Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = {ax; ay; az} и b = {nax; nay; naz}. Найдем их векторное произведение
a × b =
ijk
axayaz
bxbybz
= i (aybz — azby) — j (axbz — azbx) + k (axby — aybx) =
= i (aynaz — aznay) — j (axnaz — aznax) + k (axnay — aynax) = 0i + 0j + 0k = 0
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Пример 1. Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
Значит:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Пример 2. Доказать что вектора a = {0; 3} и b = {0; 6} коллинеарны.
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение na:
na = {2 · 0; 2 · 3} = {0; 6}
Так как b = na, то вектора a и b коллинеарны.
Пример 3. найти значение параметра n при котором вектора a = {3; 2} и b = {9; n} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
Значит:
Решим это уравнение:
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Пример 4. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
Вектора a и b коллинеарны т.к.
14 = 28 = 312
Вектора a и с не коллинеарны т.к.
15 = 210 ≠ 312
Вектора с и b не коллинеарны т.к.
54 = 108 ≠ 1212
Пример 5. Доказать что вектора a = {0; 3; 1} и b = {0; 6; 2} коллинеарны.
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение na:
na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}
Так как b = na, то вектора a и b коллинеарны.
Пример 6. найти значение параметров n и m при которых вектора a = {3; 2; m} и b = {9; n; 12} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
Решим эти уравнения:
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Содержание:
- Формула
- Примеры нахождения коллинеарного вектора
Формула
Для того чтобы вектор
$bar{a}=left(a_{x} ; a_{y}right)$ был коллинеарным вектору $bar{b}=left(b_{x} ; b_{y}right)$ необходимо, чтобы их соответствующие
координаты были пропорциональны, то есть их координаты удовлетворяли условию
$$frac{a_{x}}{b_{x}}=frac{a_{y}}{b_{y}}$$
Если векторы заданны в пространстве своими координатами:
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right), bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, тогда условие коллинеарности имеет вид:
$$frac{a_{x}}{b_{x}}=frac{a_{y}}{b_{y}}=frac{a_{z}}{b_{z}}$$
Примеры нахождения коллинеарного вектора
Пример
Задание. Даны два вектора
$bar{a}=(2 ;-3)$ и $bar{b}=(-1 ; m)$. При каком значении
$m$ эти векторы будут коллинеарными?
Решение. Для того чтобы векторы
$bar{a}$ и
$bar{b}$ были коллинеарными необходимо,
чтобы их координаты были пропорциональными, то есть удовлетворяли условию:
$$frac{a_{x}}{b_{x}}=frac{a_{y}}{b_{y}}$$
Подставим координаты заданных векторов в это равенство и найдем значение
$m$:
$$frac{2}{-1}=frac{-3}{m}$$
По пропорции имеем:
$$2 cdot m=(-1) cdot(-3) Rightarrow 2 cdot m=3 Rightarrow m=frac{3}{2}=1,5$$
Ответ. Векторы
$bar{a}$ и
$bar{b}$ будут коллинеарными при
$m=1,5$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Заданы два вектора
$bar{a}=(4 ;-m ; 1)$ и $bar{b}=(2 ;-3 ; n)$. При каких значениях
$m$ и
$n$ векторы
$bar{a}$ и
$bar{b}$ будут коллинеарными?
Решение. Для того чтобы векторы
$bar{a}$ и
$bar{b}$ были коллинеарными необходимо, чтобы их координаты
были пропорциональными, то есть чтобы выполнялись следующие равенства:
$$frac{4}{2}=frac{-m}{-3}=frac{1}{n}$$
А тогда значения неизвестных параметров
$m$ и
$n$ находим из равенств
$$frac{m}{3}=2 Rightarrow m=6$$
$$frac{1}{n}=2 Rightarrow n=frac{1}{2}=0,5$$
Ответ. Векторы
$bar{a}$ и
$bar{b}$ будут коллинеарными при
$m=6$ и $n=0,5$
Читать дальше: как найти вектор перпендикулярный вектору.
Коллинеарность векторов, условия коллинеарности векторов.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
 |
| рис. 1 |
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = < ax ; ay ; az > и b = < nax ; nay ; naz >. Найдем их векторное произведение
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
Решим это уравнение:
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
Решим эти уравнения:
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Как найти вектор коллинеарный вектору
Формула
Примеры нахождения коллинеарного вектора
Подставим координаты заданных векторов в это равенство и найдем значение $m$:
По пропорции имеем:
$$2 cdot m=(-1) cdot(-3) Rightarrow 2 cdot m=3 Rightarrow m=frac<3><2>=1,5$$
А тогда значения неизвестных параметров $m$ и $n$ находим из равенств
$$frac<3>=2 Rightarrow m=6$$ $$frac<1>=2 Rightarrow n=frac<1><2>=0,5$$
Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
любую работу
Все еще сложно?
Наши эксперты помогут разобраться
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
Условие коллинеарности векторов
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b → = λ · a → коллинеарен вектору a → , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b → коллинеарен вектору a → , его можно представить в виде λ · a → . Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.
Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b → = λ · a → или a → = μ · b → , μ ∈ R
Координатная форма условия коллинеарности векторов
Исходные данные: вектор a → задан в некоторой прямоугольной системе координат на плоскости и имеет координаты ( a x , a y ) , тогда, согласно полученному выше условию, вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y ) .
По аналогии: если вектор a → задан в трехмерном пространстве, то он будет представлен в виде координат a = ( a x , a y , a z ) , а вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y , λ · a z ) . Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.
- Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y или a x = μ · b x a y = μ · b y
- Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y b z = λ · a z или a x = μ · b x a y = μ · b y a z = μ · b z
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Если ненулевые векторы a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) коллинеарны, то согласно векторному определению произведения a → × b → = 0 → . И это также соответствует равенству: i → j → k → a x a y a z b x b y b z = 0 → , что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b → = λ · a → и a → = μ · b → , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Исходные данные: векторы a → = ( 3 — 2 2 , 1 ) и b → = ( 1 2 + 1 , 2 + 1 ) . Необходимо определить, коллинеарны ли они.
Решение
Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: b x = λ · a x b y = λ · a y Подставив заданные значения координат, получим: b x = λ · a x ⇔ 1 2 + 1 = λ · ( 3 — 2 2 ) ⇒ λ = 1 ( 2 + 1 ) · ( 3 — 2 2 ) = 1 3 2 — 4 + 3 — 2 2 = 1 2 — 1 b y = λ · a y ⇔ 2 + 1 = 1 2 — 1 · 1 ⇔ ( 2 + 1 ) · ( 2 — 1 ) = 1 ⇔ 1 ≡ 1
Т.е. b → = 1 2 — 1 · a → , следовательно, заданные векторы коллинеарны.
Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 1 , 0 , — 2 ) и b → = ( — 3 , 0 , 6 ) . Необходимо убедиться в их коллинеарности.
Решение
Т.к. b x = λ · a x b y = λ · a y b z = λ · a z ⇔ — 3 = — 3 · 1 0 = — 3 · 0 6 = — 3 · ( — 2 ) , то верным будет равенство: b → = — 3 · a → , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.
Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 1 0 — 2 — 3 0 6 = i → · 0 · 6 + j → · ( — 2 ) · ( — 3 ) + k → · 1 · 0 — k → · 0 · ( — 3 ) — j → · 1 · 6 — i → · ( — 2 ) · 0 = 0 → Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a → = ( 2 , 7 ) и b → = ( p , 3 ) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7
тогда λ = 3 7 , а p = λ · 2 ⇔ p = 6 7 .
Ответ: при p = 6 7 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Исходные данные: вектор a → = ( 2 , — 6 ) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.
Решение
Ответом может послужить, например, 1 2 · a → = ( 1 , — 3 ) или вектор 3 · a → = ( 6 , — 18 ) .
Ответ: вектор, коллинеарный заданному имеет координаты ( 1 , — 3 ) .
Исходные данные: вектор a → = ( 3 , 4 , — 5 ) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.
Решение
Вычислим длину заданного вектора по его координатам: a → = a x 2 + b x 2 + c x 2 = 3 2 + 4 2 + ( — 5 ) 2 = 5 2 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1 a → · a → = ( 3 5 2 , 4 5 2 , — 1 2 )
http://www.webmath.ru/poleznoe/formules_13_13.php
http://zaochnik.com/spravochnik/matematika/vektory/uslovie-kollinearnosti-vektorov/
В данной публикации мы рассмотрим, какие векторы называются коллинеарными и перечислим условия, при которых они являются таковыми. Также разберем примеры решения задач по этой теме.
- Условия коллинеарности векторов
- Примеры задач
Условия коллинеарности векторов
Векторы, лежащие на одной или нескольких параллельных прямых, называются коллинеарными.
Два вектора коллинеарны, если выполняется одно из условий ниже:
1. Существует такое число n, при котором a · n = b.
2. Отношения координат векторов равны. Но данное условие не может применяться, если одна из координат равняется нулю.
3. Векторное произведение равно нулевому вектору (применимо только для трехмерных задач).
Примеры задач
Задание 1
Даны векторы a = {2; 5}, b = {3; 7} и c = {6; 15}. Определим, есть ли среди них коллинеарные.
Решение:
У заданных векторов нет нулевых координат, значит мы можем применить второе условие коллинеарности.
Следовательно, коллинеарными являются только векторы a и c.
Задание 2
Выясним, при каком значении n векторы a = {4; 10} и b = {2; n} коллинеарны.
Решение:
Т.к. среди координат нет нулей, согласно второму условию мы можем составить их соотношение, чтобы рассчитать недостающий элемент.
Значит, n = 2 · 10 : 4 = 5.
Коллинеарными
называются вектора, лежащие на одной прямой или на параллельных прямых:
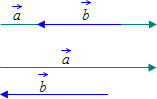
Приведенное выше определение коллинеарности двух векторов можно записать в виде формулы:
где
— некоторая константа (скаляр).
Если перейти от векторных соотношений к координатным, тогда формула принимает вид:
откуда следует, что, если два вектора коллинеарны, то выполняется следующее условие:
Наш онлайн калькулятор позволяет проверить коллинеарность двух векторов с описанием подробного хода решения на русском языке.










