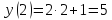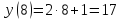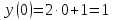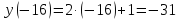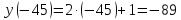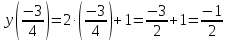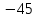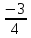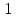Как найти значение при заданных значениях переменных

Чем алгебраические выражения отличаются от числовых? Сразу рассмотрим простой пример. Допустим, Решавру нужно рассчитать свой индекс массы тела. Известно, что ИМТ рассчитывается как отношение массы тела (кг) к росту (м) в квадрате. Решавр взвесился, замерил рост и получил следующее:

$$textbf{textcolor{blue}{ИМТ}}=frac{60~textit{кг}}{1,55^{2}~textitм}approx{25~frac{textit{кг}}{textit{м}^2}}$$

Запись выше представляет собой числовое выражение, и оно было бы совершенно бесполезно, если бы вы захотели рассчитать свой ИМТ. Но что, если представить расчет ИМТ в общем виде?

Например, вот так:

Подставляя вместо «m» и «h» соответствующие величины, можно находить ИМТ для абсолютно любого человека. В целом, запись стала универсальной. Она сообщает не столько информацию о взаимосвязи чисел, сколько инструкцию для вычисления такой информации.  

Числовое выражение	Алгебраическая дробь
$$frac{60}{1,55^2}$$	$$frac{m}{h^2}$$

Определение понятия «переменная»

Так, можно дать определение понятия «переменная»:

Переменная — математический объект, занимающий некоторое множество числовых значений.  

Пусть дана такая переменная $x$ и известно правило, задающее множество ее значений: $xinmathbb{N^+}$. Запись расшифровывается следующим образом: «В качестве значения $x$ допускается любое положительное натуральное число $mathbb{N}$».

Переменная	Множество ее значений	Примеры возможных числовых значений
$x$	$xinmathbb{N^+}$	$1, 2, 3, 4…$

Образавр объясняет: расширенный натуральный ряд

Существует несколько определений множества натуральных чисел, с включением нуля и с его исключением. Чтобы не создавать неопределенность, к множеству натуральных чисел мы будем обращаться по-разному:

🔷⠀⠀расширенный натуральный ряд $mathbb{N}$ ${0, 1, 2, 3…}$
🔷⠀⠀ряд с исключением нуля $mathbb{N^+}$ ${1, 2, 3…}$

Переменная в алгебре: пример

Выше мы не зря для примера обозначили переменную как $x$. В алгебре переменные принято записывать строчными литерами латинского алфавита $(a, b, c, x, y…)$, реже греческого $(alpha,beta,theta…)$. Греческие литеры обычно применяются как переменные значения углов.

Допустимые и недопустимые значения переменной

С другой стороны, подставлять какие угодно числа вместо переменных не всегда возможно. Некоторые математические операции могут не допускать определенные значения переменных. Чаще всего это обусловлено законами арифметики. В таком случае говорят, что запись имеет допустимые и недопустимые значения переменной.

Допустимые значения переменной в алгебраическом выражении — значения переменной, при которых выражение имеет смысл.

Повторим еще раз, но с другой «стороны»: какие значения переменных тогда называют недопустимыми? Те, при которых выражение не имеет смысл.

Рассмотрим пример:

Дана алгебраическая дробь. $frac{a^2}{a+b}$

Алгебраические выражения — даем определение

Теперь определенно ясно, что:

Алгебраические выражения — всякие записи, состоящие из переменных и чисел, связанных между собою арифметическими операциями.

Алгебраическое выражение	Числовое выражение
$x^3+4y^2-49$	$(2frac{1}{10}:2-1,8)cdot0,4+5$
Состоит из переменных, чисел, арифметических операций.	Состоит только из чисел и арифметических операций.

Синтаксис алгебраических выражений

Переменные и коэффициенты

В алгебраическом выражении «$7x^2$»:

Числовой множитель при переменной называется коэффициентом. Порядок при записи всегда следующий: вначале, если имеется, идет коэффициент, только после — переменная. Также обратите внимание, что в синтаксисе алгебраических выражений не принято указывать знак умножения между коэффициентом и переменной.  

Порядок переменных в выражении

$$frac{6(a+2b-4c)}{(a+b)^2}$$

Данная алгебраическая дробь арифметически связывает три переменные — $a$, $b$, $c$. Обращаем ваше внимание, что порядок алфавитный, не произвольный: точно так же, как, например, друг за другом в кириллице идут буквы «а», «б», «в» и так далее. Это не обязательное правило, а, скорее, правило хорошего тона.

Вычисление алгебраических выражений

7 класс.

Вычисление значений функции по формуле.

Итак, мы познакомились с функцией, узнали, что такое область определения и область значений функции. Теперь мы научимся находить значения функции по формуле, которой она задана, а также находить значения аргумента при известных значениях функции.

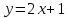
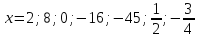
Рассмотрим пример функции: . Для того, чтобы найти значение функции, нужно знать значение аргумента. Эти значения могут быть заданы в условии задачи, а могут выбираться самостоятельно. Пусть заданы значения аргумента: . Для нахождения значений функции, необходимо подставить в формулу функции вместо х его значение (поочерёдно) и посчитать.

Для наглядности все значения удобно оформлять в таблице. В верхней строчке записываем значения х, а в нижней – значения у.

х
у

Если выбираем значения аргумента самостоятельно, то лучше это делать в порядке возрастания.

Чтобы найти значения аргумента при заданных значениях функции, сначала нужно выразить переменную х через переменную у из формулы, которой задана функция.

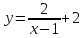
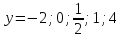
Например, дана функция . Нужно найти значения аргумента, если заданы значения функции: .

Решение. Сначала из формулы 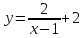выразим переменную х:

Теперь в эту формулу вместо у будем подставлять его значения:

Запишем все эти значения в таблицу.

х
у

1. Функция задана формулой . Найдите значения переменной у, если:

2. Функция задана формулой . Найдите значения переменной у, если:

3. Функция задана формулой . Найдите значения переменной у, если:

4. Функция задана формулой . Заполните таблицу, вычислив соответствующие значения функции.

x
y

1. Функция задана формулой . Заполните таблицу, вычислив соответствующие значения функции.

x
y

1. Функция задана формулой . Заполните таблицу, вычислив соответствующие значения функции.

x
y

1. Дана функция

Найдите: .

1. Дана функция

Найдите: .

1. Дана функция

Найдите: .

1. Функция задана формулой . Определите:

1. значение функции, если значение аргумента равно ;

2. значение аргумента, при котором значение функции равно .

1. Функция задана формулой . Определите:

1. значение функции, если значение аргумента равно ;

2. значение аргумента, при котором значение функции равно .

1. Дана функция . Найдите значение функции, если значение аргумента равно .

2. Дана функция . Найдите значение функции, если значение аргумента равно 1.

3. Дана функция . Найдите значение функции, если значение аргумента равно 3.

4. Дана функция . Найдите значение функции, если значение аргумента равно -3.

5. Найдите значение аргумента, при котором функция принимает значение .

6. Найдите значение аргумента, при котором функция принимает значение .

7. Найдите значение аргумента, при котором функция принимает значение .

8. Найдите значение аргумента, при котором функция принимает значение .

9. Дана функция . Найдите произведение значений функции

1. Дана функция . Найдите произведение значений функции

1. Дана функция . Найдите произведение значений функции .

2. Дана функция . Найдите произведение значений функции .

3. Для функции найдите значения и и сравните их.

4. Для функции найдите значения и и сравните их.

5. Для функции найдите значения и и сравните их.

6. Для функции найдите значения и и сравните их.

1. Функция задана формулой . Заполните таблицу:

х
у

1. Функция задана формулой . Заполните таблицу:

х
у

1. Длина (см) стального стержня при температуре изменяется по закону . На сколько миллиметров изменится длина стержня, если его температура повысится с до ?

2. Длина (см) медного стержня при температуре изменяется по закону . На сколько миллиметров изменится длина стержня, если его температура повысится с до ?

3. Составьте таблицу значений функции, заданной формулой , где , с шагом 1.

4. Составьте таблицу значений функции, заданной формулой , где , с шагом 1.

3

Данный калькулятор вычисляет значение выражения, подставляя туда значения переменных из таблицы. Удобно для проверки домашних заданий типа «Найдите значение выражения при a = 0.1, b = 2». Обозначения переменных в выражении должны совпадать с именами переменных в таблице. Если не совпадет — замены не будет и подсчитает неправильно, так что следите.

Для расчета после подстановки значений переменных используется Математический калькулятор.
Таким образом, аналогично указанному калькулятору, здесь также в математическом выражении допускается использование числа пи (pi), экспоненты (e), следующих математических операторов:

• • — сложение
• • — вычитание
• • — умножение
• / — деление
• ^ — возведение в степень

и следующих функций:

• sqrt — квадратный корень
• rootp — корень степени p, например root3(x) — кубический корень
• exp — e в указанной степени
• lb — логарифм по основанию 2
• lg — логарифм по основанию 10
• ln — натуральный логарифм (по основанию e)
• logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
• sin — синус
• cos — косинус
• tg — тангенс
• ctg — котангенс
• sec — секанс
• cosec — косеканс
• arcsin — арксинус
• arccos — арккосинус
• arctg — арктангенс
• arcctg — арккотангенс
• arcsec — арксеканс
• arccosec — арккосеканс
• versin — версинус
• vercos — коверсинус
• haversin — гаверсинус
• exsec — экссеканс
• excsc — экскосеканс
• sh — гиперболический синус
• ch — гиперболический косинус
• th — гиперболический тангенс
• cth — гиперболический котангенс
• sech — гиперболический секанс
• csch — гиперболический косеканс
• abs — абсолютное значение (модуль)
• sgn — сигнум (знак)

Область допустимых значений алгебраического выражения (сокращенно ОДЗ) — это множество значений переменной, при которых это выражение определено.

В школьном курсе алгебры есть всего пять элементарных функций, которые имеют ограниченную область определения. Вот они:

1. ОДЗ:

Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.

2. ОДЗ:

Выражение, стоящее в знаменателе дроби, не может быть равно нулю.

3. ОДЗ:

Выражение, стоящее под знаком логарифма, должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.

4. , ОДЗ:

5. Есть две функции, которые содержат «скрытую» дробь:

и

6. ОДЗ:

Степень корня — натуральное число, отличное от 1.

Таким образом, функции и имеют разную область определения.

Если выражение содержит одну или несколько функций, которые определены на ограниченном множестве значений аргумента, то для того, чтобы найти ОДЗ выражения, нужно учесть все ограничения, которые накладываются этими функциями.

Чтобы найти область допустимых значений выражения, нужно исследовать, присутствуют ли в выражении функции, которые я перечислила выше. И по мере обнаружения этих функций, записывать задаваемые ими ограничения, двигаясь «снаружи» «внутрь».

Поясню на примере:

Найти область определения функции:

Чтобы найти область определения функции, нужно найти область допустимых значений выражения, которое стоит в правой части уравнения функции

Я специально выбрала «страшную», на первый взгляд, функцию, чтобы показать вам, на какие простые операции разбивается процесс нахождения области допустимых значений.

«Просканируем» выражение, стоящее в правой части равенства:

1. Мы видим дробь:

Знаменатель дроби не равен нулю. Записываем:

2. Мы видим в знаменателе логарифм:

Выражение, стоящее под знаком логарифма должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.

3.Мы видим квадратный корень:

Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.

Теперь запишем все ограничения в систему неравенств:

Решение этой системы неравенств посмотрите в ВИДЕУРОКЕ:

Каждому выражению с переменными соответствует область допустимых значений (ОДЗ) переменных, которую ОБЯЗАТЕЛЬНО нужно учитывать при работе с этим выражением. Акцент на слове «обязательно» сделан не случайно: при решении примеров и задач халатное отношение к ОДЗ может привести к получению неверных результатов.

Чтобы у нас не возникало подобных проблем, давайте внимательно изучим все, что связано с ОДЗ. Для начала узнаем, что это такое, после этого разберем на характерных примерах, как найти ОДЗ переменных для заданного выражения, а в заключение остановимся на важности учета ОДЗ при преобразовании выражений.

Навигация по странице.

Допустимые и недопустимые значения переменных

Определение области допустимых значений переменных для выражения дается через термин допустимые значения переменной. Введем это вспомогательное определение, для чего проследим, что нас приводит к нему.

На уроках математики в школе вплоть до 7 класса познаются азы работы преимущественно с числами и числовыми выражениями. А с 7 класса начинается изучение такой математической дисциплины как алгебра, и начинается оно с того, что вводится определение выражения с переменными, а также связанное с ним определение значения выражения при выбранных значениях переменных.

Последнее определение нуждается в уточнении следующего плана. Существуют выражения, значения которых при некоторых выбранных значениях переменных вычислить невозможно. Например, невозможно вычислить значение выражения 1:a при a=0 , так как делить на нуль нельзя. Это послужило причиной введения в обиход терминов «выражение, имеющее смысл при данных значениях переменных» и «выражение, не имеющее смысла при данных значениях переменных». Говорят, что

выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение

выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Вот теперь мы обладаем всеми сведениями, позволяющими дать определение допустимых и недопустимых значений переменных:

Допустимые значения переменных – это такие значения переменных, при которых выражение имеет смысл. А значения переменных, при которых выражение не имеет смысла, называют недопустимыми значениями переменных.

Здесь лишь стоит уточнить, что если выражение содержит две, три, и большее число переменных, то речь идет о парах, тройках и т.д. допустимых значений переменных. Приведем пример. Рассмотрим выражение с тремя переменными x , y и z . Тройка значений переменных x=0 , y=1 , z=2 , она же в другой записи (0, 1, 2) , является допустимой, так как при данных значениях переменных мы можем найти значение выражения: . А тройка (1, 2, 1) – недопустимая, так как при подстановке этих значений в выражение мы придем к делению на нуль: .

Определения, озвученные в этом пункте, полностью согласуются с информацией из учебников [1, с. 6; 2, с. 11-12; 3, c. 4] .

Что такое ОДЗ?

Практически у всех, так или иначе имеющих отношение к алгебре, на слуху словосочетание «область допустимых значений», также довольно часто аббревиатуру ОДЗ можно встретить в описаниях решений, но как такового определения области допустимых значений (ОДЗ) нет в основных учебниках, используемых в школе. Поэтому интересно, откуда берет начало этот термин. Ну а с позиций практики интереснее знать, какой смысл в него вкладывают.

Под областью допустимых значений (ОДЗ) понимают множество всех допустимых значений переменных для данного выражения.

Приведем пример. Допустим, дано выражение , и записано ОДЗ: (−∞, 3)∪(3, +∞) . Последнюю запись стоит понимать так: область допустимых значений переменной z для выражения есть числовое множество (−∞, 3)∪(3, +∞) .

Другой пример. Рассмотрим выражение и относящуюся к нему запись ОДЗ: x≠y , z — любое. Она означает, что ОДЗ переменных x , y и z для данного выражения – это все такие тройки значений переменных x , y и z , для которых выполняются указанные условия x≠y , z — любое.

Завершить этот пункт хочется разговором про область допустимых значений и область определения. Часто между этими терминами стирают различия. Например, говорят про область определения выражения [4, с. 87] , под которой фактически понимают ОДЗ переменных этого выражения. Также можно столкнуться с областью определения уравнения или неравенства [5, с. 204, 220; 6, с. 188, 190] , под ней подразумевают ОДЗ переменных, на которой одновременно имеют смысл обе части уравнения или неравенства. Как тут не спутать одно с другим? Давайте будем придерживаться следующего подхода: к функциям относить область определения функции, а к выражениям – ОДЗ переменных. И на загладку приведем такое утверждение: область определения функции y=f(x) совпадает с областью допустимых значений переменной x для выражения f(x) .

Как найти ОДЗ? Примеры, решения

Прежде чем обратиться к главной теме этого пункта, нужно понимать, что значит найти ОДЗ, хотя это достаточно отчетливо ясно из определения. Это значит, что надо указать множество всех допустимых значений переменных для заданного выражения. На это можно посмотреть и с другой стороны: найти ОДЗ – это значит указать условия, которые исключают те и только те значения переменных, при которых выражение не имеет смысла. Теперь можно двигаться дальше.

Заданий с формулировкой «найти ОДЗ» не так много. Однако почти постоянно приходится преобразовывать выражения, а это неявно требует нахождения области допустимых значений для ее контроля. В этом свете вопрос, как найти ОДЗ, очень злободневен.

В поисках ответа на него поразмыслим, значения каких выражений мы не можем вычислить.

Во-первых, мы не можем вычислить значение выражения, в котором присутствует деление на нуль (или дробь со знаменателем нуль, что по сути то же самое), так как этому действию мы не придали смысла.

Во-вторых, мы не можем извлечь квадратный корень из отрицательного числа, как и корень другой четной степени, о чем мы говорим когда вводили корень из числа. Здесь же заметим, что показателями корня могут быть лишь числа 2 , 3 , 4 , и так далее, значит, значения выражений с корнями, имеющими другие показатели, мы тоже не можем вычислить.

В-третьих, вспомним про степень числа. Если степень числа с положительным целым показателем мы определили для любого действительного числа, то степень с целым отрицательным показателем мы определили уже с ограничением: для любого действительного числа, кроме числа нуль. Степени с положительным нецелым показателем мы придали смысл лишь для неотрицательных чисел, а с отрицательным нецелым показателем – лишь для положительных чисел. А еще мы не можем вычислить нуль в степени нуль.

В-четвертых, обратим внимание на логарифм числа. Его мы определили так, что не придали смысла логарифму отрицательного числа и числа нуль по любому основанию, а также логарифму положительного числа по отрицательному основанию и по основанию 1 .

В-пятых, мы не определили тангенс чисел , а также котангенс чисел (см. статью значения тригонометрических функций).

В-шестых, мы не можем найти значение арксинуса и арккосинуса числа, выходящего за рамки числового промежутка [−1, 1] в силу того, что мы так определили arcsin и arccos (см. статью arcsin, arccos, arctg, arcctg: определения, примеры).

Что нам это дает? А то, что перечисленные выше моменты и нужно учитывать при поиске ОДЗ. Как это делать, станет понятно из следующих примеров.

Укажите все допустимые значения переменных для выражения x 3 +2·x·y−4 .

Возвести в куб мы можем любое число, также мы умеем умножать любые числа, как и складывать и вычитать. Поэтому, мы можем вычислить значение заданного выражения при любых значениях переменных x и y . А это значит, что выражение x 3 +2·x·y−4 имеет смысл при любых значениях входящих в него переменных. Поэтому, ОДЗ переменных x и y для этого выражения – это множество всех таких пар (x, y) , где x – любое число и y – любое число.

(x, y) , где x – любое, y — любое.

Найти ОДЗ переменной x для выражения .

Мы видим, что данное выражение содержит дробь с нулем в знаменателе. А это значит, что ни при каком значении переменной x мы не сможем вычислить значение этого выражения, так как оно будет содержать деление на нуль. Вывод: это выражение не определено ни при каких значениях переменной x . Другими словами, ОДЗ переменной x для этого выражения есть пустое множество.

Найти ОДЗ .

Здесь нас настораживает присутствие квадратного корня. Чтобы избежать появления под корнем отрицательного числа, надо для переменных x и y потребовать выполнение условия x+2·y+3≥0 . Оно и задает искомую область допустимых значений.

множество всех пар (x, y) , для которых x+2·y+3≥0 .

В более сложных случаях приходится учитывать одновременно несколько условий из приведенного выше списка. Это дает системы неравенств, задающие ОДЗ.

Определите ОДЗ переменной x для выражения .

Во-первых, выражение в знаменателе дроби не должно обращаться в нуль, это дает первое условие . Во-вторых, выражение под знаком квадратного корня должно быть неотрицательным: x+1≥0 . В-третьих, выражение под знаком логарифма должно быть положительным, это дает третье условие x 2 +3>0 . Наконец, выражение в основании логарифма должно быть положительным и отличным от единицы, так вырисовываются еще два условия x+8>0 и x+8≠1 . Таким образом, искомая ОДЗ определяется системой следующего вида . Это система неравенств с одной переменной, решив ее, записываем ОДЗ: [−1, 0)∪(0, +∞) .

Здесь лишь заметим, что во многих случаях на практике нет необходимости в решении составленных систем.

В заключении остается сказать, что такой подход используется и тогда, когда нужно найти область определения функции.

Почему важно учитывать ОДЗ при проведении преобразований?

Решая различные задачи, нам очень часто приходится проводить тождественные преобразования выражений. Но бывает, что какое-то преобразование в одних случаях допустимо, а в других – нет. Существенную помощь в плане контроля допустимости проводимых преобразований оказывает ОДЗ. Остановимся на этом подробнее.

Суть подхода состоит в следующем: сравниваются ОДЗ переменных для исходного выражения с ОДЗ переменных для выражения, полученного в результате выполнения тождественных преобразований, и на основании результатов сравнения делаются соответствующие выводы.

Вообще, тождественные преобразования могут

• не влиять на ОДЗ;
• приводить к расширению ОДЗ;
• приводить к сужению ОДЗ.

Давайте поясним каждый случай примером.

Рассмотрим выражение x 2 +x+3·x , ОДЗ переменной x для этого выражения есть множество R . Теперь проделаем с этим выражением следующее тождественное преобразование – приведем подобные слагаемые, в результате оно примет вид x 2 +4·x . Очевидно, ОДЗ переменной x этого выражения тоже является множество R . Таким образом, проведенное преобразование не изменило ОДЗ.

Переходим дальше. Возьмем выражение x+3/x−3/x . В этом случае ОДЗ определяется условием x≠0 , которое отвечает множеству (−∞, 0)∪(0, +∞) . Это выражение тоже содержит подобные слагаемые, после приведения которых приходим к выражению x , для которого ОДЗ есть R . Что мы видим: в результате проведенного преобразования произошло расширение ОДЗ (к ОДЗ переменной x для исходного выражения добавилось число нуль).

Осталось рассмотреть пример сужения области допустимых значений после проведения преобразований. Возьмем выражение . ОДЗ переменной x определяется неравенством (x−1)·(x−3)≥0 , для его решения подходит, например, метод интервалов, в результате имеем (−∞, 1]∪[3, +∞) . А теперь преобразуем исходное выражение к виду , воспользовавшись одним из свойств корней: корень произведения равен произведению корней. ОДЗ переменной x для этого выражения определяет система линейных неравенств , решение которой дает множество [3, +∞) . Таким образом, в результате проведенного преобразования произошло сужение ОДЗ с множества (−∞, 1]∪[3, +∞) до множества [3, +∞) .

При преобразовании выражений надо строго избегать преобразований, сужающих ОДЗ. Почему? Для пояснения приведем пример.

Допустим нам нужно вычислить значение выражения при x=−1 . Если сразу подставить вместо переменной x число −1 , то мы найдем значение . А теперь представим, что мы из каких-то соображений предварительно преобразовали исходное выражение к виду , сузив тем самым ОДЗ. Вычисляем его значение, для этого подставляем вместо переменной x число −1 , и получаем выражение , которое не имеет смысла, так как под знаком корня оказывается отрицательное число. Такой подход привел нас к проблеме, которая возникла из-за того, что 2 входит в ОДЗ переменной x для исходного выражения, но уже не попадает в «суженную» ОДЗ переменной x для выражения, полученного после преобразования.

Так что надо придерживаться таких тождественных преобразований выражения, которые не изменяют ОДЗ.

А как быть с преобразованиями выражений, при которых расширяется ОДЗ? Их можно проводить, но при этом стоит придерживаться такого взгляда: полученное в результате преобразования выражение рассматривать на ОДЗ переменных исходного выражения.

Например, сокращение алгебраической дроби на x дает дробь и приводит к расширению ОДЗ от множества (−∞ 0)∪(0, +∞) до множества R . При этом можно продолжать работать с полученной дробью , но на ОДЗ переменной x для исходного выражения, то есть, на множестве (−∞ 0)∪(0, +∞) .

Еще пример. При замене суммы логарифмов lnx+ln(x+3) логарифмом произведения ln(x·(x+3)) (см. свойства логарифмов) происходит расширение ОДЗ с (0, +∞) до (−∞, −3)∪(0, +∞) . Поэтому с полученным выражением ln(x·(x+3)) дальше стоит работать на ОДЗ переменной x исходного выражения, то есть, на множестве (0, +∞) .

Итак, на каждом шаге преобразования выражения постоянно спрашивайте себя: «Не изменяет ли это преобразование ОДЗ»? Если не изменяет, то выполняйте его. Если сужает, то откажитесь от него. А если расширяет, то выполняйте его, но оставайтесь в рамках ОДЗ переменных для исходного выражения.

Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.

В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.

Допустимые и недопустимые значения переменных

Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.

Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.

Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1 : а , если а = 0 , тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут ответ. Иначе говоря, имеют смысл с имеющимися переменными.

Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.

Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.

То есть отсюда следует полное определение

Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.

Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.

Для примера рассмотрим выражение вида 1 x — y + z , где имеются три переменные. Иначе можно записать, как x = 0 , y = 1 , z = 2 , другая же запись имеет вид ( 0 , 1 , 2 ) . Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 1 0 — 1 + 2 = 1 1 = 1 . Отсюда видим, что ( 1 , 1 , 2 ) недопустимы. Подстановка дает в результате деление на ноль, то есть 1 1 — 2 + 1 = 1 0 .

Что такое ОДЗ?

Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.

Область ОДЗ – это множество значений, допустимых для данного выражения.

Рассмотрим на примере выражения.

Если имеем выражение вида 5 z — 3 , тогда ОДЗ имеет вид ( − ∞ , 3 ) ∪ ( 3 , + ∞ ) . Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.

Если имеется выражения вида z x — y , тогда видно, что x ≠ y , z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.

Область допустимых значений и область определения имеет один и тот же смысл. Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл. Область определения функции совпадает с областью допустимых значений переменной х к выражению f ( x ) .

Как найти ОДЗ? Примеры, решения

Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.

Существуют выражения, где их вычисление невозможно:

• если имеется деление на ноль;
• извлечение корня из отрицательного числа;
• наличие отрицательного целого показателя – только для положительных чисел;
• вычисление логарифма отрицательного числа;
• область определения тангенса π 2 + π · k , k ∈ Z и котангенса π · k , k ∈ Z ;
• нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [ — 1 ; 1 ] .

Все это говорит о том, как важно наличие ОДЗ.

Найти ОДЗ выражения x 3 + 2 · x · y − 4 .

Решение

В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.

Ответ: x и y – любые значения.

Найти ОДЗ выражения 1 3 — x + 1 0 .

Решение

Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.

Ответ: ∅ .

Найти ОДЗ заданного выражения x + 2 · y + 3 — 5 · x .

Решение

Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0 . То есть это и есть искомая область допустимых значений.

Ответ: множество x и y , где x + 2 · y + 3 ≥ 0 .

Определить ОДЗ выражения вида 1 x + 1 — 1 + log x + 8 ( x 2 + 3 ) .

Решение

По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x + 1 — 1 ≠ 0 . Подкоренное выражение всегда имеет смысл, когда больше или равно нулю, то есть x + 1 ≥ 0 . Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x 2 + 3 > 0 . Основание логарифма также должно иметь положительное значение и отличное от 1 , тогда добавляем еще условия x + 8 > 0 и x + 8 ≠ 1 . Отсюда следует, что искомое ОДЗ примет вид:

x + 1 — 1 ≠ 0 , x + 1 ≥ 0 , x 2 + 3 > 0 , x + 8 > 0 , x + 8 ≠ 1

Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [ − 1 , 0 ) ∪ ( 0 , + ∞ ) .

Ответ: [ − 1 , 0 ) ∪ ( 0 , + ∞ )

Почему важно учитывать ОДЗ при проведении преобразований?

При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.

• могут не влиять на ОДЗ;
• могут привести в расширению или дополнению ОДЗ;
• могут сузить ОДЗ.

Рассмотрим на примере.

Если имеем выражение вида x 2 + x + 3 · x , тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.

Если взять пример выражения x + 3 x − 3 x , то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) . Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.

Рассмотрим пример с наличием подкоренного выражения.

Если имеется x — 1 · x — 3 , тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства ( x − 1 ) · ( x − 3 ) ≥ 0 . Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) . После преобразования x — 1 · x — 3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x — 1 ≥ 0 , x — 3 ≥ 0 . При ее решении получаем, что [ 3 , + ∞ ) . Значит, ОДЗ полностью записывается так: ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) .

Нужно избегать преобразований, которые сужают ОДЗ.

Рассмотрим пример выражения x — 1 · x — 3 , когда х = — 1 . При подстановке получим, что — 1 — 1 · — 1 — 3 = 8 = 2 2 . Если это выражение преобразовать и привести к виду x — 1 · x — 3 , тогда при вычислении получим, что 2 — 1 · 2 — 3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.

Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.

Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.

Рассмотрим на примере дроби вида x x 3 + x . Если сократить на x , тогда получаем, что 1 x 2 + 1 . Тогда ОДЗ расширяется и становится ( − ∞ 0 ) ∪ ( 0 , + ∞ ) . Причем при вычислении уже работаем со второй упрощенной дробью.

При наличии логарифмов дело обстоит немного иначе.

Если имеется выражение вида ln x + ln ( x + 3 ) , его заменяют на ln ( x · ( x + 3 ) ) , опираясь на свойство логарифма. Отсюда видно, что ОДЗ с ( 0 , + ∞ ) до ( − ∞ , − 3 ) ∪ ( 0 , + ∞ ) . Поэтому для определения ОДЗ ln ( x · ( x + 3 ) ) необходимо производить вычисления на ОДЗ, то есть ( 0 , + ∞ ) множества.

При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.