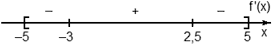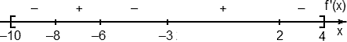12. Исследование функций с помощью производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Поиск наибольшего/наименьшего значения у произведения
(blacktriangleright) Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке ([a,b]), необходимо схематично изобразить график функции на этом отрезке.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).
(blacktriangleright) Не стоит забывать, что наибольшее/наименьшее значение функция может принимать не только во внутренних точках отрезка ([a,b]), а также на его концах.
(blacktriangleright) Наибольшее/наименьшее значение функции — это значение координаты (y=f(x)).
(blacktriangleright) Если функция задана как произведение двух других функций, то [{Large{(fcdot g)’=f’cdot g+fcdot g’}}]
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]
Задание
1
#2824
Уровень задания: Равен ЕГЭ
Найдите наименьшее значение функции (y = 2x^2cdot e^{x} — 3).
1) [y’ = 4xcdot e^{x} + 2x^2cdot e^{x} = 2x(x + 2)cdot e^x]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2x(x + 2)cdot e^x = 0qquadLeftrightarrowqquad x(x + 2) = 0,,] откуда находим корни (x_1 = -2), (x_2 = 0). Производная функции (y) существует при любом (x). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
По полученному эскизу нельзя сказать наверняка, действительно ли в точке локального минимума (x = 0) значение функции наименьшее, или же при каком-то отрицательном (x) значение функции окажется меньше, чем при (x = 0). Найдём (y(0)): [y(0) = 2cdot 0cdot e^{0} — 3 = -3,.] Рассмотрим произвольное (x_0 < 0), тогда [y(x_0) = 2{x_0}^2cdot e^{x_0} — 3,,] но ({x_0}^2geqslant 0) и (e^{x_0}geqslant 0), тогда [y(x_0) = 2{x_0}^2cdot e^{x_0} — 3geqslant 0 — 3geqslant -3,,] следовательно, наименьшее значение функции (y) равно (y(0) = -3).
Ответ: -3
Задание
2
#904
Уровень задания: Равен ЕГЭ
Найдите наименьшее значение функции (y = xcdot e^{x}cdot e — 11).
1) (y’ = e^{x}cdot e + xcdot e^{x}cdot e = (x + 1)cdot e^{x + 1}).
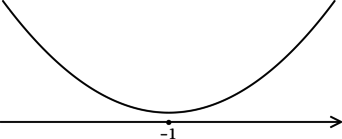
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (x + 1)cdot e^{x + 1} = 0qquadLeftrightarrowqquad x = -1] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = -1) – точка минимума функции (y).
(y(-1) = -1cdot e^0 — 11 = -12),
Итого: наименьшее значение функции (y) равно (-12).
Ответ: -12
Задание
3
#905
Уровень задания: Равен ЕГЭ
Найдите наименьшее значение функции (y = (2 — x)cdot e^{-x}cdot e^3 — 2).
1) (y’ = -e^{-x}cdot e^3 — (2 — x)cdot e^{-x}cdot e^3 = (x — 3)cdot e^{-x + 3}).
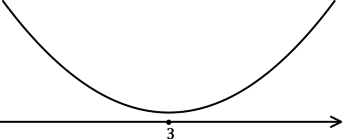
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (x — 3)cdot e^{-x + 3} = 0qquadLeftrightarrowqquad x = 3] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = 3) – точка минимума функции (y).
(y(3) = -1cdot e^0 — 2 = -3),
Итого: наименьшее значение функции (y) равно (-3).
Ответ: -3
Задание
4
#909
Уровень задания: Равен ЕГЭ
Найдите наименьшее значение функции (y = (x^2 — 14x + 34)e^{x}) на отрезке ([0; 2,5]).
1) (y’ = (2x — 14)e^{x} + e^{x}(x^2 — 14x + 34) = e^{x}(x^2 — 12x + 20)).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad e^{x}(x^2 — 12x + 20) = 0qquadLeftrightarrowqquad x^2 — 12x + 20 = 0] (так как (e^x > 0) при любом (x) и на неё можно поделить), откуда находим корни (x_1 = 2, x_2 = 10). Таким образом, [y’ = e^{x}(x — 2)(x — 10).] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
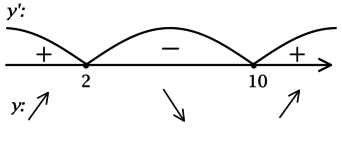
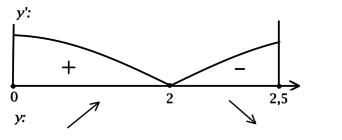
2) Найдём промежутки знакопостоянства (y’):
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([0; 2,5]):
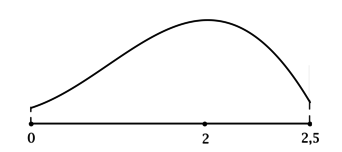
4) Эскиз графика на отрезке ([0; 2,5]):
Таким образом, (x = 2) – точка локального максимума функции (y) и наименьшее значение на ([0; 2,5]) функция достигает либо в (x = 0), либо в (x = 2,5). Сравним эти значения:
(y(0) = 34cdot e^0 = 34),
(y(2,5) = (6,25 — 35 + 34)e^{2,5} = 5,25cdot e^{2,5}). Так как (e > 2,7), то (5,25cdot e^{2,5} > 5,25cdot 2,7^{2,5} > 5,25cdot 2,7^{2} = 38,2725 > 34 = y(0)).
Итого: наименьшее значение функции (y) на ([0; 2,5]) равно (34).
Ответ: 34
Задание
5
#910
Уровень задания: Равен ЕГЭ
Найдите наибольшее значение функции (y = e^{-1}(x^2-8x+13)e^{x}) на ([-1; 5,5]).
Заметим, что (e^{-1}) – просто число, тогда
1) (y’ = e^{-1}((2x-8)e^{x}+e^{x}(x^2-8x+13)) = e^{-1}(x^2-6x+5)e^{x}).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad e^{-1}(x^2-6x+5)e^{x} = 0qquadLeftrightarrowqquad x^2-6x+5 = 0] (так как (e^x > 0) при любом (x) и на неё можно поделить), откуда находим корни (x_1 = 1, x_2 = 5). Таким образом, [y’ = e^{-1}(x — 1)(x — 5)e^{x}.] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
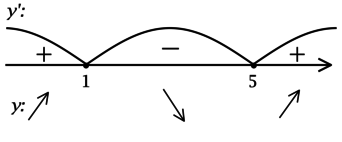
2) Найдём промежутки знакопостоянства (y’):
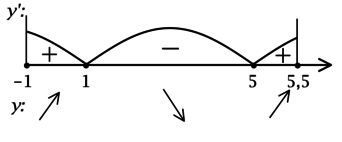
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-1; 5,5]):
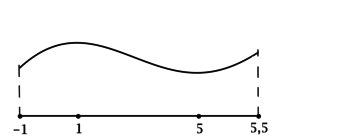
4) Эскиз графика на отрезке ([-1; 5,5]):
Таким образом, (x = 1) – точка локального максимума функции (y), (x = 5) — точка локального минимума функции и наибольшее значение на ([-1; 5,5]) функция достигает либо в (x = 1), либо в (x = 5,5). Сравним эти значения:
(y(1) = e^{-1}(1-8+13)e^{1} = 6cdot e^{-1 + 1} = 6cdot e^{0} = 6),
(y(5,5) = e^{-1}(30,25-44+13)e^{5,5} = -0,75cdot e^{-1 + 5,5} = -0,75cdot e^{4,5} < 0 < 6 = y(1)).
Итого: наибольшее значение функции (y) на ([-1; 5,5]) равно (6).
Ответ: 6
Задание
6
#907
Уровень задания: Равен ЕГЭ
Найдите наименьшее значение функции (y = (-2x + 1)cdot e^{-x}cdot e^{1,5}).
1) (y’ = -2e^{-x}cdot e^{1,5} — (-2x + 1)cdot e^{-x}cdot e^{1,5} = (2x — 3)cdot e^{-x + 1,5}).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (2x — 3)cdot e^{-x + 1,5} = 0qquadLeftrightarrowqquad x = 1,5] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
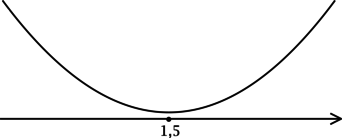
3) Эскиз графика (y):
Таким образом, (x = 1,5) – точка минимума функции (y).
(y(1,5) = -2cdot e^0 = -2),
Итого: наименьшее значение функции (y) равно (-2).
Ответ: -2
Задание
7
#906
Уровень задания: Равен ЕГЭ
Найдите наибольшее значение функции (y = (3x + 2)cdot e^{-x}cdot e^{frac{1}{3}}).
1) (y’ = 3e^{-x}cdot e^{frac{1}{3}} — (3x + 2)cdot e^{-x}cdot e^{frac{1}{3}} = (-3x + 1)cdot e^{-x + frac{1}{3}}).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad (-3x + 1)cdot e^{-x + frac{1}{3}} = 0qquadLeftrightarrowqquad x = dfrac{1}{3}] (так как (e^t > 0) при любом (t) и на неё можно поделить). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
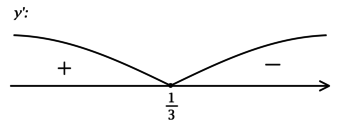
2) Найдём промежутки знакопостоянства (y’):
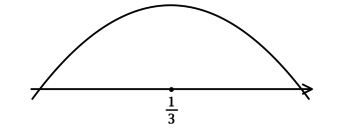
3) Эскиз графика (y):
Таким образом, (x = dfrac{1}{3}) – точка максимума функции (y).
(yleft(dfrac{1}{3}right) = 3cdot e^0 = 3),
Итого: наибольшее значение функции (y) равно (3).
Ответ: 3

УСТАЛ? Просто отдохни
Для исследования функции важно уметь определять угловой коэффициент касательной к ее графику.
Этот угловой коэффициент касательной называют производной.
Понятие производной часто используют и при решении многих других задач. Поэтому рассмотрим его подробнее.
Графический смысл производной
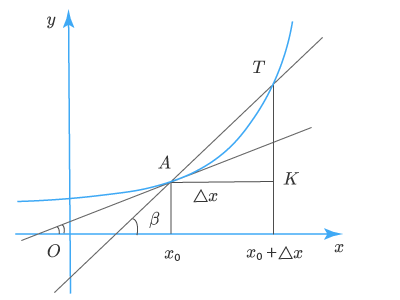
Пусть дан график функции y=f(x)y = f(x) и на нем точка АА, в которой существует касательная к графику:
Если абсцисса точки АА равна x0x_0, то ее ордината f(x0)f(x_0). Предоставим значению аргумента x0x_0 прирост ΔxΔx. Увеличенное значение аргумента х0+Δxх_0 + Δx на графике функции соответствует точка ТТ с абсциссой x0+Δxx_0 + Δx и ординатой f(x0+Δx)f(x_0 + Δx).
Через точки АА и ТТ проведем прямые АКАК и ТКТК, параллельные осям абсцисс и ординат; они пересекутся в некоторой точке КК. Тогда АК−ΔхАК — Δх – приращение аргумента, а ТК=ΔуТК = Δу – прирост функции на [x0;x0+Δx][x_0; x_0 + Δx].
Угловой коэффициент секущей ATAT равен тангенсу угла ββ, то есть отношению ΔуΔу к ΔxΔx:
tgβ=ΔyΔx=f(x0+Δx)−f(x0)Δxtgbeta =frac{Delta y}{Delta x}=frac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x}
Если ΔxΔx бесконечно мало и стремится к нулю, то секущая АТАТ, поворачиваясь вокруг точки АА, приближается к касательной, проведенной в точке АА с графиком данной функции. То есть если kk – угловой коэффициент этой касательной и ΔxΔx стремится к нулю, то
f(x0+Δx)−f(x0)Δx→kfrac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x}to k
Это число kk – производная функции f(x)f(x) в точке x0x_0.
Производной функции f(x)f(x) в точке x0x_0 называется число kk, которому соответствует дробь f(x0+Δx)−f(x0)Δxfrac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x} при Δх→0.
Производную функции f(x)f(x) в точке x0x_0 обозначают f′(x0)f'(x_0). Ее определение записывают также в виде равенства:
f′(x0)=limΔx→0 f(x0+Δx)−f(x0)Δx{f}'({{x}_{0}})=underset{Delta xto 0}{mathop{lim }},frac{f({{x}_{0}}+Delta x)-f({{x}_{0}})}{Delta x}
или
f′(x0)=limΔx→0 ΔyΔx{f}'({{x}_{0}})=underset{Delta xto 0}{mathop{lim }},frac{Delta y}{Delta x}
Задача 1
Найдите производную функции f(x)=x2f(x) = x^2 в точке x=3x = 3.
Решение
Предоставим аргументу x=3x = 3 прирост ΔxΔx. Соответствующий прирост функции Δу=(3+Δx)2−33=6Δx+Δx2Δу = (3 + Δx)^2 — 33 = 6Δx+Δx^2.
Поэтому
ΔyΔx=6Δ+Δ2Δfrac{Delta y}{Delta x}=frac{6Delta +Delta {{}^{2}}}{Delta }
Если Δx→0Δx→0, то Δy/Δx→6Δy/Δx → 6.
Ответ: f′(3)=6f ‘(3) = 6.
Так решают задачу, пользуясь определением производной функции в точке.
Задача 2
Используя формулу (1/x)′=−1/x2(1/x)’ = — 1/x^2, запишите уравнение к графику функции у=1/xу = 1/x в точке с абсциссой x0=1/2x_0 = 1/2.
Уравнение касательной к графику функции у=f(x)у = f (x) в точке с абсциссой x0x^0 в общем виде записывается так:
y=f(x0)+f′(x0)(x−x0)y=f({{x}_{0}})+{f}'({{x}_{0}})(x-{{x}_{0}})
Чтобы записать это уравнение для заданной функции, нужно найти значение f(x0)f(x_0), производную f′(x)f'(x) и значение f′(x0)f'(x_0). Для выполнения соответствующих вычислений удобно обозначить заданную функцию через f(x)f(x) и использовать табличное значение производной: (1/x)′=−1/x2.(1/x)’ = — 1/x^2.
Таким образом, если f(x)=1/xf(x) = 1/x, то f(x0)=f(1/2)=2f(x_0) = f(1/2) = 2.
Тогда f′(x0)=f′(1/2)=−4.f'(x_0) = f'(1/2) = -4.
Подставляя эти значения в уравнение касательной y=f(x0)+f′(x0)(x−x0)y=f({{x}_{0}})+{f}'({{x}_{0}})(x-{{x}_{0}}) получаем
y=2−4(x−12).y=2-4left( x-frac{1}{2} right).
То есть у=−4x+4у = -4x + 4 – искомое уравнение касательной.
Тест на тему “Производная функции в точке”
Значение производной в точке
0 =
Изучаем производные
Что такое производная?
Геометрический смысл производной
Физический смысл производной
Обобщённая таблица производных
Как найти производную?
Производная сложной функции
Что такое дифференциал функции?
Частная производная функции в точке
Как найти значение?
Постановка задачи
Найти значение частной производной функции $ u(x,y,z) $ в точке $ M(x_0,y_0,z_0) $
План решения
Частная производная в точке обозначается и вычисляется по формуле:
$$ frac{partial u}{partial x} bigg |_{M(x_0,y_0,z_0)} = frac{partial u}{partial x} (x_0,y_0,z_0) $$
$$ frac{partial u}{partial y} bigg |_{M(x_0,y_0,z_0)} = frac{partial u}{partial y} (x_0,y_0,z_0) $$
$$ frac{partial u}{partial z} bigg |_{M(x_0,y_0,z_0)} = frac{partial u}{partial z} (x_0,y_0,z_0) $$
- Находим частные производные, к примеру первого порядка:
$$ frac{partial u}{partial x}; frac{partial u}{partial y}; frac{partial u}{partial z} $$ - Подставляем координаты $ x_0,y_0,z_0 $ точки $ M $ в полученные частные производные вместо $ x,y,z $:
$$ frac{partial u}{partial x} (x_0,y_0,z_0); frac{partial u}{partial y} (x_0,y_0,z_0); frac{partial u}{partial z} (x_0,y_0,z_0) $$ - Вычисляем выражения и записываем ответ
Примеры решений
| Пример 1 |
| Найти частную производную $ u = xy + ln(y^3+z^3) $ в точке $ M(1,2,3) $ |
| Решение |
|
Берем частные производные первого порядка: $$ frac{partial u}{partial x} = y $$ $$ frac{partial u}{partial y} = x + frac{3y^2}{y^3+z^3} $$ $$ frac{partial u}{partial z} = frac{3z^2}{y^3+z^3} $$ Подставляем координаты точки $ M $ вместо $ x,y,z $ в полученные выражения и находим значения частных производных в точке: $$ frac{partial u}{partial x} (1,2,3) = 2 $$ $$ frac{partial u}{partial y} (1,2,3) = 1 + frac{3 cdot 4}{8+27} = 1 + frac{12}{35} = 1.34 $$ $$ frac{partial u}{partial z} (1,2,3) = frac{3 cdot 9}{8+27} = frac{27}{35} = 0.77 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ frac{partial u}{partial x} (1,2,3) = 2; frac{partial u}{partial y} (1,2,3) = 1.34; frac{partial u}{partial z} (1,2,3) = 0.77 $$ |
Задание 6. Геометрический смысл производной
В задаче 6 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
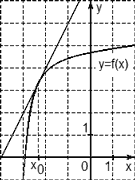
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
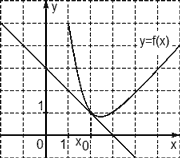
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2 − y1 = 0 − 3 = −3.
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
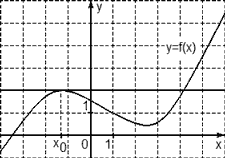
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).
- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≤ f(x).
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
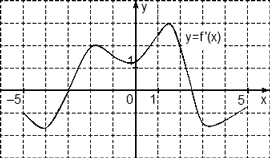
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
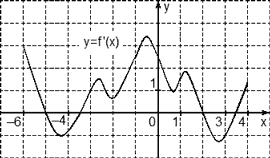
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
- Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
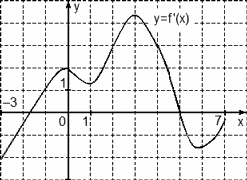
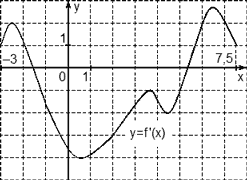
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
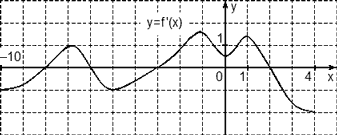
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
Как найти значение производной функции в точке х0 уравнение
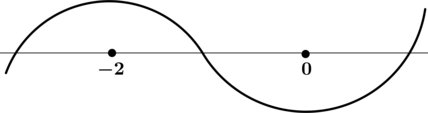
На рисунке изображен график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
Поскольку касательная параллельна прямой y = 6 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. У данной функции производная равна нулю только в точках экстремума функции. На заданном интервале функция имеет 2 максимума и 2 минимума, итого 4 экстремума. Таким образом, касательная к графику функции параллельна прямой y = 6 или совпадает с ней в 4 точках.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Найти (с решением) производную функции.
Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.
Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите выражение функции Найти производную функции f(x)
Немного теории.
Определение производной
Определение. Пусть функция ( y = f(x) ) определена в некотором интервале, содержащем внутри себя точку ( x_0 ). Дадим аргументу приращение ( Delta x ) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции ( Delta y ) (при переходе от точки ( x_0 ) к точке ( x_0 + Delta x ) ) и составим отношение ( frac<Delta y> <Delta x>). Если существует предел этого отношения при ( Delta x rightarrow 0 ), то указанный предел называют производной функции ( y=f(x) ) в точке ( x_0 ) и обозначают ( f'(x_0) ).
Для обозначения производной часто используют символ ( y’ ). Отметим, что ( y’ = f(x) ) — это новая функция, но, естественно, связанная с функцией ( y = f(x) ), определенная во всех точках (x), в которых существует указанный выше предел. Эту функцию называют так: производная функции ( y = f(x) ).
Геометрический смысл производной состоит в следующем. Если к графику функции ( y = f(x) ) в точке с абсциссой ( x=a ) можно провести касательную, непараллельную оси (y), то ( f(a) ) выражает угловой коэффициент касательной:
( k = f'(a) )
Поскольку ( k = tg(a) ), то верно равенство ( f'(a) = tg(a) ) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция ( y = f(x) ) имеет производную в конкретной точке ( x ):
$$ lim_ <Delta x to 0>frac<Delta y> <Delta x>= f'(x) $$
Это означает, что около точки (x) выполняется приближенное равенство ( frac<Delta y> <Delta x>approx f'(x) ), т.е. ( Delta y approx f'(x) cdot Delta x ).
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально» приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке (x).
Например, для функции ( y = x^2 ) справедливо приближенное равенство ( Delta y approx 2x cdot Delta x ). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение ( x ), найти ( f(x) )
2. Дать аргументу ( x ) приращение ( Delta x ), перейти в новую точку ( x+ Delta x ), найти ( f(x+ Delta x) )
3. Найти приращение функции: ( Delta y = f(x + Delta x) — f(x) )
4. Составить отношение ( frac<Delta y> <Delta x>)
5. Вычислить $$ lim_ <Delta x to 0>frac<Delta y> <Delta x>$$
Этот предел и есть производная функции в точке (x).
Если функция (y=f(x)) имеет производную в точке (x), то ее называют дифференцируемой в точке (x). Процедуру нахождения производной функции (y=f(x)) называют дифференцированием функции (y=f(x)).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция (y=f(x)) дифференцируема в точке (x). Тогда к графику функции в точке ( M(x; ; f(x)) ) можно провести касательную, причем, напомним, угловой коэффициент касательной равен ( f'(x) ). Такой график не может «разрываться» в точке (M), т. е. функция обязана быть непрерывной в точке (x).
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция (y=f(x)) дифференцируема в точке (x), то выполняется приближенное равенство ( Delta y approx f'(x) cdot Delta x ). Если в этом равенстве ( Delta x ) устремить к нулю, то и ( Delta y ) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное утверждение неверно. Например: функция ( y=|x|) непрерывна везде, в частности в точке (x=0), но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.
Еще один пример. Функция ( y=sqrt[3] ) непрерывна на всей числовой прямой, в том числе в точке (x=0). И касательная к графику функции существует в любой точке, в том числе в точке (x=0). Но в этой точке касательная совпадает с осью (y), т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид (x=0). Углового коэффициента у такой прямой нет, значит, не существует и ( f'(0) )
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если (C) — постоянное число и ( f=f(x), ; g=g(x) ) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
http://ege.sdamgia.ru/test?theme=68
http://www.math-solution.ru/math-task/derivative