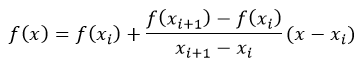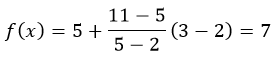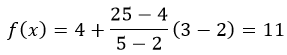Как найти значение с помощью интерполяции - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Линейная интерполяция (или просто интерполяция)^[1]
— процесс нахождения промежуточных значений величины по ее известным значениям. Многие люди могут провести интерполяцию, полагаясь исключительно на интуицию, но в этой статье описан формализованный математический подход к проведению интерполяции.

Шаги

1
Определите величину, для которой вы хотите найти соответствующее значение. Интерполяция может быть проведена для вычисления логарифмов или тригонометрических функций или для вычисления соответствующего объема или давления газа при данной температуре.^[2] Научные калькуляторы в значительной степени заменили логарифмические и тригонометрические таблицы; поэтому в качестве примера проведения интерполяции мы вычислим давление газа при температуре, значение которой не указано в справочных таблицах (или на графиках).
- В уравнении, которое мы выведем, «x» будет обозначать известную величину, а «у» — неизвестную величину (интерполированное значение). При построении графика эти значения откладываются соответственно их обозначениям — величина «x» — по оси X, величина «у» — по оси Y.
- В нашем примере под «x» будет подразумеваться температура газа, равная 37 °С.
2
В таблице или на графике найдите ближайшие значения, расположенные ниже и выше значения «x». В нашей справочной таблице не приведено давление газа при 37 °С, но приведены значения давления при 30 °С и при 40 °С. Давление газа при температуре 30 °С = 3 кПа, а давление газа при 40 °С = 5 кПа.
- Так как мы обозначили температуру в 37 °С как «x», то теперь обозначим температуру в 30 °С как x₁, а температуру в 40 °С как x₂.
- Так как мы обозначили неизвестное (интерполированное) давление газа как «у», то теперь обозначим давление в 3 кПа (при 30 °С) как у₁, а давление в 5 кПа (при 40 °С) как у₂.
3
Найдем интерполированное значение. Уравнение для нахождения интерполированного значения можно записать в виде y = y₁ + ((x — x₁)/(x₂ — x₁) * (y₂ — y₁))^[3]
- Подставим значения x, x₁, x₂ и получим: (37 — 30)/(40 — 30) = 7/10 = 0,7.
- Подставим значения у₁, у₂ и получим: (5 — 3) = 2.
- Умножив 0,7 на 2, получим 1,4. Сложим 1,4 и у₁: 1,4 + 3 = 4,4 кПа. Проверим ответ: найденное значение 4,4 кПа лежит между 3 кПа (при 30 °С) и 5 кПа (при 40 °С), а так как 37 °С ближе к 40 °С, чем к 30 °С, то и окончательный результат (4,4 кПа) должен быть ближе к 5 кПа, чем к 3 кПа.
Реклама

Советы

Если вы умеете работать с графиками, вы можете сделать грубую интерполяцию, отложив известное значение по оси X и найдя соответствующее значение на оси Y.^[4] В приведенном выше примере можно построить график, на котором по оси X откладывается температура (в десятках градусов), а по оси Y — давление (в единицах кПа). На этом графике вы можете нанести точку 37 градусов, а затем найти точку на оси Y, соответствующую этой точке (она будет лежать между точками 4 и 5 кПа). Приведенное выше уравнение просто формализует процесс мышления и обеспечивает получение точного значения.
В отличие от интерполяции, экстраполяция позволяет вычислить приблизительные значения величины вне диапазона значений, приведенных в таблицах или отображенных на графиках.^[5]

Об этой статье

Эту страницу просматривали 98 219 раз.

Была ли эта статья полезной?

Источник

Интерполяция – это способ определения промежуточных значений по дискретному набору данных.

См. онлайн калькулятор линейная интерполяция.

Формула линейной интерполяции имеет вид:

при

x_i≤x≤x_i+1

x	f(x)
x₁	f(x₁)
x	f(x)
x₂	f(x₂)

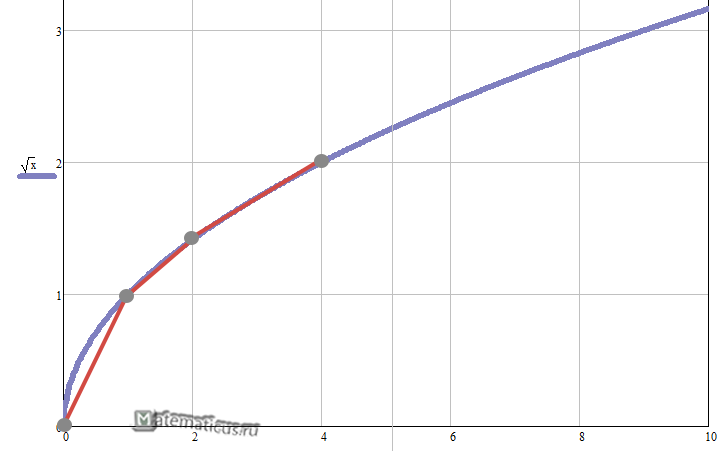
Ниже представлен график линейной интерполяции для нелинейной функции $y=sqrt{x}$

Пример 1

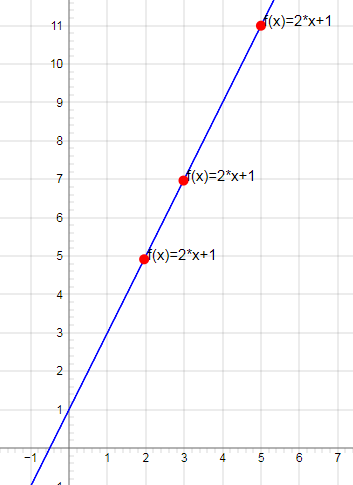
Воспользовавшись таблицей ниже, найдите неизвестное значение функции f(x) при x=3

Решение

Воспользуемся формулой линейной интерполяции, получим

Так как данные в таблице представлены для линейной функция f(x)=2x+1. Для проверки полученного значения подставим в функцию значение X=3

f(3)=2*3+1=7

Пример 2

В соответствии с представленными данными в таблице, найдите неизвестное значение функции f(x) при x=3

Решение

Применим формулу линейной интерполяции, имеем

Так как данные в таблице представлены для нелинейной квадратной функции f(x)=x². Проверим правильность, подставив в функцию значение X=3

f(3)=3²=9

Значение получилось не совсем точное, так как метод линейной интерполяции применим в основном для линейных функций, а для нелинейных функций дает результаты с определенной погрешностью в зависимости от типа функции.

29788

Источник

From Wikipedia, the free encyclopedia

Given the two red points, the blue line is the linear interpolant between the points, and the value y at x may be found by linear interpolation.

In mathematics, linear interpolation is a method of curve fitting using linear polynomials to construct new data points within the range of a discrete set of known data points.

Linear interpolation between two known points[edit]

In this geometric visualisation, the value at the green circle multiplied by the horizontal distance between the red and blue circles is equal to the sum of the value at the red circle multiplied by the horizontal distance between the green and blue circles, and the value at the blue circle multiplied by the horizontal distance between the green and red circles.

If the two known points are given by the coordinates $(x_{0},y_{0})$ and $(x_{1},y_{1})$ , the linear interpolant is the straight line between these points. For a value x in the interval $(x_{0},x_{1})$ , the value y along the straight line is given from the equation of slopes

${displaystyle {frac {y-y_{0}}{x-x_{0}}}={frac {y_{1}-y_{0}}{x_{1}-x_{0}}},}$

which can be derived geometrically from the figure on the right. It is a special case of polynomial interpolation with n = 1.

Solving this equation for y, which is the unknown value at x, gives

${displaystyle {begin{aligned}y&=y_{0}+(x-x_{0}){frac {y_{1}-y_{0}}{x_{1}-x_{0}}}\&={frac {y_{0}(x_{1}-x_{0})}{x_{1}-x_{0}}}+{frac {y_{1}(x-x_{0})-y_{0}(x-x_{0})}{x_{1}-x_{0}}}\&={frac {y_{1}x-y_{1}x_{0}-y_{0}x+y_{0}x_{0}+y_{0}x_{1}-y_{0}x_{0}}{x_{1}-x_{0}}}\&={frac {y_{0}(x_{1}-x)+y_{1}(x-x_{0})}{x_{1}-x_{0}}},end{aligned}}}$

which is the formula for linear interpolation in the interval $(x_{0},x_{1})$ . Outside this interval, the formula is identical to linear extrapolation.

This formula can also be understood as a weighted average. The weights are inversely related to the distance from the end points to the unknown point; the closer point has more influence than the farther point. Thus, the weights are ${textstyle 1-{frac {x-x_{0}}{x_{1}-x_{0}}}}$ and ${textstyle 1-{frac {x_{1}-x}{x_{1}-x_{0}}}}$ , which are normalized distances between the unknown point and each of the end points. Because these sum to 1,

${displaystyle {begin{aligned}y&=y_{0}left(1-{frac {x-x_{0}}{x_{1}-x_{0}}}right)+y_{1}left(1-{frac {x_{1}-x}{x_{1}-x_{0}}}right)\&=y_{0}left(1-{frac {x-x_{0}}{x_{1}-x_{0}}}right)+y_{1}left({frac {x-x_{0}}{x_{1}-x_{0}}}right)\&=y_{0}left({frac {x_{1}-x}{x_{1}-x_{0}}}right)+y_{1}left({frac {x-x_{0}}{x_{1}-x_{0}}}right)end{aligned}}}$

yielding the formula for linear interpolation given above.

Interpolation of a data set[edit]

Linear interpolation on a data set (red points) consists of pieces of linear interpolants (blue lines).

Linear interpolation on a set of data points (x₀, y₀), (x₁, y₁), …, (x_n, y_n) is defined as the concatenation of linear interpolants between each pair of data points. This results in a continuous curve, with a discontinuous derivative (in general), thus of differentiability class C^0 .

Linear interpolation as approximation[edit]

Linear interpolation is often used to approximate a value of some function f using two known values of that function at other points. The error of this approximation is defined as

${displaystyle R_{T}=f(x)-p(x),}$

where p denotes the linear interpolation polynomial defined above:

${displaystyle p(x)=f(x_{0})+{frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}(x-x_{0}).}$

It can be proven using Rolle’s theorem that if f has a continuous second derivative, then the error is bounded by

${displaystyle |R_{T}|leq {frac {(x_{1}-x_{0})^{2}}{8}}max _{x_{0}leq xleq x_{1}}left|f''(x)right|.}$

That is, the approximation between two points on a given function gets worse with the second derivative of the function that is approximated. This is intuitively correct as well: the «curvier» the function is, the worse the approximations made with simple linear interpolation become.

History and applications[edit]

Linear interpolation has been used since antiquity for filling the gaps in tables. Suppose that one has a table listing the population of some country in 1970, 1980, 1990 and 2000, and that one wanted to estimate the population in 1994. Linear interpolation is an easy way to do this. It is believed that it was used in the Seleucid Empire (last three centuries BC) and by the Greek astronomer and mathematician Hipparchus (second century BC). A description of linear interpolation can be found in the ancient Chinese mathematical text called The Nine Chapters on the Mathematical Art (九章算術),^[1] dated from 200 BC to AD 100 and the Almagest (2nd century AD) by Ptolemy.

The basic operation of linear interpolation between two values is commonly used in computer graphics. In that field’s jargon it is sometimes called a lerp (from linear interpolation). The term can be used as a verb or noun for the operation. e.g. «Bresenham’s algorithm lerps incrementally between the two endpoints of the line.»

Lerp operations are built into the hardware of all modern computer graphics processors. They are often used as building blocks for more complex operations: for example, a bilinear interpolation can be accomplished in three lerps. Because this operation is cheap, it’s also a good way to implement accurate lookup tables with quick lookup for smooth functions without having too many table entries.

Extensions[edit]

Comparison of linear and bilinear interpolation some 1- and 2-dimensional interpolations.
Black and red/yellow/green/blue dots correspond to the interpolated point and neighbouring samples, respectively.
Their heights above the ground correspond to their values.

Accuracy[edit]

If a C⁰ function is insufficient, for example if the process that has produced the data points is known to be smoother than C⁰, it is common to replace linear interpolation with spline interpolation or, in some cases, polynomial interpolation.

Multivariate[edit]

Linear interpolation as described here is for data points in one spatial dimension. For two spatial dimensions, the extension of linear interpolation is called bilinear interpolation, and in three dimensions, trilinear interpolation. Notice, though, that these interpolants are no longer linear functions of the spatial coordinates, rather products of linear functions; this is illustrated by the clearly non-linear example of bilinear interpolation in the figure below. Other extensions of linear interpolation can be applied to other kinds of mesh such as triangular and tetrahedral meshes, including Bézier surfaces. These may be defined as indeed higher-dimensional piecewise linear function (see second figure below).

Example of bilinear interpolation on the unit square with the z values 0, 1, 1 and 0.5 as indicated. Interpolated values in between represented by colour.

A piecewise linear function in two dimensions (top) and the convex polytopes on which it is linear (bottom)

Programming language support[edit]

Many libraries and shading languages have a «lerp» helper-function (in GLSL known instead as mix), returning an interpolation between two inputs (v0, v1) for a parameter (t) in the closed unit interval [0, 1]. Signatures between lerp functions are variously implemented in both the forms (v0, v1, t) and (t, v0, v1).

// Imprecise method, which does not guarantee v = v1 when t = 1, due to floating-point arithmetic error.
// This method is monotonic. This form may be used when the hardware has a native fused multiply-add instruction.
float lerp(float v0, float v1, float t) {
  return v0 + t * (v1 - v0);
}

// Precise method, which guarantees v = v1 when t = 1. This method is monotonic only when v0 * v1 < 0.
// Lerping between same values might not produce the same value
float lerp(float v0, float v1, float t) {
  return (1 - t) * v0 + t * v1;
}

This lerp function is commonly used for alpha blending (the parameter «t» is the «alpha value»), and the formula may be extended to blend multiple components of a vector (such as spatial x, y, z axes or r, g, b colour components) in parallel.

References[edit]

^ Joseph Needham (1 January 1959). Science and Civilisation in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press. pp. 147–. ISBN 978-0-521-05801-8.

Meijering, Erik (2002), «A chronology of interpolation: from ancient astronomy to modern signal and image processing», Proceedings of the IEEE, 90 (3): 319–342, doi:10.1109/5.993400.

External links[edit]

Equations of the Straight Line at cut-the-knot
Well-behaved interpolation for numbers and pointers
«Linear interpolation», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
«Finite-increments formula», Encyclopedia of Mathematics, EMS Press, 2001 [1994]

Источник

Интерполяция данных: соединяем точки так, чтобы было красиво

Время на прочтение
7 мин

Количество просмотров 150K

Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:

Немного матчасти

Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P₁ … P_n, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти n – 1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:

Функции f_i могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками P_i) называется сплайном.

В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.

Ставим опыты

Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
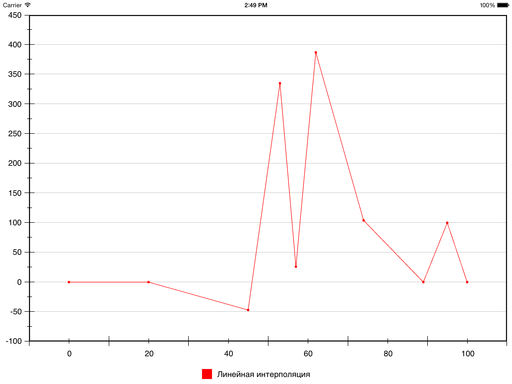
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):

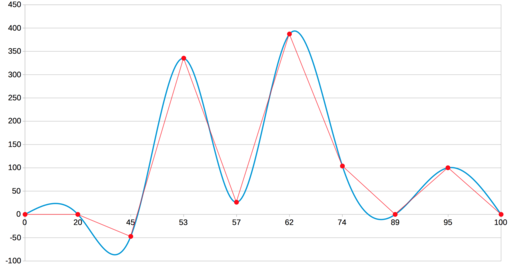
Результат линейной интерполяции этих точек выглядит так:

Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.

Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a; b], это означает, что на [a; b] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз P_i, то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.

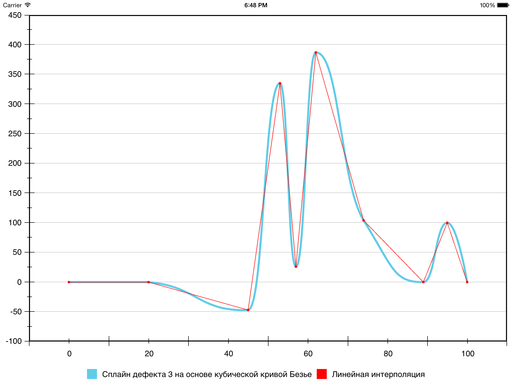
Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1. Вот как он выглядит для наших данных:

Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.

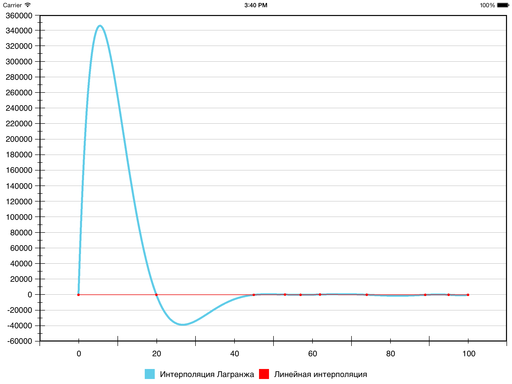
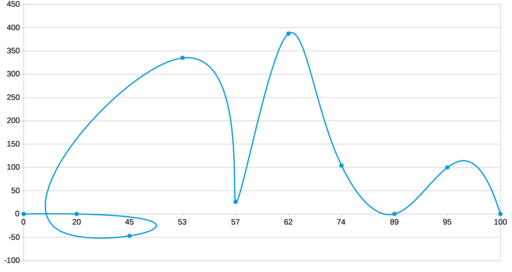
Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа. Это полиномы степени n – 1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
Но вот что получается:

Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.

В компьютерной графике очень широко применяются кривые Безье, представленные полиномами k-й степени.
Они не являются интерполирующими, так как из k + 1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k – 1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Вот пример кубической кривой Безье:

Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k-й степени (кстати, k = 1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k – 1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k = 3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (P_i), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено здесь.
Вот что получится на нашем тестовом наборе:

Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.

Думаем и экспериментируем

Можно попробовать ослабить условие гладкости: потребовать дефект 2, а не 1, то есть сохранить непрерывность одной только первой производной.
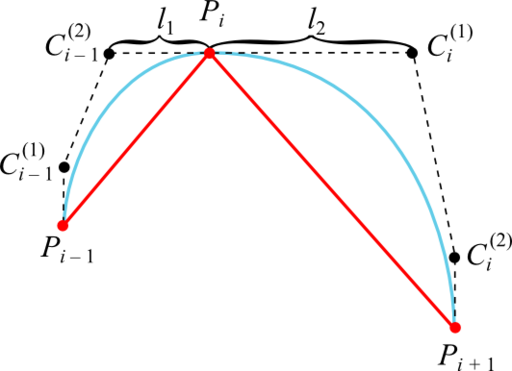
Достаточное условие достижения дефекта 2 в том, что промежуточные контрольные точки кубической кривой Безье, смежные с заданной точкой интерполируемой последовательности, лежат с этой точкой на одной прямой и на одинаковом расстоянии:

В качестве прямых, на которых лежат точки C_i – 1⁽²⁾, P_i и C_i⁽¹⁾, целесообразно взять касательные к графику интерполируемой функции в точках P_i. Это гарантирует отсутствие ложных экстремумов, так как кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).

Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:

Эвристика 1

Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C₁⁽¹⁾ и C_n – 1⁽²⁾ совпадают с точками P₁ и P_n соответственно).
В этом случае получается вот такая кривая:

Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.

К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки P_i до точек C_i – 1⁽²⁾ и C_i⁽¹⁾, но при этом сохраняем их все лежащими на одной прямой:

Эвристика для вычисления расстояний будет такой:

Эвристика 2

Расчёт l₁ и l₂ такой же, как в «эвристике 1».
При этом, однако, стоит ещё проверять, не совпали ли точки P_i и P_i + 1 по ординате, и, если совпали, полагать l₁ = l₂ = 0. Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).

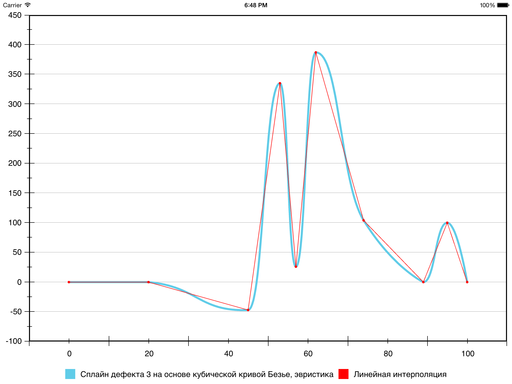
Результат получается такой:

В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы. Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:

Эвристика 3

Если абсцисса точки пересечения касательных в точках P_i(x_i, y_i) и P_i + 1(x_i + 1, y_i + 1) лежит в отрезке [x_i; x_i + 1], то l₁ либо l₂ полагаем равным нулю. В том случае, если касательная в точке P_i направлена вверх, нулю полагаем максимальное из l₁ и l₂, если вниз — минимальное.

Результат следующий:

На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код.

А как люди-то делают?

Обещанный обзор. Конечно, перед решением задачи мы посмотрели, кто чем может похвастаться, а уже потом начали разбираться, как сделать самим и по возможности лучше. Но вот как только сделали, не без удовольствия ещё раз прошлись по доступным инструментам и сравнили их результаты с плодами наших экспериментов. Итак, поехали.

MS Excel

Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.

LibreOffice Calc

В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.

Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат

Highcharts, одна из самых популярных JS-библиотек для построения диаграмм

Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).

amCharts, ещё одна популярная JS-библиотека

Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.

Coreplot, самая популярная библиотека построения графиков для iOS и OS X

Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.

aChartEngine, вроде как самая популярная библиотека построения графиков для Android

Больше всего похоже на кривую Безье степени n – 1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.

Вместо заключения

В конечном счёте получается, что из «больших ребят» лучше всех проблему решили Highcharts. Но метод, описанный в этой статье, обеспечивает ещё меньшую ошибку относительно линейной интерполяции.
Вообще, заняться этим пришлось по просьбе покупателей, которые зарепортили нам «острые углы» в качестве бага в нашем движке диаграмм. Будем рады, если описанный опыт кому-то пригодится.

Источник

Шаги

Советы

Об этой статье

Была ли эта статья полезной?

Linear interpolation between two known points[edit]

Interpolation of a data set[edit]

Linear interpolation as approximation[edit]

History and applications[edit]

Extensions[edit]

Accuracy[edit]

Multivariate[edit]

Programming language support[edit]

See also[edit]

References[edit]

External links[edit]

Интерполяция данных: соединяем точки так, чтобы было красиво

Немного матчасти

Ставим опыты

Думаем и экспериментируем

А как люди-то делают?

MS Excel

LibreOffice Calc

Highcharts, одна из самых популярных JS-библиотек для построения диаграмм

amCharts, ещё одна популярная JS-библиотека

Coreplot, самая популярная библиотека построения графиков для iOS и OS X

aChartEngine, вроде как самая популярная библиотека построения графиков для Android

Вместо заключения