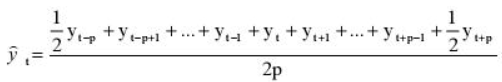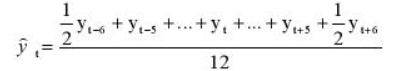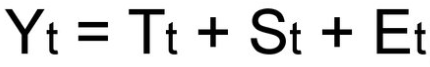Расчет сезонной компоненты в аддитивной модели
|
№ квартала. t |
Потребление |
Итого |
Скользящая |
Центрированная |
Оценка |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
6 |
||||
|
2 |
4,4 |
24,4 |
6,1 |
||
|
3 |
5 |
25,6 |
6,4 |
6,25 |
-1,25 |
|
4 |
9 |
26 |
6,5 |
6,45 |
2,55 |
|
5 |
7,2 |
27 |
6,75 |
6,625 |
0,575 |
|
6 |
4,8 |
28 |
7 |
6,875 |
-2,075 |
|
7 |
6 |
28,8 |
7,2 |
7,1 |
-1,1 |
|
8 |
10 |
29,6 |
7,4 |
7,3 |
2,7 |
|
9 |
8 |
30 |
7,5 |
7,45 |
0,55 |
|
10 |
5,6 |
31 |
7,75 |
7,625 |
-2,025 |
|
11 |
6,4 |
32 |
8 |
7,875 |
-1,475 |
|
12 |
11 |
33 |
8,25 |
8,125 |
2,875 |
|
13 |
9 |
33,6 |
8,4 |
8,325 |
0,675 |
|
14 |
6,6 |
33,4 |
8,35 |
8,375 |
-1,775 |
|
15 |
7 |
||||
|
16 |
10,8 |
Шаг
2. Найдем
оценки сезонной компоненты как разность
между фактическими уровнями ряда и
центрированными скользящими средними
(гр. 6 табл. 10.1.1). Используем эти оценки
для расчета значений сезонной компоненты
S (табл. 10.1.2). Для это найдем средние за
каждый квартал (по всем годам) оценки
сезоной компоненты Si.
В моделях с сезонной компонентой обычно
предполагается, что сезонные воздействия
за период взаимопогашаются. В
аддитивной модели это выражается в том,
что сумма значений сезонной компоненты
по всем кварталам должна быть равна
нулю.
Таблица 10.1.2
Расчет оценок сезонной компоненты в аддитивной модели
|
Показатели |
Год |
№ квартала, |
|||
|
I |
II |
III |
IV |
||
|
1 2 3 4 |
— 0,575 0,55, 0,675 |
— -2,075 -2,025 -1,775 |
-1,250 -1,100 -1,475 — |
2,550 2,700 2,875 — |
|
|
Итого |
1,800 |
-5,875 |
-3,825 |
8,125 |
|
|
Средняя |
0,600 |
-1,958 |
-1,275 |
2,708 |
|
|
Скорректированная |
0,581 |
-1,977 |
-1,294 |
2,690 |
Для данной модели
имеем:
0,6-1,958-1,275+2,708=0,075
Так как сумма всех
сезонных компонент не равна нулю, то
определяем корректирующий коэффицент:
Скорректированные
значения сезонной компоненты
найдем как разность между ее средней
оценкой
и
корректирующим
коэффициентом k.
Si
=
– k
Необходимо
опять проверить равенство нулю суммы
значений скорректированной сезонной
компоненты:
0,581-1,977-1,294+2,690=0,0
Тем самым, мы
получили следующие значений сезонной
компоненты для каждого квартала:
I
квартал: S1
=0,581
II
квартал: S2
=-1,977
III
квартал: S3
=-1,294
IV
квартал: S4
=2,690
Полученные
значения занесем в табл. 10.1.2
в последнюю строчку для соответствующих
кварталов каждого года.
Шаг
3.
Устраним влияние сезонной компоненты
из значений временного ряда потребления
электроэнергии. Для этого из каждого
уровня исходного временного ряда вычтем
значение сезонной компоненты. Получим
величины Т
+ Е = Y—
S
(столб.
4 табл. 10.1.3). Эти значения рассчитываются
за каждый момент времени и содержат
только тенденцию
и случайную компоненту.
Таблица 10.1.3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сезонная составляющая (сезонная компонента) и её оценка.
Известны данные по ВВП в России за 2008-2012 г.
|
год |
квартал |
объём ВВП, млрд.руб |
|
2008 |
1 |
8878 |
|
2 |
10238 |
|
|
3 |
11542 |
|
|
4 |
10619 |
|
|
2009 |
1 |
8335 |
|
2 |
9245 |
|
|
3 |
10411 |
|
|
4 |
10816 |
|
|
2010 |
1 |
9617 |
|
2 |
10693 |
|
|
3 |
11843 |
|
|
4 |
13019 |
|
|
2011 |
1 |
11680 |
|
2 |
13038 |
|
|
3 |
14406 |
|
|
4 |
15462 |
Построить аддитивную модель временного ряда, выделив сезонную и трендовую составляющие
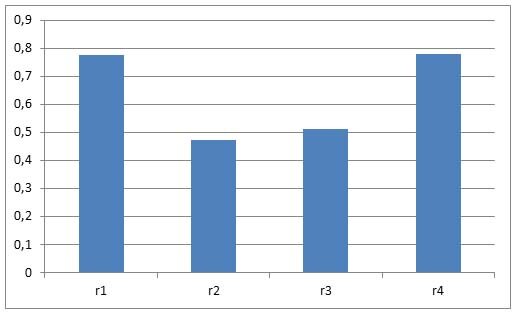
Найдём коэффициенты автокорреляции
| r1 |
0,777705 |
| r2 |
0,475503 |
| r3 |
0,513819 |
| r4 |
0,781028 |
Построим коррелограмму
По высоким значениям коэффициентов автокорреляции 1 и 4 порядка выдвигаем гипотезу о наличии тренда и сезонной составляющей .
Для оценки сезонной компоненты аддитивной модели составим таблицу
Для этого:
- Просуммируем уровни ряда последовательно за 4 квартала со сдвигом на один сезон (итого за 4 квартала)
- Найдем скользящие средние, делением каждой суммы на 4.
- Приведем скользящие средние с помощью центрирования, найдя средние значения из двух последовательных скользящих средних.
- Найдем оценки сезонной компоненты как разность между фактическим y и центрированной скользящей средней
|
t |
y |
Итого за 4 кв. |
Скользящая средняя за 4 кв. |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
|
1 |
8878 |
— |
— |
— |
— |
|
2 |
10238 |
41277 |
10319,3 |
— |
— |
|
3 |
11542 |
40734 |
10183,5 |
10251,38 |
1290,63 |
|
4 |
10619 |
39741 |
9935,3 |
10059,38 |
559,63 |
|
5 |
8335 |
38610 |
9652,5 |
9793,88 |
-1458,88 |
|
6 |
9245 |
38807 |
9701,8 |
9677,13 |
-432,13 |
|
7 |
10411 |
40089 |
10022,3 |
9862,00 |
549,00 |
|
8 |
10816 |
41537 |
10384,3 |
10203,25 |
612,75 |
|
9 |
9617 |
42969 |
10742,3 |
10563,25 |
-946,25 |
|
10 |
10693 |
45172 |
11293,0 |
11017,63 |
-324,63 |
|
11 |
11843 |
47235 |
11808,8 |
11550,88 |
292,13 |
|
12 |
13019 |
49580 |
12395,0 |
12101,88 |
917,13 |
|
13 |
11680 |
52143 |
13035,8 |
12715,38 |
-1035,38 |
|
14 |
13038 |
54586 |
13646,5 |
13341,13 |
-303,13 |
|
15 |
14406 |
— |
— |
— |
— |
|
16 |
15462 |
— |
— |
— |
— |
Рассчитаем значения сезонной компоненты
|
Показатели |
Год |
Квартал |
|||
|
1 кв. |
2 кв. |
3 кв. |
4 кв. |
||
|
1 |
1290,63 |
559,63 |
|||
|
2 |
-1458,88 |
-432,13 |
549,00 |
612,75 |
|
|
3 |
-946,25 |
-324,63 |
292,13 |
917,13 |
|
|
4 |
-1035,38 |
-303,13 |
|||
| Итого за сезон |
-3440,50 |
-1059,88 |
2131,75 |
2089,50 |
|
| Средняя оценка сезонной компоненты, |
-1146,83 |
-353,29 |
710,58 |
696,50 |
|
| Скорректированная сезонная компонента, |
-1123,57 |
-330,03 |
733,84 |
719,76 |
Все значения для расчетов возьмем из колонки «Оценка сезонной компоненты», последовательно внося их в таблицу
Сумма «Скорректированной сезонной компоненты» равна нулю.
Для расчета скорректированной сезонной компоненты определим корректирующий коэффициент.
Составим таблицу, где T + ε колонка с возможным трендом (за вычетом сезонности)
|
t |
y |
Si (скорректированная S) |
y – S = T + ε |
|
1 |
2301 |
-373,48 |
2674,48 |
|
2 |
2567 |
-139,52 |
2706,52 |
|
3 |
3050 |
266,48 |
2783,52 |
|
4 |
3064 |
246,52 |
2817,48 |
|
5 |
2891 |
-373,48 |
3264,48 |
|
6 |
3149 |
-139,52 |
3288,52 |
|
7 |
3671 |
266,48 |
3404,52 |
|
8 |
3696 |
246,52 |
3449,48 |
|
9 |
3522 |
-373,48 |
3895,48 |
|
10 |
3984 |
-139,52 |
4123,52 |
|
11 |
4645 |
266,48 |
4378,52 |
|
12 |
4979 |
246,52 |
4732,48 |
|
13 |
4441 |
-373,48 |
4814,48 |
|
14 |
5070 |
-139,52 |
5209,52 |
|
15 |
5897 |
266,48 |
5630,52 |
|
16 |
6354 |
246,52 |
6107,48 |
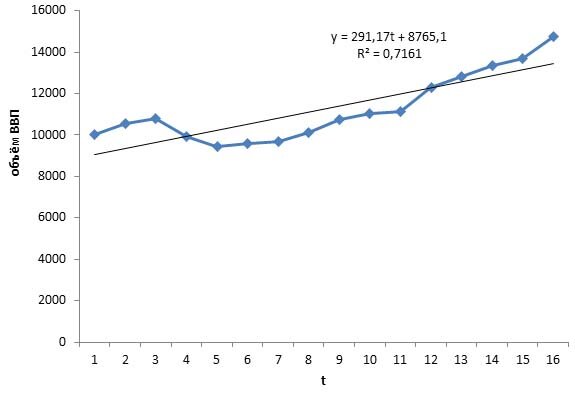
Строим график модели за вычетом сезонной компоненты
Коэффициенту детерминации очень высок (близок к 1), таким образом, полученная линейная модель может использоваться для прогнозирования
Оценим качество такой модели с помощью инструмента регрессия
| ВЫВОД ИТОГОВ | ||||
|
Регрессионная статистика |
||||
| Множественный R |
0,846 |
|||
| R-квадрат |
0,716 |
|||
| Нормированный R-квадрат |
0,696 |
|||
| Стандартная ошибка |
903,55 |
|||
| Наблюдения |
16 |
|||
| Дисперсионный анализ | ||||
|
df |
SS |
MS |
F |
|
| Регрессия |
1 |
28826034 |
28826034 |
35,30883 |
| Остаток |
14 |
11429564 |
816397,4 |
|
| Итого |
15 |
40255598 |
||
|
Коэффи-циенты |
Стандартная ошибка |
t-статистика |
P-Значение |
|
| Y-пересечение |
8765,144 |
473,824 |
18,499 |
3,09E-11 |
| t |
291,174 |
49,002 |
5,942 |
3,6E-05 |
Модель y = 291,174t + 8765,144 высокого качества, поскольку коэффициент корреляции очень высок и модель значима в целом и по параметрам при уровне значимости 95%, т.к. уровни значимости критерия Фишера и Стьюдента намного меньше 5% (0,05) – см. колонки Значимость F и P-Значение.
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
В прошлой статье мы уже разобрали, что такое временной ряд и функцию тренда. Теперь подробнее разберемся с терминологией и остановимся на одной из моделей временного ряда.
Из чего состоит временной ряд
Уровни временного ряда (Yt) представляют из себя сумму двух компонент:
- Регулярную составляющую
- Случайную составляющую
В свою очередь регулярная составляющая состоит из:
- Тренда
- Сезонности
- Циклической составляющей
Однако, в модели необязательно наличие всех этих компонент сразу.
Случайная компонента отражает влияние случайных возмущений на модель, которые по отдельности имеют незначительное воздействие, но суммарно их влияние ощущается.
То есть, в общем случае временной ряд представляет из себя наличие четырех составляющих:
- Тренд (Tt)
- Сезонность (St)
- Цикличность (Ct)
- Случайные возмущения (Et)
Циклическая компонента, по сравнению с сезонностью, имеет более длительный эффект и меняется от цикла к циклу. Поэтому, ее обычно объединяют с трендом.
Виды моделей временного ряда
Обычно, выделяют две модели временного ряда и третью — смешанную.
- Аддитивная модель
-
Мультипликативная модель
-
Смешанная модель
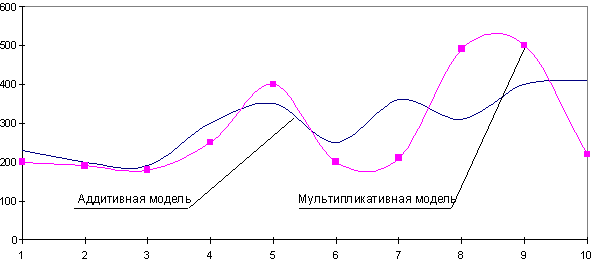
При выборе необходимой модели временного ряда смотрят на амплитуду колебаний сезонной составляющей. Если ее колебания относительно постоянны, то выбирают аддитивную модель. То есть, амплитуда колебаний примерно одинакова:
Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение этих моделей сводится к расчету тренда (Tt), сезонности (St) и случайных возмущений (Et) для каждого уровня ряда (Yt).
Алгоритм построения модели
- Выравниваем ряд с помощью скользящей средней, то есть сглаживаем ряд и отфильтровываем высокочастотные колебания.
- Рассчитываем значение сезонной компоненты St.
- Рассчитываем значения Tt с использованием полученного уравнения тренда.
- Используя полученные значения St и Tt, находим прогнозные значения уровней временного ряда.
- Оцениваем качество модели.
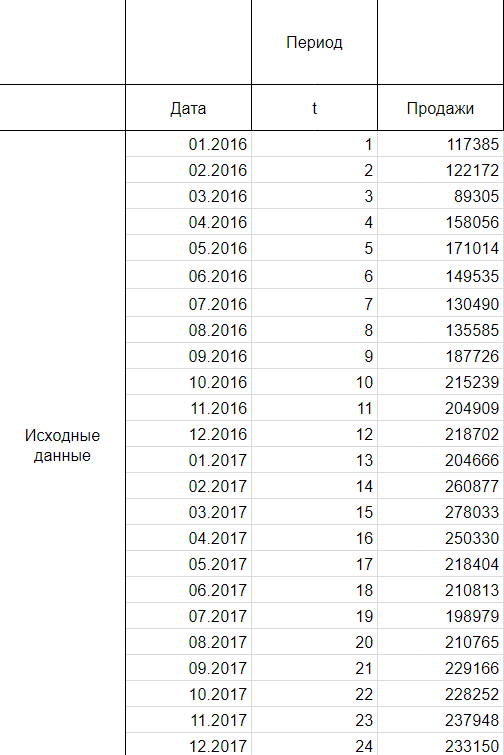
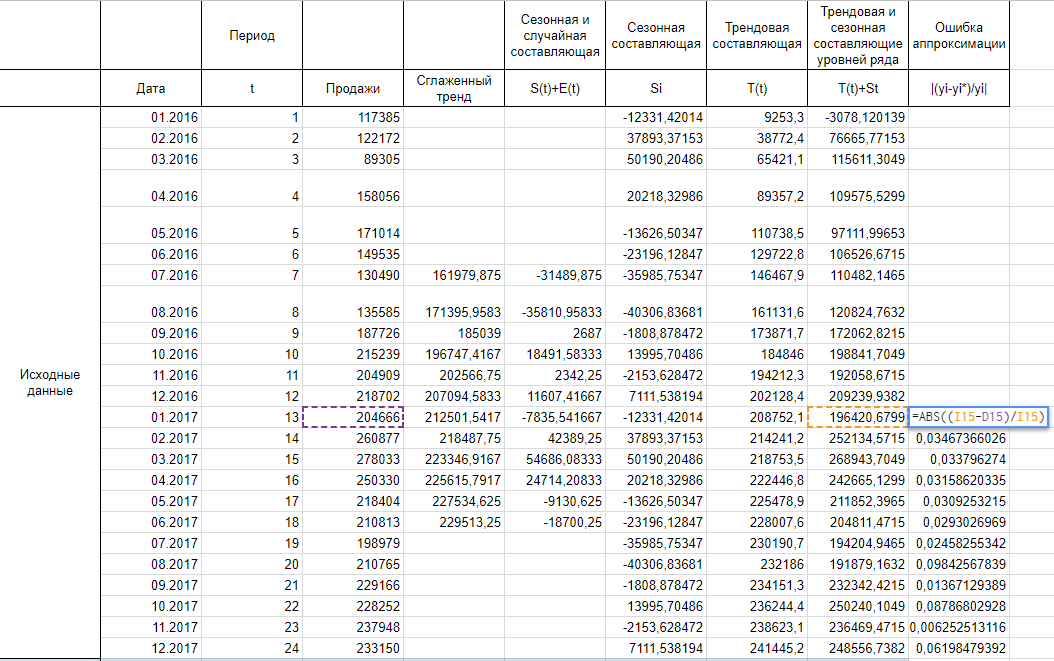
Реализация на практике
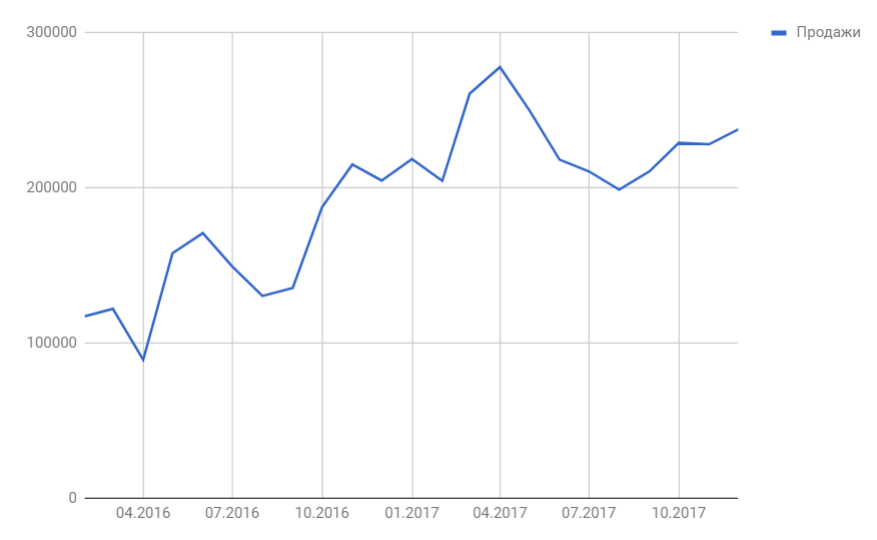
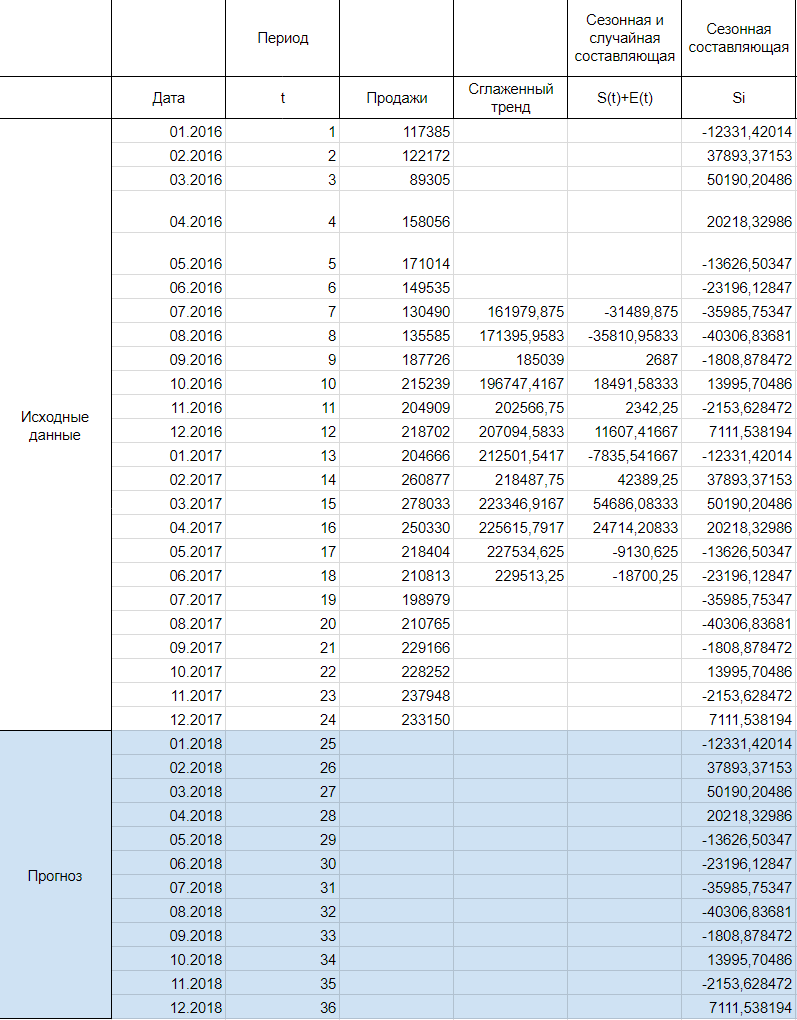
Итак, мы имеем на руках данные о продажах за 2016 и 2017 год и хотим спрогнозировать продажи на 2018 год.
Шаг 1
Следуя нашему алгоритму, мы должны сгладить временной ряд. Воспользуемся методом скользящей средней. Видим, что в каждом году есть большие пики (май-июнь 2016 и апрель 2017), поэтому возьмем период сглаживания пошире, например, месячную динамику, т.е. 12 месяцев.
Удобнее брать период сглаживания в виде нечетного числа, тогда формула для расчета уровней сглаженного ряда:
yi — фактическое значение i-го уровня ряда,
yt — значение скользящей средней в момент времени t,
2p+1 — длина интервала сглаживания.
Но так как мы решили использовать месячную динамику в виде четного числа 12, то данная формула нам не подойдет и мы воспользуемся этой:
Иными словами, мы учитываем половины от крайних уровней ряда в диапазоне, в остальном формула не претерпела больше никаких изменений. Вот ее точный вид для нашей задачи:
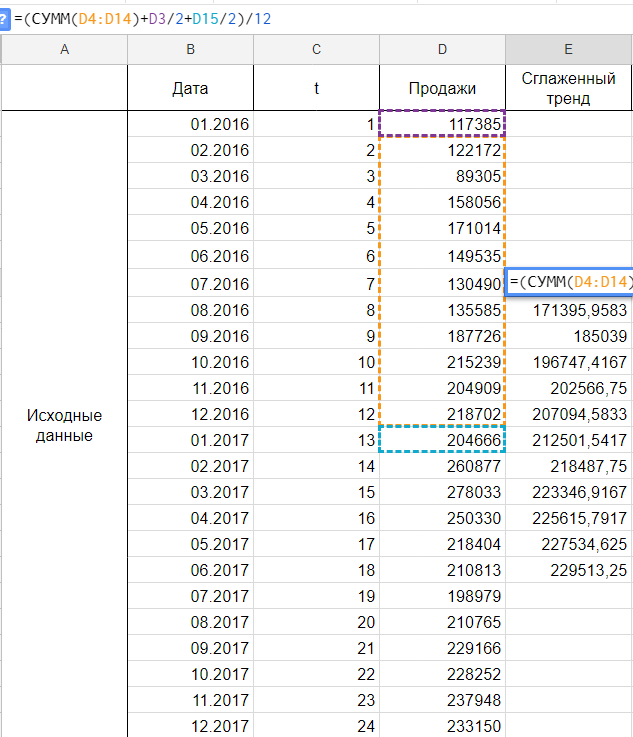
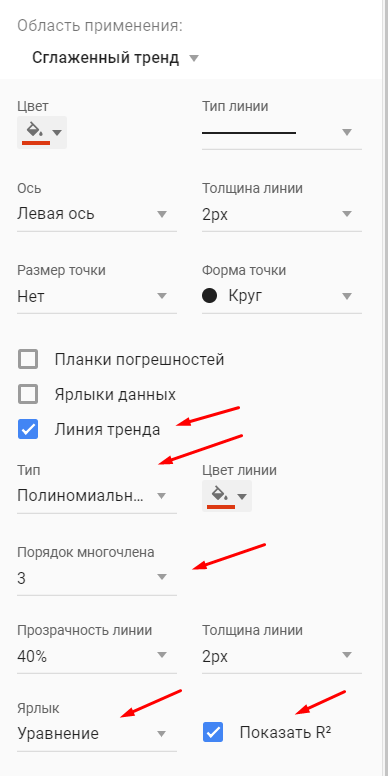
Сглаживаем наши уровни ряда и растягиваем формулу вниз:
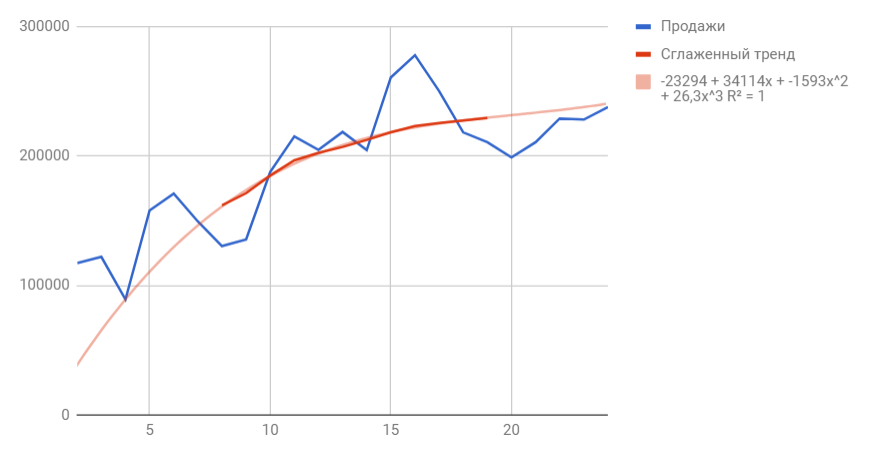
Сразу можем построить график из известных значений уровня продаж и их сглаженной. Выведем ее уравнение и значение коэффициента детерминации R^2:
В качестве сглаженной я выбрала полином третьей степени, так как он лучше всего описывал уровни временного ряда и имел наибольший R^2.
Шаг 2
Так как мы рассматриваем аддитивную модель вида:
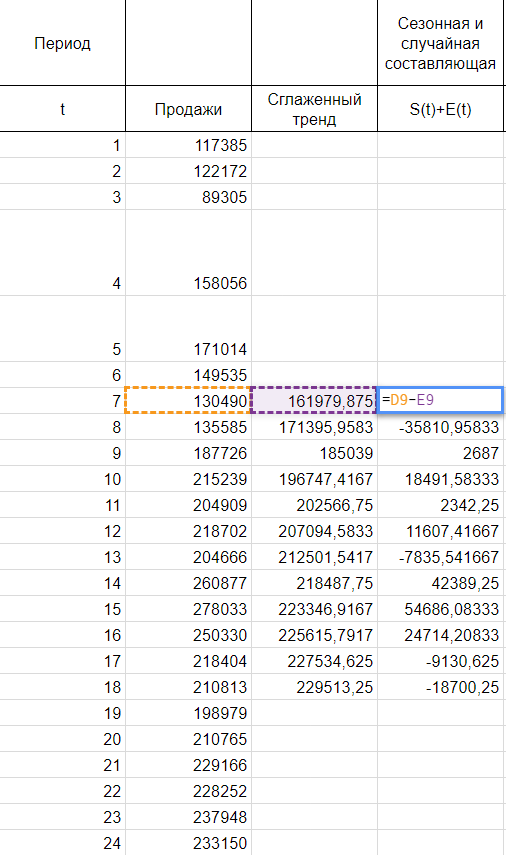
Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и значениями скользящей средней St+Et = Yt-Tt, так как Yt и Tt мы уже знаем.
Используем оценки сезонной компоненты (St+Et) для расчета значений сезонной компоненты St. Для этого найдем средние за каждый интервал (по всем годам) оценки сезонной компоненты St.
Средняя оценка сезонной компоненты находится как сумма по столбцу, деленная на количество заполненных строк в этом столбце. В нашем случае оценки сезонной составляющей расположились в строках без пересечений, поэтому сумма по столбцам состоит из одиночных значений, следовательно и среднее будет таким же. Если бы мы располагали периодом побольше, например с 2015, у нас бы добавилась еще одна строка и мы смогли бы полноценно найти среднее, поделив сумму на 2.
В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем интервалам должна быть равна нулю. Поэтому найдя значение случайной составляющей, поделив сумму средних оценок сезонной составляющей на 12, мы вычитаем ее значение из каждой средней оценки и получаем скорректированную сезонную компоненту, St.
Далее, заполняем нашу таблицу значениями сезонной составляющей дублируя ряд каждые 12 месяцев, то есть три раза:
Шаг 3
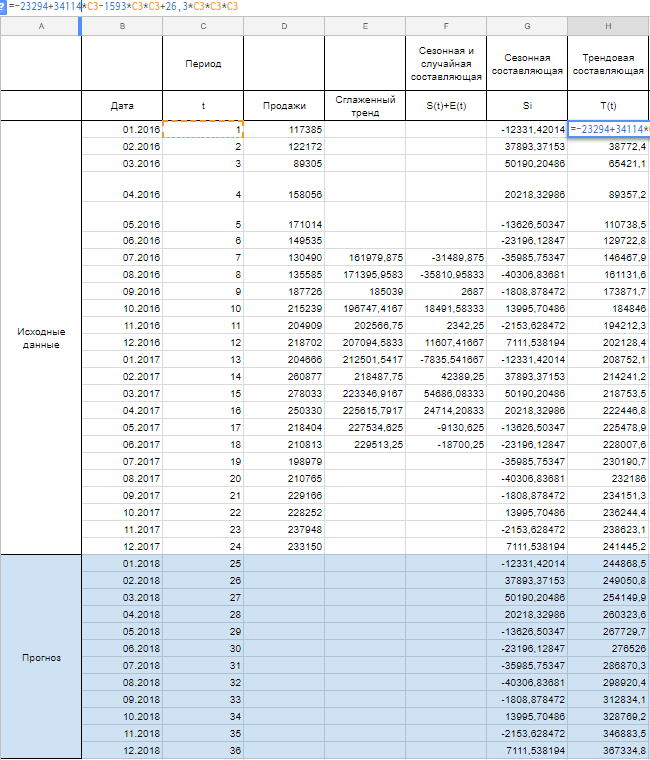
Теперь рассчитываем значения уровня тренда T(t) по тому уравнению, которое мы получили при построении сглаженного тренда на первом шаге.
T(t) = -23294+34114*t-1593*t^2+26,3*t^3
Вместо t используем значения из столбца Период из соответствующей строки.
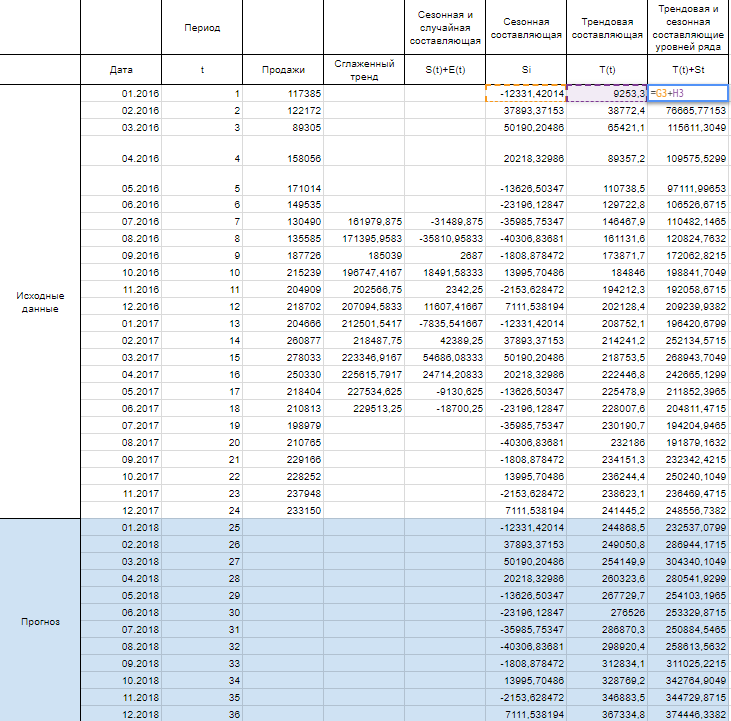
Шаг 4
Имея рассчитанные значения S(t) и T(t) мы можем рассчитать прогнозные значения уровней ряда Y(t). Для этого накладываем уровни сезонности на тренд.
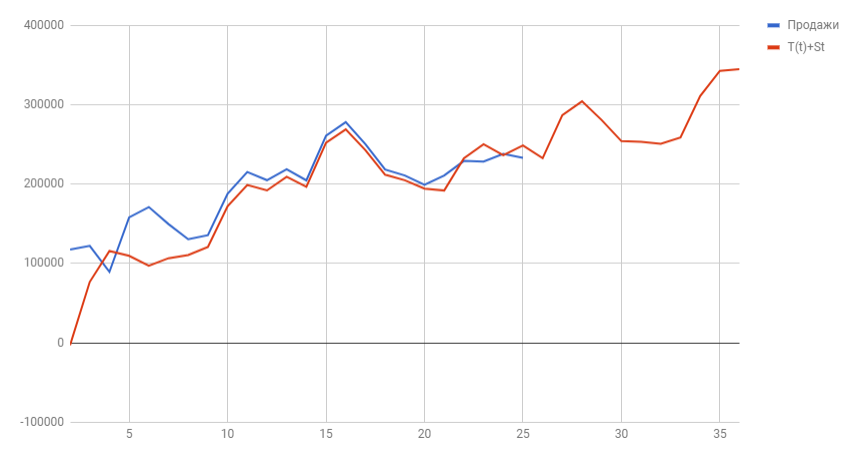
Теперь построим график известных значений Y(t) и спрогнозированных за 2018 год.
Вот мы и нашли спрогнозированные значения уровней продаж на 2018 год. Значения отражают возрастающую тенденцию и сезонные пики. Конечно, эти данные не дают 100% точности, ведь существует множество внешних воздействий, которые могут изменить направление тренда, поэтому к прогнозным значениям обычно строят доверительный интервал, это такой коридор, внутри которого могут колебаться прогнозные значения с заданной вероятностью (чаще всего выбирают 95%). Но об этом я расскажу в следующей статье.
Шаг 5
Осталось оценить точность модели. Для этого будем использовать среднюю ошибку аппроксимации, которая поможет рассчитать ошибку в относительном выражении. Иными словами, это среднее отклонение расчетных значений от фактических, которое вычисляется по формуле:
yi — спрогнозированные уровни ряда,
yi* — фактические уровни ряда,
n — количество складываемых элементов.
Модель может считаться адекватной, если:
Итак, рассчитываем ошибку аппроксимации для нашего случая. Так как в основе нашего тренда лежит полином третьей степени, прогнозные значения начинают хорошо повторять фактические значения к концу 2016 года, думаю, я думаю, поэтому корректнее было бы рассчитать ошибку аппроксимации для значений 2017 года.
Сложив весь столбец с ошибками аппроксимации и поделив на 12, получаем среднюю ошибку аппроксимации 4,13%. Это значение меньше 15% и можем сделать вывод об адекватности модели.
Не забывайте, что прогнозы не бывают точными на 100%. Любые неожиданные внешние воздействия могут развернуть значения уровней ряда в неизвестном направлении 🙂
Полезные ссылки:
- Ссылка на пример Google Sheets
- Построение функции тренда в Excel. Быстрый прогноз без учета сезонности
- Бывшев В.А. Эконометрика
- Об авторе
- Свежие записи
Раздаточный материал к Лекции 6
Изучение сезонной компоненты временных рядов
Алгоритм расчета для случая аддитивной сезонности.
1. Для описания тенденции воспользуемся процедурой скользящей средней при четной длине интервала сглаживания.
2. Рассчитаем отклонения фактических значений от уровней сглаженного ряда:
Уровни вновь полученного ряда отражают эффект сезонности и случайности.
3. Для элиминирования влияния случайных факторов определим предварительные значения сезонной составляющей как средние значения из уровней для одноименных месяцев (кварталов). Например, для временных рядов месячной динамики процедура усреднения может быть описана выражением:
где k—число целых периодов (циклов) во временном ряду, полученном на втором шаге.
Разные пределы суммирования объясняются тем, что при использовании скользящей средней с четным значением длины интервала сглаживания (l=2p) p первых и p последних уровней ряда будут потеряны (В нашем случае потери составят по 6 уровней в начале и в конце ряда).
4. Проведем корректировку первоначальных значений сезонной составляющей, вызванную тем, что суммарное воздействие сезонности на динамику предполагается нейтральным. Для аддитивного случая сумма значений сезонной составляющей для полного сезонного цикла должна быть равна нулю. Поэтому окончательные, скорректированные оценки сезонной компоненты определим с помощью следующего выражения:
m—число фаз в полном сезонном цикле (как правило, m=12 для рядов месячной динамики и m=4 для квартальных данных).
Для мультипликативной формы сезонности меняется содержание 2 и 4го этапов алгоритма. Очевидно, что на втором шаге знак вычитания необходимо заменить делением:
После получения предварительных оценок сезонности усреднением на шаге 3 следует выполнить процедуру их корректировки. Взаимопогашаемость сезонных колебаний в мультипликативной форме выражается в том, что средняя арифметическая из значений коэффициентов сезонности для полного сезонного цикла должна быть равна 1. Поэтому окончательные оценки коэффициентов сезонности получим с помощью следующего выражения:
m—число фаз в полном сезонном цикле.
Процедуру построения тренд-сезонных моделей можно описать в виде следующей последовательности шагов:
1. Оценивание сезонной составляющей с учетом характера сезонности (аддитивной или мультипликативной)
2. Сезонная корректировка (десезонализация) исходных данных.
3. Расчет параметров тренда на основе временного ряда, полученного на втором шаге.
4. Моделирование динамики исходного ряда с учетом трендовой и сезонной составляющих.
5. Оценка точности и адекватности полученной модели.
6. Использование построенной модели для прогнозирования.
Пример.
В Таблице 1 представлены квартальные данные об объемах продаж продукции фирмы за последние 4 года.
Таблица 1
Сглаживание исходного ряда с помощью скользящей средней
Год
Квартал
t
Объем продаж , тыс шт
Скользящая средняя (центрир.)
1
I
1
56,0
—
II
2
54,5
—
III
3
55,2
56,4000
IV
4
59,3
2
I
5
57,2
II
6
55,6
III
7
56,2
IV
8
60,4
3
I
9
58,4
II
10
56,9
III
11
57,1
IV
12
61,5
4
I
13
59,3
II
14
58,2
III
15
58,3
IV
16
62,6
Требуется:
1) на основе графического анализа провести исследование компонентного состава временного ряда объема продаж;
2) Рассчитать прогнозную оценку объемов продаж в первом полугодии следующего года.
Решение:
1. Графический анализ исходного временного ряда свидетельствует о наличии трендовой компоненты: имеется устойчивая, ярко выраженная тенденция роста объемов продаж в течение последних четырех лет.
Рис. 1 Квартальная динамика объемов продаж
Рисунок 1 показывает, что характер тенденции близок к линейному развитию, также отчетливо видны сезонные колебания (период колебаний равен одному году). Наблюдается устойчиво повторяющееся увеличение объемов продаж в 4м и 1м кварталах по сравнению с 3м и 2м кварталами, причем наиболее существенные «всплески» в динамике показателя просматриваются в 4м квартале. Так как амплитуда колебаний остается примерно постоянной, неизменной с течением времени, то для описания и прогнозирования динамики временного ряда можно предложить аддитивную модель.
Рис. 2 Автокорреляционная функция объемов продаж
В автокорреляционной функции наблюдается не очень тесная связь.
При анализе коэффициентов автокорреляции наблюдается наличие сезонности.
При анализе Q-статистики видно, что на первых трёх лагах Q-статистика имеет сравнительно низкие значения, что свидетельствует об отсутствии автокорреляции в первых трех лагах. Первые три коэффициента автокорреляции не являются значимыми, все остальные являются.
P-значения на первых трёх лагах значительно отличаются от нуля, что также свидетельствует об отсутствии автокорреляции.
Тенденция в ряду не очевидна. Можно сделать предположение, что либо её нет, либо она выражена неярко.
2. Проведем сглаживание исходного ряда с помощью простой скользящей средней.
Вычитая из фактических уровней значения сглаженного ряда, получим временной ряд, уровни которого отражают влияние случайных факторов и сезонности.
Предварительную оценку сезонной компоненты получим усреднением уровней временного ряда для одноименных кварталов.
Так как =0,075 (отлична от нуля), то проведем корректировку значений сезонной составляющей.
Найдем «поправку», на которую надо изменить предварительные оценки сезонности:
Скорректированные оценки сезонности приведены в таблице. Например, оценка сезонной компоненты для 1го квартала:
Таблица 2
Оценивание сезонной компоненты в аддитивной модели
№ квартала
i
Предварительная оценка сезонной компоненты
Скорректированные значения сезонной компоненты
I
1
II
2
III
3
IV
4
0,075
Рис. 3 Сезонная волна по абсолютным отклонениям
В таблице показаны основные этапы процесса прогнозирования по аддитивной модели. Сначала из исходного ряда удаляется сезонная составляющая, т.е. осуществляется сезонная корректировка (десезонализация) объема продаж. Для описания тенденции воспользуемся моделью линейного тренда, так как это согласуется с результатом графического анализа динамики показателя.
Таблица 3
Прогнозирование объема продаж с помощью
аддитивной тренд-сезонной модели
t
Объем продаж , тыс. шт.
Сезонная компонента
Десезонализированный объем продаж
Расчетные значения (линейный тренд)
Расчетные значения объема продаж
1
56,0
0,210
55,790
55,823
56,033
2
54,5
3
55,2
4
59,3
5
57,2
6
55,6
7
56,2
8
60,4
9
58,4
10
56,9
11
57,1
12
61,5
13
59,3
14
58,2
15
58,3
16
62,6
17
18
Модель имеет вид:
Расчетные уровни, полученные подстановкой последовательных значений времени t=1,2,…,16 в это уравнение, представлены в таблице.
На заключительном этапе определим расчетные уровни объема продаж по аддитивной модели, суммируя значения полученных оценок трендовой и сезонной составляющих.
Для прогнозирования объема продаж в первом полугодии следующего года оценим значения тренда при t=17 и t=18:
тыс. шт.
тыс. шт.
а затем прибавим к полученным значениям соответствующие оценки сезонной составляющей (для 1го и 2го кварталов).
Таким образом, ожидаемый объем продаж в первом полугодии
составляет:
Характеристики точности модели представлены в таблице. О высокой точности модели свидетельствуют рассчитанные абсолютные и относительные ошибки (максимальная относительная ошибка по модулю не превышает 0,5%, средняя относительная ошибка по модулю составила 0,15%)
Таблица 4
Характеристика точности аддитивной тренд-сезонной модели
t
Объем продаж , тыс. шт.
Расчетные значения объема продаж , тыс. шт.
Абсолютная ошибка, тыс. шт.
Относительная ошибка, %
1
56,0
56,033
0,033
0,059
2
54,5
3
55,2
4
59,3
5
57,2
6
55,6
7
56,2
8
60,4
9
58,4
10
56,9
11
57,1
12
61,5
13
59,3
14
58,2
15
58,3
16
62,6
В то же время необходимо отметить, что рассмотренный подход имеет существенный недостаток—предположение о неизменности во времени сезонных эффектов, что далеко не всегда соответствует реальной динамике многих экономических процессов.
Рис. 4 Ряд остатков
Рис. 5 Автокорреляционная функция остатков
Рис. 6 Нормальный вероятностный график остатков
Рис. 7 Фактические и расчетные значения объемов продаж, тыс.шт.
Применение мультипликативной модели
Таблица 5
Сглаживание исходного ряда с помощью скользящей средней
Год
Квартал
t
Объем продаж , тыс шт
Скользящая средняя (центрир.)
(индекс сезонности)
1
I
1
56,0
—
II
2
54,5
—
III
3
55,2
0,979
IV
4
59,3
2
I
5
57,2
II
6
55,6
III
7
56,2
IV
8
60,4
3
I
9
58,4
II
10
56,9
III
11
57,1
IV
12
61,5
4
I
13
59,3
II
14
58,2
III
15
58,3
IV
16
62,6
Таблица 6
Оценивание сезонной компоненты в аддитивной модели
№ квартала
i
Предварительная оценка сезонной компоненты
Скорректированные значения сезонной компоненты
I
1
II
2
III
3
IV
4
4,002
4
=4,002
Найдем «поправку», на которую надо изменить предварительные оценки сезонности:
Рис. 8 Сезонная волна по относительным отклонениям
Таблица 7
Прогнозирование объема продаж с помощью
мультипликативной тренд-сезонной модели
t
Объем продаж , тыс. шт.
Сезонная компонента
Десезонализированный объем продаж (2:3)
Расчетные значения (линейный тренд)
Расчетные значения объема продаж
(3*5)
1
2
3
4
5
6
1
56,0
1,003
55,833
55,825
55,992
2
54,5
3
55,2
4
59,3
5
57,2
6
55,6
7
56,2
8
60,4
9
58,4
10
56,9
11
57,1
12
61,5
13
59,3
14
58,2
15
58,3
16
62,6
17
18
Линейный тренд:
Таблица 8
Характеристика точности мультипликативной тренд-сезонной модели
t
Объем продаж , тыс. шт.
Расчетные значения объема продаж , тыс. шт.
Абсолютная ошибка, тыс. шт.
Относительная ошибка, %
1
56,0
2
54,5
3
55,2
4
59,3
5
57,2
6
55,6
7
56,2
8
60,4
9
58,4
10
56,9
11
57,1
12
61,5
13
59,3
14
58,2
15
58,3
16
62,6
Рис. 9 Ряд остатков
Рис. 10 Автокорреляционная функция (АКФ) остатков
Рис. 11 Нормальный вероятностный график остатков
Рис. 12 Фактические и расчетные значения объемов продаж, тыс.шт.
I. Проведем выравнивание исходных уровней ряда методом скользящей средней.
- Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы производства.
- Разделив полученные суммы на 4, найдем скользящие средние. Полученные выровненные значения уже не содержат сезонной компоненты.
- Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние. (см. Метод скользящей средней)
Расчет индекса сезонных колебаний
|
Год |
Квартал |
Объем производства |
Скользящая средняя |
Центрированная скользящая средняя |
Индекс сезонных колебаний |
|
2002 |
I |
160 |
– |
– |
– |
|
II |
20 |
– |
– |
– |
|
|
III |
150 |
(160+20+150+100):4=107,50 |
(107,50+110,00):2=108,750 |
150:108,75=1,3793 |
|
|
IV |
100 |
(20+150+100+170):4=110,00 |
(110,00+112,50):2=111,250 |
100:111,25=0,8989 |
|
|
2003 |
I |
170 |
(150+100+170+30):4=112,50 |
(112,50+115,00):2=113,750 |
170:113,75=1,4945 |
|
II |
30 |
(100+170+30+160):4=115,00 |
(115,00+117,50):2=116,250 |
30:116,25=0,2581 |
|
|
III |
160 |
(170+30+160+110):4=117,50 |
(117,50+120,00):2=118,750 |
160:118,75=1,3474 |
|
|
IV |
110 |
(30+160+110+180):4=120,00 |
(120,00+120,00):2=120,000 |
110:120,00=0,9167 |
|
|
2004 |
I |
180 |
(160+110+180+30):4=120,00 |
(120,00+122,50):2=121,250 |
180:121,25=1,4845 |
|
II |
30 |
(110+180+30+170):4=122,50 |
(122,50+120,00):2=121,250 |
30:121,25=0,2474 |
|
|
III |
170 |
(180+30+170+100):4=120,00 |
(120,00+115,00):2=117,500 |
170:117,50=1,4468 |
|
|
IV |
100 |
(30+170+100+160):4=115,00 |
(115,00+117,50):2=116,250 |
100:116,25=0,8602 |
|
|
2005 |
I |
160 |
(170+100+160+40):4=117,50 |
(117,50+118,75):2=118,125 |
160:118,125=1,3545 |
|
II |
40 |
(100+160+40+175):4=118,75 |
(118,75+125,00):2=121,875 |
40:121,875=0,3282 |
|
|
III |
175 |
(160+40+175+125):4=125,00 |
(125,00+132,50):2=128,750 |
175:128,75=1,3592 |
|
|
IV |
125 |
(40+175+125+190):4=132,50 |
(132,50+135,00):2=133,750 |
125:133,75=0,9346 |
|
|
2006 |
I |
190 |
(175+125+190+50):4=135,00 |
(135,00+136,25):2=135,625 |
190:135,625=1,4009 |
|
II |
50 |
(125+190+50+180):4=136,25 |
(136,25+137,50):2=136,875 |
50:136,875=0,3653 |
|
|
III |
180 |
(190+50+180+130):4=137,50 |
– |
– |
|
|
IV |
130 |
– |
– |
– |
II. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние. Эти оценки используются для расчета сезонной компоненты S. Для этого найдем средние оценки сезонной компоненты за каждый квартал. Для этого предварительно необходимо произвести группировку всех индексов сезонных колебаний по соответствующим временным периодам (соответственно по годам и кварталам). Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.
Расчет скорректированного индекса сезонных колебаний
|
Год |
Квартал |
Сумма |
Средний индекс |
|||
|
I |
II |
III |
IV |
|||
|
2002 |
– |
– |
1,3793 |
0,8989 |
||
|
2003 |
1,4945 |
0,2581 |
1,3474 |
0,9167 |
||
|
2004 |
1,4845 |
0,2474 |
1,4468 |
0,8602 |
||
|
2005 |
1,3545 |
0,3282 |
1,3592 |
0,9346 |
||
|
2006 |
1,4009 |
0,3653 |
– |
– |
||
|
Ĵ ср.(кварт.) |
1,4336 |
0,2997 |
1,3832 |
0,9026 |
4,0191 |
1,0048 |
|
Ĵ скоррект. |
1,4268 |
0,2983 |
1,3766 |
0,8983 |
4,0000 |
1,0000 |
Имеем: 1,4336+0,29975+1,383185+0,9026=4,0191
Определим корректирующий коэффициент как отношение 4 : 4,0191=0,995241
Обычно сумма индексов сезонности хотя и незначительно, но отличается от 4 (для четырех кварталов сумма индексов должна быть равна 4, а их средняя равна 1), для устранения этих расхождений определяется поправочный коэффициент, как отношение теоретической суммы индексов (4,0) к фактической величине их суммы.
Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки на корректирующий коэффициент.
1,4336*0,995241+0,29975*0,995241+1,383185*0,995241+0,9026*0,995241=4
Проверим условие равенства суммы значений сезонной компоненты=4:
1,4268+0,2983+1,3766+0,8983=4
III. Следующий шаг построения модели – оценка тренда. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты S. В результате получим величины: Y : S = T * E, которые содержат только тенденцию (T) и случайную компоненту (E)
|
Квартал |
Порядковый номер квартала |
Объем производства |
Сезонная компонента |
Тренд+ случайная компонента |
Выравнивание по тренду |
Тенденция c учетом сезонности |
Случайная компонента |
|
t |
Y |
S |
Y/S=T+E |
T Ỹ=93,749+2,5388t |
T*S |
E=Y/(T*S) |
|
|
I |
1 |
160 |
1,4268 |
112,14 |
96,288 |
137,382 |
1,165 |
|
II |
2 |
20 |
0,2983 |
67,04 |
98,827 |
29,482 |
0,678 |
|
III |
3 |
150 |
1,3766 |
108,96 |
101,366 |
139,540 |
1,075 |
|
IV |
4 |
100 |
0,8983 |
111,32 |
103,905 |
93,338 |
1,071 |
|
I |
5 |
170 |
1,4268 |
119,15 |
106,443 |
151,871 |
1,119 |
|
II |
6 |
30 |
0,2983 |
100,56 |
108,982 |
32,512 |
0,923 |
|
III |
7 |
160 |
1,3766 |
116,23 |
111,521 |
153,519 |
1,042 |
|
IV |
8 |
110 |
0,8983 |
122,45 |
114,060 |
102,461 |
1,074 |
|
I |
9 |
180 |
1,4268 |
126,16 |
116,599 |
166,361 |
1,082 |
|
II |
10 |
30 |
0,2983 |
100,56 |
119,138 |
35,542 |
0,844 |
|
III |
11 |
170 |
1,3766 |
123,49 |
121,676 |
167,499 |
1,015 |
|
IV |
12 |
100 |
0,8983 |
111,32 |
124,215 |
111,583 |
0,896 |
|
I |
13 |
160 |
1,4268 |
112,14 |
126,754 |
180,850 |
0,885 |
|
II |
14 |
40 |
0,2983 |
134,08 |
129,293 |
38,571 |
1,037 |
|
III |
15 |
175 |
1,3766 |
127,13 |
131,832 |
181,479 |
0,964 |
|
IV |
16 |
125 |
0,8983 |
139,15 |
134,370 |
120,706 |
1,036 |
|
I |
17 |
190 |
1,4268 |
133,17 |
136,909 |
195,339 |
0,973 |
|
II |
18 |
50 |
0,2983 |
167,60 |
139,448 |
41,601 |
1,202 |
|
III |
19 |
180 |
1,3766 |
130,76 |
141,987 |
195,458 |
0,921 |
|
IV |
20 |
130 |
0,8983 |
144,72 |
144,526 |
129,828 |
1,001 |
IV. Проведем аналитическое выравнивание по тренду. Определим трендовую компоненту (T) в мультипликативной модели. Методом наименьших квадратов (МНК) найдем оценки параметров линейного тренда. Для этого рассчитаем параметры линейного тренда, используя уровни T*E. В результате получим уравнение тренда: Ỹ=93,749+2,5388t
Подставляя в это уравнение значения t =1, 2, …20, найдем теоретические (выровненные) уровни T для каждого момента времени.
V. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (S), получим трендовую компоненту, скорректированную на величину сезонных колебаний (T*S). Расчет ошибки (случайной компоненты) в мультипликативной модели производится по формуле: E = Y /(T * S).
См. также Компоненты и сезонная декомпозиция временного ряда