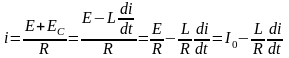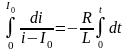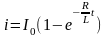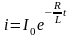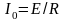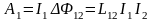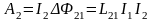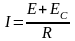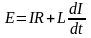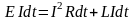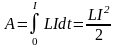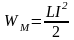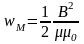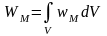Как найти значение силы тока в катушке

Что такое катушка индуктивности

Что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь «фиговинка», на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.

Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!

Индуктивность

Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC — метра.

Что такое индуктивность?  Если через  провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:

где

В — магнитное поле, Вб

I — сила тока, А

А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение

И у нас получится вот такая картина с магнитными силовыми линиями:

Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с  Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:

С научной же точки зрения, индуктивность — это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.

Самоиндукция

Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.

Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:

где

I — сила тока в катушке , А 

U — напряжение в катушке, В 

 R — сопротивление катушки, Ом

Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.

[quads id=1]

И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности — источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.

То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть  в разы больше, чем было до размыкания  цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.

Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.

Типы катушек индуктивности

Катушки индуктивности делятся в основном на два класса: с магнитным и  немагнитным сердечником. Снизу  на фото катушка с немагнитным сердечником.

Но где у нее сердечник? Воздух — это немагнитный сердечник :-).  Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным  сердечником используется, когда индуктивность не превышает 5 миллигенри.

А вот катушки индуктивности с сердечником:

В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.

Для катушек средней индуктивности используются ферритовые сердечники:

Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.

Дроссель

Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.

Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:

Также существует еще один особый вид дросселей — это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.

Что влияет на индуктивность?

От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов.  Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC — метр мне показывает ноль.

Имеется ферритовый сердечник

Начинаю вводить катушку в сердечник на самый край

LC-метр  показывает 21 микрогенри.

Ввожу катушку на середину феррита

35 микрогенри. Уже лучше.

Продолжаю вводить катушку на правый край феррита

20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине.  Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности  в переменных катушках индуктивности:

где

1 — это каркас катушки

2 — это витки катушки

3 — сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.

Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки

Индуктивность стала почти 50 микрогенри!

А давайте-ка попробуем расправим витки по всему ферриту

13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо «виток к витку».

Убавим витки катушки в два раза. Было 24 витка, стало 12.

Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз.  Вывод: чем меньше количество витков — тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.

[quads id=1]

Давайте поэкспериментируем с ферритовым кольцом.

Замеряем индуктивность

15 микрогенри

Отдалим витки катушки друг от друга

Замеряем снова

Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка  не играет никакой роли в катушке индуктивности тороидального исполнения.

Мотнем побольше витков. Было 3 витка, стало 9.

Замеряем

Офигеть! Увеличил количество витков  в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.

Если верить формулам для расчета индуктивностей, индуктивность зависит от «витков в квадрате». Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.

Обозначение на схемах

Последовательное и параллельное соединение катушек индуктивности

При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.

А при параллельном соединении получаем вот так:

При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек.  Это может привести к неправильным показаниям общей индуктивности.

Резюме

Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.

Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:

Электрические обмотки в электротехнике используются очень широко. Спектр их применения весьма огромен. Даже людям, совсем не связанных с профессией электрика, хорошо известно, что медную обмотку можно найти в таких устройствах как трансформатор, электродвигатель, электромагнит и т.д. Пожалуй в начале данной статьи стоит напомнить о самой специфике, свойствах и работе любой электрической катушки. Это позволит лучше понять рассматриваемую тему про силу тока обмотки.

Итак, основным материалом, из которого делаются электрические провода и мотаются большинство обмоток, является медь, покрытая сверху изоляционным материалом. Медь является хорошим проводником тока. Из курса физики известно, что если пропустить через провод электрический ток, то вокруг этого провода образуется магнитное поле. Сила поля зависит силы тока (чем он больше, тем сильнее будет и магнитное поле) и кучности (то есть, из максимальной вытянутости провода сделать максимальную сжатость его в объеме) (чем более провод прижат друг к другу, имея форму намотки, тем концентрированей будет и его магнитное поле).

Именно магнитные поля при взаимодействии друг с другом создают эффект притягивания или отталкивания. Внутри электродвигателя это создает механическое движение ротора и вала, что вращает нужные механизмы. Электромагнит же этим полем может притягивать к себе различные металлические предметы. Притягивание металлического язычка, что замыкает электрические контакты, лежит в основе работы обычного реле, контактора, пускателя. Помимо этого существует и обратный эффект, когда воздействие магнитного поля на электрический проводник приводит к появления электрического тока в этом самом проводнике. Это уже относится к генерации электрической энергии. Ну, и еще стоит упомянуть о таком эффекте как отставание тока катушки от электрического напряжения на ней. Он возникает именно при включении или выключении, а также непосредственно в момент изменения интенсивности электрического питания, что подается на катушку.

Как видно все эффекты, возникающие в электрической катушке, обмотке, непосредственно связаны именно с электрическим током. Для правильной работы устройства, что имеет катушку, обмотку нужны изначально правильные расчеты ее длины, сечения, способа намотки, материала сердечника (если таковой есть). Несоответствие силы тока, протекающего по обмотке, своим номинальным величинам ведет к нарушению правильности работы самого устройства.

Например, слишком большой ток, при несоответствии с нормой, будет способствовать чрезмерному нагреванию обмотки. Высокая температура будет способствовать разрушению изоляции катушки. А это приведет к последующему короткому замыканию и сгоранию этой намотки, или всего устройства в целом. Слишком большие токи в обмотке могут возникнуть по причине, либо появлению в катушке короткозамкнутых витков, либо при подаче на обмотку чрезмерного напряжения, на которое она не рассчитана изначально.

Другим примером может быть случаи, когда сила тока в обмотке меньше, чем должна быть. Это может произойти когда электрические контакты, что связаны с этой катушкой, обмоткой имеют слой окисла, нагара, что сильно ухудшает проводимость этих контактов и увеличивает сопротивление данной электрической цепи. Следовательно, в той обмотке, где имеется недостаточная сила тока, будет меньшая интенсивность магнитного поля. В катушке реле это может приводить к ее не срабатыванию или плохому прижатию контактов. В электродвигателе это снизит его рабочую мощность, а то и вовсе мотор не будет работать. В любом случае варианты переизбытка и недостатка силы тока, протекающий через обмотку ведут к ненормальной работе электротехнического устройства, а то и вовсе к выходу его из строя.

При создании обмотки на конкретное устройство учитываются множество факторов (тип устройства, место и режим его работы, тип тока, величина напряжения, частота, условия эксплуатации, уровень качества и т.д.). Мотать катушку «наобум» скорее всего не «прокатит». Как минимум нужно пользоваться хотя бы основными формулами и упрощенными расчетами. Даже один неучтенный параметр катушки, обмотки может значительно снизить эффективность работы конечного устройства.

Более распространенным случаем бывает когда изначально нормальное, рабочее устройство, содержащее обмотку, вдруг начинает работать ненормально. Тут, естественно, возникает нужда в восстановлении изначальной работоспособности. Прежде всего нужно узнать те основные параметры, характеристики, при которых электрическая обмотка будет работать нормально. Это номинальное напряжение питания, сила тока, мощность, сопротивление, тип тока (переменный или постоянный).

Причиной ненормальной работы электрической обмотки может быть как сама катушка, так и внешняя электрическая цепь. Следовательно, вначале проверяем нужное ли напряжение подается на саму катушку, и способна эта цепь обеспечить достаточную силу тока (нет ли вредного увеличение сопротивления на контактах, клеммах, прочих элементах цепи, ведущие к снижению тока). Для этого берем обычный электронный тестер, мультиметр и меряем напряжение, что должно подаваться на обмотку (сама катушка должна быть отсоединена). Если тестер показал заниженное или завышенное (что бывает гораздо реже) напряжение, то ищем причину во внешней электрической цепи.

Для проверки силы тока, который обеспечивает сама внешняя цепь, нужно взять какую-нибудь подходящую нагрузку (с сопротивлением примерно равным самой обмотке – лампочку, мощный резистор, нагреватель, подходящий кусок нихрома и т.д.). Подсоединяем эту нагрузку вместо обмотки. Переводим мультиметр в режим измерения тока и смотрим на показания. По закону ома легко посчитать силу тока и сравнить ее с измеримым результатом. Допустим, питание у нас 12 вольт, сопротивление мы взяли 12 ом. Чтобы найти силу тока по закону ома нужно напряжение (в вольтах) разделить на сопротивление (в омах), и мы получи ток (в амперах). Если внешняя цепь не может обеспечить нужную силу тока, то при измерении мы увидим заниженный ток, а при измерении напряжения в рабочем режиме будет еще и падение напряжения. Опять же, причины тогда нужно искать во внешней цепи (проверять контакты, клеммы, различные места электрического соединения, прочие электрические элементы, что относятся к этой цепи).

Допустим вы убедились, что с внешней цепью все хорошо. Теперь значит нужно проверить саму обмотку того устройства, которое не работает должным образом. Прежде всего нужно проверить сопротивление катушки.

Далее следует измеренное сопротивление сравнить с тем, что может быть указано на внешней части этой катушки. Если сравнить нес чем, то можно посмотреть в справочных данных, которые относятся именно к вашему устройству. Ну, и совсем крайний вариант, это взять метр провода такого же диаметра (сечение именно медного провода, без изоляции) и измерить на нем сопротивление. После чего приблизительно прикинуть, сколько метров может содержать эта катушка и перемножить измеренное значение на приблизительный метраж вашей катушки. Опытные электрики обычно знают, у каких катушек может быть приблизительное сопротивление, это приходит с практикой.

В большинстве случаев у катушек обычно происходит обрыв. И тут при измерении сопротивление обмотки есть только два варианта, либо сопротивление есть, либо его нет (значит на обмотке есть обрыв, который нужно найти и восстановить). Гораздо реже бываю случаи короткозамкнутых витков. То есть, это когда в целом катушка, как бы исправна, и показывает более или менее нормальное сопротивление, а на деле у нее внутри замкнулись всего несколько витков (где-то повредилась изоляция и произошло короткое замыкание нескольких витков провода). Такие катушки будут работать ненормально. Они потребляют больше тока, будут сильнее греться, их эффективность снижается, а со временем вовсе могут выйти из строя. Искать короткозамкнутые витки задача проблематичная. Тут лучше взять новую, заведомо рабочую катушку, обмотку и заменить ее.

Если для нахождения постоянного тока подойдет обычная формула закона ома (чтобы по известному сопротивлению обмотки и подаваемому напряжению вычислить значение силы тока, протекающего через эту обмотку), то для переменного тока формула будет уже иметь следующий вид:

P.S. С опытом приходит знание. Так опытный электрик скорее всего не будет проделывать ряд лишних операций, при нахождении той или иной поломки. Обычно по некоторым характерным признакам можно уже с большой уверенностью сказать, где именно нужно искать неисправность в нерабочем электрооборудовании. Так же как и приблизительное определение сопротивления обмотки, которое не обязательно измерять, а достаточно увидеть размеры этого катушки и сечение провода.

В предыдущем параграфе мы выяснили, что
требуется время, чтобы ток в катушке
индуктивности вырос или уменьшился.
Индуктивность в цепи играет роль как
бы электрической инерции. Рассмотрим
цепь (рис.31), состоящую из источника тока

,
электрического сопротивления R
и катушки индуктивности L.

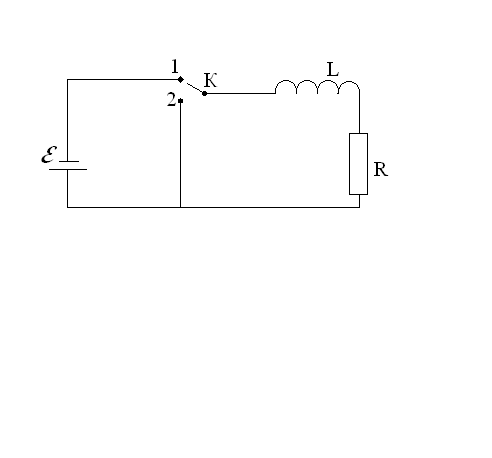
Рис.31. Индуктивность в цепи постоянного
тока.

При замыкании ключа в положение 1 в цепи,
наряду с эдс источника тока, появляется
эдс самоиндукции

и сила тока в цепи нарастает постепенно.
Если индуктивность в цепи отсутствует
(L=0), то сила тока I₀
при замыкании цепи мгновенно достигала
бы величины

.
При наличии индуктивности в цепи
мгновенное значение силы тока i
определим по закону Ома:

(2.23)

Разделив переменные, проинтегрируем
уравнение: (2.23)

,
в результате получим

. (2.24)

Таким образом, ток в цепи постепенно
увеличивается от нуля до

.
Нарастание тока происходит тем быстрее,
чем больше отношение R/L
, т.е. чем больше сопротивление цепи и
меньше её индуктивность (рис.34а).

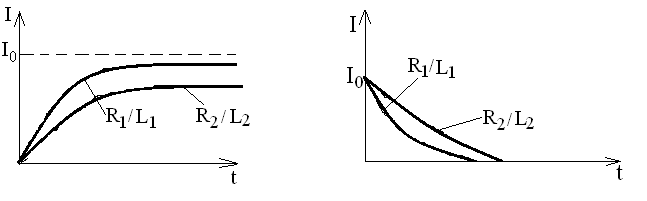
(а) (б)

Рис.32 Изменение силы тока в цепи

а) при замыкании цепи, б) при размыкании
цепи.

При отключении источника тока (ключ в
положение 2 рис.31) индуктивность L
остаётся замкнутой на сопротивление
R. Мгновенное значение
силы тока в такой цепи согласно закону
Ома, равно

. (2.25)

Пусть при t₀=0 ток в
цепи равен i=I₀.
Разделив переменные и проинтегрировав
уравнение (2.25), получим

. (2.26)

Как видно из уравнения (2.26) ток в цепи
постепенно убывает от начального
значения

до нуля. Величина тока уменьшается тем
быстрее, чем больше сопротивление цепи
R и чем меньше её индуктивность
L (рис. 32б).

§2.6. Взаимная индукция

Рассмотрим два близко расположенных
контура с токами I₁
и I₂ (рис.33).

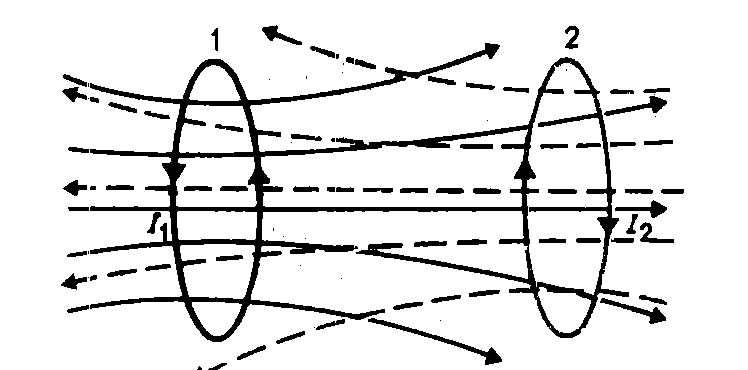
Рис.33

Эти контуры взаимосвязаны между собой
посредством магнитных потоков, создаваемых
токами I₁ и I₂.
Магнитный поток Ф₁₂ через контур
1, созданный контуром 2, пропорционален
току I₂:

Ф₁₂=L₁₂I₂
. (2.27)

В то же время контур 2 пронизывается
магнитным потоком Ф₂₁ , созданным
контуром 1, при этом

Ф₂₁=L₂₁I₁
. (2.28)

Коэффициенты L₁₂ и
L₂₁ называются
коэффициентами взаимной индукции и
имеют ту же размерность, что и индуктивность.
Величина L₁₂ и L₂₁
зависит от геометрической формы контуров
и их взаимного расположения. Покажем,
что для любых двух контуров коэффициенты
взаимной индукции всегда равны:

L₁₂=L₂₁.
(2.29)

Для этого предположим, что контур 1
выносится из магнитного поля контура
2, так, что Ф₁₂=0. Совершённая при
этом работа, согласно (1.25) равна

.
(2.30)

Если предположить, что контур 2 выносится
в область, где нет магнитного поля,
создаваемого контуром 1, то была бы
затрачена работа

.
(2.31)

Очевидно, работы А₁ и А₂
равны. Следовательно, L₁₂=L₂₁,
что и требовалось доказать.

§27. Энергия и плотность энергии магнитного поля

Возвращаемся к опытам, описанным на
стр.38 (рис.30), вспомним, что при внезапном
прерывании тока (при размыкании ключа
К) в цепи, содержащей индуктивность,
неоновая лампочка Л₃ даёт яркую
вспышку. Выясним, откуда берётся для
этого энергия. Вместе с возникновением
электрического тока создаётся магнитное
поле. С прекращением тока магнитное
поле исчезает. Для создания поля требуется
энергия, и это же количество энергии
переходит в другие виды энергии при
исчезновении магнитного поля. Таким
образом, в неоновой лампочке Л₃
(рис.32) возникает газовый разряд за счёт
энергии исчезающего магнитного поля,
созданного (локализованного) в катушке
индуктивности. Согласно закону сохранения
энергии, что энергия магнитного поля
создаётся за счёт работы источника
тока. Эта работа расходуется на нагревание
проводника и на создание постоянного
тока, с которым связано появление
магнитного поля в катушке индуктивности.

При возрастании тока в цепи, содержащей
индуктивность, возникает эдс самоиндукции,
противодействующая нарастанию тока.
По закону Ома сила тока I
в цепи равна

,
(2.32)

где

— эдс источники,

—
эдс самоиндукции, R-
сопротивление цепи.

Учитывая, что

,
перепишем уравнение (2.32) в следующем
виде:

.
Работа, совершаемая источником тока за
малый промежуток времени dt,
равна

,
(2.33)

где I²Rdt=dQ
–элементарное количество теплоты,
выделяемое в проводнике тепло, LIdt=dA
– работа, расходуемая на увеличение
силы тока от I до I+dI.
Таким образом, работа А, расходуемая на
создание постоянного тока запишется в
виде

.
(2.34)

Выражение

получило название собственной энергии
тока.

Изменение силы тока в цепи вызывает
изменение его магнитного поля. Поэтому
можно предположить, что собственная
энергия тока является энергией W_M
его магнитного поля W_M.

.
(2.35)

Таким образом, энергия W_M
магнитного поля равна работе, затраченной
источником тока на преодоление эдс
самоиндукции, пока ток увеличивается
от нуля до некоторого постоянного
значения I. Именно эта
энергия магнитного поля освобождается
в опыте (рис.32) в виде вспышки неоновой
лампы при размыкании цепи.

Рассмотрим однородное магнитное поле
длинного соленоида. Собственная энергия
тока или энергия магнитного поля
соленоида с учётом формул (1.17, 2.20, 2.35)
запишется как

,
(2.36)

где объём, занимаемый магнитным полем.

Из формулы (2.36) видно, что энергия
однородного магнитного поля пропорциональна
объёму V, занимаемого
полем. Поэтому энергия единицы объёма
поля или объёмная плотность энергии
магнитного поля для данной среды
пропорциональна квадрату магнитной
индукции:

. (2.37)

Сравнивая формулы (2.35) и (2.36) и находясь
в рамках постоянных токов и магнитных
полей, нельзя однозначно утверждать,
где локализована энергия магнитного
поля внутри проводника или в магнитном
поле, окружающем проводник с током.
Опыты с переменными во времени магнитными
полями показывают, что такие магнитные
поля могут существовать и распространяться
в пространстве без токов их поддерживающих.
Следовательно, энергия локализована в
магнитном поле.

В случае однородного магнитного поля
для расчёта энергии можно воспользоваться
формулой (2.36).

Энергию неоднородного магнитного поля
можно рассчитать, предварительно разбив
весь его объём на бесконечно малые
объёмы, содержащие энергию равную w_MdV,
и проинтегрировать по всему объёму:

. (2.38)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #