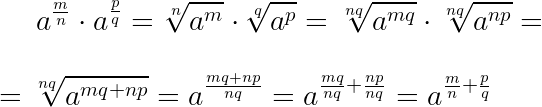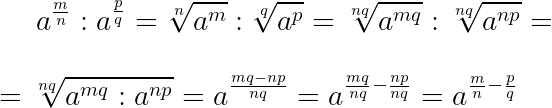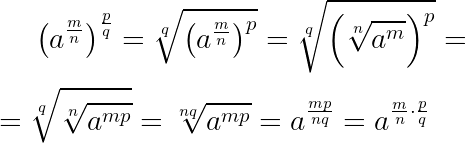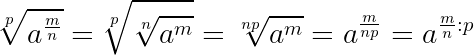Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Возведение дроби в степень
Поддержать сайт
Запомните!
При возведении в степень дроби нужно
возвести в степень и числитель, и знаменатель.
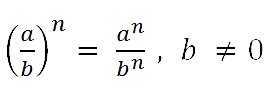
Данное свойство соответствует другой записи свойства № 5
«Степень частного», расмотренного на предыдущей странице.
Примеры возведения в степень дроби.
-
()2 =
=
=
Как возвести в степень смешанное число
Чтобы возвести в степень смешанное число, сначала избавляемся от целой
части, превращая смешанное число в неправильную дробь. После этого
возводим в степень и числитель, и знаменатель.
Пример.
Формулу возведения в степень дроби применяют как
слева направо, так и справа налево, то есть, чтобы
разделить друг на друга степени
одинаковыми показателями, можно разделить одно основание на другое,
а показатель степени оставить неизменным.
- Пример. Найти значение выражения рациональным способом.
На нашем сайте вы также можете проверить свои вычисления и
возвести число в степень онлайн.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Понятие степени
Представления о степени сложились ещё во времена существования Древнего Египта. Впервые упоминание о её вычислении встречается в знаменитом учебнике по математике Диофанта Александрийского «Арифметика». В своих трудах он описывает понятие как некоторое количество единиц, из которых состоят любые числа, увеличивающиеся до бесконечности. Он выделяет:
- квадраты, образующиеся при произведении чисел или цифр самих на себя;
- кубы, получающиеся при умножении квадрата на сторону;
- биквадраты, произведение квадрата на квадрат;
- квадрато-кубы, возникающие при умножении квадратов на кубы;
- бикубы, произведение кубов на самих себя.
Французский учёный Никола Шюке дополнил этот степенной ряд, введя отрицательный параметр. Современное же обозначение степени предложил Рене Декарт. В «Геометрии» он использовал верхний надстрочный знак для указания величины степени. Что интересно, квадрат математик продолжал обозначать как произведение чисел, то есть в виде n * n. И только потом Лейбниц настоял на универсальной записи для любого возведения в степень.
Под операцией возведения понимается бинарное действие, определяемое в результате умножения числа на себя. То есть справедлива следующая запись: di = d * d* d *… * dk, где k — число, обозначающее количество перемножаемых чисел, равное n. Например, 112 = 11 * 11 = 121. Степень, присущая числу, может быть отрицательной, рациональной, десятичной, вещественной и даже комплексной. Фактически получается, что для того, чтобы посчитать степень числа, его нужно умножить на себя столько раз, сколько указано в степенном показателе.
Но при этом существует нюанс возведения в нулевую степень. Любое число, вне зависимости от вида, в нулевой степени даст единицу. Например, (2/32)0 = 1, -1420 = 1. Выражение же ноль в нулевой степени не имеет смысла, поэтому ответ считается неопределённым.
Правило возведения дроби
В основе правила возведения дроби в степень лежит её определение с дробным показателем. Согласно ему, для решения задачи нужно отдельно возвести сначала числитель выражения, а затем знаменатель, не меняя занимаемые ими позиции. Например, дробь три шестых во второй степени будет равна: (3/6)2 = 9/36. Используя свойства сокращения дробей, числитель и знаменатель можно разделить на девять. В итоге получится равенство: (3/6)2 = 1/4.
Доказать это правило можно выполнив элементарные алгебраические действия. Для рассмотренного примера, согласно правилу арифметики, сначала необходимо выполнить деление, а после возведение в степень. Так, три разделить на шесть будет равно: 3/6 = 1/2 = 0,5. Затем полученное число следует возвести в квадрат: 0,52 = 0,5 * 0,5 = 0,25. Найденный ответ можно переписать в виде дроби 1/4, которая при сравнении полностью совпадает с ранее вычисленной.
Утверждение справедливо для любого вида дроби с произвольной степенной функцией. Например, (11 / 14)3. Используя закон, можно записать следующее: (11 / 14)3 = 113 / 143 = (11 * 11 * 11) / (14 * 14 * 14) = 1331 / 2744. Эту дробь сократить, то есть упростить, нельзя. Если нужно получить численное значение, то следует просто разделить числитель на знаменатель: 1331 : 2744 = 0,485.
Чтобы убедиться в истинности правила, можно и тут выполнить проверку. Дробь три разделить на пять в степени три можно решить, выполнив сначала деление, а после полученное число возвести в кубическую степень: (11 / 14)3 = (0,78)3 = 0,78 * 0,78 * 0,78 = 0,485. Ответ идентичен предыдущему, что и следовало доказать.
Таким образом, алгоритм возведения будет следующим:
- Выполнить арифметические действия в скобках, соблюдая первоочерёдность знаков.
- Упростить полученное выражение, которое необходимо возвести в степень.
- Числитель умножить на себя столько раз, сколько показывает определитель.
- Значение, стоящее в знаменателе, умножить на такое количество раз само на себя, которое показывает степень.
- Полученную дробь упростить или выполнить деление.
Если показатель степени небольшой, то возведение можно выполнить просто умножив дробь на саму себя необходимое число раз. Например, (2/32)3 = (2/32) * (2/32) *(2/32) = 1/4096. Алгоритм обыкновенного расчёта обычно не вызывает трудности, но часто приходиться иметь дело не только с обыкновенными дробями. При этом степень может быть даже отрицательной.
Но в любом случае нужно помнить, что если верхнюю и нижнюю часть дроби умножить или разделить на одно и то же число, то количественный показатель полученного выражения не изменится. Это важно, так как при возведении приходится часто выполнять преобразования.
Нулевая и отрицательная степень
При вычислении дроби, в показателе которой стоит ноль, исходят из свойств частного степеней с одинаковым основанием.
Так, согласно алгебраическим правилам, для простых чисел a и b, при условии, что a < b, справедливо выражение: ca / cb = ca — b. Тут нужно отметить, что основание не должно быть равным нулю, иначе получится недопустимое деление на ноль. Если a = b, то равенство можно переписать в виде: ca / cb = ca — a = c0. Так как c другой стороны частное ca / сa = 1, то можно утверждать, что с0 = 1.
Для нулевой степени такой подход использовать будет некорректно. При основании, которое равно нулю, применяя предыдущее равенство, можно записать, что ноль в степени a умноженный на ноль в степени ноль, равняется нулю с показателем a. То есть выражение может быт переписано как 0 = 0. Оно будет правильным при любом натуральном показателе, при этом не будет зависеть от того, чему равно выражение 00.
Ответ на 00 может быть любым. Поэтому для избежания путаницы считают, что решение записи 00 не имеет смысла, так же как и деление на ноль. Например, (12 / 34)0 = 120 / 340 = 1 / 1 = 1 или (-3 / 4)0 = 1, а вот для (0 / 23)0 ответ будет не определён.
Чтобы знать, как возвести дробь в отрицательную степень, нужно вспомнить свойство произведения с равными основаниями: ca * cb = ca + b. Предположив, a = -b, при условии, что основание не равняется нулю, можно записать: c−a * ca = c-a+a = a0 = 1. Несложно сделать вывод о том, что положительный и отрицательный показатель взаимно обратный. Отсюда выходит, что если число нужно возвести в отрицательную степень, то его можно представить в виде дроби: c—a = 1 / ca.
Получается, что для минусового показателя ответ определяется дробью, при условии, что основание отлично от нуля и показатель — натуральное число. Фактически необходимо перевернуть дробь и возвести её по правилу, при этом знак показателя изменить на положительный. Например, (23 / 37)-2 = 1 / (11 / 37)2 = (37 / 22)2 или (1 / 5)-2 = (5 / 1)2 = 52 = 25.
Рациональный показатель
В состав рациональных чисел входят все целые и дробные значения. По сути, ими называют значения, которые можно представить в виде обыкновенной или отрицательной дроби, как цифру ноль. При этом в числителе находится целое число, а в знаменателе – натуральное. Для того чтобы определить степень, нужно выяснить, что же представляет собой число с показателем в дробной форме.
Пусть имеется число n, которое необходимо возвести в степень a / b. Необходимо будет извлечь корень из n. Чтобы выражение соответствовало таблицам степени, должна выполняться формула: n(a / b) * b = na * b / b = na.
Используя полученное выражение, логично предположить, что ca / b = a√cb, но это лишь справедливо, когда показатель степени целый. Можно сделать вывод о том, что если выражение a√cb справедливо, что степенью числа c дробным показателем b / a является корень из c в степени b.
Если принять, что основание больше либо равно нулю, когда b является положительным числом, то буде справедливым равенство: сa / b = a√cb. При этом можно утверждать, что если основание будет равным нулю, то ответом будет тоже ноль: 0a / b = a√0b = 0.
Тут нужно оговориться, что для некоторых одночленов приведённое правило не работает. Например, для 3√ (-12 /3)2 или 4√ -122 оно верное, а для (-1 / 3)-2 / 3 или (-3 / 2)2 / 5 не имеет смысла, так как основание не может быть отрицательным. Поэтому вводится условие, по которому выражение a√ cb имеет смысл, при любых значениях неотрицательного основания.
Что же касается минусовой величины в показателе корней, оно в основании должно отличаться от нуля. Иными словами, если в любом уравнении или равенстве выражение a / b нельзя упростить (сократить), то a * i / b * I = ca — i / b —, причём степень можно заменить на ca / b.
Примеры решения
Для того чтобы понять и усвоить теорию, нужно попрактиковаться. Начинать необходимо с простых заданий, постепенно переходя к более сложным примерам. Возвести дробь в степень можно и на онлайн-калькуляторах, но желательно уметь выполнять это действие самостоятельно. Из наиболее типичных примеров, охватывающих все возможные ситуации, можно выделить следующие:
- Возведение дроби с простым показателем. Пусть дан многочлен (11 / 21)2 + (9 / 10)3 , необходимо вычислить ответ. Согласно правилу, сначала следует убрать скобки, а после выполнить сложение. Решение задания будет следующим: ( 11 * 11 ) / (21 * 21 ) + ( 9 * 9 * 9 ) / ( 10 * 10 * 10) = 121 / 441 + 729 / 100 = (121 * 1000) / (441 * 1000) + (729 * 441) / (1000 * 441) = 442489/441000.
- Решение смешанной дроби с отрицательным показателем. Определить ответ в задании вида: (2 11/12)-1 = ((2 * 12 + 11) / 12)-1 = (35 / 12)-1 = (12 / 35 )1 = 12 1 / 351 =12 / 35.
- Многоэтажные дроби . Решать их нужно после выполнения упрощения. Так, выражение вида 5 * (2 / 4) * (7 / 11 / 2))-2, решается следующим образом: 5 * (2 / 4 * (7 / 11 / 2))-2 = (((2 * 6 / 10 * 3)) / 3)-2 = (2 / 15)-2 = (15 / 2)2 = 152 / 22 = 225 / 4 = 56 1/4.
- Вычисление сложных уравнений. Определить верность выражения: (16 / 11)0 – (2 /
-1 + 4 *(-3 / 2)1/2 > e-3. Сначала следует раскрыть все скобки, а уже после выполнить алгебраические операции: (16 / 11 )0 – (2 /
-1 + 4 *(-3 / 2)2 = 1 – 8 / 2 + 4 * (9 / 4) = 1 – 4 + (-3 * (-3 ) ) / (4 * 4) = -3 + 9/16 = 9/16 – 3/1 = (9 * 1) / (16 * 1)) – (3 * 16) / (1 * 16) = 9 /16 – 48 /16 = (9 -48) / 16 = — 39 / 16 = — 2,43. Так как буквой e обозначают экспоненту, то e—3 = 2,718-3 = 0,049. Отсюда можно сделать вывод, что знак в неравенстве неверный: -2,43 < 0,049
Таким образом, чтобы возвести в степень дробь необходимо знать: правило, свойства степеней, порядок выполнения арифметических операций. А также учитывать знак показателя и вид основания.
Расчёт на онлайн-калькуляторе
В сети существуют сервисы, автоматически выполняющие арифметические операции. Воспользоваться этими сайтами может каждый, имеющий доступ к интернету. Порталы предлагают свои услуги бесплатно. С их помощью можно находить функции, рассчитывать градусы и углы, решать уравнения и неравенства, вычислять дроби и степени.
Для решения дробей со степенями на онлайн-калькуляторах не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — вести в предложенную форму задание и нажать кнопку «Рассчитать». Весь процесс вычисления занимает несколько секунд.
Полезной особенностью таких сайтов является и возможность обучиться правилам расчёта, узнать, как должны обозначаться те или иные операции и действия. Из различных калькуляторов можно выделить три наиболее популярных:
- Webmath.
- Onlinemschool.
- Сalc.by.
Сайты отличаются удобным и понятным интерфейсом. На их страницах содержится кратко изложенная теория, использующаяся для расчётов и типовые примеры.

Какими свойствами обладает степень с дробным показателем (дробная степень)?
Как выполнить возведение числа в дробную степень?
Степенью числа a (где a>0) с рациональным показателем, который равен (n/m) называется число вида: , где где m — целое число, n — натуральное число (n>1).
Таким образом, число с дробным показателем степени равно корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю.
При этом a<0 степень с дробным показателем не определяется.
Чтобы извлечь корень из степени, надо показатель степени разделить на показатель корня.
Следовательно, если показатель степени не делится на показатель корня, то получается дробная степень.
Свойства степеней с дробным показателем
Все свойства степеней из курса алгебры 7 класса выполняются и для степеней с дробными показателями.
Для упрощения вычислений при возведении числа в дробную степень удобно использовать следующее свойство корня:
Чтобы было легче решать вычислять степени с дробным показателем:
Следует обратить внимание, что основание не может быть отрицательным числом, а показатель степени может быть как положительным, так и отрицательным.
Действия над степенями с дробными показателями
Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для степеней с целым показателем.
При умножении дробных степеней с одинаковыми основаниями их показатели складываются:
При делении дробных степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя:
Чтобы возвести степень в другую степень, в случае дробных показателей, достаточно перемножить показатели степеней:
Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня:
Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.
Как посчитать дробную степень
Операции возведения числа в степень и извлечения из него корня — противоположные друг другу математические действия. Однако они могут быть совмещены в одной записи, если показатель степени числа представить в формате обыкновенной или десятичной дроби. При осуществлении записанной таким способом операции придется проделать последовательно оба этих математических действия.

Инструкция
Если в исходных условиях степень дана в формате обыкновенной дроби, то операцию нужно производить в два шага. Последовательность их на полученном результате никак не скажется — начните, например, с извлечения из числа корня той степени, которая указана в знаменателе дроби. К примеру, чтобы возвести в степень ⅔ число 64 на этом шаге из него надо извлечь кубический корень: 64^⅔ = (³√64)² = 4².
Возведите полученное на первом шаге значение в степень, равную числу, стоящему в числителе дроби. Результат этой операции и будет результатом возведения числа в дробную степень. Для примера из предыдущего шага полностью описанный ход вычислений можно записать так: 64^⅔ = (³√64)² = 4² = 16.
Исходите из простоты расчетов при определении последовательности описанных выше операций извлечения корня и возведения в степень. Например, если бы требовалось в ту же самую степень ⅔ возвести число 8, то начинать с извлечения кубического корня из восьмерки было бы нецелесообразно, так как результат был бы дробным числом. В этом случае лучше начать с возведения 8 в квадрат, а затем извлечь корень третьей степени из 64 и таким образом обойтись без дробных промежуточных значений: 8^⅔ = ³√(8²) = ³√64 = 4.
Если показатель степени в исходных данных приведен в формате десятичной дроби, то начните с преобразования его в обыкновенную дробь, а затем действуйте по описанному выше алгоритму. Например, для возведения числа в степень 0,75 трансформируйте этот показатель в обыкновенную дробь ¾, затем извлеките корень четвертой степени и возведите полученный результат в куб.
Используйте любой калькулятор, если ход вычислений значения не имеет, а важен лишь результат. Это может быть и скрипт, встроенный в поисковик Google — с его помощью найти нужное значение даже проще, чем с использованием стандартного калькулятора ОС Windows. Например, для возведения числа 15 в степень ⅗ перейдите на главную страницу сайта и введите в поле поискового запроса 15^(3/5). Результат вычислений с точностью до 8 знаков Google отобразит даже без нажатия кнопки отправки запроса: 15^(3 / 5) = 5,07755639.
Источники:
- как возводить в дробную степень
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Из статьи вы узнаете, как возвести число в дробную степень, что для этого нужно понимать и уметь. Приведены поучительные примеры с дробными степенями.
Как возводить в дробную степень
Как возвести число в натуральную степень, легко усваивают почти все учащиеся. Достаточно помножить его само на себя столько раз, сколько указано в показателе степени. Например, запись 23 означает, что число 2 нужно умножить само на себя три раза, а запись (1,4)5 значит (1,4)5=1,4*1,4*1,4*1,4*1,4.
А вот запись типа 35/6 для многих совершенно не понятна. Возникает конфликт восприятия ранее усвоенного понимания возведения числа в степень со здравым смыслом, ведь написать число помноженным само на себя 5/6 раз, просто невозможно.
Подобный вопрос возникает у тех, кто не усвоил тему извлечения из чисел корня.
Напомним, что извлечение корня из числа, это математическая операция обратная операции возведения его в степень. Она подразумевает разложение его на одинаковые множители, число которых равно показателю корня. В частности, 3√8 равно 2, ведь, как видно из приведённого ранее примера 23 = 2*2*2 = 8.
Некоторые, при изучении извлечения корня из числа упускают один факт. Корень записывается не только в виде q√a (где a некоторое число, а q – показатель корня) он может быть записан и в виде a1/q. Надеюсь, теперь смысл дробной степени вам становится ясен. q в знаменателе дроби, это и есть корень. В числителе стоит та степень, в которую указанное число нужно возвести. В данном случае она равна одному (p=1). Если бы она была равна двум (p=2), то следовало бы записать a1/q *a1/q. Эта запись равносильна a2/q. Если бы она равнялась трём (p=3), т. е. 3/q √a, то вышло бы a1/q*a1/q*a1/q.
Теперь обобщим всё выше сказанное.
ap/q = q√ap. При этом a ≥ 0, p>0 и q>1.
Если в дробную степень требуется возвести неправильную либо десятичную дробь, сначала они приводятся к виду обычной дроби, чтобы ясно стали видны числитель и знаменатель, т. е. показатели корня и степени.
О свойствах дробных степеней
Приведём самые главные свойства дробных степеней, которые чаще всего приходится использовать в вычислениях.
- [a^{p}* a^{q}=a^{p+q}]
- [a^{p} / a^{q}=a^{p-q}]
- [left(a^{p}right)^{q}=a^{p^{*} q}]
- [left(a^{*} bright)^{p}=a^{p} b^{p}]
- [(a / b)^{p}=a^{p} / b^{p}]
Из свойства 3 следует, что [left(a^{p / q}right)^{b}=a^{left(p^{*} bright) / q}]
Нет времени решать самому?
Наши эксперты помогут!
Примеры возведения в дробную степень
[81^{1 / 4}=sqrt[4]{81}=3]
[135^{9 / 10}={ }^{10} sqrt{135^{9}}]. Извлекать корень и возводить в степень не имеет смысла т. к. число
получится очень сложным, а указанная запись наиболее простая.
[left.[1(3 / 5)]^{1 / 3}=(8 / 5)^{1 / 3}={ }^{3} sqrt{(8 / 5)^{1}}={ }^{3} sqrt{(} 2^{3} / 5right)=2 /
sqrt{5} 3]. Здесь, для упрощения выражения, мы выполнили действие вынесения из-под знака корня числа 2.
Зачем нужны числа в дробной степени
Решение дробных степеней проще, чем вычисление корней. Оно занимает меньше шагов и, при наличии определённого навыка и меньше усилий. Так считают все, кто занимается математикой.



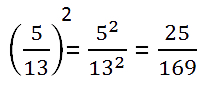
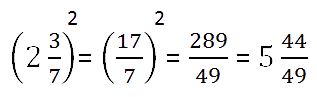
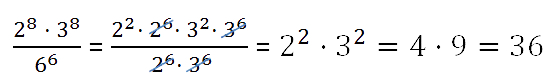





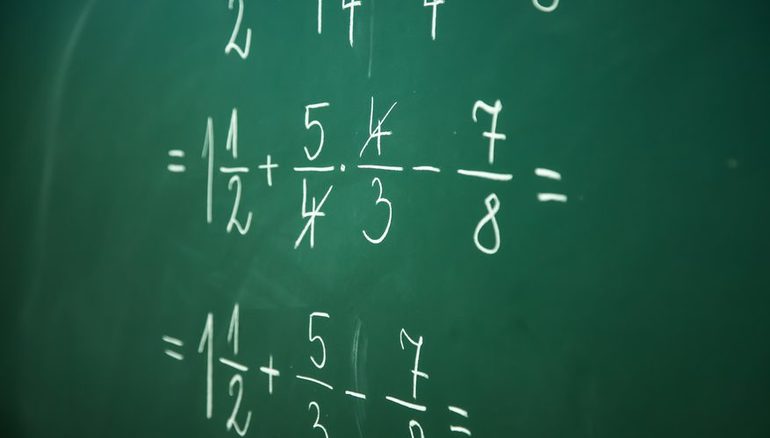

 -1 + 4 *(-3 / 2)1/2 > e-3. Сначала следует раскрыть все скобки, а уже после выполнить алгебраические операции: (16 / 11 )0 – (2 /
-1 + 4 *(-3 / 2)1/2 > e-3. Сначала следует раскрыть все скобки, а уже после выполнить алгебраические операции: (16 / 11 )0 – (2 /