Содержание:
Напомним, что каждое рациональное число можно записать в виде дроби
Определение. Пусть 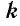
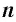
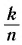
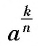
Таким образом,
Степень с рациональным показателем определяется и для основания, равного нулю (а = 0), но только тогда, когда показатель положительный.
Примеры преобразования степеней с рациональными показателями
Приведем несколько примеров преобразования степеней с рациональными показателями:
Выражения 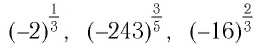
Поскольку рациональное число представимо в виде дроби неоднозначно, то возникает вопрос: не зависит ли определение степени с рациональным показателем от вида этой дроби? Например, верно ли равенство
На этот вопрос отвечает следующая теорема.
Теорема:
Для любого положительного значения 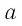
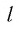
Доказательство:
Преобразуем правую часть этого равенства, используя определение степени c. рациональным показателем, а также свойства степеней и корней:
Возникает вопрос: если, например, вычислить 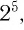
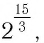
На этот вопрос отвечает следующая теорема.
Теорема:
Для любого положительного значения а при любом натуральном 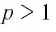
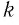
Доказательство:
Преобразуем левую часть этого равенства, пользуясь определением степени с рациональным показателем, а также свойствами степеней и корней:
Действия со степенями с рациональными показателями
Для положительных оснований все действия со степенями с рациональными показателями обладают теми же свойствами, что и действия со степенями с целыми показателями.
Теорема:
Для любых положительных значений 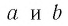
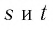
Доказательство:
Пусть
Докажем равенство (1). Преобразуем его левую часть:
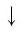
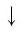



Доказательство остальных равенств аналогично доказательству равенства (1). ▲
Замечание 1. Согласно теореме 2 из п. 1.8 доказанные в этом пункте утверждения верны и в случае, когда одно из чисел 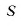
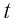
Замечание 2. Равенства (1)—(5) являются тождествами, поскольку каждое из них превращается в верное числовое равенство при любых значениях переменных, при которых входящие в это равенство выражения имеют смысл.
Следствие:
Для любых положительных значений 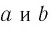
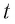
▲ Докажите эти равенства самостоятельно, используя равенства (2) и (5). ▲
Пример №1
Найти значение выражения
Решение:
Выполним преобразования:
При 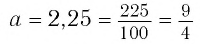
Ответ:
Пример №2
Пусть 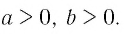
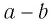
а) квадратов; б)* кубов; в) четвертых степеней.
Решение:
Пример №3
Сократить дробь
Решение:
Ответ:
Пример №4
Найти значение выражения
Решение:
Ответ:
Сравнение степеней с рациональными показателями
Теорема:
Пусть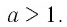
- если
— положительное рациональное число, то
- если
— рациональные числа и
Доказательство:
Докажем утверждение 1). Положительное рациональное число 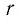
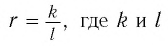
По условию 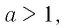
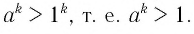
Еще раз воспользовавшись свойством степеней с натуральными показателями, получим
Утверждение 2) доказывается аналогично.
Теорема:
Пусть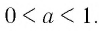
- если
— положительное рациональное число, то
- если
— рациональные числа и
Доказательство этой теоремы аналогично доказательству теоремы 1.
Пример №5
Сравнить значения выражений:
Решение:
а) Основание степеней 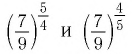
положительно и меньше 1, при этом показатель — больше показателя 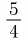
б)Для основания степеней и их показателей соответственно верны неравенства
В этом случае большему значению показателя соответствует меньшее значение степени. Поэтому имеем
в) Для основания степеней и их показателей соответственно верны неравенства
В этом случае большему значению показателя соответствует большее значение степени. Поэтому имеем
Пример №6
Сравнить 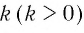
Решение:
а) Поскольку для показателей степеней верно неравенство 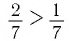
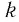
б) Поскольку для показателей степени верно неравенство 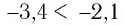
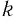
в) Поскольку для показателей степеней верно неравенство 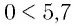
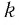
Ответ:
Степенная функция (показатель положительный)
В предыдущих классах мы изучали функции 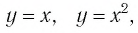
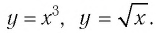
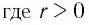
Такая функция называется степенной.
Рассмотрим степенные функции с различными положительными показателями.
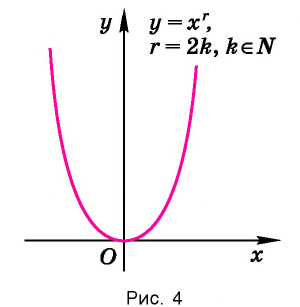
Функция y=xr где r=2k, k∈N
1. Функция
Естественная область определения выражения 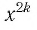
Назовем свойства функции 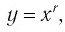
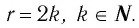
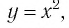
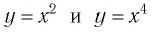
Теорема (о свойствах функции 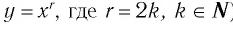
- Областью определения функции является множество R всех действительных чисел.
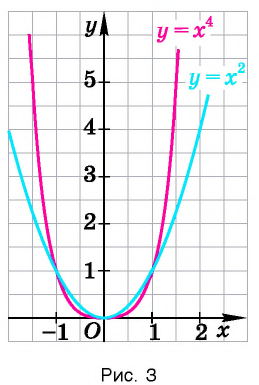
- Множеством (областью) значений функции является промежуток
- Значение функции, равное нулю (у = 0), является наименьшим, а наибольшего значения функция не имеет.
- График функции имеет с осями координат единственную точку пересечения (0; 0) — начало координат.
- Значение аргумента, равное нулю (х = 0), является нулем функции.
- Функция принимает положительные значения (у > 0) на множестве
т. е. все точки графика, кроме начала координат, лежат выше оси Ох, в I и II координатных углах.
- Функция четная; график функции симметричен относительно оси ординат.
- Функция убывающая на промежутке
и возрастающая на промежутке
- Функция не является периодической.
Убедитесь в справедливости этих свойств, используя схематичное изображение графика функции 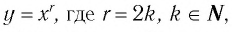
Замечание. Если 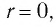
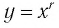
Естественная область определения выражения 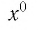
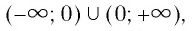
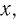
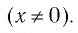
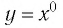
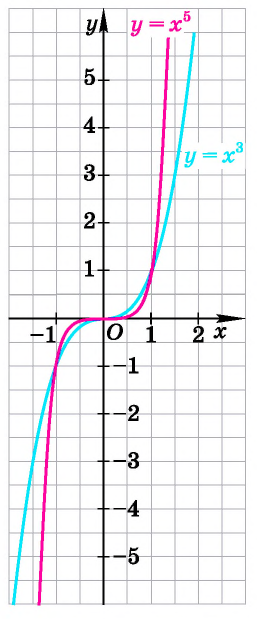
Функция y=xr где r=2k+1, k∈N
2. Функция 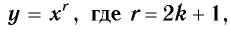
Естественная область определения выражения 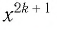
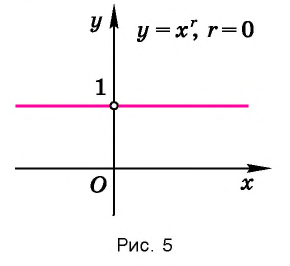
Всех действительных чисел. Оно и является областью определения функции
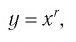
Назовем свойства функции 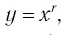
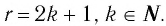
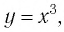
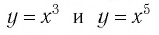
Теорема (о свойствах функции 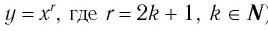
- Областью определения функции является множество R всех действительных чисел.
- Множеством (областью) значений функции является множество R всех действительных чисел.
- Функция наименьшего и наибольшего значений не имеет.
- График функции пересекает оси координат в единственной точке (0; 0) — начале координат.
- Значение аргумента, равное нулю (х = 0), является нулем функции.
- Функция принимает отрицательные значения (у < 0) на промежутке
и положительные значения (у > 0) на промежутке
т. е. график функции расположен в I и III координатных углах.
- Функция нечетная; график функции симметричен относительно начала координат.
- Функция возрастающая на области определения.
- Функция не является периодической.
Убедитесь в справедливости этих свойств, используя схематичное изображение графика функции 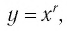
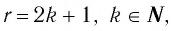
Пример №7
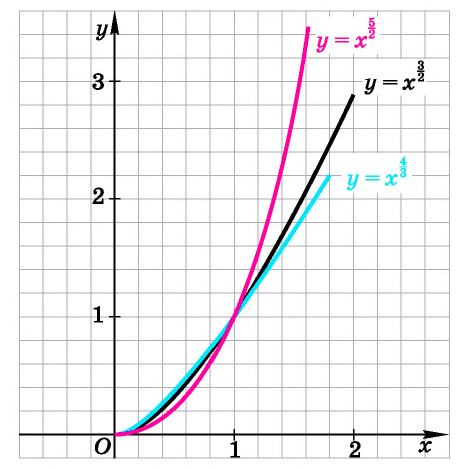
Сравнив схематичные изображения графиков функций 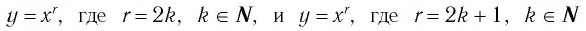
а) возрастают;
б) имеют значения разных знаков;
в) убывают;
г) принимают неотрицательные значения;
д) принимают положительные значения;
е) принимают равные значения.
Ответ:
Замечание. Если 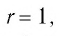
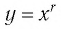
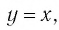
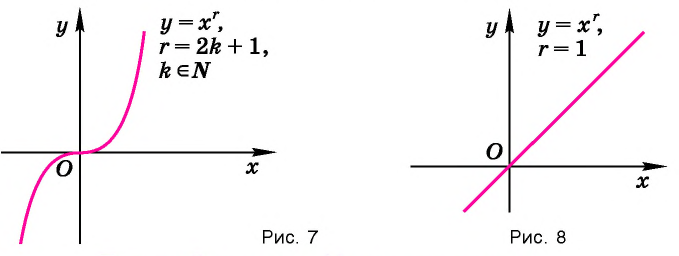
Функция y=xr, где r- рациональное нецелое число больше 1, r ∈ Q, r ∉ Z, r > 1
3. Функция 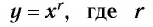
Область определения этой функции — промежуток 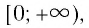
Назовем свойства этой функции. Для сравнения графики функций 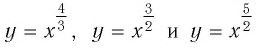
Теорема (о свойствах функции 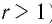
- Областью определения функции является множество
- Множеством (областью) значений функции является множество
- Значение функции, равное нулю
является наименьшим, а наибольшего значения функция не имеет.
- График функции имеет с осями координат единственную общую точку (0; 0) — начало координат.
- Значение аргумента, равное нулю (х = 0), является нулем функции.
- Функция принимает положительные значения (у > 0) на промежутке
т. е. график функции расположен в I координатном угле.
- Функция не является ни четной, ни нечетной.
- Функция возрастающая на области определения.
- Функция не является периодической.
Убедитесь в справедливости этих свойств, используя схематичное изображение графика функции 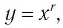
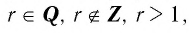
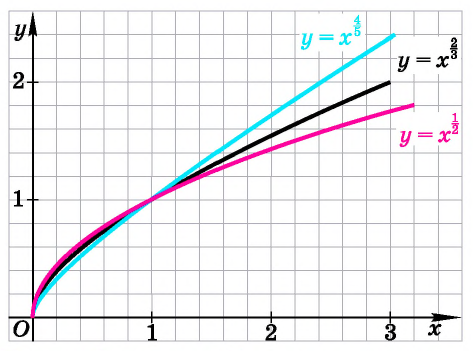
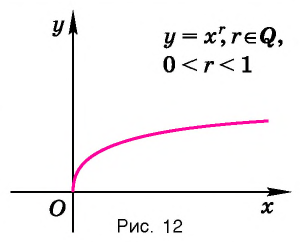
Функция y=xr, где r- рациональное положительное число меньше 1
4. Функция 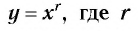
Область определения этой функции — промежуток 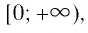
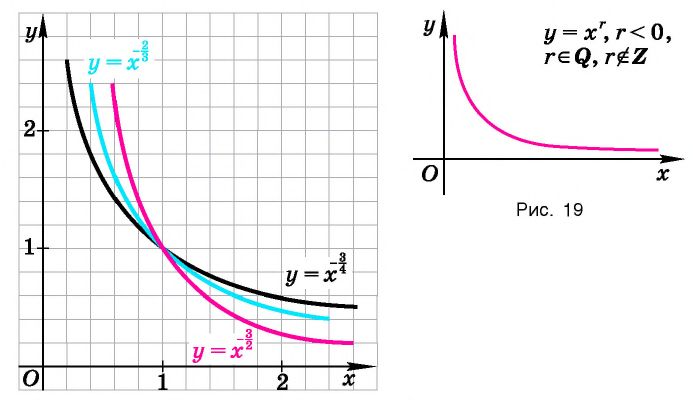
Для сравнения графики функций 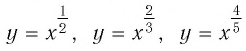
Свойства функции
где 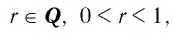
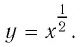
Подчеркнем, что функция 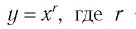
- Заказать решение задач по высшей математике
Пример №8
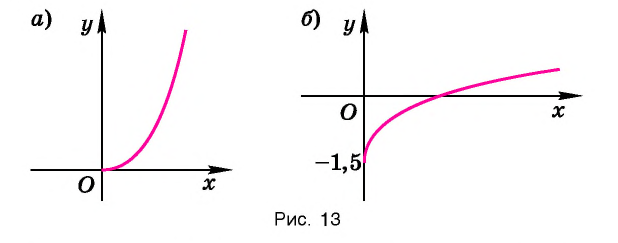
Изобразить (схематично) график функции:
Решение:
а) На рисунке 13, 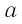
б) На рисунке 13, б схематично изображен график функции
1. Сформулируйте свойства функции
2. Сформулируйте свойства функции
3. Сформулируйте свойства функции 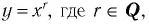
4. Изобразите схематично график функции 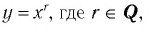
5. Что можно сказать об особенностях графика:
а) четной функции;
б) нечетной функции;
в) периодической функции?
6. Что можно сказать об особенностях области определения:
а) четной функции;
б) нечетной функции;
в) периодической функции?
Степенная функция (показатель отрицательный)
Вы изучали функцию 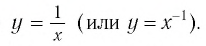
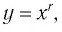
Рассмотрим еще несколько случаев степенной функции с отрицательным показателем:
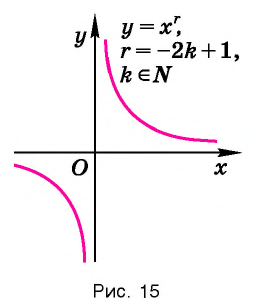
Функция y=xr, где r=-2k+1, k∈N
1. Функция
Естественная область определения выражения 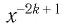
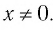
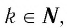
Назовем свойства функции 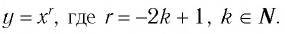
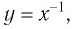
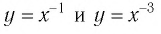
Теорема (о свойствах функции 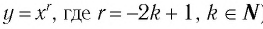
- Областью определения функции является множество всех действительных чисел, кроме нуля, т. е.
- Множеством (областью) значений функции является множество всех действительных чисел, кроме нуля, т. е.
- Наименьшего и наибольшего значений функция не имеет.
- График функции не пересекает координатных осей.
- Функция не имеет нулей.
- Функция принимает отрицательные значения (у < 0) на промежутке
и принимает положительные значения (у > 0) на промежутке
т.е. график функции расположен в I и III координатных углах.
- Функция нечетная; график функции симметричен относительно начала координат.
- Функция является убывающей на промежутке
и убывающей на промежутке
- Функция не является периодической.
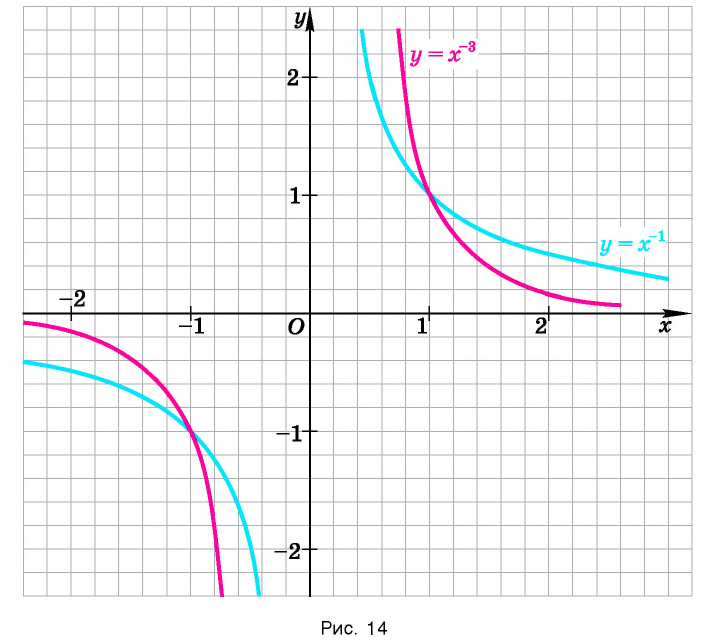
В справедливости этих свойств убедитесь, используя схематичное изображение графика функции 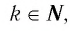
Заметим, что утверждение функция 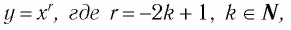
Функция y=xr, где r=-2k, k∈N
2. Функция
Естественная область определения выражения 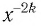
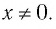
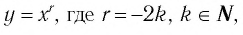
Назовем свойства функции 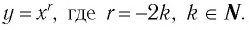
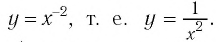
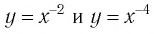
Теорема (о свойствах функции 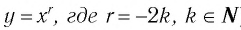
1. Областью определения функции является множество всех действительных чисел, кроме нуля, т. е.
2. Множеством (областью) значений функции является промежуток
3. Наименьшего и наибольшего значений функция не имеет.
4. График функции не пересекает координатных осей.
5. Функция не имеет нулей.
6. Функция принимает положительные значения (у > 0) на всей области определения 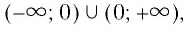
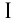
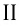
7. Функция четная; график функции симметричен относительно оси ординат.
8. Функция возрастающая на промежутке 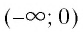
9. Функция не является периодической.
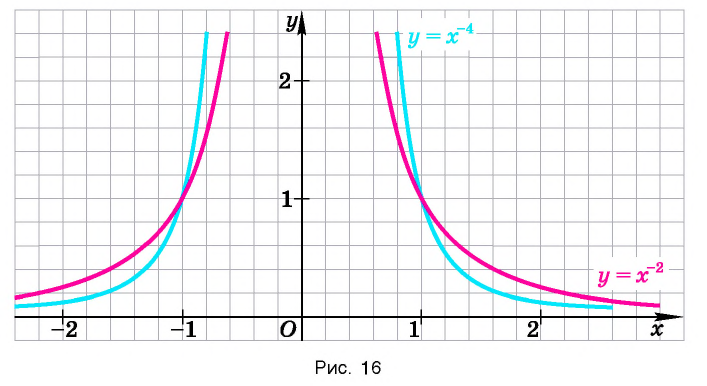
Убедитесь в справедливости свойств, используя схематичное изображение графика функции 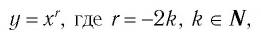
Пример №9
Сравнив изображения графиков функций 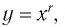
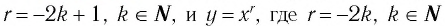
а) возрастают;
б) имеют значения разных знаков;
в) убывают;
г) принимают положительные значения;
д) принимают равные значения.
Ответ:
Функция y=xr, где r — отрицательное рациональное нецелое число
3. Функция 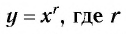
Область определения этой функции — промежуток 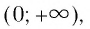
Для сравнения графики функций 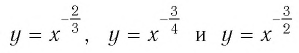
Свойства функции 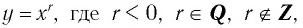
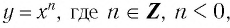
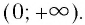
Вычисление степеней с рациональным показателем
Допустим, что равенство 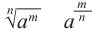
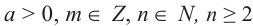
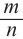
Определение: Если 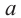
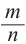
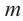
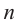
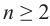
Пример:
Т.к 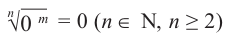
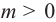
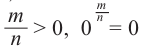
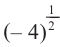
Свойства степени с рациональным показателем
Известные нам свойства степени с целым показателем справедливы и для степеней с любым рациональным показателем при положительном действительном основании.
Здесь 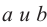
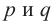
Докажите, что 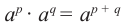
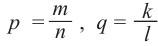
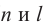
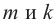
Остальные свойства доказываются аналогичным способом.
Пример: Выразите переменную 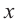
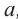
- Степень с действительным показателем
- Логарифм — формулы, свойства и примеры
- Корень из числа — нахождение и вычисление
- Теория множеств — виды, операции и примеры
- Действия с корнями нечетной степени
- Действия с корнями четной степени
- Бесконечно убывающая геометрическая прогрессия
- Периодические дроби
Мы уже знакомы с понятием степени с ЦЕЛЫМ показателем, когда в степени стоит целое число (n). Давайте разберемся, что такое степень с РАЦИОНАЛЬНЫМ показателем, когда в степени обыкновенная дробь — (a^{frac{p}{q}}).
Рациональный показатель – это выражение вида (frac{p}{q}), где (p)-некоторое целое число, а (q) – натуральное число, причем (qge2). Это строгое определение рационального показателя, но простыми словами мы будем изучать дробные степени, когда у вас в показателе стоит обыкновенная дробь.
Определение
Положительное число (a) в степени (frac{p}{q}) является арифметическим корнем степени (q) из числа (a) в степени (p):
$$ a^{frac{p}{q}}=sqrt[q]{a^p}. $$
Для того, чтобы научиться считать дробные степени, достаточно запомнить формулу из определения. Разберемся на примерах, как это работает, но нам понадобится хорошее знание арифметического корня n-й степени.
И обращаем ваше внимание, что
$$ sqrt[q]{a^p}=(sqrt[q]{a})^p,$$
Неважно в каком порядке – сначала извлечь корень и потом возвести в степень, или возвести в степень, а потом уже извлечь корень, от этого смысл выражения не теряется. Как удобнее, так и считайте. Рассмотрим несколько примеров:
Пример 1
$$ 8^{frac{2}{3}}=sqrt[3]{8^2}=(sqrt[3]{8})^2=2^2=4; $$
$$ 27^{frac{1}{3}}=sqrt[3]{27^1}=sqrt[3]{27}=3;$$
$$ 3^{frac{1}{5}}=sqrt[5]{3}; $$
$$ 7^{-frac{5}{6}}=sqrt[6]{7^{-5}}=sqrt[6]{frac{1}{7^5}}=frac{1}{sqrt[6]{7^{5}}};$$
Обратите внимание, что у обыкновенного квадратного корня двойка в показателе не пишется: пишем так (sqrt{a}), а имеем в виду (sqrt[2]{a}.)
$$ 7^{frac{1}{2}}=sqrt{7};$$
$$ 5^{frac{3}{2}}=sqrt{5^3}.$$
Пусть есть некоторое положительное число (a), целое число (p) и натуральное число (q), тогда справедливы следующие соотношения:
$$1.; a^{frac{p}{q}}=(a^{frac{1}{q}})^p,$$
$$2.; a^{frac{p}{q}}=a^{frac{p*k}{q*k}},$$
$$ 3.;a^p= a^{frac{pq}{q}}, $$
где (k) и (q) – натуральные числа большие 1.
Давайте попробуем их доказать:
Из определения степени с рациональным показателем следует, что:
$$ a^{frac{p}{q}}=sqrt[q]{a^p}=(sqrt[p]{a})^p=(a^{frac{1}{q}})^p,$$
Опять из определения и свойства корня n-й степени следует:
$$ a^{frac{p}{q}}=sqrt[q]{a^p}=sqrt[q*k]{a^{p*k}}= a^{frac{p*l}{q*k}}, $$
Третья формула на наш взгляд очевидна, просто сократить степень справа и получите исходное выражение.
Пример 2
$$8^{frac{4}{3}}=(8^{frac{1}{3}})^4=2^4=16;$$
$$4^{frac{15}{5}}=4^{frac{3}{1}}=4^3=64;$$
$$3^{-frac{6}{2}}=3^{-3}=frac{1}{3^3}=frac{1}{27}.$$
Свойства степени с рациональным показателем
Пусть (a) и (b) – некоторые положительные числа, а числа (frac{m}{n}) и (frac{c}{d}) – рациональные числа. Тогда выполняются соотношения:
$$ mathbf {1. ;a^{frac{m}{n}}*a^{frac{c}{d}}=a^{frac{m}{n}+frac{c}{d}}} $$
$$ 3^{frac{2}{5}}*3^{frac{8}{5}}=3^{frac{2}{5}+frac{8}{5}}=3^{frac{10}{5}}=3^2=9; $$
$$ 2^{frac{1}{3}}*4^{frac{4}{3}}=2^{frac{1}{3}}*(2^2)^{frac{4}{3}}=2^{frac{1}{3}}*2^{frac{8}{3}}=2^{frac{1}{3}+frac{8}{3}}=2^{frac{9}{3}}=2^3=8;$$
При умножении степеней с рациональным показателем и одинаковым основанием их показатели складываются.
$$mathbf {2. ; a^{frac{m}{n}}:a^{frac{c}{d}}=a^{frac{m}{n}-frac{c}{d}}}$$
$$ 5^{frac{8}{3}}:5^{frac{2}{3}}=5^{frac{8}{3}-frac{2}{3}}=5^{frac{6}{3}}=5^2=25;$$
При делении степеней с рациональным показателем и одинаковым основанием их показатели вычитаются.
$$mathbf {3. ; (a^{frac{m}{n}})^{frac{c}{d}}=a^{frac{m}{n}*frac{c}{d}}}$$
$$ (9^{frac{1}{3}})^{frac{3}{2}}=9^{frac{1}{3}*frac{3}{2}}=9^{frac{1}{2}}=sqrt[2]{9^1}=sqrt{9}=3;$$
При возведении степени с рациональным показателем в степень с рациональным показателем их показатели перемножаются.
$$mathbf {4. ; (a*b)^{frac{m}{n}}=a^{frac{m}{n}}*b^{frac{m}{n}}}$$
$$ (27*8)^{frac{2}{3}}=27^{frac{2}{3}}*8^{frac{2}{3}}=sqrt[3]{27^2}*sqrt[3]{8^2}=(sqrt[3]{27})^2*(sqrt[3]{8})^2=3^2*2^2=9*4=36;$$
Степень с рациональным показателем от произведения двух положительных чисел равна произведению степеней этих множителей.
$$ mathbf {5.; left(frac{a}{b}right)^{frac{m}{n}}=frac{a^{frac{m}{n}}}{b^{frac{m}{n}}}}$$
Степень с рациональным показателем от частного двух положительных чисел равна частному степеней этих чисел.
И еще два очень важных свойства степеней. Они вам понадобятся при решении показательных уравнений и неравенств.
Пусть опять есть некоторое положительное число (a>1) и дроби (frac{m}{n}) и (frac{c}{d}).
$$mathbf {6. ; При ; n gt 0 qquad a^n gt 1},$$
$$mathbf {При ; n lt 0 qquad 0 lt a^n lt 1}.$$
7. Если же (a gt 1) и (n gt m), то
$$ a^n>a^m.$$
Если ( 0 lt a lt 1 ) и (n gt m), то
$$ a^n lt a^m.$$
Разберем несколько примеров:
Пример 3
$$ 3^{-frac{3}{4}}*3^{-frac{1}{4}}=3^{-frac{3}{4}-frac{1}{4}}=3^{-1}=frac{1}{3};$$
$$ 2^{frac{1}{2}}:2^{frac{1}{4}}=2^{frac{1}{2}-frac{1}{4}}=2^{frac{1}{4}}=sqrt[4]{3};$$
$$ (5^{-frac{1}{2}})^{-4}=5^{(-frac{1}{2})*(-4)}=5^2=25; $$
$$ (0,125)^{-frac{2}{3}}*8^{-frac{2}{3}}=(0,125*8)^{-frac{2}{3}}=1^{-frac{2}{3}}=1; $$
$$ (4,4)^{frac{1}{3}}:(0,55)^{frac{1}{3}}=(frac{4,4}{0,55})^{frac{1}{3}}=8^{frac{1}{3}}=sqrt[3]{8}=2;$$
$$ 3^{frac{1}{3}} lt 3^{frac{1}{2}},$$
Так как основание степени больше единицы (3 gt 1) и (frac{1}{3} lt frac{1}{2}).
$$ (frac{1}{5})^{frac{1}{3}} gt (frac{1}{5})^{frac{1}{2}}, $$
Так как (0 lt frac{1}{5} lt 1) и (frac{1}{3} lt frac{1}{2}).
Алгебра и начала математического анализа, 10 класс
Урок №17. Степень с рациональным и действительным показателем.
Перечень вопросов, рассматриваемых в теме
1) понятие степени;
2) определение степени с рациональным и действительным показателем;
3) нахождения значения степени с действительным показателем.
Глоссарий по теме
Если n- натуральное число, 



При любом действительном х 


Но если основание степени а=0, то степень 

При 

Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Пример: вычислим
Мы можем представить 
Таким образом, мы можем записать

На основании данного примера можно сделать вывод:
Если n- натуральное число, 



Напомним, что r-рациональное число вида 
Таким образом, степень определена для любого рационального показателя r и любого положительного основания а.
Если 




Пользуясь формулой 
Рассмотрим несколько примеров:
Отметим, что все свойства степени с натуральным показателем, которые мы с вами повторили, верны для степени с любым рациональным показателем и положительным основанием, а именно, для любых рациональных чисел p и q и любых 

;
;
Разберем несколько примеров, воспользовавшись данными свойствами:
- Вычислим:
- Упростить выражение:
В числителе вынесем общий множитель ab за скобки, в знаменателе представим корни в виде дробных показателей степени:
А теперь дадим определение степени с действительным показателем, на примере 
Пусть 

Эта последовательность стремится к числу 
Числа 

Можно сделать вывод, что данная последовательность стремится к некоторому действительному числу, которое обозначают 

Опредление степени с действительным показателем.
При любом действительном х 


Но если основание степени а=0, то степень 

При 

Для степени с действительным показателем сохраняются все известные свойства степени с рациональным показателем, из которых следует теорема.
Теорема. Пусть 


Доказательство:
По условию 
а^(х₂)




Из данной теоремы вытекают три следствия:
- Пусть
Тогда
- Пусть
и

- Пусть
и

Эти теорема и следствия помогают при решении уравнений и неравенств, сравнении чисел.
Примеры и разборы решения заданий тренировочного модуля
Пример 1. Сравнить числа
Сравним показатели
Т.к. 


Поэтому по теореме
Пример 2. Решим уравнение

Поэтому уравнение можно записать так:
Получим, 
Следовательно,
Пример 3. Сравнить числа
Избавимся от корней, для это возведем оба числа в шестую степень, т.к. шесть делится — наименьшее общее кратное двух и трех:
Т.к. 0<8<9 и 


План урока:
Степень с рациональным показателем
Свойства дробных степеней и операции с ними
Сравнение степеней
Степень с рациональным показателем
Напомним, что в 7 классе мы впервые познакомились с понятием степени, причем тогда рассматривались случаи, когда показателем степени является натуральное число. В 8 классе понятие степени было расширено, теперь в него включались случаи, когда показатель являлся целым числом. Настоятельно рекомендуем перечитать соответствующие уроки. Сегодня же мы можем сделать ещё один шаг вперед и рассмотреть степени с рациональными показателями.
При расширении понятия степени важно обеспечить то, чтобы уже известные правила работы с целыми степенями работали и для дробных показателей. Одно из свойств степеней выглядит так:
(am)n = amn
Подставим в эту формулу следующие значения переменных:
а = 3
m = 1/6
n = 6
Мы специально выбрали эти числа такими, чтобы произведение mn равнялось единице:
mn = (1/6)•6 = 1
Подставляем эти значения:
(31/6)6 = 31/6•6 = 31 = 3
Получили, что
(31/6)6 = 3
Однако по определению корня n-ой степени число, дающее при возведении в шестую степень тройку, является корнем шестой степени из трех. То есть можно записать:
С помощью подобных преобразований нам удалось указать, чему равно число, возведенное в дробную степень. Аналогично можно показать, что для любого а > 0 справедлива формула:
Действительно, если возвести левую часть в n-ую степень, то получим:
(а1/n)n = a1/n•n = a
Значит, по определению корня n-ой степени
Ограничение а > 0 необходимо для того, чтобы не рассматривать случаи, когда подкоренное выражение является отрицательным.
Продолжим наши рассуждения. Чему будет равна степень аm/n? Ясно, что дробь m/n можно представить в виде:
m/n = (1/n)•m
C учетом этого выполним преобразование:
В результате несложных преобразований нам удалось получить формулу, позволяющую возводить число в степень, у которой рациональный показатель!
Приведем несколько примеров вычисления дробных степеней:
Часто при вычислениях удобнее сначала извлечь корень из числа, а потом полученный результат возвести в степень:
Напомним, что одну и ту же дробь можно представить разными способами, например:
1/2 = 2/4 = 3/6 = 4/8 = 5/10 = 0,5
Возникает вопрос – изменится ли значение дробной степени, если мы приведем дробь к новому знаменателю? Очевидно, что нет, но всё же убедимся в этом на примере. Сначала возведем в степень 1/2 число 25:
Теперь заменим дробь 1/2 на идентичную ей дробь 2/4:
Результат не изменился. В общем случае есть смысл максимально сократить дробь перед вычислением, чтобы избежать операций с большими числами. Особенно это касается десятичных дробей. Например, пусть необходимо вычислить значение выражения 810,25. По определению десятичной дроби можно записать, что 0,25 = 25/100. Тогда вычислить 810,25 можно так:
Согласитесь, возводить число 81 в 25-ую степень не очень легко! Поэтому поступим иначе. Сократим дробь 25/100:
0,25 = 25/100 = 25/(25•4) = 1/4
Теперь вычисления будет более простыми:
Вообще легко запомнить, что 0,25 = 1/4, а 0,5 = 1/2. Замена десятичных дробей обыкновенными дробями сильно упрощает вычисления. Приведем примеры:
Свойства дробных степеней и операции с ними
Когда мы изучали степени с целыми показателями, мы выяснили, что правила работы с ними ничем не отличаются от правил работы со степенями с натуральным показателем. Оказывается, эти же правила работают и для степеней с рациональным показателем. Сформулируем основные свойства дробных степеней.
Например, справедливы следующие действия:
50,5•52,5 = 50,5 + 2,5 = 53 = 125
195/3•191/3 = 195/3 + 1/3 = 192 = 361
29,36–0,37•29,361,37 = 29,36–0,37 + 1,37 = 29,361 = 29,36
Вот несколько примеров подобных вычислений:
174,5:173,5 = 174,5–3,5 = 171 = 1
49,36:46,36 = 49,36–6,36 = 43 = 64
2012:2014 = 2012–14 = 20–2
Проиллюстрируем это правило примерами:
(60,25)8 = 60,25•8 = 62 = 36
(93/2)2 = 9(3/2)•2 = 93 = 729
(254)0,125 = 254•0,125 = 250,5 = 5
Покажем, как можно применять данное правило:
41/6•161/6 = (4•64)1/6 = 641/6 = 2
0,51,5•501,5 = (0,5•50)1,5 = 251,5 = 251+0,5 = 251•250,5 = 25•5 = 125
4,90,5•100,5 = (4,9•10)0,5 = 490,5 =7
Это правило можно применять следующим образом:
3600,5:100,5 = (360:10)0,5 = 360,5 = 6
5003:503 = (500:50)3 = 103 = 1000
6,251/4:0,011/4 = (6,25:0,01)1/4 = 6251/4 = 5
Заметим, что степени очень удобны тем, что с их помощью легко упростить работу с корнями, ведь если
то верное и обратное:
То есть любое выражение с корнями в виде степени с рациональным показателем.
Пример. Вычислите значение выражения
Решение. Корней много, поэтому для удобства заменим их степенями
Получили тоже самое выражение, но в более компактном виде. Посчитаем его значение:
(91/4)1/5•39/10 = (90,25)0,2•30,9 = 90,25•0,2•30,9 = 90,05•30,9 = (32)0,05•30,9 =
=32•0,05•30,9 = 30,1•30,9 = 30,1•0,9 = 31 = 3
Ответ: 3.
Пример. Упростите выражение
(81n+1– 65•81n)0,25
Решение. Степень 81n+1можно представить как произведение:
81n+1 = 81n•811 = 81•81n
С учетом этого можно записать:
(81n+1– 65•81n)0,25 = (81•81n– 65•81n)0,25 = (81n(81 – 65))0,25 =
= (81n•16)0,25 = 810,25n •160,25 = 810,25n •161/4 = 2•810,25n
Ответ: 2•810,25n.
Сравнение степеней
Напомним, что из двух корней n-ой степени больше тот, у которого больше подкоренное выражение:
Отсюда следует вывод, что если a<b, то
а1/n<b1/n
теперь возведем каждую часть этого неравенства в степень m. Тогда получим неравенство:
аm/n<bm/n
Получили, что из двух степеней с одинаковыми показателями меньше та, у которой меньше основание (правила сравнения будем нумеровать, чтобы на них удобнее было ссылаться):
В частности, справедливы следующие неравенства:
233,75< 243,75
634/3< 644/3
0,0080,002< 0,0080,002
Здесь мы рассматривали случаи, когда показатель степени является положительным числом. А что делать, если он отрицательный? Тогда степень следует «перевернуть», воспользовавшись уже известной вам формулой:
a–n = 1/an = (1/а)n
Пример. Сравните выражения с рациональным показателем степени:
20–3,14 и 50–3,14
Решение. Избавимся от знака минус в показателе:
20–3,14 = (1/20)3,14 = 0,053,14
50–3,14 = (1/50)3,14 = 0,023,14
Получили две степени с одинаковым и, что принципиально важно, положительным показателем. Из них больше та, у которой больше основание. То есть из неравенства 0,02 < 0,05 следует, что
0,023,14< 0,053,14
Это означает, что
50–3,14< 20–3,14
Ответ: 50–3,14< 20–3,14.
Особенным является случай, когда показатель степени равен нулю. Напомним, что любое число в нулевой степени (кроме самого нуля) равно единице, а выражение 00 не имеет смысл. Это значит, что числа в нулевой степени равны друг другу, даже если у них разные основания:
250 = 260 = 1
9,360 = 9,370 = 1
18,35460 = 12,36470 = 1
Несколько сложнее сравнивать числа, у которых одинаковые основания, но различные показатели. Здесь возможны три случая – основание либо равно единице, либо больше неё, либо меньше неё.
На основании этого правила можно записать, что:
53,14< 53,15
45–0,563< 450,001
1,235–5,623< 1,235–4,958
Единица в любой степени равна самой себе. Поэтому, если у двух чисел в основании записана именно она, то они должны быть равны друг другу:
1–7,56 = 1–0,15 = 10,236 = 1 521,36 = 1
Осталось рассмотреть случай, когда основание меньше единицы (но всё равно положительное). В таком случае ситуация становится противоположной – чем больше степень, тем меньше число. Проиллюстрируем это на примере. Пусть надо сравнить числа 0,57,6 и 0,58,9. Заменим дробь 0,5 так, чтобы вместо нее получилась степень с основанием, большим единицы:
0,5 = 1/2 = 1/(21) = 2–1
Итак, 0,5 = 2–1. Тогда можно записать, что:
0,57,6 = (2–1)7,6 = 2–7,6
0,58,9 = (2–1)8,9 = 2–8,9
Такие числа мы уже умеем сравнивать. Так как
– 8,9 <– 7,6
то и
2–8,9< 2–7,6
Следовательно, 0,57,6> 0,58,9.
Например, справедливы неравенства:
0,997> 0,997,24
0,5715,36> 0,5716,47
0,490,04> 0,490,05
Рассмотрим чуть более сложное задание на сравнение степеней, где надо использовать одновременно несколько правил.
Пример. Докажите, что
0,90,9 + 0,80,8 + 0,70,7< 281/3
Решение. Напрямую вычислить значение выражений в правой и левой части затруднительно. Однако мы можем усиливать неравенство, чтобы получить более простые выражения.
Усилить неравенство – это значит увеличить его меньшую или уменьшить большую часть. Например, неравенство 10 < 20 усилится, если вместо 10 написать большее число (11 < 20), или вместо 20 написать меньшее число (10 < 19). Очевидно, что если усиленное неравенство верное, то и изначальное (ослабленное) также справедливо.
Очевидно, что можно легко посчитать значение выражения 271/3:
Также ясно, что 271/3< 281/3 (правило 1). Усилим исходное неравенство:
0,90,9 + 0,80,8 + 0,70,7< 271/3 (1)
Действительно, если (1) справедливо, то мы можем записать двойное неравенство
0,90,9 + 0,80,8 + 0,70,7< 271/3< 281/3
Опустив здесь среднюю часть, получим исходное неравенство. Так как 271/3 = 3, мы можем переписать (1) так:
0,90,9 + 0,80,8 + 0,70,7<3 (2)
Далее будем работать с левой частью. Очевидно, что 0,80,8< 0,90,8 (снова используем правило 1). С другой стороны, 0,90,8< 0,90,7 (правило 3). Значит, можно записать двойное неравенство:
0,80,8< 0,90,8<0,90,7
или просто 0,80,8<0,90,7. Абсолютно аналогично можно записать, что
0,70,8< 0,90,7<0,90,7
Или 0,70,8<0,90,7. Наконец, в силу правила (3), 0,90,9<0,90,7. Итак, имеем три неравенства:
0,90,9<0,90,7
0,80,8<0,90,7
0,70,8<0,90,7
Их левые части стоят в (2). Следовательно, можно усилить (2):
0,90,7 + 0,90,7 + 0,90,7<3
3•0,90,7< 3
Поделим обе части на 3:
0,90,7< 1
Заменим единицу равным ему выражением 10,7:
0,90,7<10,7 (4)
Из правила 1 следует, что (4) справедливо. Но мы получили его, усиливая исходное неравенство. Из справедливости более сильного неравенства следует и справедливость более слабого. Следовательно, из справедливости (4) вытекает верность исходного неравенства, которое и надо было доказать.
Степень с рациональным показателем
Ранее было определено
понятие степени с целым показателем. Выражение аn определено
для всех а и n, кроме случая а=0 при n≤0. Напомним свойства этих степеней:
Для любых чисел а, b и любых целых чисел m и п справедливы равенства:
1.
am*an=am+n;
2.
am:аn=am-n (а≠0);
3.
(аm)n = аmn;
4.
(ab) n = an*bn;
5.
(b≠0);
6.
а1=а; а0=1
(а≠0).
Отметим также следующее свойство:
Если m>n, то аm>аn при
а>1 и аm<аn при 0<а<1.
В этом разделе мы обобщим понятие степени числа, придав смысл
выражениям типа 20.3, 85/7, 4-1/2 и т. Д
Определение.
Степенью числа а>0 с рациональным
показателем r=,
где m — целое число, а n — натуральное (n > 1), называется число
Например:
При этом степень числа 0 определена только для положительных
показателей.
Сделаем ряд замечаний, связанных с понятием степени с рациональным
показателем.
Замечание 1.
Из определения степени с рациональным показателем сразу следует, что
для любого положительного а и любого рационального r число ar
положительно.
Замечание 2.
Любое рациональное число допускает различные записи его в виде дроби,
поскольку для любого натурального k. Значение ar также не
зависит от формы записи рационального числа r. В самом деле, из свойств корней
следует, что
Замечание 3.
При а < 0 рациональная степень числа а не определяется, и это не
случайно, например, значение равнялось бы
, т. е. — 2. Но, с другой стороны,
, и поэтому должно
выполняться равенство
Для степеней с рациональным показателем сохраняются основные
свойства степеней, верные для любых показателей (при условии, что
основание степени будет положительным).
1.
;
2.
;
3.
;
4.
;
5.
;
6.
если ;
7.
если .
Закрепим теоретический материал при решении примеров.
Задача 1
Представьте в виде корня из числа выражение:
a)
b)
Задача 2
Представьте выражение в виде степени с рациональным показателем:
a)
b)
Найдите значение числового выражения
Задача 3
a)
b)
a)
b)
Задание 4. Разложите на множители
a)
b)
Формулы сокращённого умножения, применённые к действиям над степенями:
1.
2.
3.
4.
Задача 5.
a)
b)
Задача 6.
·
Сравните числа .
Запишем в виде степени с
рациональным показателем
Так как
·
Сравните числа 2300
и 3200.
Запишем в виде степени с одним
показателем: ,
Так как 8<9, то
Задачи для самостоятельного решения.
1. представить
в виде корня из числа:
а)
б)
2. представить
в виде степени с рациональным показателем
а)
б)
3. Найдите значение числового выражения
а)
б)
в)
г)
д)
е)
4. Упростите
выражения
а)
б)
5. сравните
числа
а)
б)

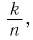
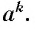
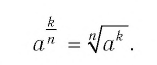

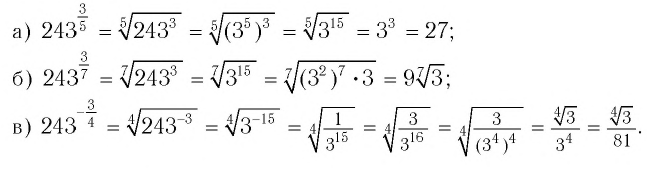
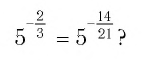
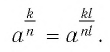
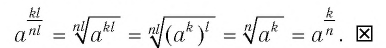
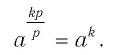
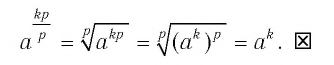
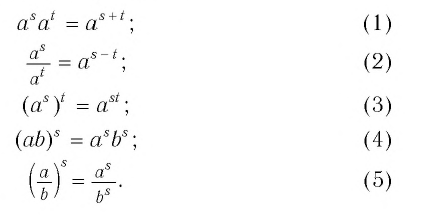
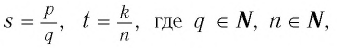
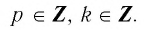
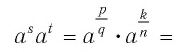
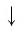
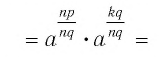

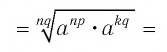

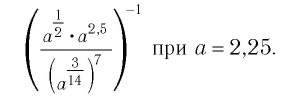
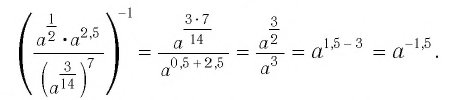
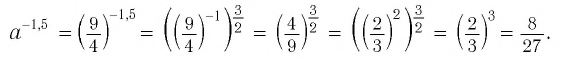
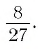
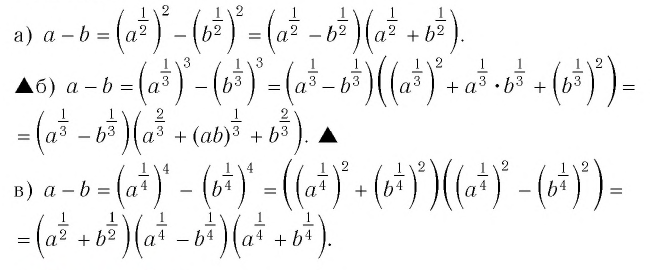
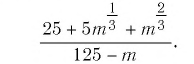
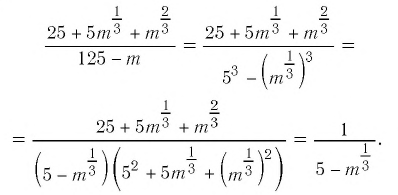
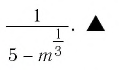
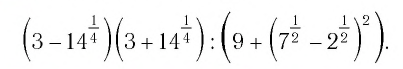
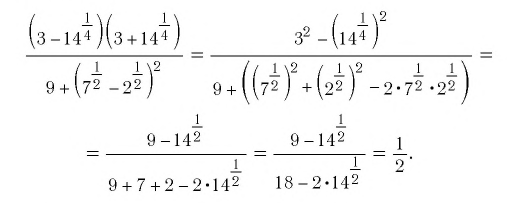
 — положительное рациональное число, то
— положительное рациональное число, то 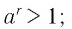
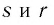 — рациональные числа и
— рациональные числа и 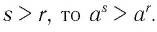
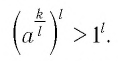
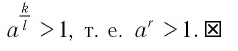
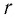 — положительное рациональное число, то
— положительное рациональное число, то 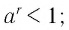
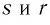 — рациональные числа и
— рациональные числа и 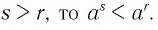
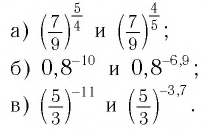
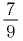
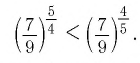
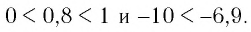
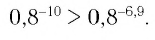
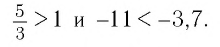
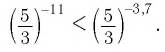
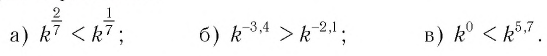
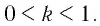
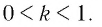
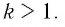
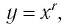
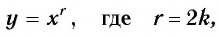
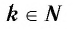
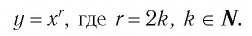
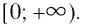
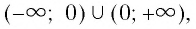 т. е. все точки графика, кроме начала координат, лежат выше оси Ох, в I и II координатных углах.
т. е. все точки графика, кроме начала координат, лежат выше оси Ох, в I и II координатных углах.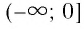 и возрастающая на промежутке
и возрастающая на промежутке 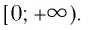
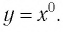
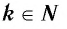
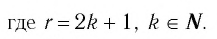
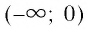 и положительные значения (у > 0) на промежутке
и положительные значения (у > 0) на промежутке 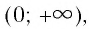 т. е. график функции расположен в I и III координатных углах.
т. е. график функции расположен в I и III координатных углах.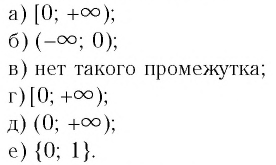
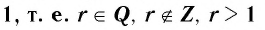
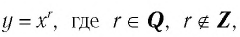
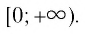
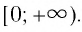
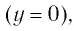 является наименьшим, а наибольшего значения функция не имеет.
является наименьшим, а наибольшего значения функция не имеет.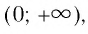 т. е. график функции расположен в I координатном угле.
т. е. график функции расположен в I координатном угле.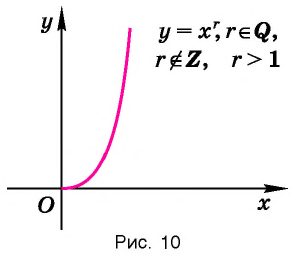
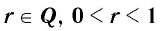
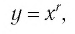
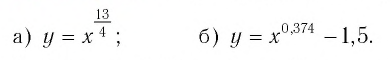
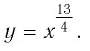
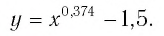
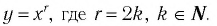
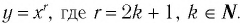


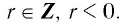
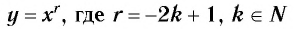
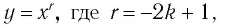
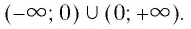
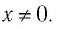
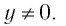
 и принимает положительные значения (у > 0) на промежутке
и принимает положительные значения (у > 0) на промежутке 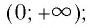 т.е. график функции расположен в I и III координатных углах.
т.е. график функции расположен в I и III координатных углах.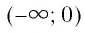 и убывающей на промежутке
и убывающей на промежутке 
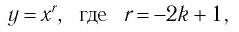
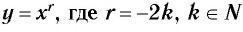
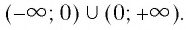
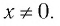
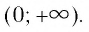
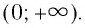
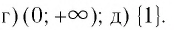
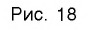
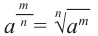
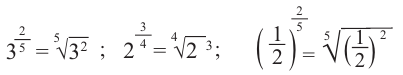

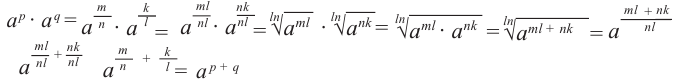
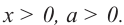









 ;
; ;
;













 Тогда
Тогда 
 и
и 
 и
и 


















































