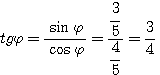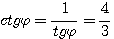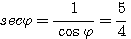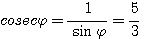Как найти значение трех других тригонометрических функций

Внимание! Эти формулы работают только если аргументы у тригонометрических функций одинаковые, т.е.

(sin^2⁡ 776^° +cos^2⁡ 776^° =1)
(tg, 3xcdot ctg, 3x=1)

Но:

(sin^2⁡x+cos^2⁡3x≠1)
(tg, xcdot ctg, y≠1)

Все формулы связи тригонометрических функций учить не надо, потому что они достаточно легко получаются друг из друга несложными преобразованиями (подробности в этих видео). Кроме того, при частом использовании они постепенно запоминаются сами.

Примеры применения формул связи

Зачем нужны формулы связи? Они позволяют найти все тригонометрические функции угла, если известна лишь одна из них, а также дают возможность упрощать выражения, доказывать тождества, решать тригонометрические уравнения, заменяя одну функцию другой и так далее.

Пример. Найдите (5sin⁡,α), если (cos,⁡α=frac{2sqrt{6}}{5}) и (α∈(frac{3π}{2};2π)). 
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:

(sin^2α+cos^2⁡α=1).

Подставим вместо косинуса его значение:

(sin^2⁡α+)((frac{2sqrt{6}}{5}))(^2=1)
(sin^2⁡α+)(frac{4cdot 6}{25})(=1)
(sin^2⁡α+)(frac{24}{25})(=1)
(sin^2⁡α=1-)(frac{24}{25})
(sin^2⁡α=)(frac{1}{25})
(sin⁡α=±)(frac{1}{5})

Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. Пожалуйста, раз и навсегда запомните, что у неполного квадратного уравнения вида (x^2=a) (при (a>0)) два корня (x_1=sqrt{a})  и (x_2=-sqrt{a}). Пусть двойка над иксом (та которая «квадрат») будет вам вечным маяком, сигнализирующим: «тут ДВА корня! Два! Не забудь!»

Вернемся к задаче. Получилось, что синус может иметь значение (frac{1}{5}), а может (-)(frac{1}{5}). И какое значение нам надо выбрать — с минусом или плюсом? Тут нам на помощь приходит информация, что (α∈(frac{3π}{2};2π)). Давайте нарисуем числовую окружность и отметим отрезок ((frac{3π}{2};2π)).

Обратите внимание – в этой четверти синус принимает только отрицательные значения (можно провести перпендикуляры до оси синусов и убедиться, что это так).

Значит, в нашем случае (sin,⁡α=-frac{1}{5}) т.е. (5sin,⁡α=5cdot(-frac{1}{5})=-1).

Ответ: (-1).

Пример.Найдите (tg,α), если (cos,⁡α=)(frac{sqrt{10}}{10}) и (α∈(frac{3π}{2};2π)). 
Решение. Есть 2 пути решения этой задачи:

— напрямую вычислить тангенс через формулу (tg^2α+1=)(frac{1}{cos^2⁡α});
— сначала с помощью тождества (sin^2⁡α+cos^2⁡α=1) найти (sin⁡,α), а потом через формулу (tg,α=)(frac{sin⁡,α}{cos⁡,α}) получить тангенс.

В учебниках обычно идут первым путем, поэтому мы пойдем вторым.

Вычисляем синус:

(sin^2⁡α+)((frac{sqrt{10}}{10})^2)(=1)
(sin^2⁡α+)(frac{10}{100})(=1)
(sin^2⁡α+)(frac{1}{10})(=1)
(sin^2⁡α=1-)(frac{1}{10})
(sin^2⁡α=)(frac{9}{10});
(sin⁡,α=±)(frac{3}{sqrt{10}})

Опять (α∈(frac{3π}{2};2π)), значит в итоге синус может быть только отрицательным. То есть, (sin⁡,α=-)(frac{3}{sqrt{10}}).
А теперь вычисляем тангенс: (tg,α=-)(frac{3}{sqrt{10}})(:)(frac{sqrt{10}}{10})(=)(-frac{3}{sqrt{10}}cdotfrac{10}{sqrt{10}})(=-)(frac{30}{10})(=-3).

Ответ: (-3).

Пример. Известно, что (tg,α=-frac{3}{4}) и (frac{π}{2}<α<π). Найдите значения трех других тригонометрических функций угла (α).
Решение. Проще всего из тангенса найти котангенс:

(ctg, α=)(frac{1}{tg, α})
(ctg,α=1:(-frac{3}{4})=1cdot(-frac{4}{3})=-frac{4}{3}).

Теперь вычислим косинус по упомянутой выше формуле:

(tg^2 α+1=)(frac{1}{cos^2⁡α})
((-)(frac{3}{4}))(^2+1=)(frac{1}{cos^2⁡α})
(frac{9}{16})(+1=)(frac{1}{cos^2⁡α})
(frac{9+16}{16})(=)(frac{1}{cos^2⁡α})
(frac{25}{16})(=)(frac{1}{cos^2⁡α})
(cos^2⁡α=)(frac{16}{25})
(cos⁡α=±)(frac{4}{5})

Опять перед нами стоит выбор плюс или минус. Отметим отрезок ((frac{π}{2};π)) на тригонометрической окружности и посмотрим какие значения принимает косинус в этой четверти, чтобы определится со знаком.

Очевидно, что косинус отрицателен в этой четверти, а значит (cos,⁡α=-)(frac{4}{5}).

Осталось найти синус:

(sin^2⁡α+cos^2⁡α=1)
(sin^2⁡α+(-)(frac{4}{5})()^2=1)
(sin^2⁡α+)(frac{16}{25})(=1)
(sin^2⁡α=1-)(frac{16}{25})
(sin^2⁡α=)(frac{9}{25})
(sin,⁡α=±)(frac{3}{5})

Опять используем круг, чтобы определить знак.

Получается, что (sin,⁡α=)(frac{3}{5}).

Ответ: (ctg,α=-)(frac{4}{3});   (cos,⁡α=-)(frac{4}{5});    (sin,α=)(frac{3}{5}).

Пример (ЕГЭ). Найдите (tg^2 α), если (5 sin^2⁡α+13 cos^2⁡α=6).
Решение. Давайте пойдем от того, что известно. В равенстве (5 sin^2⁡α+13 cos^2⁡α=6) синус заменим на косинус:

(5(1-cos^2⁡α)+13 cos^2⁡α=6)
(5-5 cos^2⁡α+13 cos^2⁡α=6)
(5+8 cos^2⁡α=6)
(8 cos^2⁡α=1)
(cos^2⁡α=)(frac{1}{8})

Поняли почему именно синус заменили на косинус, а не наоборот? И почему не надо извлекать корень, досчитывая до «чистого» косинуса? Потому что для нахождения (tg^2α) хорошо подходит формула (tg^2α+1=)(frac{1}{cos^2⁡α}) :

(tg^2 α+1=1:)(frac{1}{8})
(tg^2 α+1=1cdot)(frac{8}{1})
(tg^2 α+1=8)
(tg^2 α=7)

Ответ: (7).

Теперь еще одна задача из ЕГЭ, для наглядности мы ее решение оформили картинкой.

Пример. Упростите выражение (frac{1}{sin^2 α})(-ctg^2 α-cos^2 β).
Решение.

(frac{1}{sin^2 α})(-ctg^2 α-cos^2 β)		Самое очевидное, что можно сделать – это представить котангенс как отношение косинуса к синусу.
(=)(frac{1}{sin^2 α})(-)(frac{cos^2⁡α}{sin^2 α})(-cos^2 β=)		Приводим дроби к общему знаменателю.
(=)(frac{1-cos^2⁡α}{sin^2 α})(-cos^2 β=)		(1-cos^2⁡α) можно заменить на (sin^2 α).
(=)(frac{sin^2 α}{sin^2 α})(-cos^2 β=)		Сокращаем синусы.
(=1-cos^2 β=sin^2 β).

Пример. Докажите тождество (frac{cos^4⁡α-sin^4⁡α}{(1-sin⁡α)(1+sin⁡α)})(+2tg^2 α=)(frac{1}{cos^2 α}).
Решение.

(frac{cos^4⁡α-sin^4⁡α}{(1-sin⁡α)(1+sin⁡α)})(+2tg^2 α=)(frac{1}{cos^2 α})		Чтобы доказать это тождество, будем преобразовывать левую часть, пытаясь свести ее к правой. Поехали. Разложим числитель левой дроби по формуле разности квадратов, а знаменатель, наоборот, соберем по ней же.
(frac{(cos^2⁡α-sin^2⁡α )(cos^2 α+sin^2⁡α)}{1-sin^2⁡α})(+2tg^2 α=)(frac{1}{cos^2 α})		Очевидно, что вторая скобка числителя равна (1) (по основному тригонометрическому тождеству), а знаменатель можно заменить на (cos^2 α).
(frac{cos^2⁡α-sin^2⁡α}{cos^2 α})(+2tg^2 α=)(frac{1}{cos^2 α})		Теперь разложим тангенс по формуле (tg, α=)(frac{sin⁡,α}{cos,⁡α}).
(frac{cos^2⁡α-sin^2⁡α}{cos^2 α})(+2)(frac{sin^2⁡α}{cos^2⁡α})(=)(frac{1}{cos^2 α})		Приводим дроби к общему знаменателю.
(frac{cos^2⁡α-sin^2⁡α+2 sin^2⁡α}{cos^2 α})(=)(frac{1}{cos^2 α})		Приводим подобные слагаемые.
(frac{cos^2⁡α+sin^2⁡α}{cos^2 α})(=)(frac{1}{cos^2 α})		И вновь нас выручает основное тригонометрическое тождество
(frac{1}{cos^2 α}) (=)(frac{1}{cos^2 α})

Левая часть полностью идентична правой, то есть тождество доказано.

Как доказать все формулы связи

Свойства тригонометрических функций

Отсюда вытекает много интересных свойств и тригонометрических формул.
Во-первых, надеюсь, все знают, что в прямоугольном треугольнике самая большая сторона – это гипотенуза.
Поэтому из определения синуса и косинуса ((sin(alpha)=frac{a}{c}; quad cos(alpha)=frac{b}{c})) следует, что они всегда меньше единицы, ведь мы катет (меньшую сторону) делим на гипотенузу (большую сторону треугольника). И как мы узнаем позже, синус и косинус всегда больше минус единицы. То есть синус и косинус могут принимать только значения из промежутка:

$$ sin(alpha) in [-1;1];$$
$$ cos(alpha) in [-1;1];$$

Для тангенса и котангенса никаких ограничений нет, они могут принимать абсолютно любые значения.

Теперь выведем несколько формул, без которых нам точно потом не обойтись. Например, можно обратить внимание, что тангенс выражается через деление синуса на косинус, просто расписав их по определению:

$$frac{sin(alpha)}{cos(alpha)}=frac{frac{a}{c}}{frac{b}{c}}=frac{a}{c}*frac{c}{b}=frac{a}{b};$$

А последняя формула есть ни что иное, как определение тангенса:
$$ tg(alpha)=frac{a}{b};$$
Значит
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}.$$

Аналогичные рассуждения можно провести для котангенса:
$$frac{cos(alpha)}{sin(alpha)}=frac{frac{b}{c}}{frac{a}{c}}=frac{b}{c}*frac{c}{a}=frac{b}{a};$$
А котангенс по определению:
$$ctg(alpha)=frac{b}{a};$$
Значит
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}.$$

Кроме этого, легко заметить, что функции тангенса и котангенса взаимно обратны:
$$tg(alpha)*ctg(alpha)=frac{a}{b}*frac{b}{a}=1.$$

А теперь мы подобрались к не самой очевидной тригонометрической формуле, но одной из самых главных во всей тригонометрии. Основное тригонометрическое тождество:

$$sin^2(alpha)+cos^2(alpha)=1. qquad (1)$$

Выводится оно тоже из определений синуса и косинуса с использованием теоремы Пифагора (гипотенуза в прямоугольном треугольнике равна сумме квадратов катетов (c^2=a^2+b^2;)):
$$sin^2(alpha)+cos^2(alpha)=left(frac{a}{c}right)^2+left(frac{b}{c}right)^2=left(frac{a^2}{c^2}right)+left(frac{b^2}{c^2}right)=frac{a^2+b^2}{c^2}=frac{c^2}{c^2}=1.$$
С основным тригонометрическим тождеством вы будете сталкиваться постоянно и в 9-м и в 10-м классах.

И разберем еще две важные формулы:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
Выводится она очень легко, опять же, используя определения тангенса и косинуса. Рекомендую потренироваться и сделать это самим.
$$1+left(frac{a}{b}right)^2=frac{1}{frac{b^2}{c^2}};$$
$$left(frac{b^2}{b^2}right)+left(frac{a^2}{b^2}right)=1*frac{c^2}{b^2};$$
$$frac{b^2+a^2}{b^2}=frac{c^2}{b^2};$$
Используем теорему Пифагора:
$$frac{c^2}{b^2}=frac{c^2}{b^2};$$
Получили верное равенство, значит формула верна.

И вторая аналогичная формула для котангенса:
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)};$$
Вывод один в один, сделайте сами.

Для удобства соберем все формулы вместе.
$$sin^2(alpha)+cos^2(alpha)=1. qquad(1)$$
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}. qquad(2)$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}. qquad(3)$$
$$tg(alpha)*ctg(alpha)=1.qquad(4)$$
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)}. qquad(5)$$
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}. qquad(6)$$

Это далеко не все тригонометрические формулы, их гораздо больше. Но для начала и для 9-го класса этого вполне достаточно.

Зачем же они нужны? Оказывается, эти формулы помогают связать тригонометрические функции между собой. Посмотрите внимательно на первую формулу (1): зная, например, чему равен косинус, можно легко найти синус, и наоборот.

Пример 1
Пусть (cos(alpha) =frac{1}{2}), найдите (sin(alpha)=?)

Берем основное тригонометрическое тождество (формула (1)) и подставляем в него известный по условию задачи (cos(alpha)=frac{1}{2}:)
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(frac{1}{2}right)^2=1;$$
А дальше просто решаем получившееся уравнение относительно синуса:
$$sin^2(alpha)=1-left(frac{1}{2}right)^2;$$
$$sin^2(alpha)=1-frac{1}{4};$$
Приводим к общему знаменателю:

$$sin^2(alpha)=frac{4}{4}-frac{1}{4};$$
$$sin^2(alpha)=frac{3}{4};$$
И здесь внимательно решаем квадратное уравнение:
$$sin(alpha)=pmfrac{sqrt{3}}{2};$$
Обратите внимание на (pm). Синус может быть как положительным, так и отрицательным, так как при подстановке и возведении в квадрат минус сгорает. Значит здесь получается два ответа.

Ответ:(sin(alpha)=pmfrac{sqrt{3}}{2}.)

Аналогично, зная хотя бы одну тригонометрическую функцию, можно найти все остальные, используя тригонометрические формулы. Рассмотрим еще пример:

Пример 2
Пусть (sin(alpha) =frac{1}{3}), найдите (ctg(alpha)=?)

Смотрим на наш список формул и находим такую, в которой есть и синус и котангенс — это формула (6):
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}.$$
Подставляем известный из условия синус (sin(alpha) =frac{1}{3}):
$$1+сtg^2(alpha)=frac{1}{left(frac{1}{3}right)^2}.$$
Перевернем правую часть:
$$1+сtg^2(alpha)=left(frac{3}{1}right)^2.$$
$$1+сtg^2(alpha)=9.$$
Теперь решим уравнение и найдем котангенс:
$$сtg^2(alpha)=8.$$
$$сtg(alpha)=pmsqrt{8}=pmsqrt{4}*sqrt{2}=pm2sqrt{2}.$$

Ответ:(сtg(alpha)=pm2sqrt{2}).

Выглядит пугающе, но учить вам это НЕ НУЖНО! В некоторых школах есть изверги, которые заставляют учить такую таблицу, но в этом совершенно нет необходимости. В дальнейшем мы научимся сами выводить все значения тригонометрических функций только из маленькой таблицы.

Обратите внимание, что синус некоторого угла в треугольнике всегда положителен, неважно, тупой или острый угол. А вот косинус, тангенс и котангенс в треугольнике положительны только от острых углов и отрицательны от тупых.

Тут может возникнуть вопрос, как может существовать синус, косинус, тангенс или котангенс от тупого угла, большего чем (90^o), если мы давали определение всех тригонометрических функций через прямоугольный треугольник, в котором нет углов больших (90^o). Ну что ж, да тригонометрические функции существуют для любых углов и острых, и тупых, но для самого начала тригонометрии определения через прямоугольный треугольник нам более чем достаточно. Просто запомните выводы, которые мы сделали в предыдущем абзаце.

Рассмотрим пример на тригонометрию по типу схожий с заданиями ОГЭ. Обычно задачи сводятся просто к нахождению тригонометрической функции некоторого угла, нарисованного на рисунке:

Пример 2
По рисунку определить значение (sin(alpha)=?)

По определению синус в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. Первым делом достроим наш синий угол (angle{ABC}) до прямоугольного треугольника, для этого опустим из точки (A) высоту (AH) к (BC). Получили прямоугольный треугольник (AHB). Теперь можем воспользоваться определением синуса:
$$sin(alpha)=frac{AH}{AB};$$
По клеточкам на рисунке найдем длину отрезка (AH=15). А гипотенузу (AB) найти по клеточкам не выйдет, так как она идет по диагонали. Но мы можем найти опять по клеточкам второй катет в прямоугольном треугольнике (BH=12) и применить теорему Пифагора:
$$AB^2=AH^2+BH^2;$$
$$AB^2=15^2+12^2=225+144=369;$$
$$AB=sqrt{369}=3sqrt{41};$$
Подставим в формулу для синуса и найдем его:
$$sin(alpha)=frac{AH}{AB}=frac{15}{3sqrt{41}};$$

Ответ: (sin(alpha)= frac{15}{3sqrt{41}}.)

Разберем еще примеры посложнее на нахождение тригонометрических функций друг через друга. Некоторые даже будут из реального ЕГЭ:

Пример 3
Пусть (tg(alpha)=sqrt{3}), найти (cos(alpha)=?), если известно, что (alpha<90^o).
Задание из ЕГЭ по профильной математике.

Условие аналогично условию в примерах №1 и 2, но появилось еще какое-то ограничение на угол (alpha), пока не будем обращать на него внимания, и решаем как обычно. Воспользуемся формулой (5), в ней есть и косинус, и тангенс, как раз одна из функций нам дана, а другую надо найти:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(sqrt{3})^2=frac{1}{cos^2(alpha)};$$
$$1+3=frac{1}{cos^2(alpha)};$$
$$4=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{4};$$
$$cos(alpha)=pmfrac{1}{2}.$$

У нас опять получилось два ответа из-за квадрата. В условии сказано, что задание из первой части ЕГЭ, а значит два ответа быть не может. Для этого нам и дано, что (alpha<90^o). Это означает, что угол (alpha) острый, а значит косинус у острого угла обязательно должен быть положительный.

Ответ: (cos(alpha)=frac{1}{2}.)

Пример 4
Пусть (tg(alpha) =-2), найти (sin(alpha)=?), при (90^o<alpha<180^o).

Опять обратимся к нашим формулам (1-6) и пытаемся найти такую, в которой есть и синус и тангенс. И тут оказывается, что такой формулы нет. Но нам никто не запрещает, зная тангенс и используя формулу (5), найти косинус:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(-2)^2=frac{1}{cos^2(alpha)};$$
$$5=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{5};$$
$$cos^2(alpha)=pmsqrt{frac{1}{5}};$$
Так как согласно условию (alpha>90^o), то значение косинуса должно быть отрицательным:
$$cos(alpha)=-sqrt{frac{1}{5}};$$

А потом, уже зная косинус, по основному тригонометрическому тождеству (1) можно найти требуемый в задаче синус:
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(-sqrt{frac{1}{5}}right)^2=1;$$
$$sin^2(alpha)+frac{1}{5}=1;$$
$$sin^2(alpha)=-frac{1}{5}+1;$$
$$sin^2(alpha)=frac{4}{5};$$
$$sin(alpha)=pmsqrt{frac{4}{5}};$$
Синус у нас положительный и при острых ((alpha<90^o)) и при тупых углах ( (90<alpha<180) ):
$$sin(alpha)=sqrt{frac{4}{5}};$$

Ответ: (sin(alpha)=sqrt{frac{4}{5}}.)

Итак, зная значение хотя бы одной из четырех тригонометрических функций, при помощи формул (1-6) можно найти три оставшихся, именно для этого формулы и нужны.

Зная угол (angle{A}=60^o), мы знаем все тригонометрические функции от этого угла. Смотрите в таблицу (1):
$$sin(60^o)=frac{sqrt{3}}{2};$$
$$cos(60^o)=frac{1}{2};$$
$$tg(60^o)=sqrt{3};$$
$$ctg(60^o)=frac{1}{sqrt{3}};$$
С другой стороны, можно расписать функции по определению через отношение сторон в прямоугольном треугольнике:
$$sin(angle{A})=frac{BC}{AB};$$
$$cos(angle{A})=frac{AC}{AB};$$
$$tg(angle{A})=frac{BC}{AC};$$
$$ctg(angle{A})=frac{AC}{BC};$$

Не пугайтесь, все нам не понадобится. Воспользуемся пока формулами:
$$cos(60^o)=frac{1}{2};$$
$$cos(angle{A}=60^o)=frac{AC}{AB};$$
Нам известны косинус (angle{A}) и сторона (AC), а значит, мы можем найти гипотенузу (AB):
$$frac{1}{2}=frac{5}{AB};$$
$$AB=frac{5}{frac{1}{2}}=5*frac{2}{1}=10;$$
Нашли гипотенузу, теперь найдем последнюю сторону (BC). Для этого нам нужна любая формула с (BC), например:
$$sin(angle{A})=frac{BC}{AB};$$
Синус знаем, (AB) только что нашли — выражаем (BC):
$$BC=AB*sin(60^o)=10*frac{sqrt{3}}{2}=5*sqrt{3}.$$

Ответ: (AB=10;) (BC=5*sqrt{3}.)

Подведем итоги. Зная любую сторону в прямоугольном треугольнике и хотя бы один из острых углов, можно найти все остальные стороны при помощи тригонометрии.

Рассмотрим задачу посложнее.

Пример 6
Дан прямоугольный треугольник (bigtriangleup{ABC}), в котором угол (angle{C}=90^o), угол (tg(angle{A})=frac{1}{5}), сторона (AB=13). В треугольнике из прямого угла (angle{C}) проведена высота (CH). Найти (AH).

Первым делом обратите внимание на один очень важный факт. Если провести высоту в прямоугольном треугольнике из прямого угла, то она поделит треугольник еще на два прямоугольных. В нашем случае (bigtriangleup{ACH}) и (bigtriangleup{CHB}) тоже будут прямоугольными. А значит в них выполняются все соотношения для тригонометрических функций.
Например, в (bigtriangleup{ACH}) для угла (angle{A}) противолежащим катетом будет (CH), а прилежащим — сторона (AH), гипотенуза будет соответственно (AC). А значит можно записать формулы, следующие из определения тригонометрических функций:

$$sin(angle{A})=frac{CH}{AC};$$
$$cos(angle{A})=frac{AH}{AC};$$
$$tg(angle{A})=frac{CH}{AH};$$
$$ctg(angle{A})=frac{AH}{CH};$$

Аналогичные соотношения можно записать и для (bigtriangleup{CHB}) и (bigtriangleup{ABC}). Не буду нагромождать, запишите эти соотношения сами в качестве тренировки.

Следующий важный момент, на который следует обратить внимание — это углы в получившихся треугольниках. Обозначим угол (angle{CAB}=alpha). Тогда, так как (angle{CHA}=90^o), можно выразить угол:
$$angle{ACH}=180-angle{CAB}-angle{CHA}=180-alpha-90=90-alpha;$$
Напомню, что треугольник (bigtriangleup{ABC}) прямоугольный с прямым углом (angle{ACB}=90^o).
Значит
$$angle{HCB}=angle{ACB}-angle{ACH}=90-(90-alpha)=alpha=angle{CAB};$$

Важный факт: (angle{HCB}=angle{CAB})! А равенство этих углов само собой означает и равенство всех тригонометрических функций. То есть, например, (sin(angle{HCB})=sin(angle{ACB})). Точно так же у них равны и косинусы, и тангенсы, и даже котангенсы!

Аналогичные рассуждения можно провести для углов (angle{ACH}=angle{CBA}).
Запомните это!

А теперь приступим непосредственно к решению задачи. Нам известна гипотенуза (AB) и (tg(alpha)). По определению тангенса в (bigtriangleup{ABC}):
$$tg(angle{A})=frac{CB}{AC};$$
Либо из (bigtriangleup{ACH}):
$$tg(angle{A})=frac{CH}{AH};$$

В этих формулах есть проблема: нет известной нам стороны, гипотенузы (AB). А значит, у нас две неизвестные, и решить мы не можем.

Но зная тангенс, мы легко можем найти косинус по формуле:
$$1+tg(alpha)^2=frac{1}{cos^2(alpha)};$$
$$1+left(frac{1}{5}right)^2=frac{1}{cos^2(alpha)};$$
$$1+frac{1}{25}=frac{1}{cos^2(alpha)};$$
$$frac{26}{25}=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{frac{26}{25}}=1*frac{25}{26}=frac{25}{26};$$
$$cos(alpha)=pmsqrt{frac{25}{26}}=pmfrac{5}{sqrt{26}};$$
Так как (anglealpha) это острый угол из прямоугольного треугольника, то его косинус точно будет положительным:
$$cos(alpha)=frac{5}{sqrt{26}}.$$
Не самый приятный косинус, но что делать, будем решать так, как есть.

С другой стороны, из (bigtriangleup{ABC}):
$$cos(alpha)=frac{AC}{AB};$$
Подставим известное (AB):
$$frac{5}{sqrt{26}}=frac{AC}{13};$$
$$AC=13*frac{5}{sqrt{26}}=frac{13*5}{sqrt{26}};$$
Либо косинус еще можно расписать в (bigtriangleup{ACH}):
$$cos(alpha)=frac{AH}{AC}=frac{5}{sqrt{26}};$$
Подставим найденное (AC):
$$frac{AH}{frac{13*5}{sqrt{26}}}=frac{5}{sqrt{26}};$$
$$AH=frac{5}{sqrt{26}}*frac{13*5}{sqrt{26}}=frac{5*13*5}{26}=frac{25}{2}=12,5.$$

Ответ: (AH=12,5.)

ВИДЕО УРОК

Выражение всех тригонометрических функций через одну из них с помощью основных
тригонометрических тождеств.

Основные тригонометрические тождества позволяют определить по значению
одной из тригонометрических функций значения всех остальных.

ПРИМЕР:

Известно, что

sin x =
–³/₅,

причём

π < х <  ^3π/₂.

Найти

cos x,
tg x, ctg x.

РЕШЕНИЕ:

Из формулы

sin² α
+ cos² α = 1

получаем

cos² х  = 1 – sin² х.

подставив вместо  sin
х  его
значение, получим:

Итак,

cos² х
= ¹⁶/₂₅

значит,

либо  cos х = ⁴/₅

либо  cos х = –⁴/₅.

По условию:

π < х <  ^3π/₂,

то есть аргумент  х  принадлежит 
третьей четверти. Но в третьей четверти косинус отрицателен. Значит, из
двух указанных выше возможностей выбираем одну:

cos х
= –⁴/₅.

Зная  sin x  и  cos
х, находим  tg x  и  ctg x:

ctg x = ⁴/₃.

ОТВЕТ:

cos х = –⁴/₅,

tg x
= ³/₄,

ctg x
= ⁴/₃.

ПРИМЕР:

Дано:

sin α = ²⁰/₂₉.

Вычислить значения остальных
тригонометрических функций острого угла  α.

РЕШЕНИЕ:

Из формулы:

sin² α + соs² α = 1

имеем:

соs² α = 1 – sin² α

Подставляя вместо  sin² α  его численное значение  ²⁰/₂₉, получаем:

Следовательно:

соs α = ²¹/₂₉

Для нахождения 
tg α 
воспользуемся формулой

Получим:

tg α = ²⁰/₂₉ : ²¹/₂₉ = ²⁰/₂₁.

Отсюда, пользуясь формулой

tg α ∙ сtg α = 1,

Имеем:

ОТВЕТ:

соs α = ²¹/₂₉,

tg α = ²⁰/₂₁,

сtg α = ²¹/₂₀.

ПРИМЕР:

Определить значения тригонометрических функций угла  α, если

tg α = ³/₄

и  180° < α < 270°.

РЕШЕНИЕ:

По формуле

Находим

По формуле

Находим

Учитывая, что  sec α < 0  при 

180° < α < 270°

получим

–sec α = ⁵/₄

откуда

sec α = –⁵/₄

По формуле

Находим

сos α = – ⁴/₅.

Значения  sin α  найдём из
формулы

|sin α| = ³/₅.

Учитывая, что  sin α < 0  при 

180° < α < 270°

находим

sin α = –³/₅.

ОТВЕТ:

sin α = –³/₅,

соs α = –⁴/₅,

сtg α = ⁴/₃.

ПРИМЕР:

Известно, что

ctg x = –⁵/₁₂,

причём

^π/₂ < х < π.

Найти

sin х, cos x,
tg x.

РЕШЕНИЕ:

Из формулы

1 + ctg² α = cosec² α

находим

подставив
вместо  ctg x  его значение, получим:

Итак,

sin² х = ¹⁴⁴/₁₆₉

значит,

либо  sin х = ¹²/₁₃

либо  sin х = –¹²/₁₃.

По условию:

^π/₂ < х < π,

то есть аргумент  х  принадлежит 
второй четверти. Но во второй четверти синус положителен. Значит, из
двух указанных выше возможностей выбираем одну:

sin х = ¹²/₁₃.

Для отыскания значения  cos x  воспользуемся
формулой:

Из этой формулы находим

cos x
= ctg x ∙ sin х =

= –⁵/₁₂ ∙ ¹²/₁₃ = –⁵/₁₃.

Осталось вычислить
значение  tg x. Из равенства

находим

tg x = –¹²/₅.

ОТВЕТ:

sin х = ¹²/₁₃,

cos х = –⁵/₁₃,

tg x = –¹²/₅.

ПРИМЕР:

Дано:

сtg α = ⁴⁵/₂₈.

Вычислить остальные тригонометрические функции
острого угла  α.

РЕШЕНИЕ:

Записываем значение  tg α  как
величину, обратную  сtg α:

tg α = ²⁸/₄₅.

на основании формулы

имеем:

Возведя обе части этого
равенства в квадрат, получим:

Прибавим к обеим частям
этого равенства по единице:

Учитывая, что

sin² α + cos² α = 1,

находим:

откуда

sin α = ²⁸/₅₃.

Из формулы

Имеем, что

соs α = сtg α ∙ sin α.

В применению к данному случаю получим:

ОТВЕТ:

sin х = ²⁸/₅₃,

cos х = ⁴⁵/₅₃,

tg x = ²⁸/₄₅.

Вычисление
значений тригонометрических функций острого угла по значению одной из них надо
производить каждый раз, как было показано выше на примерах, пользуясь основными
формулами:

которые
надо твёрдо заучить.

Соотношения
между тригонометрическими функциями одного аргумента.

Если
преобразовать основные тригонометрические тождества, не предавая определённого
значения заданной функции, то можно вывести некоторые соотношения между
тригонометрическими функциями одного аргумента. Можно получить
выражения любой из тригонометрических функций через все остальные с помощью
следующих формул:

 Формулы,
приведённые в таблице, позволяют по значению одной из тригонометрических
функций находить значения всех остальных.

Во всех формулах, в
которых входят функции  tg α  или  sес α,
исключается значение

α = (2k + 1) ^π/₂,

где  k – любое целое
число, так как при этих и только при этих значениях  α  функции  tg α  или  sес α  не определены, то
есть не существуют. Во всех формулах, в которые входят функции  ctg α  или  cosес α, исключаются значения 

α = kπ,

где  k – любое целое
число, так как при этих и только при этих значениях  α  функции  ctg α  или  cosес α  не определены (не
существуют).

В тех формулах, в
которые входят радикалы, в общем случае перед радикалом следует становить
двойной знак  ±. Выбор определенного знака может быть произведён, если
дано дополнительное условие.

Пусть, например,

Если угол 
α 
находится в интервале от  0  до  π (или от  2kπ  до  2kπ + π, где  k – любое целое число), то

а если угол 
α 
находится в интервале от  π  до  2π (или от  π + 2kπ  до  2π + 2kπ, где  k – любое целое число), то

Таким образом,
выбор знака перед радикалом зависит от того промежутка, в котором
находится  α.

ПРИМЕР:

Дано:

соs α = ²/₇.

Вычислить значения остальных
тригонометрических функций острого угла  α.

РЕШЕНИЕ:

Из формулы:

sin² α + соs² α = 1

имеем:

ОТВЕТ:

ПРИМЕР:

Выразить значения
тригонометрических функций острого угла   
через  cos α.

РЕШЕНИЕ:

Из формулы:

sin² α +
cos² α = 1

находим:

Из формулы:

имеем:

и, следовательно

Подобного
рода задачи можно решать в общем виде и составить формулы, выражающие любую из
тригонометрических функций через все остальные.

ПРИМЕР:

Выразить  cos α  через все остальные тригонометрические функции
угла  α.

РЕШЕНИЕ:

Из тождества:

sin² α +
cos² α = 1

находим:

Далее из равенства

sec² α = 1 + tg² α

находим:

откуда

Заменив в полученном
равенстве

находим:

Так как

то последнее равенство примет вид:

Итак

ПРИМЕР:

Вывести выражения
тригонометрических функций острого угла   
через  tg α.

РЕШЕНИЕ:

Из формулы:

имеем:

Прибавляя к обеим частям
этих равенств по единице, получим:

или,
так как

1. Определение тригонометрических функций для угла прямоугольного треугольника

2. Значения тригонометрических функций 30, 45 и 60 градусов

    Из прямоугольного равнобедренного треугольника с гипотенузой, равной 1 и острыми углами по 45⁰ найдём:
        .

    Сведём все полученные результаты в таблицу:
                                                                                    

3. Определение тригонометрических функций на единичной окружности

    Из определения тригонометрических функций вытекают важные их свойства:
    1. Все тригонометрические функции периодические. Причём sinα и cosα имеют наименьший (главный) период Т = 2π и общий период 2πk, где k – любое целое число. У tgα и ctgα наименьший период равен π, а общий πk, где k – целое число.
    2. sinα, tgα и ctgα – нечётные функции; т.е.
        sin (– α) = – sinα, tg (– α) = – tgα, ctg (– α) = – ctgα;
        cosα – чётная функция, т.е. cos (– α ) = cosα;
    3. Знаки тригонометрических функций:
        I четверть – положительны sinα, cosα, tgα, ctgα;
        II четверть – положителен только sinα, отрицательны cosα, tgα, ctgα;
        III четверть – положительны tgα, ctgα, отрицательны sinα, cosα;
        IX четверть – положителен cosα, а sinα, tgα, ctgα – отрицательны. 

3ГОНОМЕТРИЯ     В НАЧАЛО
Нахождение значений тригонометрических функций угла по значению какой-нибудь одной из них.
Используя основные тригонометрические тождества, легко найти значения всех тригонометрических функций sin х, cos х, tg x, ctg x, sec x, cosec x, если известно значение какой-нибудь одной из них. Поясним это на конкретных примерах.
Пример   1. Найти значения   тригонометрических функций  угла φ, если известно, что sin φ = 3/5. Из тождества sin2 φ + cos2φ = 1  находим: cos2φ = 1 — sin2 φ = 16/25 Поэтому cos φ = ± 4/5 Знак + или — следует выбирать в зависимости от того,  в какой четверти оканчивается угол φ. По условию sin φ = 3/5 > 0. Значит, угол φ оканчивается либо в   1-й,  либо во 2-й четверти. 1)Если он оканчивается в 1-й четверти, то cos φ = + 4/5.    2)Если же он оканчивается во 2-й четверти, то cos φ = — 4/5. В  первом случае
Во втором случае tg φ = — 3/4;  ctg φ = —  4/3;  sес φ = —  5/4; cosec φ = 5/3
Пример 2. Найти значения тригонометрических функций угла φ, если  известно,   что  он   оканчивается  в  4-й  четверти и  tg φ = — 3/4 Используя тождество 1 + tg2 φ = sec2 φ, найдем sec φ: sec φ = /1 + tg2 φ  = /1+ (— 3/4 ) 2  =  5/4 Знак + перед радикалом мы взяли потому, что угол φ по условию оканчивается в 4-й четверти, sec φ = 1/cosφ  , а косинус угла, оканчивающегося в 4-й четверти, положителен; поэтому положителен и sec φ. Далее получаем:                 cos φ = 1/secφ = 4/5 Теперь, используя тождество sin2 φ + cos2 φ = 1, найдем   sin φ: sin φ = — / l — cos2 φ = — 3/5 . Здесь перед радикалом нужно брать знак — ,  поскольку синус угла, оканчивающегося в 4-й четверти, отрицателен. Заметим, что в данном случае рациональнее было бы   найти sin φ из тождества tg φ = sin φ/cos φ  . Однако мы сознательно  получили  sin φ  другим путем, чтобы еще раз показать, как нужно  выбирать знак (+ или —) перед радикалом. Итак, мы получили cos φ, sin φ, tg φ, sec φ. После этого легко найти значения и других тригонометрических функций угла φ: ctg φ = 1/tg φ = — 4/3  ;  cosec φ = 1/sin φ = — 5/3
Упражнения 1.  Найти   значения   тригонометрических   функций   угла   α по  следующим данным; 1) sin α = 0,6  0°<α<90°;       4) cosα = —0,8, 180°<α<270°; 2) sinα= — /2/3, π <α< 3/2  π; 5) tgα = —2,   3/2  π <α< 2π; 3) cosα= 12/13, 270°<α<360°;       6) tgα =  1/3 ,  180°<α<270°. 2.   Найти значения   тригонометрических   функций   угла  φ, если известно,  что sin φ = /2ab /a+b     (a > b > 0)  и  угол φ оканчивается не в  1-й четверти. 3.   Найти   значения   тригонометрических   функций   угла   φ, если известно, что tg φ = а2 — 1 ( |а| < 1), и угол φ оканчивается не во 2-й четверти.