Как найти значение угла по радианам

Радианная мера угла

3 ноября 2011

В школьном курсе математики есть два определения основных тригонометрических функций — синуса, косинуса, тангенса и котангенса:

1. Геометрический подход — основан на сторонах прямоугольного треугольника и их соотношениях. В этом случае все синусы и косинусы положительны, поскольку длина отрезка всегда задается положительным числом;
2. Алгебраический подход — работа ведется на тригонометрической окружности. Такой подход возникает на стыке 9—10 классов, и с этого момента синусы и косинусы вполне могут быть отрицательными. А «старые» геометрические определения становятся лишь частным случаем.

Для решения задачи B11 нужен именно алгебраический подход. Чуть позже мы убедимся, что такие задачи решаются элементарно — буквально с помощью одной формулы. Но для начала научимся быстро (буквально на лету) определять координатную четверть, в которой расположен искомый угол. В этом нам помогут следующие правила.

Переход от радианной меры к градусной

Вспомните: в 8—9 классах мы работали лишь с несколькими стандартными углами. А именно: 30°, 45° и 60°. В особо продвинутых случаях учителя рассказывали еще об углах 90° и 0°. Любые другие значения назывались «сложными», и возникновение таких углов, скорее всего, указывало на ошибку в решении.

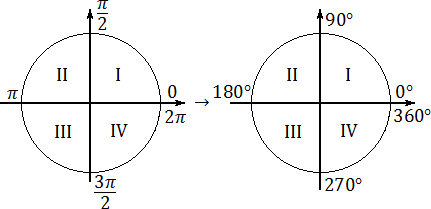
С введением тригонометрической окружности все ограничения на углы отпадают. Здесь я не буду рассказывать, как устроена тригонометрическая окружность — все это подробно описано в любом учебнике по математике. Вместо этого предлагаю обсудить другой вопрос — более важный, но которому почему-то не уделяется достаточно внимания. Речь идет о переходе от радианной меры угла к градусной.

Исторически так сложилось (и небезосновательно), что углы на тригонометрической окружности измеряют в радианах. Например, полный оборот — 360° — обозначается как 2π радиан. А всеми любимый (или ненавидимый) угол 45° равен π/4 радиан.

У многих возникает вопрос: при чем здесь число π? Ведь π ≈ 3,14. Так вот, чтобы избежать путаницы, запомните простое, но очень важное правило:

Во всех тригонометрических функциях — синусе, косинусе, тангенсе и котангенсе — можно без ущерба для здоровья заменять число π на 180°. Пишется это так: π → 180°.

Обратите внимание: данное правило работает только для тригонометрических функций! Например, мы спокойно можем записать sin π = sin 180°. Но если мы хотим найти примерную длину отрезка l = 5π, придется считать: l = 5 · π ≈ 5 · 3,14 = 15,7.

Разумеется, существует и обратное правило — переход от градусной меры угла к радианной. Однако нас это сейчас не интересует, поскольку в задачах B11 такой переход не встречается.

Теперь взгляните на конкретные примеры:

Задача. Перейдите от радианной меры угла к градусной (значение тригонометрических функций вычислять не надо):

1. sin π/3;
2. cos 7π/6;
3. tg π;
4. sin π/4;
5. tg 2π/3;
6. ctg π/2;
7. sin 3π/2;
8. cos 5π/4.

Итак, перед нами восемь тригонометрических функций, аргументы которых заданы в радианах. Мы можем перейти от радианной меры аргументов к градусной по правилу: π → 180°. Имеем:

1. sin π/3 = sin 180/3 = sin 60°;
2. cos 7π/6 = cos (7 · 180/6) = cos 210°;
3. tg π = tg 180°;
4. sin π/4 = sin 180/4 = sin 45°;
5. tg 2π/3 = tg (2 · 180/3) = tg 120°;
6. ctg π/2 = ctg 180/2 = ctg 90°;
7. sin 3π/2 = sin (3 · 180/2) = sin 270°;
8. cos 5π/4 = cos (5 · 180/4) = cos 225°.

>

Итак, вместо непонятного множителя π мы получаем вполне вменяемое число, которое можно умножать и делить по стандартным правилам.

Границы координатных четвертей

Теперь, когда мы умеем заменять радианную меру углов градусной, попробуем переписать всю тригонометрическую окружность. Это будет ключом к решению задачи B11. Основные правила останутся прежними: «нулевой градус» совпадает с положительным направлением оси ОХ, а углы откладываются в направлении против часовой стрелки. Но числа, стоящие на границах координатных четвертей, станут другими. Взгляните:



Отныне вместо непонятных «пи» и «пи-пополам» используйте простую и понятную шкалу:

1. α ∈ (0°; 90°) ⇒ это угол I координатной четверти;
2. α ∈ (90°; 180°) ⇒ II координатная четверть;
3. α ∈ (180°; 270°) ⇒ III координатная четверть;
4. α ∈ (270°; 360°) ⇒ IV координатная четверть.

Хорошая новость состоит в том, что эти правила очень быстро откладываются в голове — стоит лишь немного потренироваться. И вы точно не забудете эти числа на ЕГЭ по математике, чего нельзя сказать про радианную меру.

Если же память на числа плохая, могу посоветовать одну хитрость. Взгляните еще раз на границы координатных четвертей: 90°, 180°, 270° и 360°. Первая из них — 90° — это прямой угол, знакомый еще из курса средней школы. Его вы точно не забудете. Остальные углы отличаются друг от друга на эти же самые 90°. Взгляните: 90° + 90° = 180°; 180° + 90° = 270°; 270° + 90° = 360°. Таким образом, даже если вы забудете эти числа, их всегда можно восстановить, если просто запомнить, что прямой угол — это 90°.

А теперь разберем конкретные примеры. Будем учиться искать координатные четверти быстро, поскольку от этого умения напрямую зависит решение задачи B11.

Задача. Определите, в какой координатной четверти находится аргумент тригонометрической функции:

1. sin 8π/9;
2. tg 12π/15;
3. cos 9π/10;
4. cos 7π/18;
5. sin 3π/5;
6. ctg 5π/3;
7. tg 4π/9;
8. cos 9π/20.

Для начала переведем все углы из радиан в градусы по правилу: π → 180°. А затем найдем координатную четверть, ориентируясь по границам: 90°, 180°, 270°, 360°. Имеем:

1. sin 8π/9 = sin (8 · 180/9) = sin 160°; т.к. 160° ∈ [90°; 180°], это II четверть;
2. tg 12π/15 = tg (12 · 180/15) = tg 144°; т.к. 144° ∈ [90°; 180°], это II четверть;
3. cos 9π/10 = cos (9 · 180/10) = cos 162°; т.к. 162° ∈ [90°; 180°], это II четверть;
4. cos 7π/18 = cos (7 · 180/18) = cos 70°; т.к. 70° ∈ [0°; 90°], это I четверть;
5. sin 3π/5 = sin (3 · 180/5) = sin 108°; т.к. 108° ∈ [90°; 180°], это II четверть;
6. ctg 5π/3 = ctg (5 · 180/3) = ctg 300°; т.к. 300° ∈ [270°; 360°], это IV четверть;
7. tg 4π/9 = tg (4 · 180/9) = tg 80°; т.к. 80° ∈ [0°; 90°], это I четверть;
8. cos 9π/20 = cos (9 · 180/20) = cos 81°; т.к. 81° ∈ [0°; 90°], это I четверть.

Как видите, далеко не всегда можно найти значение самой тригонометрической функции. Например, попробуйте вычислить cos 162° или sin 108°. Зато мы всегда можем определить, в какой координатной четверти находится данный угол.

Нестандартные углы и периодичность

До сих пор мы рассматривали углы α ∈ [0°; 360°]. Но что произойдет, если, например, угол α = 420°? А как насчет отрицательных углов? Такие углы редко встречаются на ЕГЭ по математике (по крайней мере, в части B), но лучше застраховать себя от подобных «неожиданностей», поэтому предлагаю разобрать и такие задачи. Тем более, схема решения практически ничем не отличается от «стандартных» углов.

Итак, что если угол α > 360°? Судя по тригонометрической окружности, точка сделает полный оборот — а затем пройдет еще чуть-чуть. Это самое «чуть-чуть» вычисляется очень просто. Достаточно отнять от исходного угла величину 360° (иногда это приходится делать несколько раз).

С отрицательными углами работаем аналогично. Если добавлять к отрицательному углу величину 360°, мы очень скоро получим новый угол α ∈ [0°; 360°]. Таким образом, вся схема решения выглядит следующим образом:

1. Перейти от радианной меры угла к градусной. Для этого достаточно сделать замену: π → 180°;
2. Если полученный угол оказался больше 360°, отнимаем от него по 360° до тех пор, пока новый угол не окажется на отрезке [0°; 360°];
3. Аналогично, если угол будет отрицательным, увеличиваем его на 360° до тех пор, пока он не попадет в отрезок [0°; 360°];
4. Выясняем, в какой координатной четверти находится полученный угол, ориентируясь на стандартные границы: 90°, 180°, 270° и 360°.

Задача. Определите, в какой координатной четверти находится аргумент тригонометрической функции:

1. sin 21π/6;
2. cos 19π/3;
3. sin (−25π/9);
4. tg (−11π/4).

Снова переводим все углы из радиан в градусы по правилу: π → 180°. Дальше уменьшаем или увеличиваем аргумент на 360° до тех пор, пока он не окажется на отрезке [0°; 360°]. И только затем выясняем координатную четверть. Получим:

1. sin 21π/6 = sin (23 · 180/6) = sin 690°. Очевидно, что 690° > 360°, поэтому выполняем преобразование: sin 690° → sin (690° − 360°) = sin 330°. Но 330° ∈ [270°; 360°], это IV четверть;
2. cos 19π/3 = cos (19 · 180/3) = cos 1140°. Поскольку 1140° > 360°, имеем: cos 1140° → cos (1140° − 360°) = cos 780° → cos (780° − 360°) = cos 420° → cos (420° − 360°) = cos 60°. Т.к. 60° ∈ [0°; 90°], это I четверть;
3. sin (−7π/9) = sin (−7 · 180/9) = sin (−140°). Но −140° < 0°, поэтому увеличиваем угол: sin (−140°) → sin (−140° + 360°) = sin 220°. Поскольку 220° ∈ [180°; 270°], это III четверть;
4. tg (−11π/4) = tg (−11 · 180/4) = tg (−495°). Т.к. −495° < 0°, начинаем увеличивать угол: tg (−495°) → tg (−495° + 360°) = tg (−135°) → tg (−135° + 360°) = tg 225°. Это уже нормальный угол. Т.к. 225° ∈ [180°; 270°], это III четверть.

Вот и все! Обратите внимание: во втором пункте пришлось вычитать 360° три раза — и только затем получился нормальный угол. Аналогично, в четвертом пункте пришлось прибавлять два раза по 360°, чтобы выйти на положительный угол. Таким образом, добавлять и вычитать углы иногда приходится много раз — это не должно настораживать.

В заключение хочу добавить, что если вы хорошо знаете математику и быстро ориентируетесь в радианных углах, то совсем необязательно переводить их в градусы. Однако большинство людей (и не только школьники) предпочитают именно градусную меру — знакомую еще со средней школы и, как следствие, более понятную.

Смотрите также:

1. Тест к уроку «Знаки тригонометрических функций» (1 вариант)
2. Знаки тригонометрических функций
3. Что такое логарифм
4. Комбинированные задачи B12
5. Задача B2: лекарство и таблетки
6. ЕГЭ 2022, задание 6. Касательная и уравнение с параметром

Угол может измеряться следующими величинами:

1. Градусами (и соответствующими ему величинами: угловыми минутами и секундами);
2. Радианами.

Градусная мера угла

Если взять развернутый угол (это два прямых угла) и поделить его на 180 частей, то одна такая часть будет называться одним градусом. Для того, чтобы измерить градусную меру угла, необходимо посчитать, сколько раз 1 градус входит в данный угол. Полученное число и будет ответом.

Если угол таков, что его нельзя измерить целым числом, либо же он меньше единичного угла, то используют такие меры измерения как угловые минуты и секунды.

Если градус поделить на 60 частей, то одной такой частью будет минута. В свою же очередь, если минуту разделить на те же 60 частей, то полученным числом будет 1 секунда.

Радианная мера угла

Радианом называют угол, образованный дугой окружности длинной равной радиусу этой окружности.

Длина окружности равна:

l=2⋅π⋅rl=2cdotpicdot r,

где rr — радиус этой окружности.

Тогда, разделив на радиус, получаем, что полный угол в радианах равен:

lr=2⋅π⋅rr=2⋅π радианfrac{l}{r}=frac{2cdotpicdot r}{r}=2cdotpitext{ радиан}

В градусах этот же угол равен, как известно, 360∘360^{circ}.

Отсюда находим связь между радианами и градусами:

2⋅π радиан=360∘2cdotpitext{ радиан}=360^{circ}

Это та главная формула, которая нужна, чтобы переводить градусы в радианы и наоборот.

Один радиан равен:

1 радиан=360∘2⋅π≈57.3∘1text{ радиан}=frac{360^{circ}}{2cdotpi}approx57.3^{circ}

Один радиан в минутах:

1 радиан=360∘2⋅π⋅60≈3438′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60approx3438′

Один радиан в секундах:

1 радиан=360∘2⋅π⋅60⋅60≈206280′′1text{ радиан}=frac{360^{circ}}{2cdotpi}cdot60cdot60approx206280»

Перевод градусов в радианы

Если по условию известна градусная мера угла, то чтобы перевести ее в радианную, нужно сделать следующие действия: умножить ее на πpi и разделить на 180.

Перевод градусов в радианы

y радиан=π180⋅xytext{ радиан}=frac{pi}{180}cdot x

xx — значение угла в градусах;
yy — значение того же угла в радианах.

Пример 1

Переведите 45 градусов в радианную меру измерения. Ответ округлите до десятой доли.

Решение

45∘=π180⋅45 радиан≈0.8 радиан45^{circ}=frac{pi}{180}cdot 45text{ радиан}approx0.8text{ радиан}

Ответ

0.8 радиан0.8text{ радиан}

Задача

Земля совершила треть от половины оборота вокруг Солнца. На какой угол в радианах она повернулась?

Решение

Найдем сначала этот угол в градусах. Полный угол составляет 360∘360^circ. Половина от полного оборота это 180∘180^{circ}. Нам же нужна треть этого угла, то есть:

180∘3=60∘frac{180^circ}{3}=60^circ

Земля отклонилась на угол 60∘60^circ от своего начального положения. Переведем теперь этот угол в радианы:

60∘=π180⋅60 радиан≈1 радиан60^circ=frac{pi}{180}cdot 60text{ радиан}approx1text{ радиан}

Решение

1 радиан1text{ радиан}

Перевод радиан в градусы

Чтобы перевести радианы в градусы, нужно умножить угол в радианах на 180 и разделить на πpi.

Перевод радиан в градусы

y∘=180π⋅xy^{circ}=frac{180}{pi}cdot x

xx — значение угла в радианах;
yy — значение того же угла в градусах.

Пример 2

Переведите 3 радиана в градусную меру угла.

Решение

3 радиана=180π⋅3≈172∘3text{ радиана}=frac{180}{pi}cdot3approx172^circ

Ответ

172∘172^circ

Ищете, где можно заказать задачу по математике недорого? Обратитесь к нашим экспертам в данной области!

Тест по теме «Перевод градусов в радианы и наоборот»

Онлайн калькулятор для перевода углов из радиан в градусы и обратно, интерактивная таблица градусов и радиан.
Формула перевода радианов в градусы: x°=х_рад⋅180/π

Точное число чему равен 1 радиан в градусах:
1 радиан = 57.29577951308 градуса

Радиан (обозначение: рад, rad) — угол, соответствующий дуге, длина которой равна её радиусу.

Основное понятие градуса и радиана и их взаимосвязь

В математике, такое определение, как угол принято измерять градусами и радианами.

Эти два измерения угла имеют взаимосвязь и необходимо четко понимать в чем она заключается.

В данном материале, мы постараемся разобраться и вывести

основную формулу для вычисления градусов в значение радиан, и соответственно в обратном порядке.

Радианная мера — угловое значение,где  за единицу берется угол в 1 радиан. А именно, вышеупомянутая мера любого угла — это соотношение принятого угла к радиану. Из этого следует, что величина полного значения угла равняется  [2 cdot pi] радиан.

 Определяем длину окружности, по стандартной формуле:

[ l=2 cdot pi cdot r ]

Чтобы определить полный угол в радианах проводим следующие действие: [frac{l}{r}=frac{2 cdot pi cdot r}{r}=2 cdot pi] , соответственно в градусах значение будет равно 360. Отсюда следует [2 cdot pi=360^{circ}].

Какова связь между градусами и радианами?

Угол имеет градусную и радианную меру. Зная ее, можно установить связь между градусом и радианом.

Например, возьмем для примера центральный угол, который примыкает к диаметру окружности радиуса R.

Нам необходимо вычислить значение радианной меры угла. Для решения этой задачи, длину самой дуги поделить на длину радиуса окружности.

Заданный угол равен [pi] радиан. Данный угол 180 градусов и по законам математики, является развернутым. Отсюда следует, что  180 градусов эквивалентно [pi] радиан.

Данную связь можно выразить через формулу.

[text { п рад }=180 text { град. }]

Перевод радианов в градусы и соответственно в обратном порядке

Для перевода радиан в градусы и наоборот необходимо знать и применять на практике следующие формулы:

Один радиан равен: [frac{360^{circ}}{2 cdot pi} approx 57^{circ}];

Один радиан в минутах: [frac{360^{circ}}{2 cdot pi} cdot 60 approx 3438];

Один радиан в секундах: [frac{360^{circ}}{2 cdot pi} cdot 3600 approx 206280].

[ 1 text { радиан }=left(frac{180}{pi}right) text { градусов. } ]

[ 1 text { градус }=left(frac{pi}{180}right) text { рад. } ]

Рассмотрим на конкретном примере:

[1 text { радиан }=left(frac{180}{pi}right)=left(frac{180}{3,14}right)=57,324] следовательно в 1 радиане 57 градусов.

[1 text { градус }=left(frac{pi}{180}right) text { радиан }=left(frac{3,14}{180}right)=0,017] радиан (сокращенно рад.).

[text { х радиан }=left(frac{chi cdot 180}{pi}right)], дословно будет звучать как: 180 * умножить на числовое значение угла и раздели.

Соответствие градусов и радиан принято, для удобства решения сводить в таблицу.

Пример, приведен в таблице 1.

Таблица 1. Соотношение значений.

Числовые значения в градусах	Соответствующие данные радиан
1°	0,018
2°	0,035

Как мы видим  изученная тема не очень сложная. Достаточно знать основные формулы и в расчетах, и проблем не должно возникать.

Для более лучшего закрепления разберемся и решим несколько задач по вычислении градусов и радианов углов.

Задача №1

Переведите 35 градусов в радианы.

[ 35^{circ}=left(frac{pi}{180}right) cdot 35 text { радиан }=0,6 text { рад } ]

Ответ: 35°=0,6 рад.

Задача №2

Переведите 55 градусов в радианы.

[55^{circ}=left(frac{pi}{180}right) cdot 55 text { радиан}=0,9 text { paд }]

Ответ: 55°=0,9 рад.

Задача №3

Необходимо вычислить значение третьей половины полного угла.

Для начала определяем угол в градусах.

Нужно определить третью часть угла. Следовательно полный угол равняется 360 градусов, половина 180, а треть [frac{180}{3}=60] градусов.

Пользуясь формулой из задач №1 и 2, определяем значение в радианах.

[ 60^{circ}=left(frac{pi}{180}right) cdot 60 text { радиан }=1 text { рад } ]

Ответ: 1 рад.

Radians to degrees is a type of transformation used in geometry to convert angle measurements. There are two alternative methods for measuring an angle. Radians and degrees are the two units used to measure angles. Radian is the most commonly used unit in trigonometry. Various types of angles are measured in radians and then converted to degrees using a formula. This formula is discussed below.

Radians to Degrees Conversion

Two separate ways are used to measure angles. A right angle is split into 90 equal portions, which are referred to as degrees, in the Sexagesimal System. Each degree is split into 60 equal parts called minutes, which are divided further into 60 equal parts called seconds. Degree to Radian conversion can also be learned here.

• 60” = 1 minute (1’)
• 90° = 1 right angle

Radians

Angle subtended to center of a circle by radius after a complete rotation is called 2π radians. The angle in radians made by radius at the center of the circle is the ratio of length of an arc to length of a radius. If the length of the arc is equal to the length of the radius, the angle subtended at the center is called 1 radian. The unit of a radian is rad. Radian is the SI unit for measuring angles.

Degrees

Angles can also be measured in degrees. One revolution divides the circle into 360 equal parts and each part is equal to a degree. Thus, angle subtended at the center of a circle after one complete rotation is 360°. Symbol used to denote degrees is ‘°’. Degrees is not an SI unit for measuring an angle, but it is the most commonly used unit to measure an angle.

By comparing the measures of an angle for a complete rotation

• 360 Degrees = 2π Radians
• 180 Degrees = π Radians

How to Convert Degrees to Radians?

Value of 180° is equal to π radians. For converting the given angle from degrees to radians, we multiply the value of the angle in degrees by a factor of π/180.

Where the value of π = 22/7 or 3.14

Steps shown below are used for the conversion of angle in degrees to radians.

Step 1: Mark the value of the given angle in degrees

Step 2: Multiply the value obtained from the above step by π/180

Step 3: Solve the expression and rationalize the answer

Step 4: The result obtained is the measure of the angle in radian

Example: Convert 60 degrees to radians.

Solution: 

Given angle is 60 degrees

Angle in radian = Angle in degree x (π/180)

                           = 60 x (π/180)

                           = π/3

Hence, 60 degrees is equal to π/3 in radian.

Radians to Degrees Formula

Radians to Degrees formula converts the value of angle in radians to degrees. To convert the angle in radians to degrees we multiply the value in radians by 180°/π. Angles are used in two units: degrees and radians, 1 degree is expressed as 1° whereas 1 radian is expressed 1^c or 1 i.e. no unit is also used to express angle in radian. The formula for changing the angle in radians to degrees is:

Angle in Radians × 180°/π = Angle in Degrees

2π radians = 360°

π radians = 180°

1 radian = 180/π degrees = 57.296 degrees

Radians to Degrees Conversion Table

The table is given below shows the values angle in radian and their respective value in degree.

Angle in radian	Angle in degree
0	0°
π/6	30°
π/4	45°
π/3	60°
π/2	90°
π	180º
(3π)/2	270º
2π	360º

Solved Examples on Radians to Degrees

Example 1: Convert 9π/5 radians to degrees.

Solution:

Since, π radians = 180° or 1 radian = 1c = (180/π)°

Hence, (9π/5)^c = (9π/5 × 180/π)° = 324°

Thus, (9π/5)^c = 324^o

Example 2: Convert −5π/6 radians into degrees.

Solution:

We know that π radians = 180° or 1 radian = 1c = (180/π)°

Hence, (−5π/6)^c = (−5π/6 × 180/π)° = −150°

Thus, (9π/5)^c = −150°

Example 3: Convert 18π/5 into degrees.

Solution:

We know that π radians = 180° or 1 radian = 1c = (180/π)°

Hence, (18π/5)^c = (18π/5 × 180/π)° = 648°

Thus, (18π/5)^c = 648°

Example 4: Convert −3 radians into degrees.

Solution:

We know that π radians = 180° or 1 radian = 1c = (180/π)°

Hence, (−3)^c = (−3 × 180/π)° = (180 × 7 × −3/22)° = (−1719/11) = −171°(9 × 60/11)’ = −171°49’5”

Thus, (−3)^c = −171^o49’5”

Example 5: Convert 11 radians into degrees.

Solution:

We know that π radians = 180° or 1 radian = 1^c = (180/π)°

Hence, (11)^c = (11 × 180/π)° = (11 × 180 × 7/22) = 630°

Thus, (11)^c = 630°

Example 6: Convert 1 radian to degrees.

Solution:

We know that π radians = 180° or 1 radian = 1^c = (180/π)°

Hence, (1)^c = (1 × 180/π)° = (180 × 7/22) = 57°(3 × 60/11) = 57°16′(4 × 60/11)” = 57°16’21”

Thus, (1)^c = 57^o16’21”

FAQs on Radians to Degrees

Question 1: What is the Difference between Radians and Degrees?

Answer:

Radians and Degrees both are units used to measure angles. Radian is the SI unit for measurement of angle, whereas degree is the general unit used to measure angles. The relationship between them is π rad = 180°

Question 2: What is the Radian of 1 Degree?

Answer:

A complete revolution of a circle is equal to 2π radians that is equivalent to 360°, i.e. 2π rad = 360°
1° = 2π/360 rad
Thus, 1 degree is equal to π/180 radians.

Question 3: What is the value of 1 radian in degrees?

Answer:

We know that π radians are equal to 180 degrees. So, 1 radian = 57^o16’21”

Question 4: Is π radians equal to 180 degrees?

Answer:

Yes, we know that 2π radians are equal to 360 degrees. Thus, π radians equal 180 degrees.

Question 5: Why are 360 degrees equal to 2π?

Answer:

The Right angle is equal to π/2 radians. One complete revolution is considered as the length of an entire circumference of a circle divided by its radius, or 2πr / r. Thus 2π radians equals to 360 degrees,

Related Article

• Types of angles
• Pair of Angles