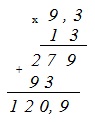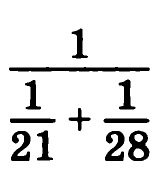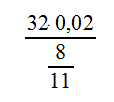Как найти значение выражения 9 класс огэ - Исправление недочетов и поиск решений вместе с Examum.ru

Задача 6 ОГЭ по математике называется «Числа и вычисления». Это действия с обыкновенными и с десятичными дробями. Действия со степенями. Сравнение чисел.

Приступим к решению задач.

Пример 1. Найдите значение выражения $frac{0,8}{1-frac{1}{9}}.$

Решение. Вспоминаем, что при вычитании дробей нужно их привести к общему знаменателю, а при делении дробей первую из них умножаем на перевёрнутую вторую.

Посчитаем, чему равен знаменатель.

$1-frac{1}{9}= frac{9}{9}-frac{1}{9}=frac{8}{9}$

Получим:
$frac{0,8}{1-frac{1}{9}}=frac{8}{10}:frac{8}{9}=frac{8}{10}cdot frac{9}{8}=frac{9}{10}=0,9 .$

Ответ: 0,9.

Пример 2. Соотнесите обыкновенные дроби с равными им десятичными дробями.

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Решение. Каждую из данных обыкновенных дробей можно представить в виде десятичной, например, используя деление в столбик.

Итак, деление выполнено. Сопоставим полученные результаты:

Ответ: 4312.

Замечание 1. Преобразование обыкновенных дробей в десятичные можно произвести и без деления в столбик. Т. к. любая десятичная дробь записывается как обыкновенная со знаменателем 10, 100, 1000 и т. д., то данные обыкновенные дроби можно «доделать» до десятичных. Для этого используем основное свойство дроби: дробь не изменится, если её числитель и знаменатель домножить на одно и тоже число.

Замечание 2. В этой задаче можно было, наоборот, преобразовывать заданные десятичные дроби в обыкновенные путём упрощения, т. е. сокращения числителя и знаменателя.

Выбирайте любой способ. Здесь важен правильный результат!

Для выполнения следующих заданий нам потребуются свойства степеней. Напомним основные из них.

Степенью называется выражение вида $boldsymbol{a^c.}$

Здесь a — основание степени, c — показатель степени.
По определению, a^1=a.

Возвести число в квадрат — значит умножить его само на себя:

Возвести число в куб — значит умножить его само на себя три раза:

Возвести число в натуральную степень n — значит умножить его само на себя n раз:

$a^n=underbrace{acdot acdot acdot acdot dots cdot a}_{n}$

По определению, ${ a}^0=1.$

Это верно для ane 0. Выражение 0^0 не определено.

Определим, что такое степень с целым отрицательным показателем.

$a^{-1}=frac{1}{a}$

$a^{-2}=frac{1}{a^2}$

$a^{-n}=frac{1}{a^n}$

Конечно, все это верно для ane 0, поскольку на ноль делить нельзя.

Соберем свойства степеней и основные формулы в одной таблице.


$a^ncdot a^m=a^{n+m}$	При перемножении степеней с одинаковыми основаниями показатели степеней складываются.
$frac{a^n}{a^m}=a^{n-m}$	При делении степеней с одинаковыми основаниями показатели степеней вычитаются.
$(a^n)^m=a^{ncdot m}$	При возведении степени в степень показатели степеней перемножаются.
$a^{-n}=frac{1}{a^n}$	При возведении в отрицательную степень получаем дробь, где единица делится на степень с положительным показателем.
	При возведении произведения двух множителей в степень каждый из этих множителей возводится в заданную степень.
$(frac{a}{b})^n=frac{a^n}{b^n}$	При возведении дроби в степень получается дробь, числитель и знаменатель которой возведены в заданную степень.
$(frac{a}{b})^{-n}=(frac{b}{a})^n$	При возведении дроби в отрицательную степень дробь переворачивается, а показатель степени становится положительным.

Пример 3. Найдите значение выражения ${{(16cdot 10}^{-2})}^2cdot {(13cdot 10}^4).$

Решение. Вычислим, используя свойства степеней:

${{(16cdot 10}^{-2})}^2cdot {(13cdot 10}^4)={16}^2cdot {left({10}^{-2}right)}^2cdot {13cdot 10}^4=256cdot 13cdot ({10}^{-4}cdot {10}^4)=3 328cdot {10}^0=3328.$

Ответ: 3328.

Пример 4. Найдите значение выражения ${5cdot 10}^{-1}+{6cdot 10}^{-2}+{4cdot 10}^{-4}.$

Решение. Вычислим, используя свойства степеней:

${5cdot 10}^{-1}+{6cdot 10}^{-2}+{4cdot 10}^{-4}=5cdot frac{1}{{10}^1}+6cdot frac{1}{{10}^2}+4cdot frac{1}{{10}^4}=$

Ответ: 0,5604.

Пример 5. Найдите значение выражения $frac{3^8cdot 3^5}{3^9}.$

Решение. Вычислим, используя свойства степеней:

$frac{3^8cdot 3^5}{3^9}=frac{3^{8+5}}{3^9}=frac{3^{13}}{3^9}=3^{13-9}=3^4=81.$

Ответ: 81.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 6 ОГЭ по математике. Числа и вычисления.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

В задании № (6) ОГЭ нужно найти значение числового выражения.

Пример:

найди значение выражения

1,2×(18+0,015)

За правильное выполнение задания даётся (1) первичный балл. За неправильное ставится (0) баллов.

Алгоритм выполнения задания

Определяем порядок вычислений, если нужно выполнить несколько математических действий.

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Проводим вычисления строго по порядку, не округляя.
Записываем ответ.

Обрати внимание!

Ответом является число или последовательность цифр, которую необходимо записать без пробелов, запятых и других дополнительных символов. Если получилась обыкновенная дробь, то ответ запиши в виде десятичной.

Как решить задание из примера?

Определим, в каком порядке выполним вычисления 1,2×(18+0,015).
Сначала — действие в скобках (сложение), а затем — умножение.
Чтобы выполнить сложение, переведём 18 в десятичную дробь (нужно числитель разделить уголком на знаменатель без остатка). 1,0−8¯8¯0,12520−16¯40−40¯018=0,125.
Выполним сложение двух десятичных дробей. 0,125+0,015 (=) 0,14.
Выполним умножение. 1,2
·0,14=0,168.
Запишем ответ в виде десятичной дроби, не округляя.
Ответ: 0,168.

Источник

Числа и высисления (действия с дробями, степени)

Задание 6 ОГЭ по математике.

Напоминаем правила операций с обыкновенными дробями:

Пример 1.Найдите
значение выражения $frac{0,8}{1-frac{1}{9}}.$

Решение. Вспоминаем,
что при вычитании дробей нужно их привести к общему знаменателю, а при делении
дробей первую из них умножаем на перевёрнутую вторую.

Посчитаем,
чему равен знаменатель.

$1-frac{1}{9}= frac{9}{9}-frac{1}{9}=frac{8}{9}$

Получим:
$frac{0,8}{1-frac{1}{9}}=frac{8}{10}:frac{8}{9}=frac{8}{10}cdot frac{9}{8}=frac{9}{10}=0,9 .$

Ответ:
0,9.

Пример
2.Соотнесите обыкновенные дроби с равными им десятичными дробями.

А. $frac{5}{8}$	Б. $frac{3}{25}$	В. $frac{1}{2}$	Г. $frac{1}{50}$
1) 0,5	2) 0,02	3) 0,12	4) 0,625

Запишите
в ответ цифры, расположив их в порядке, соответствующем буквам:

Решение.Каждую
из данных обыкновенных дробей можно представить в виде десятичной, например,
используя деление в столбик.

Итак,
деление выполнено. Сопоставим полученные результаты:

Ответ:
4312.

Степенью
называется выражение вида $boldsymbol{a^c.}$

Здесь
a — основание степени, c — показатель степени.
По определению,

Возвести
число в квадрат — значит умножить его само на себя:

Возвести
число в куб — значит умножить его само на себя три раза:

Возвести
число в натуральную степень n — значит умножить его само
на себя n раз:

$a^n=underbrace{acdot acdot acdot acdot dots cdot a}_{n}$

По
определению, ${ a}^0=1.$

Это
верно для Выражение не
определено.

Определим,
что такое степень с целым отрицательным показателем.

$a^{-1}=frac{1}{a}$

$a^{-2}=frac{1}{a^2}$

$a^{-n}=frac{1}{a^n}$

Конечно,
все это верно для поскольку на ноль делить нельзя.

Свойства
степеней и основные формулы


$a^ncdot a^m=a^{n+m}$	При перемножении степеней с одинаковыми основаниями показатели степеней складываются.
$frac{a^n}{a^m}=a^{n-m}$	При делении степеней с одинаковыми основаниями показатели степеней вычитаются.
$(a^n)^m=a^{ncdot m}$	При возведении степени в степень показатели степеней перемножаются.
$a^{-n}=frac{1}{a^n}$	При возведении в отрицательную степень получаем дробь, где единица делится на степень с положительным показателем.
	При возведении произведения двух множителей в степень каждый из этих множителей возводится в заданную степень.
$(frac{a}{b})^n=frac{a^n}{b^n}$	При возведении дроби в степень получается дробь, числитель и знаменатель которой возведены в заданную степень.
$(frac{a}{b})^{-n}=(frac{b}{a})^n$	При возведении дроби в отрицательную степень дробь переворачивается, а показатель степени становится положительным.

Пример
3.Найдите значение выражения ${{(16cdot 10}^{-2})}^2cdot {(13cdot 10}^4).$

Решение.
Вычислим, используя свойства степеней:

Ответ:
3328.

Пример
4. Найдите значение выражения ${5cdot 10}^{-1}+{6cdot 10}^{-2}+{4cdot 10}^{-4}.$

Решение.
Вычислим, используя свойства степеней:

Ответ:
0,5604.

Пример
5. Найдите значение выражения $frac{3^8cdot 3^5}{3^9}.$

Решение.
Вычислим, используя свойства степеней:

$frac{3^8cdot 3^5}{3^9}=frac{3^{8+5}}{3^9}=frac{3^{13}}{3^9}=3^{13-9}=3^4=81.$

Ответ:
81.

Источник

Шестое задание проверяет наши умения проведения вычислений. Это самое простое задание из всего модуля и требует от нас только знания арифметики. В первом задании арифметические действия будут самыми простыми. В демонстрационном варианте ОГЭ предлагается сложить две дроби: обыкновенную и десятичную. Тем не менее, в соответствии с документами о проведении ОГЭ, учащиеся должны быть готовы и к выполнению некоторых других несложных заданий. Ответом в первом задании является целое число или конечная десятичная дробь.

Итак, для успешного выполнения необходимо помнить:

порядок проведения арифметических операций – сначала производятся действия в скобках, затем возведение в степень или извлечение корня, затем умножения и деления, а затем вычитания и сложения.
правила умножения и деления в столбик
правила вычисления обыкновенных дробей

Напоминаем правила операций с обыкновенными дробями:

Рекомендуем вычислить отдельно числитель и знаменатель, а затем разделить числитель на знаменатель. Остальные рекомендации смотрите ниже при разборе типовых вариантов первого задания ОГЭ по математике. 🙂

Задание 6OM21R

Найти значение выражения 4,9 – 9,4.

Выполним вычитание десятичных дробей, где 9,4 больше по модулю, значит, ответ будет отрицательным. Итак, – (9,4 – 4,9)= – 4,5

Ответ: -4,5

pазбирался: Даниил Романович | обсудить разбор

Задание OM0606o

Найдите значение выражения:

–0,3·(–10)⁴+4·(–10)²–59

Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.

–0,3·(–10)⁴+4·(–10)²–59 =

Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:

= –0,3·10000+4·100–59 =

Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:

= –3000+400–59 =

Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:

= –2600–59 =

Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:

= –(2600+59) = –2659

Ответ: -2659

pазбирался: Даниил Романович | обсудить разбор

Задание OM0605o

Найдите значение выражения:

–13•(–9,3)–7,8

Это задание требует простого умения выполнять арифметические действия с десятичными дробями.

–13·(–9,3)–7,8 =

Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:

Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:

= 120,9–7,8 =

Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:

= 113,1

Ответ: 113,1

pазбирался: Даниил Романович | обсудить разбор

Задание OM0604o

Найдите значение выражения: ¼ + 0,07

К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной.

Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем:

0,25 + 0,07 = 0,32

Ответ: 0,32

pазбирался: Даниил Романович | обсудить разбор

Задание OM0603o

Найдите значение выражения: 1-3

Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:

1/21 + 1/28 = 4/84 + 3/84

Затем складываем:

4/84 + 3/84 = 7/84

Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:

1 / ( 7 / 84 ) = 1 •84/7 = 84/7

Далее остается поделить 84 на 7:

84 / 7 = 12

Ответ: 12

pазбирался: Даниил Романович | обсудить разбор

Задание OM0602o

Найдите значение выражения:

Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.

1/3 • (6 • (1/3) — 17 )

Проведя вычисления в скобках, получим:

1/3 • ( 6 • (1/3) — 17 ) = 1/3 • (6 /3 — 17 ) = 1/3 • ( 2 — 17 ) = 1/3 • ( -15 )

Теперь умножим полученное значение -15 на 1/3:

1/3 • ( -15 ) = -5

Ответ: -5

pазбирался: Даниил Романович | обсудить разбор

Задание OM0601o

Найдите значение выражения:

Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.

Вычислим значение знаменателя:

4,5 • 2,5

Можно произвести вычисления в столбик, тогда получим:

4,5 • 2,5 = 11,25

Либо перевести дробь к простому виду:

4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4

Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:

9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )

9 и 45 можно сократить на 9:

( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8

Ответ: 0,8

pазбирался: Даниил Романович | обсудить разбор

Источник

Перейти к содержанию

Опубликовано 31.03.2015

Найти значение выражения обычно предлагают школьникам в первой части ОГЭ (ГИА) и они достаточно просты. Для решения такого задания нужно уметь вычислять, то есть знать таблицу умножения, уметь умножать десятичные числа, понимать смысл дроби и уметь работать со степенями. Таким образом, первое задание проверяет сразу несколько умений школьника. Найти значение выражения, не умея работать с числами и степенями, невозможно.

Найти значение выражения

$( 6,8 cdot 10^{-3})(2 cdot 10^{-3})$ Решение: Перемножим 6,8 на 2, получим 13,6. Теперь умножим $10^{-3}$ на $10^{-3}$ основания степеней одинаковые, значит, складываем показатели степеней.
Получим В итоге получим $13,6 cdot 10^{-6}$ Ответ: $13,6 cdot 10^{-6}$

Найти значение выражения

$0,9 cdot (-10)^{2}-120$ Решение: $(-10)^{2}=100$ тогда $0,9 cdot (-10)^{2}-120 = 0,9 cdot 100 = 90-120=-30$ Ответ: -30.

Найти значение выражения

$3 cdot (10)^{-1}+5cdot (10)^{-3}+4cdot (10)^{-4}$ Решение: перепишем данное выражение в следующем виде Почему мы смогли так записать? Потому что мы использовали свойство степени: $10^{-n}= frac{1}{10^{n}}$ Тогда в нашем задании мы получаем $10^{-1}= frac{1}{10^{1}}$ или $10^{-1}= 0,1$ $10^{-3}= frac{1}{10^{3}}$ или $10^{-3}= 0,001$ $10^{-4}= frac{1}{10^{4}}$ или $10^{-4}= 0,0001$ Итак, имеем: Ответ: 0,3054.

Найти значение выражения

Решение: Можно просто перемножить 6,8 на 7,5, а затем, полученное число разделить столбиком на 8,5. А можно перевести десятичные дроби в обыкновенные и попробовать упростить.
$displaystyle frac{6,8 cdot 7,5}{8,5}= frac{frac{68}{10} cdot frac{75}{10}}{frac{85}{10}}= frac{68 cdot 75 cdot 10}{100 cdot 85}= frac{68 cdot 75}{10 cdot 85}$ 68 и 10 сократим на 2, а 75 и 85 на 5, тогда получим: $displaystyle frac{68 cdot 75}{10 cdot 85}= frac {34 cdot 15}{5 cdot 17}=frac {2 cdot 15}{5 cdot 1}= frac {2 cdot 3}{1 cdot 1}= 2 cdot 3 = 6$ Ответ: 6.

Найти значение выражения

Решение: $displaystyle frac{32 cdot 0,02}{frac{8}{11}}= frac{32 cdot frac{2}{100}}{frac {8}{11}}= frac{32 cdot 2 cdot 11}{100 cdot 8}=frac{4 cdot 11}{50}=frac {44}{50}=frac {22}{25}$ Ответ: $displaystyle frac{22}{25}$

( 4 оценки, среднее 4 из 5 )

Источник