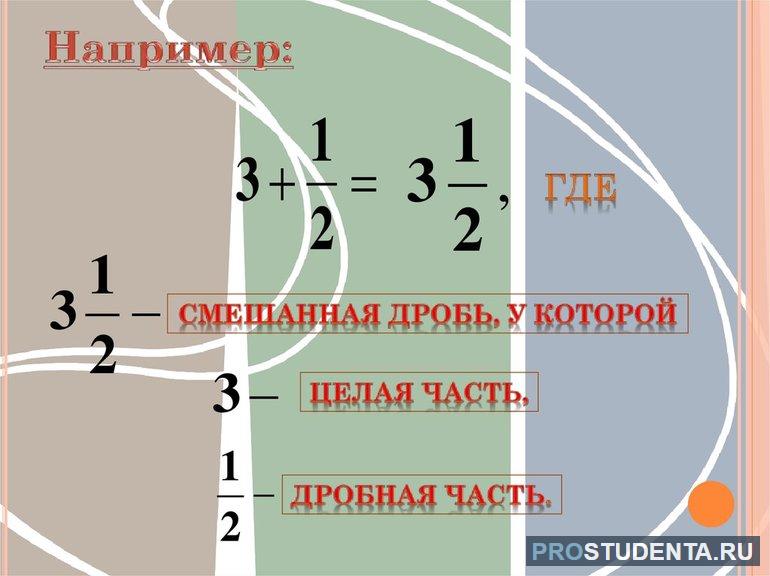
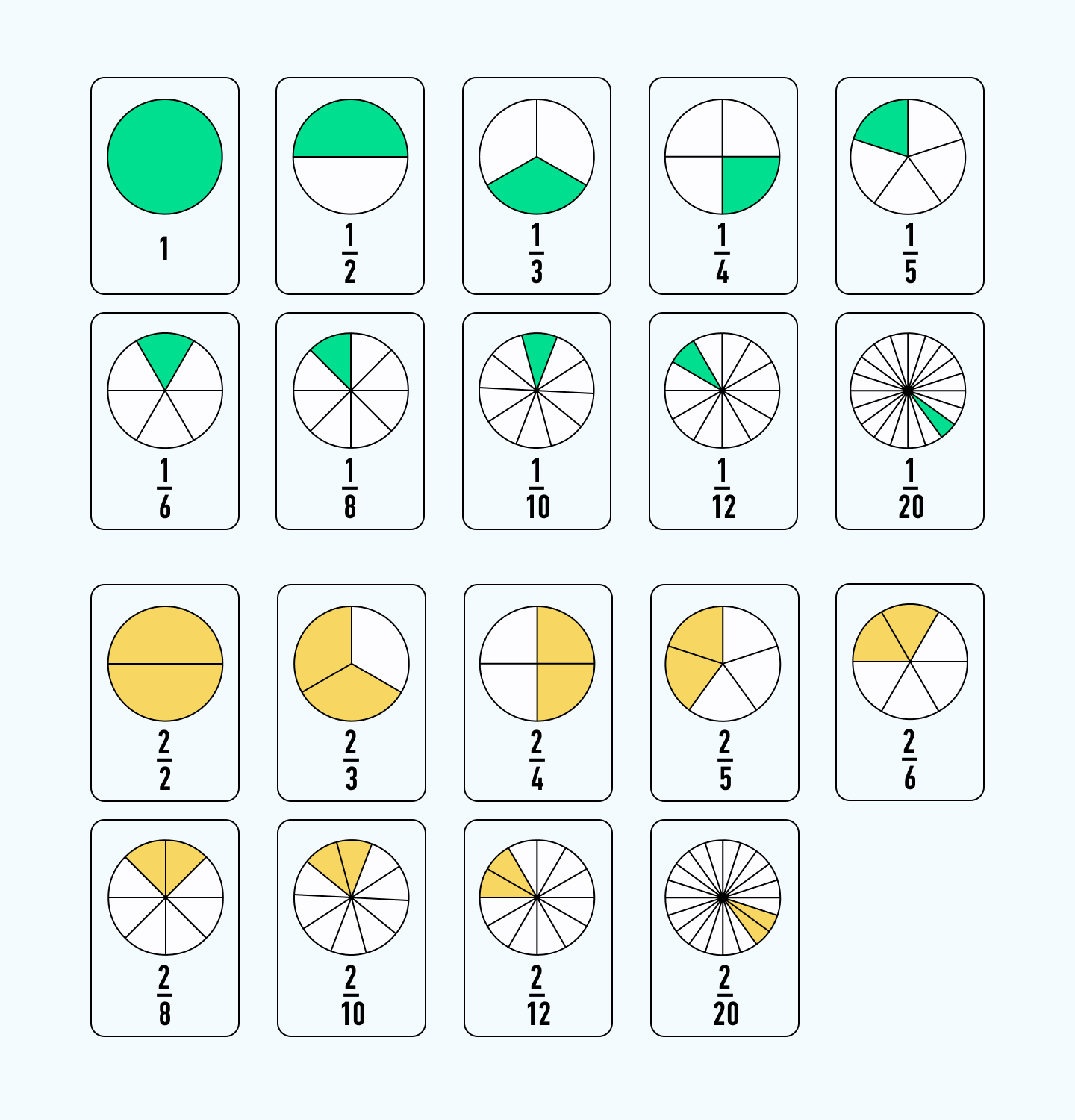
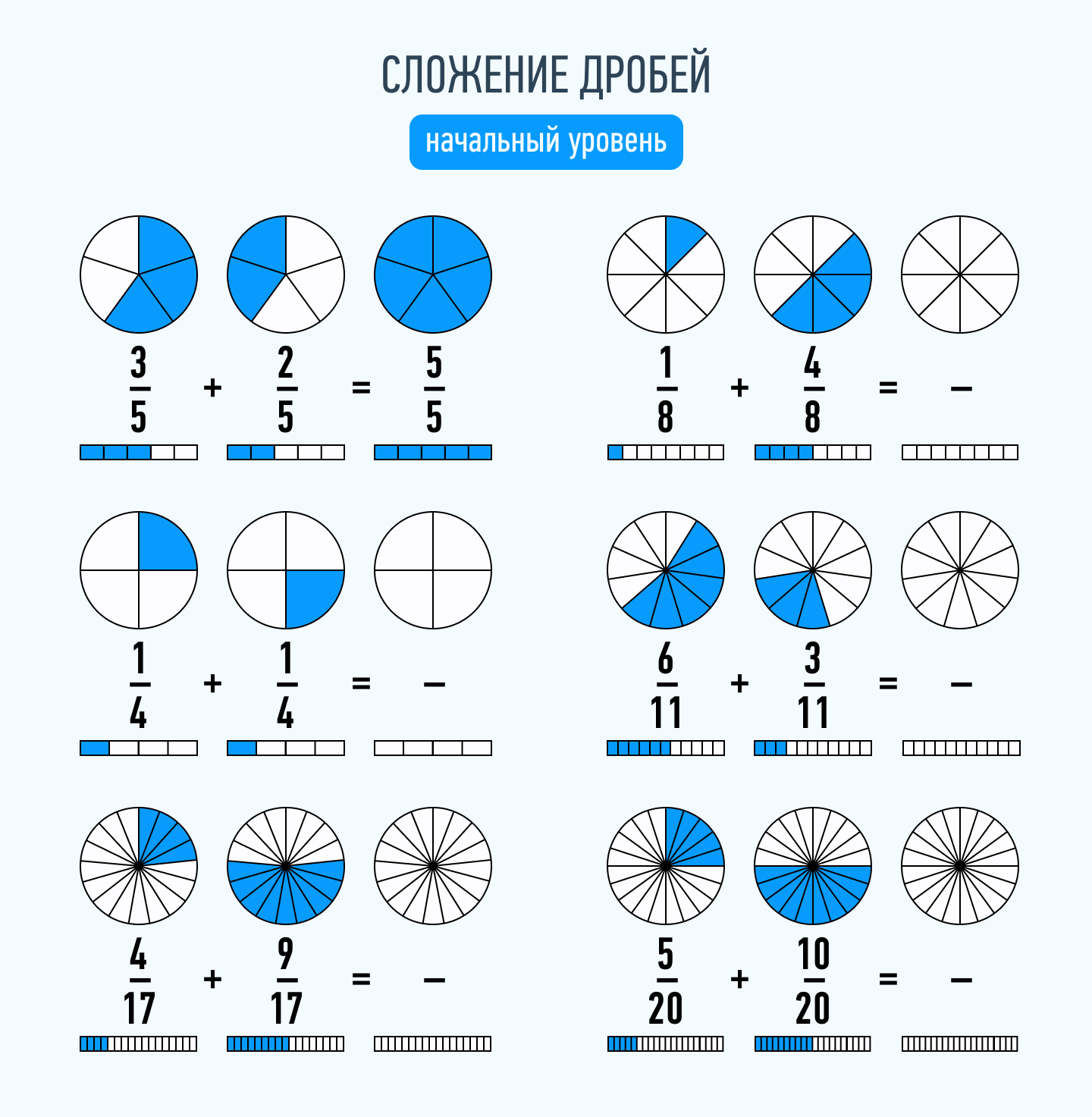
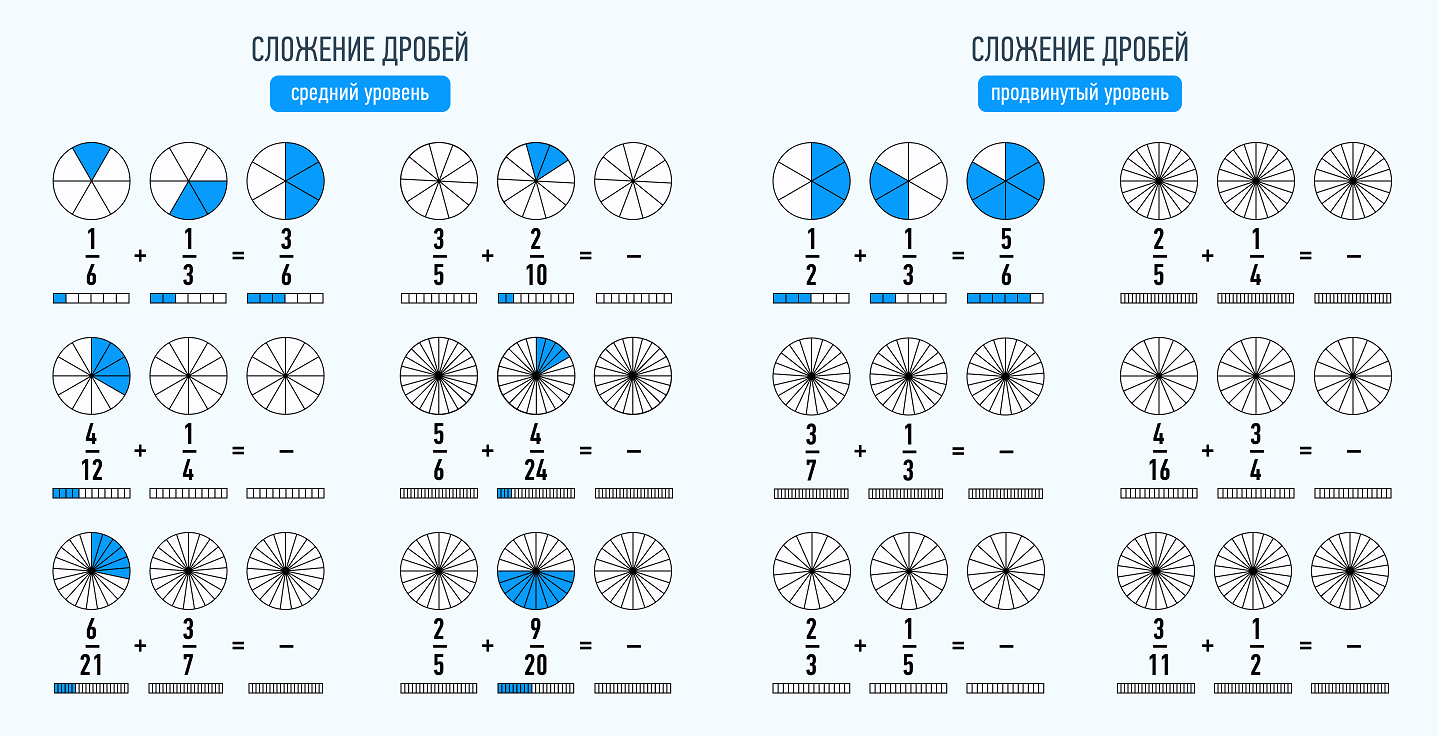
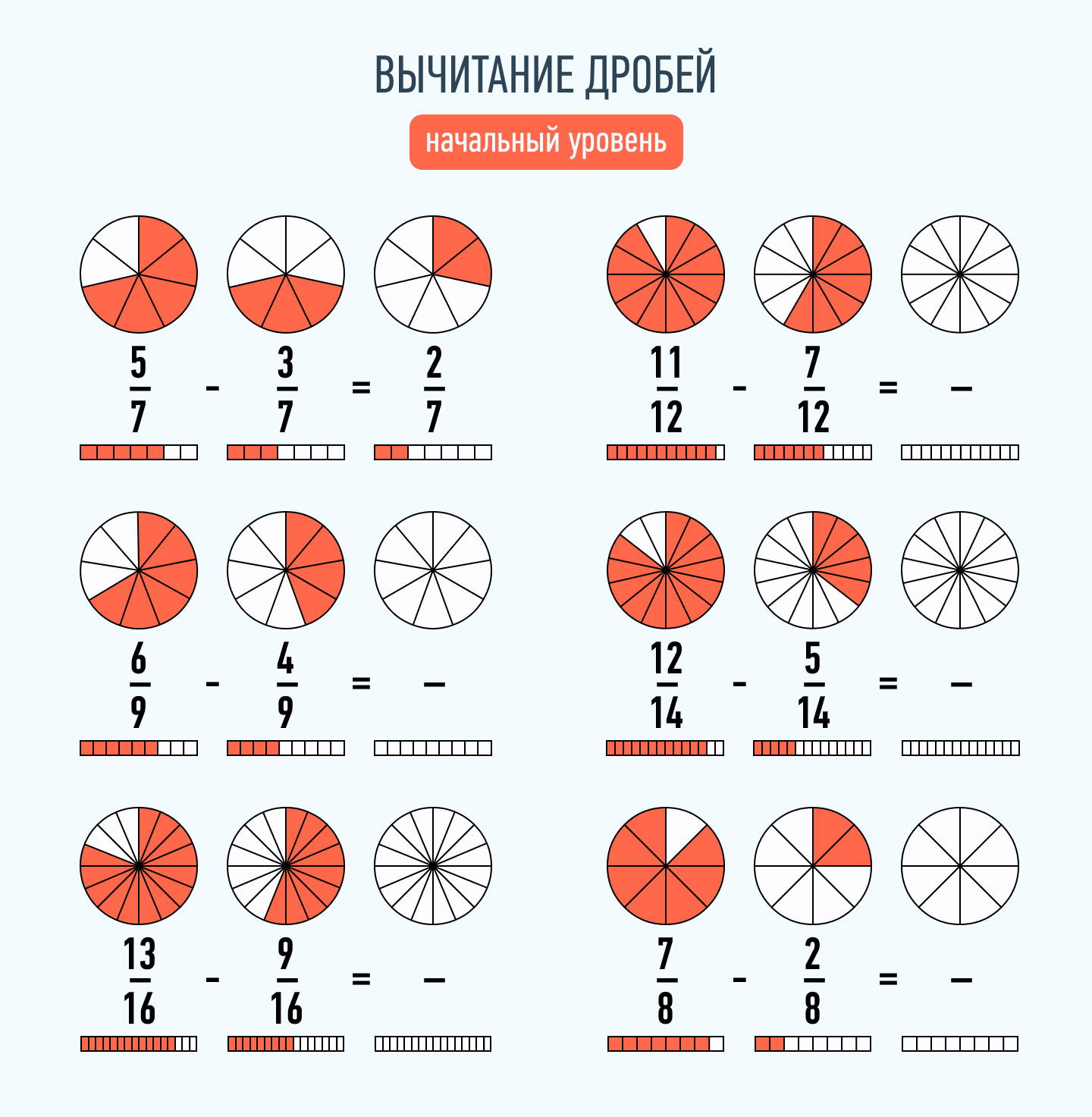
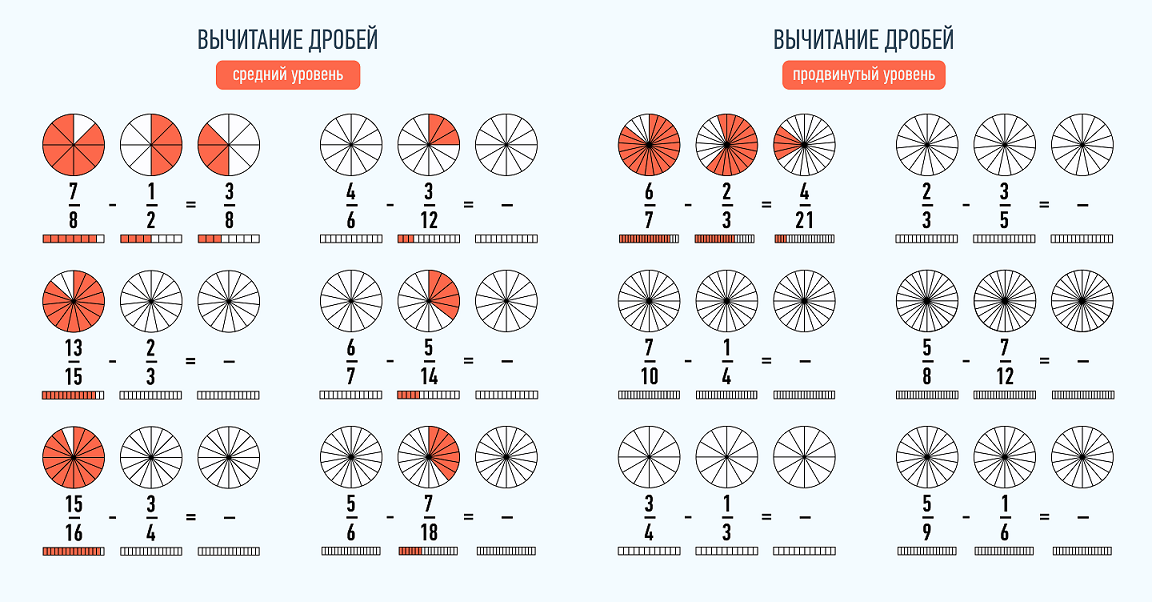
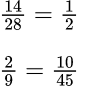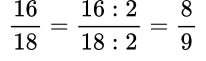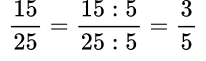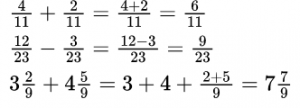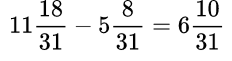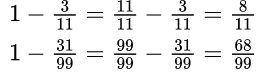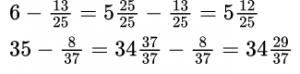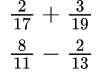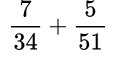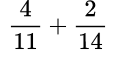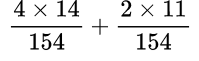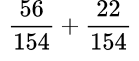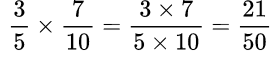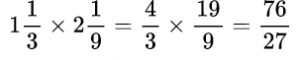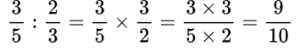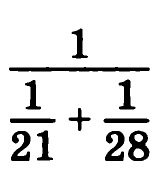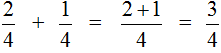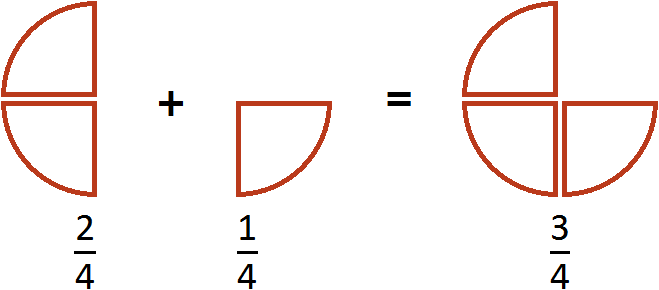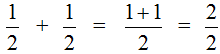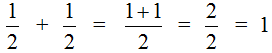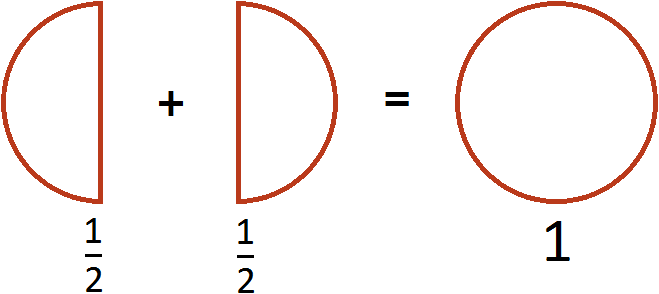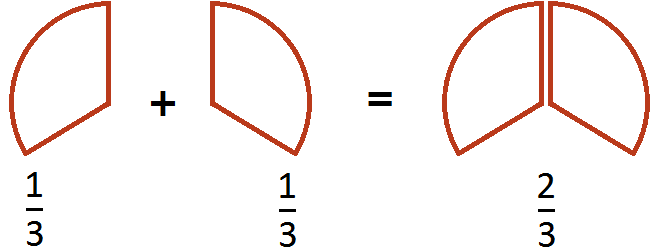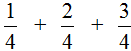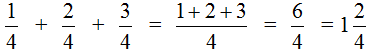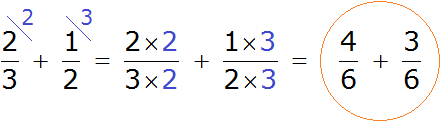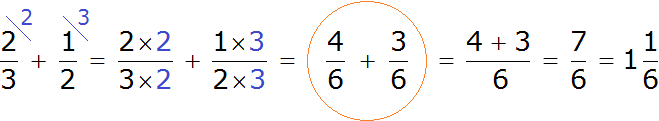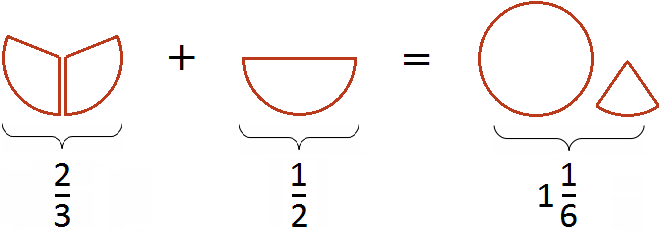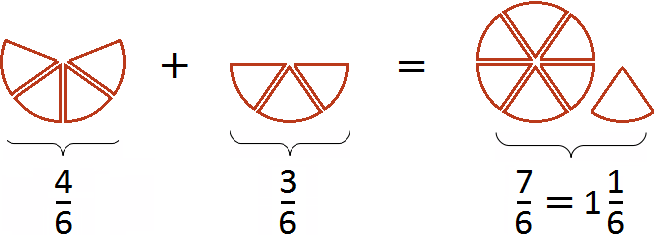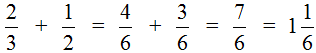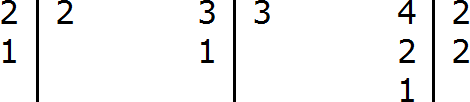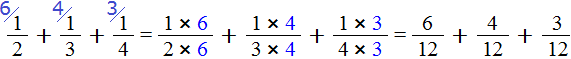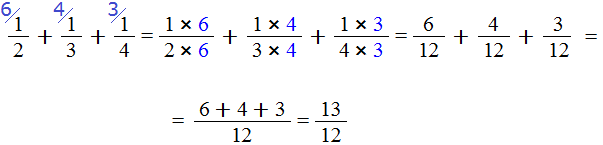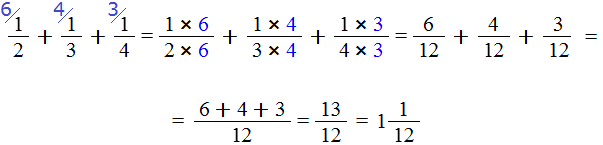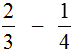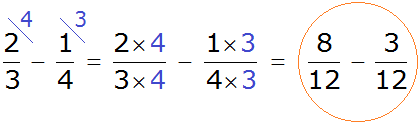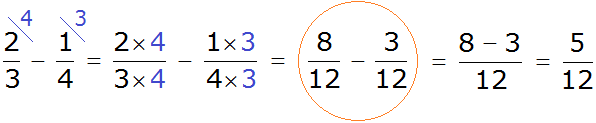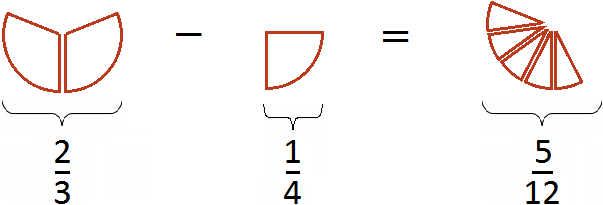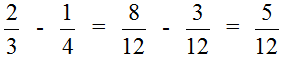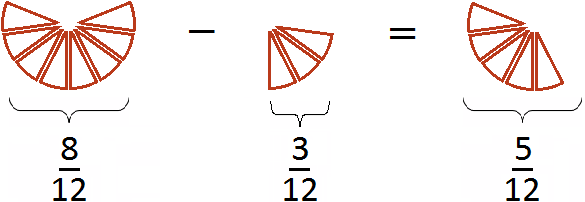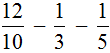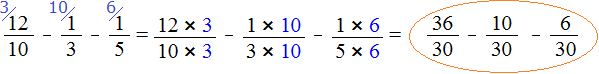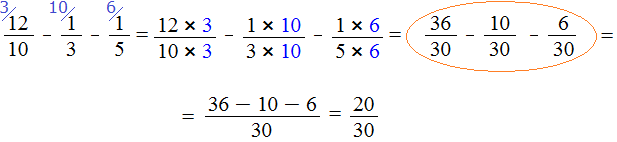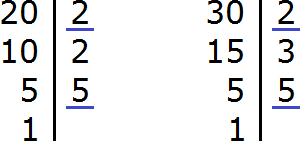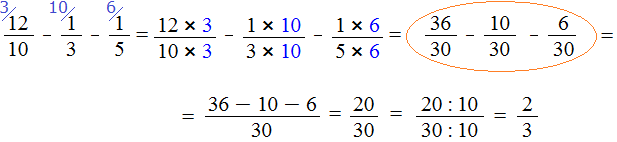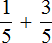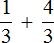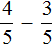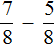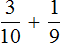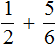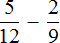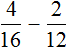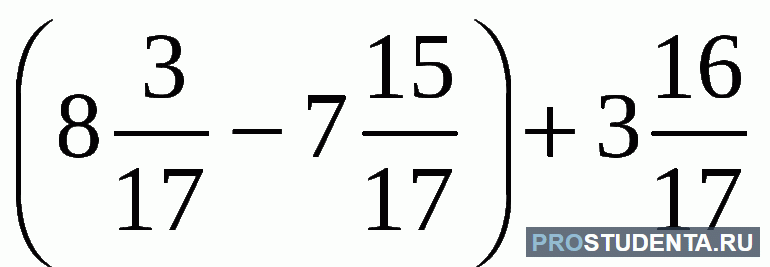Обыкновенная дробь – это запись числа в виде:
где число a называют числителем, а число b – знаменателем дроби.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Пример №1. У первой дроби можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.
Основное свойство дроби в основном применяют при сокращении обыкновенных дробей. Обыкновенные дроби бывают сократимые и несократимые.
- Сократимые – это дроби, у которых числитель и знаменатель делятся на одно и то же число.
- Несократимые – это дроби, у которых числитель и знаменатель не имеют общих делителей.
Сокращение дробей
Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.
Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби – четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:
Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.
Пример №4.
Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.
Вычитание обыкновенной дроби из целого числа
Вычитание обыкновенной дроби из единицы
Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.
Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).
Вычитание обыкновенной дроби из бóльшего числа
Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.
Пример №6.
Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.
Нахождение общего знаменателя
Наименьшее общее кратное. Приём №1.
Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.
Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7.
1. Нужно разложить на простые множители каждое число:
12=2×2×3
15=3×5
2. Затем найти одинаковые множители (подчеркиваем):
12=2×2×3
15=3×5
В данном случае это только множитель 3.
3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:
12 домножаем на 5: 12×5=60, или
15 домножаем на 2 и 2: 15×2×2=60
Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.
Перемножение знаменателей. Приём №2.
Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.
Пример №8.
Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.
Последовательный подбор. Приём №3.
Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.
Пример №9. Возьмем число 51, умножим на 2, получим 102 – видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.
После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.
Алгоритм сложения (вычитания)
- Находим общий знаменатель данных дробей.
- Находим дополнительный множитель к числителю каждой дроби, разделив общий знаменатель на числитель каждой дроби.
- Умножаем каждый числитель на дополнительный множитель.
- Выполняем сложение (вычитание) дробей с одинаковыми знаменателями.
Пример №10.
Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 – простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:
Выполняем умножение в числителе:
Выполняем сложение дробей с одинаковыми знаменателями:
Умножение обыкновенных дробей
Как перемножить дроби?
При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).
Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.
Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.
Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.
Пример №13. Нам даны смешанные дроби, переводим их в неправильные для выполнения умножения.
Деление обыкновенных дробей
Как разделить одну дробь на другую?
При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.
Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.
Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.
Пример №14. Делимое умножаем на число, обратное делителю.
Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление.
Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.
Задание OM2004
Сократите дробь 36n4n−2∙32n−1
Чтобы решить данное задание, необходимо понимать, что выполнять действия умножение и деление степеней мы можем в том случае, если они имеют одинаковые основания. Поэтому разложим на множители основание 36 нашего числителя так, чтобы вместо 36 были числа 4 и 3, которые есть в знаменателе.
(3∙3∙4)n4n−2∙32n−1
Теперь представим каждый множитель в виде степени:
3n∙3n∙4n4n−2∙32n−1
Разложим знаменатель дроби на множители по свойству степеней
3n∙3n∙4n4n∙4−2∙32n∙3−1
Теперь можно сократить числитель и знаменатель на 3n и в 4n степени
Получим дробь, которую преобразуем по свойству степеней:
14−2∙3−1 = 42∙311=16∙3=48
Ответ: 48
pазбирался: Даниил Романович | обсудить разбор
Задание OM1306o
Найдите значение выражения:
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:
теперь переходим от деления дробей к их умножению:
затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
сокращаем выражение на (a–5b):
Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений):
Подставим полученные значения в выражение и найдем конечный результат:
Ответ: 39
pазбирался: Даниил Романович | обсудить разбор
Задание OM1305o
Найдите значение выражения при x = 12:
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
Подставляем числовое значение для х в полученное выражение и находим результат:
Ответ: 0,6
pазбирался: Даниил Романович | обсудить разбор
Задание OM1304o
Найдите значение выражения
где a = 9, b = 36
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю – это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
9b² + 5a – 9b²
Приведем подобные слагаемые – это 9b² и – 9b², в числителе остается 5a. Запишем конечную дробь:
5a/b
Вычислим её значение, подставив числа из условия:
5•9/36 = 1,25
Ответ: 1,25
pазбирался: Даниил Романович | обсудить разбор
Задание OM1303o
Найдите значение выражения:
при x = √45 , y = 0,5
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель – это 15 x y, для этого необходимо первую дробь домножить на 5 y – и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y – (3 x + 5 y) = 5 y – 3 x – 5 y = – 3 x
Тогда дробь примет вид:
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: – 1/5 y
Подставим значение y = 0,5: – 1 / (5 • 0,5) = – 1 / 2,5 = – 0,4
Ответ: -0,4
pазбирался: Даниил Романович | обсудить разбор
Задание OM1302o
Найдите значение выражения:
при a = 13, b = 6,8
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй – в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:
Далее выносим из числителя второй дроби a:
Сокращаем (a-b):
И получаем:
a/2
Подставляем значение a = 13:
13 / 2 = 6,5
Ответ: 6,5
pазбирался: Даниил Романович | обсудить разбор
Задание OM0804o
Какое из данных ниже чисел является значением выражения?
Заметим, что в знаменателе присутствует разность (4 – √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² – (√14)². После этого знаменатель легко вычисляется:
16 – 14 = 2
Суммарно наши действия выглядят так:
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор
Задание OM0603o
Найдите значение выражения:
Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:
1/21 + 1/28 = 4/84 + 3/84
Затем складываем:
4/84 + 3/84 = 7/84
Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:
1 / ( 7 / 84 ) = 1 •84/7 = 84/7
Далее остается поделить 84 на 7:
84 / 7 = 12
Ответ: 12
pазбирался: Даниил Романович | обсудить разбор
Задание OM0602o
Найдите значение выражения:
Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.
1/3 • (6 • (1/3) — 17 )
Проведя вычисления в скобках, получим:
1/3 • ( 6 • (1/3) — 17 ) = 1/3 • (6 /3 — 17 ) = 1/3 • ( 2 — 17 ) = 1/3 • ( -15 )
Теперь умножим полученное значение -15 на 1/3:
1/3 • ( -15 ) = -5
Ответ: -5
pазбирался: Даниил Романович | обсудить разбор
Алла Василевская | Просмотров: 19.6k
Сложение дробей с одинаковыми знаменателями
Сложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби и
. Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить
пиццы, то получится
пиццы:
Пример 2. Сложить дроби и
.
Опять же складываем числители, а знаменатель оставляем без изменения:
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще
пиццы, то получится одна целая пицца:
Пример 3. Сложить дроби и
.
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё
пиццы, то получится
пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить
пиццы и ещё прибавить
пиццы, то получится 1 целая и ещё
пиццы.
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и
сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и
сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и
. Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить
получается
.
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить
пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и
к общему знаменателю, мы получили дроби
и
. Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь
(три кусочка из шести). Сложив эти кусочки мы получаем
(семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили
(одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?«.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения 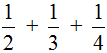
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби можно вычесть дробь
, поскольку у этих дробей одинаковые знаменатели. А вот от дроби
нельзя вычесть дробь
, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать
пиццы, то получится
пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и
к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби
и
. Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь
(три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь
и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Задания для самостоятельного решения:
Задание 1. Найдите значение выражения:
Задание 2. Найдите значение выражения:
Задание 3. Найдите значение выражения:
Задание 4. Найдите значение выражения:
Задание 5. Найдите значение выражения:
Задание 6. Найдите значение выражения:
Задание 7. Найдите значение выражения:
Задание 8. Найдите значение выражения:
Дроби — коротко о главном
Определения:
Простая дробь (обыкновенная дробь) – запись рационального числа в виде отношения двух чисел (displaystylefrac{a}{b}).
Делимое (displaystyle a) – числитель дроби, а делитель (displaystyle b) – знаменатель дроби.
Правильная дробь – дробь, у которой числитель меньше знаменателя.
Например: (displaystylefrac{2}{5}), (displaystylefrac{1}{7}) и так далее.
Неправильная дробь –дробь, у которой числитель больше или равен знаменателю.
Например: (displaystylefrac{9}{5}), (displaystylefrac{13}{2}) и так далее.
Смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.
Например: (displaystyle2frac{2}{5})( displaystyle displaystyle=frac{2cdot 5}{5}+frac{2}{5}=frac{10}{5}+frac{2}{5}=frac{12}{5}).
Десятичная дробь – обыкновенная дробь со знаменателем (displaystyle10), (displaystyle100), (displaystyle1000) и так далее, (т.е. (displaystyle{{10}^{n}}), где (displaystyle n) — натуральное число).
Например: (displaystylefrac{9}{100}) в виде десятичной дроби записывается как (displaystyle0,09),
(displaystylefrac{225}{1000}) записывается как (displaystyle0,225).
Основное свойство дроби:
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, дробь не изменится, несмотря на то, что выглядеть она будет по-другому.
Например: (displaystylefrac{1}{5}=frac{1cdot 2}{5cdot 2}=frac{2}{10}).
Действия с дробями:
Сложение/вычитание дробей
- две дроби с одинаковыми знаменателями: складываем/вычитаем их числители, а знаменатель оставляем без изменений: (displaystylefrac{a}{c}+frac{b}{c}=frac{a+b}{c})
- две обыкновенные дроби с разными знаменателями:
- приводим дроби к наименьшему общему знаменателю;
- складываем/вычитаем числители дробей, а знаменатель оставляем без изменений;
- сокращаем полученную дробь
- две смешанные дроби с разными знаменателями:
- приводим дробные части этих чисел к наименьшему общему знаменателю;
- по-отдельности складываем/вычитаем целые части и дробные части;
- если при сложении дробных частей получилась неправильная дробь, выделяем целую часть из этой дроби и прибавляем ее к полученной целой части / если дробная часть уменьшаемого меньше дробной части вычитаемого, превращаем ее в неправильную дробь, уменьшив на единицу, целую часть;
- сокращаем полученную дробь.
Умножение дробей
- умножение дроби на натуральное число: числитель умножаем на число, а знаменатель оставляем неизменным
- умножение двух обыкновенных дробей:
- перемножаем числители и знаменатели дробей;
- сокращаем полученную дробь
- умножение двух смешанных чисел:
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем полученную дробь;
- если получилась неправильная дробь преобразовываем ее в смешанную.
Деление дробей
- деление дроби на натуральное число: знаменатель дроби умножаем на число, а числитель оставляем неизменным
- деление натурального числа на дробь: число умножаем на дробь обратную данной
- деление обыкновенных дробей: умножаем первую обыкновенную дробь на дробь, обратную второй
- деление двух смешанных чисел:
- преобразовываем смешанные дроби в неправильные;
- умножаем первую дробь на дробь, обратную второй; (3) сокращаем полученную дробь; (4) если получилась неправильная дробь преобразовываем ее в смешанную.
Сокращение дроби
Чтобы сократить дробь (displaystylefrac{a}{b}) нужно найти наибольший общий делитель ее числителя и знаменателя. Если наибольший общий делитель равен (displaystyle1), то дробь сократить нельзя.
Например: (displaystylefrac{5}{15}=frac{5:5}{15:5}=frac{1}{3}).
Приведение дробей к наименьшему общему знаменателю
- найдите наименьшее общее кратное знаменателей этих дробей (наименьший общий знаменатель);
- разделите наименьший общий знаменатель на знаменатели данных дробей, т. е. найдите для каждой дроби дополнительный множитель;
- умножьте числитель и знаменатели каждой дроби на ее дополнительный множитель.
Например: (displaystylefrac{1}{3}) и (displaystylefrac{3}{4}). Наименьший общий знаменатель — (displaystyle12).
Дополнительный множитель первой дроби — (displaystyle12:3=4), дополнительный множитель второй дроби — (displaystyle12:4=3).
Следовательно: для первой дроби: (displaystylefrac{1cdot 4}{3cdot 4}=frac{4}{12}), для второй дроби: (displaystylefrac{3cdot 3}{4cdot 3}=frac{9}{12}).
Преобразования неправильной дроби в смешанную дробь
- поделите числитель дроби на ее знаменатель;
- остаток от деления запишите в числитель, знаменатель оставьте прежним;
- результат от деления запишите в качестве целой части.
Например: (displaystylefrac{17}{4}) = (displaystyle4frac{1}{4}).
Сравнение дробей:
- две дроби с одинаковыми знаменателями: больше та дробь, числитель которой больше
- две дроби с одинаковыми числителями: больше та дробь, знаменатель которой меньше
- две обыкновенные дроби: после приведения дробей к общему знаменателю, больше та дробь, числитель которой больше
Простые дроби
В данном случае от целого куска в сторонке отделенная одна доля, одна из четырех, одна четвертая.
Это простая дробь.
Простые дроби принято записывать одним из следующих способов: (displaystyle frac{1}{4}), (displaystyle {1}/{4};.)
Ты не поверишь, все эти записи означают одно и то же – одна четвертая. А что останется если забрать эту (displaystyle 1/4?) Было (displaystyle 4) из (displaystyle 4), или (displaystyle 4/4), забрали (displaystyle 1/4).
Верно, останется (displaystyle 3) дольки, (displaystyle 3) из (displaystyle 4). Запишем, как полагается, (displaystyle 3/4).
Можно даже вот так: (displaystyle 4/4-1/4=3/4)
То, что находится выше черты – это числитель (ну или слева от черты в такой записи как тут), то, что ниже – знаменатель.
Можно запомнить так: Ч – чердак. Числитель сверху 🙂
Примеры простых дробей: (displaystyle 1/5,text{ }2/4,text{ }3/10,text{ }17/3.)
Правильные и неправильные простые дроби
В этом ряду все дроби правильные, в них числитель меньше знаменателя. Кроме одной. Да-да, ты не ошибся, бывает и такое, что числитель больше знаменателя, как в этой дроби, например: (displaystyle 17/3).
Если числитель больше знаменателя, то дробь называется неправильной.
Вне зависимости от того правильная дробь или неправильная, она будет простой.
Давай остановимся на неправильной дроби (displaystyle 17/3). Что же это она неправильная?
Вспоминай пример с пирогом, там была (displaystyle 1/4) – одна часть из четырех, а тут что получается? (displaystyle 17) частей из (displaystyle 3)?
Бред какой-то! У нас в знаменателе число, которое означает, что весь пирог состоит из стольки частей! Берем (displaystyle 4) части и поучаем целый ровненький пирог. Но числитель говорит, что на данный момент у нас есть лишь одна из этих частей.
А (displaystyle 17/3)?
Что же, у нас есть (displaystyle 17) частей, а для целого пирога в данном случае надо (displaystyle 3) части. Ну так давай соберем из кусочков целые пироги и отдельно их поставим.
Как узнать сколько пирогов мы можем получить из (displaystyle 17) частей? Верно, надо на (displaystyle 3) как раз и поделить.
Если попробовать составить (displaystyle 6) пирогов, т.е. (displaystyle 3cdot 6=18), надо (displaystyle 18) частей. Не хватает. А (displaystyle 3cdot 5=15), о, хватило! Получается (displaystyle 5) целых пирогов собрали, положили в сторону. Осталось (displaystyle 17-3cdot 5=2,2), ( displaystyle 2) куска.
А для целого пирога надо ( displaystyle 3) части. В итоге у нас ( displaystyle 5) целых и ( displaystyle 2/3) (две третьих) пирога.
Много места занимает такое обозначение. А что если убрать лишние слова и оставить только ( displaystyle 5frac{2}{3}) (пять целых и две третьих).
Смешанная дробь
То, что у нас получилось (( displaystyle 5frac{2}{3})), называют смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.
То, что между ( displaystyle 5) пирогами и ( displaystyle 2/3) пирога нет никакого знака не говорит о том, что там знак умножения, как если бы мы писали ( displaystyle 2x)!!!
Запомни, между целой и дробной частями можно поставить знак плюс, вот так: ( displaystyle 5frac{2}{3}=5+frac{2}{3}).
Так же можно проделать и обратное действие, т.е. преобразование из смешанной дроби в неправильную дробь.
Ты же знаешь, как это сделать?
Преобразование из смешанной дроби в неправильную дробь.
Конечно, нужно умножить знаменатель дроби (в случае с , (displaystyle5frac{2}{3}) знаменатель равен ( displaystyle 3)), умножить знаменатель…, верно, на (displaystyle5) и прибавить нецелую часть, а именно – ( displaystyle 2) .
В результате получим исходное ( displaystyle 17/3).
Сложение дробей
Самый простой вариант, когда дроби, которые надо сложить, имеют одинаковый знаменатель.
Ты же еще не забыл, что это такое, правда?
Например, ( displaystyle 2/5+1/5). Вспомнив пример с кусочками пирога, думаю, ты без проблем догадаешься, что если складывать равные дольки одного пирога, то знаменатель меняться не будет, а складываются лишь числители.
Сложение будет выглядеть следующим образом: ( displaystyle frac{2}{5}+frac{1}{5}=frac{2+1}{5}=frac{3}{5}). Не сложно догадаться и как складывать смешанные дроби.
Отдельно складываются целые и дробные части:
( displaystyle 2frac{2}{3}+4frac{1}{3}=6frac{2+1}{3}=6frac{3}{3}=7).
А что, если знаменатели у дробей разные, а? Например, ( displaystyle 2/3+1/2).
И тут ты сразу вспоминаешь, что мы проходили приведение дробей к общему знаменателю, и, наконец, становится понятно, зачем это было учить!
В данном примере общим знаменателем будет число ( displaystyle 6), как наименьшее общее кратное чисел ( displaystyle 2) и ( displaystyle 3). ( displaystyle frac{2}{3}+frac{1}{2}=frac{4}{6}+frac{3}{6}=frac{7}{6}=1frac{1}{6}).
Поскольку ты теперь умеешь приводить неправильную дробь к смешанной дроби, то открою тебе секрет, что это является не просто хорошим тоном, но и обязательным действием при упрощении выражений, после получения ответа избавиться от неправильных дробей.
С десятичными дробями все еще проще.
Сложение делается, как и с обычными числами, только не забывай про запятую. Вот тебе пример: (displaystyle15,2+2,91).
Я предлагаю решать так: удобнее всего вычитать в столбик, расположив одну дробь под другой, но при этом запятая должна стоять строго под запятой вне зависимости от количества знаков до и после нее.
Как ты видишь, у второй дроби после запятой было на один знак больше. Для достижения одинакового количества знаков, я добавил еще один ноль в конце первой дроби.
Невероятно, но после последнего знака после запятой ты можешь добавить сколько угодно нулей, и это не изменит смысла дроби!
Вычитание дробей
Вычитание дробей практически ни чем не отличается от сложения, ну разве что знаком. А так, вычитается знаменатель из знаменателя, при сохранении общего числителя неизменным, а в случае если знаменатели разные, дроби приводятся к общему знаменателю.
Но куда же без специфики, тут она тоже присутствует.
Если ты вычитаешь одну смешанную дробь из другой, то в случае, если дробная часть уменьшаемой дроби меньше, чем у той, которую ты вычитаешь, то нужно уменьшить целую часть дроби на один и перенести в дробную часть, и вычитать из целой части целую, а из дробной дробную.
Что-нибудь понятно хоть чуточку? – Ладно, смотри пример, сейчас разберешься!
( displaystyle 4frac{1}{3}-2frac{2}{3}=3frac{4}{3}-2frac{2}{3}=1frac{2}{3}) – как ты видишь, в дробной части, тут из ( displaystyle 1/3) вычитается ( displaystyle 2/3).
Но, очевидно, что, не привлекая «кусочки» от целого пирога, вычитание совершить нельзя. Для этого один пирог режут на куски и добавляют их к дробной части.
Получается, что уже из ( displaystyle 4/3) вычитают ( displaystyle 2/3), а тут уж нет проблем.
А с десятичными дробями все то же самое, что и было при сложении.
Вот тебе пример:
Есть вопросы по нему? Думаю, все логично и понятно, если нет, то еще раз посмотри, как делали сложение.
Умножение дробей
Умножать дробь на число — элементарно! ( displaystyle 4cdot frac{2}{3} ) — вот пример, это произведение четырех и ( displaystyle 2/3), не путай с ( displaystyle 4frac{2}{3}) — это четыре целых, две третьих!!! Ну, так вот, ( displaystyle 4cdot frac{2}{3} =frac{4cdot 2}{3}=frac{8}{3}=2frac{2}{3}).
Просто умножаешь число на числитель, а знаменатель не трогаешь!
Умножение смешанной дроби на число: ( displaystyle 4cdot 2frac{2}{5}) . Умножаешь и целую, и дробную части на ( displaystyle 4). Вот как это выглядит: ( displaystyle 4cdot 3frac{2}{5}=12frac{8}{5}=13frac{3}{5}).
Все сложнее при умножении дроби на дробь.
Алгоритм умножения дроби на дробь
- Если дробь смешанная, привести ее к виду обыкновенной неправильной дроби;
- Перемножить числители дробей, перемножить знаменатели дробей;
- Записать результат умножения числителей в числитель, а знаменателей, в знаменатель.
Заметь, что для умножения дробей с разными знаменателями не нужно приводить их к общему знаменателю!
Вот как все делается: ( displaystyle 3frac{2}{5}cdot 2frac{1}{3}=frac{17}{5}cdot frac{7}{3}=frac{119}{15}=7frac{14}{15}).
Умножение десятичных дробей на число или на десятичную дробь делается просто в столбик, и без запятых. Главное не забыть что?
Правильно, после умножения поставить запятую, отсчитав справа столько знаков, сколько было в сумме у двух множителей до умножения.
Например: ( displaystyle 17,3cdot 5,1=88,23). В множителях было в сумме два знака справа от запятой, можно просто перемножить ( displaystyle 173) и ( displaystyle 51), а потом к результату дописать запятую, отсчитав два знака справа.
Ученики изучают на уроках математики в 5 классе смешанные дроби и примеры работы с ними. Однако не всегда усваивают теоретический материал, а на практике не могут решать задачи с обыкновенными дробными величинами. Специалисты нашли выход с этой ситуации, предложив специальные алгоритмы для оптимизации вычислений без ошибок. Для их изучения необходимы определенные базовые знания.
Оглавление:
- Общие сведения
- Конвертация смешанного числа
- Приведение к единому знаменателю
- Вычитание и суммирование
- Произведение и частное
- Возведение в степень и корень
Общие сведения
Запись чисел не всегда выполняется с применением целых значений. Иногда величина может выражаться обыкновенными или десятичными дробными выражениями. Первая может преобразовываться во вторую. Допустима также и обратная операция. Следует отметить, что обыкновенные дроби бывают трех типов:
- Правильными.
- Неправильными.
- Смешанными.
Для объяснения различия между ними необходимо записать величину в математической форме «w/v». В первом случае, когда дробное выражение является правильным, его числитель «w» меньше знаменателя «v» (w<v). Если оно считается неправильным, то величина числителя «v» всегда будет больше, чем «w», т. е. v>w. При этом дробное число нужно «превратить» в смешанное.
Смешанной называется обыкновенная дробь, состоящая из целого компонента и дробной части. Она имеет такой вид: 3[2/7]. Следует отметить, что любое дробное тождество обыкновенного вида может быть записано в виде десятичного. Для этого достаточно просто разделить числитель на знаменатель, т. е. ½=0,5.
Кроме того, над смешанными числами можно совершать любые арифметические операции.
К последним относятся следующие:
- «*» — произведение.
- «/» — нахождение частного или деление.
- «+» — сложение.
- «-» — вычитание.
- «^n» — возведение в степень.
- «^(1/n)» — извлечение корня.
Для совершения любой операции рекомендуется преобразовать смешанное число в неправильное дробное выражение. Далее необходимо разобрать подробно методику выполнения этой операции.
Конвертация смешанного числа
Конвертация смешанной дроби в обыкновенную применяется для оптимизации вычислений при выполнении арифметических операций. Она выполняется по следующей методике:
- Записать величину: С[w/v].
- Перемножить знаменатель и целую часть, а затем прибавить числитель: (vC+w)/v.
- Выполнить математические операции по расчету знаменателя, записав окончательный результат.
На практике необходимо разобрать реализацию методики в математике для 5 класса на примере смешанной дроби «3[2/7]». Конвертация выглядит таким образом:
- 3[2/7].
- (7*3+2)/7.
- 23/7.
Однако существует обратная операция по преобразованию неправильного дробного числа в смешанное. Она применяется для решения заданий, в которых нужно записать окончательный ответ. Оставлять его в виде неправильной дроби не рекомендуется, т. к. за это могут снизить оценку. Алгоритм имеет следующий вид:
- Записать искомое число.
- Разделить числитель на знаменатель, выделив целую часть.
- Преобразовать числитель, воспользовавшись формулой: w’=w-vС.
- Записать результат: w’/v.
Однако при изучении конкретного алгоритма рекомендуется разобрать его на примере. Для этого нужно взять число «23/7», и представить его в виде неправильного дробного тождества:
- 23/7.
- С=23/7=3.
- w’=w-Cv=23−3*7=2/7
- 3[2/7].
Используя алгоритмы преобразования смешанного числа, можно сравнивать, приводить к общему знаменателю, делить, перемножать, складывать и вычитать дроби, а также возводить в степень и извлекать корень.
Приведение к единому знаменателю
Операцию приведения смешанных чисел к общему знаменателю рекомендуется выполнять только при сравнении, сложении и вычитании.
Существует три способа выполнения этого действия, перед которым обязательно следует конвертировать смешанное число в неправильную дробь.
Методика зависит от знаменателей дробей (w/v и u/z):
- v/z — целое число, при условии, что v>z.
- Знаменатели v и z cодержат общие множители.
- Невыполнение первого и второго правил.
В первом случае приводить дроби к единому знаменателю очень просто. Для этого нужно записать общее значение «v», а над числителем второго выражения — коэффициент «v/z». Выполнить арифметические преобразования, и написать искомое дробное тождество. Математическая форма имеет следующий вид: [w+u*v/z]/v.
Если знаменатели содержат общие множители, то нужно найти наименьшее общее кратное (НОК). Для этого необходимо разложить их на простые множители. Далее требуется выделить один или совокупность общих элементов. Затем перемножить их с сомножителями, которые не повторяются. Полученный результат и будет общим знаменателем.
Однако бывает случай, когда первые два метода применить невозможно. Для получения единого знаменателя достаточно перемножить v и z между собой, записав коэффициенты над числителями «крест-накрест». Математическая запись операции сложения имеет следующий вид: [wz+vu]/(vz). Следует отметить, что вместо суммирования дробных величин, значения можно сравнивать или вычитать друг с друга.
Изучив вспомогательные операции над смешанными величинами (конвертации и приведения к единому знаменателю), можно переходить к методикам выполнения арифметических действий. Сначала следует рассмотреть сумму и разность.
Вычитание и суммирование
Для сложения двух смешанных дробей необходимо руководствоваться определенной методикой. Она имеет такой вид:
- Преобразовать обе величины в неправильные дроби.
- Привести к общему знаменателю.
- Выполнить сложение числителей, записав окончательный результат.
Операция вычитания выполняется по такому же алгоритму, что и сложение. Однако используется знак вычитания, а не суммирования. Следует отметить, что при сложении и вычитании смешанные числа можно не преобразовывать в неправильные дробные выражения при эквивалентности их знаменателей одному значению.
В этом случае методика будет выглядеть немного по-другому:
- Записать два выражения дробного типа.
- Отнять из одной целой части другую.
- Выполнить операцию разности числителей.
- Написать результат.
Следует отметить, что специалисты рекомендуют сразу ознакомиться с оптимизацией решения. Это значит, что при равенстве знаменателей нет необходимости преобразовывать смешанные числа в неправильные дроби. Задания должны решаться простыми способами, которые позволяют избежать множества ошибок.
Далее можно перейти к более сложным операциям произведения и деления смешанных выражений дробного типа.
Произведение и частное
Для операций умножения и деления нет необходимости приводить смешанные выражения к единому знаменателю. Арифметические действия выполняются по различным алгоритмам. Методика определения результата произведения выглядит таким образом:
- Написать смешанные величины.
- Преобразовать значения в первом пункте в неправильные дробные выражения.
- Перемножить числители между собой, а затем знаменатели.
- При необходимости вынести общий множитель, и сократить дробь на него.
Операция получения частного похожа на произведение, но существует некоторая особенность.
Последнюю часто забывают выполнить начинающие математики.
Алгоритм деления смешанных величин имеет такой вид:
- Записать смешанные значения, и переконвертировать их в неправильные дробные тождества.
- Поменять местами числитель и знаменатель второй дроби.
- Выполнить операцию умножения, записав результат.
Следует отметить, что обязательным условием при делении является «переворот» второй дроби, а также замена знака деления «:» на умножение «*». Это правило не нужно забывать, поскольку только его соблюдение позволит решить пример без ошибок. Следующими операциями являются возведение в степень и извлечение корня.
Возведение в степень и корень
Операции возведения в степень и изъятия корня похожи между собой, поскольку последний можно записать в виде первой, которая представлена обыкновенной дробью. Например, кубический радикал (корень) имеет математическую форму записи в виде «(8)^(1/3)».
Если числитель степени имеет величину отличную от единицы, то нужно число возвести в степень при числителе, а затем изъять радикал в знаменателе. Иными словами, (2)^(4/2)=(16)^(½)=4.
Методики возведения смешанного тождества в степень и извлечения радикала похожи между собой.
Алгоритм выглядит следующим образом:
- Преобразовать смешанное выражение в неправильное дробное.
- Возвести числитель и знаменатель в заданную степень или извлечь из них корень.
- Записать результат.
Следует отметить, что после получения результата дробь можно сократить, а затем преобразовать в смешанную. Этот прием является правилом «хорошего тона» в математике. Математическим «этикетом» пользуются во всем мире. Это свидетельствует о том, что каждый ученый приводит свои исследования или расчеты к читабельной форме представления, чтобы его наработками могли воспользоваться и другие специалисты.
Таким образом, при выполнении различных операций над смешанными дробными числами необходимо руководствоваться специальными алгоритмами, а также знать, как производятся операции конвертирования в неправильные дробные формы.
Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.
Как объяснить суть дробей ребенку?
Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.
Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.
Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.
Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.
Что нужно знать о дробях?
1. Дробь — число нецелое, оно обозначает количество долей целого.
2. Дробь меньше целого.
3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.
Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.
Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.
Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.
Что такое смешанные дроби?
В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.
У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.
Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть. А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.
Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.
Примеры:
- 14/5 = (5*2+4) / 5 = 2 4/5
- 21/6 = (6*3+ 3) / 6 = 3 3/6
Задание:
Выделите целую часть из неправильных дробей:
- 15/4,
- 22/12,
- 30/7.
Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.
Примеры:
- 3 1/8 = (3*8+1) / 8 = 25/8
- 7 4/9 = (7*9+4) / 9 = 67/9
Задание:
1. Преобразовать в смешанное число неправильную дробь:
- 27/4,
- 18/5,
- 45/7.
2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:
- 3 4/5;
- 12 7/11.
Десятичные дроби
Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.
Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.
Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».
Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления применяется человечеством с самых древних времен. Она интуитивна понятна и проста.
Задание:
Преобразовать следующие дроби в десятичные:
- 8/10,
- 4/100,
- 7/1000.
Сокращение дробей
Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.
Пример 1. Сократить дробь 8/12
Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:
8/12 = 8:4 / 12:4 = 2/3
Пример 2. Сократить дробь 10/25
Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:
10/25 = 10:5 / 25:5 = 2/5
Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.
Задание:
Сократите следующие дроби:
- 6/18,
- 20/40;
- 7/21.
Сложение дробей
Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.
Примеры:
- 1/7 + 2/7 = 3/7
- 3/8 + 5/8 = 8/8 = 1
Задание:
Выполни сложение дробей с одинаковыми знаменателями:
Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.
Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:
- 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
- 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.
Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:
- 3*6 / 7*6 = 18/42;
- 2*7 / 6*7 = 14/42.
Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:
- 18/42 + 14/42 = 32/42
Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.
Задание:
Выполни сложение дробей с разными знаменателями:
Вычитание дробей
Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.
Пример:
7/9 — 2/9 = (7-2) / 9 = 5/9
Задание:
Выполни вычитание дробей с одинаковыми знаменателями:
Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.
Пример:
6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70
Задание:
Выполни вычитание дробей с разными знаменателями:
Умножение дробей
Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.
Умножение обыкновенных дробей
В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.
Пример:
2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10
Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.
Пример:
24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21
Умножение смешанных дробей
Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.
Пример:
4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24
Задание:
Выполните умножение дробей:
- 5/7 * 6/8;
- 6/11 * 2/3;
- 2 3/7 * 4 5/9;
- 4 6/7 * 7 9/10.
Деление дробей
Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый знаменатель).
Пример:
4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7
Бывают ситуации, когда дробь нужно разделить на целое число. В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.
Пример:
5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18
Задание:
Выполните деление дробей:
- 6/11 : 3;
- 7/15 : 2;
- 9/12 : 4.
Сравнение дробей
Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.
Пример:
1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.
Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.
Пример:
1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.
Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби. Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.
Пример:
Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.
Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно. Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.
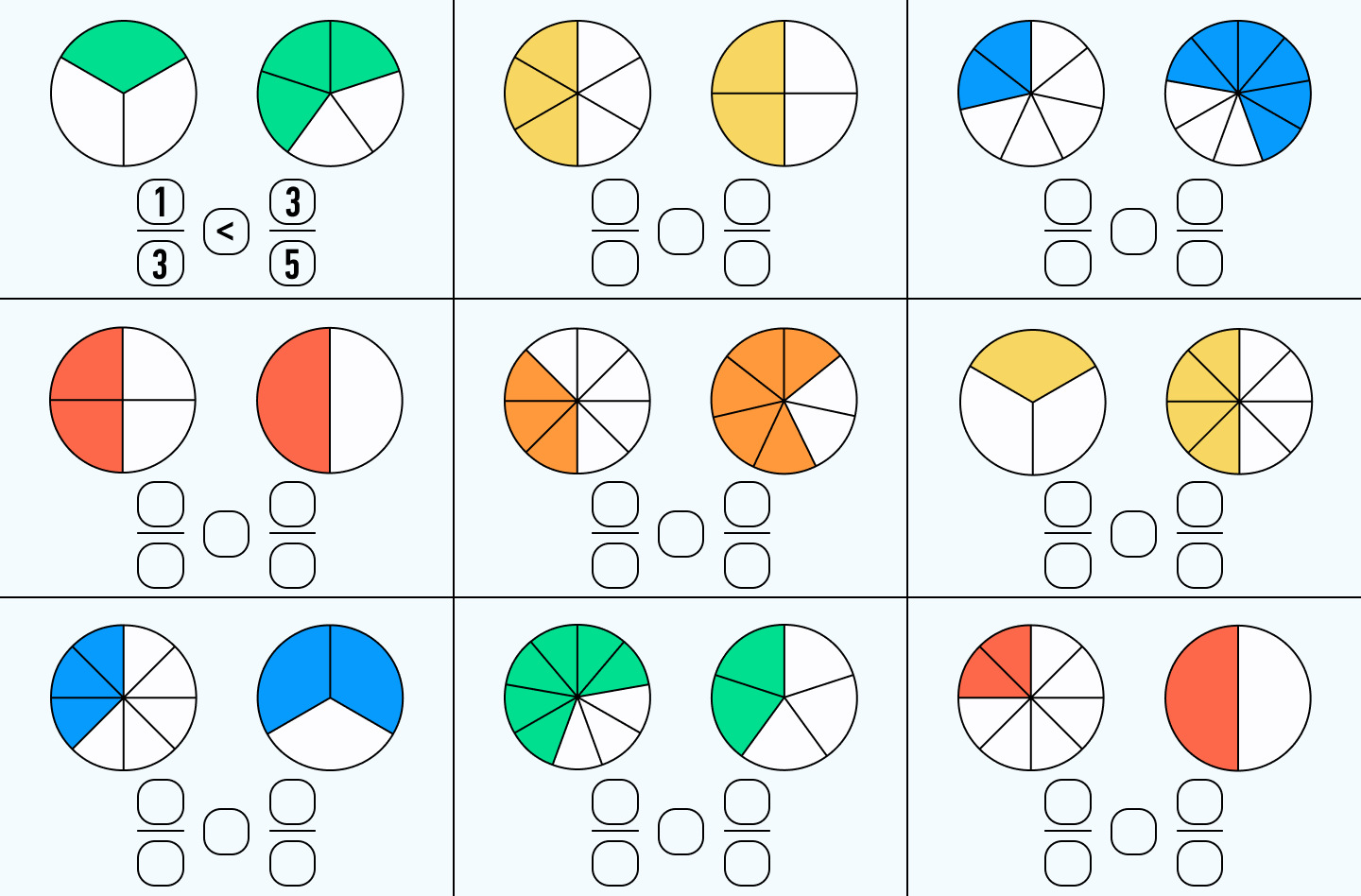
Задание:
Определите, какие дроби изображены на рисунке, и сравните их:
Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.


Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Читайте также:
- Таблица умножения для детей
- Как объяснить ребенку состав числа?