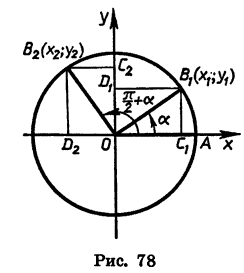
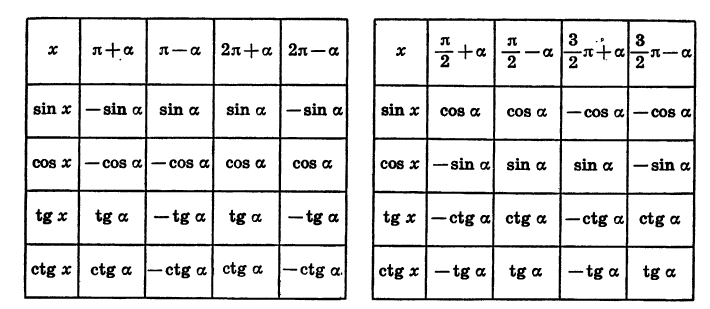
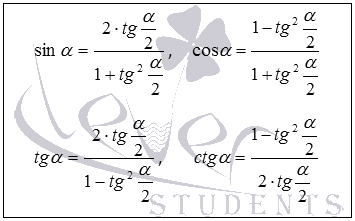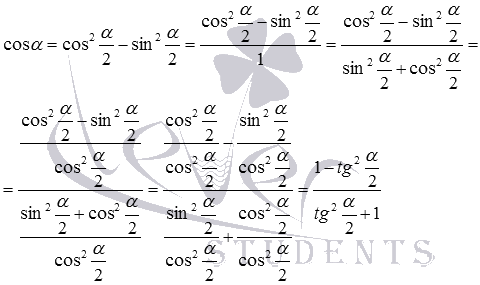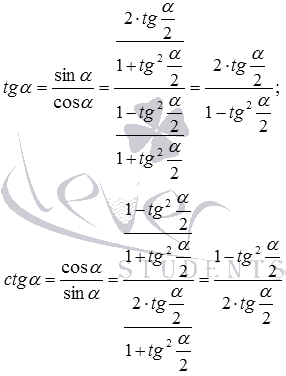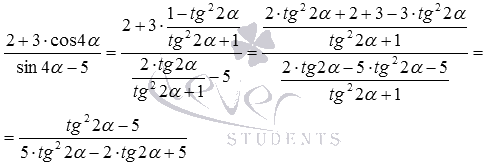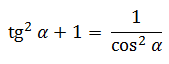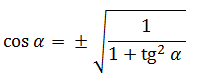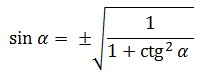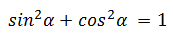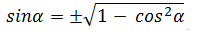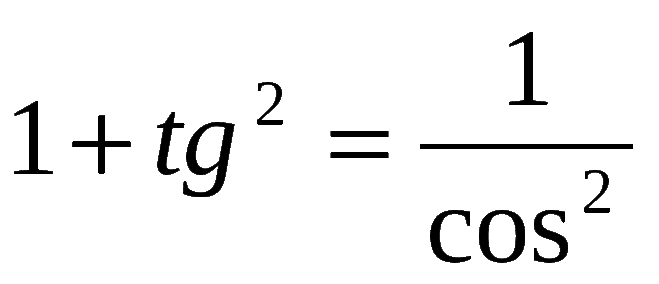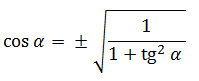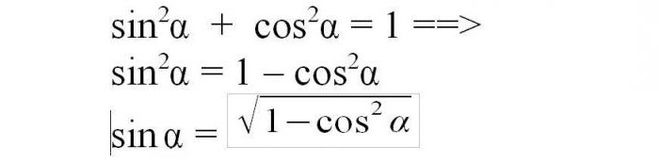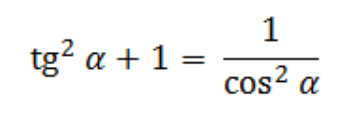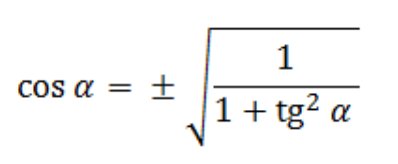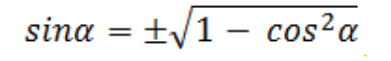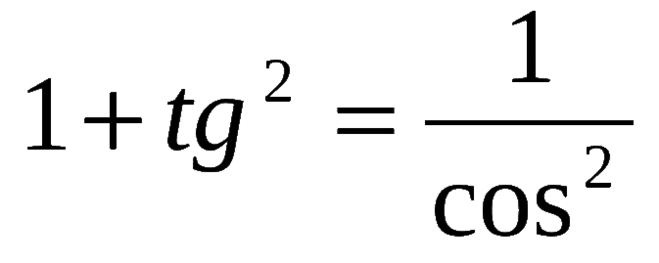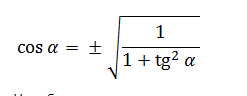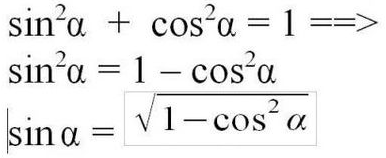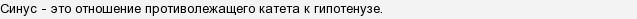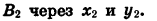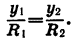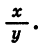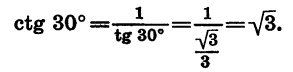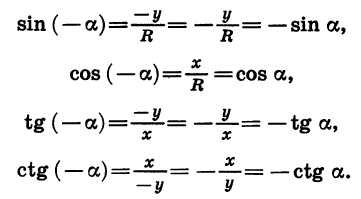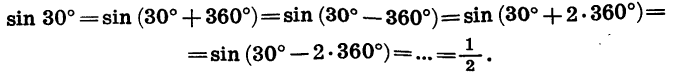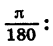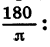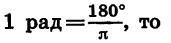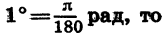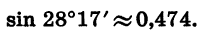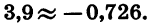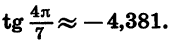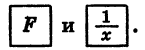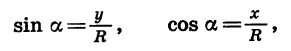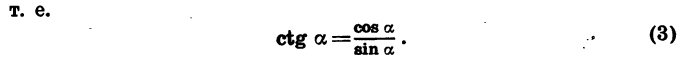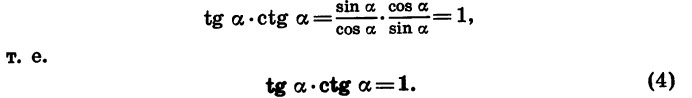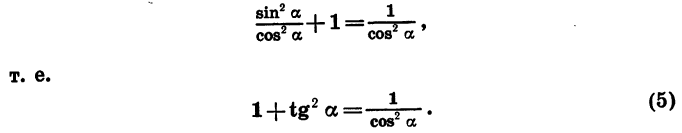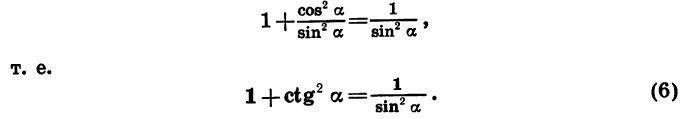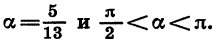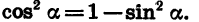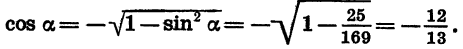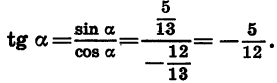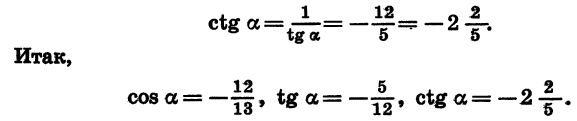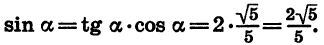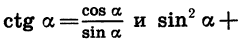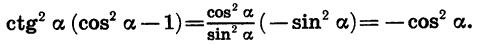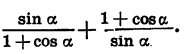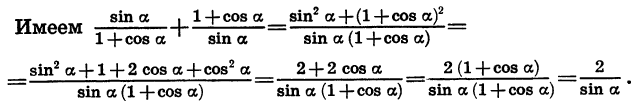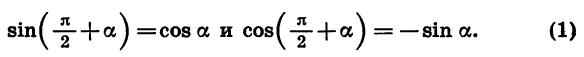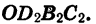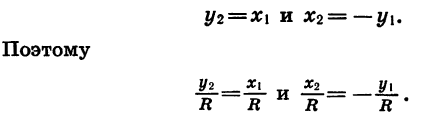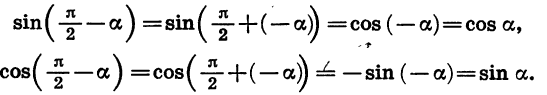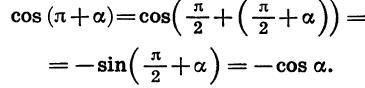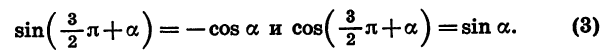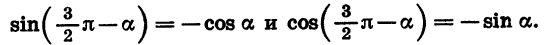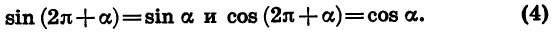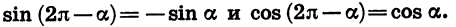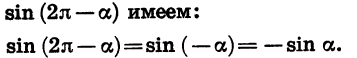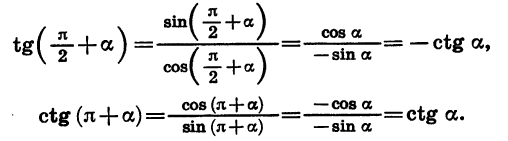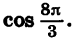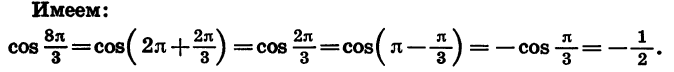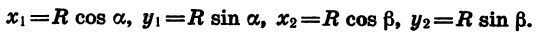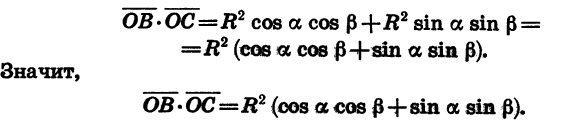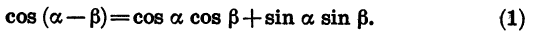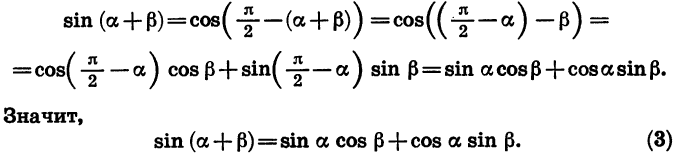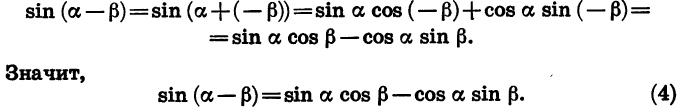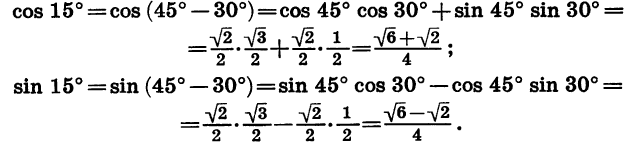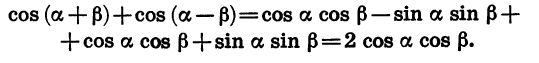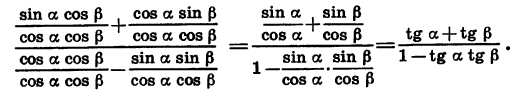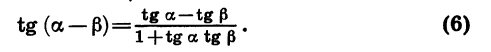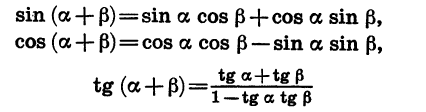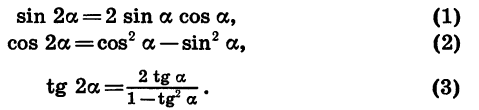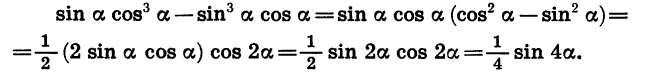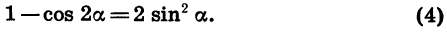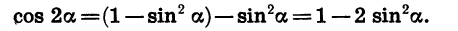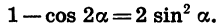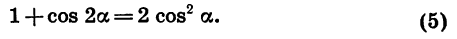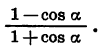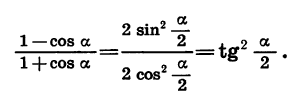|
Как найти синус, если известен тангенс? Как найти косинус, если известен тангенс? довольно часто при решении уравнений и упрощении тригонометрических выражений требуется найти синус или косинус через тангенс. Для этого существуют специальные формулы. Итак, для нахождения косинуса нужно извлечь квадратный корень из дроби в числителе которой единица, а в знаменателе выражение единица плюс тангенс в квадрате. А вот для того, чтобы найти синус нужно извлечь квадратный корень из выражения один минус дробь в числителе которой единица, а в знаменателе выражение единица плюс тангенс в квадрате. Но нужно обратить на знак синуса и косинуса, в зависимости от того в какой четверти находится угол. И если синус находим, то в 3 и 4 четвертях он будет отрицателен, а если косинус, то во второй и третьей. система выбрала этот ответ лучшим Ксарфакс 4 года назад Косинус через тангенс Для того, чтобы найти значение косинуса по известному тангенсу, нужно воспользоваться одним из тригонометрических тождеств. Сумма квадрата тангенса и единицы равна отношению единицы и квадрата косинуса. Отсюда можно выразить косинус: Наличие знака ± связано с тем, что в одних четвертях косинус угла может быть положительным, а в других — отрицательным. То есть в условии задачи должна оговариваться четверть, в которой находится угол. ** Пример. tgα = 1/√3, α находится в 1 четверти (0 < α < 90). Найдём косинус: cosα = √ ( 1 / (1 + 1/3)) = √ ( 1 / (4/3)) = √ (3/4) = √3/2. Итак, если тангенс равен 1/√3, то косинус равен √3/2. Нетрудно догадаться, что мы имели дело с углом 30°. Синус через тангенс Здесь также понадобятся тригонометрические тождества. Можно пойти двумя путями: 1) Выразить котангенс через тангенс и найти синус по котангенсу. 2) Найти косинус по тангенсу, а затем воспользоваться основным тригонометрическим тождеством. ** Пример. tgα = √3, α находится в 1 четверти (0 < α < 90). Найдём котангенс: ctga = 1 / tgα = 1 / √3. Теперь найдём синус: sina = √ ( 1 / (1 + 1/3)) = √ ( 1 / (4/3)) = √ (3/4) = √3/2. Или: cosa = √ ( 1 / (1 + 3)) = √ (1/4) = 1/2. sina = √ (1 — 1/4) = √ (3/4) = √3/2. Таким образом, если тангенс равен √3, то синус равен √3/2. Здесь также понятно, что это угол 60°. СергейНиколаев 5 месяцев назад Для этого существуют вполне определённые математические тригонометрические формулы. Например, косинус любого угла можно найти, зная его тангенс, исходя из соотношения что он равен корню квадратному из дроби, в числителе которой будет единица, а в знаменателе квадрат тангенса плюс единица. Только надо учитывать момент, что он может быть положительным и отрицательным. Зная косинус, несложно вычислить и синус любого угла, если вспомнить, что сумма их квадратов всегда равна единице. Также можно найти котангенс этого угла, разделив 1 на тангенс, а дальше воспользоваться аналогичной приведённой в первом абзаце формулой для синуса и котангенса. Optorius 6 месяцев назад Синус и косинус через тангенс можно найти: 1 — По таблице значений тригонометрических функций некоторых углов. 2 — Через вычисления по формулам тригонометрических тождеств. Сначала находим косинус, затем по нему синус. 3 — Через универсальные тригонометрические подстановки (полуугловые подстановки). Такой способ обычно используют при вычислении интегралов, он дает приближенный результат. Для примера: Возьмем tg = √3. По таблице sin = √3/2 ≈ 0,866. По второму способу sin = √(1-1/4) ≈ 0,866. По третьему способу sin = √3/(7/4) ≈ 0,9897. Дмитрий Подкопаев 3 года назад Приведу на всякий случай, на мой взгляд, наиболее общий способ нахождения синуса и косинуса по тангенсу. Как говорится определил знак подставил в выражение и получил ответ. В алгебре и геометрии очень часто при решении задач используются тригонометрические формулы, которые чаще называют тригонометрическими тождествами. Из любого тригонометрического тождества несложно вывести новую формулу, необходимую для нахождения одной из величин, входящих в его состав. ************************************************************************ Для того, чтобы найти косинус угла, зная его тангенс, возьмем тригонометрическое тождество: . Из данного тождества выводим новую формулу для вычисления косинуса: Не забываем, что косинус может принимать как положительные, так и отрицательные значения в зависимости от четверти нахождения угла. ************************************************************************ Для вычисления синуса угла через его тангенс можно действовать по-разному. Например, вычислить по выведенной выше формуле косинус угла, а затем воспользоваться еще одним тригонометрическим тождеством и вывести из него формулу для вычисления синуса угла: Алиса в Стране 3 года назад В тригонометрических тождествах нет, конечно, ничего сложного, вот только запомнить их все так, чтобы не пользоваться справочными материалами, обычному человеку достаточно трудно, поэтому всегда приходится где-то искать эти формулы. Вот одна из них: Из нее то мы и будем получать формулу для выполнения задания из вопроса, а именно — нахождения косинуса через тангенс, проведя несложные преобразования, получим: Как видите, действительно все очень просто. Теперь, найдя косинус, воспользуемся основным тригонометрическим тождеством, преобразуем его, чтобы найти синус через уже найденный косинус, формула такая: RIOLIt 5 лет назад конечно тангенс угла- это отношение синуса этого угла к косинусу того же угла- условно- а/б= с и а= с*в, в= а/с, сразу видно, что, кроме с, что- нибудь еще должно быть дано иначе не расколоть задачку, разве с будет равно 1 или еще какому замечательному значению, позволяющему определить величину угла угла. Krustall 8 месяцев назад Синус, косинус и тангенс являются тригонометрическими функциями. Исторически они возникли как отношения между сторонами прямоугольного треугольника, поэтому их удобнее вычислять через прямоугольный треугольник. Однако через него могут быть выражены только тригонометрические функции острых углов. Для тупых углов вам нужно будет вставить окружность. Иногда, необходимо найти синус или косинус через тангенс. Для этого существуют специальные формулы. Итак, чтобы найти косинус, нужно извлечь квадратный корень из дроби, в числителе которой единица, а в знаменателе выражение единица плюс тангенс к квадрату. Но чтобы найти синус, нужно извлечь квадратный корень из выражения один минус дробь в числителе которого единица, а в знаменателе выражение равно единице плюс касательная к квадрату. Но нужно обращать внимание на знак синуса и косинуса в зависимости от того, в какой четверти находится угол. И если мы найдем синус, то в 3-й и 4-й четвертях он будет отрицательным, а если косинус — во 2 и 3. Если говорить о тангенсе угла, то является отношением синуса по отношению к косинусу. Так, следует воспользоваться тригонометрическим тождеством. Согласно ему выводится формула, которую используем для того, чтобы вычислить косинус. Вы можете вычислить по формуле, а также воспользуюсь еще 1 тригонометрическим тождеством, выведя формула вычислить: Лара Изюминка 2 года назад Итак , чтобы найти синус нужно взять корень из выражения 1 деленное на 1 плюс тангенс в квадрате. Далее по основному тригонометрическому тождесьву можно найти косинус. Для этого нужно извлечь квадратный корень их 1 минус только что найденнный синус в квадрате. sin=sqrt(1/(1+((1/tg)**2))) cos=sqrt(1/(1+((1/ctg)**2))) Знаете ответ? |
Смотрите также: Что такое тангенс, катангенс, синус, косинус, секанс, касеканс? Как найти тангенс, если известен косинус и синус? Как выучить значения косинусов, синусов, тангенсов? Какова этимология слов «тангенс, котангенс, синус, косинус, тон»? А вам в жизни когда нибудь приходились столкнуться с косинусами, синусами? Как легко запомнить тригонометрический круг (единичную окружность)? Как узнать синус угла в треугольнике если известны синусы остальных углов? Определите знак выражения и как вы нашли? Sin имеет много рациональных значений, а в таблицах мало, почему (см.)? Для чего и где нужны математические Sin и Cos? |
Универсальная тригонометрическая подстановка, вывод формул, примеры.
В этой статье мы поговорим об универсальной тригонометрической подстановке. Она подразумевает выражение синуса, косинуса, тангенса и котангенса какого-либо угла через тангенс половинного угла. Более того, такая замена проводится рационально, то есть, без корней.
Сначала мы запишем формулы, выражающие синус, косинус, тангенс и котангенс через тангенс половинного угла. Дальше покажем вывод этих формул. А в заключение рассмотрим несколько примеров использования универсальной тригонометрической подстановки.
Навигация по странице.
Синус, косинус, тангенс и котангенс через тангенс половинного угла
Для начала запишем четыре формулы, выражающие синус, косинус, тангенс и котангенс угла 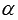
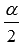
Указанные формулы справедливы для всех углов 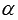
Вывод формул
Разберем вывод формул, выражающих синус, косинус, тангенс и котангенс угла через тангенс половинного угла. Начнем с формул для синуса и косинуса.
Представим синус и косинус по формулам двойного угла как 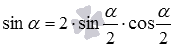
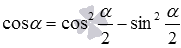
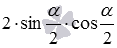
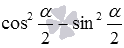
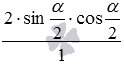
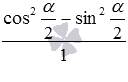
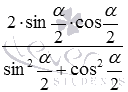
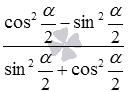
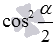
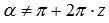
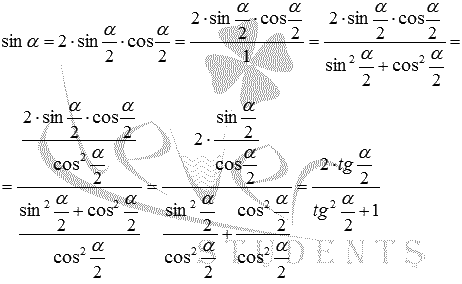
и
На этом вывод формул, выражающих синус и косинус через тангенс половинного угла, закончен.
Осталось вывести формулы для тангенса и котангенса. Теперь, учитывая полученные выше формулы, и формулы 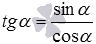
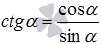
Итак, мы вывели все формулы для универсальной тригонометрической подстановки.
Примеры использования универсальной тригонометрической подстановки
Для начала рассмотрим пример применения универсальной тригонометрической подстановки при преобразовании выражений.
Приведите выражение 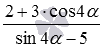
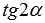
Здесь следует использовать универсальную тригонометрическую подстановку. Применим к косинусу и синусу четырех альфа формулы, выражающие их через тангенс половинного угла. В результате останется лишь упростить вид полученного выражения, имеем
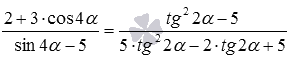
Как мы уже сказали в самом начале статьи, основное предназначение универсальной тригонометрической подстановки заключается в преобразовании исходного рационального тригонометрического выражения, содержащего синус, косинус, тангенс и котангенс, к рациональному выражению с одной единственной тригонометрической функцией, а именно, с тангенсом половинного угла. А такое преобразование особенно полезно при решении тригонометрических уравнений определенного вида, а также при интегрировании тригонометрических функций.
Источник
Основное тригонометрическое тождество
9 класс, 10 класс, ЕГЭ/ОГЭ
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
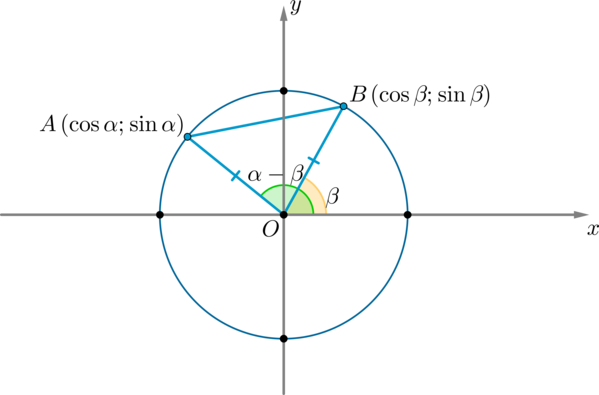
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
Образовался прямоугольный треугольник OA1B.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.

Задачка 2. Найдите значение cos α,
если:
Подставляем значения sin α:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Источник
Основные тригонометрические формулы и тождества sin, cos, tg, ctg
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
Формулы понижения степени
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
Произведение тригонометрических функций
Формулы произведения тригонометрических функций
Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка
Источник
Тригонометрические формулы. Их вывод
Наиболее часто встречающиеся тригонометрические формулы:
(blacktriangleright) Основные тождества: [begin <|l|l|>hline sin^2 alpha+cos^2 alpha =1& mathrm, alpha cdot mathrm, alpha =1 \ &(sinalphane 0, cosalphane 0)\[0.5ex] hline &\ mathrm, alpha=dfrac<sin alpha> <cos alpha>&mathrm, alpha =dfrac<cos alpha> <sin alpha>\&\ 1+mathrm^2, alpha =dfrac1 <cos^2 alpha>& 1+mathrm^2, alpha=dfrac1<sin^2 alpha>\&\ (cosalphane 0)& (sinalphane 0) \ hline end]
(blacktriangleright) Формулы сложения углов: [begin <|l|r|>hline &\ sin<(alphapm beta)>=sinalphacdot cosbetapm sinbetacdot cosalpha & cos<(alphapm beta)>=cosalphacdot cosbeta mp sinalphacdot sinbeta\ &\ hline &\ mathrm, (alphapm beta)=dfrac<mathrm, alphapm mathrm, beta><1 mp mathrm, alphacdot mathrm, beta> & mathrm, (alphapmbeta)=-dfrac<1mp mathrm, alphacdot mathrm, beta><mathrm, alphapm mathrm, beta>\&\ cosalphacosbetane 0&sinalphasinbetane 0\ hline end]
(blacktriangleright) Формулы понижения степени: [begin <|lc|cr|>hline &&&\ sin^2alpha=dfrac<1-cos<2alpha>>2 &&& cos^2alpha=dfrac<1+cos<2alpha>>2\&&&\ hline end]
(blacktriangleright) Формулы произведения функций: [begin <|c|>hline \ sinalphasinbeta=dfrac12bigg(cos<(alpha-beta)>-cos<(alpha+beta)>bigg)\\ cosalphacosbeta=dfrac12bigg(cos<(alpha-beta)>+cos<(alpha+beta)>bigg)\\ sinalphacosbeta=dfrac12bigg(sin<(alpha-beta)>+sin<(alpha+beta)>bigg)\\ hline end]
(blacktriangleright) Выражение синуса и косинуса через тангенс половинного угла: [begin <|l|r|>hline &\ sin<2alpha>=dfrac<2mathrm, alpha><1+mathrm^2, alpha> & cos<2alpha>=dfrac<1-mathrm^2, alpha><1+mathrm^2, alpha>\&\ cosalphane 0 & sinalphane 0\ hline end]
(blacktriangleright) Формула вспомогательного аргумента: [begin <|c|>hline text<Частный случай>\ hline \ sinalphapm cosalpha=sqrt2cdot sin<left(alphapm dfrac<pi>4right)>\\ sqrt3sinalphapm cosalpha=2sin<left(alphapm dfrac<pi>6right)>\\ sinalphapm sqrt3cosalpha=2sin<left(xpm dfrac<pi>3right)>\\ hline text<Общий случай>\ hline\ asinalphapm bcosalpha=sqrtcdot sin<(alphapm phi)>, cosphi=dfrac a<sqrt>, sinphi=dfrac b<sqrt>\\ hline end]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
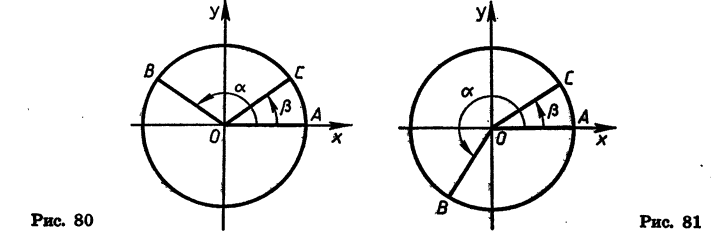
(AB^2=AO^2+BO^2-2AOcdot BOcdot cos(alpha-beta)=1+1-2cos(alpha-beta) (1)) (т.к. (AO=BO=R) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
Таким образом, сравнивая равенства ((1)) и ((2)) :
Отсюда и получается наша формула.
(blacktriangleright) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения (sin x=cos(90^circ-x)) и (cos x=sin (90^circ-x)) :
(blacktriangleright) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) (sin 2alpha=sin(alpha+alpha)=sinalphacosalpha+sinalphacosalpha=2sinalphacosalpha)
разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0 Rightarrow mathrm,2alpha=0) ):
5) (sin3alpha=sin(alpha+2alpha)=sinalphacos2alpha+cosalphasin2alpha=sinalpha(1-2sin^2alpha)+cosalphacdot 2sinalphacosalpha=)
6) Аналогично выводится, что (cos3alpha=cos(alpha+2alpha)=4cos^3alpha-3cosalpha)
(blacktriangleright) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) (cos2alpha=2cos^2alpha-1 Rightarrow cos^2alpha=dfrac<1+cos2alpha>2)
2) (cos2alpha=1-2sin^2alpha Rightarrow sin^2alpha=dfrac<1-cos2alpha>2)
(blacktriangleright) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
Получим: (cos(alpha+beta)+cos(alpha-beta)=2cosalphacosbeta Rightarrow cosalphacosbeta=dfrac12Big(cos(alpha-beta)+cos(alpha+beta)Big))
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
3) Сложим формулы синуса суммы и синуса разности двух углов:
(blacktriangleright) Вывод формул суммы/разности функций:
Получили формулу суммы косинусов.
Получили формулу разности косинусов.
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
Аналогично выводится формула суммы котангенсов.
(blacktriangleright) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
(разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0) и (sin2alpha=0) ):)
(blacktriangleright) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
(asin x+bcos x=sqrtleft(dfrac a<sqrt>sin x+ dfrac b<sqrt>cos x right)=sqrtbig(a_1sin x+b_1cos xbig))
(sqrt,big(cos phi sin x+sin phicos xbig)=sqrt,sin (x+phi)) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: [<large,sin (x+phi),>> quad text <где >cos phi=dfrac a<sqrt>] Заметим, что мы могли бы, например, принять за (cos phi=b_1, sin phi=a_1) и тогда формула выглядела бы как [asin x+bcos x=sqrt,cos (x-phi)]
(blacktriangleright) Рассмотрим некоторые частные случаи формул вспомогательного угла:
(a) sin xpmcos x=sqrt2,left(dfrac1<sqrt2>sin xpmdfrac1<sqrt2>cos xright)=sqrt2, sin left(xpmdfrac<pi>4right))
(b) sqrt3sin xpmcos x=2left(dfrac<sqrt3>2sin xpm dfrac12cos xright)=2, sin left(xpmdfrac<pi>6right))
(c) sin xpmsqrt3cos x=2left(dfrac12sin xpmdfrac<sqrt3>2cos xright)=2,sinleft(xpmdfrac<pi>3right))
Источник
Формулы тригонометрии
Формул в тригонометрии много.
Запомнить их механически очень сложно, почти невозможно. На занятиях многие школьники и студенты пользуются распечатками на форзацах учебников и тетрадей, плакатами на стенах, шпаргалками, наконец. А как быть на экзамене?
Однако, если Вы присмотритесь к этим формулам повнимательнее, то обнаружите, что все они взаимосвязаны и обладают определенной симметрией. Давайте проанализируем их с учетом определений и свойств тригонометрических функций, чтобы определить тот минимум, который действительно стоит выучить наизусть.
I группа. Основные тождества
sin 2 α + cos 2 α = 1;
tgα = ____ sinα cosα ; ctgα = ____ cosα sinα ;
Эта группа содержит самые простые и самые востребованные формулы. Большинство учащихся их знает. Но если всё-таки есть трудности, то чтобы запомнить первые три формулы, мысленно представьте себе прямоугольный треугольник с гипотенузой равной единице. Тогда его катеты будут равны, соответственно, sinα по определению синуса (отношение противолежащего катета к гипотенузе) и cosα по определению косинуса (отношение прилежащего катета к гипотенузе).
Последние две формулы можно не запоминать досимвольно. Они встречаются реже. И если потребуются, то Вы всегда сможете вывести их на черновике заново. Для этого достаточно подставить вместо тангенса или контангенса их определения через дробь (формулы вторая и третья, соответственно) и привести выражение к общему знаменателю. Но важно помнить, что такие формулы, которые связывают квадраты тангенса и косинуса, и квадраты котангенса и синуса существуют. Иначе, Вы можете не догадаться, какие преобразования необходимы для решения той или иной конкретной задачи.
Если рекомендации понятны, нажмите кнопку 
II группа. Формулы сложения
sin(α + β) = sinα·cosβ + cosα·sinβ;
sin(α − β) = sinα·cosβ − cosα·sinβ;
cos(α + β) = cosα·cosβ − sinα·sinβ;
cos(α − β) = cosα·cosβ + sinα·sinβ;
tg(α + β) = tgα + tgβ _________ 1 − tgα·tgβ ;
sin(−α) = − sin(α); cos(−α) = cos(α); tg(−α) = − tg(α).
Из всех тригонометрических функций только косинус является четной функцией и не изменяет свой знак при смене знака аргумента (угла), остальные функции являются нечетными. Нечетность функции, фактически, означает, что знак минус можно вносить и выносить за знак функции. Поэтому, если Вам встретится тригонометрическое выражение с разностью двух углов, всегда можно будет понимать его как сумму положительного и отрицательного углов.
Например, sin(x − 30º) = sin( x + (−30º) ).
Дальше пользуемся формулой суммы двух углов и разбираемся со знаками:
sin( x + (−30º) ) = sinx·cos(−30º) + cosx·sin(−30º) =
= sinx·cos30º − cosx·sin30º.
Таким образом все формулы, содержащие разность углов, можно просто пропустить при первом заучивании. Затем стоит научиться восстанавливать их в общем виде сначала на черновике, а потом и мысленно.
Это поможет в дальнейшем быстрее догадываться о том, какие преобразования нужно применить для решения той или иной задачи из тригонометрии.
Если рекомендации понятны, нажмите кнопку 
Ш группа. Формулы кратных аргументов
cos2α = cos 2 α − sin 2 α ;
tg2α = 2tgα _______ 1 − tg 2 α ;
sin3α = 3sinα − 4sin 3 α ;
Необходимость в использовании формул для синуса и косинуса двойного угла возникает очень часто, для тангенса тоже нередко. Эти формулы следует знать наизусть. Тем более, что трудностей в их заучивании нет. Во-первых, формулы короткие. Во-вторых, их легко контролировать по формулам предыдущей группы, исходя из того, что 2α = α + α. 
sin(α + β) = sinα·cosβ + cosα·sinβ;
sin(α + α) = sinα·cosα + cosα·sinα;
sin2α = 2sinα·cosα.
Однако, если Вы быстрее выучили эти формулы, а не предыдущие, то можно поступать и наоборот: вспоминать формулу для суммы двух углов можно по соответствующей формуле для двойного угла.
Например, если нужна формула косинуса суммы двух углов:
1) вспоминаем формулу для косинуса двойного угла: cos2x = cos 2 x − sin 2 x;
2) расписываем её длинно: cos(x + x) = cosx·cosx − sinx·sinx;
3) заменяем один х на α, второй на β: cos(α + β) = cosα·cosβ − sinα·sinβ.
Потренируйтесь аналогично восстанавливать формулы для синуса суммы и тангенса суммы. В ответственных случаях, таких как например ЕГЭ, проверяйте точность восстановленных формул по известным значениям функций для основных углов первой четверти: 0º, 30º, 45º, 60º, 90º.
Проверка предыдущей формулы (полученной заменой в строке 3):
пусть α = 60°, β = 30°, α + β = 90°,
тогда cos(α + β) = cos90° = 0, cosα = cos60° = 1/2, cosβ = cos30° = √3 _ /2, sinα = sin60° = √3 _ /2, sinβ = sin30° = 1/2;
подставляем значения в формулу: 0 = (1/2)·( √3 _ /2) − ( √3 _ /2)·(1/2);
0 ≡ 0, ошибок не обнаружено.
Если ВСЕ рекомендации понятны, нажмите кнопку 
sinα + sinβ = 2·sin α + β ____ 2 ·cos α − β ____ 2 ;
sinα − sinβ = 2·sin α − β ____ 2 ·cos α + β ____ 2 ;
cosα + cosβ = 2·cos α + β ____ 2 ·cos α − β ____ 2 ;
cosα − cosβ = −2·sin α − β ____ 2 ·sin α + β ____ 2 ;
tgα + tgβ = sin(α + β) ________ cosα·cosβ ;
sin90º − sin30º = sin90º + sin(−30º) = 2·sin 90º + (−30º) __________ 2 ·cos 90º − (−30º) __________ 2 =
= 2·sin30º·cos60º = 2·(1/2)·(1/2) = 1/2.
Таким образом, формулы разности синусов и тангенсов не обязательно сразу заучивать наизусть.
С суммой и разностью косинусов дело обстоит сложнее. Эти формулы не взаимозаменяемы. Но опять же, пользуясь четностью косинуса, можно запомнить следующие правила.
Сумма cosα + cosβ не может изменить свой знак ни при каких изменениях знаков углов, поэтому произведение также должно состоять из четных функций, т.е. двух косинусов.
Знак разности cosα − cosβ зависит от значений самих функций, значит знак произведения должен зависеть от соотношения углов, поэтому произведение должно состоять из нечетных функций, т.е. двух синусов.
И всё-таки эта группа формул не самая лёгкая для запоминания. Это тот случай, когда лучше меньше зубрить, но больше проверять. Чтобы не допустить ошибки в формуле на ответственном экзамене, обязательно сначала запишите её на черновике и проверьте двумя способами. Сначала подстановками β = α и β = −α, затем по известным значениям функций для простых углов. Для этого лучше всего брать 90º и 30º, как это было сделано в примере выше, потому что полусумма и полуразность этих значений, снова дают простые углы, и Вы легко можете увидеть, как равенство становится тождеством для верного варианта. Или, наоборот, не выполняется, если Вы ошиблись.
Пример проверки формулы cosα − cosβ = 2·sin α − β ____ 2 ·sin α + β ____ 2 для разности косинусов с ошибкой !
1) Пусть β = α, тогда cosα − cosα = 2·sin α − α _____ 2 ·sin α + α _____ 2 = 2sin0·sinα = 0·sinα = 0. cosα − cosα ≡ 0.
2) Пусть β = − α, тогда cosα − cos(− α) = 2·sin α − (−α) _______ 2 ·sin α + (−α) _______ 2 = 2sinα·sin0 = 0·sinα = 0. cosα − cos(− α) = cosα − cosα ≡ 0.
Эти проверки показали, что функции в формуле использованы правильно, но из-за того, что тождество получалось вида 0 ≡ 0, могла быть пропущена ошибка со знаком или коэффициентом. Делаем третью проверку.
3) Пусть α = 90º, β = 30º, тогда cos90º − cos30º = 2·sin 90º − 30º ________ 2 ·sin 90º + 30º ________ 2 = 2sin30º·sin60º = 2·(1/2)·( √3 _ /2) = √3 _ /2.
cos90 − cos30 = 0 − √3 _ /2 = − √3 _ /2 ≠ √3 _ /2.
Ошибка была действительно в знаке и только в знаке перед произведением.
Если ВСЕ рекомендации понятны, нажмите кнопку 
sinα·sinβ = 1 _ 2 · ( cos(α − β) − cos(α + β) ) ;
cosα·cosβ = 1 _ 2 · ( cos(α − β) + cos(α + β) ) ;
Рассмотрим пример: нужно преобразовать произведение sin5x·cos3x в сумму двух тригонометрических функций.
Поскольку в произведение входят и синус, и косинус, то берём из предыдущей группы формулу для суммы синусов, которую уже выучили, и записываем её на черновике.
sinα + sinβ = 2·sin α + β ____ 2 ·cos α − β ____ 2
Заменяем в формуле на черновике значения углов, выраженные через переменные α и β, на значения углов, выраженные через переменную x.
Получим sin8x + sin2x = 2·sin5x·cos3x
Делим обе части равества на 2 и записываем его на чистовик справа налево sin5x·cos3x = 1 _ 2 (sin8x + sin2x). Ответ готов.
Если рекомендации понятны, нажмите кнопку 
VI группа. Формулы понижения степени
cos 2 α = 1 + cos2α _________ 2 ;
sin 2 α = 1 − cos2α _________ 2 ;
cos 3 α = 3cosα + cos3α ____________ 4 ;
Первые две формулы этой группы очень нужны. Применяются часто при решении тригонометрических уравнений, в том числе уровня единого экзамена, а также при вычислении интегралов, содержащих подинтегральные функции тригонометрического типа.
Возможно, будет легче запомнить их в следующей «одноэтажной» форме
2cos 2 α = 1 + cos2α;
2 sin 2 α = 1 − cos2α,
а разделить на 2 всегда можно в уме или на черновике.
Необходимость в использовании следующих двух формул (с кубами функций) на экзаменах встречается гораздо реже. В другой обстановке у Вас всегда будет время воспользоваться черновиком. При этом возможны следующие варианты:
1) Если Вы помните последние две формулы III-ей группы, то пользуйтесь ими, чтобы выражать sin 3 α и cos 3 α путем несложных преобразований.
2) Если в последних двух формулах этой группы Вы заметили элементы симметрии, которые способствуют их запоминанию, то записывайте «эскизы» формул на черновике и проверяйте их по значениям основных углов.
3) Если, кроме того, что такие формулы понижения степени существуют, Вы о них ничего не знаете, то решайте задачу поэтапно, исходя из того, что sin 3 α = sin 2 α·sinα и прочих выученных формул. Потребуются формулы понижения степени для квадрата и формулы преобразования произведения в сумму.
Если рекомендации понятны, нажмите кнопку 
VII группа. Половинный аргумент
sin α _ 2 = ± √ 1 − cosα ________ 2 ; _____
cos α _ 2 = ± √ 1 + cosα ________ 2 ; _____
Не вижу смысла в заучивании наизусть этой группы формул в том виде, в котором они представлены в учебниках и справочниках. Если Вы понимаете, что α есть половина от 2α, то этого достаточно, чтобы быстро вывести нужную формулу половинного аргумента, исходя из первых двух формул понижения степени.
Это касается также тангенса половинного угла, формула для которого получается делением выражения для синуса на соответствующее выражение для косинуса.
Не забудьте только при извлечении квадратного корня поставить знак ±.
Если рекомендации понятны, нажмите кнопку 
VIII группа. Универсальная подстановка
sinα = 2tg(α/2) _________ 1 + tg 2 (α/2) ;
cosα = 1 − tg 2 (α/2) __________ 1 + tg 2 (α/2) ;
Если рекомендации понятны, нажмите кнопку 
IX группа. Формулы приведения.
X группа. Значения для основных углов.
Пример задачи на использование формул тригонометрии
Имеем две разные функции sin() и cos() и четыре! разных аргумента 5x, 3x, 8x и 6x. Без предварительных преобразований свести к простейшим типам тригонометрических уравнений не получится. Поэтому сначала пробуем заменить произведения на суммы или разности функций.
Делаем это так же, как в примере выше (см. раздел Преобразование произведения функций в сумму или разность).
Выражая из этих равенств произведения, подставляем их в уравнение. Получим:
Умножаем на 2 обе части уравнения, раскрываем скобки и приводим подобные члены
Итак, уравнение sin8x − sin14x = 0 равносильно уравнению sin3x·cos11x = 0, которое, в свою очередь, равносильно совокупности двух простейших уравнений sin3x = 0 и cos11x = 0. Решая последние, получаем две серии ответов
x1 = πn/3, nϵZ
x2 = π/22 + πk/11, kϵZ
Если Вы обнаружили ошибку или опечатку в тексте, сообщите о ней, пожалуйста, на электронный адрес mathematichka@yandex.ru. Буду весьма признательна.
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте ссылки.
Источник
2
Как найти синус и косинус через тангенс?
Как найти синус, если известен тангенс?
Как найти косинус, если известен тангенс?
6 ответов:
7
0
Косинус через тангенс
Для того, чтобы найти значение косинуса по известному тангенсу, нужно воспользоваться одним из тригонометрических тождеств.
Сумма квадрата тангенса и единицы равна отношению единицы и квадрата косинуса.
Отсюда можно выразить косинус:
Наличие знака ± связано с тем, что в одних четвертях косинус угла может быть положительным, а в других — отрицательным.
То есть в условии задачи должна оговариваться четверть, в которой находится угол.
**
Пример.
tgα = 1/√3, α находится в 1 четверти (0 < α < 90).
Найдём косинус: cosα = √ ( 1 / (1 + 1/3)) = √ ( 1 / (4/3)) = √ (3/4) = √3/2.
Итак, если тангенс равен 1/√3, то косинус равен √3/2.
Нетрудно догадаться, что мы имели дело с углом 30°.
<hr />
Синус через тангенс
Здесь также понадобятся тригонометрические тождества.
Можно пойти двумя путями:
1) Выразить котангенс через тангенс и найти синус по котангенсу.
2) Найти косинус по тангенсу, а затем воспользоваться основным тригонометрическим тождеством.
**
Пример.
tgα = √3, α находится в 1 четверти (0 < α < 90).
Найдём котангенс: ctga = 1 / tgα = 1 / √3.
Теперь найдём синус: sina = √ ( 1 / (1 + 1/3)) = √ ( 1 / (4/3)) = √ (3/4) = √3/2.
Или:
cosa = √ ( 1 / (1 + 3)) = √ (1/4) = 1/2.
sina = √ (1 — 1/4) = √ (3/4) = √3/2.
Таким образом, если тангенс равен √3, то синус равен √3/2.
Здесь также понятно, что это угол 60°.
1
0
конечно тангенс угла- это отношение синуса этого угла к косинусу того же угла- условно- а/б= с и а= с*в, в= а/с, сразу видно, что, кроме с, что- нибудь еще должно быть дано иначе не расколоть задачку, разве с будет равно 1 или еще какому замечательному значению, позволяющему определить величину угла угла.
1
0
В алгебре и геометрии очень часто при решении задач используются тригонометрические формулы, которые чаще называют тригонометрическими тождествами. Из любого тригонометрического тождества несложно вывести новую формулу, необходимую для нахождения одной из величин, входящих в его состав.
****************<wbr />*****************<wbr />*****************<wbr />*****************<wbr />*****
Для того, чтобы найти косинус угла, зная его тангенс, возьмем тригонометрическое тождество:
.
Из данного тождества выводим новую формулу для вычисления косинуса:
Не забываем, что косинус может принимать как положительные, так и отрицательные значения в зависимости от четверти нахождения угла.
****************<wbr />*****************<wbr />*****************<wbr />*****************<wbr />*****
Для вычисления синуса угла через его тангенс можно действовать по-разному.
Например, вычислить по выведенной выше формуле косинус угла, а затем воспользоваться еще одним тригонометрическим тождеством и вывести из него формулу для вычисления синуса угла:
1
0
В тригонометрических тождествах нет, конечно, ничего сложного, вот только запомнить их все так, чтобы не пользоваться справочными материалами, обычному человеку достаточно трудно, поэтому всегда приходится где-то искать эти формулы. Вот одна из них:
Из нее то мы и будем получать формулу для выполнения задания из вопроса, а именно — нахождения косинуса через тангенс, проведя несложные преобразования, получим:
Как видите, действительно все очень просто.
Теперь, найдя косинус, воспользуемся основным тригонометрическим тождеством, преобразуем его, чтобы найти синус через уже найденный косинус, формула такая:
0
0
sin=sqrt(1/(1+((1/tg)**2)))
cos=sqrt(1/(1+((1/ctg)**2)))
0
0
Если говорить о тангенсе угла, то является отношением синуса по отношению к косинусу. Так, следует воспользоваться тригонометрическим тождеством. Согласно ему выводится формула, которую используем для того, чтобы вычислить косинус.
Вы можете вычислить по формуле, а также воспользуюсь еще 1 тригонометрическим тождеством, выведя формула вычислить:
Читайте также
Функция 1/cos X называется секансом. Название происходит от латинского слова secans — секущая. Того же происхождения слова сектор (лат. sector — отсекающий, отделяющий), секатор (садовые ножницы, от лат. secare — сечь, резать) и др. А какое отношение к этому имеет пчела? Все знают, что пчела — насекомое. Это слово в русском языке (от глаголов насекать, сечь) — калька, то есть буквальный перевод, с французского insecte (отсюда и термин инсектицид), которое произошло от латинского insectum — «насеченное, с насечками». В свою очередь латинское слово — калька с древнегреческого ἔντομον — насекомое (от ἐντομή — надрез). От этого греческого слова в русском языке — термин энтомология — область зоологии, изучающая насекомых. Так что секанс и насекомое — этимологические родственники.
1) Можно объяснить, например, так.
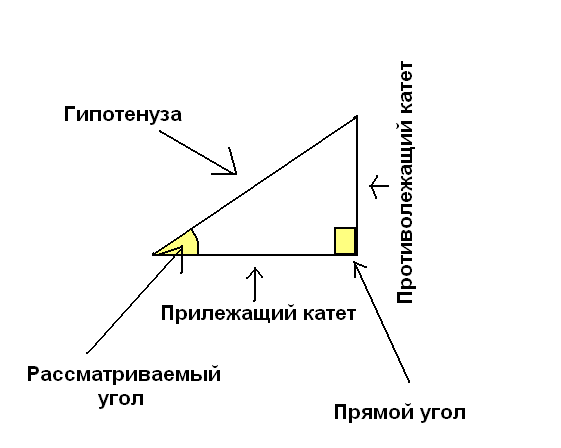
Покажите ему картинку, которую я привёл ниже:
Объясните, что синус и косинус бывают только у треугольников, у которых есть прямой угол, то есть у прямоугольных треугольников. Хотя сами по себе синус и косинус имеют отношение только к углу. Треугольник — это лишь вспомогательная фигура, помогающая понять и рассчитать их.
Если есть прямой угол, тогда:
Стороны, касающиеся этого угла называются катетами.
А сторона, которая не касается — гипотенузой.
Также, у такого треугольника есть ещё два острых угла.
Синус и косинус могут быть только с параметром угол. То есть для одного острого угла этого треугольника одни синус и косинус, а для другого — другие.
Определение синуса:
Определение косинуса:
На рассматриваемом рисунке рассматривается один из углов и написано где относительно него противолежащий и прилежащий катеты.
Противолежащий катет — это катет, находящийся противоположно от рассматриваемого угла. Рассматриваемый угол — это тот угол, для которого мы хотим найти синус или косинус.
А прилежащий катет — это катет, примыкающий к этому углу.
А гипотенуза — это третья сторона.
Так вот, по определению синусов и косинусов они — это отношение их к гипотенузе.
То есть чтобы найти синус, нужно поделить длину противолежащего катета на длину гипотенузы, а чтобы найти косинус, нужно поделить длину прилежащего катета на длину гипотенузы.
2) Но это ещё не всё.
Можно ещё объяснить и по-другому:
Если угол, для которого необходимо найти синус и косинус вписать в окружность таким образом, как на рисунке ниже, то синусом будет длина вертикального отрезка, а косинусом — горизонтального, исходя из того, что радиус окружности равен единице. Как видно из рисунка, образованная гипотенуза является одновременно и радиусом этой окружности, а эти отрезки — это катеты.
При данном рассмотрении синусов и косинусов нет такой привязки к треугольнику, поэтому тут можно также рассматривать и тупые и даже развёрнутые углы. Правда тогда придётся приписывать знак к синусу или косинусу при условии попадения линии гипотенузы в другие сегменты круга. Там, где на рисунке написан X, это имеет отношение к косинусу, а где Y — к синусу.
Какие знаки нужно приписывать при попадении гипотенузы в эти сегменты:
левый верхний: к косинусу знак минус
правый верхний: ничего
левый нижний: и к синусу и к косинусу знак минус
правый нижний: к синусу знак минус
При попадании между сегментами — так как указано на рисунке:
Если известны только углы, то
C=180-arcsin(sin A)-arcsin(sin B)
Если известна хоть одна сторона, то есть теорема синусов.
a/sin A = b/sin B = c/sin C = 2R
Зная одну сторону и два синуса, можно найти и третий синус, и остальные две стороны.
И заодно радиус описанной окружности, но это уже другая задача.
А надо ли так усложнять решение. Из известных соотношений, найти гипотенузу, которая и будет равна 20. А дальше Пифагор,- 20 в квадрате минус 12 в той же степени, и после простого извлечения корня, получаем величину,- 16.Тригонометрию, вместе с логарифмированием, лучше оставлять в покое…)
Мне нет.
Я всегда догадывалась, что высшая математика для избранных. Я готова согласиться, что математика одна из основных наук, все в мире подчиненно математическим законам. Так же математика отлично развивает мышление и логику.
Но все-таки, я считаю, что косинусы и синусы должны изучать люди, которые целенаправленно выбрали математику своей профессией! Когда я училась в колледже на гуманитарном направлении, и мне приходилось заниматься с репетитором чтобы получить зачет по синусам и косинусам, я чувствовала как меня лишают права выбора. Я же уже выбрала другой путь, я бы лучше это врем потратила на дополнительные уроки английского или другого языка.
Тригонометрические функции любого угла и определение синуса, косинуса, тангенса и котангенса:
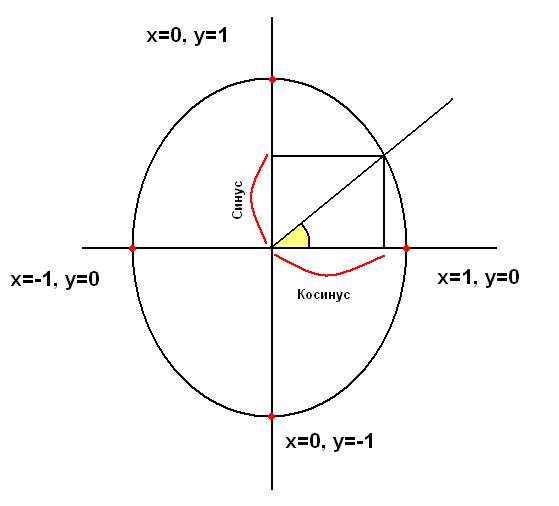
Отметим на оси х справа от начала координат точку А и проведем через нее окружность с центром в точке О (рис. 64). Радиус OA будем называть начальным радиусом.
Повернем начальный радиус около точки О на 70° против часовой стрелки. При этом он перейдет в радиус ОВ. Говорят, что угол поворота равен 70°. Если повернуть начальный радиус около точки О на 70° по часовой стрелке, то он перейдет в радиус ОС. В этом случае говорят, что угол поворота равен —70°. Углы поворота в 70° и —70° показаны стрелками на рисунке 64.
Вообще при повороте против часовой стрелки угол поворота считают положительным, а при повороте по часовой стрелке — отрицательным.
Из курса геометрии известно, что мера угла в градусах выражается числом от 0 до 180. Что касается угла поворота, то он может выражаться в градусах каким угодно действительным числом от 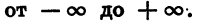
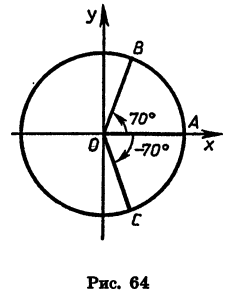
радиус повернуть против часовой стрелки на 180°, а потом еще на 30°, то угол поворота будет равен 210°. Если начальный радиус сделает полный оборот против часовой стрелки, то угол поворота будет равен 360°; если он сделает полтора оборота в том же направлении, то угол поворота будет равен 540° и т. д. На рисунке 65 стрелками показаны углы поворота в 405° и -200°.
Рассмотрим радиусы OA и ОВ (рис. 66). Существует бесконечно много углов поворота, при которых начальный радиус OA переходит в радиус ОВ. Так, если 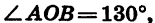
Пусть при повороте на угол а начальный радиус OA переходит в радиус ОВ. В зависимости от того, в какой координатной четверти окажется радиус ОВ, угол а называют углом этой четверти. Так, если 0° < а < 90°, то а — угол I четверти; если 90° < а <180°, то а — угол II четверти; если 180° < а < 270°, то а — угол III четверти; если 270° < а < 360°, то а — угол IV четверти. Очевидно, что при прибавлении к углу целого числа оборотов получается угол той же четверти. Например, угол в 430° является углом I четверти, так как 430° = 360°+ 70° и 0°<70°<90°; угол в 920° является углом III четверти, так как 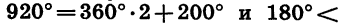
Углы 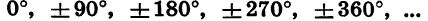
В курсе геометрии были определены синус, косинус и тангенс угла а при 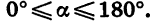
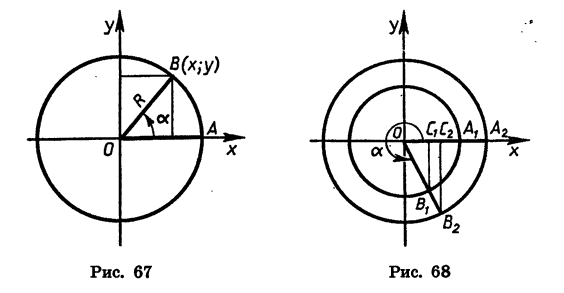
Пусть при повороте около точки О на угол а начальный радиус OA переходит в радиус ОВ (рис. 67).
Синусом угла а называется отношение ординаты точки В к длине радиуса.
Косинусом утла а называется отношение абсциссы точки В к длине радиуса.
Тангенсом угла а называется отношение ординаты точки В к ее абсциссе.
Котангенсом угла а называется отношение абсциссы точки В к ее ординате.
Если координаты точки В равны х и у, а длина начального радиуса равна R, то
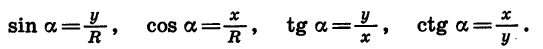
В курсе геометрии было показано, что значения синуса, косинуса и тангенса угла а, где 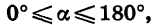
Покажем, например, что sin а не зависит от R.
Пусть при повороте луча 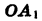
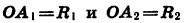
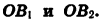
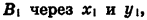
Опустим перпендикуляры из точек 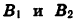
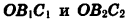
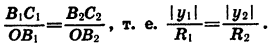
Так как точки 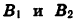
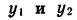
Заметим, что это равенство верно и в том случае, когда точки 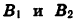
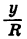
Выражения sin а и cos а определены при любом а, так как для любого угла поворота можно найти соответствующие значения дробей 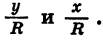
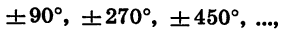
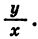
Каждому допустимому значению а соответствует единственное значение sin a, cos а, tg а и ctg а. Поэтому синус, косинус, тангенс и котангенс являются функциями угла а. Их называют тригонометрическими функциями.
Можно доказать, что областью значений синуса и косинуса является промежуток [—1; 1], а областью значений тангенса и котангенса — множество всех действительных чисел.
Приведем примеры вычисления значений тригонометрических функций.
Пример:
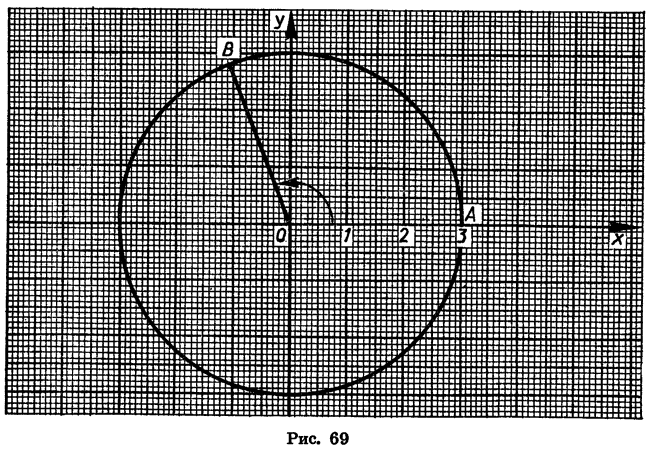
Найдем с помощью чертежа приближенные значения sin 110°, cos 110°, tg 110° и ctg 110°.
Начертим окружность с центром в начале координат и радиусом OA = R = 3 (рис. 69). Повернем радиус OA на 110°. Получим радиус ОВ. Найдем по рисунку координаты х и у точки В: 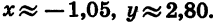
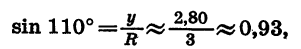
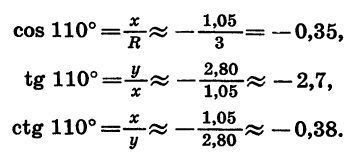
В таблице приведены известные из курса геометрии значения синуса, косинуса и тангенса углов 0°, 30°, 45°, 60° и 90°. Прочерк сделан в том случае, когда выражение не имеет смысла.
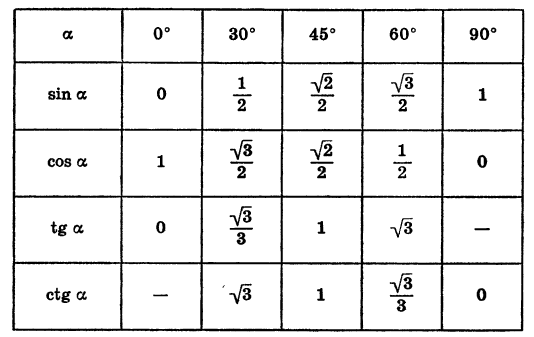
Значения котангенса могут быть получены из значений тангенса, так как котангенс угла является числом, обратным тангенсу этого же угла. Поэтому, например,
Пример:
Найдем синус, косинус, тангенс и котангенс углов 180° и 270°.
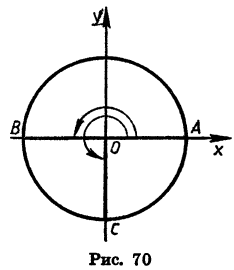
При повороте на 180° около точки О радиус OA, равный 1, (рис. 70) переходит в радиус ОВ, а при повороте на 270° — в радиус ОС.
Так как точка В имеет координаты х = — 1 и у = 0, то
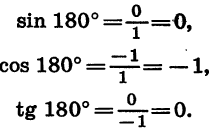
Так как точка С имеет координаты х = 0 и у = —1, то

Напомним, что выражения ctg 180° и tg 270° не имеют смысла.
Свойства синуса, косинуса, тангенса и котангенса
Рассмотрим некоторые свойства тригонометрических функций.
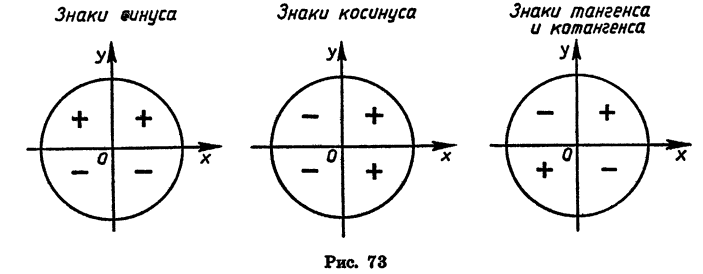
Выясним сначала, какие знаки имеют синус, косинус, тангенс и котангенс в каждой из координатных четвертей.
Пусть при повороте радиуса OA, равного R, на угол а точка А перешла в точку В с координатами х и у (см. рис. 67).
Так как 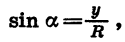
В I и II четвертях у > 0, а в III и IV четвертях у < 0. Значит, sin a > 0, если а является углом I или II четверти, и sin a < 0, если а является углом III или IV четверти.
Знак cos а зависит от знака х, так как 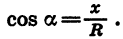
Так как 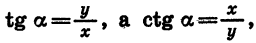
Знаки синуса, косинуса, тангенса и котангенса в каждой из четвертей показаны на рисунке 73.
Выясним теперь вопрос о четности и нечетности тригонометрических функций.
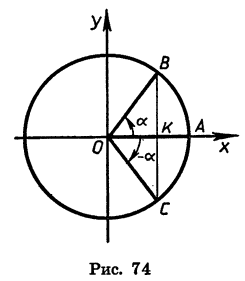
Пусть при повороте на угол а радиус OA переходит в радиус ОВ, а при повороте на угол — а в радиус ОС х (рис. 74). Соединив отрезком точки В и С, получим равнобедренный треугольник ВОС. Луч OA является биссектрисой угла ВОС. Значит, отрезок ОК является медианой и высотой треугольника ВОС. Отсюда следует, что точки В и С симметричны относительно оси абсцисс.
Пусть координаты точки В равны х и у, тогда координаты точки С равны х и -у. Пользуясь этим, найдем, что
Мы получили формулы, выражающие зависимость между синусами, косинусами, тангенсами и котангенсами противоположных углов:
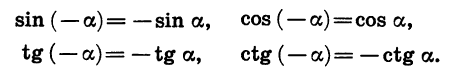
Например:
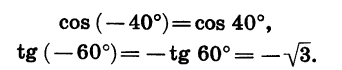
Итак, синус, тангенс и котангенс являются нечетными функциями, а косинус является четной функцией.
Рассмотрим еще одно свойство тригонометрических функций.
Если при повороте радиуса OA на угол а получен радиус ОВ (см. рис. 67), то тот же радиус получится и при повороте OA на угол, отличающийся от а на целое число оборотов. Отсюда следует, что при изменении угла на целое число оборотов значения синуса, косинуса, тангенса и котангенса не изменяются.
Например:
Рассмотренные свойства позволяют свести нахождение значений синуса, косинуса, тангенса и котангенса любого угла к нахождению их значений для неотрицательного угла, меньшего 360°.
Пример:
Найдем sin 765° и cos ( — 1170°). Имеем:
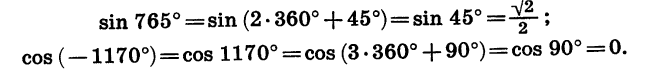
Радианная мера угла. Вычисление значении тригонометрических функции с помощью микрокалькулятора
Как известно, углы измеряются в градусах, минутах, секундах. Эти единицы измерения связаны между собой соотношениями
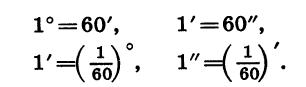
Кроме указанных, используется также единица измерения углов, называемая радианом.
Углом в один радиан называют центральный угол, которому соответствует длина дуги, равная длине радиуса окружности.
Угол, равный 1 рад, изображен на рисунке 75.
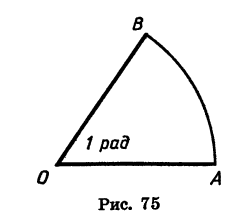
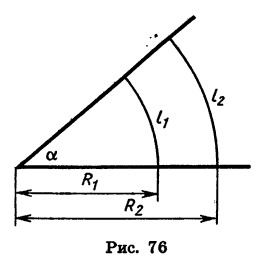
Радианная мера угла, т. е. величина угла, выраженная в радианах, не зависит О А от длины радиуса. Это следует из того, что фигуры, ограниченные углом и дугой окружности с центром в вершине этого угла, подобны между собой (рис. 76).
Установим связь между радиан-ным и градусным измерениями углов.
Углу, равному 180°, соответствует полуокружность, т. е. дуга, длина l которой равна
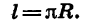
Чтобы найти радианную меру этого угла, надо длину дуги l разделить на длину радиуса R. Получим:
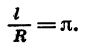
Следовательно, радианная мера угла в 180° равна
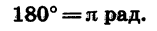
Отсюда получаем, что радианная мера угла в 1° равна
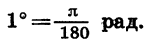
Приближенно 1° равен 0,017 рад.
Из равенства 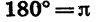
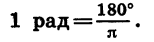
Приближенно 1 рад равен 57°.
Рассмотрим примеры перехода от радианной меры к градусной и от градусной меры к радианной.
Пример:
Выразим в градусах 4,5 рад.
Так как
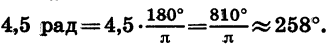
Пример:
Найдем радианную меру угла в 72°.
Так как
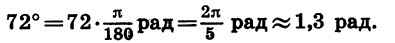
При записи радианной меры угла обозначение «рад» часто опускают. Например, вместо равенства 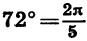
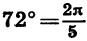
Выразим в радианной мере углы 30°, 45°, 60°, 90°, 270° и 360°. Получим:
Радианная мера угла часто используется в тригонометрических выражениях. Так, запись sirfl означает синус угла в 1 радиан, запись sin ( — 2,5) означает синус угла в —2,5 радиана, запись 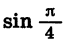
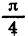
Значения тригонометрических функций для углов, выраженных как в градусах, так и в радианах, можно находить, используя микрокалькулятор. Так, с помощью микрокалькулятора «Электроника БЗ-З6» значения синуса, косинуса и тангенса вычисляют следующим образом. Переводят переключатель «ГРАД — РАД», находящийся в нижней части корпуса, в положение «ГРАД», если угол задан в градусах, или в положение «РАД», если угол задан в радианах. Вводят угол, нажимают клавишу 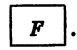
Пример:
Найдем с помощью микрокалькулятора значение выражения с точностью до 0,001:
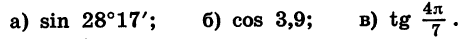
а) Установим переключатель в положение «ГРАД», затем выразим 28°17′ в градусах и нажмем «последовательно клавиши 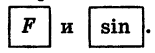
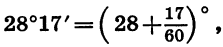

Получаем, что
б) Устанавливаем переключатель в положение «РАД» и находим значение cos 3,9 по программе:
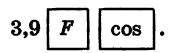
Получаем, что cos
в) Переключатель устанавливаем в положение «РАД». При нахождении значения выражения 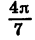
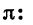
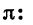
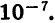

Получаем, что
Отметим, что для вычисления котангенса угла надо сначала найти значение тангенса этого угла, а потом обратное число, нажав клавиши
Основные тригонометрические формулы
Соотношения между тригонометрическими функциями одного и того же угла:
Рассмотрим, как связаны между собой синус и косинус одного и того же угла.
Пусть при повороте радиуса OA вокруг точки О на угол а получен радиус ОВ (рис. 77). По определению
где х — абсцисса точки В, у — ее ордината, a R — длина радиуса OA. Отсюда

Так как точка В принадлежит окружности с центром в начале координат, радиус которой равен R, то ее координаты удовлетворяют уравнению
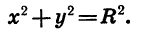
Подставив в это уравнение вместо х и у выражения R cos а и R sin а, получим:
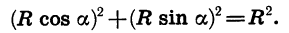
Разделив обе части последнего равенства на 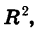

Равенство (1) верно при любых значениях а. Выясним теперь, как связаны между собой тангенс, синус и косинус одного и того же угла.
По определению 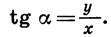
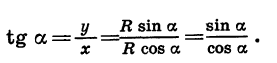
Таким образом,
Аналогично
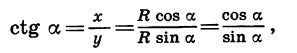
Равенство (2) верно при всех значениях а, при которых cos 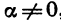
С помощью формул (1) — (3) можно получить другие формулы, выражающие соотношения между тригонометрическими функциями одного и того же угла.
Из равенств (2) и (3) получим:
Равенство (4) показывает, как связаны между собой тангенс и котангенс угла а. Оно верно при всех значениях а, при которых tg а и ctg а имеют смысл.
Заметим, что формулу (4) можно получить и непосредственно из определения тангенса и котангенса.
Выведем теперь формулы, выражающие соотношения между тангенсом и косинусом, а также между котангенсом и синусом одного и того же угла.
Разделив обе части равенства (1) на 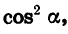
Если обе части равенства (1) разделить на 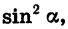
т. е.
Равенство (5) верно, когда cos 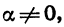
Равенства (1) — (6) являются тождествами. Их называют основными тригонометрическими тождествами. Рассмотрим примеры использования этих тождеств для нахождения значений тригонометрических функций по известному значению одной из них.
Пример:
Найдем cos a, tg а и ctg а, если известно, что sin
Найдем сначала cos а. Из формулы 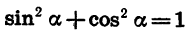
Так как а является углом II четверти, то его косинус отрицателен. Значит,
Зная синус и косинус угла а, можно найти его тангенс:
Для отыскания котангенса угла а удобно воспользоваться формулой tg a • ctg a = 1. Имеем:
Пример:
Известно, что 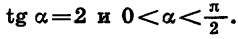
Воспользовавшись формулой 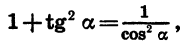
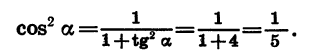
По условию угол a является углом I четверти, поэтому его косинус положителен. Значит,
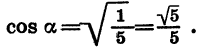
Зная cos а и tg а, можно найти sin а. Из формулы 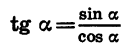
По известному tg а легко найти ctga:
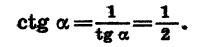
Итак,
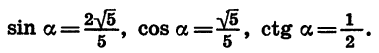
Применение основных тригонометрических формул к преобразованию выражении
Мы уже встречались с некоторыми простейшими преобразованиями тригонометрических выражений. Рассмотрим более сложные примеры.
Пример:
Упростим выражение
Воспользовавшись формулами 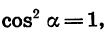
Пример:
Упростим выражение
Пример:
Докажем тождество
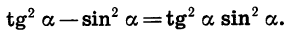
Преобразуем левую часть данного равенства:
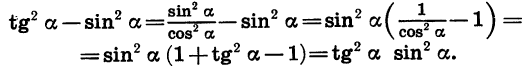
Мы получили выражение, стоящее в правой части равенства. Таким образом, тождество доказано.
Формулы приведения
Тригонометрические функции углов вида 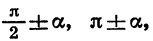
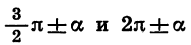
Выведем сначала формулы приведения для синуса и косинуса.
Докажем, что для любого а
Повернем радиус OA, длина которого равна R, на угол а и на угол 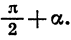
Опустим из точки В1 перпендикуляры 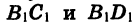
Повернем прямоугольник 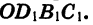
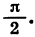
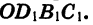
Отсюда следует, что ордината точки В2 равна абсциссе точки В1, а абсцисса точки В2 равна числу, противоположному ординате точки В1. Обозначим координаты точки B1 через 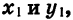
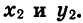
Значит,
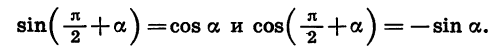
Из формул (1) следует, что
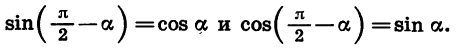
Действительно, представим разность 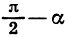
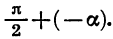
Формулы приведения для синуса и косинуса угла 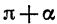
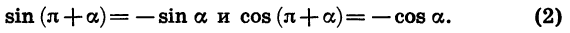
Для доказательства достаточно представить 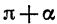
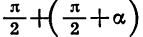
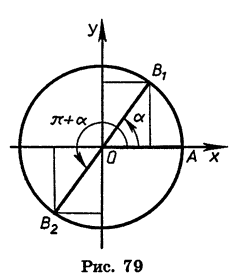
Заметим, что к формулам (2) легко прийти и из геометрических соображений (рис. 79). При повороте радиуса OA на угол а и на угол 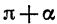
начала координат точек равны по модулю и противоположны по знаку. Отсюда следует, что 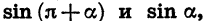
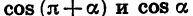
Из формул (2) следует, что
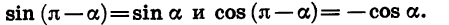
Для доказательства достаточно представить 
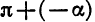
Формулы приведения для синуса и косинуса угла 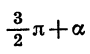
Чтобы доказать формулы (3), достаточно представить 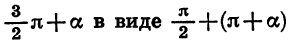
Из формул (3) нетрудно получить, что
Наконец, формулы приведения для синуса и косинуса угла 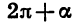
Справедливы также формулы
Например, для
Формулы приведения для тангенса и котангенса можно получить с помощью формул приведения для синуса и косинуса. Например:
Все формулы приведения сведем в две таблицы, поместив в первой из них формулы для углов 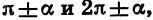
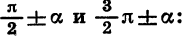
Цо таблицам легко проследить закономерности, имеющие место для формул приведения. Эти закономерности позволяют сформулировать правило, с помощью которого можно записать любую формулу приведения, не прибегая к таблице:
Функция в правой части равенства берется с тем же знаком, какой имеет исходная функция, если считать, что угол а является углом 1 четверти;
для углов 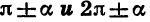
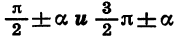
Пример:
Выразим 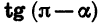
Если считать, что a — угол I четверти, то 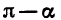
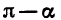
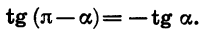
С помощью формул приведения нахождение значений тригонометрических функций любого угла можно свести к нахождению значений тригонометрических функций угла от 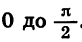
Пример:
Найдем значение
Пример:
Найдем значение sin (— 585°).
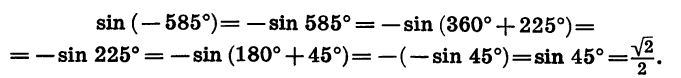
Формулы сложения и их следствия
Выведем формулы, выражающие тригонометрические функции суммы и разности двух углов через тригонометрические функции этих углов.
Повернем радиус OA, равный R, около точки О на угол а и на угол 
Найдем скалярное произведение векторов 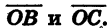
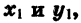
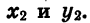
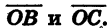
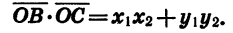
Выразим скалярное произведение 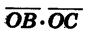

Подставив значения 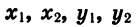
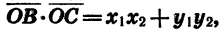
С другой стороны, по теореме о скалярном произведении векторов имеем:

Угол ВОС между векторами 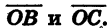

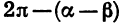
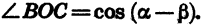
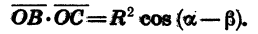
Так как 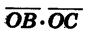
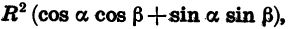
Формулу (1) называют формулой косинуса разности.
Косинус разности двух углов равен произведению косинусов этих углов плюс произведение синусов этих углов.
С помощью формулы (1) легко получить формулу косинуса суммы:
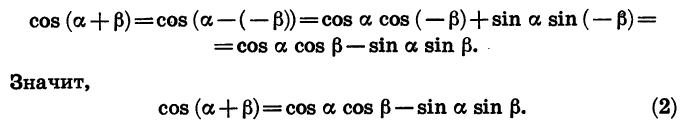
Косинус суммы двух углов равен произведению косинусов этих углов минус произведение синусов этих углов.
Выведем теперь формулы синуса суммы и синуса разности. Используя формулы приведения и формулу (1), получим:
Синус суммы двух углов равен произведению синуса первого угла на косинус второго плюс произведение косинуса первого угла на синус второго.
Для синуса разности имеем:
Синус разности двух углов равен произведению синуса первого угла на косинус второго минус произведение косинуса первого угла на синус второго.
Формулы (1) — (4) называют формулами сложения для синуса и косинуса.
Приведем примеры использования формул сложения.
Пример:
Вычислим cos 15° и sin 15°. Представим 15° в виде разности 45° — 30°. Тогда
Пример:
Упростим выражение 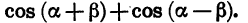
Используя формулы (1) — (4), можно вывести формулы сложения для тангенса и котангенса. Выведем, например, формулу тангенса суммы:
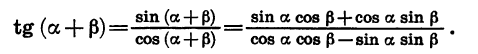
Разделим числитель и знаменатель полученной дроби на произведение cos a cos 
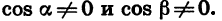
Значит,
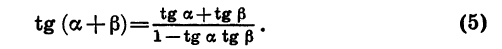
Аналогично можно доказать, что
Формулы двойного угла
Формулы сложения позволяют выразить sin 2a, cos 2a и tg 2a через тригонометрические функции угла a. Положим в формулах

Эти тождества называют формулами двойного угла.
Приведем примеры применения формул двойного угла для нахождения значений тригонометрических функций и преобразования тригонометрических выражений.
Пример:
Найдем значение sin 2а, зная, что cosa = — 0,8 и a — угол III четверти.
Сначала вычислим sin а. Так как a — угол III четверти, то sin а < 0. Поэтому
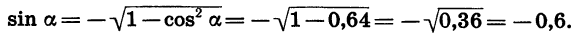
По формуле синуса двойного угла
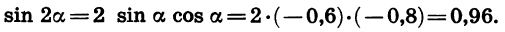
Пример:
Упростим выражение
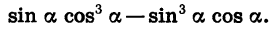
Вынесем за скобки sin a cos a и воспользуемся формулами двойного угла:
Из формулы (2) следует, что
Действительно, выразив cos 2a через sin a, получим:
Отсюда
Аналогично, выразив cos 2a через cos a, получим:
Формулы (4) и (5) используются в вычислениях и преобразованиях.
Пример:
Упростим выражение
Применим формулы (4) и (5) к выражениям 1 — cos а и 1 + cos а, представив а в виде произведения 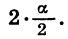
Формулы суммы и разности тригонометрических функции
Сумму и разность синусов или косинусов можно представить в виде произведения тригонометрических функций. Формулы, на которых основано такое преобразование, могут быть получены из формул сложения.
Чтобы представить в виде произведения сумму sin a + sin 
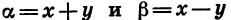
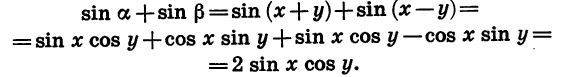
Из равенств a = x + y и 
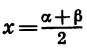
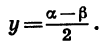
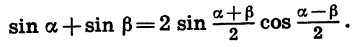
Мы получили формулу суммы синусов двух углов.
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.
Аналогично можно вывести формулы разности синусов, суммы и разности косинусов.
Формула разности синусов:
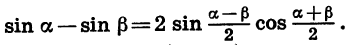
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы.
Формула суммы косинусов:
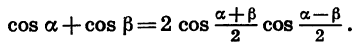
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы, этих углов на косинус их полуразности.
Формула разности косинусов:
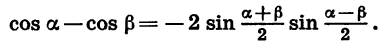
Разность косинусов двух углов равна взятому со знаком *минус» удвоенному произведению синуса полусуммы этих углов на синус их полуразности.
Учитывая, что 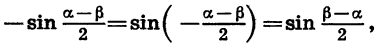
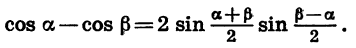
Приведем примеры применения полученных формул.
Пример:
Упростим сумму sin 10° + sin 50°.
Воспользовавшись формулой суммы синусов, получим:
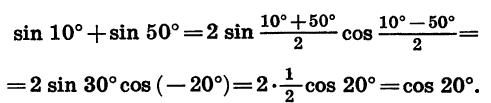
Пример:
Представим в виде произведения разность
Воспользовавшись формулой приведения, представим данное выражение в виде разности косинусов и преобразуем ее в произведение. Тогда
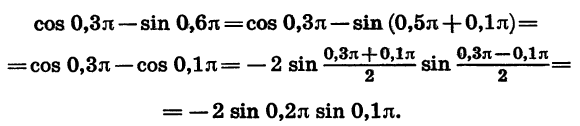
Пример:
Представим в виде произведения выражение 1 — sin а.
Так как 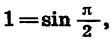
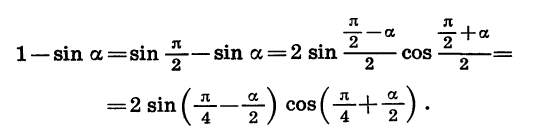
Эту задачу можно решить иначе:
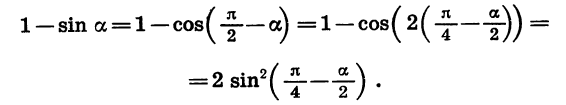
С помощью формул приведения первое из полученных выражений можно преобразовать во второе и наоборот.
Вычисление значений тригонометрических выражений
Возможно вам будут полезны эти страницы:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи?
Как перевести тангенс в косинус формула:
- cos(a)=(+-)1/sqrt(1+(tg(a))^2)
Косинус через тангенс, перевести tg в cos, калькулятор — онлайн
tg φ:
cos φ:
±
Поделиться в соц сетях:
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн — косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о «Использование сердечного индекса Руфье в медико-спортивном контроле». Проба Руфье — представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в