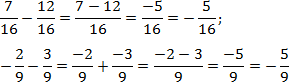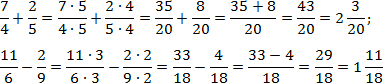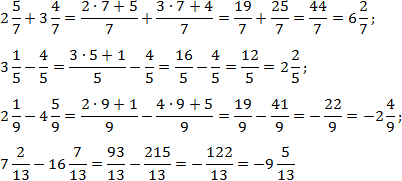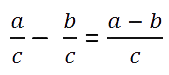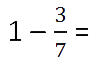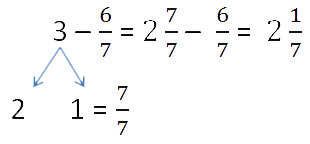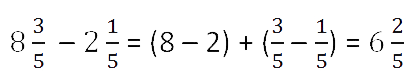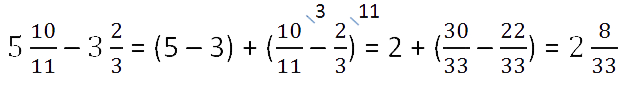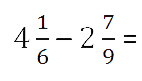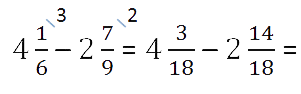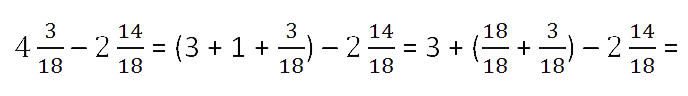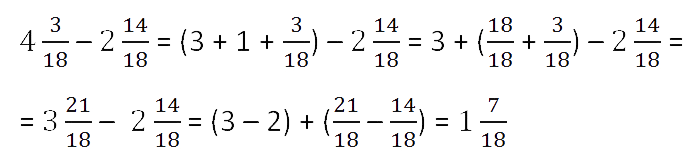Как найти значение выражения с дробями вычитание

Сложение и вычитание дробей

30 июля 2011

Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.

Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.

Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.

Задача. Найдите значение выражения:

Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:

Как видите, ничего сложного: просто складываем или вычитаем числители — и все.

Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.

Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.

Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!

Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.

Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:

1. Плюс на минус дает минус;
2. Минус на минус дает плюс.

Разберем все это на конкретных примерах:

Задача. Найдите значение выражения:

В первом случае все просто, а во втором внесем минусы в числители дробей:

Что делать, если знаменатели разные

Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.

Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю», поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:

Задача. Найдите значение выражения:

В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.

Что делать, если у дроби есть целая часть

Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.

Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:

1. Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
2. Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
3. Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.

Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:

Задача. Найдите значение выражения:

Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:

Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.

Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.

Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.

Резюме: общая схема вычислений

В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:

1. Если в одной или нескольких дробях выделена целая часть, переведите эти дроби в неправильные;
2. Приведите все дроби к общему знаменателю любым удобным для вас способом (если, конечно, этого не сделали составители задач);
3. Сложите или вычтите полученные числа по правилам сложения и вычитания дробей с одинаковыми знаменателями;
4. Если возможно, сократите полученный результат. Если дробь оказалась неправильной, выделите целую часть.

Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.

Смотрите также:

1. Тест к уроку «Сложение и вычитание дробей» (легкий)
2. Приведение дробей к общему знаменателю
3. Тест к уроку «Десятичные дроби» (1 вариант)
4. Метод узлов в задаче B5
5. Задача B5: площадь кольца
6. Сфера, вписанная в куб

При вычитании дробей, как и при сложении, могут встретиться несколько случаев.

Вычитание дробей с одинаковыми знаменателями

При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают
числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.

Пример.

В буквенном виде правило вычитания дробей с одинаковыми знаменателями
записывают так:

Вычитание правильной дроби из единицы

Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде
неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.

Пример.

Знаменатель вычитаемой дроби равен 7, значит, единицу представляют как неправильную
дробь

и вычитают по правилу вычитания дробей с одинаковыми знаменателями.

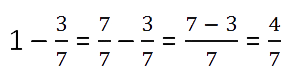
Вычитание правильной дроби из целого числа

Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число
в виде смешанного числа.

Для этого занимаем единицу в натуральном числе и представляем её в виде неправильной дроби,
знаменатель которой равен знаменателю вычитаемой дроби.

Пример.

В примере единицу мы заменили неправильной дробью

и вместо 3 записали смешанное
число и от дробной части отняли дробь.

Вычитание смешанных чисел

При вычитании смешанных чисел отдельно из целой части вычитают целую часть, а из дробной части
вычитают дробную часть.

При подобных расчётах могут встретиться разные случаи.

Первый случай вычитания смешанных чисел

У дробных частей одинаковые знаменатели и числитель дробной части
уменьшаемого (из чего вычитаем) больше или равен числителю дробной части вычитаемого
(что вычитаем).

Пример.

Второй случай вычитания смешанных чисел

У дробных частей разные знаменатели.

В этом случае вначале нужно

привести к общему знаменателю
дробные части, а затем
выполнить вычитание целой части из целой, а дробной из дробной.

Пример.

Третий случай вычитания смешанных чисел

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Пример.

Так как у дробных частей разные знаменатели, то как и
во втором случае, вначале приведём обыкновенные дроби к общему знаменателю.

Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого.

3 < 14

Поэтому, вспомнив
вычитание правильной дроби из целого числа, займём единицу из целой части и представим
эту единицу в виде неправильной дроби с одинаковым знаменателем и числителем равным 18.

Сложим полученную неправильную дробь

и дробную часть
уменьшаемого и получим:

Все рассмотренные случаи можно описать с помощью правил вычитания
смешанных чисел.

• Привести дробные части уменьшаемого и вычитаемого к наименьшему общему знаменателю.
• Если дробная часть уменьшаемого меньше дробной части
  вычитаемого, то занимаем у целой части уменьшаемого единицу. Эту единицу
  превращаем в неправильную дробь с одинаковым числителем и знаменателем равными наименьшему общему знаменателю.
• Прибавляем полученную неправильную дробь к дробной части уменьшаемого.
• Вычитаем из целой части целую, а из дробной — дробную.
• Проверяем, нельзя ли сократить и выделить целую часть в конечной дроби.

---

Ваши комментарии

Оставить комментарий:

---

Перед тем как перейти к сложению дробей, вспомним теоретические основы. Итак, дробь — это форма записи числа:

где a — числитель, b — знаменатель.

Дробь называется правильной — если числитель меньше знаменателя (к примеру, 1/3), неправильной — если числитель больше знаменателя (например, 5/2).

Вычитание обыкновенных дробей

Вычитание дробей — это арифметическое действие, в результате которого получается новое число, содержащее разность заданных чисел.

Разберем на конкретных примерах: как находить разность дробей с одинаковыми и разными знаменателями, как из натурального числа вычесть дробь и наоборот, познакомимся с вычитанием смешанных дробей.

Вычитание дробей с одинаковыми знаменателями

Чтобы вычесть дроби с одинаковыми знаменателями нужно из числителя первой дроби вычесть числитель второй, а знаменатели оставить без изменения. В общем виде это будет выглядеть следующим образом:

Пример 1:

7 8

—

2 8

Решение:

7 8

—

2 8

=

7 — 2 8

=

5 8

Таким образом, чтобы вычесть дроби с одинаковыми знаменателями нужно найти разность их числителей, а знаменатель оставить без изменения.

Как вычитать дроби с разными знаменателями

В общем виде, вычитание дробей с разными знаменателями, выглядит следующим образом:

a b

—

c d

=

a ∙ m1 — c ∙ m2 e

где e — наименьший общий знаменатель (НОЗ — наименьшее число, которое делится без остатка и на b и на d), m1 и m2 — дополнительные множители (m1 = e : b, m2 = e : d).

Пример 3:

5 3

—

2 7

Решение:

5 3

—

2 7

=

5 ∙ 7 21

—

2 ∙ 3 21

=

35 21

—

6 21

=

35 — 6 21

=

29 21

=

1

8 21

Подробнее про нахождение НОЗ — смотрите тут.

Как из целого числа вычесть дробь?

Вычитание обыкновенной дроби из целого числа, сводится к представлению целого числа в виде дроби, в которой знаменатель будет единицей, а числитель самим числом, к примеру:

Дальнейшее вычисление происходит по стандартному алгоритму.

Как из обыкновенной дроби вычесть целое число?

Порядок действий, при вычитании целого числа из дробного, аналогичен, т.е. представляем целое число в виде дроби со знаменателем — 1 и находим разность, согласно представленным выше алгоритмам вычитания.

Как вычитать смешанные дроби?

Вычитание смешанных дробей сводится к переводу их к неправильному виду и дальнейшим действиям согласно вышеописанным алгоритмам. Перевод смешанного числа в неправильную дробь, в общем виде, выглядит следующим образом:

Пример 4:

3

2 4

—

3 5

Решение:

3

2 4

—

3 5

=

3 ∙ 4 + 2 4

—

3 5

=

14 4

—

3 5

=

14 ∙ 5 20

—

3 ∙ 4 20

=

70 20

—

12 20

=

70 — 12 20

=

58 20

=

29 10

=

2

9 10

Правила вычитания дробей

Резюмируя вышесказанное, выведем общий алгоритм вычитания дробей:

• Если дробь смешанная — приводим её к неправильному виду;
• Если дроби имеют одинаковые знаменатели — из числителя первой дроби вычитаем числитель второй;
• Если дроби имеют разные знаменатели — находим НОЗ и дополнительные множители, находим разность числителей;
• При необходимости сокращаем и приводим к неправильному виду.

Смотрите также:

• Смотрите также
• Калькуляторы
• Последние примеры

Калькулятор вычитания дробей

Оцените материал:

Загрузка…