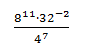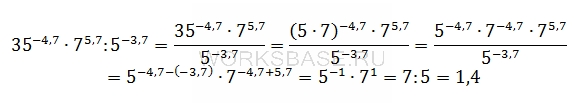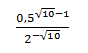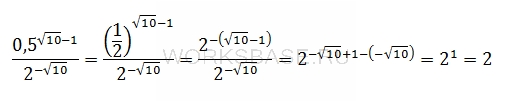Формулировка задачи: Найдите значение выражения (степени, с разными основаниями).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 2 (Действия со степенями).
Рассмотрим, как решаются подобные задачи на примере.
Пример задачи 1:
Найдите значение выражения 80,76 ∙ 640,12.
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:

Ответ: 8
Пример задачи 2:
Найдите значение выражения: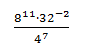
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:

Ответ: 512
Пример задачи 3:
Найдите значение выражения 35-4,7 ∙ 75,7 : 5-3,7.
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
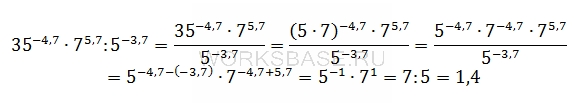
Ответ: 1,4
Пример задачи 4:
Найдите значение выражения: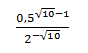
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
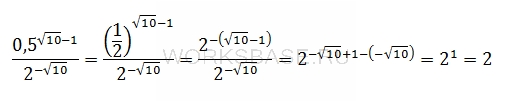
Ответ: 2
Поделитесь статьей с одноклассниками «Найдите значение выражения (степени, с разными основаниями) – как решать».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
Действия со степенями и корнями
1. При умножении степеней с одинаковыми основаниями показатели
складываются, а основание остаётся прежним:
.
Например, .
2. При делении степеней с одинаковыми основаниями показатели
степеней вычитаются, а основание остаётся прежним:
.
Например, .
3. При возведении степени в степень показатели
степеней перемножаются, а основание остаётся прежним:
.
Например, .
4. Степень произведения равна произведению степеней множителей:
.
Например, .
5. Степень частного равна частному степеней делимого и делителя:
.
Например, .
Пример 1. Найти значение выражения
.
Решение. В данном случае в явной форме ни одно из свойств степени
с натуральным показателем применить нельзя, так как все степени имеют разные основания.
Запишем некоторые степени в другом виде:
(степень произведения равна произведению степеней множителей),
(при умножении степеней с одинаковыми основаниями показатели складываются, а основание
остаётся прежним, при возведении степени в степень показатели степеней перемножаются,
а основание остаётся прежним).
Теперь получим:
В данном примере были использованы первые четыре свойства степени
с натуральным показателем.
Свойства степеней и корней интенсивно используются при упрощении выражений в задачах
математического анализа, например, для нахождения производной параметрически заданной функции
и
производной функции, заданной неявно.
Имеют место следующие тождества:
1) ;
2) ;
3) .
Выполнить действия со степенями самостоятельно, а затем посмотреть решения
Пример 2. Найти значение выражения
.
Пример 3. Найти значение выражения
.
1. Корень k-й степени из произведения неотрицательных
чисел равен произведению корней той же степени из сомножителей:
,
где
(правило извлечения корня из произведения).
2. Если ,
то
(правило извлечения корня из дроби).
3. Если ,
то
(правило извлечения корня из корня).
4. Если ,
то
(правило возведения корня в степень).
5. Если ,
то ,
где ,
т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и
то же число.
6. Если ,
то ,
т. е. большему положительному подкоренному выражению соответствует и большее значение
корня.
7. Все указанные выше формулы часто применяются в обратном порядке
(т. е. справа налево). Например:
(правило умножения корней),
(правило деления корней),
.
8. Правило вынесения множителя из-под знака корня. При
.
9. Обратная задача — внесение множителя под знак корня. Например,
10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим
некоторые типичные случаи.
а) ,
так как .
Например, .
б)
Например,
в)
и т. д.
Другие темы в блоке «Школьная математика»
function-x.ru
Решение примеров со степенями
| Решение | Преобразуем, степени в числителе по свойству , а степени из знаменателя поднимем в числитель, при этом они изменят знак:
Далее воспользуемся тем фактом, что при умножении степеней с одинаковыми основаниями показатели степеней складываются Используя свойства степеней: и , получим: |
ru.solverbook.com
Умножение чисел со степенями с разными основаниями
Действия со степенями и корнями
Свойства степени с натуральным показателем
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним:
.
Например, .
2. При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним:
.
Например, .
3. При возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним:
.
Например, .
4. Степень произведения равна произведению степеней множителей:
.
Например, .
5. Степень частного равна частному степеней делимого и делителя:
.
Например, .
Пример 1. Найти значение выражения
.
Решение. В данном случае в явной форме ни одно из свойств степени с натуральным показателем применить нельзя, так как все степени имеют разные основания. Запишем некоторые степени в другом виде:
(степень произведения равна произведению степеней множителей),
(при умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним, при возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним).
Теперь получим:
В данном примере были использованы первые четыре свойства степени с натуральным показателем.
Свойства степеней и корней интенсивно используются при упрощении выражений в задачах математического анализа, например, для нахождения производной параметрически заданной функции и производной функции, заданной неявно.
Нет времени вникать в решение? Можно заказать работу!
Степень с целым и дробным показателем
Имеют место следующие тождества:
1) ;
2) ;
3) .
Выполнить действия со степенями самостоятельно, а затем посмотреть решения
Пример 2. Найти значение выражения
.
Пример 3. Найти значение выражения
.
Преобразования арифметических корней
1. Корень k-й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: , где (правило извлечения корня из произведения).
2. Если , то (правило извлечения корня из дроби).
3. Если , то (правило извлечения корня из корня).
4. Если , то (правило возведения корня в степень).
5. Если , то , где , т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.
6. Если , то , т. е. большему положительному подкоренному выражению соответствует и большее значение корня.
7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например:
(правило умножения корней),
(правило деления корней),
.
8. Правило вынесения множителя из-под знака корня. При .
9. Обратная задача — внесение множителя под знак корня.
Правило умножение степеней с разными основаниями
Например,
10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи.
а) , так как .
Например, .
б)
Например,
в)
и т. д.
11. Применение тождеств сокращённого умножения к действиям с арифметическими корнями:
1) ;
2) ;
3)
К началу страницы
Другие темы в блоке «Школьная математика»
Действия с дробями
Решение квадратных уравнений
Решение дробных уравнений с преобразованием в квадратное уравнение
Действия со степенями и корнями
Свойства степени с натуральным показателем
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним:
.
Например, .
2. При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним:
.
Например, .
3. При возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним:
.
Например, .
4. Степень произведения равна произведению степеней множителей:
.
Например, .
5. Степень частного равна частному степеней делимого и делителя:
.
Например, .
Пример 1. Найти значение выражения
.
Решение. В данном случае в явной форме ни одно из свойств степени с натуральным показателем применить нельзя, так как все степени имеют разные основания. Запишем некоторые степени в другом виде:
(степень произведения равна произведению степеней множителей),
(при умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним, при возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним).
Теперь получим:
В данном примере были использованы первые четыре свойства степени с натуральным показателем.
Свойства степеней и корней интенсивно используются при упрощении выражений в задачах математического анализа, например, для нахождения производной параметрически заданной функции и производной функции, заданной неявно.
Нет времени вникать в решение? Можно заказать работу!
Степень с целым и дробным показателем
Имеют место следующие тождества:
1) ;
2) ;
3) .
Выполнить действия со степенями самостоятельно, а затем посмотреть решения
Пример 2. Найти значение выражения
.
Пример 3. Найти значение выражения
.
Преобразования арифметических корней
1. Корень k-й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: , где (правило извлечения корня из произведения).
Что делать со степенями при сложении и вычитании числа?
Если , то (правило извлечения корня из дроби).
3. Если , то (правило извлечения корня из корня).
4. Если , то (правило возведения корня в степень).
5. Если , то , где , т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.
6. Если , то , т. е. большему положительному подкоренному выражению соответствует и большее значение корня.
7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например:
(правило умножения корней),
(правило деления корней),
.
8. Правило вынесения множителя из-под знака корня. При .
9. Обратная задача — внесение множителя под знак корня. Например,
10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи.
а) , так как .
Например, .
б)
Например,
в)
и т. д.
11. Применение тождеств сокращённого умножения к действиям с арифметическими корнями:
1) ;
2) ;
3)
К началу страницы
Другие темы в блоке «Школьная математика»
Действия с дробями
Решение квадратных уравнений
Решение дробных уравнений с преобразованием в квадратное уравнение
Действия со степенями и корнями
Свойства степени с натуральным показателем
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним:
.
Например, .
2. При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним:
.
Например, .
3. При возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним:
.
Например, .
4. Степень произведения равна произведению степеней множителей:
.
Например, .
5. Степень частного равна частному степеней делимого и делителя:
.
Например, .
Пример 1. Найти значение выражения
.
Решение. В данном случае в явной форме ни одно из свойств степени с натуральным показателем применить нельзя, так как все степени имеют разные основания. Запишем некоторые степени в другом виде:
(степень произведения равна произведению степеней множителей),
(при умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним, при возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним).
Теперь получим:
В данном примере были использованы первые четыре свойства степени с натуральным показателем.
Свойства степеней и корней интенсивно используются при упрощении выражений в задачах математического анализа, например, для нахождения производной параметрически заданной функции и производной функции, заданной неявно.
Нет времени вникать в решение? Можно заказать работу!
Степень с целым и дробным показателем
Имеют место следующие тождества:
1) ;
2) ;
3) .
Выполнить действия со степенями самостоятельно, а затем посмотреть решения
Пример 2. Найти значение выражения
.
Пример 3. Найти значение выражения
.
Преобразования арифметических корней
1. Корень k-й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: , где (правило извлечения корня из произведения).
2. Если , то (правило извлечения корня из дроби).
3. Если , то (правило извлечения корня из корня).
Алгебра – 7 класс. Умножение и деление степеней
Если , то (правило возведения корня в степень).
5. Если , то , где , т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.
6. Если , то , т. е. большему положительному подкоренному выражению соответствует и большее значение корня.
7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например:
(правило умножения корней),
(правило деления корней),
.
8. Правило вынесения множителя из-под знака корня. При .
9. Обратная задача — внесение множителя под знак корня. Например,
10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи.
а) , так как .
Например, .
б)
Например,
в)
и т. д.
11. Применение тождеств сокращённого умножения к действиям с арифметическими корнями:
1) ;
2) ;
3)
К началу страницы
Другие темы в блоке «Школьная математика»
Действия с дробями
Решение квадратных уравнений
Решение дробных уравнений с преобразованием в квадратное уравнение
Действия со степенями и корнями
Свойства степени с натуральным показателем
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним:
.
Например, .
2. При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним:
.
Например, .
3. При возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним:
.
Например, .
4. Степень произведения равна произведению степеней множителей:
.
Например, .
5. Степень частного равна частному степеней делимого и делителя:
.
Например, .
Пример 1. Найти значение выражения
.
Решение. В данном случае в явной форме ни одно из свойств степени с натуральным показателем применить нельзя, так как все степени имеют разные основания. Запишем некоторые степени в другом виде:
(степень произведения равна произведению степеней множителей),
(при умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним, при возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним).
Теперь получим:
В данном примере были использованы первые четыре свойства степени с натуральным показателем.
Свойства степеней и корней интенсивно используются при упрощении выражений в задачах математического анализа, например, для нахождения производной параметрически заданной функции и производной функции, заданной неявно.
Нет времени вникать в решение? Можно заказать работу!
Степень с целым и дробным показателем
Имеют место следующие тождества:
1) ;
2) ;
3) .
Выполнить действия со степенями самостоятельно, а затем посмотреть решения
Пример 2. Найти значение выражения
.
Пример 3. Найти значение выражения
.
Преобразования арифметических корней
1. Корень k-й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: , где (правило извлечения корня из произведения).
2. Если , то (правило извлечения корня из дроби).
3. Если , то (правило извлечения корня из корня).
Как умножить степени с разными основаниями и показателями?
Если , то (правило возведения корня в степень).
5. Если , то , где , т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.
6. Если , то , т. е. большему положительному подкоренному выражению соответствует и большее значение корня.
7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например:
(правило умножения корней),
(правило деления корней),
.
8. Правило вынесения множителя из-под знака корня. При .
9. Обратная задача — внесение множителя под знак корня. Например,
10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи.
а) , так как .
Например, .
б)
Например,
в)
и т. д.
11. Применение тождеств сокращённого умножения к действиям с арифметическими корнями:
1) ;
2) ;
3)
К началу страницы
Другие темы в блоке «Школьная математика»
Действия с дробями
Решение квадратных уравнений
Решение дробных уравнений с преобразованием в квадратное уравнение
Действия со степенями и корнями
Свойства степени с натуральным показателем
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним:
.
Например, .
2. При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним:
.
Например, .
3. При возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним:
.
Например, .
4. Степень произведения равна произведению степеней множителей:
.
Например, .
5. Степень частного равна частному степеней делимого и делителя:
.
Например, .
Пример 1. Найти значение выражения
.
Решение. В данном случае в явной форме ни одно из свойств степени с натуральным показателем применить нельзя, так как все степени имеют разные основания. Запишем некоторые степени в другом виде:
(степень произведения равна произведению степеней множителей),
(при умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним, при возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним).
Теперь получим:
В данном примере были использованы первые четыре свойства степени с натуральным показателем.
Свойства степеней и корней интенсивно используются при упрощении выражений в задачах математического анализа, например, для нахождения производной параметрически заданной функции и производной функции, заданной неявно.
Нет времени вникать в решение? Можно заказать работу!
Степень с целым и дробным показателем
Имеют место следующие тождества:
1) ;
2) ;
3) .
Выполнить действия со степенями самостоятельно, а затем посмотреть решения
Пример 2. Найти значение выражения
.
Пример 3. Найти значение выражения
.
Преобразования арифметических корней
1. Корень k-й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: , где (правило извлечения корня из произведения).
2. Если , то (правило извлечения корня из дроби).
3. Если , то (правило извлечения корня из корня).
4. Если , то (правило возведения корня в степень).
5. Если , то , где , т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.
6. Если , то , т. е. большему положительному подкоренному выражению соответствует и большее значение корня.
7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например:
(правило умножения корней),
(правило деления корней),
.
8. Правило вынесения множителя из-под знака корня. При .
Свойства степени
Обратная задача — внесение множителя под знак корня. Например,
10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи.
а) , так как .
Например, .
б)
Например,
в)
и т. д.
11. Применение тождеств сокращённого умножения к действиям с арифметическими корнями:
1) ;
2) ;
3)
К началу страницы
Другие темы в блоке «Школьная математика»
Действия с дробями
Решение квадратных уравнений
Решение дробных уравнений с преобразованием в квадратное уравнение
Степень с натуральным показателем и её свойства
Степень с натуральным показателем и ее свойства.
Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен a:
an =
В выражении an :
— число а (повторяющийся множитель) называют основанием степени
— число n (показывающее сколько раз повторяется множитель) – показателем степени
Например:
25 = 2·2·2·2·2 = 32,
здесь:
2 – основание степени,
5 – показатель степени,
32 – значение степени
Отметим, что основание степени может быть любым числом.
Вычисление значения степени называют действием возведения в степень. Это действие третьей ступени. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание).
Для записи больших чисел часто применяются степени числа 10. Так, расстояние от земли до солнца примерно равное 150 млн. км, записывают в виде 1,5 · 108
Каждое число большее 10 можно записать в виде: а · 10n , где 1 < a < 10 и n – натуральное число. Такая запись называется стандартным видом числа.
Например: 4578 = 4,578 · 103 ;
103000 = 1,03 · 105.
Свойства степени с натуральным показателем:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываются
am · an = am + n
например: 71.7 · 7 — 0.9 = 71.7+( — 0.9) = 71.7 — 0.9 = 70.8
Как умножать и делить степени? Что делают при умножении и делении степеней?
При делении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаются
am / an = am — n ,
где, m > n,
a ? 0
например: 133.8 / 13 -0.2 = 13(3.8 -0.2) = 133.6
3. При возведении степени в степень основание остается прежним, а показатели степеней перемножаются.
(am )n = a m · n
например: (23)2 = 2 3·2 = 26
4. При возведении в степень произведения в эту степень возводится каждый множитель
(a · b)n = an · b m ,
например:(2·3)3 = 2n · 3 m ,
5. При возведении в степень дроби в эту степень возводятся числитель и знаменатель
(a / b)n = an / bn
например: (2 / 5)3 = (2 / 5) · (2 / 5) · (2 / 5) = 23 / 53
pasmr21.ru
Как умножить степени с разными основаниями и показателями?
1) Если умножаются 2 числа с одинаковыми основаниями, но разными показателями, то общее основание возводится в сумму степеней.:
Пример
3⁴*3³=3⁴⁺³=3⁷
2) Если основания разные, а показатели одинаковые. В этом случае мы возводим в степень произведение оснований.
aⁿ*bⁿ=(ab)ⁿ
Пример:
5²*2²=(5*2)²=10²=100
3) Если основания разные и показатели разные, то тут 2 варианта:
1. Выделяем одинаковое основание, т.е. раскладываем один из множителей.
Представим число b=a*c
Пример
2. Приводим к общему показателю:
Пример
Оцени ответ
nebotan.com
Найдите значение выражения (степени, с разными основаниями) – как решать
Формулировка задачи: Найдите значение выражения (степени, с разными основаниями).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 2 (Действия со степенями).
Рассмотрим, как решаются подобные задачи на примере.
Пример задачи 1:
Найдите значение выражения 80,76 ∙ 640,12.
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Ответ: 8
Пример задачи 2:
Найдите значение выражения:
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Ответ: 512
Пример задачи 3:
Найдите значение выражения 35-4,7 ∙ 75,7 : 5-3,7.
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Ответ: 1,4
Пример задачи 4:
Найдите значение выражения:
Решение:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Ответ: 2
Поделитесь статьей с одноклассниками «Найдите значение выражения (степени, с разными основаниями) – как решать».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
worksbase.ru
Обобщение понятия степени и решение примеров со степенями
Здравствуйте. Многие ученики испытывают сложности при решении заданий, в которых встречаются выражения с корнями. В данной статье я попытаюсь обобщить материал по темам «Радикал» и «Степень». Покажу как решать некоторые задания. Если у Вас во время прочтения статьи появятся вопросы, Вы можете записаться ко мне на занятие, я с радостью помогу Вам во всем разобраться, помогу с решением именно Ваших задач!
1. Свойства степеней и корней
Степенью числа а с натуральным показателем n называется произведение n множителей, каждый из которых равняется а.
Степень числа а с показателем n обозначают an, например:
В общем случае при n > 1 имеем
Число a называется основой степени, число n — показателем степени.
Приведем основные свойства действий со степенями.
Приведенные свойства обобщаются для любых показателей степени
Часто в вычислениях используются степени с рациональным показателем. При этом удобным оказалось такое обозначение:
Корнем n— ой степени из числа а называется число b, n— я степень которого равняется a:
Корень также называется радикалом.
Корень нечетной степени n всегда существует. Корень четной степени 2n из отрицательного числа не существует. Существуют два противоположных числа, которые являются корнями четной степени из положительного числа а > 0. Положительный корень n— ой степени из положительного числа называют арифметическим корнем.
Из формул (3), (4) вытекают такие свойства радикалов
Если степень корня n = 2, то показатель корня обычно не пишется.
Пример 1.1. Найти значение выражения
Подкоренное выражение разложим на простые множители:
Пример 1.2. Упростить выражение
Имеем:
Пример 1.3. Извлечь корень
Имеем:
Пример 1.4. Упростить выражение
Поскольку при
2. Действия с радикалами
1) Преобразование корня по формуле называется внесением множителя под знак радикала.
Пример 2.1. Внести множитель под знак корня 5√2.
Исходя из формулы (7) получим
Пример 2.2. Внести множитель под знак радикала x√y при x< 0.
Имеем равенство
2) Преобразование корня исходя из формулы называется вынесением множителя из-под знака радикала.
Пример 2.3. Вынести множитель из-под знака корня в выражении
Получим:
Пример 2.4. Вынести множитель из-под знака корня
Имеем:
Пример 2.5. Вынести множитель из-под знака корня:
Радикалы вида , где a, b — рациональные числа, называются подобными. Их можно прибавлять и отнимать:
Пример 2.6. Упростить:
Пример 2.7. Сложить радикалы:
Пример 2.8. Выполнить действие:
Заметим, что равенство не выполняется. В этом можно убедиться на таком примере:
Приведем примеры умножения радикалов.
Пример 2.9.
Аналогично освобождаются от кубических иррациональностей в знаменателе:
Рассмотрим более сложные примеры рационализации знаменателей:
Чтобы перемножить радикалы с разными степенями, их сначала превращают в радикалы с одинаковыми степенями.
Пример 2.10. Перемножим радикалы:
Во время умножения радикалов можно использовать формулы сокращенного умножения. Например:
Если радикалы находятся в знаменателе дроби, то, используя свойства радикалов, можно избавиться от иррациональности.
Пример 2.11. Рационализируем знаменатели дробей
Выражения называются сопряженными. Произведение сопряженных выражений не содержит радикалов:
Это свойство используется для рационализации знаменателей.
Пример 2.12. Избавиться от иррациональности в знаменателе:
Избавимся от иррациональности в знаменателе дроби:
3. Вычисление иррациональных выражений
С помощью свойств корней можно упрощать и вычислять иррациональные выражения.
Пример 3.1. Вычислить
Выполним последовательно действия:
Пример 3.2. Вычислить:
Выполним действия.
Часто используется формула двойного радикала:
Пример 3.3. Исходя из формулы (8) находим:
Пример 3.4. Вычислить
Исходя из формулы (8) находим:
Окончательно получаем:
Аналогично вычисляются кубические корни. Имеем:
Возводим обе части равенства в куб:
Сравнивая выражения при √с, получаем однородную систему уравнений:
Поделив уравнение почленно, приходим к уравнению для z = y/x:
Пример 3.5. Вычислить значение радикала
После возведения в куб уравнения приходим к системе уравнений:
Поделив почленно первое уравнение на второе, получим уравнение для z= y/x:
По схеме Горнера находим корень z = — ½
Из системы уравнений и уравнения y/x = — ½ находим x = 2, y = -1. Итак,
Пример 3.6. Вычислить .
Возьмем .
Возведя обе части уравнения в куб, получаем откуда вытекает система уравнений
Система уравнений имеет очевидное решение x= 1, y= 1.
Поэтому .
Вычисляем радикал
Окончательно имеем a = — 1.
Пример 3.7. Вычислить
Поскольку
Дальше имеем:
Итак, a = — 2.
Пример 3.8. Вычислить
Возведем уравнение в куб, воспользовавшись равенством .
Получили для x кубическое уравнение
или x3 – 3x – 18 = 0,
имеет корни
Во множестве действительных чисел имеем корень x = 3.
4. Оценки для радикалов
Если
Это неравенство можно использовать для доведения неровностей, которые содержат радикалы.
Пример 4.1. Доказать, что .
Возведя неравенство в шестую степень, получим очевидное неравенство
Можно приводить радикалы к одной и то й же самой степени :
Пример 4.2. Оценим .
Поскольку
При преобразовании неравенств можно использовать символ V, понимая под ним знаки « > », « < », или « ».
Пример 4.3. Какое число больше
.
Поскольку
На этом все. Напоминаю, что Вы можете записываться ко мне на занятия в расписании, я с радостью помогу Вам с любыми вопросами по математике или высшей математике.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Свойства степени
Наверное, ни для кого не является секретом, что большинство математических утверждений, прежде, чем установится, проходят несколько этапов. Давайте подробно рассмотрим, как же.
Первый этап – это, конечно же, когда человек замечает некоторую одну и ту же закономерность в ряде случаев.
Второй этап – формулировка закономерности. Говоря проще, человек пытается предположить, что данная закономерность действует не только в одном конкретном случае, а и во всех подобных.
Третий этап – человек пытается доказать то, что закономерность, которую он подметил, а потом сформулировал, верна, то есть он пытается ее доказать. Но что же значит доказать, что утверждение верно? Конечно же, это значит объяснить верность предположений, но при этом опираться необходимо обязательно только лишь на уже проверенные факты, теоремы и утверждения.
Теперь давайте рассмотрим подробнее, непосредственно, свойства степеней.
Итак, первое свойство: aH * aK = aH+K
Проверим данное свойство на примере: 22 * 23 = 22+3. Как видим, утверждение правильное. Мы можем взять еще несколько подобных примеров, и все время будет получать только лишь верный результат.
Второе свойство (подобное к первому, за исключением нескольких различий в знаках). В данном случае мы будем иметь дело с делением: aH : aK = aH-K
Проверяем данное свойство также на примере: : 22 : 23 = 22-3. Опять-таки получили верный результат.
Третье свойство: (aH)K = aH*K
Опять же проверяем на примере: (22)3 = 26. Получили очередное правильное свойство.
Исходя из вышеуказанных формул и примеров, легко выводятся три основных правила, связанные со свойством степеней:
- Если у степени одинаковое основание, показатели разные, а сами основания умножаются, то мы можем преобразоваться это в степень с одним основанием, а показатели степени просто суммируются.
- Если у степени одинаковое основание, показатели разные, а сами основания делятся, то мы можем преобразоваться это в степень с одним основанием, а показатели степени просто вычитаются.
- Если мы хотим возвести степень в степень, то необходимо просто перемножить показатели степени.
Например: 2^2+3^2
| Свойства степени | |||||||||
|
|||||||||
|
|||||||||
|
|||||||||
|
|||||||||
|
|||||||||
|
mateshka.ru
Итоговый экзамен по математике сдают все. Те, кто поступает на гуманитарные специальности (филология, юриспруденция, международные отношения) выбирают базовый уровень — вопросы в нем легче, а оценки «3» достаточно для получения аттестата. Профильный уровень сдают будущие экономисты, инженеры и программисты — на этих специальностях без знания математики не обойтись, ее обязательно изучают на первых курсах. Но это непростой предмет. Даже в профильных математических классах не всегда дают достаточно знаний. Если ваша цель — поступление в топовый вуз на техническую специальность, без курсов подготовки к ЕГЭ не обойтись. Это касается не только профильного уровня, но и ЕГЭ по математике базового. «Задание 2, как решать?» — часто спрашивают школьники, сдающие этот экзамен. В этой статье мы проведем разбор задания 2 из ЕГЭ по математике профильного и базового уровня.
Теория
В задании 2 ЕГЭ по профильной математике теория достаточно простая. Это номер базового уровня сложности, он приносит 1 балл. Выпускникам дается график (иногда — диаграмма), нужно проанализировать его в соответствии с условием. Определение аргумента функции, поиск максимального и минимального значения — навыки, которые нужны для этого задания ЕГЭ. 2 часть математики профильного уровня тоже содержит номера с графиками, поэтому эта теория пригодится и там. То, что нужно знать для решения задания 2 ЕГЭ по математике профильного уровня:
функция и ее график;
- оси абсцисс и ординат;
- промежутки возрастания и убывания функции;
- области определения и значения функции;
- максимум и минимум функции;
- наибольшее и наименьшее значения на промежутке;
- диаграммы;
- цена деления на графике.
Перечисленные понятия нужны для сдачи любого уровня ЕГЭ. Но задание 2 по базовой математике проверяет другие навыки. В нем выпускник должен произвести вычисления со степенями. Этот номер тоже считается легким, однако для его выполнения нужно знать куда больше теории. Формулы для ЕГЭ по базовой математике, к заданию 2:
- определение степени — an = a • a • a … • a, где n — натуральное число. a называют основанием степени, n — показателем.
- a0 = 1.
- a1 = a.
- a-n = 1 / an.
- anm=man.
- an • am = an+m.
- an • bn = (a • b)n.
- an / am = an-m.
- an / bn = (a / b)n.
Разбор задания 2
Решение задания 2 по математике ЕГЭ мы начнем с профильного уровня.
Задача. Замеры температуры проводились в течение 3 дней. Какой была минимальная температура 18 апреля?
Решение. Подобное задание 2 на ЕГЭ по математике профильного уровня кажется очень простым, однако в нем легко ошибиться. Обратим внимание на два момента: «18 апреля» и «минимальная». Для начала отсекаем колонки, относящиеся к 19 и 20 апреля — про них ничего не спрашивают. После этого ищем самую низкую точку и находим ее ординату.
Ответ: 6.
Задача. В помещении стоит кондиционер с датчиком температуры. Когда она достигает определенного максимального значения, кондиционер включается. Когда комната остужается до необходимой температуры, кондиционер автоматически выключается. На графике показана зависимость температуры от времени. Укажите, сколько минут кондиционер был выключен.
Решение. В этом номере важно умение логически рассуждать. Когда кондиционер отключен, температура увеличивается. На графике это показывается ростом функции вверх. Чтобы определить, сколько минут кондиционер был выключен, нужно найти область возрастания функции. Это промежуток между числами 6 и 9 на оси абсцисс. Теперь мы ищем время: 9 — 6 = 3.
Ответ: 3.
За выполнение такого простого номера можно получить 1 балл на экзамене по математике. Разбор задания 2 ЕГЭ мы продолжим базовым уровнем. Здесь встречаются несколько типов вопросов: степенные выражения с одинаковыми и разными основаниями, поиск частного, произведения и суммы. Чтобы посмотреть все существующие виды заданий, зайдите на «Решу ЕГЭ» по базовой математике. Задание 2 там представлено более чем 40 вариантами. А в рамках этой статьи мы разберем несколько примеров задания 2 из ЕГЭ по математике базового уровня.
 Найти значение выражения
Найти значение выражения
Задача. 4 • 72 + 6 • 72.
Решение. У слагаемых есть общий множитель, который мы можем вынести за скобку. После этого считаем выражение в скобке, потом возводим число в степень и перемножаем: (4 + 6) • 72 = 10 • 72 = 10 • 49 = 490.
Ответ: 490.
Найти значение выражения (разные основания)
Задача. 80,76 • 640,12.
Решение. Нужно привести степени к одинаковому основанию, представив 64 как 82. После этого их можно перемножить: 80,76 • 640,12 = 80,76 • (8)2*0,12 = 80,76+0,24 = 81 = 8.
Ответ: 8.
Найти значение выражения (одинаковые основания)
Задача. 26 • 2-2 / 22.
Решение. В данном примере расчеты можно провести сразу же. Умножение степеней с одинаковым основанием заменяем на сложение показателей, деление — на их вычитание: 26 + (-2) — 2 = 26 — 4 = 22 = 4.
Ответ: 4.
 Найти частное от деления
Найти частное от деления
Задача. 1,6 • 102 : 4 • 10-2.
Решение. У степеней одинаковое основание, поэтому мы можем поделить их, найдя разность показателей. После этого мы делим числа без степеней и выполняем умножение: 1,6 : 4 • 102 — (-2) = 1,6 : 4 • 104 = 1,6 : 4 • 10000 = 0,4 • 10000 = 4000.
Ответ: 4000.
Найти произведение
Задача. 4 • 105 • 2,3 • 10-7.
Решение: Степени имеют одинаковые основания, поэтому мы можем умножить их, сложив показатели. После этого результат умножаем на остальные числа: 4 • 2,3 • 105 + (-7) = 4 • 2,3 • 10-2 = 4 • 2,3 • 0,01 = 9,2 • 0,01 = 0,092.
Ответ: 0,092.
Найти сумму
Задача. 9,4 • 102 + 2,1 • 103.
Решение. Мы возводим числа в степень, затем выполняем умножение и сложение: 9,4 • 100 + 2,1 • 1000 = 940 + 2100 = 3040.
Ответ: 3040.
Теперь вы знаете чуть больше теории для ЕГЭ по математике. Задание 2 из профильного уровня достаточно легкое (хотя без практики тут тоже не обойтись), а вот в базе придется рассуждать и выполнять вычисления. Но и его можно выполнить без труда, если должным образом подготовиться к ЕГЭ. Однако, лучший результат всегда дают занятия с опытными преподавателями, знающими специфику экзамена. Если нанимать репетитора для вас дорого, обратите внимание на курсы. Там разбирают не только задание 2 ЕГЭ по математике, но и многие другие номера, в том числе вторую часть. Грамотная подготовка — ключ к хорошим баллам, а значит, и месту на бюджете.
Формулировка задачи: Найдите значение выражения (степени, с разными основаниями).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 2 (Действия со степенями).
Рассмотрим, как решаются подобные задачи на примере.
Пример задачи 1:
Найдите значение выражения 8 0,76 ∙ 64 0,12 .
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Пример задачи 2:
Найдите значение выражения:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Пример задачи 3:
Найдите значение выражения 35 -4,7 ∙ 7 5,7 : 5 -3,7 .
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Пример задачи 4:
Найдите значение выражения:
Найдем значение выражения. Для этого приведем числа к одинаковому основанию и выполним необходимые действия:
Поделитесь статьей с одноклассниками «Найдите значение выражения (степени, с разными основаниями) – как решать».
Есть другой способ решения?
Предложите другой способ решения задачи «Найдите значение выражения (степени, с разными основаниями)». Возможно, он окажется более понятным для кого-нибудь:
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , ( 2 + 1 ) 5 , ( − 0 , 1 ) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , ( a 2 ) 3 . А также степени с нулевым показателем: 5 0 , ( a + 1 ) 0 , 3 + 5 2 − 3 , 2 0 . И степени с целыми отрицательными степенями: ( 0 , 5 ) 2 + ( 0 , 5 ) — 2 2 .
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 — 3 · 3 · 3 1 2 , 2 3 , 5 · 2 — 2 2 — 1 , 5 , 1 a 1 4 · a 1 2 — 2 · a — 1 6 · b 1 2 , x π · x 1 — π , 2 3 3 + 5 .
В качестве показателя может выступать переменная 3 x — 54 — 7 · 3 x — 58 или логарифм x 2 · l g x − 5 · x l g x .
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Вычислите значение степенного выражения 2 3 · ( 4 2 − 12 ) .
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · ( 4 2 − 12 ) = 2 3 · ( 16 − 12 ) = 2 3 · 4 .
Нам остается заменить степень 2 3 ее значением 8 и вычислить произведение 8 · 4 = 32 . Вот наш ответ.
Ответ: 2 3 · ( 4 2 − 12 ) = 32 .
Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 .
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Ответ: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Представьте выражение со степенями 9 — b 3 · π — 1 2 в виде произведения.
Решение
Представим число 9 как степень 3 2 и применим формулу сокращенного умножения:
9 — b 3 · π — 1 2 = 3 2 — b 3 · π — 1 2 = = 3 — b 3 · π — 1 3 + b 3 · π — 1
Ответ: 9 — b 3 · π — 1 2 = 3 — b 3 · π — 1 3 + b 3 · π — 1 .
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 и ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3 . Раскрыв скобки, мы можем привести подобные слагаемые в основании степени ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) и получить степенное выражение более простого вида a 2 · ( x + 1 ) .
Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:
- a r · a s = a r + s ;
- a r : a s = a r − s ;
- ( a · b ) r = a r · b r ;
- ( a : b ) r = a r : b r ;
- ( a r ) s = a r · s .
В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n , где m и n – натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0 .
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Представьте выражение a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 в виде степени с основанием a .
Решение
Для начала используем свойство возведения в степень и преобразуем по нему второй множитель ( a 2 ) − 3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:
a 2 , 5 · a − 6 : a − 5 , 5 = a 2 , 5 − 6 : a − 5 , 5 = a − 3 , 5 : a − 5 , 5 = a − 3 , 5 − ( − 5 , 5 ) = a 2 .
Ответ: a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 = a 2 .
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .
Решение
Если мы применим равенство ( a · b ) r = a r · b r , справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .
Есть еще один способ провести преобразования:
3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · ( 3 · 7 ) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21
Ответ: 3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21
Дано степенное выражение a 1 , 5 − a 0 , 5 − 6 , введите новую переменную t = a 0 , 5 .
Решение
Представим степень a 1 , 5 как a 0 , 5 · 3 . Используем свойство степени в степени ( a r ) s = a r · s справа налево и получим ( a 0 , 5 ) 3 : a 1 , 5 − a 0 , 5 − 6 = ( a 0 , 5 ) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .
Ответ: t 3 − t − 6 .
Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Упростить степенное выражение 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 .
Решение
Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = 3 · 5 2 3 · 5 1 3 — 3 · 5 2 3 · 5 — 2 3 — 2 — x 2 = = 3 · 5 2 3 + 1 3 — 3 · 5 2 3 + — 2 3 — 2 — x 2 = 3 · 5 1 — 3 · 5 0 — 2 — x 2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 — 2 — x 2 = — 12 2 + x 2
Ответ: 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = — 12 2 + x 2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .
Решение
а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a , следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3 . Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3 не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a 0 , 3 :
a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a
б) Обратим внимание на знаменатель:
x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 — x 1 3 · 2 · y 1 6 + 2 · y 1 6 2
Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т.е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x и y выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2
Ответ: а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .
Сократите дробь: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 , б) a 1 4 — b 1 4 a 1 2 — b 1 2 .
Решение
а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .
30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 )
б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a 1 4 — b 1 4 a 1 2 — b 1 2 = a 1 4 — b 1 4 a 1 4 2 — b 1 2 2 = = a 1 4 — b 1 4 a 1 4 + b 1 4 · a 1 4 — b 1 4 = 1 a 1 4 + b 1 4
Ответ: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 ) , б) a 1 4 — b 1 4 a 1 2 — b 1 2 = 1 a 1 4 + b 1 4 .
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Выполните действия x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 .
Решение
Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:
x 1 2 — 1 · x 1 2 + 1
x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 — x 1 2 — 1 · x 1 2 — 1 x 1 2 + 1 · x 1 2 — 1 · 1 x 1 2 = = x 1 2 + 1 2 — x 1 2 — 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 — x 1 2 2 — 2 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2
Теперь умножаем дроби:
4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · x 1 2
Произведем сокращение на степень x 1 2 , получим 4 x 1 2 — 1 · x 1 2 + 1 .
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 — 1 · x 1 2 + 1 = 4 x 1 2 2 — 1 2 = 4 x — 1 .
Ответ: x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = 4 x — 1
Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 .
Решение
Мы можем произвести сокращение дроби на ( x 2 , 7 + 1 ) 2 . Получаем дробь x 3 4 x — 5 8 · x 2 , 7 + 1 .
Продолжим преобразования степеней икса x 3 4 x — 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x — 5 8 · 1 x 2 , 7 + 1 = x 3 4 — — 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .
Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .
Ответ: x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение ( x + 1 ) — 0 , 2 3 · x — 1 можно заменить на x 3 · ( x + 1 ) 0 , 2 .
Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Представьте выражение x 1 9 · x · x 3 6 в виде степени.
Решение
Область допустимых значений переменной x определяется двумя неравенствами x ≥ 0 и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞ ) .
На этом множестве мы имеем право перейти от корней к степеням:
x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6
Используя свойства степеней, упростим полученное степенное выражение.
x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3
Ответ: x 1 9 · x · x 3 6 = x 1 3 .
Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0 .
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .
Теперь поделим обе части равенства на 7 2 · x . Это выражение на ОДЗ переменной x принимает только положительные значения:
5 · 5 — 3 · 5 x · 7 x — 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 2 · x — 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 x · 7 x — 2 · 7 2 · x 7 2 · x = 0
Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x — 3 · 5 x 7 x — 2 = 0 .
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x — 3 · 5 7 x — 2 = 0 , которое равносильно 5 · 5 7 x 2 — 3 · 5 7 x — 2 = 0 .
Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .
Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 — 5 · log 2 3 или log 3 27 9 + 5 ( 1 — log 3 5 ) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
- Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15 - Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17 - Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.
Нельзя заменять сумму (3 3 + 3 2 ) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2 ) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
m : a n =—>
= a m − n , где « a » — любое число, не равное нулю, а « m », « n » — любые натуральные числа такие, что « m > n ».
- Записать частное в виде степени
(2b) 5 : (2b) 3 = (2b) 5 − 3 = (2b) 2 - Вычислить.
= 11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
- Пример. Решить уравнение. Используем свойство частного степеней.
3 8 : t = 3 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
-
Пример. Упростить выражение.
4 5m + 6 · 4 m + 2 : 4 4m + 3 = 4 5m + 6 + m + 2 : 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
=
=
=
=
= 2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2 ) на 4 1 . Это понятно, если посчитать (4 3 −4 2 ) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n ) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
- Пример.
(a 4 ) 6 = a 4 · 6 = a 24 - Пример. Представить 3 20 в виде степени с основанием 3 2 .
По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:
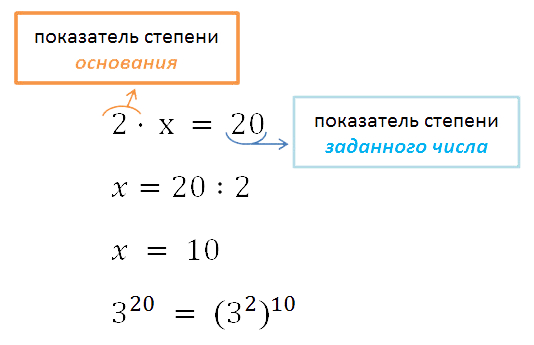
Свойства 4
Степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
(a · b) n = a n · b n , где « a », « b » — любые рациональные числа; « n » — любое натуральное число.
- Пример 1.
(6 · a 2 · b 3 · c ) 2 = 6 2 · a 2 · 2 · b 3 · 2 · с 1 · 2 = 36 a 4 · b 6 · с 2 - Пример 2.
(−x 2 · y) 6 = ( (−1) 6 · x 2 · 6 · y 1 · 6 ) = x 12 · y 6
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n )= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
- Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000 - Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4
Свойства 5
Степень частного (дроби)
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a : b) n = a n : b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.
- Пример. Представить выражение в виде частного степеней.
(5 : 3) 12 = 5 12 : 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.

 функция и ее график;
функция и ее график; Найти значение выражения
Найти значение выражения Найти частное от деления
Найти частное от деления