При изучении систем
случайных величин всегда следует
обращать внимание на степень и характер
их зависимости. Эта зависимость может
быть более или менее тесной.
Понятие о независимых
случайных величинах — одно из важных
понятий теории вероятностей.
Определение
1.
Случайная величина Y
называется
независимой от случайной величины
X,
если
закон распределения величины Y
не
зависит от того, какое значение приняла
величина X.
Для
непрерывных случайных величин условие
независимости Y
от
X
может
быть записано в виде:
|
|
(5.5.1) |
Напротив,
в случае, если Y
зависит
от X,
то
|
|
(5.5.2) |
Докажем,
что зависимость
или независимость случайных величин
всегда взаимны: если
величина Y
не
зависит от X,
то
и величина X
не
зависит от Y.
Действительно,
пусть Y
не
зависит от X,
тогда
|
|
Плотность совместного
распределения согласно (5.4.5) и (5.4.6) можно
записать
|
|
(5.5.3) |
откуда, получим:
|
|
что и требовалось
доказать.
Так
как зависимость и независимость случайных
величин всегда взаимны, можно дать новое
определение независимых случайных
величин.
Определение
2.
Случайные величины X
и Y
называются независимыми, если закон
распределения каждой из них не зависит
от того, какое значение приняла другая.
В
противном случае величины X
и
Y
называются
зависимыми.
Для независимых
непрерывных случайных величин теорема
умножения законов распределения
принимает вид:
|
|
(5.5.4) |
т.е.
плотность
распределения системы независимых
случайных величин равна произведению
плотностей распределения отдельных
величин, входящих в систему.
Остановимся,
несколько подробнее на важных понятиях
о «зависимости» и «независимости»
случайных величин.
Понятие
«зависимости» случайных величин, которым
мы пользуемся в теории вероятностей,
несколько отличается от обычного
понятия «зависимости» величин,
которым мы оперируем в математике.
Действительно, обычно под «зависимостью»
величин подразумевают только один тип
зависимости—полную, жесткую, так
называемую функциональную
зависимость.
Две величины X
и
Y
называются
функционально зависимыми, если, зная
значение одной из них, можно точно
указать значение другой.
В
теории вероятностей мы встречаемся с
другим, более общим, типом зависимости
— с вероятностной
или
«стохастической» зависимостью. Если
величина Y
связана
с величиной X
вероятностной
зависимостью, то, зная значение X,
нельзя
указать точно значение Y,
а
можно указать только ее закон распределения,
зависящий от того, какое значение приняла
величина X.
Вероятностная
зависимость между случайными величинами
очень часто встречается на практике.
Если случайные величины X
и
Y
находятся
в вероятностной зависимости, это не
означает, что с изменением величины
X
величина
Y
изменяется
вполне определенным образом; это лишь
означает, что с изменением величины X
величина
Y
имеет
тенденцию также изменяться (например,
возрастать или убывать при возрастании
X).
Рассмотрим,
например, две такие случайные величины:
X
—
рост наугад взятого человека, Y
—
его вес. Очевидно, величины X
и
Y
находятся
в определенной вероятностной зависимости;
она выражается в том, что в общем люди
с большим ростом имеют больший вес.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Функции
- Связи между величинами. Функция
В окружающем нас мире мы часто встречаемся с зависимостями между различными величинами. Например, периметр квадрата зависит от длины его стороны, площадь круга зависит от длины его радиуса, объем прямоугольного параллелепипеда зависит от трех его измерений (длины, ширины и высоты).
Рассмотрим несколько примеров.
Пример 1. Периметр квадрата изменяется, если изменяется его сторона. Если 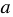
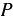
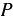
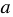
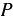
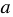
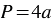
С помощью этой формулы можно, выбрав произвольную длину стороны квадрата, найти соответствующее значение периметра квадрата. Поэтому переменную 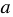
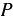
Обратите внимание, эта формула задает правило, с помощью которого по значению независимой переменной можно однозначно найти значение зависимой переменной.
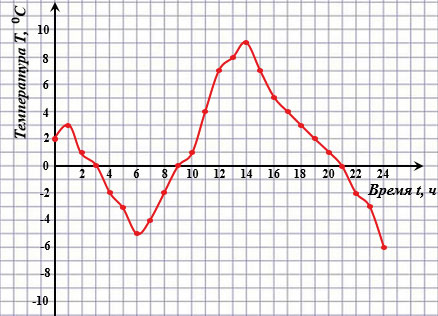
Пример 2. На рисунке ниже изображен график зависимости температуры воздуха 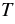
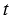
С помощью этого графика для каждого момента времени 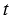
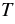
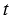
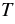
Обратите внимание, этот график задает правило, с помощью которого по значению независимой переменной можно однозначно найти значение зависимой переменной.
Мы рассмотрели две различные модели зависимостей, при этом для каждой из них выполняется следующее:
указано правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной. Это правило называют функцией, а соответствующую зависимость одной переменной от другой — функциональной.
Как правило, независимую переменную обозначают буквой 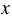
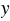
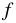
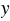
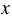
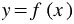
Независимую переменную еще называют аргументом функции.
Все значения, которые принимает независимая переменная (аргумент), образуют область определения функции. Так, в примере 1 областью определения функции являются все положительные числа; в примере 2 — все неотрицательные числа, не превосходящие 24.
Для функции 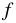
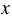
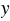
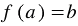
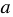
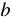
Все значения, которые принимает зависимая переменная, образуют область значений функции. Так, в примере 1 область значений функции — это все положительные числа, в примере 2 — все числа не меньшие 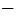
Советуем посмотреть:
Способы задания функции
График функции
Линейная функция, ее график и свойства
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 782,
Мерзляк, Полонский, Якир, Учебник
Номер 807,
Мерзляк, Полонский, Якир, Учебник
Номер 822,
Мерзляк, Полонский, Якир, Учебник
Номер 826,
Мерзляк, Полонский, Якир, Учебник
Номер 882,
Мерзляк, Полонский, Якир, Учебник
Номер 1042,
Мерзляк, Полонский, Якир, Учебник
Номер 1212,
Мерзляк, Полонский, Якир, Учебник
Номер 1214,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 309,
Мерзляк, Полонский, Якир, Учебник
Номер 322,
Мерзляк, Полонский, Якир, Учебник
Номер 334,
Мерзляк, Полонский, Якир, Учебник
Номер 337,
Мерзляк, Полонский, Якир, Учебник
Номер 341,
Мерзляк, Полонский, Якир, Учебник
Номер 352,
Мерзляк, Полонский, Якир, Учебник
Номер 359,
Мерзляк, Полонский, Якир, Учебник
Номер 415,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 433,
Мерзляк, Полонский, Якир, Учебник
Случайные величины называются независимыми, если закон распределения одной из них не зависит от того какое значение принимает другая случайная величина.
Понятие зависимости случайных величин является очень важным в теории вероятностей.
Условные распределения независимых случайных величин равны их безусловным распределениям.
Определим необходимые и достаточные условия независимости случайных величин.
Теорема. Для того, чтобы случайные величины Х и Y Были независимы, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих.
Аналогичную теорему можно сформулировать и для плотности распределения:
Теорема. Для того, чтобы случайные величины Х и Y Были независимы, необходимо и достаточно, чтобы плотность совместного распределения системы (X, Y) была равна произведению плотностей распределения составляющих.
Определение. Корреляционным моментом MXy Случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин.
Практически используются формулы:
Для дискретных случайных величин:
Для непрерывных случайных величин:
Корреляционный момент служит для того, чтобы охарактеризовать связь между случайными величинами. Если случайные величины независимы, то их корреляционный момент равен нулю.
Корреляционный момент имеет размерность, равную произведению размерностей случайных величин Х и Y. Этот факт является недостатком этой числовой характеристики, т. к. при различных единицах измерения получаются различные корреляционные моменты, что затрудняет сравнение корреляционных моментов различных случайных величин.
Для того, чтобы устранить этот недостаток применятся другая характеристика – коэффициент корреляции.
Определение. Коэффициентом корреляции Rxy случайных величин Х и Y называется отношение корреляционного момента к произведению средних квадратических отклонений этих величин.
Коэффициент корреляции является безразмерной величиной. Коэффициент корреляции независимых случайных величин равен нулю.
Свойство: Абсолютная величина корреляционного момента двух случайных величин Х и Y не превышает среднего геометрического их дисперсий.
Свойство: Абсолютная величина коэффициента корреляции не превышает единицы.
Случайные величины называются Коррелированными, если их корреляционный момент отличен от нуля, и Некоррелированными, если их корреляционный момент равен нулю.
Если случайные величины независимы, то они и некоррелированы, но из некоррелированности нельзя сделать вывод о их независимости.
Если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными.
Часто по заданной плотности распределения системы случайных величин можно определить зависимость или независимость этих величин.
Наряду с коэффициентом корреляции степень зависимости случайных величин можно охарактеризовать и другой величиной, которая называется Коэффициентом ковариации. Коэффициент ковариации определяется формулой:
Пример. Задана плотность распределения системы случайных величин Х и Y.
Выяснить являются ли независимыми случайные величины Х и Y.
Для решения этой задачи преобразуем плотность распределения:
Таким образом, плотность распределения удалось представить в виде произведения двух функций, одна из которых зависит только от Х, а другая – только от У. Т. е. случайные величины Х и Y независимы. Разумеется, они также будут и некоррелированы.
| < Предыдущая | Следующая > |
|---|
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Дискретной называют двумерную величину, составляющие которой дискретны.
Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Закон
распределения дискретной двумерной случайной величины может быть задан:
а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;
б) аналитически, например в виде функции распределения.
Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность
, надо просуммировать
вероятности столбца
. Аналогично сложив
вероятности строки
получим вероятность
.
Пусть
составляющие
и
дискретны и имеют соответственно следующие
возможные значения:
;
.
Условным распределением составляющей
при
(j сохраняет одно и то же
значение при всех возможных значениях
) называют совокупность
условных вероятностей:
Аналогично
определяется условное распределение
.
Условные
вероятности составляющих
и
вычисляют соответственно по формулам:
Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Ковариация (корреляционный момент)
Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки
.
Ковариацию
(корреляционный момент) можно найти по формуле:
Свойства ковариации
Свойство 1.
Ковариация двух независимых случайных величин равна нулю.
Свойство 2.
Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.
Свойство 3.
Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.
Коэффициент корреляции
Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.
Формула коэффициента корреляции:
Две
случайные величины
и
называют коррелированными, если их коэффициент
корреляции отличен от нуля.
и
называют некоррелированными величинами, если
их коэффициент корреляции равен нулю
Свойства коэффициента корреляции
Свойство 1.
Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.
Свойство 2.
Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.
Свойство 3.
Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Линейная регрессия
Рассмотрим
двумерную случайную величину
, где
и
– зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины
в виде линейной функции величины
:
где
и
– параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.
Линейная
средняя квадратическая регрессия
на
имеет вид:
Коэффициент
называют
коэффициентом регрессии
на
, а прямую
называют
прямой среднеквадратической регрессии
на
.
Аналогично
можно получить прямую среднеквадратической регрессии
на
:
Смежные темы решебника:
- Двумерная непрерывная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Задача 1
Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.
Требуется:
—
определить одномерные законы распределения случайных величин X и Y;
— найти
условные плотности распределения вероятностей величин;
—
вычислить математические ожидания mx и my;
—
вычислить дисперсии σx и σy;
—
вычислить ковариацию μxy;
—
вычислить коэффициент корреляции rxy.
| xy | 3 | 5 | 8 | 10 | 12 |
| -1 | 0.04 | 0.04 | 0.03 | 0.03 | 0.01 |
| 1 | 0.04 | 0.07 | 0.06 | 0.05 | 0.03 |
| 3 | 0.05 | 0.08 | 0.09 | 0.08 | 0.05 |
| 6 | 0.03 | 0.04 | 0.04 | 0.06 | 0.08 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Задана
дискретная двумерная случайная величина (X,Y).
а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X; в) построить регрессию случайной величины X на Y; г) найти коэффициент ковариации; д) найти
коэффициент корреляции.
| Y | X | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 30 | 0.05 | 0.03 | 0.02 | 0.01 | 0.01 |
| 40 | 0.03 | 0.02 | 0.02 | 0.04 | 0.01 |
| 50 | 0.05 | 0.03 | 0.02 | 0.02 | 0.01 |
| 70 | 0.1 | 0.03 | 0.04 | 0.03 | 0.01 |
| 90 | 0.1 | 0.04 | 0.01 | 0.07 | 0.2 |
Задача 3
Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.
|
x y |
1 | 2 | 3 |
| 1.5 | 0.03 | 0.02 | 0.02 |
| 2.9 | 0.06 | 0.13 | 0.03 |
| 4.1 | 0.4 | 0.07 | 0.02 |
| 5.6 | 0.15 | 0.06 | 0.01 |
Задача 4
Двумерная
случайная величина (X,Y) распределена по закону
| XY | 1 | 2 |
| -3 | 0,1 | 0,2 |
| 0 | 0,2 | 0,3 |
| -3 | 0 | 0,2 |
Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.
Задача 5
Случайные
величины ξ и η имеют следующий совместный закон распределения:
P(ξ=1,η=1)=0.14
P(ξ=1,η=2)=0.18
P(ξ=1,η=3)=0.16
P(ξ=2,η=1)=0.11
P(ξ=2,η=2)=0.2
P(ξ=2,η=3)=0.21
1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.
2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).
3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}
4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.
Задача 6
Дан закон
распределения двумерной случайной величины (ξ,η):
| ξ=-1 | ξ=0 | ξ=2 | |
| η=1 | 0,1 | 0,1 | 0,1 |
| η=2 | 0,1 | 0,2 | 0,1 |
| η=3 | 0,1 | 0,1 | 0,1 |
1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания Mξ,
Mη и дисперсии Dξ, Dη
2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).
3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?
4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти Mγ и Dγ.
Задача 7
Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.
| XY | 1 | 2 | 4 |
| -2 | 0,25 | 0 | 0,25 |
| 1 | 0 | 0,25 | 0 |
| 3 | 0 | 0,25 | 0 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 8
Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.
| YX | -1 | 1 |
| -1 | 0,4 | 0,1 |
| 1 | 0,2 | 0,3 |
Задача 9
Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:
| X=-3 | X=0 | X=1 | |
| Y=-2 | 0,3 | ? | 0,1 |
| Y=1 | 0,1 | 0,1 | 0,2 |
Задача 10
Совместный
закон распределения пары
задан таблицей:
| xh | -1 | 0 | 1 |
| -1 | 1/12 | 1/4 | 1/6 |
| 1 | 1/4 | 1/12 | 1/6 |
Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.
Задача 11
Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции rxy?
| X | 20 | 25 | 30 | 35 |
| P | 0.1 | 0.1 | 0.4 | 0.4 |
и
Задача 12
Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):
| XY | 0 | 1 | 2 |
| -1 | ? | 0,1 | 0,2 |
| 1 | 0,1 | 0,2 | 0,3 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:
| ξη | -1 | 1 | 2 |
| 0 | 1/7 | 2/7 | 1/7 |
| 1 | 1/7 | 1/7 | 1/7 |
Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?
Задача 14
Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.
| XY | 2,3 | 2,9 | 3,1 | 3,4 |
| 0,2 | 0,15 | 0,15 | 0 | 0 |
| 2,8 | 0 | 0,25 | 0,05 | 0,01 |
| 3,3 | 0 | 0,09 | 0,2 | 0,1 |
Задача 15
Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.
| xy | 1 | 4 |
| -10 | 0,1 | 0,2 |
| 0 | 0,3 | 0,1 |
| 20 | 0,2 | 0,1 |
Задача 16
Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:
а) законы
распределения ее компонент и их числовые характеристики;
b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.
с)
ковариацию и коэффициент корреляции случайных величин X и Y;
d) составить матрицу ковариаций и матрицу корреляций;
e) вероятность попадания в область, ограниченную линиями y=16-x2 и y=0.
f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.
| XY | -1 | 0 | 1 | 2 |
| -1 | 0 | 1/6 | 0 | 1/12 |
| 0 | 1/18 | 1/9 | 1/12 | 1/9 |
| 2 | 1/6 | 0 | 1/9 | 1/9 |
Задача 17
Совместный
закон распределения случайных величин X и Y задан таблицей:
|
XY |
0 |
1 |
3 |
|
0 |
0,15 |
0,05 |
0,3 |
|
-1 |
0 |
0,15 |
0,1 |
|
-2 |
0,15 |
0 |
0,1 |
Найдите:
а) закон
распределения случайной величины X и закон распределения
случайной величины Y;
б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.
Задача 18
Известен
закон распределения двумерной случайной величины (X,Y).
а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);
б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;
в)
построить поле распределения и линию регрессии Y по X и X по Y;
г)
вычислить корреляционный момент (коэффициент ковариации) μxy и
коэффициент корреляции rxy.
|
|
5 | 20 | 35 |
| 100 | — | — | 0.05 |
| 115 | — | 0.2 | 0.15 |
| 130 | 0.15 | 0.35 | — |
| 145 | 0.1 | — | —- |