Как найти значение золотого сечения

https://ria.ru/20221116/sechenie-1832065968.html

Гармония во всем: что такое золотое сечение и способы его применения

Золотое сечение: что это такое, пропорции, принцип, применение в архитектуре и строительстве

Гармония во всем: что такое золотое сечение и способы его применения

«Божественная гармония» или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке,… РИА Новости, 16.11.2022

2022-11-16T21:08

2022-11-16T21:08

2022-11-16T21:08

общество

европа

греция

ле корбюзье (шарль-эдуар жаннере-гри)

леонардо да винчи

https://cdnn21.img.ria.ru/images/07e6/0b/10/1832031636_0:318:3076:2048_1920x0_80_0_0_74519bda270895480ff99027b7b160ec.jpg

МОСКВА, 16 ноя — РИА Новости. «Божественная гармония» или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке, природе, архитектуре, искусстве. Что такое ряд чисел Фибоначчи, принцип расчета и метод построения на основе пропорций – в материале РИА Новости.Золотое сечение»Определенные пропорции повсеместно используются в дизайне и архитектуре, фотографии и очень часто наблюдаются в естественной природе», – говорит Ренат Мансуров, профессиональный фотограф, фотохудожник, лауреат и участник международных фотоконкурсов.История»Первым про золотое сечение писал еще Евклид в “Началах”, которые в свое время были вторые по популярности после Библии. Людям свойственно искать закономерности везде, даже там где их нет, поэтому число “фи” всегда было темой для религиозных спекуляций. Леонардо да Винчи, например, считал, что золотое сечение является выражением божественной сущности Троицы», – комментирует Максим Господинко, диджитал-художник, дизайнер, основатель Spoils.По словам эксперта, про эту пропорцию писал Ян Чихольд, использовал Малевич, Монферран построил по ней Исаакиевский собор.»Но, как мне кажется, острое желание привязать всё мироздание к одному закону больше говорит о людях прошлого, чем о самом мире. Ум человека плохо переносит множественность, неточность моделей и просто хаос. Из этой особенности и происходит когнитивное “удобство”, когда порядок и закономерность всё-таки находятся», – отмечает Максим Господинко.»Впервые термин «золотое сечение» («goldener Schnitt») употребил в эпоху резкого роста европейской секуляризации в примечании ко второму изданию своей «Чистой элементарной математики» в 1835 году доктор философии Мартин Ом. Термин был известен ранее (из текста следует, что Ом не сам его придумал), и в дальнейшем быстро распространился в европейской литературе», – поясняет Сергей Дементьев, эксперт сервиса meta-luxury недвижимости «Душа объекта».Эксперт отмечает, что до Ома это соотношение благодаря трактату монаха францисканца Луки Пачоли, изданному в соавторстве с Леонардо да Винчи, с 1509 года именовали в Европе «божественной пропорцией» (лат. «Divina Proportione», итал. «Proporzione Divina»).По мнению Сергея Дементьева, «божественная пропорция» («золотое сечение») как известная концепция красоты (еще древнегреческий скульптор Поликлет сформировал альтернативные правила красоты, а в 20-м веке модернист архитектор Ле Корбюзье разработал собственную систему пропорционирования) обязана своему появлению упадку веросознания: Эпоха Возрождения в Европе – именно историческая попытка Ренессанса веросознания в новых его формах через умозрение и затем деятельное воплощение в культуре (художественное творчество, архитектура, строительство, парковый, ландшафтный и интерьерный дизайн и т.д.).Пионеры Возрождения Пачоли и Леонардо да Винчи («Тайная вечеря» и «Мона Лиза» вписаны в геометрические фигуры) обратили свое внимание на античность, где еще в «Началах» Евклид (ок. 300 лет до нашей эры) говорил о делении отрезка в крайнем и среднем отношении («ἄκρος καὶ μέσος λόγος»), полагая, что на числах построено все мироздание, на идеи Витрувия (ок. 80-70 гг. до нашей эры — после 13 г. до нашей эры), изложенные в «Десяти книгах об архитектуре» (лат. «De architectura libri decem») о применении математики к искусству архитектуры.Пропорции золотого сеченияО том, как высчитывать золотые пропорции, рассказал эксперт в сфере фотографии Ренат Мансуров.»Если взять для примера линию и разделить ее на две части так, чтобы длинная соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной, получится золотая пропорция», – поясняет он. К слову, она равна всегда 1,618, и это так называемое число «фи» обозначается греческой буквой φ — от имени древнегреческого скульптора Фидия.Ренат Мансуров отмечает, что в правильном прямоугольнике соотношение сторон соответствует золотому сечению.»Интересен этот прямоугольник тем, что сколько бы ни отрезали от него квадратов, он всегда будет оставлять после себя кусочек с золотым соотношением сторон и так до бесконечности», – говорит Ренат Мансуров.Золотое сечение в математикеИтальянский астроном и математик Фибоначчи вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Эта закономерность известна как ряд Фибоначчи.»Если представить два квадрата, поставленных рядом, потом добавить квадрат с удвоенной стороной, то получится квадрат 2 на 2. Далее добавить по спирали против часовой стрелки сумму двух предыдущих квадратов. Получится квадрат с длинной стороны три квадрата, далее добавить к стороне квадрата предыдущую сторону, получится 5, потом 8 потом 13 и 21, каждое последующее число — это сумма сложения с предыдущим, то есть получается такая последовательность, которую и вывел Фибоначчи: 0,1,1,2,3,5,8,13,21 и т.д.», – поясняет Ренат Мансуров.0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и до бесконечности. А при делении последующего числа на предыдущее получается коэффициент золотого сечения. По мере возрастания чисел соотношение приближается к 1,618. К примеру, числа 3 и 5, их соотношение равно 1,666, а если взять 13 и 21, то получается уже 1,625. Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленное значение 0,62.А если в каждом квадрате построить дугу из одного угла к другому, то получится так называемая спираль Фибоначчи.Правило золотого сеченияНа практике золотое сечение представляет собой пропорцию, соотношение сторон прямоугольника, отрезков определенной длины, других геометрических форм или сопряженных размерных характеристик реальных объектов.Метод золотого сечения»Если построить прямоугольник, используя метод, указанный выше, и встроить в этот прямоугольник линии, используя числа золотого сечения, то получится разграничение прямоугольника несколькими линиями. И если говорить о композиции, то размещая объекты на линиях или их пересечениях, можно максимально выделить эти объекты как смысловые центры, и наоборот, чем дальше от этих точек, тем труднее будет улавливать смысловой центр», – поясняет Ренат Мансуров.Если же совместить спираль Фибоначчи и эту сетку, то получится практически инструкция по использованию золотого сечения в фотографии, живописи и дизайне.Где можно увидеть золотое сечениеЕсли разделить обычное куриное яйцо мысленно пополам в самой широкой его части, то получатся правильные золотые пропорции. Пропорции здания Парфенона в Греции, спирали раковин, пропорции тела человека, спиральные галактики и растения, и еще много всего вокруг.ПриродаПо словам Рената Мансурова, примеров этих золотых чисел и спиралей найти в природе можно множество. «Распределение семян подсолнуха, спиральные раковины, спиральные галактики, соотношения пропорций человеческого тела, и например, если внимательно посмотреть на нераскрытую еловую шишку или ананас с торца, то можно увидеть эти спирали», – отмечает эксперт.Свою точку зрения озвучил Максим Господинко.»У растения есть важная задача — наиболее оптимально расположить свои листья или лепестки, для того чтобы уловить больше солнечного света или просто уместить больше семян. В некоторых случаях есть возможность делать это только по плотной спирали (ананас, еловая шишка, подсолнечник). Кажется, что перед таким растением стоит сложная математическая задача — на какой угол сдвинуть следующую семечку или лепесток, но на самом деле вопрос лишь в том, насколько сильное создается отталкивание от уже существующего элемента.И так складывается, что угол отклонения от предыдущего листка действительно очень близок к отношению «фи», – комментирует эксперт. – Ни одно рациональное отношение не подходит, потому что при повороте под такими углами возникают колонны-лучи с большими дырами, а как мы знаем, семена подсолнечника уложены красивыми спиралями, число которых как раз соответствует числам из ряда Фибоначчи и дыр там никаких нет».По словам Максима Господинко, ряд Фибоначчи можно легко образовать, взяв ноль и единицу, а каждое последующее за ними получить из суммы двух предыдущих. «Моделировать растение конечно не умеет, насколько мне известно, и не знает количества рядов спиралей, а усилие отталкивания следующего элемента регулируется поколениями и естественным отбором, но в итоге приходит именно к “фи”», – отмечает специалист.ЧеловекПропорции золотого сечения прослеживаются и на примере тела человека. К золотой формуле приравнивается абсолютно все: кости, ладони и пальцы, пропорции участков на лице, расстояние вытянутых рук по отношению к телу. Пропорции таковы:ИскусствоМножество произведений искусства и архитектурных шедевров сделаны по принципам золотого сечения. Египетские и пирамиды Майя, греческий Парфенон и так далее. Картины известных художников тоже выполнены с учетом правил золотого сечения.Прослеживаются такие пропорции и в музыкальных произведениях Шуберта, Моцарта, Баха, Шопена и прочих.»Для дизайнера и художника вопрос о золотом сечении стоит лишь в разрезе более широкой темы — пропорционирования. Не каждый использует этот инструмент, хоть и должен, но часто амбициозный художник, схватившись за “божественную истину”, начинает транслировать лишь её, упуская суть художественного высказывания, передачу образа. Пропорция – лишь инструмент и, очевидно, инструмент не должен идти вперёд задачи. Если образ не понят художником, его невозможно передать», – говорит Максим Господинко. Но тем не менее, переоценить важность этой пропорции сложно. Часто чувствительный художник сам интуитивно может расположить элементы в соответствии с “фи”, также оно является достаточно простым инструментом, чтобы создать изящную композицию даже в самых простых вещах.Примеры использования в живописи.Примеры использования золотого сечения в дизайне логотипов.Применение золотого сеченияПримеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений и создании проекта дома, в современном дизайне интерьера при планировании и зонировании пространства, расстановки мебели и даже цветовом оформлении, а также в ландшафтном дизайне при выкладке закрученных дорожек, расположении растений на клумбах и других элементов.Так, к примеру, при строительстве квартир и домов отношение самой большой комнаты к площади всей квартиры равно как 0,62 к 1, меньшее помещение делают с таким же соотношением к площади большей комнаты. Так, кухня – к меньшей комнате, прихожая к кухне, санузел к прихожей, а балкон – к санузлу.Кроме того, с помощью золотого сечения подбирают и цветовое оформление. В интерьере применяют соотношение 10-30-60, основанное на золотом сечении. В пространстве используют три основных цвета: первый – доминирующий, охватывает 60% комнаты (стены и пол). Второй оттенок составляет 30% – мебель. И третий, 10%, приходится на декор.»Существует множество вариантов золотого сечения. Но все они, так или иначе, основаны на числах Фибоначчи. Какие то из них популярны, какие то не очень, но о чем мы говорим сегодня, это то, что выработалось за последние столетия — это явно золотой стандарт, – говорит Ренат Мансуров. – Конечно, нужно понимать, что творчество остается творчеством и отходить от стандарта не возбраняется, но и совсем идти наперекор этим пропорциям не стоит».По мнению эксперта, теория золотого сечения и «божественных пропорций» довольно популярна, но наука не стоит на месте, и сейчас активно исследуются теории восприятия с научной точки зрения. «То, что работает на практике не одно столетие, однозначно должно напоминать каждый раз о том, что эти пропорции проверены временем и сотнями тысяч творческих людей: фотографы, художники, дизайнеры и архитекторы каждый день работают и используют золотые пропорции в своей работе.Высчитывать миллиметры и микроны в надежде сделать ваше творчество золотым, наверное, не стоит, но и забывать о приятных для глаза пропорциях наверняка не нужно», – говорит Ренат Мансуров.Как это делать правильно, каждый решает самостоятельно, существует множество приемов композиции и работы с психологией восприятия, которые вместе могут улучшить работу в разы. «Учитесь правильно и не останавливайтесь в изучении художественных и композиционных приемов, и ваше творчество будет сиять оригинальностью и легкостью восприятия», – советует Ренат Мансуров.Второе золотое сечениеВторое золотое сечение вытекает из основного сечения и дает отношение 44: 56.Максим Господинко отмечает, что золотое сечение – не единственная пропорция, приятная глазу человека, есть “серебряное сечение”. Две величины находятся в «серебряном сечении», если отношение суммы меньшей и удвоенной большей величины к большей то же самое, что и отношение большей величины к меньшей. Также можно отметить, что порядок разлинованной в клетку тетради приятнее полного хаоса чистого листа (если не брать пропорцию самого его формата за порядок).По словам эксперта, пропорция тетрадки в клетку ничем не хуже золотого сечения, но действие на человека она оказывает иное, как будто организуя простейший порядок — один к одному. «Если бы мы использовали такой поворот угла в подсолнухе, то получили бы одну линию семян, в случае с 1/4 — крест. Каждой задаче — свое решение. В случае с растениями им нужно как раз самое иррациональное число. Примечательно, что именно такое число и прослыло божественным», – говорит Максим Господинко.Мифы о золотом сечении»Можно спекулировать на тему того, что где-то в глубине восприятия человека лежит именно закономерность ряда Фибоначчи, вероятно, где-то мы так же решали геометрическую задачу поворота на нужный угол по спирали, может быть, всё живое, так или иначе помнит этот опыт. Но чтобы не очаровываться золотым сечением чрезмерно, можно обратить внимание на любовь человека к зигзагам и орнаментам. Далеко не обязательно строить бабушкин ковёр по “фи”, чтобы на него было приятнее смотреть, чем на голую стену, – считает Максим Господинко. – Оказывается, этот вид визуального комфорта обусловлен строением визуального кортекса человеческого мозга, и такие орнаменты, как мы можем увидеть в традиционных культурах, ложатся в него как недостающий кусочек удобного паззла вместо хаотичного визуального потока внешней среды. Резной наличник лучше голых ставень. Кружева лучше минимализма. Природа лучше асфальта. Потому что экономят ресурсы человека, показывая привычные и близкие формы».

https://ria.ru/20210121/litso-1593906541.html

https://radiosputnik.ria.ru/20220201/piramida-1769426771.html

https://ria.ru/20181111/1532496249.html

европа

греция

2022

Новости

ru-RU

https://ria.ru/docs/about/copyright.html

https://xn--c1acbl2abdlkab1og.xn--p1ai/

https://cdnn21.img.ria.ru/images/07e6/0b/10/1832031636_345:0:3076:2048_1920x0_80_0_0_d15c886e20acd2d1355969b43de06ca8.jpg

общество, европа, греция, ле корбюзье (шарль-эдуар жаннере-гри), леонардо да винчи

Число Ф (фи), которое называют золотым сечением или серединой, является одним из самых загадочных терминов в математике и физике. Интересно, что оно часто встречается в повседневной жизни, хотя многие об этом никогда не задумывались. Даже люди, не знакомые с правилом золотого сечения, видят его, сами того не понимая. Проводились эксперименты: испытуемым показывали случайные лица и просили назвать наиболее привлекательные. Таковыми оказывались лица, в которых находили золотые соотношения между различными величинами – шириной лица, глаз, линии бровей, носа.  Таким образом, инстинктивно человек видит приближенное к пропорциям, которые считаются идеальными.

Что такое золотое сечение?

Это пропорция, полученная делением в крайнем и среднем отношении. Также это называют гармоническим делением. Как вычисляется золотая середина? В выражении математическим языком эта величина представляет собой соотношение двух величин a и b, где известно, что а>b, и имеет место такое равенство: a/b=(a+b)/a. Представив, что a и b – это части одного отрезка, можно сказать: отношение меньшей части к большей равно отношению большей части к целому. Золотое сечение обозначают 21-й буквой греческого алфавита – Ф (произносится как «фи»).

Данное число бесконечно, как и Пи, показывающее отношение длины окружности к диаметру. Выглядит оно так: 1.6180339887498948420… Соответственно, округляют Ф до 1,618.

История золотого сечения

У этой величины несколько названий. Среди них – божественная пропорция и асимметричная симметрия. Считается, что в науку метод золотого деления внес Пифагор в VI веке до нашей эры. В свою очередь он узнал об этом у египтян и вавилонян. Ведь то, что они использовали соотношения золотого деления доказывают пропорции пирамид, храмов, барельефов, предметов быта и украшений.

Встречается данное правило и в другой древней архитектуре. Например, пирамида Гизы имеет высоту 146,6 метров, а каждая сторона основания достигает 230,5 метров. Если рассчитать отношение длины стороны к высоте, получаем 1,5717, а это совсем рядом со значением Ф. Греческий скульптор и математик Фидий, живший в V веке до нашей эры с применением правила золотого деления создавал скульптуры для Парфенона. Универсальным связующим звеном математических отношений назвал золотое сечение Платон. А Евклид еще в IV веке до нашей эры увидел золотое сечение в пентаграмме.

С данным понятием непосредственно связана последовательность Фибоначчи. Известный математик создал последовательный ряд чисел, и если взять любые два очередных числа, то их отношение будет очень близко к Ф. При этом по мере возрастания чисел, соотношение всё больше приближается к 1,618. К примеру, если взять 3 и 5, то соотношение равно 1,666, а если 13 и 21, то получается уже 1,625. Равное значению Ф дает отношение 144 и 233.

«Золотые» фигуры

Принцип золотого сечения используется для построения геометрических фигур. И считается, что полученные таким образом фигуры, выглядят наиболее изящными. Это подтверждают многократно проведенные эксперименты. Внимание испытуемых больше привлекают именно такие фигуры.

Самым простым примером является прямоугольник, при вычислении отношения сторон которого получаем значение Ф. Еще один замечательный пример – правильный пятиугольник. Все его диагонали делят друг друга на отрезки, связанные золотой пропорцией, а каждый конец – это золотой треугольник. При вершине такого треугольника образуется угол в 36 градусов, а основание делит боковую сторону в пропорции золотого сечения. Внутри пятиугольника строится пентаграмма.

Древнегреческий ученый Архимед, первым отметил, что если от золотого прямоугольника последовательно отсекать квадраты, соединяя противоположные точки четвертью окружности, получается изящная спираль.

Золотое сечение в изобразительном искусстве

В эпоху Возрождения при создании картин и скульптур великие мастера применяли золотое сечение, чтобы достичь баланс красоты. Наиболее яркими примерами являются творения Леонардо да Винчи. С помощью этого правила художник определял пропорции в работе «Тайная вечеря». Это видно при исследовании размеров стола, стен, элементов интерьера. Также божественная пропорция прослеживается в картинах «Мона Лиза» и «Витрувианский Человек». Такие великие художники, как Микеланджело, Рафаэль, Рембрандт, Сальвадор Дали и другие, использовали золотое сечение при создании своих шедевров.

Примеры золотого сечения в жизни и в природе

Ежедневно мы можем наблюдать идеальные пропорции:

• Грудная и брюшная части тела бабочки соотносятся в золотой пропорции. А при сложенных крыльях это прекрасное создание представляет собой правильный треугольник с равными сторонами.
• У стрекозы длины хвоста и корпуса относятся так же, как общая длина тела к хвосту.
• В пропорциях тела ящерицы также прослеживается данный принцип.
• Большинство яиц птиц можно вписать в золотой прямоугольник.
• Последовательность Фибоначчи видна в развитии растений, в расположении чешуек в шишках, зерен в подсолнухах.
• Спирально растет бараний рог, плетет паутину паук.
• Интересно, что если напугать стадо северных оленей, то животные будут разбегаться по спирали.
• В форме двойной спирали представлена молекула ДНК.
• Цветки разных растений, а также морские звезды имеют форму правильного пятиугольника.

Как видно, примеров с правильными пропорциями в природе и повседневной жизни предостаточно. Не даром золотое сечение называют божественной пропорцией. Вероятно, именно этим правилом руководствовался создатель в процессе заполнения Вселенной живыми и неживыми объектами. То, что соответствует этому правилу, кажется нам наиболее привлекательным.

В мире много интересных вещей, изучение нового делает нас умнее, способствует развитию мозга и мышления. Советуем вам обязательно находить время на познание нового. А чтобы было легче усваивать и запоминать большие объемы информации, рекомендуем тренажеры Викиум. Регулярно используя их для тренировок мозга, вы сможете улучшить память, внимательность, логику и аналитические способности.

Эта гармония поражает своими масштабами…

Здравствуйте, друзья!

Вы что-нибудь слышали о Божественной гармонии или Золотом сечении? Задумывались ли о том, почему нам что-то кажется идеальным и красивым, а что-то отталкивает?

Если нет, то вы удачно попали на эту статью, потому что в ней мы обсудим золотое сечение, узнаем что это такое, как оно выглядит в природе и в человеке. Поговорим о его принципах, узнаем что такое ряд Фибоначчи и многое многое другое, включая понятие золотой прямоугольник и золотая спираль.

Да, в статье много изображений, формул, как-никак, золотое сечение — это еще и математика. Но все описано достаточно простым языком, наглядно. А еще, в конце статьи, вы узнаете, почему все так любят котиков =)

Что такое золотое сечение?

Если по-простому, то золотое сечение — это определенное правило пропорции, которое создает гармонию?. То есть, если мы не нарушаем правила этих пропорций, то у нас получается очень гармоничная композиция.

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому.

Но, кроме этого, золотое сечение — это математика: у него есть конкретная формула и конкретное число. Многие математики, вообще, считают его формулой божественной гармонии, и называют «асимметричной симметрией».

До наших современников золотое сечение дошло со времен Древней Греции, однако, бытует мнение, что сами греки уже подсмотрели золотое сечение у египтян. Потому что многие произведения искусства Древнего Египта четко построены по канонам этой пропорции.

Золотое сечение в математике

Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.

В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:

Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:

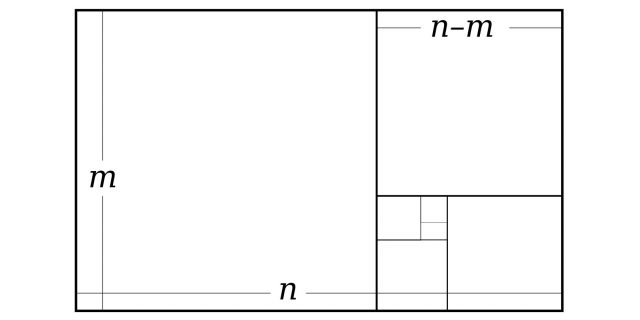
Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.

Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:

Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.

Ряд Фибоначчи и золотое сечение

Продолжаем творить и наблюдать за магией математики и золотого сечения. В средние века был такой товарищ — Фибоначчи (или Фибоначи, везде по-разному пишут). Любил математику и задачи, была у него и интересная задачка с размножением кроликов =) Но не в этом суть. Он открыл числовую последовательность, числа в ней так и зовутся «числа Фибоначчи».

Сама последовательность выглядит так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… и дальше до бесконечности.

Если словами, то последовательность Фибоначчи — это такая последовательность чисел, где каждое последующее число, равно сумме двух предыдущих.

Причем здесь золотое сечение? Сейчас увидите.

Спираль Фибоначчи

Чтобы увидеть и прочувствовать всю связь числового ряда Фибоначчи и золотого сечения, нужно снова взглянуть на формулы.

Иными словами, с 9-го члена последовательности Фибоначчи мы начинаем получать значения золотого сечения. И если визуализировать всю эту картину, то мы увидим, как последовательность Фибоначчи создает прямоугольники все ближе и ближе к золотому прямоугольнику. Вот такая вот связь.

Теперь поговорим о спирали Фибоначчи, ее еще называют «золотой спиралью».

Золотая спираль — логарифмическая спираль, коэффициент роста которой равен φ4, где φ — золотое сечение.

В общем и целом, с точки зрения математики, золотое сечение — идеальная пропорция. Но на этом ее чудеса только начинаются. Принципам золотого сечения подчинен почти весь мир, эту пропорцию создала сама природа. Даже эзотерики, и те, видят в ней числовую мощь. Но об этом точно не в этой статье будем говорить, поэтому, чтобы ничего не пропустить, можете подписаться на обновления сайта.

Золотое сечение в природе, человеке, искусстве

Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» — это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.

И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.

Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.

Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.

Пропорции золотого сечения в человеке

Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.

Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:

• от плеч до макушки к размеру головы = 1:1.618

• от пупка до макушки к отрезку от плеч до макушки = 1:1.618

• от пупка до коленок и от коленок до ступней = 1:1.618

• от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618

Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».

Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.

Золотое сечение в природе и ее явлениях

Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:

• в завитках человеческого уха мы можем увидеть золотую спираль;

• ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;

• и в молекуле ДНК;

• по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.

Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, — спланировано по принципу золотого сечения.

Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:

• Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.

• Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.

• Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.

• Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.

По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.

Абсолютно во всем живом и не живом можно прочесть высшую красоту и гармонию.

Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет. Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил.

Золотое сечение в искусстве

Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.

• Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.

• В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.

• В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.

• Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.

• Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.

Золотые котики Фибоначчи

Ну и, наконец, о котиках! Вы задумывались о том, почему все так любят котеек? Они же ведь заполонили Интернет! Котики везде и это чудесно =)

А все дело в том, что кошки — идеальны! Не верите? Сейчас докажу вам это математически!

Видите? Тайна раскрыта! Котейки идеальны с точки зрения математики, природы и Вселенной =)

* Я шучу, конечно. Нет, кошки, действительно, идеальны) Но математически их никто не измерял, наверное.

На этом, в общем-то, все, друзья! Мы увидимся в следующих статьях. Удачи вам!

P. S. Изображения взяты с сайта medium.com.

Что такое золотое сечение

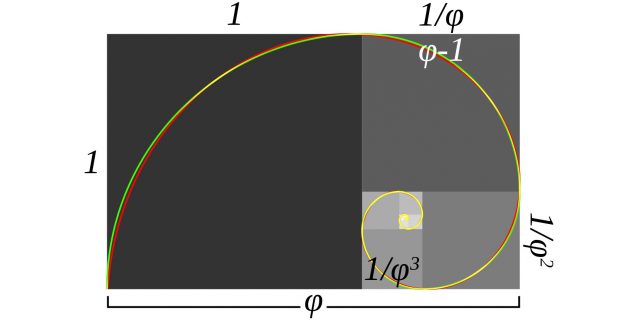
Это соотношение двух неравных чисел, при котором большее так же относится к меньшему, как сумма этих чисел к большему. Золотое сечение равно примерно 1,618, или 1,62, если округлить, и обозначается греческой буквой φ, «фи» — от имени древнегреческого скульптора Фидия. Считается, что он использовал такие пропорции при оформлении Парфенона.

Наиболее известные графические представления золотого сечения — это прямоугольник с соотношением сторон примерно 62:48 и построенная в нём спираль.

1 / 0

«Золотой прямоугольник» можно разделить на такие же, только меньшего размера. Изображение: Dicklyon / Wikimedia Commons

2 / 0

«Золотая спираль» (красная), вписанная в «золотой прямоугольник». Изображение: Silverhammermba & Jahobr / Wikimedia Commons

Золотое сечение тесно связано с числами Фибоначчи. Это ряд чисел, каждое из которых равняется сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Чем дальше продолжается этот ряд, тем ближе соотношение соседних чисел в нём к 1,618. Например, 3/2=1,5; 8/5=1,6, а 34/21= 1,619.

Почему золотое сечение так популярно

Впервые им заинтересовались ещё древнегреческие математики Пифагор и Евклид. Они считали, что на числах построено всё мироздание и с их помощью можно объяснить любой феномен. Неудивительно, что элегантное соотношение так заинтересовало античных мыслителей.

Вслед за ними золотым сечением увлеклись многие выдающиеся учёные и деятели искусства. Например, Леонардо да Винчи, Альбрехт Дюрер, Иоганн Кеплер, Ле Корбюзье, Сальвадор Дали и Ричард Пенроуз.

Его считают «божественной пропорцией»

Название «золотое сечение» придумал немецкий математик XIX века Мартин Ом. До него это соотношение именовали «божественной пропорцией».

Из‑за приписываемых характеристик золотое сечение старались применять как можно чаще. Так, во времена Возрождения это число считалось идеальным способом для выбора размера. «Золотой прямоугольник», например, нередко использовали при создании книг и картин. А линию пояса называли границей золотого сечения человеческого тела.

Некоторые и поныне считают эту пропорцию секретом привлекательности и примером универсальной гармонии, приятной человеческому глазу. Например, о золотом сечении любят говорить пластические хирурги. А ещё это число популярно как никакое другое в математике.

Его можно встретить в природе

Числа Фибоначчи и спирали, подобные золотому сечению, часто обнаруживаются в природе. Например, в количестве лепестков у цветов или форме растений.

Его обнаруживают в произведениях архитектуры и искусства

Например, «божественные пропорции» находят в Парфеноне и египетских пирамидах. Также широко распространено заблуждение, что «Мона Лиза» написана в соответствии с числом φ.

Почему универсальность золотого сечения — миф

Однако при тщательном изучении становится понятно, что эта пропорция не так уж всеобъемлюща.

Божественность золотого сечения преувеличивается

Золотому сечению придают больше значения, чем есть в действительности. Красивые узоры и налёт таинственности сделали из обычного геометрического соотношения математический миф, который, к примеру, очень любят нумерологи.

Чаще всего вещи причисляют к золотому сечению с большими допущениями. Ни о какой точности и математической универсальности в таком случае говорить не приходится. Поэтому при желании можно обнаружить «божественные пропорции» где угодно.

В природе золотое сечение не так уж распространено

Его находят далеко не везде. Например, у маков всегда четыре лепестка, а в ряд Фибоначчи четвёрка не входит. Также нередко встречается четырёхлистный клевер. Раковины морских моллюсков похожи на спираль золотого сечения, но всё-таки другие. У них больше витков, и расстояние между ними меньше. Ни у одного моллюска коэффициент скручивания раковины и близко не равен 1,62. Это видно даже невооружённым глазом:

1 / 0

Спираль морского моллюска. Изображение: Florian Elias Rieser / Wikimedia Commons

2 / 0

Спираль Фибоначчи, близкая к золотому сечению. Изображение: Jahobr / Wikimedia Commons

В человеческом теле же столько точек, от которых можно производить измерение, что при желании реально найти золотое сечение где угодно. Вот только с большой вероятностью у разных людей «божественную пропорцию» придётся искать в разных местах, так как мы можем сильно отличаться друг от друга.

В искусстве оно тоже встречается не так уж часто

Изучение 565 картин выдающихся художников показало, что в среднем соотношение сторон в работах составляет 1,34. Это явно не дотягивает до золотого сечения. Учёные не находят его даже в произведениях Леонардо да Винчи.

Археологические исследования не подтверждают и того, что древние греки могли использовать золотое сечение при постройке Парфенона. Из более чем 100 памятников древнегреческой архитектуры это число нашлось в пропорциях только четырёх объектов: башни, алтаря, гробницы и надгробия. Не могли пользоваться золотым сечением и древние египтяне, не обладавшие достаточным уровнем технологий, чтобы точно высчитывать пропорции.

Кому золотое сечение может быть полезно на самом деле

Современная математика использует золотое сечение и числа Фибоначчи при описании фракталов — фигур, которые проявляют самоподобие.

Знание о числе φ играет важную роль в изучении хаоса и изменяющихся (динамических) систем. Оно помогает понять, как природа развивается и самоорганизуется.

Также числа Фибоначчи полезны при решении некоторых сложных задач. Например, с помощью этих чисел советский математик Юрий Матиясевич доказал, что не существует универсального алгоритма решения уравнений с как минимум двумя неизвестными.

Читайте также 💆‍♂️👩‍🔬

• Продолжите последовательность! 10 мини-задач для разминки мозга
• Как округлять числа
• Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
• Гимнастика для ума: 10 увлекательных задач с числами
• 10 увлекательных задач от советского математика

Что это? Золотое сечение – это математическая формула, соотношение двух неравных чисел. Его еще называют божественной пропорцией. Правило третей, золотая спираль – всё это визуальное отображения этого универсального правила.

Где используется? Золотое сечение применимо везде, где есть место графике, рисунку, фотографии. Сфера дизайна – не исключение. Конечно, это не единственное правило гармонии, но, пожалуй, самое известное.

Что такое золотое сечение

Это отношение двух разных по величине чисел, когда большее из них относится к меньшему так же, как и общая их сумма относится к большему. Соотношение золотого сечения равняется около 1,618. Его обозначают греческой литерой Ф (читается как «фи») в честь древнегреческого скульптора Фидия, который применял эти пропорции при создании храма Парфенон.

Одним из популярных способов представления золотого сечения является прямоугольник с соотношением сторон 62 на 48 и построенной внутри спиралью.

История золотого сечения

Согласно истории, данное понятие для научного использования ввел Пифагор, философ и математик Древней Греции. Предполагается, что ученый позаимствовал знание у жителей Египта и Вавилонии.

Если посмотреть на соотношение сторон пирамид, храмов и предметов домашнего обихода у древних египтян, а также на украшения из саркофага царя Тутанхамона, то очевидно, что все они создавались по принципу золотого сечения.

Архитектор из Франции Ле Корбюзье заметил, что рельеф храма египетского правителя Сети I, как и в рельефе изображения царя Рамзеса, тоже создавались по этому правилу. Соотношения золотого деления были обнаружены и в рельефе гробницы, на котором изображен высокопоставленный чиновник Хесира.

Скачать
файл

Жители Древней Греции хорошо владели геометрией. Арифметике, например, они учились по геометрическим фигурам уже в детстве. А квадрат Пифагора и его диагональ служили основой для создания динамических прямоугольников.

Сам термин «золотое сечение» впервые ввел в обиход математик из Германской империи Мартин Ом в 19 веке. До того времени правило имело название «божественная пропорция».

Из-за уникальных свойств она пользовалась большой популярностью. Например, в эпоху Возрождения число 1,618 было идеальным при выборе размера. Его часто применяли для создания картин и книг. А линия талии в то время считалась границей золотого сечения в теле человека.

Многие люди и сегодня уверены, что соблюдение данного правила считается залогом красоты и внешней гармонии. Эту тему активно обсуждают пластические хирурги.

Золотое сечение Фибоначчи

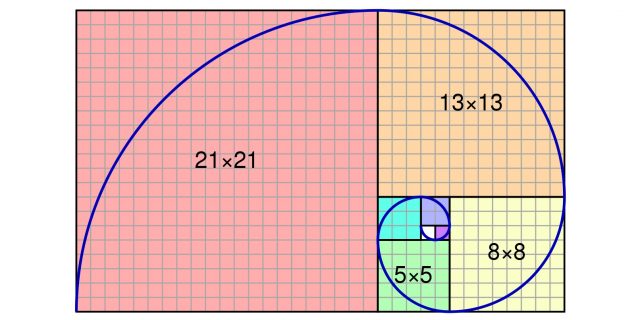
В конце 12 века математик из Италии Леонардо Пизанский, известный по прозвищу Фибоначчи, открыл последовательность чисел, связанных с золотой пропорцией. Суть в том, что если взять любые 2 числа из ряда итальянского математика, то соотношение между ними почти такое же, как на примерах золотого сечения. Особенность последовательности Фибоначчи в том, что каждое новое число всегда равняется сумме 2-х предыдущих. Пример: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д.

По мере увеличения ряда, отношения между числами становится все ближе к 1,618. Разделив, к примеру, 8 на 5, мы получим около 1,6. А соотношение 34 на 21 уже дает 1,619, если округлить. Каждое число ряда является логичным в последовательности Фибоначчи.

Такие соотношения из-за приближения к показателю золотого деления можно использовать при построении золотого прямоугольника. Эта фигура считается одной из самых гармоничных в геометрии, что позволяет применять пропорции Пифагора в любом виде изобразительного искусства.

Золотой прямоугольник тесно связан с золотой спиралью, которая строится методом размещения смежных между собой квадратов по алгоритму Фибоначчи.

Золотое сечение в природе

Пропорции золотого сечения можно наблюдать во всех природных и научных проявлениях. В представленном списке мы рассмотрим наиболее удивительные случаи.

• Лепестки у цветов. Нередки случаи, когда их количество соответствует числовому ряду «Ф». По мнению Дарвина, все лепестки растений располагаются так, чтобы получать как можно больше солнечного света и остальных необходимых для жизни ресурсов.
• Головки у семян. Во многих случаях семена цветов начинают расти посередине головки семени и появляются снаружи, заполняя собой пространство. В качестве примера можно привести семена подсолнуха.
• Шишки у сосен. Семена, находящиеся в их семенных коробочках, произрастают вверх противоположно друг другу по спирали. Расстояние между ними обычно совпадает с соотношениями чисел из последовательности Фибоначчи.
• Ветки у деревьев. На примере их формирования и расщепления также можно заметить правило золотого ряда. То же самое относится и к развитию корневых систем у растений и водорослей.
• Раковины. Большинство из них демонстрируют нам правило золотого сечения. Например, это можно сказать об улитках и наутилусах.

• Спиральные галактики. Млечный Путь содержит в себе несколько рукавов, представленных в виде изогональных спиралей с шагом около 12 градусов. Их форма соответствует форме золотой спирали, при том над каждой такой галактикой можно начертить золотой прямоугольник.
• Ураганы. В большинстве случаев, изнутри они устроены согласно последовательности ряда «фи».
• Пальцы на руках у людей. Все участки пальцев от начала основания и до запястья увеличивается в соотношении по Фибоначчи.
• Тела людей и животных. Расстояние у людей от пупка до пола, а также от темени и до пупка — это яркий пример закона золотого сечения. Помимо человека такую пропорцию можно наблюдать и у других организмов (например, у дельфинов и пчел).
• Молекулы ДНК. Все они содержат соотношение 34 на 21 ангстрем в каждом полном спиральном цикле. А вы уже знаете, что эти цифры — часть ряда Фибоначчи.

Как мы видим, примеров, где можно увидеть пропорции и соотношения по принципу золотого правила, довольно много. Помимо случаев, описанных выше, 1,618 постоянно встречается в точных науках, биологии и других областях жизни. Поэтому свое альтернативное название — божественное сечение, правило полностью оправдывает. Ведь материальный мир словно был создан по этому закону.

Золотое сечение в фотографии

Гармоническая пропорция напрямую связана с правилом третей — другой неотъемлемой схемой для работы с визуалом. По сути, оно продолжает золотое сечение так же, как, например, фотография рождается из художественного творчества.

Основное различие заключается в соотношении сторон. Так, в принципе третей кадр разделяется на 3 одинаковые части, а в божественной пропорции он делится на 1:0.618:1.

Отсюда следует, что правило третей можно назвать более простой версией золотого сечения, но полностью рабочей.

Например, сегодня большинство камер, в том числе и в смартфонах, имеет разлинованную сетку третей, что позволяет пользователям гармонично выстраивать композицию из фото и видео.

Чем следует руководствоваться при съемке?

• Точки пересечения. Благодаря размещению нужного объекта по линиям, сделать снимок будет намного удобнее.
• Диагональная композиция. Линию можно прочертить самостоятельно из верхнего угла кадра в нижний, а можно использовать объекты, находящиеся в этой последовательности, которые формируют эту линию. Наличие разных диагоналей позволяет получить динамичный кадр. Восходящая, например, из правого нижнего угла в левый верхний придаст фотографии веселое настроение, а нисходящая — грустное.
• Пропорции. Чаще всего это относится к взаимосвязи объектов на нескольких планах снимка. Это тоже вариант золотого сечения, только представленный в соотношении объектов. Например, на заднем плане к большему объекту на переднем плане (либо наоборот).
• Линия горизонта. Когда вы делаете снимок на природе либо в городской инфраструктуре, нужно расположить горизонтальную линию кадра на одной из горизонтальных линий третей. То же самое относится и к общему плану фотографии/видео. Это даст более качественный результат.
• Правило «воздуха». Не забывайте про свободные участки между объектами. Если вы делаете фотографию человека, то оставьте немного пространства от его головы до границы кадра. А в ситуации, когда он смотрит налево, разместите человека по правым точкам пересечения линий (верно и обратное).

Золотое сечение в дизайне

Божественная пропорция делает современный дизайн более упорядоченным. Легкий и быстрый способ использования этого — умножить размер одного элемента на 1,618. Результат покажет, каким должен быть размер следующего объекта.

Применение формулы золотого сечения в типографике

Определяющими факторами в данной области являются 3 составляющие: размер шрифта, ширина линии и высота строки. Их необходимо подбирать в правильных пропорциях.

Увеличивая и уменьшая шрифт, а также ширину текста, можно определить, какую высоту следует задать буквам. Установлено, что оптимальным для удобства читателей количеством является 70-80 символов на строку. Когда длина текста превышает этот показатель, его читабельность сильно снижается.

Для примера возьмем текст из 3 строк и определим в нем 3 части: «А», «Б» и «В». Допустим, строка «В» содержит меньше ценной информации, чем «А» и «Б». В связи с этим, текст внутри строки «В» должен иметь шрифт размером 10. Чтобы установить размер контента на строке «Б» (второй по значимости контента), надо умножить 10 на 1,618.

В разработке логотипов

Большинство популярных брендов, например, «Твиттер», «Эппл» и «Пепси», применяют знания божественного сечения, когда создают фирменный логотип.

Поэтому вы тоже можете пользоваться правилом чисел «Ф» при создании сетки. Полученный результат станет вашей опорой в разработке графического рисунка.

Золотое сечение в архитектуре

Зодчие прошлого применяли принцип божественного деления при создании памятников. Мавзолей-мечеть Тадж-Махал, например, относится к одному из 7 чудес света. Когда его возводили, мастера пользовались правилом золотого сечения.

Применение этого знания в современной архитектуре дает возможность добиться баланса между шириной и высотой сооружения. Популярным методом построить гармоничное здание является использование свойств золотого прямоугольника.

Стоит добавить, что золотое сечение дает возможность творить разнообразные формы. При их создании нет необходимости строго следовать прямоугольной структуре. Золотое деление позволяет дизайнерам применять полученные формы как основу для работы.

Разработка проектов и формирование макетов

Чтобы сделать макеты качественными, нужно учесть 2 главные составляющие: отдельные визуальные элементы и как они будут связаны между собой.

Есть много способов формирования макетов. Например — расположение «Z». Оно дает увидеть путь, по которому проходит посетитель на веб странице, а также схему того, как он смотрит на элементы.

Еще одно востребованное правило компоновки — это применение золотой спирали. Она более эффективно, если в дизайне достаточно много элементов, различающихся между собой, но предназначенные для расположения на одном макете. Благодаря использованию правил сечения внимание посетителей ненавязчиво, но эффективно притягивается к середине спирали, в которой можно расположить главный элемент контента.

Некоторые считают, что золотое сечение в большей или меньшей степени присутствует в каждом успешном дизайне. Рассказать о востребованной концепции бывает полезным в общении с заказчиком или когда нужно показать свой проект публично. Действительно ли «божественная пропорция» очень эффективна или это мнение преувеличено? Обсуждение данного вопроса в творческой сфере продолжается и сегодня.