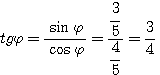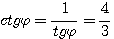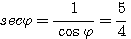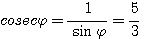Как найти значения функций если известен синус - Исправление недочетов и поиск решений вместе с Examum.ru

Внимание! Эти формулы работают только если аргументы у тригонометрических функций одинаковые, т.е.

(sin^2⁡ 776^° +cos^2⁡ 776^° =1)
(tg, 3xcdot ctg, 3x=1)

Но:

(sin^2⁡x+cos^2⁡3x≠1)
(tg, xcdot ctg, y≠1)

Все формулы связи тригонометрических функций учить не надо, потому что они достаточно легко получаются друг из друга несложными преобразованиями (подробности в этих видео). Кроме того, при частом использовании они постепенно запоминаются сами.

Примеры применения формул связи

Зачем нужны формулы связи? Они позволяют найти все тригонометрические функции угла, если известна лишь одна из них, а также дают возможность упрощать выражения, доказывать тождества, решать тригонометрические уравнения, заменяя одну функцию другой и так далее.

Пример. Найдите (5sin⁡,α), если (cos,⁡α=frac{2sqrt{6}}{5}) и (α∈(frac{3π}{2};2π)).
Решение. Нам известен косинус, найти надо синус. А что связывает синус и косинус? Основное тригонометрическое тождество:

(sin^2α+cos^2⁡α=1).

Подставим вместо косинуса его значение:

(sin^2⁡α+)((frac{2sqrt{6}}{5}))(^2=1)
(sin^2⁡α+)(frac{4cdot 6}{25})(=1)
(sin^2⁡α+)(frac{24}{25})(=1)
(sin^2⁡α=1-)(frac{24}{25})
(sin^2⁡α=)(frac{1}{25})
(sin⁡α=±)(frac{1}{5})

Внимание! Последняя строчка – место, где теряется огромное количество баллов на ЕГЭ! Это одна из самых популярных ошибок – забыть отрицательный корень. Пожалуйста, раз и навсегда запомните, что у неполного квадратного уравнения вида (x^2=a) (при (a>0)) два корня (x_1=sqrt{a}) и (x_2=-sqrt{a}). Пусть двойка над иксом (та которая «квадрат») будет вам вечным маяком, сигнализирующим: «тут ДВА корня! Два! Не забудь!»

Вернемся к задаче. Получилось, что синус может иметь значение (frac{1}{5}), а может (-)(frac{1}{5}). И какое значение нам надо выбрать — с минусом или плюсом? Тут нам на помощь приходит информация, что (α∈(frac{3π}{2};2π)). Давайте нарисуем числовую окружность и отметим отрезок ((frac{3π}{2};2π)).

Обратите внимание – в этой четверти синус принимает только отрицательные значения (можно провести перпендикуляры до оси синусов и убедиться, что это так).

Значит, в нашем случае (sin,⁡α=-frac{1}{5}) т.е. (5sin,⁡α=5cdot(-frac{1}{5})=-1).

Ответ: (-1).

Пример.Найдите (tg,α), если (cos,⁡α=)(frac{sqrt{10}}{10}) и (α∈(frac{3π}{2};2π)).
Решение. Есть 2 пути решения этой задачи:

— напрямую вычислить тангенс через формулу (tg^2α+1=)(frac{1}{cos^2⁡α});
— сначала с помощью тождества (sin^2⁡α+cos^2⁡α=1) найти (sin⁡,α), а потом через формулу (tg,α=)(frac{sin⁡,α}{cos⁡,α}) получить тангенс.

В учебниках обычно идут первым путем, поэтому мы пойдем вторым.

Вычисляем синус:

(sin^2⁡α+)((frac{sqrt{10}}{10})^2)(=1)
(sin^2⁡α+)(frac{10}{100})(=1)
(sin^2⁡α+)(frac{1}{10})(=1)
(sin^2⁡α=1-)(frac{1}{10})
(sin^2⁡α=)(frac{9}{10});
(sin⁡,α=±)(frac{3}{sqrt{10}})

Опять (α∈(frac{3π}{2};2π)), значит в итоге синус может быть только отрицательным. То есть, (sin⁡,α=-)(frac{3}{sqrt{10}}).
А теперь вычисляем тангенс: (tg,α=-)(frac{3}{sqrt{10}})(:)(frac{sqrt{10}}{10})(=)(-frac{3}{sqrt{10}}cdotfrac{10}{sqrt{10}})(=-)(frac{30}{10})(=-3).

Ответ: (-3).

Пример. Известно, что (tg,α=-frac{3}{4}) и (frac{π}{2}<α<π). Найдите значения трех других тригонометрических функций угла (α).
Решение. Проще всего из тангенса найти котангенс:

(ctg, α=)(frac{1}{tg, α})
(ctg,α=1:(-frac{3}{4})=1cdot(-frac{4}{3})=-frac{4}{3}).

Теперь вычислим косинус по упомянутой выше формуле:

(tg^2 α+1=)(frac{1}{cos^2⁡α})
((-)(frac{3}{4}))(^2+1=)(frac{1}{cos^2⁡α})
(frac{9}{16})(+1=)(frac{1}{cos^2⁡α})
(frac{9+16}{16})(=)(frac{1}{cos^2⁡α})
(frac{25}{16})(=)(frac{1}{cos^2⁡α})
(cos^2⁡α=)(frac{16}{25})
(cos⁡α=±)(frac{4}{5})

Опять перед нами стоит выбор плюс или минус. Отметим отрезок ((frac{π}{2};π)) на тригонометрической окружности и посмотрим какие значения принимает косинус в этой четверти, чтобы определится со знаком.

Очевидно, что косинус отрицателен в этой четверти, а значит (cos,⁡α=-)(frac{4}{5}).

Осталось найти синус:

(sin^2⁡α+cos^2⁡α=1)
(sin^2⁡α+(-)(frac{4}{5})()^2=1)
(sin^2⁡α+)(frac{16}{25})(=1)
(sin^2⁡α=1-)(frac{16}{25})
(sin^2⁡α=)(frac{9}{25})
(sin,⁡α=±)(frac{3}{5})

Опять используем круг, чтобы определить знак.

Получается, что (sin,⁡α=)(frac{3}{5}).

Ответ: (ctg,α=-)(frac{4}{3}); (cos,⁡α=-)(frac{4}{5}); (sin,α=)(frac{3}{5}).

Пример (ЕГЭ). Найдите (tg^2 α), если (5 sin^2⁡α+13 cos^2⁡α=6).
Решение. Давайте пойдем от того, что известно. В равенстве (5 sin^2⁡α+13 cos^2⁡α=6) синус заменим на косинус:

(5(1-cos^2⁡α)+13 cos^2⁡α=6)
(5-5 cos^2⁡α+13 cos^2⁡α=6)
(5+8 cos^2⁡α=6)
(8 cos^2⁡α=1)
(cos^2⁡α=)(frac{1}{8})

Поняли почему именно синус заменили на косинус, а не наоборот? И почему не надо извлекать корень, досчитывая до «чистого» косинуса? Потому что для нахождения (tg^2α) хорошо подходит формула (tg^2α+1=)(frac{1}{cos^2⁡α}) :

(tg^2 α+1=1:)(frac{1}{8})
(tg^2 α+1=1cdot)(frac{8}{1})
(tg^2 α+1=8)
(tg^2 α=7)

Ответ: (7).

Теперь еще одна задача из ЕГЭ, для наглядности мы ее решение оформили картинкой.

Пример. Упростите выражение (frac{1}{sin^2 α})(-ctg^2 α-cos^2 β).
Решение.

(frac{1}{sin^2 α})(-ctg^2 α-cos^2 β)		Самое очевидное, что можно сделать – это представить котангенс как отношение косинуса к синусу.
(=)(frac{1}{sin^2 α})(-)(frac{cos^2⁡α}{sin^2 α})(-cos^2 β=)		Приводим дроби к общему знаменателю.
(=)(frac{1-cos^2⁡α}{sin^2 α})(-cos^2 β=)		(1-cos^2⁡α) можно заменить на (sin^2 α).
(=)(frac{sin^2 α}{sin^2 α})(-cos^2 β=)		Сокращаем синусы.
(=1-cos^2 β=sin^2 β).

Пример. Докажите тождество (frac{cos^4⁡α-sin^4⁡α}{(1-sin⁡α)(1+sin⁡α)})(+2tg^2 α=)(frac{1}{cos^2 α}).
Решение.

(frac{cos^4⁡α-sin^4⁡α}{(1-sin⁡α)(1+sin⁡α)})(+2tg^2 α=)(frac{1}{cos^2 α})		Чтобы доказать это тождество, будем преобразовывать левую часть, пытаясь свести ее к правой. Поехали. Разложим числитель левой дроби по формуле разности квадратов, а знаменатель, наоборот, соберем по ней же.
(frac{(cos^2⁡α-sin^2⁡α )(cos^2 α+sin^2⁡α)}{1-sin^2⁡α})(+2tg^2 α=)(frac{1}{cos^2 α})		Очевидно, что вторая скобка числителя равна (1) (по основному тригонометрическому тождеству), а знаменатель можно заменить на (cos^2 α).
(frac{cos^2⁡α-sin^2⁡α}{cos^2 α})(+2tg^2 α=)(frac{1}{cos^2 α})		Теперь разложим тангенс по формуле (tg, α=)(frac{sin⁡,α}{cos,⁡α}).
(frac{cos^2⁡α-sin^2⁡α}{cos^2 α})(+2)(frac{sin^2⁡α}{cos^2⁡α})(=)(frac{1}{cos^2 α})		Приводим дроби к общему знаменателю.
(frac{cos^2⁡α-sin^2⁡α+2 sin^2⁡α}{cos^2 α})(=)(frac{1}{cos^2 α})		Приводим подобные слагаемые.
(frac{cos^2⁡α+sin^2⁡α}{cos^2 α})(=)(frac{1}{cos^2 α})		И вновь нас выручает основное тригонометрическое тождество
(frac{1}{cos^2 α}) (=)(frac{1}{cos^2 α})

Левая часть полностью идентична правой, то есть тождество доказано.

Как доказать все формулы связи

Источник

3ГОНОМЕТРИЯ В НАЧАЛО

Нахождение значений тригонометрических функций угла по значению какой-нибудь одной из них.

Используя основные тригонометрические тождества, легко найти значения всех тригонометрических функций sin х, cos х, tg x, ctg x, sec x, cosec x, если известно значение какой-нибудь одной из них. Поясним это на конкретных примерах.

Пример 1. Найти значения тригонометрических функций угла φ, если известно, что sin φ = ³/₅.

Из тождества sin² φ + cos²φ = 1 находим: cos²φ = 1 — sin² φ = ¹⁶/₂₅

Поэтому cos φ = ± ⁴/₅

Знак + или — следует выбирать в зависимости от того, в какой четверти оканчивается угол φ.

По условию sin φ = ³/₅ > 0.

Значит, угол φ оканчивается либо в 1-й, либо во 2-й четверти.
1)Если он оканчивается в 1-й четверти, то cos φ = + ⁴/₅.
2)Если же он оканчивается во 2-й четверти, то cos φ = — ⁴/₅.

В первом случае

Во втором случае

tg φ = — ³/₄; ctg φ = — ⁴/₃; sес φ = — ⁵/₄; cosec φ = ⁵/₃

Пример 2. Найти значения тригонометрических функций угла φ, если известно, что он оканчивается в 4-й четверти и tg φ = — ³/₄

Используя тождество 1 + tg² φ = sec² φ, найдем sec φ:

sec φ = /1 + tg² φ = /1+ (— ³/₄) ² = ⁵/₄

Знак + перед радикалом мы взяли потому, что угол φ по условию оканчивается в 4-й четверти, sec φ = ¹/_cos_φ , а косинус угла, оканчивающегося в 4-й четверти, положителен; поэтому положителен и sec φ.

Далее получаем: cos φ = ¹/_sec_φ = ⁴/₅

Теперь, используя тождество sin² φ + cos² φ = 1, найдем sin φ:

sin φ = — / l — cos² φ = — ³/₅ .

Здесь перед радикалом нужно брать знак — , поскольку синус угла, оканчивающегося в 4-й четверти, отрицателен.

Заметим, что в данном случае рациональнее было бы найти sin φ из тождества tg φ = ^sin^φ/_cos_φ . Однако мы сознательно получили sin φ другим путем, чтобы еще раз показать, как нужно выбирать знак (+ или —) перед радикалом.

Итак, мы получили cos φ, sin φ, tg φ, sec φ. После этого легко найти значения и других тригонометрических функций угла φ:

ctg φ = ¹/_tg_φ = — ⁴/₃ ; cosec φ = ¹/_sin_φ = — ⁵/₃

Упражнения

1. Найти значения тригонометрических функций угла α по следующим данным;

1) sin α = 0,6 0°<α<90°; 4) cosα = —0,8, 180°<α<270°;

2) sinα= — ^/²/₃, π <α< ³/₂π; 5) tgα = —2, ³/₂π <α< 2π;

3) cosα= ¹²/₁₃, 270°<α<360°; 6) tgα = ¹/₃ , 180°<α<270°.

2. Найти значения тригонометрических функций угла φ, если известно, что
sin φ = ^/^2ab /_a+b (a > b > 0) и угол φ оканчивается не в 1-й четверти.

3. Найти значения тригонометрических функций угла φ, если известно, что tg φ = а² — 1 ( |а| < 1), и угол φ оканчивается не во 2-й четверти.

Источник

Как найти угол имея цифровое значение синуса, косинуса, тангенса,котангенса? например есть значение sin a=0,3452 какой угол этому соответствует?

Функции: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), называются тригонометрическими. Они выражают зависимости длин сторон от углов треугольника при гипотенузе. Определяются отношением какой-либо из сторон треугольника к другой. То есть, показывают, насколько одна сторона больше другой. Это отношение может быть характерно только для строго определенного угла. Выражаются тригонометрические функции в безразмерных единицах.

Если известно значение какой-либо тригонометрической функции (в данном случае, синуса — sin), а требуется найти соответствующий ему угол в градусах, то нужно:

найти обратную тригонометрическую функцию, так называемую «arc»: arcsin, arccos, arctg, arcctg.. Эти функции находятся: по таблицам Брадиса, в которых для каждого угла приведены свои — строго определенные значения тригонометрических функций (таблицами Брадиса пользовались в «докомпьютерный век»), с помощью «инженерных» калькуляторов или компьютерными программами, в частности — Excel. Для того, чтобы определить значение угла по таблицам Брадиса, нужно водить пальцем по их строкам (с тысячами значений), где найти нужную величину (то ли 5, то ли 6 знаков после запятой). И увидеть соответствующее ему значение угла. Так что, с помощью Excel это делается несравненно быстрее и точнее.
Однако функции arc показывают значение в радианах. Искомый угол равен 0,35245 радиан. Если нужно в градусах, то следуют применить еще и формулу перевода радиан в градусы.

asin

Определение значения arcsin угла (в радианах) и значения в градусах — с помощью функций Excel

Итак, ответ получен:

Синусу угла альфа со значением 0,3452 соответствует угол 20,194 градуса.

автор вопроса выбрал этот ответ лучшим

RIOLIt
[176K]

6 лет назад

Данному значению синуса соответствует угол- немногим более 20 градусов, это- по таблице, а если есть значение гипотенузы, то- по отношению- можно найти катет и другие элементы треугольника и- возможно- все улы, здесь- главное- зацепка- кончик ниточки, чтобы размотать весь клубочек,( а имея в

хозяйстве инженерный калькулятор, можно сразу- по функции найти угол с точностью до н- ого знака после запятой…)

Можно без компьютера, без калькулятора, без таблиц Брадиса найти этот угол. Для этого нужен такой инструмент, как транспортир. Можно воспользоваться угломером. Если есть чертежный прибор, который еще называют кульман, то и им. Но сначала высисляют катет и гипотенузу. Чем больше длина, тем точгее. Допустим, гипотенуза 100 мм, тогда противолежащий катет будет равен 100*0,3452=34,52мм. Берем клетчатую бумагу, по вертикали откладываем 35 мм от горизонтальной линии вверх. Из верхней точки циркулем с разведенными ножками на 100 мм делаем засечку на глризонтальной линии. Соединяем три точки линиями и измеряем угол.

Если честно, то в повседневной жизни не припомню, чтобы приходилось определять углы по синусу или тагенсу. Вот строить углы приходится постоянно. Например, нужно обрезать плинтуса под углом 45 градусов. Никакой транспортир или угломер не нужен. На заводе плинтус обрезан под прямым углом, тогда просто отмеряешь два одинаковых катета и проводишь гипотенузу, угол получантся сам собой. Так же легко строить углы 30 и 60 градусов, так как гипотенуза равна двум противолежащим катетам.

Еще углы можно измерять смартфоном илитпланшетом, если в нем установлено приложение по измерению углов, очень удобная штука, не надо покупать строительный уровень.

bezdelnik
[34.1K]

6 лет назад

Найти угол имея цифровое значение синуса, косинуса, тангенса можно по таблицам Брадиса, на логарифмической линейке или на калькуляторе. Если sin a=0,3452, то a=20,194… градуса. Можно найти приближенное значение тригонометрических функций по их графикам, для синуса и косинуса это графики синусоиды и косинусоиды. Найдя значения синуса и косинуса значения тангенса и котангенса можно вычислить по формулам tg a = Sin a /Cos a, ctg a = Cos a/Sin a

DartFallen
[68.2K]

6 лет назад

Я открою Вам одну старую и великую тайну! Все эти величины давно вычислены и сведены в таблицу. Носит она название таблицы Браддиса.

Когда я учился в старших классах у каждого ученика была желтенькая такая брошюрка, в которой и представлены многие данные и не только для градусной меры углов. Величины эти постоянные и периодического пересчета не требуют.

Вот как-то так…

Blockphild
[0]

8 месяцев назад

Зачем так все сложно и это в век компьютеров? Иди сюда -> https://allcalc.ru/node/1039

вставляй величины катетов и гипотенуз —> жми на кнопку -> ВЫЧИСЛИТЬ и вот тебе результат в градусах и радианах.

Недостаток: нужно иметь интернет

Не надо никаких там EXCEL, таблиц Брадисов и прочей ерунды, мы в 21 веке живем, все делается очень быстро.

Успехов!

bezdelnik
[34.1K]

5 лет назад

Для некоторых значений тригонометрических функций соответствующие углы общеизвестны из учебников по математике. Например,для углов 0°, 30°, 45°, 60°, 90° синус равен 0, 1/2, √2/2, √3/2, 1 ,соответственно, а косинус такие же значения в обратном порядке. Это должны знать все получившие среднее школьное образование.

Знаете ответ?

Смотрите также:

В треугольнике АВС угол С равен 90°, АВ=10, АС=√51. Как найти sin A?

Как вычислить площадь параллелограма по формуле S=a·b·sin A с след.данными?

В треугольнике ABC угол C = 90°, sin A = 4/5, AC=9. Найти AB. Как решить?

Как доказать теорему о равенстве синусов острых углов?

Как построить угол, если известен синус?

Если синус X равен 1, чему равен косинус X(см)?

Как найти котангенс, тангенс, синус, косинус?

Как выучить таблицу значений синуса, косинуса, тангенса разных углов?

Перечислите все формулы, объединяющие синус, косинус, тангенс и котангенс?

Как записать две различные функции для синуса и косинуса?

Источник

Как найти значение тригонометрических функции

Тригонометрические функции вначале возникли как инструменты абстрактных математических вычислений зависимостей величин острых углов в прямоугольном треугольнике от длин его сторон. Сейчас они очень широко применяются как в научных, так и в технических областях человеческой деятельности. Для практических вычислений тригонометрических функций от заданных аргументов можно использовать разные инструменты — ниже описано несколько наиболее доступных из них.

Инструкция

Воспользуйтесь, например, устанавливаемой по умолчанию вместе с операционной системой программой-калькулятором. Она открывается выбором пункта «Калькулятор» в папке «Служебные» из подраздела «Стандартные», помещенного в раздел «Все программы». Этот раздел можно найти, открыв щелчком по кнопке «Пуск» главное меню операционной системы. Если вы используете версию Windows 7, то имеете возможность просто ввести слово «Калькулятор» в поле «Найти программы и файлы» главного меню, а затем щелкнуть по соответствующей ссылке в результатах поиска.

Введите значение угла, для которого надо рассчитать тригонометрическую функцию, а потом кликните по соответствующей этой функции кнопке — sin, cos или tan. Если вас интересуют обратные тригонометрические функции (арксинус, арккосинус или калькулятора функции на противоположные.

В более ранних версиях ОС (например, Windows XP) для доступа к тригонометрическим функциям надо раскрыть в меню калькулятора раздел «Вид» и выбрать строку «Инженерный». Кроме того, вместо кнопки Inv в интерфейсе старых версий программы присутствует чекбокс с такой же надписью.

Можно обойтись и без калькулятора, если у вас есть доступ в интернет. В сети много сервисов, которые предлагают по-разному организованные вычислители тригонометрических функций. Один их наиболее удобных вариантов встроен в поисковую систему Nigma. Перейдя на ее главную страницу, просто введите в поле поискового запроса интересующее вас значение — например, «арктангенс 30 градусов». После нажатия кнопки «Найти!» поисковик рассчитает и покажет результат вычисления — 0,482347907101025.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

План урока:

Основные тригонометрические функции

Взаимосвязь между тригонометрическими функциями

Тригонометрические функции стандартных углов

Поиск тангенса на квадратной решетке

Основные тригонометрические функции

Пусть есть некоторый прямоугольный треугольник АBС, у которого∠С = 90°. Обозначим какой-нибудь его острый угол, например, ∠А, греческой буквой α. В треугольнике есть два катета. Тот из них, который, непосредственно является одной из сторон угла α, называют прилежащим катетом. Другой катет именуют противолежащим. Ещё одна сторона треугольника – это гипотенуза, для которой не надо уточнять, прилежащая она или противолежащая относительно острого угла:

Отношения этих трех сторон друг к другу имеют особое наименование.

Для обозначения этих трех величин (их именуют тригонометрическими функциями) используют сокращения sin, cos и tg. При этом после этого сокращения может писаться как обозначение угла греческой буквой, так и обычное обозначение с помощью больших латинских букв:

Задание. Найдите значения тригонометрических функций для∠А в ∆АBС, длины сторон которого указаны на рисунке:

Решение. Просто пользуемся определениями каждой функции:

Задание. Найдите величину тригонометрических функций угла∠В в ∆АBС, показанном на рисунке:

Решение. На первый взгляд кажется, что задание повторяет предыдущее, но это не так. В данном случае нам надо вычислять функции не для∠А, а для ∠В. Для него противолежащим катетом уже будет АС, а прилежащим – ВС. Тогда можно записать, что

Задание. В прямоугольном ∆АBС гипотенуза АB имеет длину 10, а sin∠A = 0,2. Найдите величину ВС.

Решение. Запишем синус как отношение двух сторон:

Задание. В прямоугольном ∆АBС АС = 8, cos∠A = 0,4. Какова длина гипотенузы АB?

Решение. Выразим известный нам косинус как отношение двух отрезков:

Принципиально важно то, что если в двух прямоугольных треугольниках острые углы одинаковы, то и значение их синусов, косинусов и тангенсов также будут одинаковы. Действительно, пусть у ∆АBС и ∆А₁В₁С₁ одинаковы∠А и ∠А₁, а ∠С и ∠С₁ – прямые:

Тогда у них совпадает по два угла, а это означает, что ∆АBС и ∆А₁В₁С₁ подобны. Из этого подобия вытекает пропорция:

Отсюда можно сделать вывод:

Другими словами, значение тригонометрической функции угла зависит только от величины угла (его градусной меры) и НЕ зависит от того, в каком прямоугольном треугольнике этот угол построен. Действительно, с помощью калькулятора или компьютера можно всегда посчитать синус для какого-то угла, если известна его величина в градусах.

Задание. Найдите тангенс угла, изображенного на рисунке:

Решение. Нам надо самостоятельно достроить угол до прямоугольного треугольника. Удобней всего просто построить вертикальную линию, длину которой будет удобно измерить с помощью клеточек. Например, можно сделать такое построение:

Тогда тангенс можно получить, поделив вертикальный отрезок (он здесь оказывается противолежащим катетом) на горизонтальный:

Заметим, что мы могли построить и треугольник с другими размерами, однако во всех случаях величина тангенса будет одной и той же:

Ответ: 0,5

Задание. Постройте такой угол, что его тангенс будет равен 1,5.

Решение. Если тангенс равен 1,5, то это означает, что противолежащий катет в 1,5 раза длиннее прилежащего катета треугольника. В 1,5 раза отличаются, например, числа 2 и 3. Значит, если мы построим треугольник с катетами 2 и 3, то мы получим необходимый нам угол:

Взаимосвязь между тригонометрическими функциями

Оказывается, что одну тригонометрическую функцию угла, например, синус, можно найти и все остальные функции, используя буквально две формулы. Для их вывода снова построим прямоугольный ∆АBС и обозначим его∠А как α:

Запишем для α все 3 тригонометрические функции:

Для вывода второй важной формулы возведем синус и косинус в квадрат, а потом сложим их:

В итоге у нас получилось так называемое основное тригонометрическое тождество:

Задание. Известно, что синус некоторого угла в прямоугольном треугольнике составляет 0,6. Найдите его косинус и тангенс.

Решение. Обозначим этот угол как α. По условию sin α = 0,6. С помощью основного тригонометрического тождества находим косинус:

имеет не одно, а два решения: 0,8 и (– 0,8). Однако понятно, что так как все длины в геометрии – это положительные числа, то и их отношение также должно быть положительным. Поэтому в прямоугольном треугольнике тригонометрические функции могут быть только положительными, и корень (– 0,8) можно отбросить.

Далее находим тангенс:

Задание. Известен косинус острого угла, который равен 7/25. Вычислите синус и тангенс угла.

Решение. Сначала определяем синус угла:

Задание. Известен тангенс острого угла, он составляет 15/8. Найдите синус и косинус угла.

Решение. Данная задача сложнее двух предыдущих, так как две известные нам тригонометрические формулы не позволяют сразу по тангенсу вычислить две другие функции. Сначала используем формулу, в которой тангенс вообще присутствует:

Мы смогли выразить синус через косинус. Теперь можно использовать и вторую формулу:

Теперь можно вычислить и синус:

Заметим важное обстоятельство – так как гипотенуза всегда длиннее катетов, то и синус с косинусом в прямоугольном треугольнике всегда меньше единицы. На тангенс же подобных ограничений нет.

Задание. В прямоугольном ∆АBС гипотенуза АB равна 20, а cos∠A = 0,8. Вычислите длину ВС.

Решение. Если бы нам был дан синус, мы могли бы сразу найти ВС, но нам известен косинус. Здесь можно предложить два алгоритма решения задачи. Первый метод заключается в том, что мы сначала находим синус, пользуясь тригонометрическими формулами:

Второй метод решения задачи заключается в том, что сначала с помощью косинуса найти неизвестный катет АС:

Тригонометрические функции стандартных углов

Итак, мы выяснили, что тригонометрические функции зависят от градусной меры угла. Попытаемся вычислить их для некоторых стандартных значений.

Начнем с угла в 30°. Построим прямоугольный ∆АBС с∠А = 30°:

Ещё из 7-ого класса нам известно, что в таком треугольнике гипотенуза вдвое длиннее, чем катет, лежащий напротив угла в 30°:

Далее можно найти и тангенс 30°:

Вернемся к рассматриваемому нами ∆АBС, в котором∠А = 30°. Ясно, что другой его острый угол, ∠В, будет составлять 90 – 30 = 60°:

Снова используем тот факт, что гипотенуза АB будет длиннее катета ВС в 2 раза:

Ещё один стандартный угол, для которого легко можно рассчитать значение его тригонометрических функций – это 45°. Рассмотрим прямоугольный ∆АBС, в котором один из острых углов составляет 45°. Тогда и другой острый угол должен также составлять 45°, ведь их сумма в прямоугольном треугольнике равна 90°:

Но если в треугольнике 2 угла одинаковы, то он – равнобедренный, то есть катеты АС и ВС равны:

Итак, в результате нам удалось получить 9 стандартных значений, которые можно представить в виде единой таблицы тригонометрических функций:

Задание. Составьте формулу для вычисления площади прямоугольного треугольника, если известен один из его катетов (он равен a) и острый угол, прилегающий к этому катету (он обозначается как α). Далее найдите c помощью формулы площадь треугольника, если а = 5 и α = 45°.

Решение. Как известно, площадь прямоугольного треугольника рассчитывается по формуле:

Задание. В прямоугольном ∆АBС к гипотенузе ВС проведена высота АН. Отрезок НВ имеет длину 16. Известно, что sinα = 0,6. Какова длина СН?

Решение. Сначала, зная sinα, найдем сosα и tgα:

Теперь заметим, что на рисунке угол α – это не только ∠АBС. Действительно, в ∆АBС

Нам известен отрезок АН и tg∠САН, поэтому можно найти СН:

Поиск тангенса на квадратной решетке

Рассмотрим задание, которое часто встречается на экзаменах и вызывает большие затруднения. На рисунке показан угол, требуется высчитать его тангенс:

Ясно, что для нахождения тангенса надо построить какой-нибудь прямоугольный треугольник, однако проблема заключается в том, что обе стороны угла не являются ни горизонтальными, ни вертикальными линиями, а потому провести к ним перпендикуляр у многих не получается. Рассмотрим, как это делается.

Посмотрим на нижнюю линию. Она представляет собой поднимающуюся прямую, причем на каждые 2 клеточки, которые эта прямая проходит вправо, приходится подъем на 1 клеточку вверх.

Оказывается, что для построения перпендикуляра к ней необходимо от какой-нибудь ее точки вести наклонную прямую, у которой, наоборот, на каждые две клеточки подъема будет приходиться 1 клетка движения вбок, причем не вправо, а влево:

Теперь, чтобы найти тангенс, надо просто поделить длину красного отрезка (он здесь оказывается противолежащим катетом) на длину зеленого отрезка. Несложно заметить, что эти отрезки одинаковы, так как являются гипотенузами в двух равных прямоугольных ∆АBС и ∆CDF:

Естественно, что отношение одинаковых отрезков равно единице, поэтому и тангенс также равен единице. Заметим, что прямой угол можно было получить, проведя перпендикуляр к нижней линии в другой точке:

Более того, перпендикуляр можно провести и к верхней стороне угла. Она представляет собой линию, которая поднимается вправо, и на каждые три клетки движения вверх приходится одна клетка смещения вправо:

Соответственно, чтобы построить к ней перпендикуляр, надо от одной из ее точек начать двигаться вправо и вниз, причем на 3 клетки движения вбок будет приходиться только 1 клетка движения вниз:

Во всех этих случаях зеленые и красные отрезки одинаковы, а потому тангенс равен единице.

Объясним, почему для построения перпендикуляра надо использовать именно такой метод. Пусть на квадратной решетке начерчена прямая АС, к которой надо провести перпендикуляр. Построив горизонтальную (показана зеленым цветом) линию АB и вертикальную (показана красным) линию ВС, мы достоим ее до прямоугольного ∆АBС. Далее отложим от точки С уже вертикально отрезок CD, равный АB, а далее от D – горизонтальный отрезок, равный ВС:

Обозначим∠А как α, тогда ∠АСВ будет составлять 90° – α. Заметим, что ∆АBС и ∆СDF – равные, так как они прямоугольные и у них одинаковы катеты:

Теперь обратим внимание на три угла, вершины которых лежат в точке С. Это ∠АСВ, ∠FCD и ∠АСF. Они вместе образуют развернутый угол ВСD, то есть их сумма составляет 180°. Но ∠АСВ и ∠FCD мы уже выразили через величину α. Тогда можно вычислить и третий угол ∠АСF:

Получили, что отрезки АС и СF действительно перпендикулярны.

Задание. Найдите тангенс угла, показанного на рисунке:

Решение. Если попытаться провести прямую, перпендикулярную нижней стороне угла, то в результате этот перпендикуляр просто не пересечется со второй стороной:

Поэтому перпендикуляр следует проводить к верхней стороне:

Теперь осталось найти отношение длин красного (здесь это противолежащий катет) зеленого отрезка. Конечно, и длины можно найти по теореме Пифагора, однако есть и более простой метод. Возьмем в качестве единичного отрезок, который получается, если на квадратной решетке сделать два шага вбок и один вверх. Этот отрезок будет укладываться на красном катете ровно 3 раза, а на зеленом – ровно 2 раза, то есть прилежащий катет равен трем единичным отрезкам, а противолежащий – двум. Тогда их отношение составляет 3/2 = 1,5

Ответ: 1,5

Источник