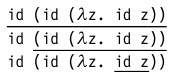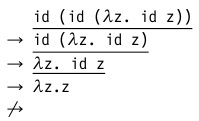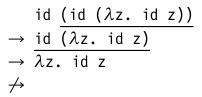Как найти значения лямбда

λ-исчисление. Часть первая: история и теория

Идею, короткий план и ссылки на основные источники для этой статьи мне подал хабраюзер z6Dabrata, за что ему огромнейшее спасибо.

UPD: в текст внесены некоторые изменения с целью сделать его более понятным. Смысловая составляющая осталась прежней.

Вступление

Возможно, у этой системы найдутся приложения не только
в роли логического исчисления. (Алонзо Чёрч, 1932)

Вообще говоря, лямбда-исчисление не относится к предметам, которые «должен знать каждый уважающий себя программист». Это такая теоретическая штука, изучение которой необходимо, когда вы собираетесь заняться исследованием систем типов или хотите создать свой функциональный язык программирования. Тем не менее, если у вас есть желание разобраться в том, что лежит в основе Haskell, ML и им подобных, «сдвинуть точку сборки» на написание кода или просто расширить свой кругозор, то прошу под кат.

Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.

Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…

λ-исчисление: основные понятия

Синтаксис

В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции,

только хардкор

. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.

Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.

Термы:

переменная:	x
лямбда-абстракция (анонимная функция):	λx.t, где x — аргумент функции, t — её тело.
применение функции (аппликация):	f x, где f — функция, x — подставляемое в неё значение аргумента

Соглашения о приоритете операций:

Может показаться, будто нам нужны какие-то специальные механизмы для функций с несколькими аргументами, но на самом деле это не так. Действительно, в мире чистого лямбда-исчисления возвращаемое функцией значение тоже может быть функцией. Следовательно, мы можем применить первоначальную функцию только к одному её аргументу, «заморозив» прочие. В результате получим новую функцию от «хвоста» аргументов, к которой применим предыдущее рассуждение. Такая операция называется каррированием (в честь того самого Хаскелла Карри). Выглядеть это будет примерно так:

f = λx.λy.t	Функция с двумя аргументами x и y и телом t
f v w	Подставляем в f значения v и w
(f v) w	Эта запись аналогична предыдущей, но скобки явно указывают на последовательность подстановки
((λy.[x → v]t) w)	Подставили v вместо x. [x → v]t означает «тело t, в котором все вхождения x заменены на v»
[y → w][x → v]t	Подставили w вместо y. Преобразование закончено.

И напоследок несколько слов об области видимости. Переменная x называется связанной, если она находится в теле t λ-абстракции λx.t. Если же x не связана какой-либо вышележащей абстракцией, то её называют свободной. Например, вхождения x в x y и λy.x y свободны, а вхождения x в λx.x и λz.λx.λy.x(y z) связаны. В (λx.x)x первое вхождение x связано, а второе свободно. Если все переменные в терме связаны, то его называют замкнутым, или комбинатором. Мы с вами будем использовать следующий простейший комбинатор (функцию тождества): id = λx.x. Она не выполняет никаких действий, а просто возвращает без изменений свой аргумент.

Процесс вычисления

Рассмотрим следующий терм-применение:

(λx.t) y

Его левая часть — (λx.t) — это функция с одним аргументом x и телом t. Каждый шаг вычисления будет заключаться в замене всех вхождений переменной x внутри t на y. Терм-применение такого вида носит имя редекса (от reducible expression, redex — «сокращаемое выражение»), а операция переписывания редекса в соответствии с указанным правилом называется бета-редукцией.

Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:

(λx.x) ((λx.x) (λz. (λx.x) z)),

который для простоты можно переписать как

id (id (λz. id z))

(напомним, что id — это функция тождества вида λx.x)

В этом терме содержится три редекса:

1. Полная β-редукция. В этом случае каждый раз редекс внутри вычисляемого терма выбирается произвольным образом. Т.е. наш пример может быть вычислен от внутреннего редекса к внешнему:
   
2. Нормальный порядок вычислений. Первым всегда сокращается самый левый, самый внешний редекс.
   
3. Вызов по имени. Порядок вычислений в этой стратегии аналогичен предыдущей, но к нему добавляется запрет на проведение сокращений внутри абстракции. Т.е. в нашем примере мы останавливаемся на предпоследнем шаге:
   
   Оптимизированная версия такой стратегии (вызов по необходимости) используется Haskell. Это так называемые «ленивые» вычисления.
4. Вызов по значению. Здесь сокращение начинается с самого левого (внешнего) редекса, у которого в правой части стоит значение — замкнутый терм, который нельзя вычислить далее.
   
   Для чистого лямбда-исчисления таким термом будет λ-абстракция (функция), а в более богатых исчислениях это могут быть константы, строки, списки и т.п. Данная стратегия используется в большинстве языков программирования, когда сначала вычисляются все аргументы, а затем все вместе подставляются в функцию.

Если в терме больше нет редексов, то говорят, что он вычислен, или находится в нормальной форме. Не каждый терм имеет нормальную форму, например (λx.xx)(λx.xx) на каждом шаге вычисления будет порождать самоё себя (здесь первая скобка — анонимная функция, вторая — подставляемое в неё на место x значение).

Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение

(λx.λy. x) z ((λx.x x)(λx.x x))

Этот терм имеет нормальную форму z несмотря на то, что его второй аргумент такой формой не обладает. На её-то вычислении и зависнет стратегия вызова по значению, в то время как стратегия вызова по имени начнёт с самого внешнего терма и там определит, что второй аргумент не нужен в принципе. Вывод: если у редекса есть нормальная форма, то «ленивая» стратегия её обязательно найдёт.

Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y. Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y, а z — первоначальный терм имел бы вид(λx.λz.x)y и после редукции выглядел бы как λz.y. Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.

Так же бывает, что у нас есть абстракция λx.t x, причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t. Такое преобразование называется η-конверсией.

На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Список источников

1. «What is Lambda Calculus and should you care?», Erkki Lindpere
2. «Types and Programming Languages», Benjamin Pierce
3. Вики-конспект «Лямбда-исчисление»
4. «Учебник по Haskell», Антон Холомьёв
5. Лекции по функциональному программированию

Лямбда-исчисление (англ. lambda calculus) — формальная система, придуманная в 1930-х годах
Алонзо Чёрчем. Лямбда-функция является, по сути, анонимной функцией.
Эта концепция показала себя удобной и сейчас активно используется во многих
языках программирования.

Лямбда-исчисление

Определение:

Лямбда-выражением (англ. -term) называется выражение, удовлетворяющее следующей грамматике: где — множество всех строк над фиксированным алфавитом .

Пробел во втором правиле является терминалом грамматики. Иногда его обозначают как @, чтобы он не сливался с другими символами в выражении.

В первом случае функция является просто переменной.
Во втором происходит аппликация (применение) одной функции к другой.
Это аналогично вычислению функции-левого операнда на аргументе-правом операнде.
В третьем — абстракция по переменной. В данном случае происходит
создание функции одного аргумента с заданными именем аргумента и телом функции.

Рассмотрим, например, -терм . Эта функция принимает аргумент и
возвращает его неизменённым. Например,
. Аналогично, .

Еще примеры:

Иногда -термы пишут по другому. Для краткости подряд идущие лямбды заменяют на одну. Например:

Приоритет операций

• Аппликация:
• Абстракция забирает себе всё, до чего дотянется:
• Скобки играют привычную роль группировки действий

Свободные и связанные переменные

Связанными переменными называются все переменные, по которым выше в
дереве разбора были абстракции. Все остальные переменные называются свободными.

Например, в , и связана, а — свободна. А в
в своём первом вхождении переменная свободна, а во втором — связана.

Связанные переменные — это аргументы функции. То есть для функции они являются локальными.

Рассмотрим функции и . В первой из них при взгляде на
понятно, что она имеет отношение к переменной, по которой производилась
абстракция. Если по одной и той же
переменной абстракция производилась более одного раза, то переменная связана
с самым поздним (самым нижним в дереве разбора) абстрагированием. Например, в
, переменная связана с самой правой абстракцией
по .

α-эквивалентность

Определение:

-эквивалентностью (англ. -equivalence) — называется наименьшее соотношение эквивалентности на такое что: для любого если и замкнуто относительно следующих правил:

Функции и являются -эквивалентными,
а и — нет.

β-редукция

Определение:

-редукция (англ. -reduction) — это наименьшее соотношение на такое что и замкнуто относительно следующих правил

Определение:

Через обозначают сведение к с помощью одной -редукции. А через — за ноль или более.

В -редукции вполне возможна функция вида . Во время подстановки вместо внутренняя переменная не заменяется — действует принцип локальной переменной. Но принято считать, что таких ситуаций не возникает и все переменные называются разными именами.

Каррирование

Определение:

Каррирование (англ. carrying) — преобразование функции от многих переменных в функцию, берущую свои аргументы по одному. Для функции типа оператор каррирования выполняет преобразование . Таким образом берет аргумент типа и возвращает функцию типа . С интуитивной точки зрения, каррирование функции позволяет фиксировать ее некоторый аргумент, возвращая функцию от остальных аргументов. Таким образом, представляет собой функцию типа .

Нотация Де Брауна

Существует также альтернативное эквивалентное определение -исчисления.
В оригинальном определении для обозначения переменных использовались имена,
и была проблема с тем, что не были запрещены одинаковые имена в разных
абстракциях.

От этой проблемы можно избавиться следующим образом. Вместо имени переменной
будет храниться натуральное число — количество абстракций в дереве разбора,
на которое нужно подняться, чтобы найти ту лямбду, с которой данная переменная
связана. В данной нотации получаются несколько более простые определения
свободных переменных и -редукции.

Грамматику нотации можно задать как:

Примеры выражений в этой нотации:

Standart	de Bruijn
$lambda x.x$	$lambda .0$
$lambda z.z$	$lambda .0$
$lambda x. lambda y.x$	$lambda . lambda .1$
$lambda x. lambda y. lambda s. lambda z.x s (y s z)$	$lambda . lambda . lambda . lambda .3 1(2 1 0)$
$(lambda x.x x)(lambda x.x x)$	$(lambda .0 0)(lambda .0 0)$
$(lambda x. lambda x.x)(lambda y.y)$	$(lambda .lambda .0)(lambda .0)$

Переменная называется свободной, если ей соответствует число, которое больше
количества абстракций на пути до неё в дереве разбора.

При -редукции же нужно будет ко всем свободным переменным заменяющего
дерева при каждой замене прибавить число, равное разницы уровней раньше и сейчас.
Это будет соответствовать тому, что эта переменная продолжит «держаться» за
ту же лямбду, что и раньше.

Нумералы Чёрча и программирование на -исчислении

Определение

Введём на основе лямбда-исчисления аналог натуральных чисел, основанный на идее,
что натуральное число — это или ноль, или увеличенное на единицу натуральное
число.

Каждое число будет функцией двух аргументов: какой-то функции и начального значения.
Число будет раз применять функцию к начальному значению и возвращать
результат. Если такому «числу» дать на вход функцию и в качестве
начального значения, то на выходе как раз будет ожидаемое от функции число:
.

+1

Функция, прибавляющая к числу, должна принимать первым аргументом число.
Но число — функция двух аргументов. Значит, эта функция должна принимать три
аргумента: «число» , которое хочется увеличить, функция, которую надо будет
раз применить, и начальное значение.

Здесь — раз применённая к функция . Но нужно применить
раз. Отсюда .

Сложение

Сложение двух чисел похоже на прибавление единицы. Но только надо прибавить не единицу, а второе число.

раз применить к применённому раз к

Умножение

Умножение похоже на сложение, но прибавлять надо не единицу, а второе число.
Или, в терминах нумералов Чёрча, в качестве применяемой несколько раз
функции должна быть не , а функция, применяющая раз .

Здесь — функция, которая раз применит к тому, что дадут ей на
вход. С помощью -редукции можно немного сократить эту формулу

Возведение в степень

It’s a kind of magic

Логические значения

Функции двух аргументов, возвращающие первый и второй, соответственное, аргументы.
Забавный факт: . Эти функции сделаны такими для того,
чтобы красиво написать функцию :

Если ей в качестве первого аргумента дадут , то вернётся , иначе — .

Стандартные функции булевой логики:

Ещё одной важной функцией является функция проверки, является ли число нулём:

Функция выглядит несколько странно. — функция, которая независимо
от того, что ей дали на вход, возвращает . Тогда, если в качестве
будет дан ноль, то функция, по определению нуля, не выполнится ни разу, и будет
возвращено значение по умолчанию . Иначе же функция будет запущено, и
вернётся .

Пара

Функция принимает два значения и запаковывает их в пару так, чтобы к ним можно было обращаться по и . В и вместо в будет подставлено или , возвращающие, соответственно, первый и второй аргументы, то есть или , соответственно.

Вычитание

В отличие от всех предыдущих функций, вычитание для натуральных чисел определено только в случае, если уменьшаемое больше вычитаемого. Положим в противном случае результат равным нулю. Пусть уже есть функция, которая вычитает из числа единицу. Тогда на её основе легко сделать, собственно, вычитание.

Это то же самое, что раз вычесть единицу из .

Осталось, собственно, функция для вычитания единицы. Однако, это не так просто, как может показаться на первый взгляд. Проблема в том, что, имея функцию, которую нужно применить для того, чтобы продвинуться вперёд, продвинуться назад будет проблематично. Если попробовать воспользоваться идеей о том, чтобы, начав от нуля, идти вперёд, и пройти на один шаг меньше, то будет не очень понятно, как же остановиться ровно за один шаг до конца. Для реализации вычитания единицы сделаем следующее. раз выполним следующее: имея пару построим пару . Тогда после шагов во втором элементе пары будет записано число , которое и хочется получить.

Если вы ничего не поняли, не огорчайтесь. Вычитание придумал Клини, когда ему вырывали зуб мудрости. А сейчас наркоз уже не тот.

Сравнение

Так как вычитание определено таким способом, чтобы для случая, в котором уменьшаемое больше, чем вычитаемое, возвращать ноль, можно определить сравнение на больше-меньше через него. Равными же числа и считаются, если .

Комбинатор неподвижной точки

Попробуем выразить в лямбда-исчислении какую-нибудь функцию, использующую рекурсию. Например, факториал.

Мы столкнулись с проблемой. В определении функции используется функция . При формальной замене, получим бесконечную функцию. Можно попытаться решить эту проблему следующим образом

Определение:

Неподвижной точкой лямбда-функции назовём такую функцию , что .

Лямбда исчисление обладаем замечательным свойством: у каждой функции есть неподвижная точка!

Рассмотрим следующую функцию.

Заметим, что .
Или, что то же самое,

Рассмотрим функцию

Как было показано выше, , то есть, , где — искомая функция, считающая факториал.

Это даст функцию, которая посчитает факториал числа. Но делать она это будет мееедленно-меееедленно. Для того, чтобы посчитать потребовалось сделать 66066 -редукций.

Наиболее известным комбинатором неподвижной точки является -комбинатор, введенный известным американским ученым Хаскеллом Карри как

Деление

Воспользовавшись идеей о том, что можно делать рекурсивные функции, сделаем функцию, которая будет искать частное двух чисел.

И остатка от деления

Проверка на простоту

— принимает число, которое требуется проверить на простоту и то, на что его надо опытаться поделить, перебирая это от до . Если на что-нибудь разделилось, то число — составное, иначе — простое.

Следующее простое число. — следующее, больше либо равное заданного, — следующее, большее заданного.

пропрыгает простых чисел вперёд. принимает число и пропрыгивает столько простых чисел вперёд, начиная с двойки.

…и всего через 314007 -редукций вы узнаете, что третье простое число — семь!

Списки

Для работы со списками чисел нам понадобятся следующие функции:

• — возвращает пустой список
• — принимает первый элемент и оставшийся список, склеивает их
• — вернуть голову списка
• — вернуть хвост списка

Список будем хранить в следующем виде: . При этом, голова списка будет храниться как показатель степени при .

Выводы

На основе этого всего уже можно реализовать эмулятор машины тьюринга: с помощью пар, списков чисел можно хранить состояния. С помощью рекурсии можно обрабатывать переходы. Входная строка будет даваться, например, закодированной аналогично списку: пара из длины и числа, характеризующего список степенями простых. Я бы продолжил это писать, но уже на операции я не дождался окончания выполнения. Скорость лямбда-исчисления как вычислителя печальна.

Примеры (слабонервным не смотреть)

fact

head

tail

См. также

• Неразрешимость задачи вывода типов в языке с зависимыми типами

Источники информации

• Lectures on the Curry Howard — Isomorphism
• Д. Штукенберг. Лекции
• Английская Википедия
• Русская Википедия
• Игра про крокодилов

Лямбда-исчисление (Часть I)

---

Содержание

• Обзор
• Простой пример
• Синтаксис лямбда-исчислений
  • Тест для самопроверки #1
  • Тест для самопроверки #2
• Проблемы с простым правилом переписывания
• Бета-редукция
• Нормальная форма
  • Нормальный и аппликативный порядок редукции
    • Тест для самопроверки #3
    • Тест для самопроверки #4
• Теорема Чёрча-Россера
  • Доказательство следствия 1
  • Доказательство следствия 2
  • Доказательство теоремы Чёрча-Россера
    • 3 задания
    • Задание 1
    • Задание 2
    • Задание 3
      • Тест для самопроверки #5
    • Окончательное доказательство

Обзор

Лямбда-исчисление — это модель вычислений, открытая Чёрчем в начале 1930-х. Лямбда-исчисление и машина Тьюринга
эквивалентны в том плане, что функция, определенная с помощью одной из этих систем, может быть выражена с помощью
другой.

Вот некоторые пункты сравнения:

Лямбда-исчисление	Машина Тьюринга
Создает основу для функциональных ЯП (LISP, Scheme, ML).	Создает основу для императивных ЯП (Pascal, ADA, C).
Мы пишем лямбда-выражение для каждой функции. Ввод и вывод также лямбда-выражение.	Создается новая машина для вычисления каждой функции. Ввод и вывод записан на ленту

Простой пример

Вот простой пример лямбда-выражения, которое определяет функцию «увеличить на единицу»:

λx.x+1

(Заметим, что это выражение не служит примером чистых лямбда-выражений, потому что использует оператор +, который
не является частью чистых лямбда-выражений; тем не менее, этот пример проще понять, чем пример с чистыми
лямбда-выражениями.)

В этом примере определяется функция одного аргумента, который обозначен ‘x’. Телом функции является «x+1». Заметим,
что функция не имеет имени (иначе говоря, это анонимная функция). Что бы вычислить эту функцию необходимо передать ей
аргумент, например:

(λx.x+1)3

В этом примере λx.x+1 является функцией, а 3 её аргументом; а всё в целом представляет собой лямбда-выражение.

Вычисление подразумевает перезаписывание:

(λx.x+1)3 ⇒ 3+1 ⇒ 4

Пока что под перезаписью можете понимать замену внутри функции всех вхождений параметра ‘x’ на аргумент (а затем, для
не чистых лямбда-выражений, которые включают операторы наподобие сложения, применение этих операторов). Более точное
определение будет приведено далее.

Синтаксис лямбда-исчислений

Синтаксис (чистых) лямбда-исчислений может быть определен следующим образом:

1. Переменные являются лямбда-выражениями (обозначаются одной буквой в нижнем регистре).
2. Если M и N являются лямбда-выражениями, то возможны записи вида:
3. (M)
4. λid.M
5. MN

Вот и все!

Правило 2.1 гласит, что мы можем добавлять скобки к выражениям. Правило 2.2 дает определение абстракции: функция с
формальным параметром id и телом M. Правило 2.3 задаёт аппликацию: применение или вызов одного
лямбда-выражения к другому (M применяется к N).

Заметим, что чистые лямбда-исчисление исключают константы, типы и примитивные операторы (+, *, …). Также заметим, что
по соглашению аппликация является лево ассоциативной: ABC означает (AB)C а не A(BC). Аппликация имеет приоритет выше,
чем абстракция: λx.AB означает λx.(AB) а не (λx.A)B

Правила выше определяют язык лямбда-выражений, который можно выразить используя контекстно-свободную грамматику:

exp	→	ID
	|	( exp )
	|	λ ID . exp	// абстракция
	|	exp exp	// аппликация

Как уже говорилось выше, при вычислении лямбда-выражений используется перезаписывание; для каждой аппликации в теле
функции заменяются все вхождения формального параметра (переменной) на значение фактического параметра
(лямбда-выражение).

Будет проще понять, если для лямбда-выражений вместо текста мы будем использовать дерево с абстрактным синтаксисом. Вот
простой пример, приведенный выше:

(λx.x+1)3

И дерево с абстрактным синтаксисом (где λ это абстракция, а apply — аппликация):

        apply
        /   
       λ     3
      / 
     x   +
        / 
       x   1

Для перезаписи дерева с абстрактным синтаксисом мы ищем аппликации функции к аргументам и для каждой из них заменяем
формальный параметр аргументом в теле функции. Чтобы это сделать мы должны найти узел apply у которого левая часть
является лямбда-узлом, так как только лямбда-узлы представляют функции.

1. Правое поддерево узла apply является аргументом.
2. Левое поддерево узла apply (с лямбда-выражением в корневом узле) является функцией.
3. Левый лист лямбда-выражения — это формальный параметр.
4. Правый лист лямбда-выражения — это тело функции.

В нашем примере только один узел apply; аргумент 3, функция λx.x+1; формальный параметр x, тело функции x+1.
Приведем переписывание:

        apply      =>      +
        /                / 
       λ     3           3   1
      / 
     x   +
        / 
       x   1

А вот пример с двумя аппликациями:

(λx.x+1)((λy.y+2)3)

Первое лямбда-выражение определяет функцию «увеличить на единицу». Аргументом этой функции является аппликация, которая
применяет функцию «увеличить на 2» к значению 3. Построим дерево с абстрактным синтаксисом и один из способов перезаписи
(отдавая приоритет самой правой аппликации):

        apply         =>   apply     =>  apply   =>  +  =>  6
       /                  /            /         / 
      λ       apply       λ     +       λ     5    5   1
     /        /        /    /      / 
    x   +     λ    3    x   + 3   2   x   +
       /    /            /            / 
      x   1 y   +         x   1         x   1
               / 
              y   2

В целом, различные стратегии порядка выбора аппликаций для перезаписи приводят к различным последствиям. Проблема будет
пояснена далее.

---

Тест для самопроверки #1

Сделайте переписывание ещё раз, при этом выберите другую аппликацию первой.

Ответ

---

Заметим, что результат переписывания не чистого лямбда-выражения может являться константой (как в примере выше), но
результат может быть также лямбда-выражением: переменной, абстракцией или аппликацией.
Для чистых лямбда-выражений результат переписывания всегда будет лямбда-выражением.

1. (λf.λx.fx)λy.y+1

   Первое лямбда-выражение определяет функцию, аргумент f которой также является функцией, а тело λx.fx
   является другой функцией (которая принимает аргумент x и вызывает с ним f). Ниже приведены дерево с абстрактным
   синтаксисом и переписывание; возможно вы захотите попробовать нарисовать их сами.

        apply      =>   λ        =>    λ        λx.x+1
       /              /             / 
      λ       λ       x  apply       x   +    
     /      /          /             / 
    f   λ   y   +       λ     x        x   1
       /      /      / 
      x  apply y  1   y   +
         /              / 
        f    x          y   1
    

   Обратите внимание, что результатом переписывания является функция. Также заметим, хотя в этом примере и используются
   2 узла «apply», только один из них имеет лямбда-узел, поэтому переписывание может быть начато только одним способом.

2. (λx.λy.x)(λz.z)

   В этом примере первая лямбда принимает один аргумент x, и возвращает функцию, которая игнорирует свой собственный
   аргумент (y), просто возвращая x. В данном случае значение передаваемое как x является функцией.

               apply            λ         λy.λz.z
              /               / 
             λ       λ    =>  y   λ
            /      /           / 
           x   λ   z   z        z   z
              / 
             y   x
    

---

Тест для самопроверки #2

Нарисуйте дерево с абстрактным синтаксисом и выполните переписывание для лямбда-выражения:

(λx.λy.xy)(λz.z)

Ответ

---

Проблемы с простым правилом переписывания

Вспомним, что неточное определение переписывания аппликации (λx.M)N означает «M с заменой на N всех
вхождений x. Однако, с этим определением две проблемы:

Проблема #1: В действительности, мы не хотим заменять все вхождения x. Что бы понять почему, посмотрим на
следующее не чистое лямбда-выражение:

(λx.(x + ((λx.x+1)3)))2

Выражение можно сократить до 6; внутреннее выражение:

(λx.x+1)3

принимает один аргумент 3, прибавляет 1, итого 4. Внешнее выражение

(λx.(x + 4))2

принимает один один аргумент, значение 2, прибавляет 4, итого 6.

Однако, если мы в первую очередь произведём замену во внешней аппликации используя простое правило переписывния, то
получим следующий результат:

      apply
       /
      λ  2
     / 
    x   +                     +
       /                    / 
      x  apply     =>       2  apply     =>  +    => 5
          /     (неверная      /          / 
         λ   3   аппликация)   λ   3       2   +
        /                    /              / 
       x   +                 x   +           2   1
          /                    / 
         x   1                 2   1

Получен неверный результат (5 вместо 6), потому что мы заменили все вхождения x во внутреннем выражении значением,
переданным как параметр для внешнего выражения.

Проблема #2: Рассмотрим чистое лямбда-выражение

((λx.λy.x)y)z

Это выражение похоже на предыдущее, но в этот раз при применяем λx.λy.x к двум аргументам (y и z)
вместо одного аргумента (λz.z). При вызове с двумя аргументами выражение λx.λy.x должно вернуть
свой первый аргумент, в данном случае результатом переписывания должен быть y. Однако, если мы будем использовать
простое правило переписывания и заменим все вхождения формального параметра x на y, то получим:

(λy.y)z

и после переписывания этого выражения получаем

z

т.е. был получен второй аргумент вместо первого! Данный пример иллюстрирует проблему конфликта имен.

Что бы понять как исправть эту проблему необходимо разобраться с областью видимости, включающую в себя следующие
понятия:

• Связанная переменная: переменная, которая связана с некоторой лямбдой.
• Свободная переменная: переменная, которая не связана ни с одной лямбдой.

Интуитивно понятно, что в лямбда-выражении M переменная x является связанной, если в дереве с абстрактным
синтаксисом x встречается в поддереве лямбды, у которой левой ветвью является x:

                λ
               / 
              x  /
                /  
               /    
              /..x...
                 |
                 здесь x связан

Приведем точное определение свободных и связанных переменных:

• В выражении «x» переменная x свободная (нет связанных переменных).
• В выражении «λx.M» каждый x в M связанный, каждая свободная в M является свободной и в λx.M;
  любая связанная в M переменная также является связанной в λx.M.
• В выражении MN
  • Свободные в MN переменные являются объединением двух множеств: свободных в M и свободных в N переменных.
  • Связанные в MN переменные также являются объединением двух множеств: связанных в M и связанных в N переменных.

Заметим, что переменная может встречаться несколько раз в одном лямбда-выражении; некоторые её вхождения могут быть
свободными, а некоторые связанными. Таким образом, переменная является одновременно и свободной и связанной, но
каждое вхождение либо связанной, либо свободной (но не вместе). Например, в следующем лямбда-выражении свободными
переменными являются {y,x}, а связанными {y}:

            (λx.y)(λy.yx)
                |     ||
                |     |свободная
            свободная |
                    связанная

Для того, что бы решить проблему #1 в данном лямбда-выражении

(λx.M)N

вместо замены всех вхождений x в M и N мы заменим все свободные вхождения в M с N. Пример:

                       +----- M ---------+
                       |                 |
                   (λx. x + ((λx.x + 1)3)) 2
                        |        |
                        |        |
                   свободный   связанный
                      в M        в M

                     => 2 + ((λx.x + 1)3)

С проблемой #2 дело в том, что переменная y, которая была свободным аргументом в исходном лямбда-выражении, становится
связанной после переписывания (использования аргумента для замены всех вхождений формального параметра), потому, что она
попадает в контекст лямбды, у которой, так уж случилось, аргумент тоже назван y:

    ((λx.λy.x)y)z
              |
              |
       свободная, но станет связанной после аппликации

Для решения проблемы #2 мы воспользуемся преобразованием под названием альфа-редукция. Идея в том, что названия
формальных параметров не важны; поэтому переименуем их таким образом, что бы избежать конфликта. Альфа-редукция
используется для преобразования выражений вида λx.M. Оно переименовывает все вхождения x, которые являются
свободными в M в некоторую другую переменную z, которая не встречается в M (т.е. λx становится
λz). Переменная z отсутствует в M, поэтому мы можем переименовать x в z; т.е.

λx.λy.x+y альфа-редукция => λz.λy.z+y

Приведем псевдокод для альфа-редукции.

alphaReduce(M: lambda-expression,
            x: id,
            z: id) {

  // предварительное условие: z не встречается в M
  // постусловие: вернуть M с заменой всех свободных вхождений x на z

  case M of {

    VAR(x): return VAR(z)

    VAR(y): return VAR(y)

    APPLY(e1, e2): return APPLY(alphaReduce(e1, x, z), alphaReduce(e2, x, z))

    LAMBDA(x,e): return LAMBDA(x,e)

    LAMBDA(y,e): return LAMBDA(y, alphaReduce(e, x, z))
  }
}

Замечание: другой способ для решения проблемы #2 это использование так называемой нотации де Брауна, которая
использует целые числа вместо обозначений. Её изучение будет домашним заданием.

Бета-редукция

Наконец-то мы готовы дать точное определение переписыванию:

• оно называется бета-редукцией или бета-упрощением;
• оно определяется при помощи подстановки (которая в свою очередь использует альфа-редукцию).

Для бета-редукции используется следующая нотация:

(λx.M)N →_β M[N/x]

Левая часть ((λx.M)N) называется редекс (redex), а правая (M[N/x]) называется контрактус
(contractum). Нотация обозначает M с заменеными свободными вхождениями x на N без конфликта имен. Мы говорим, что
(λx.M)N упрощается до M с подстановкой N в x. Далее приведен псевдокод для замены.

substitute(M: lambda-expression,
           x: id,
           N: lambda-expression) {

  // когда замена вызвана в первый раз M является телом функции в виде λx.M

  case M of {
    VAR(x): return N

    VAR(y): return M

    LAMBDA(x,e): return M // в том случае, если отсутствуют свободные вхождения
                          // x в M, т.е. нечего заменять;
                          // заметим, что это решает проблему #1

    LAMBDA(y,e):
       if (y не является свободной в N)
       then return LAMBDA(y,substitute(e,x,N)) // замена x на N в теле
                                               // лямбда-выражения
       else { // y имеет свободные вхождения в N; здесь решается проблема #2
          let y' идентификатор, не являющийся не x и не y, и 
                 не входящий не в N, не в e;
          let e' = alphaReduce(e,y,y');
          return LAMBDA(y',substitute(e',x,N))
       }

    APPLY(e1,e2): return APPLY(substitute(e1,x,N), substitute(e2,x,N))
  }
}

Что бы проиллюстрировать работу бета-редукции, рассмотрим предыдущий пример проблемы #2. Далее приведены шаги
бета-редукции:

        ((λx.λy.x)y)z
                ->  ((λy.x)[y/x])z   // заменяем x на y в теле "λy.x"
                ->  ((λy'.x)[y/x])z  // после альфа-редукции
                ->  (λy'.y)z         // первая бета-редукция завершена!
                ->  y[z/y']          // замена y' на z в "y"
                ->  y                // вторая бета-редукция завершена!

Обратим внимание, что термин «бета-упрощение» не совсем верно, поскольку применение бета-редукции не всегда дает
меньшее лямбда-выражение. По факту, бета-редукция:

• уменьшает
• увеличивает
• не изменяет

длину лямбда-выражения. Далее будут приведены примеры. В первом случае результатом бета-редукции является исходное
выражение (т.е. длина не изменилась); во-втором примере лямбда-выражение становится длинее; а в-третьем примере
сначало выражение становится длинее, а затем короче.

• (λx.xx)(λx.xx) → (λx.xx)(λx.xx)
• (λx.xxx)(λx.xxx) → (λx.xxx)(λx.xxx)(λx.xxx) → (λx.xxx)(λx.xxx)(λx.xxx)(λx.xxx)
• (λx.xx)(λa.λb.bbb) → (λa.λb.bbb)(λa.λb.bbb) → λb.bbb

Нормальная форма

Как мы уже обсуждали ранее, вычисление лямбда-выражений влечет в себе их переписывание применяя бета-редукцию. Помиимо
этого, существует ещё одна операция под названием бета-расширение, которую мы так же можем использовать. По
определению, лямбда-выражение e1 бета-расширяется в e2, если e2 бета-упрощается до e1. Например, выражение

xy

beta-expands to each of the following:

    (λa.a)xy
    (λa.xy)(λz.z)
    (λa.ay)x

Вычисления останавливаются, когда уже больше нет редексов (не осталось аппликаций функций и аргументов). Мы говорим, что
лямбда-выражение без редексов находится в нормальной форме. Также, лямбда-выражение имеет нормальную форму, если
существует последовательность бета-редукций и/или бета-расширений, которые приводят к нормальной форме.

Отсюда мы получаем несколько интересных вопросов о нормальной форме:

1. В: Правда, что каждое лямбда-выражение имеет нормальную форму?

   О: Нет, например (λz.zz)(λz.zz). Заметим, что это и не должно быть удивительным, поскольку так как
   лямбда-выражения эквивалентны Машине Тьюринга, а мы знаем, что Машина Тьюринга может не суметь остановиться
   (например, программа может попасть в вечный цикл или бесконечную рекурсию).

2. В: Если лямбда-выражение имеет нормальную форму, можем ли мы перейти к ней используя только бета-редукцию, или нам
   понадобится использовать бета-расширения?

   О: Должно хватить бета-редукций (это одно из следствий теоремы Чёрча-Россера, уже не за горами!)

3. В: Если лямбда-выражение имеет нормальную форму, при любой ли последовательности редукций мы к ней придем?

   О: Нет. Рассмотрим следующее лямбда-выражение:

   (λx.λy.y)((λz.zz)(λz.zz))

   Это лямбда-выражение содержет два редекса: первый это всё выражение целиком (аппликация (λx.λy.y) к
   его аргументу); второе — это аргумент: ((λz.zz)(λz.zz)). Второй редекс как раз является примером
   лямбда-выражения без нормальной формы — каждый раз применяя к нему бета-редукцию мы получаем то же самое выражение.
   Очевидно, что если мы будем выбирать этот редекс для упрощения, то мы никогда не найдём нормальную форму для всего
   выражения. Хотя, если мы упростим первый редекс, мы получим λy.y, что и является нормальной формой.
   Следовательно, последовательность наших упрощений может определить, получим мы нормальную форму или нет.

4. В: Существует ли стратегия для выбора бета-редукций, которая точно позволит придти к нормальной форме, если, конечно,
   такая существует?

   О: Да! Она называется редукция нормального порядка, и ниже мы дадим ей определние.

Нормальный и аппликативный порядок редукции

Определение: самый крайний редекс не является частью другово редекса (Аналогично, самый глубокий редекс не
содержит внутри других редексов). В терминах дерева с абстрактным синтаксисом, узел apply является самым крайним
редексом, если

• он является редексом (его левая ветвь — лямбда), и
• он не содержит узлов apply в дереве, которое также является редексом.

Пример:

                            apply  <-- не редекс
                           /     
    крайний редекс --> apply      apply <-- ещё один крайний редекс
                      /          /    
                     λ     ...   λ      apply  <-- редекс, но не крайний
                    /          /      /        
                  ... ...      ... ... λ    ...

При нормальной редукции всегда выбирается самый левый из крайних редексов (поэтому нормальную редукцию ещё
иногда называют лево-ориентированной редукцией).

Нормальная редукция похожа на передачу аргументов по имени, где вы вычисляете входящий параметр только если используется
соответствующий формальный. Если формальный параметр не используется, то входящий можно и не вычислять. Самый левый
редекс не может являться частью аргумента для другово редекса; т.е. редукция скорее похожа на вычисление тела функции,
чем на вычисление агрумента. Если функция игнорирует свой аргумент, то редукция этого редекса может «удалить» остальные
редексы (которые задают аргумент); при этом редукция аргумента никогда не «удалит» функцию. Интуитивно понятно почему
нормальная редукция приведет к нормальной форме, если такая существует, даже если другие последовательности редукций к
нормальной форме не приводят.

---

Тест для самопроверки #3

Заполните неполное дерево с абстрактным синтаксисом данное выше (для иллюстрации крайнего редекса) таким образом, что бы
итоговое лямбда-выражение имело нормальную форму, и единственным способом придти к ней был бы выбор самого левого
редекса (вместо любых других) хотя бы один раз.

Ответ

---

Вы наверное думаете, хорошо ли всегда использовать нормальную редукцию (NOR). К сожалению, нет; проблема в том, что
NOR иногда крайне не эффектина. Такая же проблема возникает при передаче параметров по имени: если формальный аргумент
часто используется в функции, и вы вычисляете параметр в каждом вхождении, а вычисление ресурсо-затратно, то было бы
лучше вычислить его один раз. Это приводит к определению другого полезного порядка вычисления: аппликативная
редукция (AOR). Для AOR мы всегда выбираем самый левый из внутренних редексов. AOR соответствует передаче
параметров по значению: все вычисляются (единожно) перед вызовом функции (или, в терминах лямбда-выражений, аргументы
упрощаются перед применением функции). Преимущество AOR заключается в эффективности: если формальный параметр
встречается много раз в теле функции, тогда с NOR аргумент будет упрощен много раз, в то время как для AOR только раз.
Минус AOR в том, что она может не свернуть лямбда-выражение, имеющее нормальную форму.

Стоит отметить, что для языков программирования существует решение под названием вычисление при необходимости,
взявшее лучшее из обеих стратегий. Вычисление при необходимости похоже на передачу аргументов по имени в том плане, что
параметр вычисляется только когда используется соответствующий формальный; хотя, различие в том, что когда используется
вычисление при необходимости, результат вычислений записывается и затем используется для каждого последущего
использования формального. В отсутствии побочных эффектов (что вызывает необходимость каждый раз вычислять параметр,
т.к. получаются различные значения), вычисление по имени и вычисление по необходимости эквивалентны в плане вычисленных
значениях (хотя и вычисление по необходимости эффективнее).

---

Тест для самопроверки #4

Напишите лямбда-выражение, которое может быть приведено к нормальной форме используя NOR или AOR, но AOR должно быть
эффективнее.

Ответ

---

Теорема Чёрча-Россера

Настало время для первой теоремы: Теорема Чёрча-Россера. Для начала зададим новое определение:

Говорят, что A → B если существует последовательность нуля или более альфа и/или бета редукций, которая
преобразует А в B.

Теорема: если (X0 → X1) и (X0 → X2), тогда существует x3, для которого справедливо (X1 → X3) и (X2 → X3).
Проиллюстрируем:

         X0
       /    
      /      
     /        
    v          v
   X1          X2
              /
             /
            /
           /
        v  v
         X3

где стрелки обозначают последовательности одного или более альфа и/или бета редукций.

Следствия: если X имеет нормальную форму Y, то

1. X может быть приведено к Y используя только альфа и/или бета редукции (расширения не обязательны), и
2. Y единственно (из-за альфа-редукции); т.е., X не имеет других нормальных форм.

Для начала мы предположим что теорема верна, докажем оба следствия, затем мы докажем саму теорему. Для простоты мы
будем использовать нотацию де Брауна; т.е. альфа-редукция не используется.

Доказательство следствия 1

Перед доказательством следствия 1 заметим, что X has normal form Y означает, что мы можем привести X к Y используя
последовательность чередующихся бета-редукций и бета-расширений. Графически это выглядит так:

                         ^
                       /
               ^      /
             /      /    ......  
            /      /              
           X       v                
                                     v
                                     Y

где стрелки вверх обозначают последовательность бета-расширений, а вниз — бета-редукции. Заметим, что последовательность
не может закончиться расширением, так как Y является нормальной формой.

Мы докажем Следствие 1 используя математическую индукцию по числу изменений направления получая из X Y.

Основные случаи

1. Нуль изменений направления. Так как последовательность не может закончиться расширением, изображение может быть
   только таким:

               X
                
                 
                  v
                  Y
    

   т.е. мы получили Y из X используя ноль или больше бета-редукций, на этом всё.

2. Одно изменение направления, т.е. изображение следующее:

    
                 W
                ^ 
              /    
             /      
            /        v
           X         Y
    

   т.е. мы используем несколько бета-расширений что бы получить из X некоторое лямбда-выражение W, затем мы используем
   несколько бета-редукций, что бы из W получить Y. Поскольку каждое бета-расширение является обратным к бета-редукции,
   то мы можем получить X из W (точно так же, как и Y из W), т.е. мы получаем следующее изображение:

                  W
                /   
               /     
              /       
             v         v
             X         Y
    

   Теорма Чёрча-Россера утверждает, что существует Z такой, что и X и Y можно упростить до Z:

                 W
               /   
              /     
             v       v
            X         Y
                    /
                   /
               v   v
                 Z
    

   Так как Y (по условию) в нормальной форме, то Y = Z, и на самом деле наше изображение выглядит так:

                 W
               /  
              /    |
             v     |
            X      |
                  |
                 /
               v v
                Y
    

   что означает, что X можно упростить до Y без расширений.

   Теперь мы введём индукцию:

   Предположение индукции: Если X имеет нормальную форму Y, и возможно привести X к Y используя последовательность
   длины n (n gt;= 1) чередующихся бета-расширений и бета-редукций, то мы можем привести X к Y используя только
   бета-редукций.

   Теперь мы покажем, что Следствие 1 справедливо для n+1 изменения направления. Изобразим графически:

    
                 W
                ^             ^            ^ 
              /             /            /    
             /             /            /      
            /        v     /        v    /        v
           X           ...           ...           Y
    
       <--1 изменение --> <-- n изменений направления -->
    

   Обратите внимание на некое лямбда-выражение W (вверху на изображении), такое что:

   1. Мы можем получить W из X используя серию бета-редукций, и
   2. мы можем получить W из Y используя бета-расширения и редукции с n изменений направления.

   По гипотезе индукции, второй пункт означает, что мы можем получить Y из W используя только бета-редукции:

    
               W
                
                 
                  v
                  Y
    

   Комбинируя с пунктом 1 получаем:

    
                 W
                ^  
              /     
             /       
            /         v
           X          Y
    

   Другими словами, мы можем получить W из X используя только бета-редукции, и Y из W используя только бета-редукции.
   Аналогично второму пункту доказательства, получаем, что мы можем получить Y из X используя только бета-редукции.

Доказательство следствия 2

Вспомним, что Следствие 2 гласит: если лямбда X имеет нормальную форму Y, тогда Y единственно (следует из
альфа-редукции), т.е. X не имеет других нормальных форм. Докажем от противного: Пусть Y и Z — две различные
нормальные формы для X. По Следствию 1 X можно привести к Y и Z:

                X
              /   
             /     
            /       
           v         v
           Y         Z

По теореме Чёрча-Россера существует W такое, что

                X
              /  
             /    
            v      v
           Y        Z
                  /
                 /
              v  v
                W

Поскольку по предположению Y и Z уже находятся в нормальной форме, то никаких упрощений не требуется — Y = W = Z,
и X не имеет двух разных нормальных форм.

Доказательство теоремы Чёрча-Россера

Вспомним теорему:

если (X0 → X1) и (X0 → X2), тогда существует x3, для которого справедливо (X1 → X3) и (X2 → X3).

Где → обозначает одну или больше бета-редукций (так как мы планируем использовать нотацию де Брауна;
т.е. альфа-редукция не используется).

Мы будем доказывать «заполняя алмаз» из X0 в X3; т.е. графически в виде:

                      X0
                    /   
                  W1     Z1
                 /    /   
               W2     A     X2
              /     /    /
            X1     B     C
                 /    /
                D     E
                    /
                    F  = X3

Другими словами, мы бы хотели показать, что для каждой лямбды справедливо следующее: если возможно взять 2 разных
«шага» (две разные бета-редукции) для термов A B, то возможно придти к терму C произведя одну бета-редукцию из A
и одну из B. Если мы сможем доказать это, то мы придём к желаемому X3, построенному согласно изображению выше.

К сожалению, идея не вполне работает — т.е. в целом, предположение о том, что получить C можно произведя одну
бета-редукцию из A и одну из B ложно. Далее приведен пример, который проиллюстрирует это. * обозначает
редекс, который упрощается до y.

        X0 = (λx.xx)(*)
            /          
           /            
        (**)             (λx.xx)y
                            /
                           /
                          /
        (y*) или (*y)     /
                        /
                       /
                     (yy)

Обратим внимание на то, что в примере в исходном терме X0 два редекса: сама * и редекс, который принимает как
аргумент *. Итого, у нас два возможных пути развития для X0: в (**) или в (λx.xx)y. Хотя мы и
можем придти к терму (yy) из обоих выражений, для (**) потребуется два шага.

Итак, для доказательства теоремы Чёрча-Россера дадим определение:

Определение (золотое свойство): Отношение ~~> над термами обладает золотым свойством, тогда и только тогда, когда

Из ( X0 ~~> X1) и ( X0 ~~> X2) следует существование X3, такого, что ( X1 ~~> X3 ) и ( X2 ~~> X3 )

Замечание:

1. Теорема Чёрча-Россера гласит, что отношение бета-редукций обладает золотым свойством (т.е. если X бета-упрощается
   и до A и до B за нуль или больше шагов, то тогда и A и B бета-упрощаются до C за нуль или больше шагов).
2. Предыдущий пример доказывает, что одна бета-редукция не обладает золотым свойством (просто потому, что если
   X бета-упрощается до A и B за один шаг, не значит, что и A и B бета-упрощаются до C за один шаг).

3 задания

Для доказательства теормы Чёрча-Россера мы выполним три следующих задания:

1. Дать определение параллельной редукции (обозначается как ⇒).
2. Доказать, что X бета-упрощается до Y тогда и только тогда, когда X ⇒ Y*.
3. Доказать, что ⇒ обладает золотым свойством.

Итак, мы докажем, что ⇒* (последовательность нуля или больше параллельных редукций) обладает золотым свойством, и
что оно идеально подходит для доказательства теоремы Чёрча-Россера.

---

Ответ 1

        apply         =>    +     =>  +   =>  +  =>  6
       /                  /        /      / 
      λ       apply     apply 1     +   1   5   1
     /        /        /        / 
    x   +     λ    3    λ   3    3    2
       /    /        /      
      x   1 y   +     y   +    
               /        / 
	      y   2     y   2

Ответ 2

     apply      =>       λ     =>        λ      λy.y
    /                  /              / 
   λ       λ           y   apply       y   y
  /      /              /     
 x   λ   z   z           λ       y
    /                  / 
   y  apply            z   z
     /     
    x       y

Ответ 3

Одно из возможных решений:

           apply
       /           
    apply            apply
   /               /     
  L       L        L       apply
 /      /       /     /       
x   x   x   y    x   x  L         L
                       /        / 
                      x  apply  x   apply
                        /         /     
                       x       x  x       x

Ответ 4

Одно из возможных решений:

       apply1
     /        
    /          
   L            apply3
  /           /      
 x   apply2   L        a
     /      / 
    x     x y   y         

В этом примере всего два редекса: apply1 и apply3. apply1 самый крайний, а apply3 внутренний.

Если мы будем применять NOR (сначала упростив apply1), то мы получим две копии apply3 (заменяя два вхождения x в
поддереве apply2). Нам потребуется упростить каждый вместо apply3, итого три редукции.

А если мы применим AOR (в первую очередь упростив apply3), то мы заменим поддерево с корнем в apply3 на выражение a.
Теперь, когда мы упростим apply1, то мы получим (а а) — выражение в нормальной форме. Итого всего две редукции.

Лямбда-исчисление

А сегодня немного теории. Я не считаю, что лямбда-исчисление является необходимым знанием для любого программиста. Однако, если вам нравится докапываться до истоков, чтобы понять на чем основаны многие языки программирования, вы любознательны и стремитесь познать все в этом мире или просто хотите сдать экзамен по функциональном программированию (как, например, я), то этот пост для вас.

Что это такое

Лямбда-исчисление — это формальная система, то есть набор объектов, формул, аксиом и правил вывода. Благодаря таким системам с помощью абстракций моделируется теория, которую можно использовать в реальном мире, и при этом выводить в ней новые математически доказуемые утверждения. Например, язык запросов SQL основан на реляционном исчислении. Благодаря математической базе, на которой он существует, оптимизаторы запросов могут анализировать алгебраические свойства операций и влиять на скорость работы.

Но речь сегодня не о SQL, а о функциональных языках. Именно для них лямбда-исчисление является основой. Функциональные языки далеко не столь популярны, как, например, объектно-ориентированные, но тем не менее прочно занимают свою нишу. Кроме того, многие идеи из функционального программирования и лямда-исчисления постепенно прокрадываются в другие языки, под видом новых фич.

Если вы изучали формальные языки, то знаете о таком понятии как Машина Тьюринга. Эта вычислительная абстракция определяет класс вычислимых функций. Этот класс столь важен, так как по тезису Черча он эквивалентен понятию алгоритма. Другими словами, любую программу, которую можно запрограммировать на вычислительном устройстве, можно воспроизвести и на машине Тьюринга. А для нас главное то, что лямбда-исчисление по мощности эквивалентно машине Тьюринга и определяет этот же класс функций. Причем создателем лямбда-исчисления является тот самый Алонзо Черч!

Основные понятия

В нотации лямбда-исчисления есть всего три типа выражений:

1. Переменные: ` x, y, z `
2. Абстракция — декларация функции: ` lambda x.E ` . Определяем функцию с параметром ` x ` и телом ` E `.
3. Аппликация — применение функции ` E_1 ` к аргументу ` E_2 ` : ` E_1 E_2`

Сразу пара примеров:

• Тождественная функция: ` lambda x. x `
• Функция, вычисляющая тождественную функцию: ` lambda x.(lambda y . y) `

Соглашения

Несколько соглашений для понимания, в каком порядке правильно читать выражения:

1. Аппликация лево-ассоциативна. То есть выражение ` x y z ` читается как ` (x y) z `.
2. В абстракции группируем скобки вправо. Другими словами, читая абстракцию необходимо распространять ее максимально вправо насколько возможно. Пример: выражение ` lambda x. x lambda y . x y z ` эквивалентно ` lambda x. (x (lambda y . ((x y) z))) ` , так как абстракция функции с аргументом ` x ` включила в себя все выражение. Следом было проведено включение абстракцией с аргументом ` y ` и ,наконец, в теле этой функции были расставлены скобки для аппликации.

Области видимости переменных

Определим контекст переменной, в котором она может быть использована.
Абстракция ` lambda x.E ` связывает переменную ` x `. В результате мы получаем следующие понятия:

1. ` x ` — связанная переменная в выражении .
2. ` E ` — область видимости переменной ` x `.
3. Переменная свободна в ` E ` , если она не связана в ` E ` . Пример: ` lambda x. x (lambda y. x y z) ` . Cвободная переменная — ` z ` .

Взглянем на следующий пример: ` lambda x. x (lambda x. x) x ` .

Понимание лямбда-выражений существенно усложняется, когда переменные с разными значениями и контекстами используют идентичные имена. Поэтому впредь мы будем пользоваться следующим соглашением: связанные переменные необходимо переименовывать для того, чтобы они имели уникальные имена в выражении. Это возможно благодаря концептуально важному утверждению: выражения, которые могут быть получены друг из друга путем переименования связанных переменных, считаются идентичными. Важность этого утверждения в том, что функции в исчислении определяются лишь своим поведением, и имена функций не несут никакого смысла. То есть, функции ` lambda x. x ` , ` lambda y. y ` , ` lambda z. z ` на самом деле одна тождественная функция.

Вычисление лямбда-выражений

Вычисление выражений заключается в последовательном применении подстановок. Подстановкой ` E’ ` вместо ` x ` в ` E ` (запись: ` [E’//x]E ` ) называется выполнение двух шагов:

1. Альфа-преобразование. Переименование связанных переменных в ` E ` и ` E’ ` , чтобы имена стали уникальными.
2. Бета-редукция. По сути единственная значимая аксиома исчисления. Подразумевает замену ` x ` на ` E’ ` в ` E ` .
   Рассмотрим несколько примеров подстановок:

• Преобразование к тождественной функции. ` (lambda f. f (lambda x. x)) (lambda x. x) -> ` (пишем подстановку) ` -> [lambda x. x // f] f ( lambda x. x)) = ` (делаем альфа-преобазование) ` = [(lambda x. x) // f] f (lambda y. y)) = ` (производим бета-редукцию) ` = (lambda x. x) (lambda y. y) -> ` (еще одна подстановка) ` -> [lambda y. y // x] x = lambda y. y `
• Бесконечные вычисления. ` (lambda x. x x)(lambda x. x x) -> [lambda x. x x // x]x x = [lambda y. y y // x] x x = ` ` = (lambda y. y y)(lambda y. y y) -> … `
• Также небольшой пример, почему нельзя пренебрегать альфа-преобразованием. Рассмотрим выражение ` (lambda x. lambda y. x) y ` . Если не выполнить первый шаг, результатом будет тождественная функция ` lambda y. y ` . Однако, после правильного выполнения подстановки с заменой ` y ` на ` z ` мы получим совсем другой результат ` lambda z. y ` , то есть константную функцию.

Функции нескольких переменных

Для того чтобы использовать функции нескольких переменных добавим в исчисление новую операцию ` add ` : она применяется к двум аргументам и является синтаксическим сахаром для следующих вычислений: ` (lambda x. lambda y. add x y) E_1 E_2 -> ([E_1 // x] lambda y. add x y) E_2 = ` ` (lambda y. add E_1 y) E_2 -> ` ` [E_2 // y] add E_1 y = add E_1 E_2 `

Как результат мы получили функцию от одного аргумента, которая возвращает еще одну функцию от одного аргумента. Такое преобразование называется каррирование (в честь Хаскелла Карри назвали и язык программирования, и эту операцию), а функция, возвращающая другую, называется функцией высшего порядка.

Порядок вычислений

Бывают ситуации, когда произвести вычисление можно несколькими способами. Например, в выражении ` (lambda y. (lambda x. x) y) E ` сначала можно подставлять ` y ` вместо ` x ` во внутреннее выражение, либо ` E ` вместо ` y ` во внешнее. Теорема Черча-Рассера говорит о том, что в не зависимости от последовательности операций, если вычисление завершится, результат будет одинаков. Тем не менее, эти два подхода принципиально отличаются. Рассмотрим их подробнее:

1. Вызов по имени. В вычислении всегда в первую очередь применяются самые внешние подстановки. Другими словами, нужно вычислять аргумент уже после подстановки в функцию. Кроме того нельзя использовать редукцию внутри абстракции. Пример: ` (lambda y. (lambda x. x) y) ((lambda u. u) (lambda v. v)) -> ` (применяем редукцию к внешней функции) ` -> (lambda x. x) ((lambda u. u) (lambda v. v)) -> ` (вновь подставляем, не меняя аргумент) ` -> (lambda u. u) (lambda v. v) = lambda v. v `
2. Вызов по значению. В этом способе вычисление проходит ровно наоборот, то есть сначала вычисляется аргумент функции. При этом редукция внутри абстракции также не применяется. Пример: ` (lambda y. (lambda x. x) y) ((lambda u. u) (lambda v. v)) -> ` (вычисляем аргумент функции) ` -> (lambda y. (lambda x. x) y) (lambda v. v) -> (lambda x. x) (lambda v. v) -> lambda v. v `

Из практических отличий этих двух подходов отметим, то что вычисление по значению более сложно в реализации и редко используется для всех вычислений в неисследовательских языках. Однако, второй подход может не привести к завершению вычисления. Пример: ` (lambda x. lambda z.z) ((lambda y. y y) (lambda u. u u)) ` . При вычислении аргумента мы попадаем в бесконечный цикл, в то время как, проводя вычисления по имени функции, мы сразу получим тождественную функцию.

Кодирование типов

В чистом лямбда-исчислении есть только функции. Однако, программирование трудно представить без различных типов данных. Идея заключается в том, чтобы закодировать поведение конкретных типов в виде функций.

1. Булевые значения. Поведение типа можно описать как функцию, выбирающую одно из двух. Тогда значения выглядят так: ` true = lambda x. lambda y. x ` и ` false = lambda x. lambda y. y `
2. Натуральные числа. Каждое натуральное число может быть описано как функция, проитерированная заданное число раз. Выпишем несколько первых чисел ( ` f ` — функция, которую итерируем, а ` s ` — начальное значение):
   • ` 0 = lambda f. lambda s. s `
   • ` 1 = lambda f. lambda s. f s `
   • ` 2 = lambda f. lambda s. f (f s) `
3. Операции с натуральными числами.
   • Следующее число. ` succ n = lambda f. lambda s. f (n f s) ` . Аргумент функции — число ` n ` , которое, будучи так же функцией, принимает еще два аргумента: начальное значение и итерируемую функцию. Для числа ` n ` один раз применяем функцию ` f ` и получаем следующее число.
   • Сложение. ` add n_1 n_2 = n_1 succ n_2 ` . Для сложения чисел ` n_1 ` и ` n_2 ` нужно одному из слагаемых передать в параметры функцию ` succ `, как итерруемую функцию, и другое слагаемое, как начальное значение. В результате мы увеличим заданное число на единицу необходимое число раз.
   • Умножение. ` mult n_1 n_2 = n_1 (add n_2) 0 ` . В роли итерируемой функции для множителя ` n_1 ` выступает функция ` succ ` с аргументом ` n_2 ` , а в роли начального значения уже определенное число ` 0 ` . То есть мы определяем умножение как прибавление ` n_2 ` к нулю ` n_1` раз.

Аналогично, с помощью лямбда-исчисления можно выразить любые конструкции языков программирования, такие как циклы, ветвления, списки и тд.

Заключение

Лямбда-исчисление — очень мощная система, которая позволяет писать любые программы. Однако, непосредственно программирование на лямбда-исчислении получается черезчур громоздким и неудобным. Тем не менее, чистое лямбда-исчисление предназначено вовсе не для программирования на нем, а для изучения существующих и создания новых языков программирования. А следующим шагом на пути к типовым функциональным языкам является типизированное лямбда-исчисление — расширение чистого исчисления типовыми метками.

По материалу лекций Салищева С. И.

Written on

October
21st
,
2017
by

Alexey Kalina

Feel free to share!

Lambda calculus (also written as λ-calculus) is a formal system in mathematical logic for expressing computation based on function abstraction and application using variable binding and substitution. It is a universal model of computation that can be used to simulate any Turing machine. It was introduced by the mathematician Alonzo Church in the 1930s as part of his research into the foundations of mathematics.

Lambda calculus consists of constructing lambda terms and performing reduction operations on them. In the simplest form of lambda calculus, terms are built using only the following rules:^[a]

The reduction operations include:

If De Bruijn indexing is used, then α-conversion is no longer required as there will be no name collisions. If repeated application of the reduction steps eventually terminates, then by the Church–Rosser theorem it will produce a β-normal form.

Variable names are not needed if using a universal lambda function, such as Iota and Jot, which can create any function behavior by calling it on itself in various combinations.

Explanation and applications[edit]

Lambda calculus is Turing complete, that is, it is a universal model of computation that can be used to simulate any Turing machine.^[2] Its namesake, the Greek letter lambda (λ), is used in lambda expressions and lambda terms to denote binding a variable in a function.

Lambda calculus may be untyped or typed. In typed lambda calculus, functions can be applied only if they are capable of accepting the given input’s «type» of data. Typed lambda calculi are weaker than the untyped lambda calculus, which is the primary subject of this article, in the sense that typed lambda calculi can express less than the untyped calculus can. On the other hand, typed lambda calculi allow more things to be proven. For example, in the simply typed lambda calculus it is a theorem that every evaluation strategy terminates for every simply typed lambda-term, whereas evaluation of untyped lambda-terms need not terminate. One reason there are many different typed lambda calculi has been the desire to do more (of what the untyped calculus can do) without giving up on being able to prove strong theorems about the calculus.

Lambda calculus has applications in many different areas in mathematics, philosophy,^[3] linguistics,^[4][5] and computer science.^[6] Lambda calculus has played an important role in the development of the theory of programming languages. Functional programming languages implement lambda calculus. Lambda calculus is also a current research topic in category theory.^[7]

History[edit]

The lambda calculus was introduced by mathematician Alonzo Church in the 1930s as part of an investigation into the foundations of mathematics.^[8][c] The original system was shown to be logically inconsistent in 1935 when Stephen Kleene and J. B. Rosser developed the Kleene–Rosser paradox.^[9][10]

Subsequently, in 1936 Church isolated and published just the portion relevant to computation, what is now called the untyped lambda calculus.^[11] In 1940, he also introduced a computationally weaker, but logically consistent system, known as the simply typed lambda calculus.^[12]

Until the 1960s when its relation to programming languages was clarified, the lambda calculus was only a formalism. Thanks to Richard Montague and other linguists’ applications in the semantics of natural language, the lambda calculus has begun to enjoy a respectable place in both linguistics^[13] and computer science.^[14]

Origin of the λ symbol[edit]

There is some uncertainty over the reason for Church’s use of the Greek letter lambda (λ) as the notation for function-abstraction in the lambda calculus, perhaps in part due to conflicting explanations by Church himself. According to Cardone and Hindley (2006):

By the way, why did Church choose the notation “λ”? In [an unpublished 1964 letter to Harald Dickson] he stated clearly that it came from the notation “” used for class-abstraction by Whitehead and Russell, by first modifying “” to “” to distinguish function-abstraction from class-abstraction, and then changing “” to “λ” for ease of printing.

This origin was also reported in [Rosser, 1984, p.338]. On the other hand, in his later years Church told two enquirers that the choice was more accidental: a symbol was needed and λ just happened to be chosen.

Dana Scott has also addressed this question in various public lectures.^[15]
Scott recounts that he once posed a question about the origin of the lambda symbol to Church’s former student and son-in-law John W. Addison Jr., who then wrote his father-in-law a postcard:

Dear Professor Church,

Russell had the iota operator, Hilbert had the epsilon operator. Why did you choose lambda for your operator?

According to Scott, Church’s entire response consisted of returning the postcard with the following annotation: «eeny, meeny, miny, moe».

Informal description[edit]

Motivation[edit]

Computable functions are a fundamental concept within computer science and mathematics. The lambda calculus provides simple semantics for computation which are useful for formally studying properties of computation. The lambda calculus incorporates two simplifications that make its semantics simple.
The first simplification is that the lambda calculus treats functions «anonymously;» it does not give them explicit names. For example, the function

can be rewritten in anonymous form as

(which is read as «a tuple of x and y is mapped to «).^[d] Similarly, the function

can be rewritten in anonymous form as

where the input is simply mapped to itself.^[d]

The second simplification is that the lambda calculus only uses functions of a single input. An ordinary function that requires two inputs, for instance the function, can be reworked into an equivalent function that accepts a single input, and as output returns another function, that in turn accepts a single input. For example,

can be reworked into

This method, known as currying, transforms a function that takes multiple arguments into a chain of functions each with a single argument.

Function application of the function to the arguments (5, 2), yields at once

,

whereas evaluation of the curried version requires one more step

// the definition of has been used with in the inner expression. This is like β-reduction.

// the definition of has been used with . Again, similar to β-reduction.

to arrive at the same result.

The lambda calculus[edit]

The lambda calculus consists of a language of lambda terms, that are defined by a certain formal syntax, and a set of transformation rules for manipulating the lambda terms. These transformation rules can be viewed as an equational theory or as an operational definition.

As described above, having no names, all functions in the lambda calculus are anonymous functions. They only accept one input variable, so currying is used to implement functions of several variables.

Lambda terms[edit]

The syntax of the lambda calculus defines some expressions as valid lambda calculus expressions and some as invalid, just as some strings of characters are valid C programs and some are not. A valid lambda calculus expression is called a «lambda term».

The following three rules give an inductive definition that can be applied to build all syntactically valid lambda terms:^[e]

Nothing else is a lambda term. Thus a lambda term is valid if and only if it can be obtained by repeated application of these three rules. However, some parentheses can be omitted according to certain rules. For example, the outermost parentheses are usually not written. See §Notation, below for when to include parentheses

An abstraction denotes an § anonymous function^[g] that takes a single input x and returns t. For example, is an abstraction for the function using the term for t. The name is superfluous when using abstraction.
binds the variable x in the term t. The definition of a function with an abstraction merely «sets up» the function but does not invoke it. See §Notation below for usage of parentheses

An application   represents the application of a function t to an input s, that is, it represents the act of calling function t on input s to produce .

There is no concept in lambda calculus of variable declaration. In a definition such as (i.e. ), in lambda calculus y is a variable that is not yet defined. The abstraction is syntactically valid, and represents a function that adds its input to the yet-unknown y.

Parentheses may be used and might be needed to disambiguate terms. For example,

1. which is of form —an abstraction, and
2. which is of form    —an application.

The examples 1 and 2 denote different terms; except for the scope of the parentheses they would be the same. But example 1 is a function definition, while example 2 is function application. Lambda variable x is a placeholder in both examples.

Here, example 1 defines a function , where is , an anonymous function , with input ; while example 2,  , is M applied to N, where is the lambda term being applied to the input which is . Both examples 1 and 2 would evaluate to the identity function .

Functions that operate on functions[edit]

In lambda calculus, functions are taken to be ‘first class values’, so functions may be used as the inputs, or be returned as outputs from other functions.

For example, represents the identity function, , and represents the identity function applied to . Further, represents the constant function , the function that always returns , no matter the input. In lambda calculus, function application is regarded as left-associative, so that means .

There are several notions of «equivalence» and «reduction» that allow lambda terms to be «reduced» to «equivalent» lambda terms.

Alpha equivalence[edit]

A basic form of equivalence, definable on lambda terms, is alpha equivalence. It captures the intuition that the particular choice of a bound variable, in an abstraction, does not (usually) matter.
For instance, and are alpha-equivalent lambda terms, and they both represent the same function (the identity function).
The terms and are not alpha-equivalent, because they are not bound in an abstraction.
In many presentations, it is usual to identify alpha-equivalent lambda terms.

The following definitions are necessary in order to be able to define β-reduction:

Free variables[edit]

The free variables
^[h] of a term are those variables not bound by an abstraction. The set of free variables of an expression is defined inductively:

For example, the lambda term representing the identity has no free variables, but the function has a single free variable, .

Capture-avoiding substitutions[edit]

Suppose , and are lambda terms, and and are variables.
The notation indicates substitution of for in in a capture-avoiding manner. This is defined so that:

For example, , and .

The freshness condition (requiring that is not in the free variables of ) is crucial in order to ensure that substitution does not change the meaning of functions.

For example, a substitution that ignores the freshness condition could lead to errors: . This erroneous substitution would turn the constant function into the identity .

In general, failure to meet the freshness condition can be remedied by alpha-renaming first, with a suitable fresh variable.
For example, switching back to our correct notion of substitution, in the abstraction can be renamed with a fresh variable , to obtain , and the meaning of the function is preserved by substitution.

In a functional programming language where functions are first class citizens, this systematic change in variables to avoid capture of a free variable can introduce an error, when returning functions as results.^[16]

β-reduction[edit]

The β-reduction rule^[b] states that an application of the form reduces to the term . The notation is used to indicate that β-reduces to .
For example, for every , . This demonstrates that really is the identity.
Similarly, , which demonstrates that is a constant function.

The lambda calculus may be seen as an idealized version of a functional programming language, like Haskell or Standard ML.
Under this view, β-reduction corresponds to a computational step. This step can be repeated by additional β-reductions until there are no more applications left to reduce. In the untyped lambda calculus, as presented here, this reduction process may not terminate.
For instance, consider the term .
Here .
That is, the term reduces to itself in a single β-reduction, and therefore the reduction process will never terminate.

Another aspect of the untyped lambda calculus is that it does not distinguish between different kinds of data.
For instance, it may be desirable to write a function that only operates on numbers. However, in the untyped lambda calculus, there is no way to prevent a function from being applied to truth values, strings, or other non-number objects.

Formal definition[edit]

Definition[edit]

Lambda expressions are composed of:

• variables v₁, v₂, …;
• the abstraction symbols λ (lambda) and . (dot);
• parentheses ().

The set of lambda expressions, Λ, can be defined inductively:

1. If x is a variable, then x ∈ Λ.
2. If x is a variable and M ∈ Λ, then (λx.M) ∈ Λ.
3. If M, N ∈ Λ, then (M N) ∈ Λ.

Instances of rule 2 are known as abstractions and instances of rule 3 are known as applications.^[17][18]

Notation[edit]

To keep the notation of lambda expressions uncluttered, the following conventions are usually applied:

• Outermost parentheses are dropped: M N instead of (M N).
• Applications are assumed to be left associative: M N P may be written instead of ((M N) P).^[19]
• When all variables are single-letter, the space in applications may be omitted: MNP instead of M N P.^[20]
• The body of an abstraction extends as far right as possible: λx.M N means λx.(M N) and not (λx.M) N.
• A sequence of abstractions is contracted: λx.λy.λz.N is abbreviated as λxyz.N.^[21][19]

Free and bound variables[edit]

The abstraction operator, λ, is said to bind its variable wherever it occurs in the body of the abstraction. Variables that fall within the scope of an abstraction are said to be bound. In an expression λx.M, the part λx is often called binder, as a hint that the variable x is getting bound by prepending λx to M. All other variables are called free. For example, in the expression λy.x x y, y is a bound variable and x is a free variable. Also a variable is bound by its nearest abstraction. In the following example the single occurrence of x in the expression is bound by the second lambda: λx.y (λx.z x).

The set of free variables of a lambda expression, M, is denoted as FV(M) and is defined by recursion on the structure of the terms, as follows:

1. FV(x) = {x}, where x is a variable.
2. FV(λx.M) = FV(M) {x}.^[i]
3. FV(M N) = FV(M) ∪ FV(N).^[j]

An expression that contains no free variables is said to be closed. Closed lambda expressions are also known as combinators and are equivalent to terms in combinatory logic.

Reduction[edit]

The meaning of lambda expressions is defined by how expressions can be reduced.^[22]

There are three kinds of reduction:

• α-conversion: changing bound variables;
• β-reduction: applying functions to their arguments;
• η-reduction: which captures a notion of extensionality.

We also speak of the resulting equivalences: two expressions are α-equivalent, if they can be α-converted into the same expression. β-equivalence and η-equivalence are defined similarly.

The term redex, short for reducible expression, refers to subterms that can be reduced by one of the reduction rules. For example, (λx.M) N is a β-redex in expressing the substitution of N for x in M. The expression to which a redex reduces is called its reduct; the reduct of (λx.M) N is M[x := N].

If x is not free in M, λx.M x is also an η-redex, with a reduct of M.

α-conversion[edit]

α-conversion, sometimes known as α-renaming,^[23] allows bound variable names to be changed. For example, α-conversion of λx.x might yield λy.y. Terms that differ only by α-conversion are called α-equivalent. Frequently, in uses of lambda calculus, α-equivalent terms are considered to be equivalent.

The precise rules for α-conversion are not completely trivial. First, when α-converting an abstraction, the only variable occurrences that are renamed are those that are bound to the same abstraction. For example, an α-conversion of λx.λx.x could result in λy.λx.x, but it could not result in λy.λx.y. The latter has a different meaning from the original. This is analogous to the programming notion of variable shadowing.

Second, α-conversion is not possible if it would result in a variable getting captured by a different abstraction. For example, if we replace x with y in λx.λy.x, we get λy.λy.y, which is not at all the same.

In programming languages with static scope, α-conversion can be used to make name resolution simpler by ensuring that no variable name masks a name in a containing scope (see α-renaming to make name resolution trivial).

In the De Bruijn index notation, any two α-equivalent terms are syntactically identical.

Substitution[edit]

Substitution, written M[x := N], is the process of replacing all free occurrences of the variable x in the expression M with expression N. Substitution on terms of the lambda calculus is defined by recursion on the structure of terms, as follows (note: x and y are only variables while M and N are any lambda expression):

x[x := N] = N

y[x := N] = y, if x ≠ y

(M₁ M₂)[x := N] = M₁[x := N] M₂[x := N]

(λx.M)[x := N] = λx.M

(λy.M)[x := N] = λy.(M[x := N]), if x ≠ y and y ∉ FV(N) See above for the FV

To substitute into an abstraction, it is sometimes necessary to α-convert the expression. For example, it is not correct for (λx.y)[y := x] to result in λx.x, because the substituted x was supposed to be free but ended up being bound. The correct substitution in this case is λz.x, up to α-equivalence. Substitution is defined uniquely up to α-equivalence.

β-reduction[edit]

β-reduction captures the idea of function application. β-reduction is defined in terms of substitution: the β-reduction of (λx.M) N is M[x := N].^[b]

For example, assuming some encoding of 2, 7, ×, we have the following β-reduction: (λn.n × 2) 7 → 7 × 2.

β-reduction can be seen to be the same as the concept of local reducibility in natural deduction, via the Curry–Howard isomorphism.

η-reduction[edit]

η-reduction (eta reduction) expresses the idea of extensionality,^[24] which in this context is that two functions are the same if and only if they give the same result for all arguments. η-reduction converts between λx.f x and f whenever x does not appear free in f.

η-reduction can be seen to be the same as the concept of local completeness in natural deduction, via the Curry–Howard isomorphism.

Normal forms and confluence[edit]

For the untyped lambda calculus, β-reduction as a rewriting rule is neither strongly normalising nor weakly normalising.

However, it can be shown that β-reduction is confluent when working up to α-conversion (i.e. we consider two normal forms to be equal if it is possible to α-convert one into the other).

Therefore, both strongly normalising terms and weakly normalising terms have a unique normal form. For strongly normalising terms, any reduction strategy is guaranteed to yield the normal form, whereas for weakly normalising terms, some reduction strategies may fail to find it.

Encoding datatypes[edit]

The basic lambda calculus may be used to model booleans, arithmetic, data structures and recursion, as illustrated in the following sub-sections.

Arithmetic in lambda calculus[edit]

There are several possible ways to define the natural numbers in lambda calculus, but by far the most common are the Church numerals, which can be defined as follows:

0 := λf.λx.x

1 := λf.λx.f x

2 := λf.λx.f (f x)

3 := λf.λx.f (f (f x))

and so on. Or using the alternative syntax presented above in Notation:

0 := λfx.x

1 := λfx.f x

2 := λfx.f (f x)

3 := λfx.f (f (f x))

A Church numeral is a higher-order function—it takes a single-argument function f, and returns another single-argument function. The Church numeral n is a function that takes a function f as argument and returns the n-th composition of f, i.e. the function f composed with itself n times. This is denoted f⁽ⁿ⁾ and is in fact the n-th power of f (considered as an operator); f⁽⁰⁾ is defined to be the identity function. Such repeated compositions (of a single function f) obey the laws of exponents, which is why these numerals can be used for arithmetic. (In Church’s original lambda calculus, the formal parameter of a lambda expression was required to occur at least once in the function body, which made the above definition of 0 impossible.)

One way of thinking about the Church numeral n, which is often useful when analysing programs, is as an instruction ‘repeat n times’. For example, using the PAIR and NIL functions defined below, one can define a function that constructs a (linked) list of n elements all equal to x by repeating ‘prepend another x element’ n times, starting from an empty list. The lambda term is

λn.λx.n (PAIR x) NIL

By varying what is being repeated, and varying what argument that function being repeated is applied to, a great many different effects can be achieved.

We can define a successor function, which takes a Church numeral n and returns n + 1 by adding another application of f, where ‘(mf)x’ means the function ‘f’ is applied ‘m’ times on ‘x’:

SUCC := λn.λf.λx.f (n f x)

Because the m-th composition of f composed with the n-th composition of f gives the m+n-th composition of f, addition can be defined as follows:

PLUS := λm.λn.λf.λx.m f (n f x)

PLUS can be thought of as a function taking two natural numbers as arguments and returning a natural number; it can be verified that

PLUS 2 3

and

5

are β-equivalent lambda expressions. Since adding m to a number n can be accomplished by adding 1 m times, an alternative definition is:

PLUS := λm.λn.m SUCC n ^[25]

Similarly, multiplication can be defined as

MULT := λm.λn.λf.m (n f)^[21]

Alternatively

MULT := λm.λn.m (PLUS n) 0

since multiplying m and n is the same as repeating the add n function m times and then applying it to zero.
Exponentiation has a rather simple rendering in Church numerals, namely

POW := λb.λe.e b^[1]

The predecessor function defined by PRED n = n − 1 for a positive integer n and PRED 0 = 0 is considerably more difficult. The formula

PRED := λn.λf.λx.n (λg.λh.h (g f)) (λu.x) (λu.u)

can be validated by showing inductively that if T denotes (λg.λh.h (g f)), then T⁽ⁿ⁾(λu.x) = (λh.h(f⁽ⁿ⁻¹⁾(x))) for n > 0. Two other definitions of PRED are given below, one using conditionals and the other using pairs. With the predecessor function, subtraction is straightforward. Defining

SUB := λm.λn.n PRED m,

SUB m n yields m − n when m > n and 0 otherwise.

Logic and predicates[edit]

By convention, the following two definitions (known as Church booleans) are used for the boolean values TRUE and FALSE:

TRUE := λx.λy.x

FALSE := λx.λy.y

Then, with these two lambda terms, we can define some logic operators (these are just possible formulations; other expressions are equally correct):

AND := λp.λq.p q p

OR := λp.λq.p p q

NOT := λp.p FALSE TRUE

IFTHENELSE := λp.λa.λb.p a b

We are now able to compute some logic functions, for example:

AND TRUE FALSE

≡ (λp.λq.p q p) TRUE FALSE →_β TRUE FALSE TRUE

≡ (λx.λy.x) FALSE TRUE →_β FALSE

and we see that AND TRUE FALSE is equivalent to FALSE.

A predicate is a function that returns a boolean value. The most fundamental predicate is ISZERO, which returns TRUE if its argument is the Church numeral 0, and FALSE if its argument is any other Church numeral:

ISZERO := λn.n (λx.FALSE) TRUE

The following predicate tests whether the first argument is less-than-or-equal-to the second:

LEQ := λm.λn.ISZERO (SUB m n),

and since m = n, if LEQ m n and LEQ n m, it is straightforward to build a predicate for numerical equality.

The availability of predicates and the above definition of TRUE and FALSE make it convenient to write «if-then-else» expressions in lambda calculus. For example, the predecessor function can be defined as:

PRED := λn.n (λg.λk.ISZERO (g 1) k (PLUS (g k) 1)) (λv.0) 0

which can be verified by showing inductively that n (λg.λk.ISZERO (g 1) k (PLUS (g k) 1)) (λv.0) is the add n − 1 function for n > 0.

Pairs[edit]

A pair (2-tuple) can be defined in terms of TRUE and FALSE, by using the Church encoding for pairs. For example, PAIR encapsulates the pair (x,y), FIRST returns the first element of the pair, and SECOND returns the second.

PAIR := λx.λy.λf.f x y

FIRST := λp.p TRUE

SECOND := λp.p FALSE

NIL := λx.TRUE

NULL := λp.p (λx.λy.FALSE)

A linked list can be defined as either NIL for the empty list, or the PAIR of an element and a smaller list. The predicate NULL tests for the value NIL. (Alternatively, with NIL := FALSE, the construct l (λh.λt.λz.deal_with_head_h_and_tail_t) (deal_with_nil) obviates the need for an explicit NULL test).

As an example of the use of pairs, the shift-and-increment function that maps (m, n) to (n, n + 1) can be defined as

Φ := λx.PAIR (SECOND x) (SUCC (SECOND x))

which allows us to give perhaps the most transparent version of the predecessor function:

PRED := λn.FIRST (n Φ (PAIR 0 0)).

Additional programming techniques[edit]

There is a considerable body of programming idioms for lambda calculus. Many of these were originally developed in the context of using lambda calculus as a foundation for programming language semantics, effectively using lambda calculus as a low-level programming language. Because several programming languages include the lambda calculus (or something very similar) as a fragment, these techniques also see use in practical programming, but may then be perceived as obscure or foreign.

Named constants[edit]

In lambda calculus, a library would take the form of a collection of previously defined functions, which as lambda-terms are merely particular constants. The pure lambda calculus does not have a concept of named constants since all atomic lambda-terms are variables, but one can emulate having named constants by setting aside a variable as the name of the constant, using abstraction to bind that variable in the main body, and apply that abstraction to the intended definition. Thus to use f to mean N (some explicit lambda-term) in M (another lambda-term, the «main program»), one can say

(λf.M) N

Authors often introduce syntactic sugar, such as let,^[k] to permit writing the above in the more intuitive order

let f =N in M

By chaining such definitions, one can write a lambda calculus «program» as zero or more function definitions, followed by one lambda-term using those functions that constitutes the main body of the program.

A notable restriction of this let is that the name f be not defined in N, for N to be outside the scope of the abstraction binding f; this means a recursive function definition cannot be used as the N with let. The letrec^[l] construction would allow writing recursive function definitions.

Recursion and fixed points[edit]

Recursion is the definition of a function using the function itself. A definition containing itself inside itself, by value, leads to the whole value being of infinite size. Other notations which support recursion natively overcome this by referring to the function definition by name. Lambda calculus cannot express this: all functions are anonymous in lambda calculus, so we can’t refer by name to a value which is yet to be defined, inside the lambda term defining that same value. However, a lambda expression can receive itself as its own argument, for example in  (λx.x x) E. Here E should be an abstraction, applying its parameter to a value to express recursion.

Consider the factorial function F(n) recursively defined by

F(n) = 1, if n = 0; else n × F(n − 1).

In the lambda expression which is to represent this function, a parameter (typically the first one) will be assumed to receive the lambda expression itself as its value, so that calling it – applying it to an argument – will amount to recursion. Thus to achieve recursion, the intended-as-self-referencing argument (called r here) must always be passed to itself within the function body, at a call point:

G := λr. λn.(1, if n = 0; else n × (r r (n−1)))

with  r r x = F x = G r x  to hold, so  r = G  and

F := G G = (λx.x x) G

The self-application achieves replication here, passing the function’s lambda expression on to the next invocation as an argument value, making it available to be referenced and called there.

This solves it but requires re-writing each recursive call as self-application. We would like to have a generic solution, without a need for any re-writes:

G := λr. λn.(1, if n = 0; else n × (r (n−1)))

with  r x = F x = G r x  to hold, so  r = G r =: FIX G  and

F := FIX G  where  FIX g := (r where r = g r) = g (FIX g)

so that  FIX G = G (FIX G) = (λn.(1, if n = 0; else n × ((FIX G) (n−1))))

Given a lambda term with first argument representing recursive call (e.g. G here), the fixed-point combinator FIX will return a self-replicating lambda expression representing the recursive function (here, F). The function does not need to be explicitly passed to itself at any point, for the self-replication is arranged in advance, when it is created, to be done each time it is called. Thus the original lambda expression (FIX G) is re-created inside itself, at call-point, achieving self-reference.

In fact, there are many possible definitions for this FIX operator, the simplest of them being:

Y := λg.(λx.g (x x)) (λx.g (x x))

In the lambda calculus, Y g  is a fixed-point of g, as it expands to:

Y g

(λh.(λx.h (x x)) (λx.h (x x))) g

(λx.g (x x)) (λx.g (x x))

g ((λx.g (x x)) (λx.g (x x)))

g (Y g)

Now, to perform our recursive call to the factorial function, we would simply call (Y G) n,  where n is the number we are calculating the factorial of. Given n = 4, for example, this gives:

(Y G) 4

G (Y G) 4

(λr.λn.(1, if n = 0; else n × (r (n−1)))) (Y G) 4

(λn.(1, if n = 0; else n × ((Y G) (n−1)))) 4

1, if 4 = 0; else 4 × ((Y G) (4−1))

4 × (G (Y G) (4−1))

4 × ((λn.(1, if n = 0; else n × ((Y G) (n−1)))) (4−1))

4 × (1, if 3 = 0; else 3 × ((Y G) (3−1)))

4 × (3 × (G (Y G) (3−1)))

4 × (3 × ((λn.(1, if n = 0; else n × ((Y G) (n−1)))) (3−1)))

4 × (3 × (1, if 2 = 0; else 2 × ((Y G) (2−1))))

4 × (3 × (2 × (G (Y G) (2−1))))

4 × (3 × (2 × ((λn.(1, if n = 0; else n × ((Y G) (n−1)))) (2−1))))

4 × (3 × (2 × (1, if 1 = 0; else 1 × ((Y G) (1−1)))))

4 × (3 × (2 × (1 × (G (Y G) (1−1)))))

4 × (3 × (2 × (1 × ((λn.(1, if n = 0; else n × ((Y G) (n−1)))) (1−1)))))

4 × (3 × (2 × (1 × (1, if 0 = 0; else 0 × ((Y G) (0−1))))))

4 × (3 × (2 × (1 × (1))))

24

Every recursively defined function can be seen as a fixed point of some suitably defined function closing over the recursive call with an extra argument, and therefore, using Y, every recursively defined function can be expressed as a lambda expression. In particular, we can now cleanly define the subtraction, multiplication and comparison predicate of natural numbers recursively.

Standard terms[edit]

Certain terms have commonly accepted names:^[27][28][29]

I := λx.x

S := λx.λy.λz.x z (y z)

K := λx.λy.x

B := λx.λy.λz.x (y z)

C := λx.λy.λz.x z y

W := λx.λy.x y y

ω or Δ or U := λx.x x

Ω := ω ω

I is the identity function. SK and BCKW form complete combinator calculus systems that can express any lambda term — see
the next section. Ω is UU, the smallest term that has no normal form. YI is another such term.
Y is standard and defined above, and can also be defined as Y=BU(CBU), so that Yg=g(Yg). TRUE and FALSE defined above are commonly abbreviated as T and F.

Abstraction elimination[edit]

If N is a lambda-term without abstraction, but possibly containing named constants (combinators), then there exists a lambda-term T(x,N) which is equivalent to λx.N but lacks abstraction (except as part of the named constants, if these are considered non-atomic). This can also be viewed as anonymising variables, as T(x,N) removes all occurrences of x from N, while still allowing argument values to be substituted into the positions where N contains an x. The conversion function T can be defined by:

T(x, x) := I

T(x, N) := K N if x is not free in N.

T(x, M N) := S T(x, M) T(x, N)

In either case, a term of the form T(x,N) P can reduce by having the initial combinator I, K, or S grab the argument P, just like β-reduction of (λx.N) P would do. I returns that argument. K throws the argument away, just like (λx.N) would do if x has no free occurrence in N. S passes the argument on to both subterms of the application, and then applies the result of the first to the result of the second.

The combinators B and C are similar to S, but pass the argument on to only one subterm of an application (B to the «argument» subterm and C to the «function» subterm), thus saving a subsequent K if there is no occurrence of x in one subterm. In comparison to B and C, the S combinator actually conflates two functionalities: rearranging arguments, and duplicating an argument so that it may be used in two places. The W combinator does only the latter, yielding the B, C, K, W system as an alternative to SKI combinator calculus.

Typed lambda calculus[edit]

A typed lambda calculus is a typed formalism that uses the lambda-symbol () to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered (see Kinds of typed lambda calculi). From a certain point of view, typed lambda calculi can be seen as refinements of the untyped lambda calculus but from another point of view, they can also be considered the more fundamental theory and untyped lambda calculus a special case with only one type.^[30]

Typed lambda calculi are foundational programming languages and are the base of typed functional programming languages such as ML and Haskell and, more indirectly, typed imperative programming languages. Typed lambda calculi play an important role in the design of type systems for programming languages; here typability usually captures desirable properties of the program, e.g. the program will not cause a memory access violation.

Typed lambda calculi are closely related to mathematical logic and proof theory via the Curry–Howard isomorphism and they can be considered as the internal language of classes of categories, e.g. the simply typed lambda calculus is the language of Cartesian closed categories (CCCs).

Reduction strategies[edit]

Whether a term is normalising or not, and how much work needs to be done in normalising it if it is, depends to a large extent on the reduction strategy used. Common lambda calculus reduction strategies include:^[31][32][33]

Normal order

The leftmost, outermost redex is always reduced first. That is, whenever possible the arguments are substituted into the body of an abstraction before the arguments are reduced.

Applicative order

The leftmost, innermost redex is always reduced first. Intuitively this means a function’s arguments are always reduced before the function itself. Applicative order always attempts to apply functions to normal forms, even when this is not possible.

Full β-reductions

Any redex can be reduced at any time. This means essentially the lack of any particular reduction strategy—with regard to reducibility, «all bets are off».

Weak reduction strategies do not reduce under lambda abstractions:

Call by value

A redex is reduced only when its right hand side has reduced to a value (variable or abstraction). Only the outermost redexes are reduced.

Call by name

As normal order, but no reductions are performed inside abstractions. For example, λx.(λy.y)x is in normal form according to this strategy, although it contains the redex (λy.y)x.

Strategies with sharing reduce computations that are «the same» in parallel:

Optimal reduction

As normal order, but computations that have the same label are reduced simultaneously.

Call by need

As call by name (hence weak), but function applications that would duplicate terms instead name the argument, which is then reduced only «when it is needed».

Computability[edit]

There is no algorithm that takes as input any two lambda expressions and outputs TRUE or FALSE depending on whether one expression reduces to the other.^[11] More precisely, no computable function can decide the question. This was historically the first problem for which undecidability could be proven. As usual for such a proof, computable means computable by any model of computation that is Turing complete. In fact computability can itself be defined via the lambda calculus: a function F: N → N of natural numbers is a computable function if and only if there exists a lambda expression f such that for every pair of x, y in N, F(x)=y if and only if f x =_β y,  where x and y are the Church numerals corresponding to x and y, respectively and =_β meaning equivalence with β-reduction. See the Church–Turing thesis for other approaches to defining computability and their equivalence.

Church’s proof of uncomputability first reduces the problem to determining whether a given lambda expression has a normal form. Then he assumes that this predicate is computable, and can hence be expressed in lambda calculus. Building on earlier work by Kleene and constructing a Gödel numbering for lambda expressions, he constructs a lambda expression e that closely follows the proof of Gödel’s first incompleteness theorem. If e is applied to its own Gödel number, a contradiction results.

Complexity[edit]

The notion of computational complexity for the lambda calculus is a bit tricky, because the cost of a β-reduction may vary depending on how it is implemented.^[34]
To be precise, one must somehow find the location of all of the occurrences of the bound variable V in the expression E, implying a time cost, or one must keep track of the locations of free variables in some way, implying a space cost. A naïve search for the locations of V in E is O(n) in the length n of E. Director strings were an early approach that traded this time cost for a quadratic space usage.^[35] More generally this has led to the study of systems that use explicit substitution.

In 2014 it was shown that the number of β-reduction steps taken by normal order reduction to reduce a term is a reasonable time cost model, that is, the reduction can be simulated on a Turing machine in time polynomially proportional to the number of steps.^[36] This was a long-standing open problem, due to size explosion, the existence of lambda terms which grow exponentially in size for each β-reduction. The result gets around this by working with a compact shared representation. The result makes clear that the amount of space needed to evaluate a lambda term is not proportional to the size of the term during reduction. It is not currently known what a good measure of space complexity would be.^[37]

An unreasonable model does not necessarily mean inefficient. Optimal reduction reduces all computations with the same label in one step, avoiding duplicated work, but the number of parallel β-reduction steps to reduce a given term to normal form is approximately linear in the size of the term. This is far too small to be a reasonable cost measure, as any Turing machine may be encoded in the lambda calculus in size linearly proportional to the size of the Turing machine. The true cost of reducing lambda terms is not due to β-reduction per se but rather the handling of the duplication of redexes during β-reduction.^[38] It is not known if optimal reduction implementations are reasonable when measured with respect to a reasonable cost model such as the number of leftmost-outermost steps to normal form, but it has been shown for fragments of the lambda calculus that the optimal reduction algorithm is efficient and has at most a quadratic overhead compared to leftmost-outermost.^[37] In addition the BOHM prototype implementation of optimal reduction outperformed both Caml Light and Haskell on pure lambda terms.^[38]

Lambda calculus and programming languages[edit]

As pointed out by Peter Landin’s 1965 paper «A Correspondence between ALGOL 60 and Church’s Lambda-notation»,^[39] sequential procedural programming languages can be understood in terms of the lambda calculus, which provides the basic mechanisms for procedural abstraction and procedure (subprogram) application.

Anonymous functions[edit]

For example, in Python the «square» function can be expressed as a lambda expression as follows:

The above example is an expression that evaluates to a first-class function. The symbol lambda creates an anonymous function, given a list of parameter names, x – just a single argument in this case, and an expression that is evaluated as the body of the function, x**2. Anonymous functions are sometimes called lambda expressions.

For example, Pascal and many other imperative languages have long supported passing subprograms as arguments to other subprograms through the mechanism of function pointers. However, function pointers are not a sufficient condition for functions to be first class datatypes, because a function is a first class datatype if and only if new instances of the function can be created at run-time. And this run-time creation of functions is supported in Smalltalk, JavaScript and Wolfram Language, and more recently in Scala, Eiffel («agents»), C# («delegates») and C++11, among others.

Parallelism and concurrency[edit]

The Church–Rosser property of the lambda calculus means that evaluation (β-reduction) can be carried out in any order, even in parallel. This means that various nondeterministic evaluation strategies are relevant. However, the lambda calculus does not offer any explicit constructs for parallelism. One can add constructs such as Futures to the lambda calculus. Other process calculi have been developed for describing communication and concurrency.

Semantics[edit]

The fact that lambda calculus terms act as functions on other lambda calculus terms, and even on themselves, led to questions about the semantics of the lambda calculus. Could a sensible meaning be assigned to lambda calculus terms? The natural semantics was to find a set D isomorphic to the function space D → D, of functions on itself. However, no nontrivial such D can exist, by cardinality constraints because the set of all functions from D to D has greater cardinality than D, unless D is a singleton set.

In the 1970s, Dana Scott showed that if only continuous functions were considered, a set or domain D with the required property could be found, thus providing a model for the lambda calculus.^[40]

This work also formed the basis for the denotational semantics of programming languages.

Variations and extensions[edit]

These extensions are in the lambda cube:

• Typed lambda calculus – Lambda calculus with typed variables (and functions)
• System F – A typed lambda calculus with type-variables
• Calculus of constructions – A typed lambda calculus with types as first-class values

These formal systems are extensions of lambda calculus that are not in the lambda cube:

• Binary lambda calculus – A version of lambda calculus with binary I/O, a binary encoding of terms, and a designated universal machine.
• Lambda-mu calculus – An extension of the lambda calculus for treating classical logic

These formal systems are variations of lambda calculus:

• Kappa calculus – A first-order analogue of lambda calculus

These formal systems are related to lambda calculus:

• Combinatory logic – A notation for mathematical logic without variables
• SKI combinator calculus – A computational system based on the S, K and I combinators, equivalent to lambda calculus, but reducible without variable substitutions

See also[edit]

Further reading[edit]

• Abelson, Harold & Gerald Jay Sussman. Structure and Interpretation of Computer Programs. The MIT Press. ISBN 0-262-51087-1.
• Hendrik Pieter Barendregt Introduction to Lambda Calculus.
• Henk Barendregt, The Impact of the Lambda Calculus in Logic and Computer Science. The Bulletin of Symbolic Logic, Volume 3, Number 2, June 1997.
• Barendregt, Hendrik Pieter, The Type Free Lambda Calculus pp1091–1132 of Handbook of Mathematical Logic, North-Holland (1977) ISBN 0-7204-2285-X
• Cardone and Hindley, 2006. History of Lambda-calculus and Combinatory Logic. In Gabbay and Woods (eds.), Handbook of the History of Logic, vol. 5. Elsevier.
• Church, Alonzo, An unsolvable problem of elementary number theory, American Journal of Mathematics, 58 (1936), pp. 345–363. This paper contains the proof that the equivalence of lambda expressions is in general not decidable.
• Church, Alonzo (1941). The Calculi of Lambda-Conversion. Princeton: Princeton University Press. Retrieved 2020-04-14. (ISBN 978-0-691-08394-0)
• Frink Jr., Orrin (1944). «Review: The Calculi of Lambda-Conversion by Alonzo Church» (PDF). Bull. Amer. Math. Soc. 50 (3): 169–172. doi:10.1090/s0002-9904-1944-08090-7.
• Kleene, Stephen, A theory of positive integers in formal logic, American Journal of Mathematics, 57 (1935), pp. 153–173 and 219–244. Contains the lambda calculus definitions of several familiar functions.
• Landin, Peter, A Correspondence Between ALGOL 60 and Church’s Lambda-Notation, Communications of the ACM, vol. 8, no. 2 (1965), pages 89–101. Available from the ACM site. A classic paper highlighting the importance of lambda calculus as a basis for programming languages.
• Larson, Jim, An Introduction to Lambda Calculus and Scheme. A gentle introduction for programmers.
• Michaelson, Greg (10 April 2013). An Introduction to Functional Programming Through Lambda Calculus. Courier Corporation. ISBN 978-0-486-28029-5.^[41]
• Schalk, A. and Simmons, H. (2005) An introduction to λ-calculi and arithmetic with a decent selection of exercises. Notes for a course in the Mathematical Logic MSc at Manchester University.
• de Queiroz, Ruy J.G.B. (2008). «On Reduction Rules, Meaning-as-Use and Proof-Theoretic Semantics». Studia Logica. 90 (2): 211–247. doi:10.1007/s11225-008-9150-5. S2CID 11321602. A paper giving a formal underpinning to the idea of ‘meaning-is-use’ which, even if based on proofs, it is different from proof-theoretic semantics as in the Dummett–Prawitz tradition since it takes reduction as the rules giving meaning.
• Hankin, Chris, An Introduction to Lambda Calculi for Computer Scientists, ISBN 0954300653

Monographs/textbooks for graduate students

• Morten Heine Sørensen, Paweł Urzyczyn, Lectures on the Curry–Howard isomorphism, Elsevier, 2006, ISBN 0-444-52077-5 is a recent monograph that covers the main topics of lambda calculus from the type-free variety, to most typed lambda calculi, including more recent developments like pure type systems and the lambda cube. It does not cover subtyping extensions.
• Pierce, Benjamin (2002), Types and Programming Languages, MIT Press, ISBN 0-262-16209-1 covers lambda calculi from a practical type system perspective; some topics like dependent types are only mentioned, but subtyping is an important topic.

Documents

• Achim Jung, A Short Introduction to the Lambda Calculus-(PDF)
• Dana Scott, A timeline of lambda calculus-(PDF)
• Raúl Rojas, A Tutorial Introduction to the Lambda Calculus-(PDF)
• Peter Selinger, Lecture Notes on the Lambda Calculus-(PDF)
• Marius Buliga, Graphic lambda calculus
• Lambda Calculus as a Workflow Model by Peter Kelly, Paul Coddington, and Andrew Wendelborn; mentions graph reduction as a common means of evaluating lambda expressions and discusses the applicability of lambda calculus for distributed computing (due to the Church–Rosser property, which enables parallel graph reduction for lambda expressions).

Notes[edit]

References[edit]

Some parts of this article are based on material from FOLDOC, used with permission.

External links[edit]

• Graham Hutton, Lambda Calculus, a short (12 minutes) Computerphile video on the Lambda Calculus
• Helmut Brandl, Step by Step Introduction to Lambda Calculus
• «Lambda-calculus», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• David C. Keenan, To Dissect a Mockingbird: A Graphical Notation for the Lambda Calculus with Animated Reduction
• L. Allison, Some executable λ-calculus examples
• Georg P. Loczewski, The Lambda Calculus and A++
• Bret Victor, Alligator Eggs: A Puzzle Game Based on Lambda Calculus
• Lambda Calculus Archived 2012-10-14 at the Wayback Machine on Safalra’s Website Archived 2021-05-02 at the Wayback Machine
• LCI Lambda Interpreter a simple yet powerful pure calculus interpreter
• Lambda Calculus links on Lambda-the-Ultimate
• Mike Thyer, Lambda Animator, a graphical Java applet demonstrating alternative reduction strategies.
• Implementing the Lambda calculus using C++ Templates
• Shane Steinert-Threlkeld, «Lambda Calculi», Internet Encyclopedia of Philosophy
• Anton Salikhmetov, Macro Lambda Calculus