На этой странице вы узнаете
- Можно ли представить прогресс в виде монотонной функции?
- Где можно встретить идеальную симметрию?
- Как сломать функцию?
В восточных боевых искусствах спортсмены разбивают доски руками. А вот плотники для разрезания досок используют пилу, то есть вспомогательный инструмент. Так стоит ли нам справлять с параметрами голыми руками? Или проще взять специальный инструмент? Такая же дилемма может встать и в решении задач с параметром.
Монотонность функции
В математике пилу, разумеется, не используют. Зато мы можем использовать свойства функции, которые и будут нашей опорой при решении задач с параметром. Давайте попробуем собрать свой “ящик с инструментами”.
Возможно, до детального знакомства с темой, вам захочется вспомнить «Определение и график функции».
Многим из нас знакома монотонная и скучная работа. Например, удалять с телефона ненужные фотографии или стирать пометки из учебника, прежде чем вернуть его в школьную библиотеку. Приходится повторять одно и то же действие на протяжении всего цикла работы — это утомительно и однообразно.
Монотонная функция так же, как и работа, не меняет своих свойств на всем промежутке.
Монотонная функция — функция, строго возрастающая или строго убывающая на промежутке.
Разберемся со “строгостью” функций.
Строго возрастающая функция на промежутке — функция, большему значению аргумента которой из промежутка соответствует большее значение функции.
Иными словами: чем больше х, тем больше у.
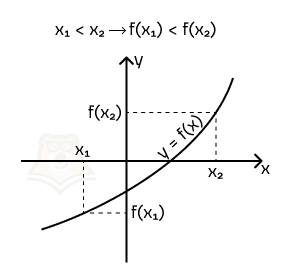
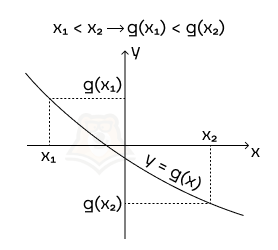
Строго убывающая функция на промежутке — функция, большему значению аргумента которой соответствует меньшее значение функции.
Или чем больше х, тем меньше у.
Идеальная картина: чем больше мы работаем, тем лучше наш результат. С каждым днем мы все растем, становимся лучше и избегаем ошибок. То есть наш прогресс — это монотонная функция.
К сожалению, реальность несколько другая. Прогресс никогда не будет монотонной функцией, всегда будут взлеты и падения. Ошибки — неотъемлемая часть обучения, поэтому нельзя бояться неудач. Если представить прогресс человека в виде функции, то она постоянно будет менять промежутки возрастания на промежутки убывания и обратно.
Что еще можно сказать про возрастание функции? Вспомним «Производную», а именно — ее знаки на промежутках возрастания и убывания функции:
- если производная положительна на некотором промежутке, то функция возрастает на этом промежутке;
- если производная отрицательна на некотором промежутке, то функция убывает на этом промежутке.
Свойства монотонной функции
Монотонные функции обладают своими свойствами, которые могут пригодиться при решении задач.
Свойство 1. Монотонная функция принимает свое значение единственный раз.
Это можно проследить по графику: для каждого значения у будет единственное значение х.
Свойство 2. Если две функции f(x) и h(x) возрастают на промежутке, то функция y = f(x) + h(x) также будет возрастать.
Это же свойство будет работать и с убыванием функции.
Если две функции f(x) и h(x) убывают на промежутке, то функция
y = f(x) + h(x) также будет убывать.
Свойство 3. Если функции f(x) и h(x) возрастают на промежутке, то функция y = f(x) * h(x) тоже будет возрастать при
и
Аналогично и с убыванием.
Пример 1. При каких значениях параметра а любое решение уравнения 4x7 + 2x + a = 0 принадлежит отрезку [−1;1].
Решение.
Шаг 1. Какой является эта функция: возрастающей или убывающей? Проверим это с помощью производной.
Заметим, что поскольку х стоит в четной степени, то какое бы число мы ни подставили в производную, оно будет положительно. Значит, эта функция строго возрастает.
Шаг 2. Как определить, что решение уравнения будет лежать в заданном отрезке? Решением уравнения будет пересечение функции и оси х. То есть точка этого пересечения должна лежать между −1 и 1 включительно.
На графике это будет выглядеть так:
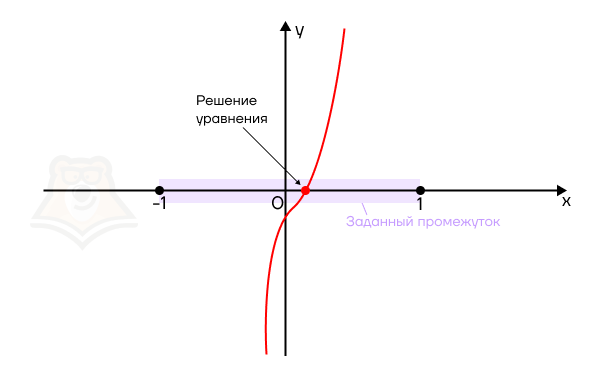
А вот такие случаи нам уже не подходят, поскольку решение уравнения будет лежать за пределами заданного промежутка.
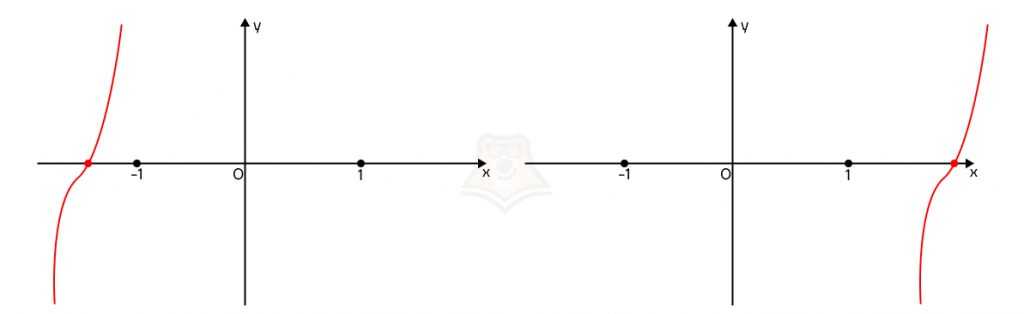
Шаг 3. При x = — 1 функция отрицательна, а при x = 1 функция будет положительна при любом положении в заданном промежутке. Следовательно, мы можем задать ее положение на графике с помощью значения функции при x = — 1 и x = 1.
Шаг 4. Получаем два условия, которые должны выполниться одновременно, то есть систему.
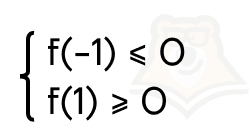
Шаг 5. Решаем первое неравенство системы:
Решаем второе неравенство системы:
Следовательно, условия будут выполняться при
Ответ:
Итак, в наш ящик с инструментами отправляется монотонность функции, ее возрастание и убывание.
Четность функции
Четной функцией называется такая функция, график которой симметричен относительно оси Оу.
Для такой функции будет выполняться условие f(x) = f( — x).
В природе идеальная симметрия почти не встречается: даже на миллиметр, но одна сторона животного, растения или человека будет отличаться от другой. Идеальная симметрия встречается в математике, в четной функции. Симметрия часто используется в искусстве и архитектуре для создания гармоничной композиции. Если посмотреть на планы и фасады некоторых храмов и дворцов, созданных много лет назад, то окажется, что части здания располагаются симметрично относительно оси.
Четность функции — это точно не универсальный инструмент, как, например, молоток. Скорее это редкий ключ, который будет большую часть времени просто лежать в ящике, но пригодится в самый ответственный момент.
Четность можно применить, когда в функции стоят модули, четные степени, четные корни и другие условия, с которыми минус “не дружит”.
Шаг 1. Перенести все слагаемые в одну сторону и ввести f(x).
Шаг 2. Проверить функцию на четность. Для этого нужно удостовериться, что условие f(x) = f( — x) выполняется.
Четная функция имеет четное количество корней, кроме случая
х = 0, когда корень всего один.
Шаг 3. Подставить х = 0.
Шаг 4. Рассмотреть данные значения в зависимости от условия задачи.
Почему функция имеет четное количество корней, кроме случая х = 0? Возьмем зеркало и попробуем подвигать карандаш относительно него. При этом само зеркало будет осью у.
На какое бы расстояние мы не отодвинули карандаш, в зеркале всегда будет его отражение. Следовательно, мы получим два карандаша.
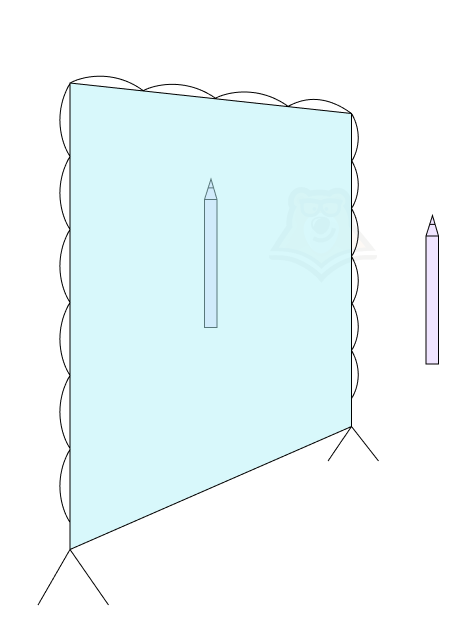
Но если мы приложим карандаш к самому зеркалу, то два карандаша объединятся в один. Условно мы можем сказать, что получили один карандаш.
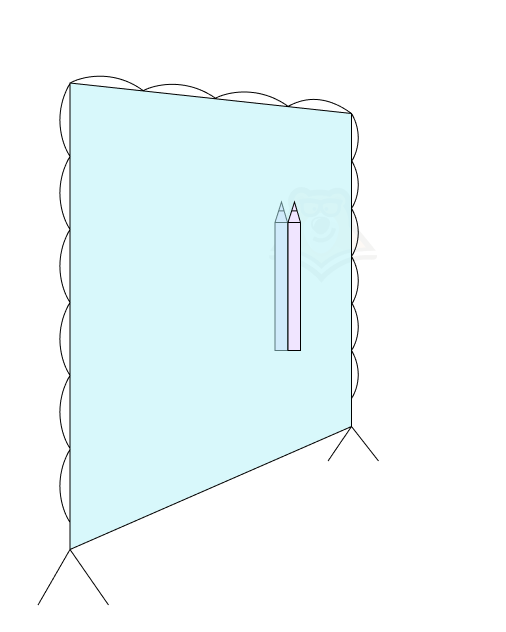
Такая же логика и с корнями четной функции: пока они не будут лежать на зеркале, то есть на оси у, их всегда будет два.
Пример 2. Найдите все значения параметра а, при каждом из которых уравнение
sqrt{a^2+x^2}=a^2-a-14-cos5x
имеет единственное решение.
Решение.
Шаг 1. Введем две функции:
Будем действовать согласно алгоритму. Первый шаг мы уже сделали. Теперь убедимся, что полученные функции четные.
f(-x)=sqrt{a^2+(-x^2)}=sqrt{a^2+x^2}
— функция четная.
g(-x)=a^2-a-14-cos5(-x)=a^2-a-14-cos5x
— функция четная.
Шаг 2. Поскольку функции четные, то при решении уравнения х будет появляться второе решение ( — x). Вспоминаем зеркало: уравнение будет иметь единственное решение только при x = 0.
Шаг 3. Подставим x = 0 в наше уравнение.
sqrt{a^2+0^2} =a^2-a-14-cos5*0
Подробнее про такое преобразование можно прочесть в статье «Модуль».
Шаг 4. Раскроем модуль двумя способами.
— этот корень отрицательный, а значит, он не подходит к условию раскрытия модуля.
— в этом случае нам подходит только корень
Шаг 5. Получаем корни
и
Проверим, что при них действительно получается решение x = 0.
Шаг 6. a = 5
sqrt{5^2+x^2}=5^2-5-14-cos5x
— решение только при x=0.
sqrt{(-sqrt{15})^2+x^2}=(-sqrt{15})^2+sqrt{15}-14-cos5x
sqrt{-15+x^2}=1+sqrt{15}-cos5x
— решение только при x=0.
Следовательно, корни найдены верно.
Ответ: 5, -√15
В ящик с инструментами отправляется четность функции.
Значение функции
В заданиях с параметрами могут встречаться области определений и значений функции, наибольшее и наименьшее значения. Подробнее про эти свойства в обычных функциях можно прочитать в статье «Исследование функции с помощью производной».
Обычно эти свойства функции применяются в заданиях, где просят исследовать функцию, а не найти количество решений. Как их применять? Рассмотрим на примере.
Пример 1. Найдите все значения параметра а, при каждом из которых функция f(x) = — x2 + 4|a2 -x|+ 6x имеет хотя бы одну точку минимума.
Решение. Для начала немного упростим функцию и раскроем модуль.
При
f(x)=-x^2+4a^2-4x+6x=-x^2+2x+4a^2
— мы получили квадратное уравнение.
Оно задает параболу с ветвями, направленными вниз. Ее вершина будет в точке
При
f(x)=-x^2-4a^2+4x+6x=-x^2+10x-4a^2
— мы получили квадратное уравнение.
Оно задает параболу с ветвями, направленными вниз. Ее вершина будет в точке
На графике должно получиться две параболы, которые объединятся в одну фигуру, похожую на горы. Как эти горы могут располагаться относительно друг друга?
Первая гора может быть выступом для второй горы. То есть одна гора плавно будет перетекать в другую.
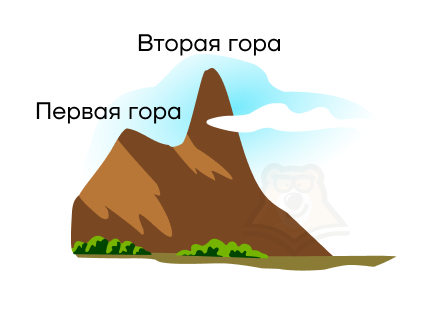
Они могут находиться рядом друг с другом, а между ними будет перевал.
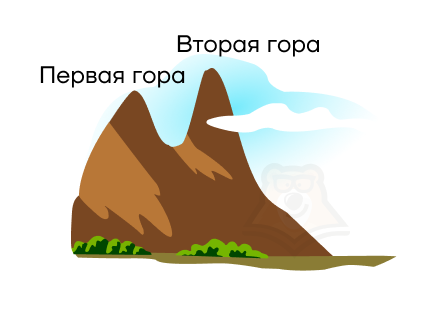
Вторая гора может быть выступом в первой горе.
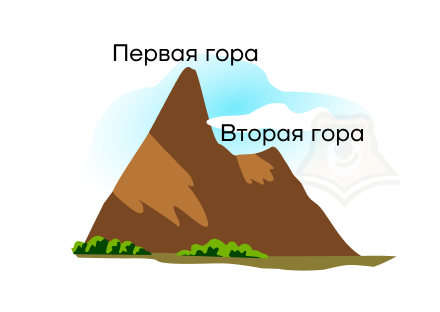
Случай, когда горы находятся на разных материках планеты, мы не рассматриваем, поскольку они обязательно должны быть связаны между собой, иначе бы задавались разными функциями.
Теперь мы можем построить примерные графики функций. При этом в значении a2 будет перелом, поскольку в этой точке происходит переход от первого случая раскрытия модуля ко второму. Эта точка будет называться точкой излома.
Точка излома — точка, в которой одна функция переходит в другую из-за раскрытия модуля.
Если в функции появляется модуль, ее график будет состоять из нескольких ветвей параболы или прямых. Это связано с тем, что при раскрытии модуля получается две разные функции, соответственно, они имеют разные графики.
Однако при построении графика всей функции, два графика объединяются в один. В точке их соединения, то есть точке излома, функция меняет свое направление.
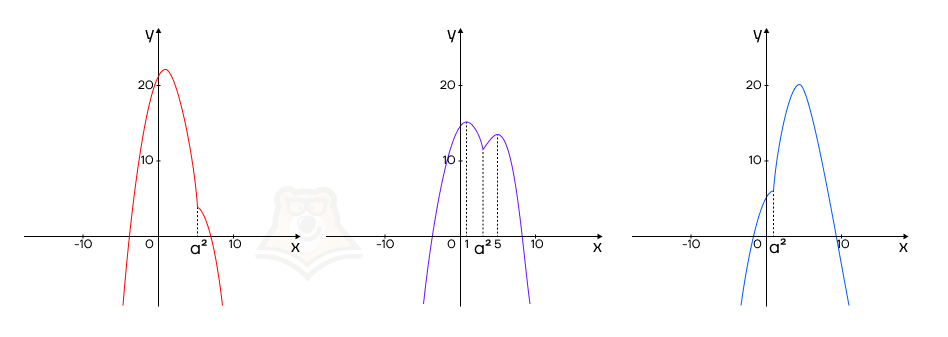
Заметим, что точка минимума — точка, где функция перестает убывать и начинает возрастать — есть только во втором случае, когда каждая “гора” имеет вершину, а точка a2 лежит между ними.
Следовательно, получаем неравенство 1 < a2 < 5. Разобьем его на системы из двух неравенств:
Решим первое неравенство системы:
(a-sqrt{5})(a+sqrt{5})<0
Решим второе неравенство системы:
ain(-infty;-1)cup(1;+infty)
Осталось найти ответ для системы.

Отсюда
ain(-sqrt{5};-1)cup(1;sqrt{5})
Ответ:
ain(-sqrt{5};-1)cup(1;sqrt{5})
Для удобства решения таких заданий мы можем вывести алгоритм.
Шаг 1. Раскрыть модули.
Шаг 2. Рассмотреть полученные функции и проанализировать их. Например, если получаются параболы, то нужно определить направление ветвей и положение ветвей.
Шаг 3. Проанализировать точку излома: найти все случаи, где она может находиться в зависимости от значений параметра.
Шаг 4. Найти значения параметра для каждого подходящего случая.
Вот мы и собрали инструменты для решения параметров с помощью свойств функций. В наш ящик вошли:
- монотонность функции;
- возрастание и убывание функции;
- четность функции и ее симметрия;
- область определения и область значений функций;
- наибольшее и наименьшее значение функции и точки экстремума.
Фактчек
- Монотонная функция — функция, строго возрастающая или строго убывающая на промежутке. Если при решении задач с параметром доказать, что функция монотонно возрастает или монотонно убывает, можно применить свойство производных. Это же свойство можно применить и для доказательства монотонности функции.
- Производная положительна на промежутках возрастания функции и отрицательна на промежутках убывания.
- Четной функцией называется такая функция, график которой симметричен относительно оси Оу. Для такой функции будет выполняться условие f(x)=f(-x). Это же условие можно применять для доказательства четности функции.
- В четной функции всегда будет два решения, кроме случая х = 0. При х = 0 у функции будет единственное решение.
- Точка излома — точка, в которой одна функция переходит в другую из-за раскрытия модуля. Зная точки излома, можно проанализировать поведение функции.
Проверь себя
Задание 1.
На заданном промежутке функция монотонно возрастает. Чему будет равна производная функции на этом промежутке?
- Производная функции будет отрицательна.
- Производная функции будет положительна.
- Производная функции будет равна 0.
- Невозможно определить производную, не зная функцию.
Задание 2.
Выберите верные утверждения для убывающей функции.
- Чем больше значение х, тем больше значение у.
- Чем больше значение х, тем меньше значение у.
- Производная функции положительна.
- Производная функции отрицательна.
Задание 3.
Дана четная функция. Сколько будет решений при х = 0?
- Четыре решения.
- Два решения.
- Одно решение.
- Решений не будет.
Задание 4.
Что такое точка излома?
- Точка, в которой одна функция переходит в другую из-за раскрытия модуля.
- Любая точка на функции, в которой график меняет свое направление.
- Точки экстремума.
- Асимптоты функции.
Ответы: 1. — 2 2. — 24 3. — 3 4. — 1.
Цель данной работы – изучение различных способов решения задач с параметрами.
Возможность и умение решать задачи с параметрами демонстрируют владение методами
решения уравнений и неравенств, осмысленное понимание теоретических сведений,
уровень логического мышления, стимулируют познавательную деятельность. Для
развития этих навыков необходимы длительнее усилия, именно поэтому в профильных
10-11 классах с углубленным изучением точных наук введен курс: “Математический
практикум”, частью которого является решение уравнений и неравенств с
параметрами. Курс входит в число дисциплин, включенных в компонент учебного
плана школы.
Успешному изучению методов решения задач с параметрами могут помочь
элективный или факультативный курсы, или компонент за сеткой по теме: “Задачи с
параметрами”.
Рассмотрим четыре больших класса задач с параметрами:
- Уравнения, неравенства и их системы, которые необходимо решить для
любого значения параметра, либо для значений параметра, принадлежащих
определенному множеству. - Уравнения, неравенства и их системы, для которых требуется определить
количество решений в зависимости от значения параметра. - Уравнения, неравенства и их системы, для которых требуется найти все те
значения параметра, при которых указанные уравнения (системы, неравенства)
имеют заданное число решений. - Уравнения, неравенства и их системы, для которых при искомых значениях
параметра множество решений удовлетворяет заданным условиям в области
определения.
Методы решений задач с параметрами.
1. Аналитический метод.
Это способ прямого решения, повторяющий стандартные процедуры нахождения
ответа в задачах без параметра.
Пример 1. Найдите все значения параметра
a, при которых уравнение:
(2a – 1)x2 + ax + (2a – 3) =0 имеет не более
одного корня.
Решение:
При 2a
– 1 = 0 данное уравнение квадратным не является, поэтому случай
a =1/2 разбираем отдельно.
Если a = 1/2, то уравнение принимает вид
1/2x – 2 = 0, оно имеет один корень.
Если a ≠ 1/2,
то уравнение является квадратным; чтобы оно имело не более одного корня
необходимо и достаточно, чтобы дискриминант был неположителен:
D = a2 – 4(2a – 1)(2a – 3) = -15a2
+ 32a – 12;
Чтобы записать окончательный ответ, необходимо понять,
2. Графический метод.
В зависимости от задачи (с переменной x
и параметром a)
рассматриваются графики в координатной плоскости (x;y)
или в плоскости (x;a).
Пример 2. Для каждого значения параметра a
определите количество решений уравнения
.
Решение:
Заметим, что количество решений уравнения
равно количеству точек пересечения графиков функций
и y = a.
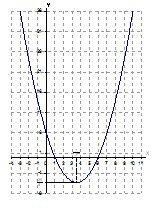
График функции
показан на рис.1.
Рис.1
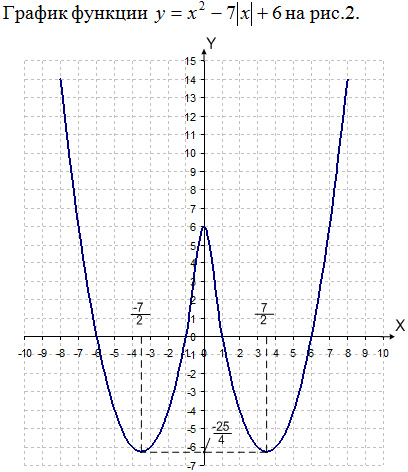
Рис. 2
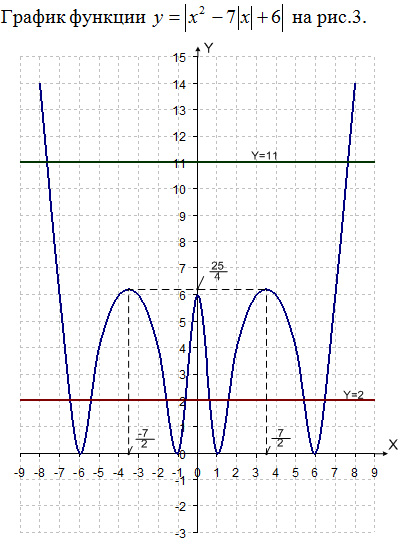
Рис. 3
y = a – это горизонтальная прямая. По графику несложно
установить количество точек пересечения в зависимости от a
(например, при a =
11 – две точки пересечения; при a
= 2 – восемь точек пересечения).
Ответ: при a < 0 – решений нет; при a
= 0 и a = 25/4 – четыре решения; при
0 < a < 6 – восемь решений; при a
= 6 – семь решений; при
6 < a < 25/4 – шесть решений; при a >
25/4 – два решения.
3. Метод решения относительно параметра.
При решении этим способом переменные х и а принимаются
равноправными, и выбирается та переменная, относительно которой аналитическое
решение становится более простым. После упрощений нужно вернуться к исходному
смыслу переменных х и а и закончить решение.
Пример 3. Найти все значения параметра а , при каждом из которых
уравнение
= —ax +3a +2 имеет единственное решение.
Решение:
Будем решать это уравнение заменой переменных. Пусть
= t , t ≥ 0
, тогда x = t2 + 8 и
уравнение примет вид at2 + t + 5a – 2 = 0
. Теперь задача состоит в том, чтобы найти все а,
при которых уравнение at2 + t + 5a – 2 =
0 имеет единственное неотрицательное решение. Это имеет
место в следующих случаях.
1) Если а = 0, то уравнение имеет единственное решение t
= 2.
Решение некоторых типов уравнений и неравенств с параметрами.
Задачи с параметрами помогают в формировании логического мышления, в
приобретении навыков исследовательской деятельности.
Решение каждой задачи своеобразно и требует к себе индивидуального,
нестандартного подхода, поскольку не существует единого способа решения таких
задач.
Ⅰ. Линейные уравнения.
Задача № 1.
При каких значениях параметра b
уравнение
не имеет корней?
Ⅱ. Степенные уравнения, неравенства и их системы.
Задача №2. Найти все значения параметра a,
при которых множество решений неравенства:
содержит число 6, а также содержит два отрезка длиной 6, не имеющие общих точек.
Решение:
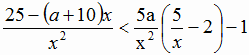
Преобразуем обе части неравенства.
Для того, чтобы множество решений неравенства содержало число 6, необходимо и
достаточно выполнение условия:
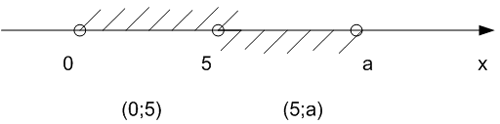
При a > 6 множество
решений неравенства:
.
Интервал (0;5) не может содержать ни одного отрезка
длины 6. Значит, два непересекающихся отрезка длины 6 должны содержаться в
интервале (5; a).
Это
Ⅲ. Показательные уравнения, неравенства и системы.
Задача № 3. В области определения функции
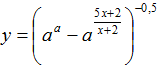
все целые положительные числа и сложили их. Найти все значения, при которых
такая сумма будет больше 5, но меньше 10.
Решение:
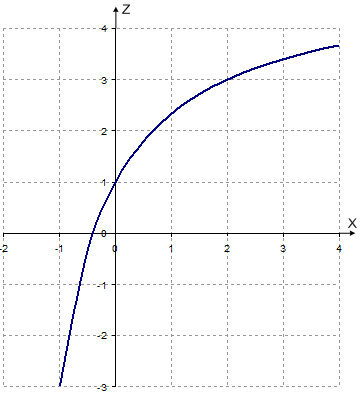
1) Графиком дробно-линейной функции
является гипербола. По условию x > 0. При
неограниченном возрастании х дробь
монотонно убывает и приближается к нулю, а значения функции z возрастают
и приближаются к 5. Кроме того, z(0) = 1.
Рис. 5
2) По определению степени область определения D(y)
состоит из решений неравенства
.
При a = 1 получаем неравенство, у которого решений
нет. Поэтому функция у нигде не определена.
3) При 0 < a < 1 показательная функция с
основанием а убывает и неравенство
равносильно неравенству
. Так как x > 0 , то z(x) >
z(0) = 1 . Значит, каждое положительное значение х
является решением неравенства
. Поэтому для таких а указанную в условии сумму нельзя найти.
4) При a > 1 показательная функция с основанием
а возрастает и неравенство
равносильно неравенству
. Если a ≥ 5,
то любое положительное число является его решением, и указанную в условии сумму
нельзя найти. Если 1 < a < 5, то множество
положительных решений – это интервал (0;x0)
, где a = z(x0) .
5) Целые числа расположены в этом интервале подряд, начиная с 1. Вычислим
суммы последовательно идущих натуральных чисел, начиная с 1 : 1; 1+2 = 3; 1+2+3
= 6; 1+2+3+4 = 10;… Поэтому указанная сумма будет больше 5 и меньше 10, только
если число 3 лежит в интервале (0;x0),
а число 4 не лежит в этом интервале. Значит, 3 < x0
≤ 4 . Так как
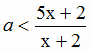
возрастает на
,
то z(3) < z(x0)
≤ z(4) .
Решение иррациональных уравнений и неравенств, а также уравнений, неравенств
и систем, содержащих модули рассмотрены в Приложении 1.
Задачи с параметрами являются сложными потому, что не существует единого
алгоритма их решения. Спецификой подобных задач является то, что наряду с
неизвестными величинами в них фигурируют параметры, численные значения которых
не указаны конкретно, но считаются известными и заданными на некотором числовом
множестве. При этом значения параметров существенно влияют на логический и
технический ход решения задачи и форму ответа.
По статистике многие из выпускников не приступают к решению задач с
параметрами на ЕГЭ. По данным ФИПИ всего 10% выпускников приступают к решению
таких задач, и процент их верного решения невысок: 2–3%,
поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе
задач с параметрами, учащимися школ по-прежнему остается актуальным.
Уравнения с параметрами.
Исследование и решение уравнений с параметрами считается не самым простым разделом школьной математики. Однако, параметр, как понятие, часто воспринимается школьниками гораздо более сложным, чем есть в действительности. Здесь в первом пункте представлены очень простые вводные примеры использования параметров в уравнениях. Те, для кого это понятие не составляет большой трудности, могут сразу перейти к решению задач, которые представлены ниже.
Что такое уравнение с параметром?
Допустим нам нужно решить уравнение 2х + 5 = 2 − x.
Решение: 2x + x = 2 − 5; 3x = −3; x = −3/3 = −1.
Теперь нужно решить уравнение 2x + 5 = 3 − x.
Решение: 2x + x = 3 − 5; 3x = −2; x = −2/3
Затем нужно решить уравнение 2x + 5 = 0,5 − x.
Решение: 2x + x = 0,5 − 5; 3x = −4,5; x = −4,5/3 = −1,5.
А потом может потребоваться решить уравнение 2x + 5 = 10,7 − x или уравнение 2x + 5 = −0,19 − x.
Понятно, что уравнения похожи, а потому их решение будет сопровождаться теми же действиями, что выше. Возникает естественный вопрос — сколько можно делать одно и то же?
Уменьшим себе трудозатраты. Заметим, что все эти уравнения отличаются только одним числом в правой части. Обозначим это число символом a .
Получим уравнение 2х + 5 = a − х,
где a — переменная величина, вместо которой можно подставить нужное числовое значение и получить нужное уравнение. Эта переменная и называется параметром.
Решим это уравнение так же, как и все предыдущие.
Решение: 2х + 5 = a − x; 2x + x = a − 5; 3x = a − 5; x = (a − 5)/3.
Теперь для того, чтобы найти ответы для двух последних примеров, мы можем не повторять полностью всё решение каждого уравнения, а просто подставить в полученную формулу для х числовое значение параметра а:
x = (10,7 − 5)/3 = 5,7/3 = 1,9;
x = (−0,19 − 5)/3 = −5,19/3 = −1,73.
Таким образом, под термином «уравнение с параметром», фактически, скрывается целое семейство «почти одинаковых уравнений» , которые отличаются друг от друга только одним числом (одним слагаемым или одним коэффициентом) и одинаково решаются. Параметр — это число, которое меняется от уравнения к уравнению.
Полученную формулу для корня уравнения мы можем запрограммировать на компьютере. Достаточно будет только ввести значение параметра a, чтобы получить решение любого такого уравнения.
Рассмотрим еще один пример.
Замечаем, что они похожи друг на друга и отличаются только первым коэффициентом. Обозначим его, например, символом k.
Решим уравнение kх + 5 = 2 − x с параметром k.
С помощью этой формулы вычислим все ответы для приведенных уравнений.
x = −3/(2 + 1) = −1
x = −3/(3 + 1) = −0,75
x = −3/(−4 + 1) = 1
x = −3/(17 + 1) = −1/6
Можем ли мы теперь запрограммировать эту формулу и сказать, что с её помощью можно решить любое аналогичное уравнение?
Запрограммировать можем. Компьютер справится как с очень большими значениями коэффициента, так и с очень маленькими.
Например, если введём k = 945739721, то для уравнения заданного вида будет получен корень примерно равный −0,0000000031721201195353831188, если k = 0,0000004, то получим корень ≈ −2,9999988000004799998080000768.
Но, если мы введем в программу, казалось бы, более простое значение k = −1, то компьютер зависнет.
Почему?
Посмотрим внимательнее на формулу x = −3/(−1 + 1) = −3/0. Деление на ноль.
Посмотрим на соответствующее уравнение −1·х + 5 = 2 − x.
Преобразуем его −х + x = 2 − 5.
Оказывается, оно равносильно уравнению 0 = −3 (. ) и не может иметь корней.
Таким образом, из общего подхода к решению «почти одинаковых уравнений» могут существовать исключения, о которых нужно позаботиться отдельно. Т.е. провести предварительное исследование всего семейства уравнений. Именно этому и учатся на уроках математики с помощью так называемых задач с параметрами.
Графические способы решения уравнений
Сначала вспомним, что представляет собой графический способ решения обычного уравнения (без параметра).
Пусть дано уравнение вида f(x) = g(x) . Построим графики функций y = f(x) и y = g(x) и найдём точки пересечения этих графиков. Абсциссы точек пересечения и есть корни уравнения.
Для быстрого построения эскизов графиков повторите еще раз графики элементарных функций, которые изучаются в школьном курсе математики, и правила преобразования графиков функций.
Рассмотрим примеры.
1. Решить уравнение
2х + 5 = 2 − x
Ответ: x = −1.
2. Решить уравнение
2х 2 + 4х − 1 = 2х + 3
3. Решить уравнение
log2х = −0,5х + 4
Ответ: x = 2.
Первые два из приведенных уравнений вы можете решить и аналитически, так как это обычные линейное и квадратное уравнения. Второе уравнение содержит функции разных классов — степенную (здесь линейную) и трансцендентную (здесь логарифмическую). Для таких случаев выбор способов решения у школьников очень ограничен. Фактически, единственным доступным способом является именно графическое решение.
Внимание: Для корней, найденных графическим способом, обязательна проверка! Вы уверены, что на третьем рисунке пересечение именно в точке х = 4 , а не в точке 3,9 или 4,1? А если на реальном экзамене у вас нет возможности построить график достаточно точно? На чертеже «от руки» разброс может быть еще больше. Поэтому алгоритм действий должен быть следующим:
- Предварительный вывод: х ≈ 4.
- Проверка: log24 = −0,5·4 + 4; 2 = −2 + 4; 2 ≡ 2.
- Окончательный вывод х = 4.
Чтобы графически решать уравнения с параметрами надо строить не отдельные графики, а их семейства.
Решение уравнений с параметрами с помощью графиков.
Задача 1.
Найти все значения параметра q при которых уравнение |x + 1| − |x − 3| − x = q 2 − 8q + 13 имеет ровно 2 корня.
При каждом значении параметра q можно вычислить значение выражения q 2 − 8q + 13 . Результат обозначим переменной а.
Т.е. примем q 2 − 8q + 13 = a и решим уравнение с параметром |x + 1| − |x − 3| − x = a
Строим график функции y = |x + 1| − |x − 3| − x , расположенной в левой части уравнения.
Для этого разобьём числовую ось на отрезки точками, в которых каждый из встречающихся модулей принимает нулевое значение.

Для каждого из этих участков раскроем модули с учётом знаков.
Вспомним: по определению |x| = x, если х ≥ 0, и |x| = −x, если х Чтобы проверить знаки модулей на участке достаточно подставить любое промежуточное значение x из этого отрезка, например, −2, 0 и 4.
Таким образом на участке I, где −∞ имеем −(x + 1) + (x − 3) − x = − x − 4.
Следовательно, должны построить график функции y = − x − 4 .
Это линейная функция. Её график прямая линия, которую можно построить по двум точкам, например, x = 0, y = −4 и у = 0, x = −4. Cтроим всю прямую бледной линией, а затем выделяем часть графика, относящуюся только к рассматриваемому участку.
Аналогично, разбираемся с оставшимися двумя участками.
На участке II, где −1 имеем (x + 1) + (x − 3) − x = x − 2
и должны построить соответствующую часть графика функции y = x − 2 .
На участке III, где 3 , имеем (x + 1) − (x − 3) − x = − x + 4
и должны построить соответствующую часть графика функции y = − x + 4 .
Последовательное построение итогового графика показано ниже. (Чтобы увеличить рисунок, нужно щелкнуть по нему левой кнопкой мыши.)
Замечание: если вы освоили тему Преобразование графиков функций, то с этой частью задачи сможете справиться быстрее, чем показано в примере.
Итак, построение графика функции, расположенной в левой части уравнения, мы завершили. Посмотрим, что находится в правой части.
График функции y = a представляет собой прямую линию, параллельную оси абсцисс (Ox), и пересекающую ось ординат (Oy) в точке а. Так как а — параметр, который может принимать разные значения, то нужно построить целое семейство таких параллельных линий, пересекающих ось ординат на разной высоте. Очевидно, что все графики семейства построить мы не сможем, поскольку их бесконечное множество. Изобразим для примера несколько штук в районе уже построенного графика функции. Ниже прямые семейства y = a показаны красным цветом.
Из рисунка видно, что количество точек пересечения каждой из красных прямых с ранее построенным (зелёным) графиком зависит от высоты, на которой расположена эта прямая, т.е. от параметра а. Прямые, расположенные ниже y = −3 , пересекают график в одной точке, а значит эти уравнения имеют только одно решение. Прямые, проходящие на уровне −3 имеют по три точки пересечения, значит соответствующие уравнения будут иметь по три решения. Прямые, расположенные выше точки y = 1 , снова имеют только по одной точке пересечения.
Ровно две точки пересечения с зелёным графиком будут иметь только прямые y = 1 и y = −3 . Соответствующие уравнения будут иметь ровно два корня, что и требовалось определить в задании.
Однако мы нашли значения введённого нами параметра а, при котором заданное уравнение имеет 2 корня, а вопрос задачи состоял в том, чтобы найти все значения параметра q. Для этого придётся решить следующую совокупность уравнений: 
Это обычные квадратные уравнения, которые решаются через дискриминант или по теореме Виета. 
Таким образом, окончательный ответ: <2;4;6>.
Задача 2.
Найти все значения параметра a, при которых уравнение (2 − x)x(x − 4) = a имеет ровно 3 корня.
Рассмотрим функцию y = (2 − x)x(x − 4) . Видно, что если раскрыть скобки, то старший член будет −х 3 . Т.е. графиком функции должна быть кубическая парабола, причем на при x, стремящемcя к +∞, y → −∞, а при x, стремящемся к −∞, y → +∞.
Поскольку уравнение (2 − x)x(x − 4) = 0 имеет три корня 2, 0 и 4, то график функции будет пересекать ось абсцисс трижды.
Понятно, что при упомянутых условиях график непрерывной функции должен иметь участок с «волной». Строим от руки эскиз графика.
Правая часть уравнения y = a такая же, как в предыдущей задаче. Поэтому дальнейшие построения не требуют комментариев. Смотрите рисунки. Чтобы увеличить, используйте щелчок мышью.





Из рисунков видно, что прямые, отделяющие линии с тремя точками пересечения от других случаев, проходят через экстремумы кубической функции. Поэтому определяем значения ymax и ymin через производную. (Исследовать функцию полностью не нужно, так как примерное положение точек экстремума мы видим на эскизе графика.) Обратите внимание на то, что при вычислении значений функции используются точные значения x и формулы сокращенного умножения. Приближенные значения в промежуточных вычислениях не используют.
Ответ:
Задача для самостоятельного решения
Задача 3.
При каком наибольшем отрицательном значении параметра а уравнение 
Ответ: -1,625
Задача реального экзамена ЗНО-2013 (http://www.osvita.ua/).
Переход на главную страницу сайта «Математичка».
Есть вопросы? пожелания? замечания?
Обращайтесь — mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.
Что такое параметр? Простые задачи с параметрами
Одна из сложных задач Профильного ЕГЭ по математике — задача с параметрами. В ЕГЭ 2022 года это №17. И даже в вариантах ОГЭ они есть. Что же означает это слово — параметр?
Толковый словарь (в который полезно время от времени заглядывать) дает ответ: «Параметр — это величина, характеризующая какое-нибудь основное свойство устройства, системы, явления или процесса».
Хорошо, параметр — это какая-либо характеристика, свойство системы или процесса.
Вот, например, ракета выводит космический аппарат в околоземное пространство. Как вы думаете — какие параметры влияют на его полет?
Если корабль запустить с первой космической скоростью, приближенно равной 7,9 км/с, он выйдет на круговую орбиту.
Вторая космическая скорость, приближенно равная 11,2 км/с, позволяет космическому кораблю преодолеть поле тяжести Земли. Третья космическая скорость, приближенно равная 16,7 км/с, дает возможность преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы.
А если скорость меньше первой космической? Значит, тонны металла, топлива и дорогостоящей аппаратуры рухнут на землю, сопровождаемые репликой растерянного комментатора: «Кажется, что-то пошло не так».
Скорость космического корабля можно — параметр, от которого зависит его дальнейшая траектория и судьба. Конечно, это не единственный параметр. В реальных задачах науки и техники, задействованы уравнения, включающие функции многих переменных и параметров, а также производные этих функций.
1. Теперь пример из школьной математики.
Все мы помним, что такое квадратное уравнение. Это уравнение вида , где коэффициент а не равен нулю.
Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.
Дискриминант квадратного уравнения:
Если 
Если , квадратное уравнение имеет единственный корень
Если 


Если при , уравнение имеет единственный корень.
Если 
В нашем уравнении с — параметр, величина, которая принимать любые значения. Но от этого параметра с зависит количество корней данного уравнения.
Для того чтобы уверенно решать задачи с параметрами, необходимо отличное знание и алгебры, и планиметрии.
И еще две простые задачи с параметром.
2. Найдите значение параметра p, при котором уравнение имеет 2 различных корня.
Квадратное уравнение имеет два различных корня, когда 
Найдем дискриминант уравнения
Т.к. 
Вспомним, как решаются квадратичные неравенства (вы проходили это в 9 классе).
Найдем корни квадратного уравнения . Это и
Разложим левую часть неравенства на множители:
Рисуем параболу с ветвями вверх. Она пересекает ось р в точках и
3. При каких значениях параметра k система уравнений не имеет решений?
Оба уравнения системы — линейные. График линейного уравнения — прямая. Запишем уравнения системы в привычном для нас виде, выразив у через х:
Первое уравнение задает прямую с угловым коэффициентом . Второе уравнение — прямую с угловым коэффициентом -2.
Система уравнений не имеет решений, если эти прямые не пересекаются, то есть параллельны. Это значит, что и .
Действительно, в этом случае первое уравнение задает прямую , а второе — параллельную ей прямую
Уравнения с параметром
Разделы: Математика
Справочный материал
Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.
Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.
Если 1 – а = 0, т.е. а = 1, то х0 = -2 корней нет
Если 1 – а 0, т.е. а 1, то х =
Пример 4.
Если а = 1, то 0х = 0
х – любое действительное число
Если а = -1, то 0х = -2
Корней нет
Если а 1, а -1, то х = 
Это значит, что каждому допустимому значению а соответствует единственное значение х.
если а = 5, то х =
=
;
Дидактический материал
3. а = 
4. + 3(х+1)
5. = –
6. =
Ответы:
- При а1 х =;
- При а3 х = ;
- При а1, а-1, а0 х = ;
при а = 1 х – любое действительное число, кроме х = 1
- При а2, а0 х = ;
- При а-3, а-2, а0, 5 х =
- При а + с0, с0 х = ;
Квадратные уравнения с параметром
Пример 1. Решить уравнение
х = –
В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.
Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16
a =
a =
Если а -4/5 и а 1, то Д > 0,
х =
х = – = –
Пример 2. При каких значениях параметра а уравнение
х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?
| В итоге | 4(а – 1)(а – 6) > 0 — 2(а + 1) 0 |
а 6 а > — 1 а > 5/9 |
6 |
Пример 3. Найдите значения а, при которых данное уравнение имеет решение.
Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а
4а 2 – 16 0
4а(а – 4) 0
а(а – 4)) 0
Ответ: а 0 и а 4
Дидактический материал
1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?
2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?
3. При каких значениях а уравнение (а 2 – 6а + 
4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?
5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?
Показательные уравнения с параметром
Пример 1.Найти все значения а, при которых уравнение
9 х – (а + 2)*3 х-1/х +2а*3 -2/х = 0 (1) имеет ровно два корня.
Решение. Умножив обе части уравнения (1) на 3 2/х , получим равносильное уравнение
3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)
Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или
Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log32 , или х 2 – хlog32 + 1 = 0.
Это уравнение не имеет действительных корней, так как его Д = log 2 32 – 4 х+1/х = а то х + 1/х = log3а, или х 2 – хlog3а + 1 = 0. (3)
Уравнение (3) имеет ровно два корня тогда и только тогда, когда
Д = log 2 32 – 4 > 0, или |log3а| > 2.
Если log3а > 2, то а > 9, а если log3а 9.
Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?
Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х1 = -3, х2 = а = >
а – положительное число.
Дидактический материал
1. Найти все значения а, при которых уравнение
25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.
2. При каких значениях а уравнение
2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?
3. При каких значениях параметра а уравнение
4 х — (5а-3)2 х +4а 2 – 3а = 0 имеет единственное решение?
Ответ:
- 0 25/2
- при а = 1, а = -2,2
- 0 0, х1/4 (3)
х = у
| Если а = 0, то – | 2у + 1 = 0 2у = 1 у = 1/2 х = 1/2 х = 1/4 |
Не выполняется (2) условие из (3).
Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.
Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).
Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х
Выражая х из (1) и подставляя в (2), получаем неравенство
2 – а > 1 – а (3)
Чтобы решить неравенство (3), построим графики функций у = 2 – а и у = 1 – а.
Решения неравенства (3) образуют промежуток (а0; 2), где а0 2
а0 =
Ответ: x + 9a 3 ) = x имеет ровно два корня.
Ответы:
-
при а 16.06.2009
http://urok.1sept.ru/articles/534897

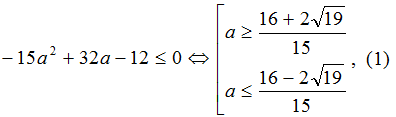
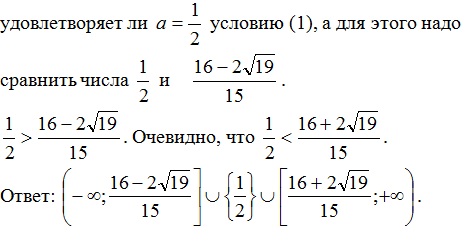
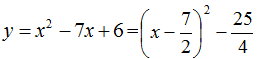

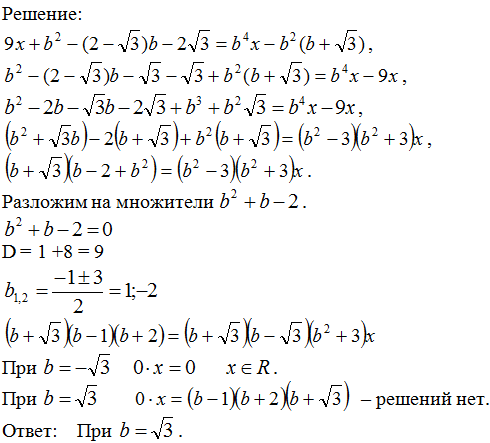
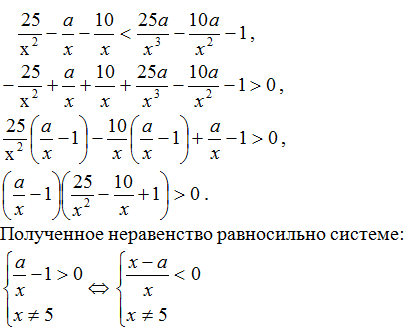
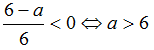
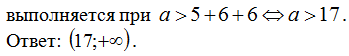
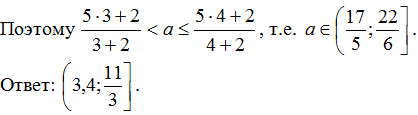








 =
=  ;
;