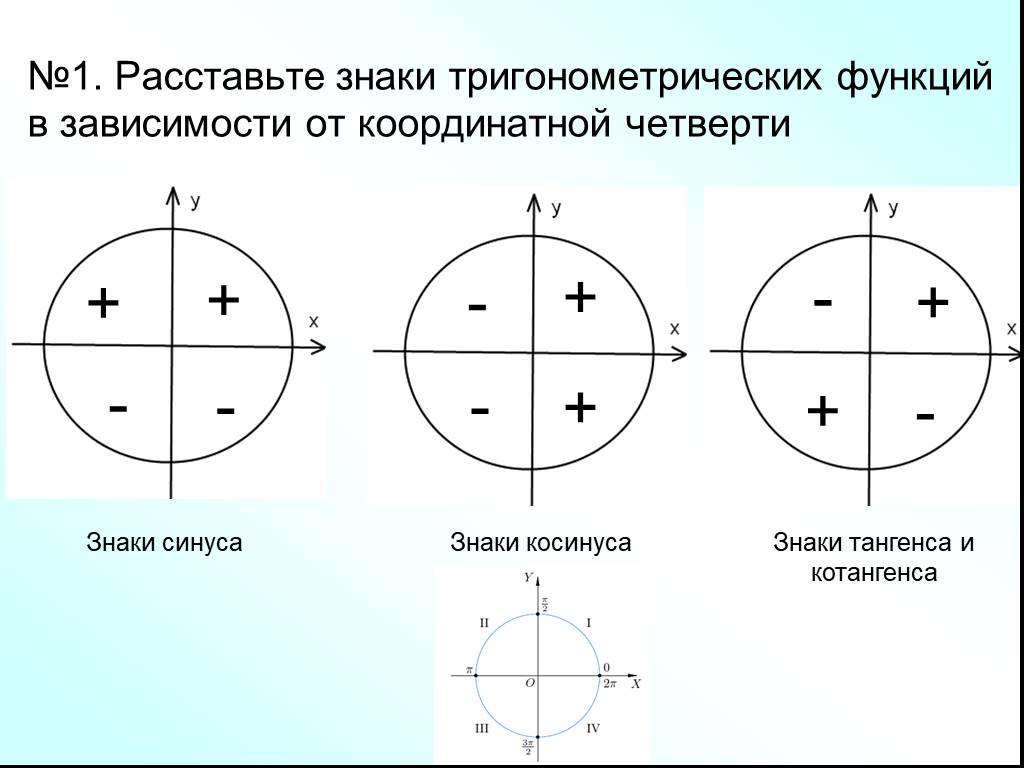
Знаки тригонометрических функций
5 ноября 2011
- Знаки триг. функций
Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.
Синус угла α — это ордината (координата
y
) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
Косинус угла α — это абсцисса (координата
x
) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
Тангенс угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты
y
к координате
x
.
Обозначение: sin α =
y
; cos α =
x
; tg α =
y
:
x
.
Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:
Синим цветом обозначено положительное направление оси
OY
(ось ординат), красным — положительное направление оси
OX
(ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:
- sin α > 0, если угол α лежит в
I
или
II
координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата
y
). А координата
y
будет положительной именно в
I
и
II
координатных четвертях;
- cos α > 0, если угол α лежит в
I
или
IV
координатной четверти. Потому что только там координата
x
(она же — абсцисса) будет больше нуля;
- tg α > 0, если угол α лежит в
I
или
III
координатной четверти. Это следует из определения: ведь tg α =
y
:
x
, поэтому он положителен лишь там, где знаки
x
и
y
совпадают. Это происходит в
I
координатной четверти (здесь
x
> 0,
y
> 0) и
III
координатной четверти (
x
< 0,
y
< 0).
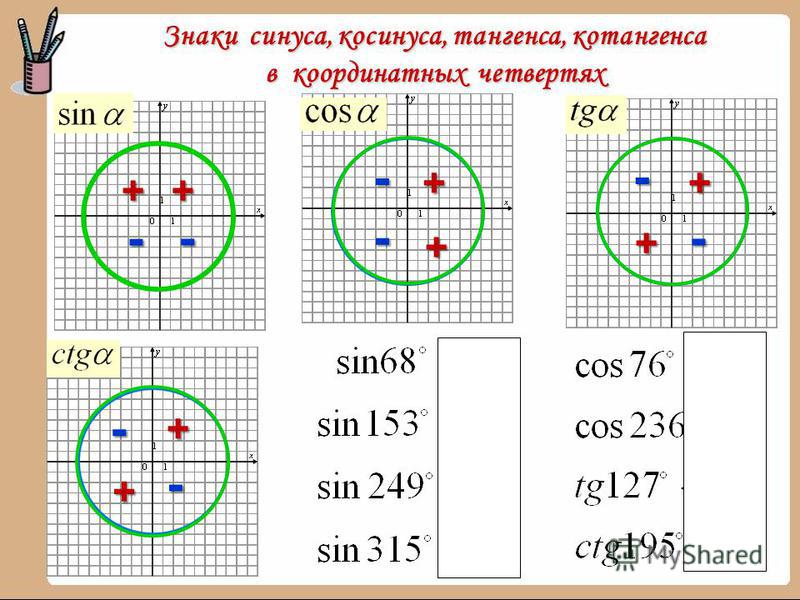
Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:
Заметьте: в своих рассуждениях я ни разу не говорил о четвертой тригонометрической функции — котангенсе. Дело в том, что знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.
Теперь предлагаю рассмотреть примеры, похожие на задачи B11 из пробного ЕГЭ по математике, который проходил 27 сентября 2011. Ведь лучший способ понять теорию — это практика. Желательно — много практики. Разумеется, условия задач были немного изменены.
Задача. Определите знаки тригонометрических функций и выражений (значения самих функций считать не надо):
- sin (3π/4);
- cos (7π/6);
- tg (5π/3);
- sin (3π/4) · cos (5π/6);
- cos (2π/3) · tg (π/4);
- sin (5π/6) · cos (7π/4);
- tg (3π/4) · cos (5π/3);
- ctg (4π/3) · tg (π/6).
План действий такой: сначала переводим все углы из радианной меры в градусную (π → 180°), а затем смотрим в какой координатной четверти лежит полученное число. Зная четверти, мы легко найдем знаки — по только что описанным правилам. Имеем:
- sin (3π/4) = sin (3 · 180°/4) = sin 135°. Поскольку 135° ∈ [90°; 180°], это угол из
II
координатной четверти. Но синус во
II
четверти положителен, поэтому sin (3π/4) > 0;
- cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из
III
координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) < 0;
- tg (5π/3) = tg (5 · 180°/3) = tg 300°. Поскольку 300° ∈ [270°; 360°], мы находимся в
IV
четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) < 0;
- sin (3π/4) · cos (5π/6) = sin (3 · 180°/4) · cos (5 · 180°/6) = sin 135° · cos 150°. Разберемся с синусом: т.к. 135° ∈ [90°; 180°], это
II
четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова
II
четверть, косинусы там отрицательны. Поэтому cos (5π/6) < 0. Наконец, следуя правилу «плюс на минус дает знак минус», получаем: sin (3π/4) · cos (5π/6) < 0;
- cos (2π/3) · tg (π/4) = cos (2 · 180°/3) · tg (180°/4) = cos 120° · tg 45°. Смотрим на косинус: 120° ∈ [90°; 180°] — это
II
координатная четверть, поэтому cos (2π/3) < 0. Смотрим на тангенс: 45° ∈ [0°; 90°] — это
I
четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) < 0;
- sin (5π/6) · cos (7π/4) = sin (5 · 180°/6) · cos (7 · 180°/4) = sin 150° · cos 315°. Работаем с синусом: поскольку 150° ∈ [90°; 180°], речь идет о
II
координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это
IV
координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
- tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это
II
четверть, т.е. tg (3π/4) < 0. Аналогично, угол 300° ∈ [270°; 360°] — это
IV
четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) < 0;
- ctg (4π/3) · tg (π/6) = ctg (4 · 180°/3) · tg (180°/6) = ctg 240° · tg 30°. Смотрим на аргумент котангенса: 240° ∈ [180°; 270°] — это
III
координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это
I
координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.
В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.
Задача. Найдите sin α, если sin2 α = 0,64 и α ∈ [π/2; π].
Поскольку sin2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это
II
координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.
Задача. Найдите cos α, если cos2 α = 0,04 и α ∈ [π; 3π/2].
Действуем аналогично, т.е. извлекаем квадратный корень: cos2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о
III
координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.
Задача. Найдите sin α, если sin2 α = 0,25 и α ∈ [3π/2; 2π].
Имеем: sin2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это
IV
координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.
Задача. Найдите tg α, если tg2 α = 9 и α ∈ [0; π/2].
Все то же самое, только для тангенса. Извлекаем квадратный корень: tg2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это
I
координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!
Смотрите также:
- Радианная мера угла
- Тест к уроку «Знаки тригонометрических функций» (1 вариант)
- Тест к параграфу «Что такое логарифм» (легкий)
- Сводный тест по задачам B12 (1 вариант)
- Изюм и виноград (смеси и сплавы)
- Задача B4: транзит нефти
Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
|
|
|||||||||||||||||||||||||||||
|
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление
|
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
||||||||||||||||||||||||||||
|
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. |
|||||||||||||||||||||||||||||
|
Коды баннеров проекта DPVA.ru Консультации и техническая |
Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator |
Определение и знаки тригонометрических функций
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Определение и знаки тригонометрических функций
2. Угол поворота
у
ОР0 — неподвижный луч
1
II
Р
I
1Р0
О
-1
ОР — подвижный луч
III
IV
-1
х
Угол поворота соответствует
длине пути, пройденного
точкой Р от начального
положения Р0
Угол поворота можно измерить
двумя мерами : градусной и
радианной
3.

• Приняв точку пересечения
окружности с
положительной частью оси
Ох за начало отсчета;
• Выбрав положительное
направление – против
часовой стрелки,
отрицательное – по
часовой стрелке;
• Отложив от начала
отсчета дугу в 1 рад, мы
получим, что
тригонометрическая
окружность в некотором
смысле «эквивалентна»
понятию «числовая
прямая».
y
1
1
«+»
0
0
1
« »
x
4. Тригонометрические функции
Определение. Тригонометрические функции — это
неалгебраические функции, устанавливающие
зависимость между сторонами и углами треугольника.
Тригонометрические функции угла α определяются при
помощи числовой окружности, а также из
прямоугольного треугольника (для острых углов).
5. Определение синуса
• Синусом угла х называется ордината точки,
полученной поворотом точки (1; 0) вокруг начала
координат на угол х (обозначается sin x).
sin x
x
(1;0)
6. Определение косинуса
• Косинусом угла х называется абсцисса точки,
полученной поворотом точки (1; 0) вокруг начала
координат на угол х (обозначается cos x).
x
cos x
(1;0)
7. Определение тангенса
• Тангенсом угла х называется отношение синуса
угла х к косинусу угла х.
sin
tg
cos
x
(1;0)
tg x
8. Определение котангенса
• Котангенсом угла х называется отношение косинуса
угла х к синусу угла х.
cos
сtg
sin
9. Тригонометрическая окружность
ЗНАКИ тригонометрических функций
sin a
+
+
–
–
tg a
cos a
–
+
–
+
ctg a
–
+
–
+
+
–
+
–
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ
ЗНАЧЕНИЙ СИНУСА, КОСИНУСА,
ТАНГЕНСА И КОТАНГЕНСА
sin α
cos α
Область
опреде- (- ∞;+ ∞) (- ∞;+ ∞)
ления
Область
значений
1;1 1;1
tg α
2
+
ctg α
n n
n-целое число
(- ∞;+ ∞)
n-целое число
(- ∞;+ ∞)
ТАБЛИЦА ЗНАЧЕНИЙ
ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
α
0° 30° 45° 60° 90° 180° 270° 360°
0
6
4
3
π
3
2
sin α 0
1
2
2
2
2
3
2
1
0
-1
0
cos α 1
3
2
2
2
1
2
0
-1
0
1
3
3
1
3
—
0
—
0
0
—
0
—
tg α 0
ctg α —
3
1
3
3
2π
14.
3 2 3
1
3
3
3sin +2cos -tg =3∙ +2∙ — 3 =
— 3= + 3- 3=
2
2
2
2
2
2
6
6
3
Задание:Вычислить
15. Учебник «Алгебра и начала анализа» (10 кл.)
Стр.178 № 563(2,3,4)
Стр.179 № 567
Стр.179 № 566
English
Русский
Правила
Знаки тригонометрических функций
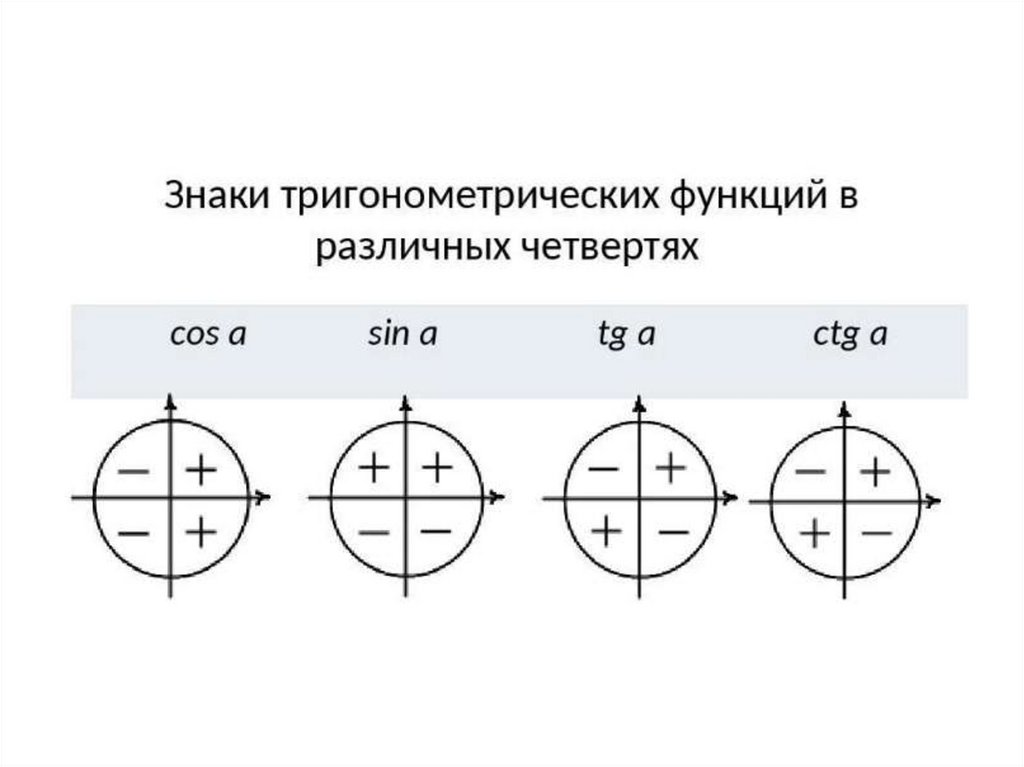
Знаки тригонометрических функций в каждом квадранте
Мы знаем, что cos α = x
/ r . Поскольку r > 0, знак функции косинуса зависит только от знака x . Следовательно, косинус положительный в 1-й и 4-й квадрантах и отрицательный во 2-й и 3-й квадрантах.
Рис. 1.
Рассмотрим синусоидальную функцию (sin alpha = frac{y}{r}.) Ее знак определяется знаком (y.). Следовательно, синус положителен в ( 1text{st}) и (2text{nd}) квадранты, а отрицательное — в (3text{rd}) и (4text{th}) квадрантах.
Рис. 2.
Ясно, что обратные функции (sec alpha = frac{1}{{cos alpha }}) и (csc alpha = frac{1}{{sin alpha }}) имеют те же знаки, что и (cos alpha) и (sin alpha,) соответственно.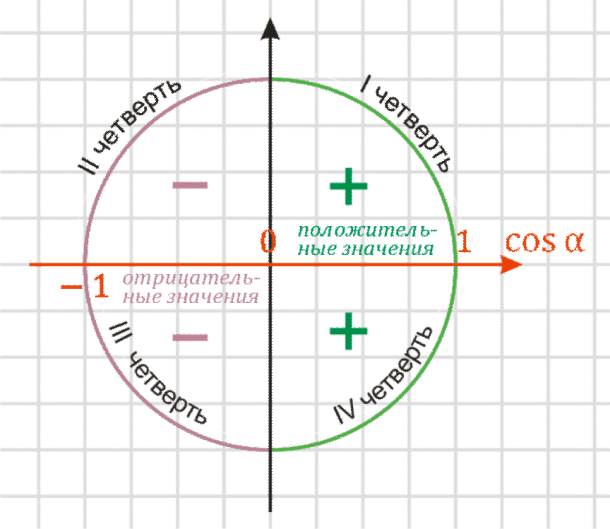
Знаки тангенса и котангенса зависят от знаков синуса и косинуса. Тангенс и котангенс положительны, когда (x) и (y) оба положительны или оба отрицательны. Это происходит в квадрантах (1text{st}) и (3text{rd}). В квадрантах (2text{nd}) и (4text{th}) эти функции отрицательны.
Рисунок 3.
Мы можем обобщить эту информацию в следующей таблице:
Рисунок 4.
Оценка тригонометрических функций
Для нахождения тригонометрической функции любого угла удобно использовать понятие исходного угла. Это включает в себя следующие шаги:
- Определите опорный угол для заданного угла в стандартном положении. Угол отсчета всегда острый.
- Вычислите значение тригонометрической функции для опорного угла. 92}альфа = 1.]
Зная одну из тригонометрических функций угла и квадрант, в котором лежит угол, мы можем определить все остальные тригонометрические функции этого угла. Это можно сделать с помощью перечисленных выше тождеств и определений тригонометрических функций.
Обратите внимание, что если тригонометрическое выражение содержит частное, оно справедливо только для тех углов, при которых знаменатель не равен нулю.
См. решенные проблемы на стр. 2.
Как определить знаки тригонометрических функций
Тригонометрия является неотъемлемой частью математики. Изучение тригонометрии не ограничивается только нахождением функций или использованием тригонометрического калькулятора, но также предполагает знание знаков тригонометрических функций как целостного понятия. Знаки тригонометрических функций будут зависеть от углов крайних сторон. Зная, в какой четверти лежит конечная сторона угла, можно определить его знак.
Есть восемь областей, которые могут иметь конечную сторону угла — в четырех квадрантах или вдоль осей в квадрантных углах (положительное или отрицательное направление). В каждой ситуации знаки тригонометрических функций имеют разное значение.
Что такое тригонометрические функции?
Давайте на минутку освежим в памяти тригонометрические функции.
Тригонометрические функции, также называемые круговыми функциями, представляют собой различные углы треугольника. Эти тригонометрические функции устанавливают отношения между углами и сторонами треугольника. Основными тригонометрическими функциями являются синус, секанс, тангенс, косинус, косеканс и котангенс.
Углы синус, косинус и тангенс являются основными функциями, а остальные являются производными от этих основных функций.
Шесть функций тригонометрии обычно определяются с помощью прямоугольного треугольника.
Основные тригонометрические формулы следующие:
Функция синуса: Функция синуса представляет собой отношение длины, противоположной углу А, к длине гипотенузы.
– Sin A= Противоположный/гипотенуза
Функция cos: Функция cos представляет собой отношение длины стороны, примыкающей к углу A, к длине гипотенузы.
– Cos A= Смежная/Гипотенуза
Функция тангенса: Функция тангенса – это отношение длины противоположной стороны к длине примыкающей стороны к углу A.
– Tan A= Противоположная/Смежная
Синус и cos также можно использовать для определения Tan.
– Tan A= Sin A/Cos A
Остальные три функции, секанс, косеканс и котангенс, получаются из обратной величины косинуса, синуса и тангенса.
– Sec A= 1/ Cos A= гипотенуза/ смежный
– Cosec A= 1/ Sin A= Гипотенуза/ Противоположная
– Cot A = 1/ Tan A = Примыкающая/ Противоположная
Тригонометрический калькулятор может определять значения различных функций. Вы можете ввести два значения и легко ответить на третье. Однако необходимо запоминать формулы тригонометрии.
Знаки тригонометрических функций
Тригонометрические функции синуса, косинуса, тангенса и котангенса основаны на знаках координат x и y в соответствующих четырех квадрантах.
Расстояние от начала до точки всегда положительное. Однако знаки координат x и y могут быть положительными или отрицательными.
- В первом квадранте все функции положительны, поскольку все координаты x и y положительны.
- Во втором квадранте синус вместе с косекансом положителен. Все остальные четыре отрицательные.
- В третьем квадранте тангенс и котангенс положительны, а остальные отрицательны.
- В четвертом квадранте косинус и секанс положительны, а остальные четыре функции отрицательны.
Обратное число имеет тот же знак, что и исходное число.
Вот небольшая хитрость, чтобы запомнить функции по квадрантам. Помните правило ASTC, которое можно запомнить как «Добавить сахар в кофе». Первая буква первого слова — «А», что означает, что все тригонометрические функции положительны в первом квадранте. Первая буква второго слова, «S», указывает на то, что синус и его обратный косой угол во втором квадранте положительны. Первая буква третьего слова, «Т», указывает на то, что тангенс и обратный Котан положительны в третьем квадранте. Наконец, первая буква последнего слова «C» указывает на то, что косинус и его обратный секанс положительны в четвертом квадранте.
Тригонометрическая функция Квадрант I Квадрант II Квадрант III III Квадрант IV
SIN α положительный положительный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный
COS α положительный отрицательный отрицательный положительный положительный
TAN α положительный положительный положительный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный
Cosec α -положительный положительный отрицательный отрицательный Отрицательный Положительный
кроватка α Положительный Отрицательный Положительный Отрицательный
Таблица, показывающая квадранты
В этой таблице суммируются знаки различных тригонометрических функций в разных квадрантах.
Значения квадрантных углов
Тригонометрическая функция 0 π/2 π 3π/2
SIN α 0 1 0 -1
COS α 1 0 -1 0
TAN α 0 Неопределенные 0 Не определено
COSEC α Не определено 0 Не определено 0
с α 1 Не определено -1 Не определено
COT α Не определено 1 не определенный -1
.
Когда значение не определено, коэффициент для этой конкретной функции делится на ноль. Эти точки технически не входят в область действия этой функции.
Из таблицы видно, что областью определения синуса и косиса являются все числа.
Другие виды тригонометрии
Раздел тригонометрии, изучающий отношение сторон прямоугольного треугольника, называется основной тригонометрией. Благодаря прогрессу ученых сегодня используются еще три вида тригонометрии: плоская, сферическая и аналитическая.
Плоская тригонометрия вычисляет углы простых треугольников. Этот угол имеет в основном три вершины на поверхности, и все стороны представляют собой прямые линии. Сумма плоскости равна 180 вместо обычных 90.
Сферическая тригонометрия используется для вычисления углов треугольников, нарисованных на сфере. Мера всех углов в этой ветви тригонометрии значительнее 180 градусов. Переменные широты и долготы используются вместе с тригонометрическими функциями. Как правило, для определения расстояний картографы и энтузиасты навигации регулярно используют сферическую тригонометрию.
- В первом квадранте все функции положительны, поскольку все координаты x и y положительны.
ВИДЕО УРОК
Длина радиуса-вектора
всегда число положительное. Проекции его на координатные оси – величины
алгебраические и в зависимости от координатных четвертей имеют следующие знаки:
в I четверти
ах > 0; ау > 0;
во II четверти
ах < 0; ау > 0;
в III четверти
ах < 0; ау < 0;
в IV четверти
ах > 0; ау < 0.
Функция sin α.
В силу того, что для тригонометрической функции sin α число 2π (или 360°) является периодом, достаточно исследовать
знаки этой функции на каком-нибудь промежутке изменения α длиной 2π, например для значений
α от 0 до 2π;
0 ≤ α < 2π (0° ≤ α < 360°).
Если угол α заключён
между 0 и π (0° и 180°), то ордината
у
конца М
подвижного радиуса ОМ единичной окружности положительна, а
следовательно, и синус угла α, составленного с
осью Ох этим
радиусом, положителен. На чертеже
показано несколько положений подвижного радиуса:
ОМ1, ОМ2, … , ОМ5.
Если же угол α заключён
между π и 2π (180° и 360°), то ордината
у
конца М
подвижного радиуса ОМ отрицательна,
а следовательно, и sin α на этом промежутке отрицательный.
Теперь, пользуясь равенством
sin (α + 2kπ) = sin α,
получаем заключение о знаке синуса для любых значений α:
1) если 2kπ <
α < π + 2kπ, то
sin α ˃ 0,
2) если π + 2kπ < α < 2π + 2kπ, то
sin α < 0.
Соответственно
тригонометрическая функция имеет знаки, указанные на рисунку.
ПРИМЕР:
Определите знак тригонометрической
функции:
sin 3π/4.
РЕШЕНИЕ:
sin 3π/4. = sin (3 ∙ 180°/4) = sin 135°.
Поскольку
135° ∈ [90°, 180°],
это угол из
II координатной четверти.
Синус во II четверти
положителен, поэтому
sin 3π/4 ˃ 0.
Функция cos α.
Исследуем знаки cos α также на промежутке изменения α от 0 до 2π (от 0° до 360°).
Если угол α заключён
между 0 и π/2 (0° и 90°), то абсцисса
х
конца М
подвижного радиуса ОМ единичной окружности положительна,
а следовательно, и косинус угла α, составленного
с осью Ох этим
радиусом ОМ, – положительный.
Если угол α заключён
между π/2 и 3π/2 (90° и 270°), то абсцисса
точки М отрицательна, а следовательно, и cos α – отрицательный.
Если же угол
α заключён
между 3π/2 и 2π (270° и 360°), то как видно из чертежа
cos α – положительный.
Пользуясь равенством
cos (α + 2kπ) = cos α,
получаем
1) если 2kπ ≤
α < π/2 + 2kπ,
то
cos α ˃ 0,
2) если π/2 + 2kπ <
α < 3π/2 + 2kπ,
то
cos α < 0,
3) если 3π/2 + 2kπ <
α < 2π + 2kπ, то
cos α ˃ 0.
Соответственно
тригонометрическая функция имеет знаки, указанные на рисунку.
ПРИМЕР:
Определите знак тригонометрической
функции:
cos 7π/6.
РЕШЕНИЕ:
cos 7π/6. = cos (7 ∙ 180°/6) = cos 210°.
Поскольку
210° ∈ [180°, 270°],
это угол из
III координатной четверти.
Косинус в III четверти отрицателен, поэтому
cos 7π/6 < 0.
Функция tg α.
Так как периодом
функций tg α и сtg α является
π (или 180°), исследуем знаки tg α и сtg α при изменении
α от 0 до π (от 0° до 180°). Если угол оканчивается
в I четверти
(0 < α < π/2 или 0° < α < 90°), то продолжение
подвижного радиуса ОМ единичной окружности, образующего с осью Ох
угол α, пересечёт ось тангенсов в точке Т,
ордината которой положительна. Это означает, что тангенсы углов,
оканчивающихся в I четверти – положительны.
Если же угол α
оканчивается во II четверти (π/2 < α < π или 90° < α < 180°), то продолжение
подвижного радиуса ОМ единичной окружности, образующего с осью Ох
угол α, пересечёт ось тангенсов в точке Т,
ордината которой отрицательна. Следовательно, тангенсы углов,
оканчивающиеся во II четверти, отрицательны.
В силу периодичности функции tg α имеем, что тангенсы углов, оканчивающихся
в III четверти, положительны, а в IV четверти –
отрицательны.
И вообще, так как
tg (α + kπ) = tg α,
имеем:
1) если kπ <
α < kπ + π/2, то
tg α ˃ 0,
2) если kπ + π/2 < α < kπ + π, то
tg α < 0.
где k – любое целое число.
Соответственно
тригонометрическая функция tg α имеет знаки, указанные на рисунку.
ПРИМЕР:
Определить, какой знак имеет выражение:
tg 2.
РЕШЕНИЕ:
Так как π/2 < 2 < π, то угол 2
рад будет углом II четверти, поэтому
tg 2 < 0.
ОТВЕТ: Знак –
Функция сtg α.
Аналогично приходим к выводу:
если 0 < α < π/2, то
сtg α ˃ 0,
если π/2 < α < π, то
сtg α < 0,
если π < α < 3π/2, то
сtg α ˃ 0,
если 3π/2 < α < 2π , то
сtg α < 0.
И вообще:
1) если kπ <
α < π/2 + kπ, то
сtg α ˃ 0,
2) если kπ + π/2 < α < kπ + π, то
сtg α < 0.
где k – любое целое число.
Соответственно
тригонометрическая функция сtg α имеет знаки, указанные на рисунку.
ПРИМЕР:
Определите знак тригонометрической
функции:
сtg 5π/3.
РЕШЕНИЕ:
сtg 5π/3 = сtg (5 ∙ 180°/3) = сtg 300°.
Поскольку
300° ∈ [270°, 360°],
это угол из
IV координатной четверти.
Котангенс в IV четверти отрицателен, поэтому
сtg 5π/3 < 0.
ПРИМЕР:
Определите знак выражения:
sin 3π/4 ∙ cos 5π/6.
РЕШЕНИЕ:
sin 3π/4 ∙ cos 5π/6 =
sin (3 ∙ 180°/4) ∙ cos (5 ∙ 180°/6) =
sin 135° ∙ cos 150°.
Разберёмся с синусом. Так как
135° ∈ [90°, 180°],
это угол из
II координатной четверти.
Синус во II четверти положителен,
поэтому
sin 3π/4 ˃ 0.
Разберёмся с косинусом. Так как
150° ∈ [90°, 180°],
это угол из
II координатной четверти.
Косинус во II четверти отрицателен,
поэтому
cos 5π/6 < 0.
Получили произведение, в
котором множители разных знаков.
Пользуясь правилом
<<плюс на минус даёт знак минус>>,
получаем
sin 3π/4 ∙ cos 5π/6 < 0.
ПРИМЕР:
Определите знак выражения:
cos 2π/3 ∙ tg π/4.
РЕШЕНИЕ:
cos 2π/3 ∙ tg π/4 =
cos (2 ∙ 180°/3) ∙ tg (180°/4) =
cos 120° ∙ tg 45°.
Разберёмся с косинусом. Так как
120° ∈ [90°, 180°],
это угол из
II координатной четверти.
Косинус во II четверти отрицателен,
поэтому
cos 2π/3 < 0.
Разберёмся с тангенсом. Так как
45° ∈ [0°, 90°],
это угол из
I координатной четверти.
Тангенс в I четверти положителен,
поэтому
tg π/4 ˃ 0.
Получили произведение, в
котором множители разных знаков. Пользуясь правилом
<<минус на плюс даёт минус>>,
получаем
cos 2π/3 ∙ tg π/4 < 0.
ПРИМЕР:
Определите знак выражения:
sin 5π/6 ∙ cos 7π/4.
РЕШЕНИЕ:
sin 5π/6 ∙ cos 7π/4 =
sin (5 ∙ 180°/6) ∙ cos (7 ∙ 180°/4) =
sin 150° ∙ cos 315°.
Разберёмся с синусом. Так как
150° ∈ [90°, 180°],
это угол из
II координатной четверти.
Синус во II четверти положителен,
поэтому
sin 5π/6 ˃ 0.
Разберёмся с косинусом. Так как
315° ∈ [270°, 360°],
это угол из
IV координатной четверти.
Косинус в IV четверти положителен,
поэтому
cos 5π/6 < 0.
Получили произведение, в
котором множители одного знака.
Пользуясь правилом
<<плюс на плюс даёт знак плюс>>,
получаем
sin 5π/6 ∙ cos 7π/4 ˃ 0.
ПРИМЕР:
Определите знак выражения:
tg 3π/4 ∙ cos 5π/3.
РЕШЕНИЕ:
tg 3π/4 ∙ cos 5π/3 =
tg (3 ∙ 180°/4) ∙ cos (5 ∙ 180°/3) =
tg 135° ∙ cos 300°.
Разберёмся с тангенсом. Так как
135° ∈ [90°, 180°],
это угол из
II координатной четверти.
Тангенс во II четверти отрицателен,
поэтому
tg 3π/4 < 0.
Разберёмся с косинусом. Так как
300° ∈ [270°, 360°],
это угол из
IV координатной четверти.
Косинус в IV четверти положителен,
поэтому
cos 5π/3 ˃ 0.
Получили произведение, в
котором множители разных знаков. Пользуясь правилом
<<минус на плюс даёт минус>>,
получаем
tg 3π/4 ∙ cos 5π/3 < 0.
ПРИМЕР:
Определите знак выражения:
сtg 4π/3 ∙ tg π/6.
РЕШЕНИЕ:
сtg 4π/3 ∙ tg π/6 =
сtg (4 ∙ 180°/3) ∙ tg (180°/6) =
сtg 240° ∙ tg
30°.
Разберёмся с котангенсом. Так
как
240° ∈ [180°, 270°],
это угол из
III координатной четверти.
Котангенс в III четверти положителен,
поэтому
сtg 4π/3 ˃ 0.
Разберёмся с тангенсом. Так как
30° ∈ [0°, 90°],
это угол из
I координатной четверти.
Тангенс в I четверти положителен,
поэтому
tg π/6 ˃ 0.
Получили произведение, в
котором множители одинаковых знаков. Пользуясь правилом
<<плюс на плюс даёт плюс>>,
получаем
сtg 4π/3 ∙ tg π/6 ˃ 0.
ПРИМЕР:
Определите знак выражения:
cos 123° × tg 231° × sin 312°.
РЕШЕНИЕ:
Так как
123° – угол II четверти,
231° – угол III четверти,
312° – угол IV четверти, то
cos 123° < 0, tg 231° ˃ 0, sin 312° < 0
и их произведение будет
величиной положительной, то есть
cos 123° × tg 231° × sin 312° ˃ 0.
ОТВЕТ:
Знак +
Задания к уроку 7
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 16. Решение косоугольных треугольников
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований
В этой статье мы рассмотрим тригонометрический круг и введем определения тригонометрических функций с помощью тригонометрического круга .
Впервые с определением синуса, косинуса, тангенса и котангенса школьники встречаются в восьмом классе в курсе геометрии. Напомню эти определения. Рассмотрим прямоугольный треугольник: Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
tg A=a/c; tg C=c/a.
Эти определения тригонометрических функций удобно использовать при решении геометрических задач, связанных с нахождением сторон и углов в прямоугольном треугольнике, однако они не улучшают понимания того, что из себя представляют тригонометрические функции именно как функции.
Часто во время занятий со школьниками я сталкиваюсь с тем, что они не понимают, откуда «взялись» тригонометрические функции, что они из себя представляют, и как их «готовить», чтобы легко решать уравнения и неравенства, содержащие тригонометрические функции.
Предлагаю вам посмотреть ВИДЕОУРОК, чтобы понять, что такое синус, косинус, тангенс и котангенс, как они между собой связаны, и как легко определять знаки тригонометрических функций без использования таблиц.
Косинусом угла α называется абсцисса (то есть координата по оси OX) точки на единичной окружности, соответствующей данному углу α.
Синусом угла α называется ордината (то есть координата по оси OY ) точки на единичной окружности, соответствующеий данному углу α.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса (x), синус — ордината (y).
Поскольку радиус окружности равен 1, для любого угла и синус, и косинус находятся в пределах от −1 до 1:
−1 ≤ cos α ≤ 1, −1 ≤ sin α ≤ 1.
Основное тригонометрическое тождество является следствием теоремы Пифагора (квадрат гипотенузы равен сумме квадратов катетов):
sin 2 α+ cos 2 α = 1
Чтобы узнать знаки синуса и косинуса какого-либо угла, находим на нашей окружности точку, соответствующую данному углу α, смотрим, положительны или отрицательны её координаты по x (это косинус угла α) и по y (это синус угла α).
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и 13»
Знаки тригонометрических функций
Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.
угла α — это ордината (координата y ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты y к координате x .
Обозначение: sin α = y ; cos α = x ; tg α = y : x .
Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:
- sin α > 0, если угол α лежит в I или II координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата y ). А координата y будет положительной именно в I и II координатных четвертях;
- cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только там координата x (она же — абсцисса) будет больше нуля;
- tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x , поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти ( x y II координатной четверти. Но синус во II четверти положителен, поэтому sin (3π/4) > 0;
- cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из III координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) IV четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) II четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова II четверть, косинусы там отрицательны. Поэтому cos (5π/6) II координатная четверть, поэтому cos (2π/3) I четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) II координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это IV координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
- tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это II четверть, т.е. tg (3π/4) IV четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) III координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это I координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.
В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.
Задача. Найдите sin α, если sin 2 α = 0,64 и α ∈ [π/2; π].
Поскольку sin 2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.
Задача. Найдите cos α, если cos 2 α = 0,04 и α ∈ [π; 3π/2].
Действуем аналогично, т.е. извлекаем квадратный корень: cos 2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.
Задача. Найдите sin α, если sin 2 α = 0,25 и α ∈ [3π/2; 2π].
Имеем: sin 2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.
Задача. Найдите tg α, если tg 2 α = 9 и α ∈ [0; π/2].
Все то же самое, только для тангенса. Извлекаем квадратный корень: tg 2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!
Знаки функций на числовой окружности
Числовая окружность
В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac , frac , frac , 10π, -frac )) разбирается в этой статье .
Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:
1) Начало отсчета находится в крайней правой точке окружности;
2) Против часовой стрелки — положительное направление; по часовой – отрицательное;
3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);
4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).
Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.
Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.
Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).
Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).
Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:
Длина числовой окружности равна (2π) или примерно (6,28).
А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.
Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?
Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.
Какие точки соответствуют числам (1), (2) и т.д?
Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.
При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.
2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.
К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac ),(-frac ),(frac ), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).
Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
Такая вот математическая полигамия.
И следствие из этого правила:
Все значения одной точки на числовой окружности можно записать с помощью формулы:
Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .
В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .
Что надо запомнить про числовую окружность:
Знаки тригонометрических функций
Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.
угла α — это ордината (координата y ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты y к координате x .
Обозначение: sin α = y ; cos α = x ; tg α = y : x .
Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:
- sin α > 0, если угол α лежит в I или II координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата y ). А координата y будет положительной именно в I и II координатных четвертях;
- cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только там координата x (она же — абсцисса) будет больше нуля;
- tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x , поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти ( x y II координатной четверти. Но синус во II четверти положителен, поэтому sin (3π/4) > 0;
- cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из III координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) IV четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) II четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова II четверть, косинусы там отрицательны. Поэтому cos (5π/6) II координатная четверть, поэтому cos (2π/3) I четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) II координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это IV координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
- tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это II четверть, т.е. tg (3π/4) IV четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) III координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это I координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.
В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.
Задача. Найдите sin α, если sin 2 α = 0,64 и α ∈ [π/2; π].
Поскольку sin 2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.
Задача. Найдите cos α, если cos 2 α = 0,04 и α ∈ [π; 3π/2].
Действуем аналогично, т.е. извлекаем квадратный корень: cos 2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.
Задача. Найдите sin α, если sin 2 α = 0,25 и α ∈ [3π/2; 2π].
Имеем: sin 2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.
Задача. Найдите tg α, если tg 2 α = 9 и α ∈ [0; π/2].
Все то же самое, только для тангенса. Извлекаем квадратный корень: tg 2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!
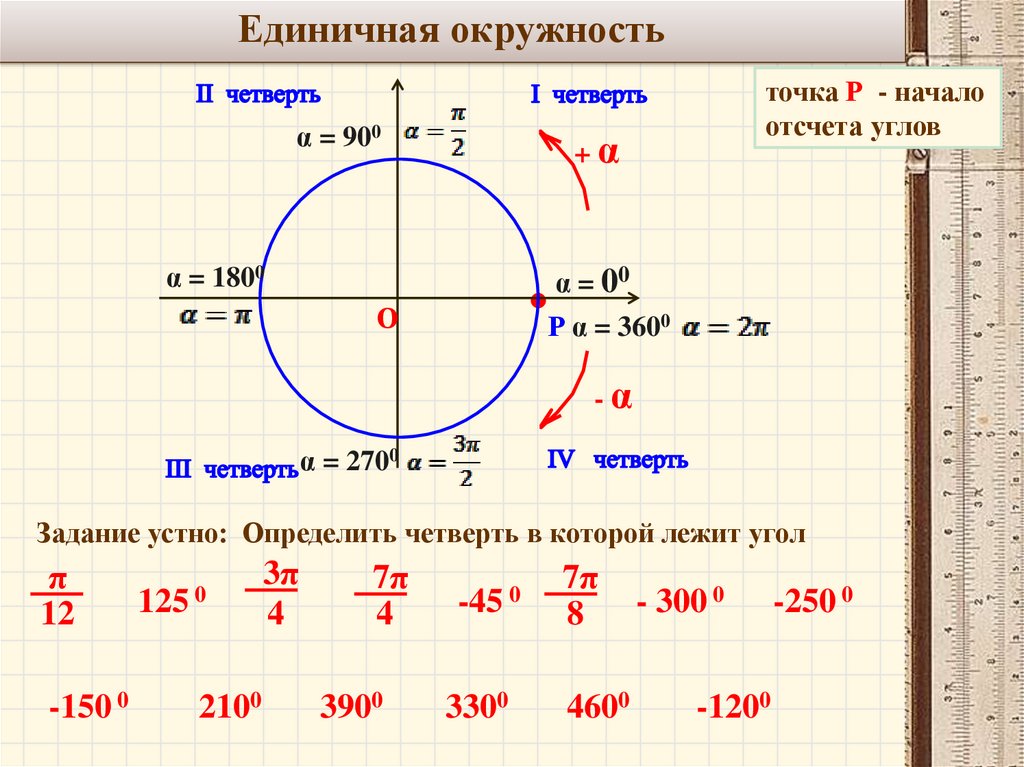
Единичная окружность
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
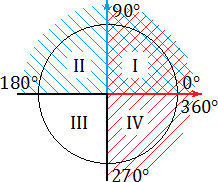
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
http://www.berdov.com/ege/trigonometry/sign/
http://b4.cooksy.ru/articles/znaki-funktsiy-na-chislovoy-okruzhnosti
Знаки тригонометрических функций
Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.
угла α — это ордината (координата y ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты y к координате x .
Обозначение: sin α = y ; cos α = x ; tg α = y : x .
Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:
- sin α > 0, если угол α лежит в I или II координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата y ). А координата y будет положительной именно в I и II координатных четвертях;
- cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только там координата x (она же — абсцисса) будет больше нуля;
- tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x , поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти ( x < 0, y < 0).
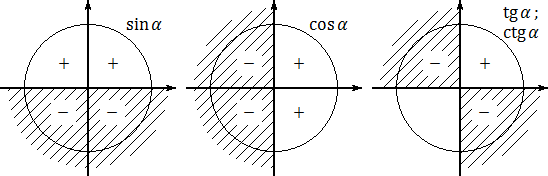
Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:
Заметьте: в своих рассуждениях я ни разу не говорил о четвертой тригонометрической функции — котангенсе. Дело в том, что знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.
Теперь предлагаю рассмотреть примеры, похожие на задачи B11 из пробного ЕГЭ по математике, который проходил 27 сентября 2011. Ведь лучший способ понять теорию — это практика. Желательно — много практики. Разумеется, условия задач были немного изменены.
- sin (3π/4);
- cos (7π/6);
- tg (5π/3);
- sin (3π/4) · cos (5π/6);
- cos (2π/3) · tg (π/4);
- sin (5π/6) · cos (7π/4);
- tg (3π/4) · cos (5π/3);
- ctg (4π/3) · tg (π/6).
План действий такой: сначала переводим все углы из радианной меры в градусную (π → 180°), а затем смотрим в какой координатной четверти лежит полученное число. Зная четверти, мы легко найдем знаки — по только что описанным правилам. Имеем:
- sin (3π/4) = sin (3 · 180°/4) = sin 135°. Поскольку 135° ∈ [90°; 180°], это угол из II координатной четверти. Но синус во II четверти положителен, поэтому sin (3π/4) > 0;
- cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из III координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) < 0;
- tg (5π/3) = tg (5 · 180°/3) = tg 300°. Поскольку 300° ∈ [270°; 360°], мы находимся в IV четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) < 0;
- sin (3π/4) · cos (5π/6) = sin (3 · 180°/4) · cos (5 · 180°/6) = sin 135° · cos 150°. Разберемся с синусом: т.к. 135° ∈ [90°; 180°], это II четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова II четверть, косинусы там отрицательны. Поэтому cos (5π/6) < 0. Наконец, следуя правилу «плюс на минус дает знак минус», получаем: sin (3π/4) · cos (5π/6) < 0;
- cos (2π/3) · tg (π/4) = cos (2 · 180°/3) · tg (180°/4) = cos 120° · tg 45°. Смотрим на косинус: 120° ∈ [90°; 180°] — это II координатная четверть, поэтому cos (2π/3) < 0. Смотрим на тангенс: 45° ∈ [0°; 90°] — это I четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) < 0;
- sin (5π/6) · cos (7π/4) = sin (5 · 180°/6) · cos (7 · 180°/4) = sin 150° · cos 315°. Работаем с синусом: поскольку 150° ∈ [90°; 180°], речь идет о II координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это IV координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
- tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это II четверть, т.е. tg (3π/4) < 0. Аналогично, угол 300° ∈ [270°; 360°] — это IV четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) < 0;
- ctg (4π/3) · tg (π/6) = ctg (4 · 180°/3) · tg (180°/6) = ctg 240° · tg 30°. Смотрим на аргумент котангенса: 240° ∈ [180°; 270°] — это III координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это I координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.
В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.
Задача. Найдите sin α, если sin 2 α = 0,64 и α ∈ [π/2; π].
Поскольку sin 2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.
Задача. Найдите cos α, если cos 2 α = 0,04 и α ∈ [π; 3π/2].
Действуем аналогично, т.е. извлекаем квадратный корень: cos 2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.
Задача. Найдите sin α, если sin 2 α = 0,25 и α ∈ [3π/2; 2π].
Имеем: sin 2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.
Задача. Найдите tg α, если tg 2 α = 9 и α ∈ [0; π/2].
Все то же самое, только для тангенса. Извлекаем квадратный корень: tg 2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!
Знаки тригонометрических функций по четвертям
У математики есть одно классное преимущество перед другими предметами – здесь запоминать надо по минимуму, ведь подавляющее большинство теорем или свойств можно вывести из предыдущих тем. Это касается и знаков тригонометрических функций — их совершенно точно не нужно учить, достаточно просто помнить определение синуса и косинуса.
Тем, кто забыл, напомню:
— синус – это ордината точки на числовой окружности;
— косинус – это абсцисса точки на числовой окружности.
Значит, чтоб определить знак синуса достаточно найти точку на числовой окружности и взглянуть положительная у неё ордината или отрицательная. Аналогично у косинуса — найдите точку на числовой окружности и проведите перпендикуляр до оси косинусов: если попали в положительную часть оси, значит косинус положителен, в отрицательную — отрицателен. C тангенсом и котангенсом разберетесь сами? Если нет, пишите вопросы в комментарии!
Бонус:
Определения и знаки синуса, косинуса, тангенса угла
Тип урока: систематизации знаний и промежуточного контроля.
Оборудование: тригонометрический круг, тесты, карточки с заданиями.
Цели урока: систематизировать изученный теоретический материал по определениям синуса, косинуса, тангенса угла; проверить степень усвоения знаний по данной теме и применение на практике.
Задачи:
- Обобщить и закрепить понятия синуса, косинуса и тангенса угла.
- Формировать комплексное представление о тригонометрических функциях.
- Способствовать выработке у учащихся желания и потребности изучения тригонометрического материала; воспитывать культуру общения, умение работать в группах и потребности в самообразовании.
«Кто смолоду делает и думает сам, тот
становится потом, надёжнее, крепче, умнее.
I. Организационный момент
Класс представлен тремя группами. В каждой группе консультант.
Учитель сообщает тему, цели и задачи урока.
II. Актуализация знаний (фронтальная работа с классом)
1) Работа в группах по заданиям:
1. Сформулировать определение sin угла.
– Какие знаки имеет sin α в каждой координатной четверти?
– При каких значениях имеет смысл, выражение sin α, и какие значения оно может принимать?
2. Вторая группа те – же вопросы для cos α.
3. Третья группа ответы готовит по тем же вопросам tg α и ctg α.
В это время трое учащихся самостоятельно работают у доски по карточкам (представители разных групп).
Практическая работа.
С помощью единичной окружности вычислить для угла 50 , 210 и – 210 значения sin α, cos α и tg α.
Определить знак выражения: tg 275; cos 370; sin 790; tg 4,1 и sin 2.
1) Вычислить:
2) Сравнить: cos 60 и cos 2 30 – sin 2 30
2) Устно:
а) Предложен ряд чисел: 1; 1,2; 3; , 0, , – 1. Среди них есть лишние. Какое свойство sin α или cos α могут выражать эти числа (Может ли sin α или cos α принимать эти значения).
б) Имеет ли смысл выражение: cos (–); sin 2; tg 3: ctg (– 5); ; ctg0;
ctg (– π). Почему?
в) Существует ли наименьшее и наибольшее значение sin или cos, tg, ctg.
г) Верно ли?
1) α = 1000 является углом II четверти;
2) α = – 330 является углом IV четверти.
д) Числам соответствует одна и та же точка на единичной окружности.
3) Работа у доски
№ 567 (2; 4) – Найти значение выражения
№ 583 (1-3) Определить знак выражения
Домашнее задание: таблица в тетради. № 567(1, 3) № 578
III. Усвоение дополнительных знаний. Тригонометрия в ладони
Учитель: Оказывается, значения синусов и косинусов углов «находятся» на вашей ладони. Протяните руку (любую) и разведите как можно сильнее пальцы (как на плакате). Приглашается один ученик. Мы измеряем углы между нашими пальцами.
Берется треугольник, где есть угол в 30, 45 и 60 90 и прикладываем вершину угла к бугру Луны на ладони. Бугор Луны находится на пересечении продолжений мизинца и большого пальца. Одну сторону совмещаем с мизинцем, а другую сторону – с одним из остальных пальцев.
Оказывается между мизинцем и большим пальцем угол 90, между мизинцем и безымянным – 30, между мизинцем и средним – 45, между мизинцем и указательным – 60. И это у всех людей без исключения
Если пальцы считать лучами, исходящими из бугра Луны на ладони, то можно считать, что направление мизинца соответствует началу отсчета углов, т.е. 0.
Введем нумерацию пальцев:
мизинец № 0 – соответствует 0,
безымянный № 1 – соответствует 30,
средний № 2 – соответствует 45,
указательный № 3 – соответствует 60,
большой № 4 – соответствует 90.

 Введите свой запрос:
Введите свой запрос: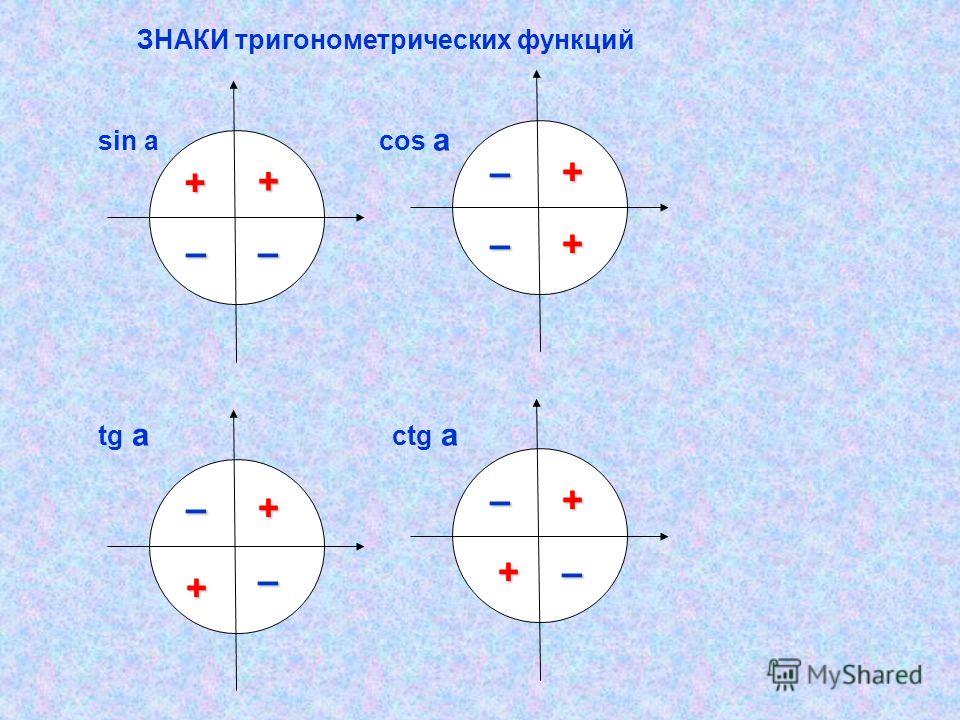 Обратите внимание, что если тригонометрическое выражение содержит частное, оно справедливо только для тех углов, при которых знаменатель не равен нулю.
Обратите внимание, что если тригонометрическое выражение содержит частное, оно справедливо только для тех углов, при которых знаменатель не равен нулю.  Тригонометрические функции, также называемые круговыми функциями, представляют собой различные углы треугольника. Эти тригонометрические функции устанавливают отношения между углами и сторонами треугольника. Основными тригонометрическими функциями являются синус, секанс, тангенс, косинус, косеканс и котангенс.
Тригонометрические функции, также называемые круговыми функциями, представляют собой различные углы треугольника. Эти тригонометрические функции устанавливают отношения между углами и сторонами треугольника. Основными тригонометрическими функциями являются синус, секанс, тангенс, косинус, косеканс и котангенс.