Как найти знак выражения тригонометрия

Знаки тригонометрических функций

5 ноября 2011

• Знаки триг. функций

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.

Синус угла α — это ордината (координата

y

) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

Косинус угла α — это абсцисса (координата

x

) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

Тангенс угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты

y

к координате

x

.

Обозначение: sin α =

y

; cos α =

x

; tg α =

y

:

x

.

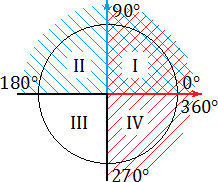
Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:

Синим цветом обозначено положительное направление оси

OY

(ось ординат), красным — положительное направление оси

OX

(ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:

1. sin α > 0, если угол α лежит в

   I

   или

   II

   координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата

   y

   ). А координата

   y

   будет положительной именно в

   I

   и

   II

   координатных четвертях;

2. cos α > 0, если угол α лежит в

   I

   или

   IV

   координатной четверти. Потому что только там координата

   x

   (она же — абсцисса) будет больше нуля;

3. tg α > 0, если угол α лежит в

   I

   или

   III

   координатной четверти. Это следует из определения: ведь tg α =

   y

   :

   x

   , поэтому он положителен лишь там, где знаки

   x

   и

   y

   совпадают. Это происходит в

   I

   координатной четверти (здесь

   x

   > 0,

   y

   > 0) и

   III

   координатной четверти (

   x

   < 0,

   y

   < 0).

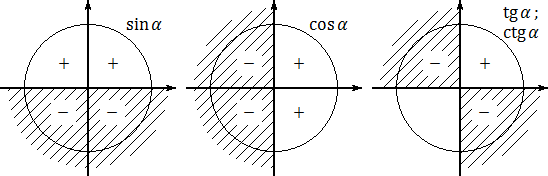
Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:

Заметьте: в своих рассуждениях я ни разу не говорил о четвертой тригонометрической функции — котангенсе. Дело в том, что знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.

Теперь предлагаю рассмотреть примеры, похожие на задачи B11 из пробного ЕГЭ по математике, который проходил 27 сентября 2011. Ведь лучший способ понять теорию — это практика. Желательно — много практики. Разумеется, условия задач были немного изменены.

Задача. Определите знаки тригонометрических функций и выражений (значения самих функций считать не надо):

1. sin (3π/4);
2. cos (7π/6);
3. tg (5π/3);
4. sin (3π/4) · cos (5π/6);
5. cos (2π/3) · tg (π/4);
6. sin (5π/6) · cos (7π/4);
7. tg (3π/4) · cos (5π/3);
8. ctg (4π/3) · tg (π/6).

План действий такой: сначала переводим все углы из радианной меры в градусную (π → 180°), а затем смотрим в какой координатной четверти лежит полученное число. Зная четверти, мы легко найдем знаки — по только что описанным правилам. Имеем:

1. sin (3π/4) = sin (3 · 180°/4) = sin 135°. Поскольку 135° ∈ [90°; 180°], это угол из

   II

   координатной четверти. Но синус во

   II

   четверти положителен, поэтому sin (3π/4) > 0;

2. cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из

   III

   координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) < 0;

3. tg (5π/3) = tg (5 · 180°/3) = tg 300°. Поскольку 300° ∈ [270°; 360°], мы находимся в

   IV

   четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) < 0;

4. sin (3π/4) · cos (5π/6) = sin (3 · 180°/4) · cos (5 · 180°/6) = sin 135° · cos 150°. Разберемся с синусом: т.к. 135° ∈ [90°; 180°], это

   II

   четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова

   II

   четверть, косинусы там отрицательны. Поэтому cos (5π/6) < 0. Наконец, следуя правилу «плюс на минус дает знак минус», получаем: sin (3π/4) · cos (5π/6) < 0;

5. cos (2π/3) · tg (π/4) = cos (2 · 180°/3) · tg (180°/4) = cos 120° · tg 45°. Смотрим на косинус: 120° ∈ [90°; 180°] — это

   II

   координатная четверть, поэтому cos (2π/3) < 0. Смотрим на тангенс: 45° ∈ [0°; 90°] — это

   I

   четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) < 0;

6. sin (5π/6) · cos (7π/4) = sin (5 · 180°/6) · cos (7 · 180°/4) = sin 150° · cos 315°. Работаем с синусом: поскольку 150° ∈ [90°; 180°], речь идет о

   II

   координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это

   IV

   координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;

7. tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это

   II

   четверть, т.е. tg (3π/4) < 0. Аналогично, угол 300° ∈ [270°; 360°] — это

   IV

   четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) < 0;

8. ctg (4π/3) · tg (π/6) = ctg (4 · 180°/3) · tg (180°/6) = ctg 240° · tg 30°. Смотрим на аргумент котангенса: 240° ∈ [180°; 270°] — это

   III

   координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это

   I

   координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.

В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.

Задача. Найдите sin α, если sin² α = 0,64 и α ∈ [π/2; π].

Поскольку sin² α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это

II

координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.

Задача. Найдите cos α, если cos² α = 0,04 и α ∈ [π; 3π/2].

Действуем аналогично, т.е. извлекаем квадратный корень: cos² α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о

III

координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.

Задача. Найдите sin α, если sin² α = 0,25 и α ∈ [3π/2; 2π].

Имеем: sin² α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это

IV

координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.

Задача. Найдите tg α, если tg² α = 9 и α ∈ [0; π/2].

Все то же самое, только для тангенса. Извлекаем квадратный корень: tg² α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это

I

координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!

Смотрите также:

1. Радианная мера угла
2. Тест к уроку «Знаки тригонометрических функций» (1 вариант)
3. Тест к параграфу «Что такое логарифм» (легкий)
4. Сводный тест по задачам B12 (1 вариант)
5. Изюм и виноград (смеси и сплавы)
6. Задача B4: транзит нефти

Знаки тригонометрических функций

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.

угла α — это ордината (координата y ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты y к координате x .

Обозначение: sin α = y ; cos α = x ; tg α = y : x .

Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:

Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:

1. sin α > 0, если угол α лежит в I или II координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата y ). А координата y будет положительной именно в I и II координатных четвертях;
2. cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только там координата x (она же — абсцисса) будет больше нуля;
3. tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x , поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти ( x < 0, y < 0).

Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:

Заметьте: в своих рассуждениях я ни разу не говорил о четвертой тригонометрической функции — котангенсе. Дело в том, что знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.

Теперь предлагаю рассмотреть примеры, похожие на задачи B11 из пробного ЕГЭ по математике, который проходил 27 сентября 2011. Ведь лучший способ понять теорию — это практика. Желательно — много практики. Разумеется, условия задач были немного изменены.

1. sin (3π/4);
2. cos (7π/6);
3. tg (5π/3);
4. sin (3π/4) · cos (5π/6);
5. cos (2π/3) · tg (π/4);
6. sin (5π/6) · cos (7π/4);
7. tg (3π/4) · cos (5π/3);
8. ctg (4π/3) · tg (π/6).

План действий такой: сначала переводим все углы из радианной меры в градусную (π → 180°), а затем смотрим в какой координатной четверти лежит полученное число. Зная четверти, мы легко найдем знаки — по только что описанным правилам. Имеем:

1. sin (3π/4) = sin (3 · 180°/4) = sin 135°. Поскольку 135° ∈ [90°; 180°], это угол из II координатной четверти. Но синус во II четверти положителен, поэтому sin (3π/4) > 0;
2. cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из III координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) < 0;
3. tg (5π/3) = tg (5 · 180°/3) = tg 300°. Поскольку 300° ∈ [270°; 360°], мы находимся в IV четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) < 0;
4. sin (3π/4) · cos (5π/6) = sin (3 · 180°/4) · cos (5 · 180°/6) = sin 135° · cos 150°. Разберемся с синусом: т.к. 135° ∈ [90°; 180°], это II четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова II четверть, косинусы там отрицательны. Поэтому cos (5π/6) < 0. Наконец, следуя правилу «плюс на минус дает знак минус», получаем: sin (3π/4) · cos (5π/6) < 0;
5. cos (2π/3) · tg (π/4) = cos (2 · 180°/3) · tg (180°/4) = cos 120° · tg 45°. Смотрим на косинус: 120° ∈ [90°; 180°] — это II координатная четверть, поэтому cos (2π/3) < 0. Смотрим на тангенс: 45° ∈ [0°; 90°] — это I четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) < 0;
6. sin (5π/6) · cos (7π/4) = sin (5 · 180°/6) · cos (7 · 180°/4) = sin 150° · cos 315°. Работаем с синусом: поскольку 150° ∈ [90°; 180°], речь идет о II координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это IV координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
7. tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это II четверть, т.е. tg (3π/4) < 0. Аналогично, угол 300° ∈ [270°; 360°] — это IV четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) < 0;
8. ctg (4π/3) · tg (π/6) = ctg (4 · 180°/3) · tg (180°/6) = ctg 240° · tg 30°. Смотрим на аргумент котангенса: 240° ∈ [180°; 270°] — это III координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это I координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.

В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.

Задача. Найдите sin α, если sin 2 α = 0,64 и α ∈ [π/2; π].

Поскольку sin 2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.

Задача. Найдите cos α, если cos 2 α = 0,04 и α ∈ [π; 3π/2].

Действуем аналогично, т.е. извлекаем квадратный корень: cos 2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.

Задача. Найдите sin α, если sin 2 α = 0,25 и α ∈ [3π/2; 2π].

Имеем: sin 2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.

Задача. Найдите tg α, если tg 2 α = 9 и α ∈ [0; π/2].

Все то же самое, только для тангенса. Извлекаем квадратный корень: tg 2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!

Знаки тригонометрических функций по четвертям

У математики есть одно классное преимущество перед другими предметами – здесь запоминать надо по минимуму, ведь подавляющее большинство теорем или свойств можно вывести из предыдущих тем. Это касается и знаков тригонометрических функций — их совершенно точно не нужно учить, достаточно просто помнить определение синуса и косинуса.

Тем, кто забыл, напомню:
— синус – это ордината точки на числовой окружности;
— косинус – это абсцисса точки на числовой окружности.

Значит, чтоб определить знак синуса достаточно найти точку на числовой окружности и взглянуть положительная у неё ордината или отрицательная. Аналогично у косинуса — найдите точку на числовой окружности и проведите перпендикуляр до оси косинусов: если попали в положительную часть оси, значит косинус положителен, в отрицательную — отрицателен. C тангенсом и котангенсом разберетесь сами? Если нет, пишите вопросы в комментарии!

Бонус:

Определения и знаки синуса, косинуса, тангенса угла

Тип урока: систематизации знаний и промежуточного контроля.

Оборудование: тригонометрический круг, тесты, карточки с заданиями.

Цели урока: систематизировать изученный теоретический материал по определениям синуса, косинуса, тангенса угла; проверить степень усвоения знаний по данной теме и применение на практике.

Задачи:

• Обобщить и закрепить понятия синуса, косинуса и тангенса угла.
• Формировать комплексное представление о тригонометрических функциях.
• Способствовать выработке у учащихся желания и потребности изучения тригонометрического материала; воспитывать культуру общения, умение работать в группах и потребности в самообразовании.

«Кто смолоду делает и думает сам, тот
становится потом, надёжнее, крепче, умнее.

I. Организационный момент

Класс представлен тремя группами. В каждой группе консультант.
Учитель сообщает тему, цели и задачи урока.

II. Актуализация знаний (фронтальная работа с классом)

1) Работа в группах по заданиям:

1. Сформулировать определение sin угла.

– Какие знаки имеет sin α в каждой координатной четверти?
– При каких значениях имеет смысл, выражение sin α, и какие значения оно может принимать?

2. Вторая группа те – же вопросы для cos α.

3. Третья группа ответы готовит по тем же вопросам tg α и ctg α.

В это время трое учащихся самостоятельно работают у доски по карточкам (представители разных групп).

Практическая работа.
С помощью единичной окружности вычислить для угла 50 , 210 и – 210 значения sin α, cos α и tg α.

Определить знак выражения: tg 275; cos 370; sin 790; tg 4,1 и sin 2.

1) Вычислить:
2) Сравнить: cos 60 и cos 2 30 – sin 2 30

2) Устно:

а) Предложен ряд чисел: 1; 1,2; 3; , 0, , – 1. Среди них есть лишние. Какое свойство sin α или cos α могут выражать эти числа (Может ли sin α или cos α принимать эти значения).
б) Имеет ли смысл выражение: cos (–); sin 2; tg 3: ctg (– 5); ; ctg0;
ctg (– π). Почему?
в) Существует ли наименьшее и наибольшее значение sin или cos, tg, ctg.
г) Верно ли?
1) α = 1000 является углом II четверти;
2) α = – 330 является углом IV четверти.
д) Числам соответствует одна и та же точка на единичной окружности.

3) Работа у доски

№ 567 (2; 4) – Найти значение выражения
№ 583 (1-3) Определить знак выражения

Домашнее задание: таблица в тетради. № 567(1, 3) № 578

III. Усвоение дополнительных знаний. Тригонометрия в ладони

Учитель: Оказывается, значения синусов и косинусов углов «находятся» на вашей ладони. Протяните руку (любую) и разведите как можно сильнее пальцы (как на плакате). Приглашается один ученик. Мы измеряем углы между нашими пальцами.
Берется треугольник, где есть угол в 30, 45 и 60 90 и прикладываем вершину угла к бугру Луны на ладони. Бугор Луны находится на пересечении продолжений мизинца и большого пальца. Одну сторону совмещаем с мизинцем, а другую сторону – с одним из остальных пальцев.
Оказывается между мизинцем и большим пальцем угол 90, между мизинцем и безымянным – 30, между мизинцем и средним – 45, между мизинцем и указательным – 60. И это у всех людей без исключения

Если пальцы считать лучами, исходящими из бугра Луны на ладони, то можно считать, что направление мизинца соответствует началу отсчета углов, т.е. 0.
Введем нумерацию пальцев:

мизинец № 0 – соответствует 0,
безымянный № 1 – соответствует 30,
средний № 2 – соответствует 45,
указательный № 3 – соответствует 60,
большой № 4 – соответствует 90.

Алгебра и начала математического анализа, 10 класс

Урок №31. Знаки синуса, косинуса и тангенса

Перечень вопросов, рассматриваемых в теме

1) Знаки синуса, косинуса, тангенса и котангенса;

2)Зависимость знаков синуса, косинуса, тангенса и котангенса от положения точки, движущейся по тригонометрической окружности, от произвольного угла;

3) Знаки тригонометрического выражения.

Глоссарий по теме

Число (пи) – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,14.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Какие знаки имеюткоординаты точки в зависимости от их положения в системе координат?

У точек первой четверти

у точек второй четверти

у точек третьей четверти

у точек четвёртой четверти

Пример.

В какой координатной четверти находятся точки с указанными координатами

Ответ:

A	B	C	D	E	F
2	4	2	3	1	4

А если точка находится на тригонометрической окружности, то как узнать зависимость знака координат точки от угла поворота вокруг начала координат?

Сегодня на уроке мы узнаем знаки синуса, косинуса, тангенса и котангенса, научимся определять положение точки на тригонометрической окружности в зависимости от комбинации знаков синуса и косинуса, тангенса и котангенса.

1.Рассмотрим единичную окружность в прямоугольной системе координат хОу.

Точка Р(1;0) при повороте вокруг начала координат на угол переместилась в точку Рₐ. Определим её координаты.

Синусом углаявляется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол .

Косинусом углаявляется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол .

Если угол то точка Рₐ находится в первой четверти, здесь , значит

, .

Если угол , то точка Рₐ находится во второй четверти, здесь , , значит , .

Если угол , то точка Рₐ находится в третьей четверти, здесь , , значит

, .

Если угол , то точка Рₐ находится в четвертой четверти, здесь , , значит ,

На рисунке видно какие знаки имеет синус, а какие косинус.

Примеры и разбор решения заданий тренировочного модуля

Пример1. Определить знаки синуса и косинуса угла .

Решение: Выясним, в какой четверти находится точка, полученная поворотом на угол .

во второй четверти синусы положительны, косинусы отрицательны.

Ответ:

Пример 2. Определить знаки синуса и косинуса угла .

Решение: Полный угол, при котором точка «обойдёт» всю окружность, равен .

а это значит, что точка после 2 оборотов окажется в первой четверти, где синус и косинус положительны.

Ответ:

Пример 3.

Определить знаки синуса и косинуса угла .

Решение: Угол отрицательный, значит точка получена поворотом по часовой стрелке.

в 4 четверти синусы отрицательны, косинусы положительны.

Ответ: синус отрицательный, косинус положительный.

Пример 4.

Определить знаки .

Решение: Знаем, что, а . Значит, . Точка во второй четверти.

Ответ:

2.Знаки тангенса и котангенса.

Тангенс это отношение синуса угла к его косинусу:

Котангенс это отношение косинуса угла к его синусу: .

Тангенс и котангенс будут положительными там, где синус и косинус имеют одинаковые знаки. Это первая и третья четверти. Синус и косинус имеют разные знаки во второй и четвёртой четвертях, здесь тангенс и котангенс будут отрицательны. На рисунке изображены знаки тангенса и котангенса.

Пример 5.

Определить знак тангенса угла

Решение , угол второй четверти

Ответ:

Пример 6.

Определить знак тангенса угла .

Решение: Угол в третьей четверти, тангенс положительный.

Ответ:

Вывод: чтобы определить знаки синуса, косинуса, тангенса и котангенса, нужно:

1. выяснить в какой координатной четверти находится угол;
2. знак синусов такой же, как ордината точки (у).
3. знак косинусов такой же, как абсцисса точки (х).
4. тангенсы и котангенсы положительны там, где синус и косинус имеют одинаковые знаки(1ч. и 4ч.), отрицательны, где синус и косинус имеют противоположные знаки (2ч. и 3ч.).

ВИДЕО УРОК

Длина радиуса-вектора

всегда число положительное. Проекции его на координатные оси – величины
алгебраические и в зависимости от координатных четвертей имеют следующие знаки:

в  I  четверти   
а_х > 0;    а_у > 0;

во  II  четверти   
а_х < 0;    а_у > 0;

в  III  четверти   
а_х < 0;    а_у < 0;

в  IV  четверти   
а_х > 0;    а_у < 0.

Функция  sin α.

В силу того, что для тригонометрической функции  sin α  число  2π (или 360°)  является периодом, достаточно исследовать
знаки этой функции на каком-нибудь промежутке изменения  α  длиной  2π, например для значений 
α  от  0  до  2π;

0 ≤ α < 2π (0° ≤ α < 360°).

Если угол  α  заключён
между  0  и  π (0°  и  180°), то ордината 
у 
конца  М 
подвижного радиуса  ОМ  единичной окружности положительна, а
следовательно, и синус угла  α, составленного с
осью  Ох  этим
радиусом, положителен. На чертеже

показано несколько положений подвижного радиуса:

ОМ₁, ОМ₂, … , ОМ₅.

Если же угол  α  заключён
между  π  и  2π (180°  и  360°), то ордината 
у 
конца  М 
подвижного радиуса  ОМ  отрицательна,

а следовательно, и  sin α  на этом промежутке отрицательный.

Теперь, пользуясь равенством

sin (α + 2kπ) = sin α,

получаем заключение о знаке синуса для любых значений  α:

1)  если  2kπ <
α < π + 2kπ, то

sin α ˃ 0,

2)  если  π + 2kπ < α < 2π + 2kπ, то

sin α < 0.

Соответственно
тригонометрическая функция имеет знаки, указанные на рисунку.

ПРИМЕР:

Определите знак тригонометрической
функции:

sin ^3π/₄.

РЕШЕНИЕ:

sin ^3π/₄. = sin (3 ∙ ¹⁸⁰°/₄) = sin 135°.

Поскольку  

135° ∈ [90°, 180°],

это угол из 
II  координатной четверти.

Синус во  II  четверти
положителен, поэтому

sin ^3π/₄ ˃ 0.

Функция  cos α.

Исследуем знаки  cos α  также на промежутке изменения α  от  0  до  2π (от  0°  до  360°).

Если угол  α  заключён
между  0  и  ^π/₂ (0°  и  90°), то абсцисса 
х 
конца  М 
подвижного радиуса  ОМ  единичной окружности положительна,

а следовательно, и косинус угла  α, составленного
с осью  Ох  этим
радиусом  ОМ, – положительный.

Если угол  α  заключён
между  ^π/₂  и  ^3π/₂ (90°  и  270°), то абсцисса 
точки  М  отрицательна, а следовательно, и  cos α – отрицательный.

Если же угол 
α  заключён
между  ^3π/₂  и  2π (270°  и  360°), то как видно из чертежа

cos α – положительный.

Пользуясь равенством

cos (α + 2kπ) = cos α,

получаем

1)  если  2kπ ≤
α < ^π/₂ + 2kπ,
то

cos α ˃ 0,

2)  если  ^π/₂ + 2kπ <
α < ^3π/₂ + 2kπ,
то

cos α < 0,

3)  если  ^3π/₂ + 2kπ <
α < 2π + 2kπ, то

cos α ˃ 0.

Соответственно
тригонометрическая функция имеет знаки, указанные на рисунку.

ПРИМЕР:

Определите знак тригонометрической
функции:

cos ^7π/₆.

РЕШЕНИЕ:

cos ^7π/₆. = cos (7 ∙ ¹⁸⁰°/₆) = cos 210°.

Поскольку  

210° ∈ [180°, 270°],

это угол из 
III  координатной четверти.

Косинус  в  III  четверти отрицателен, поэтому

cos ^7π/₆ < 0.

Функция  tg α.

Так как периодом
функций  tg α  и  сtg α  является 
π (или  180°), исследуем знаки  tg α  и  сtg α  при изменении 
α  от  0  до  π (от  0°  до  180°). Если угол оканчивается
в  I  четверти
(0 < α < ^π/₂  или  0° < α < 90°), то продолжение
подвижного радиуса  ОМ  единичной окружности, образующего с осью  Ох 
угол  α, пересечёт ось тангенсов в точке  Т,

ордината которой положительна. Это означает, что тангенсы углов,
оканчивающихся в  I  четверти – положительны.

Если же угол  α 
оканчивается во  II  четверти (^π/₂ < α < π или  90° < α < 180°), то продолжение
подвижного радиуса  ОМ  единичной окружности, образующего с осью  Ох 
угол  α, пересечёт ось тангенсов в точке  Т,

ордината которой отрицательна. Следовательно, тангенсы углов,
оканчивающиеся во  II  четверти, отрицательны.

В силу периодичности функции  tg α  имеем, что тангенсы углов, оканчивающихся
в  III  четверти, положительны, а в  IV  четверти –
отрицательны.

И вообще, так как

tg (α + kπ) = tg α,

имеем:

1)  если  kπ <
α < kπ + ^π/₂, то

tg α ˃ 0,

2)  если  kπ + ^π/₂ < α < kπ + π, то

tg α < 0.

где  k – любое целое число.

Соответственно
тригонометрическая функция  tg α  имеет знаки, указанные на рисунку.

ПРИМЕР:

Определить, какой знак имеет выражение:

tg 2.

РЕШЕНИЕ:

Так как  ^π/₂ < 2 < π, то угол  2
рад  будет углом  II  четверти, поэтому

tg 2 < 0.

ОТВЕТ:  Знак  –

Функция  сtg α.

Аналогично приходим к выводу:

если  0 < α < ^π/₂, то

сtg α ˃ 0,

если  ^π/₂ < α < π, то

сtg α < 0,

если  π < α < ^3π/₂, то

сtg α ˃ 0,

если  ^3π/₂ < α < 2π , то

сtg α < 0.

И вообще:

1)  если  kπ <
α < ^π/₂ + kπ,  то

сtg α ˃ 0,

2)  если  kπ + ^π/₂ < α < kπ + π, то

сtg α < 0.

где  k – любое целое число.

Соответственно
тригонометрическая функция  сtg α  имеет знаки, указанные на рисунку.

ПРИМЕР:

Определите знак тригонометрической
функции:

сtg ^5π/₃.

РЕШЕНИЕ:

сtg ^5π/₃ = сtg (5 ∙ ¹⁸⁰°/₃) = сtg 300°.

Поскольку  

300° ∈ [270°, 360°],

это угол из 
IV  координатной четверти.

Котангенс  в  IV  четверти отрицателен, поэтому

сtg ^5π/₃ < 0.

ПРИМЕР:

Определите знак выражения:

sin ^3π/₄ ∙ cos ^5π/₆.

РЕШЕНИЕ:

sin ^3π/₄ ∙ cos ^5π/₆ =

sin (3 ∙ ¹⁸⁰°/₄) ∙ cos (5 ∙ ¹⁸⁰°/₆) =

sin 135° ∙ cos 150°.

Разберёмся с синусом. Так как  

135° ∈ [90°, 180°],

это угол из 
II  координатной четверти.

Синус во  II  четверти положителен,
поэтому

sin ^3π/₄ ˃ 0.

Разберёмся с косинусом. Так как
 

150° ∈ [90°, 180°],

это угол из 
II  координатной четверти.

Косинус во  II  четверти отрицателен,
поэтому

cos ^5π/₆ < 0.

Получили произведение, в
котором множители разных знаков.

Пользуясь правилом

<<плюс на минус даёт знак минус>>,

получаем

sin ^3π/₄ ∙ cos ^5π/₆ < 0.

ПРИМЕР:

Определите знак выражения:

cos ^2π/₃ ∙ tg ^π/₄.

РЕШЕНИЕ:

cos ^2π/₃ ∙ tg ^π/₄ =

cos (2 ∙ ¹⁸⁰°/₃) ∙ tg (¹⁸⁰°/₄) =

cos 120° ∙ tg 45°.

Разберёмся с косинусом. Так как
 

120° ∈ [90°, 180°],

это угол из 
II  координатной четверти.

Косинус во  II  четверти отрицателен,
поэтому

cos ^2π/₃ < 0.

Разберёмся с тангенсом. Так как
 

45° ∈ [0°, 90°],

это угол из 
I  координатной четверти.

Тангенс в  I  четверти положителен,
поэтому

tg ^π/₄ ˃ 0.

Получили произведение, в
котором множители разных знаков. Пользуясь правилом

<<минус на плюс даёт минус>>,

получаем

cos ^2π/₃ ∙ tg ^π/₄ < 0.

ПРИМЕР:

Определите знак выражения:

sin ^5π/₆ ∙ cos ^7π/₄.

РЕШЕНИЕ:

sin ^5π/₆ ∙ cos ^7π/₄ =

sin (5 ∙ ¹⁸⁰°/₆) ∙ cos (7 ∙ ¹⁸⁰°/₄) =

sin 150° ∙ cos 315°.

Разберёмся с синусом. Так как  

150° ∈ [90°, 180°],

это угол из 
II  координатной четверти.

Синус во  II  четверти положителен,
поэтому

sin ^5π/₆ ˃ 0.

Разберёмся с косинусом. Так как
 

315° ∈ [270°, 360°],

это угол из 
IV  координатной четверти.

Косинус в  IV  четверти положителен,
поэтому

cos ^5π/₆ < 0.

Получили произведение, в
котором множители одного знака.

Пользуясь правилом

<<плюс на плюс даёт знак плюс>>,

получаем

sin ^5π/₆ ∙ cos ^7π/₄  ˃ 0.

ПРИМЕР:

Определите знак выражения:

tg ^3π/₄ ∙ cos ^5π/₃.

РЕШЕНИЕ:

tg ^3π/₄ ∙ cos ^5π/₃ =

tg (3 ∙ ¹⁸⁰°/₄) ∙ cos (5 ∙ ¹⁸⁰°/₃) =

tg 135° ∙ cos 300°.

Разберёмся с тангенсом. Так как
 

135° ∈ [90°, 180°],

это угол из 
II  координатной четверти.

Тангенс во  II  четверти отрицателен,
поэтому

tg ^3π/₄ < 0.

Разберёмся с косинусом. Так как
 

300° ∈ [270°, 360°],

это угол из 
IV  координатной четверти.

Косинус в  IV  четверти положителен,
поэтому

cos ^5π/₃ ˃ 0.

Получили произведение, в
котором множители разных знаков. Пользуясь правилом

<<минус на плюс даёт минус>>,

получаем

tg ^3π/₄ ∙ cos ^5π/₃ < 0.

ПРИМЕР:

Определите знак выражения:

сtg ^4π/₃ ∙ tg ^π/₆.

РЕШЕНИЕ:

сtg ^4π/₃ ∙ tg ^π/₆ =

сtg (4 ∙ ¹⁸⁰°/₃) ∙ tg (¹⁸⁰°/₆) =

сtg 240° ∙ tg
30°.

Разберёмся с котангенсом. Так
как  

240° ∈ [180°, 270°],

это угол из 
III  координатной четверти.

Котангенс в  III  четверти положителен,
поэтому

сtg ^4π/₃ ˃ 0.

Разберёмся с тангенсом. Так как
 

30° ∈ [0°, 90°],

это угол из 
I  координатной четверти.

Тангенс в  I  четверти положителен,
поэтому

tg ^π/₆ ˃ 0.

Получили произведение, в
котором множители одинаковых знаков. Пользуясь правилом

<<плюс на плюс даёт плюс>>,

получаем

сtg ^4π/₃ ∙ tg ^π/₆  ˃ 0.

ПРИМЕР:

Определите знак выражения:

cos 123° × tg 231° × sin 312°.

РЕШЕНИЕ:

Так как

123° – угол  II  четверти,

231° – угол  III  четверти,

312° – угол  IV  четверти, то 

cos 123° < 0, tg 231° ˃ 0, sin 312° < 0 

и их произведение будет
величиной положительной, то есть

cos 123° × tg 231° × sin 312° ˃ 0.

ОТВЕТ: 

Знак  +

Знаки тригонометрических функций

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.

угла α — это ордината (координата y ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты y к координате x .

Обозначение: sin α = y ; cos α = x ; tg α = y : x .

Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:

Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:

1. sin α > 0, если угол α лежит в I или II координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата y ). А координата y будет положительной именно в I и II координатных четвертях;
2. cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только там координата x (она же — абсцисса) будет больше нуля;
3. tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x , поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти ( x y II координатной четверти. Но синус во II четверти положителен, поэтому sin (3π/4) > 0;
4. cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из III координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) IV четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) II четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова II четверть, косинусы там отрицательны. Поэтому cos (5π/6) II координатная четверть, поэтому cos (2π/3) I четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) II координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это IV координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
5. tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это II четверть, т.е. tg (3π/4) IV четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) III координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это I координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.

В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.

Задача. Найдите sin α, если sin 2 α = 0,64 и α ∈ [π/2; π].

Поскольку sin 2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.

Задача. Найдите cos α, если cos 2 α = 0,04 и α ∈ [π; 3π/2].

Действуем аналогично, т.е. извлекаем квадратный корень: cos 2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.

Задача. Найдите sin α, если sin 2 α = 0,25 и α ∈ [3π/2; 2π].

Имеем: sin 2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.

Задача. Найдите tg α, если tg 2 α = 9 и α ∈ [0; π/2].

Все то же самое, только для тангенса. Извлекаем квадратный корень: tg 2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!

Тригонометрия: определение тригонометрических функций

В этой статье мы рассмотрим тригонометрический круг и введем определения тригонометрических функций с помощью тригонометрического круга .

Впервые с определением синуса, косинуса, тангенса и котангенса школьники встречаются в восьмом классе в курсе геометрии. Напомню эти определения. Рассмотрим прямоугольный треугольник: Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:

sin A=a/b; sin C=c/b

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:

cos A=c/b; cos C= a/b

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:

tg A=a/c; tg C=c/a.

Эти определения тригонометрических функций удобно использовать при решении геометрических задач, связанных с нахождением сторон и углов в прямоугольном треугольнике, однако они не улучшают понимания того, что из себя представляют тригонометрические функции именно как функции.

Часто во время занятий со школьниками я сталкиваюсь с тем, что они не понимают, откуда «взялись» тригонометрические функции, что они из себя представляют, и как их «готовить», чтобы легко решать уравнения и неравенства, содержащие тригонометрические функции.

Предлагаю вам посмотреть ВИДЕОУРОК, чтобы понять, что такое синус, косинус, тангенс и котангенс, как они между собой связаны, и как легко определять знаки тригонометрических функций без использования таблиц.

Косинусом угла α называется абсцисса (то есть координата по оси OX) точки на единичной окружности, соответствующей данному углу α.

Синусом угла α называется ордината (то есть координата по оси OY ) точки на единичной окружности, соответствующеий данному углу α.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса (x), синус — ордината (y).

Поскольку радиус окружности равен 1, для любого угла и синус, и косинус находятся в пределах от −1 до 1:

−1 ≤ cos α ≤ 1, −1 ≤ sin α ≤ 1.

Основное тригонометрическое тождество является следствием теоремы Пифагора (квадрат гипотенузы равен сумме квадратов катетов):

sin 2 α+ cos 2 α = 1

Чтобы узнать знаки синуса и косинуса какого-либо угла, находим на нашей окружности точку, соответствующую данному углу α, смотрим, положительны или отрицательны её координаты по x (это косинус угла α) и по y (это синус угла α).

Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и 13»

Знаки тригонометрических функций по четвертям — примеры определения

Общая информация

Раздел математики, который занимается изучением тригонометрических функций, называется тригонометрией. К функциям относятся следующие: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существуют также и обратные им функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).

Для нахождения знаков тригонометрических функций по четвертям рекомендуется применять специальный «инструмент». Он называется окружностью синусов и косинусов. Однако по ней можно находить не только функции, которые соответствуют ее названию, но и другие. Делается это с помощью тригонометрических тождеств.

Специалисты рекомендуют для понимания материала получить базовые знания об углах и основных тригонометрических функциях. Следует применять принцип «от простого к сложному», поскольку нужно учитывать физиологические особенности головного мозга.

Виды углов

Важной «ступенью» в освоении тригонометрии является идентификация углов. Они делятся на 7 видов. Кроме того, существует еще два типа классификации по знаку: положительные и отрицательные.

Для составления критериев, по которым математики классифицируют углы, необходимо ввести некоторую переменную. Пусть существует некоторый угол a, градусная мера которого составляет x градусов. Необходимо рассмотреть 7 случаев, в которых он измеряется только в градусной размерности:

Последний случай встречается очень часто в различных задачах, в которых следует вычислить определенное значение, упростить тригонометрическое выражение или использовать формулы приведения, а также найти разность между функциями.

Градус — это не единственная единица измерения размерности угла. Существует также и радиан, который пользуется большей популярностью, чем предыдущая единица. Согласно статистике, которая составлена математиками, при решении задач с тригонометрическим уклоном многие используют радиан (около 95,88%). Это объясняется удобством, поскольку в основном применяется тригонометрическая окружность для быстрого нахождения значений функций. Перевод одной единицы в другую осуществляется с помощью двух простых соотношений:

1. В радианы: P = (a * ПИ) / 180.
2. В градусы: а = (P * 180) / ПИ.

Существует 2 метода перевода: автоматизированный и ручной. В первом случае следует применять специальные радианные таблицы, программы и тригонометрическую окружность. Во втором — пользоваться формулами для преобразований. Если очень часто приходится решать задачи подобного типа, то можно создать свой инструмент. Для этого потребуется табличный процессор EXCEL. Необходимо вбить в ячейки две формулы, и тогда ручной метод «превратится» в автоматизированный.

Смысл функций

Тригонометрические функции используются не только в математике, но и в других дисциплинах (физике, электронике, микросхемотехнике, акустике и так далее). С их помощью можно описывать законы изменения различных периодических величин.

Для определения функции необходимо представить прямоугольный треугольник. Его стороны называются катетами и гипотенузой. Угол между двумя катетами является прямым, то есть он равен 90 градусам.

Синус угла — значение, которое вычисляется отношением линейного размера противолежащего катета к гипотенузе прямоугольного треугольника. Если выразить величину через отношение прилежащего катета к гипотенузе, то она называется косинусом угла. Величина, полученная при отношении двух катетов — противолежащего к прилежащему, называется тангенсом. В случае с котангенсом, необходимо поменять числитель и знаменатель местами, то есть отношение прилежащего к противолежащему. Следует также напомнить, что все четыре функции обладают периодичностью. Для sin и cos период соответствует 2 ПИ, а для tg и ctg — ПИ.

Обратными тригонометрическими функциями являются arcsin, arccos, arctg и arcctg. Их необходимо использовать в том случае, когда нужно найти угол по заданному значению. Для этих целей применяются таблицы Брадиса, тригонометрический калькулятор и программное обеспечение, а также круг синусов и косинусов.

Определение знака

Достоверность результата зависит от правильного решения. Неверный знак функции способен кардинально его изменить. Для безошибочного определения значений потребуются еще кое-какие знания. К ним относятся следующие: понятие о системе координат и теорема Пифагора, а также умение чертить окружность с определенным радиусом.

Системы координат, которые применяются при решении задач бывают полярными и декартовыми. Последние используются чаще, чем первые. Полярные применяются для решения задач из области высшей математики, а также в других сложных дисциплинах с физико-математическим уклоном.

Дополнительные сведения

Для определения знака применяется обыкновенная система координат с двумя осями. Одна из них (ОХ) является осью абсцисс, а другая (ОУ) — ординат. Ее центром, который совпадает с центром тригонометрической окружности, является точка «О». Очень часто для работы необходимо знание теоремы Пифагора. Ее формулировка имеет следующий вид: в любом прямоугольном треугольнике выполняется равенство квадрата гипотенузы и суммы квадратов катетов. Вторая формулировка записывается в виде формулы: с^2 = a^2 + b^2 (c, a и b — гипотенуза и два катета соответственно).

Необходимо обратить внимание на следующий факт: сумма всех углов треугольника составляет 180 градусов, то есть является развернутым углом. Математически утверждение можно записать следующим образом через углы а, b и c: а + b + c = 180. Кроме того, существуют и другие соотношения между острыми углами прямоугольного треугольника: cos (a) = sin (b), cos (b) = sin (a), tg (a) = ctg (b), и tg (b) = ctg (a).

Чтобы найти знаки тангенса и котангенса по четвертям, используются такие соотношения: tg (a) = sin (a) / cos (a) и ctg (a) = cos (a) / sin (a).

Построение окружности

Сделать «инструмент», который значительно ускорит процесс решения задач довольно просто. Для этого нужно построить декартовую систему координат и единичную окружность с центром в точке О (точка пересечения осей абсцисс и ординат). Горизонтальная ось обозначается «х», а вертикальная — «у».

Рекомендуется чертить произвольную окружность. Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:

1. Координаты заключаются в круглые скобки и разделяются «;».
2. На первом месте стоит значение, соответствующее оси абсцисс, а на втором — ординат: (x;y).

Окружность пересекает оси в четырех точках: (1;0), (0;1), (-1;0) и (0;-1). Четвертями называются области, которые делят систему координат на четыре равные части. Отсчет выполняется от первой четверти (x>0 и y>0) против часовой стрелки:

1. Значения по x и y больше 0 соответствуют первой четверти (I).
2. II: x 0.
3. III: x 0 и y 0 и ctg>0.
4. -sin(ПИ + ПИ/4) = -sin(ПИ/4) = -cos(ПИ/4) = -sqrt(2)/2.
5. tg(ПИ/4) = ctg(ПИ/4) = -sin(ПИ/4) / -cos(ПИ/4) = 1.

После расчетов нужно выполнить проверку знаков. В III четверти больше нуля только тангенс и котангенс. Однако бывают случаи, когда значение градусной меры угла превышает 360.

Свыше 2ПИ

Существует определенный тип задач, в которых величина градусной меры угла свыше 360 градусов. Например, следует вычислить значения тригонометрических функций угла -26ПИ/6. Решается она следующим образом:

1. Следует выделить целую часть из -26ПИ/6 и привести к удобному виду: 26/6 = 4 + 2/6 = 4 + 1/3. Угол находится в IV четверти (движение по часовой стрелке).
2. -sin(4ПИ + ПИ/3) = -sin(ПИ/3) = — sqrt(3)/2.
3. cos(ПИ/3) = 1/2.
4. -tg(ПИ/3) = — sqrt(3).
5. -сtg(ПИ/3) = — 1/sqrt(3).

Во втором, четвертом и пятом пунктах функции являются нечетными. Если посмотреть на график, то движение осуществляется по часовой стрелке, поскольку угол является отрицательным числом. Функция косинуса является четной. Ее числовое значение — положительная величина. Последним этапом считается проверка знаков. Угол находится в IV четверти. Значения функций совпадают.

Таким образом, при решении задач по тригонометрии следует применять тригонометрическую окружность, с помощью которой можно безошибочно определять знак функции.

источники:

http://ege-ok.ru/2011/12/29/trigonometriya-opredelenie-trigonom

http://nauka.club/matematika/znaki-trigonometricheskikh-funktsiy.html