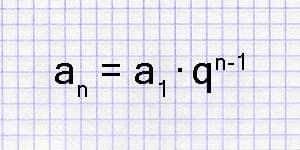На сайте уже есть калькулятор для геометрической прогрессии — Геометрическая прогрессия, который позволяет найти сумму ее членов. Однако бывает еще и другая задача — по двум заданным соседним членам геометрической прогрессии найти знаменатель и ее первый член. Понятно, что в такой постановке задачи речь идет о возрастающей геометрической прогрессии, первый член которой, также как и знаменатель, являются целыми числами.
Со знаменателем все понятно, два соседних члена геометрической прогрессии связаны соотношением
,
откуда
А вот чтобы получить первый член, надо делить каждый предыдущий на q, пока не перестанут получаться целые значения. Последнее целое значение и будет первым членом геометрической прогрессии. Собственно, чтобы не утомляться таким делением, и написан калькулятор ниже.
Геометрическая прогрессия. Знаменатель и первый член
Член геометрической прогрессии
Следующий член геометрической прогрессии
Первый член геометрической прогрессии
Знаменатель геометрической прогрессии
Калькулятор геометрической прогрессии
Геометрическая прогрессия – такая последовательность чисел, в которой каждое следующее число получается путем умножения предыдущего на знаменатель прогрессии. Пример такой прогрессии: 4, 8, 16, 32, 64, где первый член – 4, знаменатель – 2, количество членов – 5. Если первый член прогрессии и ее знаменатель > 0, то это – возрастающая последовательность. Если знаменатель от нуля до единицы, то последовательность убывает.
Свойства геометрической прогрессии
Зная соседние члены, знаменатель q можно найти по формуле:
q = bn+1bn.
Скопировать «Геометрическая прогрессия»:
Последние вычисления
Комментарии к калькулятору
Количество комментариев: 2
21.10.2020
Лена
Получила 5!
18.10.2020
Лена
Во, как раз нам по домашке ГП задали, сейчас посчитаем)
Геометрическая прогрессия — это числовая последовательность, в которой все ее члены расположены в порядке, подчиняющемся определенной закономерности. Формула геометрической прогрессии определяет, что каждое следующее число будет получено умножением предыдущего на знаменатель прогрессии — постоянное число, не меняющее свое значение в пределах одной последовательности.
bn=b1 q(n-1)
В зависимости от знаменателя прогрессии, выписанные члены геометрической прогрессии могут давать различный вид ряда. Если знаменатель является числом положительным, больше 1 (k > 1), тогда он будет увеличивать значение каждого следующего числа. Такая прогрессия будет монотонно возрастать на протяжении всего ряда. Если знаменатель — положительный, но находится между 0 и 1 (0 < k < 1), тогда он будет каждый раз уменьшать значение следующего члена, и такая прогрессия будет называться бесконечно убывающая геометрическая прогрессия.
Если для все возрастающей последовательности, можно только найти сумму первых членов геометрической прогрессии, то сумма членов бесконечно убывающей прогрессии будет равна вполне конкретному числовому значению, которое может рассчитать калькулятор. Третий случай представлен отрицательным знаменателем (k < 0), тогда прогрессия становится знакочередующейся, то есть первые члены геометрической прогрессии определяют порядок знаков для всей последовательности чисел. Как знаменатель геометрической прогрессии, так и первый член геометрической прогрессии по определению не могут быть равны нулю.
Существует всего несколько формул геометрической прогрессии, из которых можно вывести все необходимые для решения конкретных задач:
• Формула первого члена геометрической прогрессии;
• Формула n члена геометрической прогрессии;
• Формула суммы первых членов геометрической прогрессии;
• Формула суммы бесконечно убывающей геометрической прогрессии;
• Формула знаменателя геометрической прогрессии.
Таким образом, если условиями задана геометрическая прогрессия с хотя бы двумя параметрами из всех выше представленных, для нее можно будет найти любую из всех прочих переменных.
Геометрическая прогрессия – это последовательность чисел, каждое следующее из которых отличается от предыдущего в q раз, где q называют иначе знаменателем геометрической прогрессии.
bn=bn-1×q
Зная первый член геометрической прогрессии и ее знаменатель, можно также найти любой другой член прогрессии, умножив первый член на знаменатель в степень n-1.
bn=b1×qn-1
Любая геометрическая прогрессия является бесконечной, но если взять заданное количество ее членов, то можно найти сумму геометрической прогрессии. Для этого необходимо умножить первый член геометрической прогрессии на разности единицы и знаменателя прогрессии в степени, равной по значению количеству членов, и разделить на простую разность единицы и знаменателя.
Если знаменатель геометрической прогрессии находится в промежутке от -1 до 1, то каждый следующий член прогрессии будет меньше предыдущего. Такая геометрическая прогрессия называется бесконечно убывающей, и она будет стремиться к конкретному числовому значению. Зная первый член прогрессии и знаменатель, можно найти сумму убывающей геометрической прогрессии, которая представлена приблизительным числом (числом, к которому эта сумма стремится).
Калькулятор онлайн.
Решение геометрической прогрессии.
Дано: b1, q, n
Найти: bn и первых n членов.
Эта математическая программа находит ( b_n ) и первых ( n ) членов
геометрической прогрессии, исходя из заданных пользователем чисел ( b_1, q ) и ( n ).
Числа ( b_1) и ( q ) можно задать не только целые, но и дробные. Причём, дробное число можно ввести в виде десятичной
дроби ( ( 2,5 ) ) и в виде обыкновенной дроби ( ( -5frac{2}{7} ) ).
Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Правила ввода чисел
Числа ( b_1) и ( q ) можно задать не только целые, но и дробные.
Число ( n) может быть только целое положительное.
Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так 2.5 или так 2,5
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод:
Результат: ( -frac{2}{3} )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод:
Результат: ( -1frac{2}{3} )
Введите числа b1, q, n
Наши игры, головоломки, эмуляторы:
Немного теории.
Числовая последовательность
В повседневной практике часто используется нумерация различных предметов, чтобы указать порядок их расположения. Например,
дома на каждой улице нумеруются. В библиотеке нумеруются читательские абонементы и затем располагаются в порядке присвоенных
номеров в специальных картотеках.
В сберегательном банке по номеру лицевого счёта вкладчика можно легко найти этот счёт и посмотреть, какой вклад на нём лежит.
Пусть на счёте № 1 лежит вклад а1 рублей, на счёте № 2 лежит вклад а2 рублей и т. д. Получается числовая последовательность
a1, a2, a3, …, aN
где N — число всех счетов. Здесь каждому натуральному числу n от 1 до N поставлено в соответствие число an.
В математике также изучаются бесконечные числовые последовательности:
a1, a2, a3, …, an, … .
Число a1 называют первым членом последовательности, число a2 — вторым членом последовательности,
число a3 — третьим членом последовательности и т. д.
Число an называют n-м (энным) членом последовательности, а натуральное число n — его номером.
Например, в последовательности квадратов натуральных чисел 1, 4, 9, 16, 25, …, n2, (n + 1)2, …
а1 = 1 — первый член последовательности; аn = n2 является n-м членом последовательности;
an+1= (n + 1)2 является (n + 1)-м (эн плюс первым) членом последовательности.
Часто последовательность можно задать формулой её n-го члена.
Например, формулой ( a_n=frac{1}{n}, ; n in mathbb{N} ) задана последовательность
( 1, ; frac{1}{2} , ; frac{1}{3} , ; frac{1}{4} , dots,frac{1}{n} , dots )
Геометрическая прогрессия
Рассмотрим равносторонний треугольник со стороной 4 см. Построим треугольник, вершинами которого являются середины сторон данного
треугольника. По свойству средней линии треугольника сторона второго треугольника равна 2 см. Продолжая аналогичные построения,
получим треугольники со сторонами ( 1, ; frac{1}{2}, ; frac{1}{4} ) см и т.д. Запишем последовательность длин сторон этих
треугольников: ( 4, ; 2, ; 1, ; frac{1}{2}, ; frac{1}{4}, ; frac{1}{8}, dots )
В этой последовательности каждый её член, начиная со второго, равен предыдущему, умноженному на одно и то же число ( frac{1}{2} )
Определение.
Числовая последовательность
b1, b2, b3, …, bn, …
называется геометрической прогрессией если для всех натуральных n выполняется равенство
bn+1 = bnq,
где ( b_n neq 0 ), q — некоторое число, не равное нулю.
Из этой формулы следует, что ( frac{ b_{n+1}}{b_n}=q ). Число q называется знаменателем геометрической прогрессии.
По определению геометрической прогрессии
( b_{n+1} = b_n q, quad b_{n-1}=frac{b_n}{q}, )
откуда
( b_n^2 = b_{n-1}b_{n+1}, quad n>1 )
Если все члены геометрической прогрессии положительны, то ( b_n=sqrt{b_{n-1}b_{n+1}} ), т.е. каждый член прогрессии, начиная
со второго, равен среднему геометрическому двух соседних с ним членов. Этим объясняется название «геометрическая» прогрессия.
Отметим, что если b1 и q заданы, то остальные члены геометрической прогрессии можно вычислить по рекуррентной формуле
bn+1 = bnq. Однако для больших n это трудоёмко. Обычно пользуются формулой n-го члена.
По определению геометрической прогрессии
b2 = b1q,
b3 = b2q = b1q2,
b4 = b3q = b1q3 и т.д.
Вообще,
( b_n = b_1q^{n-1} )
так как n-й член геометрической прогрессии получается из первого члена умножением (n-1) раз на число q.
Эту формулу называют формулой n-го члена геометрической прогрессии.
Также не сложно получить формулу для нахождения n-ого члена геометрической прогрессии зная m-ый член.
Запишем формулы n-го члена геометрической прогрессии и m-го члена:
( b_n = b_1q^{n-1} )
$$ b_m = b_1q^{m-1} Rightarrow b_1 = frac{b_m}{q^{m-1}} $$
Подставляя b1 в первое равенство получим:
$$ b_n = frac{b_m}{q^{m-1}} cdot q^{n-1} = b_m cdot q^{n-1-(m-1)} = b_m cdot q^{n-m} $$
Таким образом мы получили формулу для нахождения n-ого члена геометрической прогрессии зная m-ый член:
( b_n = b_m cdot q^{n-m} )
Сумма n первых членов геометрической прогрессии
Найдем сумму
S = 1 + 3 + 32 + 33 + 34 + 35.
Умножим обе части равенства на 3:
3S = 3 + 3 + 32 + 33 + 34 + 35 + 36.
Перепишем эти два равенства так:
S = 1 + (3 + 32 + 33 + 34 + 35),
3S = (3 + 3 + 32 + 33 + 34 + 35) + 36.
Выражения, стоящие в скобках, одинаковы. Поэтому, вычитая из нижнего равенства верхнее, получаем:
3S — S = 36 — 1, 2S = 36 — 1,
$$ S=frac{3^6 — 1}{2} = frac{729 — 1}{2} = 364 $$
Рассмотрим теперь произвольную геометрическую прогрессию ( b_1, ; b_1q, ; dots, ; b_1q^n, ; dots ) знаменатель
которой ( q neq 1 ).
Пусть Sn — сумма n первых членов этой прогрессии:
( S_n = b_1 + b_1q + b_1q^2 + … + b_1q^{n-1} )
Тогда сумма n первых членов геометрической прогрессии со знаменателем ( q neq 1 ) равна
$$ S_n = frac{b_1(q^n-1)}{q-1} $$
Можно получить ещё одну формулу для нахождения суммы n первых членов геометрической прогрессии:
$$ S_n = frac{b_1(q^n-1)}{q-1} = frac{b_1q^n — b_1}{q-1} = frac{b_1q^{n-1} cdot q — b_1}{q-1} $$
Так как ( b_n=b_1q^{n-1} ), то можно подставить ( b_n ) в предыдущее выражение:
$$ S_n = frac{b_n q — b_1}{q-1} $$