Как нашли радиус земного шара - Исправление недочетов и поиск решений вместе с Examum.ru

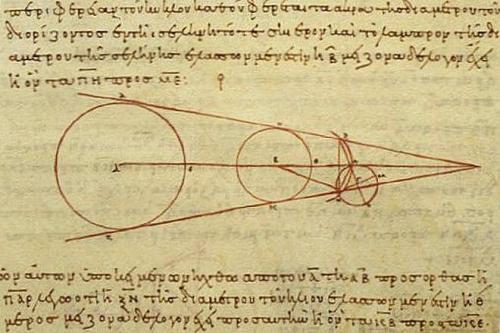
В наши дни окружность Земли можно измерить с помощью измерительной аппаратуры и спутников. Но можно и не изобретать никаких хитроумных инструментов, как это сделал Эратосфен более 2000 лет назад. Он вычислил размеры Земли, не покидая стен библиотеки, где работал.

Как Эратосфен измерил окружность Земли?

Эратосфен

Эратосфен — греческий ученый, живший в египетском городе Александрии с 276 года по 196 год до нашей эры. Работал он в Александрийском мусейоне. Отчасти это был музей, отчасти научный центр того времени.

В музее был ботанический сад, виварий, астрономическая обсерватория и лаборатории. Одни ученые мужи вели научные диспуты в аудитории музея, другие трапезничали и беседовали в триклинии (то есть в столовой).

Интересный факт: греческий ученый Эратосфен вычислил окружность Земли более 2000 лет назад.

Эратосфен заведовал библиотекой мусейона, в которой хранилось около 100 тысяч книг, написанных на свитках папируса (разновидность бумаги, сделанной из волокон растения папируса). Эратосфен интересовался всем на свете. Он изучал философию, историю и естественные науки, был театральным критиком. Многие коллеги по мусейону считали его дилетантом, то есть человеком, который всем интересуется, но ничего не знает по истине глубоко.

Как Эратосфен измерил окружность Земли?

От проезжих путешественников Эратосфен услышал о необычном явлении, которое они наблюдали в Сиене, городе, расположенном далеко к югу от Александрии. Путешественники рассказали, что в полдень первого дня лета — в самый продолжительный день в году — в Сиене исчезали тени. Солнце в это время стояло прямо над головой, лучи его падали на землю отвесно вниз. Внимательно вглядываясь в воду водоема, можно было рассмотреть отражение Солнца на дне.

Интересный факт: окружность Земли равна приблизительно 40000 километров.

Эратосфен съездил в Сиену и убедился в этом сам. Вернувшись в Александрию, он обнаружил, что и в самый длительный день года в полдень стены мусейона продолжали отбрасывать тень на землю. Основываясь на этом простом наблюдении, он смог вычислить окружность Земли. Вот как он это сделал.

Вычисления окружности

Эратосфен знал, что из – за громадного расстояния от Земли до Солнца, лучи последнего достигают и Сиены и Александрии параллельными лучами. То есть лучи Солнца, падающие на землю в Александрии, параллельны лучам, падающим на землю в Сиене в то же время. Если бы Земля была плоской, то тени исчезали бы на ней повсеместно 21 июня. Но так как, рассуждал он, Земля искривлена, то в Александрии, удаленной от Сиены на 500 миль (1 миля равна 1,609 километра) к северу, местные стены и колонны наклонены по отношению к сиенским стенам и колон нам под некоторым углом.

Вычисления окружности

Итак, в полдень первого дня лета Эратосфен измерил тень, отбрасываемую обелиском, стоявшим неподалеку от мусейона. Зная высоту обелиска, он смог легко вычислить длину линии, соединяющей вершину обелиска и конец тени. Получился воображаемый треугольник. После того как треугольник был «очерчен», оставалось, используя известные к тому времени правила геометрии, вычислить его углы. И Эратосфен их вычислил. Он нашел, что угол отклонения обелиска от солнечного луча составляет чуть больше 7 градусов.

Так как в Сиене вертикальные предметы не отбрасывали тени, то угол между ними и солнечным лучом составлял ноль градусов. Короче, никакого угла не было. Это означало, что Александрия отстоит по земной окружности от Сиены на 7 градусов. Такой угол между городами — это ¹/50 часть окружности. Всякая окружность содержит 360 градусов, земная окружность в этом смысле не исключение. Эратосфен умножил расстояние между Сиеной и Александрией — 500 миль — на 50 и получил значение окружности Земли. Оно оказалось равным 25 тысячам миль. Современные ученые, измерившие с помощью высококлассной техники окружность Земли, нашли ее равной 24 894 тысяч миль. Все таки Эратосфен оказался первоклассным ученым, а не дилетантом.

Определение расстояний на земной поверхности

В настоящее время существует целая наука — геодезия, которая занимается определением расстояний на земной поверхности. Геодезисты используют специальные приборы для определения угловых расстояний. Они изучают колебания силы тяжести на нашей планете, чтобы выявить истинную форму Земли. Для вычисления углов используют спутники. Такой спутник перемещается в вершину воображаемого треугольника, два других его угла помещают в заданных точках на земной поверхности.

Как вычислили окружность Земли

Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Источник

После получения образования, имея почти энциклопедические познания, Эратосфен начал свою научную деятельность, впоследствии став известным, благодаря своим работам. Так, в один прекрасный момент, царь Птолемей III пригласил Эратосфена из Афин в Александрию заведовать великой Александрийской библиотекой.

Источник

Earth radius
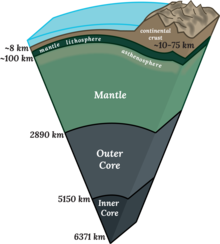
Cross section of Earth’s Interior
General information
Unit system	astronomy, geophysics
Unit of	distance
Symbol	R_🜨 or , ${displaystyle {mathcal {R}}_{mathrm {eE} }^{mathrm {N} }}$
Conversions
1 R_🜨 in …	… is equal to …
SI base unit	6.3781×10⁶ m^[1]
Metric system	6,357 to 6,378 km
English units	3,950 to 3,963 mi

Earth radius (denoted as R_🜨 or ) is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly 6,378 km (3,963 mi) (equatorial radius, denoted a) to a minimum of nearly 6,357 km (3,950 mi) (polar radius, denoted b).

A nominal Earth radius is sometimes used as a unit of measurement in astronomy and geophysics, which is recommended by the International Astronomical Union to be the equatorial value.^[1]

A globally-average value is usually considered to be 6,371 kilometres (3,959 mi) with a 0.3% variability (±10 km) for the following reasons.
The International Union of Geodesy and Geophysics (IUGG) provides three reference values: the mean radius (R₁) of three radii measured at two equator points and a pole; the authalic radius, which is the radius of a sphere with the same surface area (R₂); and the volumetric radius, which is the radius of a sphere having the same volume as the ellipsoid (R₃).^[2] All three values are about 6,371 kilometres (3,959 mi).

Other ways to define and measure the Earth’s radius involve the radius of curvature. A few definitions yield values outside the range between polar radius and equatorial radius because they include local or geoidal topography or because they depend on abstract geometrical considerations.

Introduction[edit]

Earth’s rotation, internal density variations, and external tidal forces cause its shape to deviate systematically from a perfect sphere.^[a] Local topography increases the variance, resulting in a surface of profound complexity. Our descriptions of Earth’s surface must be simpler than reality in order to be tractable. Hence, we create models to approximate characteristics of Earth’s surface, generally relying on the simplest model that suits the need.

Each of the models in common use involve some notion of the geometric radius. Strictly speaking, spheres are the only solids to have radii, but broader uses of the term radius are common in many fields, including those dealing with models of Earth. The following is a partial list of models of Earth’s surface, ordered from exact to more approximate:

The actual surface of Earth
The geoid, defined by mean sea level at each point on the real surface^[b]
A spheroid, also called an ellipsoid of revolution, geocentric to model the entire Earth, or else geodetic for regional work^[c]
A sphere

In the case of the geoid and ellipsoids, the fixed distance from any point on the model to the specified center is called «a radius of the Earth» or «the radius of the Earth at that point».^[d] It is also common to refer to any mean radius of a spherical model as «the radius of the earth». When considering the Earth’s real surface, on the other hand, it is uncommon to refer to a «radius», since there is generally no practical need. Rather, elevation above or below sea level is useful.

Regardless of the model, any radius falls between the polar minimum of about 6,357 km and the equatorial maximum of about 6,378 km (3,950 to 3,963 mi). Hence, the Earth deviates from a perfect sphere by only a third of a percent, which supports the spherical model in most contexts and justifies the term «radius of the Earth». While specific values differ, the concepts in this article generalize to any major planet.

Physics of Earth’s deformation[edit]

Rotation of a planet causes it to approximate an oblate ellipsoid/spheroid with a bulge at the equator and flattening at the North and South Poles, so that the equatorial radius a is larger than the polar radius b by approximately aq. The oblateness constant q is given by

${displaystyle q={frac {a^{3}omega ^{2}}{GM}},,}$

where ω is the angular frequency, G is the gravitational constant, and M is the mass of the planet.^[e] For the Earth 1/q ≈ 289, which is close to the measured inverse flattening 1/f ≈ 298.257. Additionally, the bulge at the equator shows slow variations. The bulge had been decreasing, but since 1998 the bulge has increased, possibly due to redistribution of ocean mass via currents.^[4]

The variation in density and crustal thickness causes gravity to vary across the surface and in time, so that the mean sea level differs from the ellipsoid. This difference is the geoid height, positive above or outside the ellipsoid, negative below or inside. The geoid height variation is under 110 m (360 ft) on Earth. The geoid height can change abruptly due to earthquakes (such as the Sumatra-Andaman earthquake) or reduction in ice masses (such as Greenland).^[5]

Not all deformations originate within the Earth. Gravitational attraction from the Moon or Sun can cause the Earth’s surface at a given point to vary by tenths of a meter over a nearly 12-hour period (see Earth tide).

Radius and local conditions[edit]

Al-Biruni’s (973–1048) method for calculation of the Earth’s radius simplified measuring the circumference compared to taking measurements from two locations distant from each other.

Given local and transient influences on surface height, the values defined below are based on a «general purpose» model, refined as globally precisely as possible within 5 m (16 ft) of reference ellipsoid height, and to within 100 m (330 ft) of mean sea level (neglecting geoid height).

Additionally, the radius can be estimated from the curvature of the Earth at a point. Like a torus, the curvature at a point will be greatest (tightest) in one direction (north–south on Earth) and smallest (flattest) perpendicularly (east–west). The corresponding radius of curvature depends on the location and direction of measurement from that point. A consequence is that a distance to the true horizon at the equator is slightly shorter in the north–south direction than in the east–west direction.

In summary, local variations in terrain prevent defining a single «precise» radius. One can only adopt an idealized model. Since the estimate by Eratosthenes, many models have been created. Historically, these models were based on regional topography, giving the best reference ellipsoid for the area under survey. As satellite remote sensing and especially the Global Positioning System gained importance, true global models were developed which, while not as accurate for regional work, best approximate the Earth as a whole.

Extrema: equatorial and polar radii[edit]

The following radii are derived from the World Geodetic System 1984 (WGS-84) reference ellipsoid.^[6] It is an idealized surface, and the Earth measurements used to calculate it have an uncertainty of ±2 m in both the equatorial and polar dimensions.^[7] Additional discrepancies caused by topographical variation at specific locations can be significant. When identifying the position of an observable location, the use of more precise values for WGS-84 radii may not yield a corresponding improvement in accuracy.^{[clarification needed]}

The value for the equatorial radius is defined to the nearest 0.1 m in WGS-84. The value for the polar radius in this section has been rounded to the nearest 0.1 m, which is expected to be adequate for most uses. Refer to the WGS-84 ellipsoid if a more precise value for its polar radius is needed.

The Earth’s equatorial radius a, or semi-major axis, is the distance from its center to the equator and equals 6,378.1370 km (3,963.1906 mi).^[8] The equatorial radius is often used to compare Earth with other planets.

The Earth’s polar radius b, or semi-minor axis, is the distance from its center to the North and South Poles, and equals 6,356.7523 km (3,949.9028 mi).

Location-dependent radii[edit]

Three different radii as a function of Earth’s latitude. R is the geocentric radius; M is the meridional radius of curvature; and N is the prime vertical radius of curvature.

Geocentric radius[edit]

The geocentric radius is the distance from the Earth’s center to a point on the spheroid surface at geodetic latitude φ:

${displaystyle R(varphi )={sqrt {frac {(a^{2}cos varphi )^{2}+(b^{2}sin varphi )^{2}}{(acos varphi )^{2}+(bsin varphi )^{2}}}}}$

where a and b are, respectively, the equatorial radius and the polar radius.

The extrema geocentric radii on the ellipsoid coincide with the equatorial and polar radii.
They are vertices of the ellipse and also coincide with minimum and maximum radius of curvature.

Radii of curvature[edit]

Principal radii of curvature[edit]

There are two principal radii of curvature: along the meridional and prime-vertical normal sections.

Meridional[edit]

In particular, the Earth’s meridional radius of curvature (in the north–south direction) at φ is:^[9]

${displaystyle M(varphi )={frac {(ab)^{2}}{{big (}(acos varphi )^{2}+(bsin varphi )^{2}{big )}^{frac {3}{2}}}}={frac {a(1-e^{2})}{(1-e^{2}sin ^{2}varphi )^{frac {3}{2}}}}={frac {1-e^{2}}{a^{2}}}N(varphi )^{3},.}$

where is the eccentricity of the earth. This is the radius that Eratosthenes measured in his arc measurement.

Prime vertical[edit]

The length PQ, called the prime vertical radius, is . The length IQ is equal to $,e^{2}N(phi )$ . .

If one point had appeared due east of the other, one finds the approximate curvature in the east–west direction.^[f]

This Earth’s prime-vertical radius of curvature, also called the Earth’s transverse radius of curvature, is defined perpendicular (orthogonal) to M at geodetic latitude φ^[g] and is:^[9]

${displaystyle N(varphi )={frac {a^{2}}{sqrt {(acos varphi )^{2}+(bsin varphi )^{2}}}}={frac {a}{sqrt {1-e^{2}sin ^{2}varphi }}},.}$

N can also be interpreted geometrically as the normal distance from the ellipsoid surface to the polar axis.^[10]
The radius of a parallel of latitude is given by .^[11]^[12]

Polar and equatorial radius of curvature[edit]

The Earth’s meridional radius of curvature at the equator equals the meridian’s semi-latus rectum:

b²/a = 6,335.439 km

The Earth’s prime-vertical radius of curvature at the equator equals the equatorial radius, N = a.

The Earth’s polar radius of curvature (either meridional or prime-vertical) is:

a²/b = 6,399.594 km

Derivation[edit]

Extended content
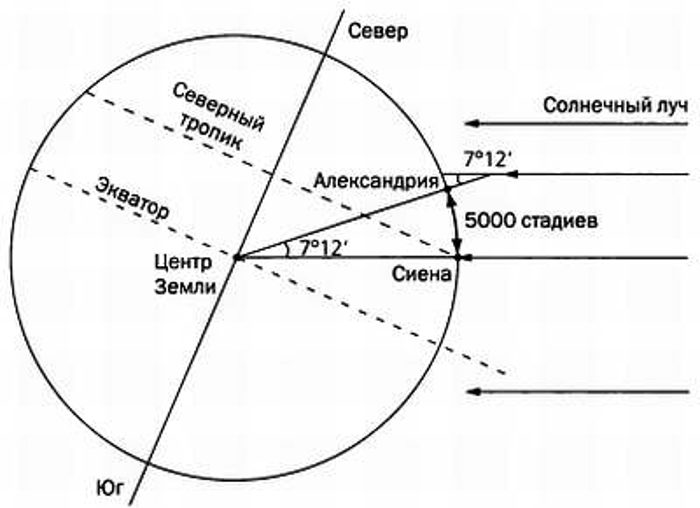
The principal curvatures are the roots of Equation (125) in:^[13] ${displaystyle (EG-F^{2}),kappa ^{2}-(eG+gE-2fF),kappa +(eg-f^{2})=0=det(A-kappa ,B),}$ where in the first fundamental form for a surface (Equation (112) in^[13]): ${displaystyle ds^{2}=sum _{ij}a_{ij}dw^{i}dw^{j}=E,dvarphi ^{2}+2F,dvarphi ,dlambda +G,dlambda ^{2},}$ E, F, and G are elements of the metric tensor: ${displaystyle A=a_{ij}=sum _{nu }{frac {partial r^{nu }}{partial w^{i}}}{frac {partial r^{nu }}{partial w^{j}}}=left[{begin{array}{ll}E&F\F&Gend{array}}right],}$ ${displaystyle r=[r^{1},r^{2},r^{3}]^{T}=[x,y,z]^{T}}$ , ${displaystyle w^{1}=varphi }$ , ${displaystyle w^{2}=lambda ,}$ in the second fundamental form for a surface (Equation (123) in^[13]): ${displaystyle 2D=sum _{ij}b_{ij}dw^{i}dw^{j}=e,dvarphi ^{2}+2f,dvarphi ,dlambda +g,dlambda ^{2},}$ e, f, and g are elements of the shape tensor: ${displaystyle B=b_{ij}=sum _{nu }n^{nu }{frac {partial ^{2}r^{nu }}{partial w^{i}partial w^{j}}}=left[{begin{array}{ll}e&f\f&gend{array}}right],}$ ${displaystyle n={frac {N}{\|N\|}}}$ is the unit normal to the surface at , and because ${displaystyle {frac {partial r}{partial varphi }}}$ and ${displaystyle {frac {partial r}{partial lambda }}}$ are tangents to the surface, ${displaystyle N={frac {partial r}{partial varphi }}times {frac {partial r}{partial lambda }}}$ is normal to the surface at . With for an oblate spheroid, the curvatures are ${displaystyle kappa _{1}={frac {g}{G}}}$ and ${displaystyle kappa _{2}={frac {e}{E}},,}$ and the principal radii of curvature are ${displaystyle R_{1}={frac {1}{kappa _{1}}}}$ and ${displaystyle R_{2}={frac {1}{kappa _{2}}}.}$ The first and second radii of curvature correspond, respectively, to the Earth’s meridional and prime-vertical radii of curvature. Geometrically, the second fundamental form gives the distance from to the plane tangent at .

Extended content

The principal curvatures are the roots of Equation (125) in:^[13]

${displaystyle (EG-F^{2}),kappa ^{2}-(eG+gE-2fF),kappa +(eg-f^{2})=0=det(A-kappa ,B),}$

where in the first fundamental form for a surface (Equation (112) in^[13]):

${displaystyle ds^{2}=sum _{ij}a_{ij}dw^{i}dw^{j}=E,dvarphi ^{2}+2F,dvarphi ,dlambda +G,dlambda ^{2},}$

E, F, and G are elements of the metric tensor:

${displaystyle A=a_{ij}=sum _{nu }{frac {partial r^{nu }}{partial w^{i}}}{frac {partial r^{nu }}{partial w^{j}}}=left[{begin{array}{ll}E&F\F&Gend{array}}right],}$

${displaystyle r=[r^{1},r^{2},r^{3}]^{T}=[x,y,z]^{T}}$ , ${displaystyle w^{1}=varphi }$ , ${displaystyle w^{2}=lambda ,}$

in the second fundamental form for a surface (Equation (123) in^[13]):

${displaystyle 2D=sum _{ij}b_{ij}dw^{i}dw^{j}=e,dvarphi ^{2}+2f,dvarphi ,dlambda +g,dlambda ^{2},}$

e, f, and g are elements of the shape tensor:

${displaystyle B=b_{ij}=sum _{nu }n^{nu }{frac {partial ^{2}r^{nu }}{partial w^{i}partial w^{j}}}=left[{begin{array}{ll}e&f\f&gend{array}}right],}$

${displaystyle n={frac {N}{|N|}}}$ is the unit normal to the surface at , and because
${displaystyle {frac {partial r}{partial varphi }}}$ and ${displaystyle {frac {partial r}{partial lambda }}}$ are tangents to the surface,

${displaystyle N={frac {partial r}{partial varphi }}times {frac {partial r}{partial lambda }}}$

is normal to the surface at .

With for an oblate spheroid, the curvatures are

${displaystyle kappa _{1}={frac {g}{G}}}$

and ${displaystyle kappa _{2}={frac {e}{E}},,}$

and the principal radii of curvature are

${displaystyle R_{1}={frac {1}{kappa _{1}}}}$

and ${displaystyle R_{2}={frac {1}{kappa _{2}}}.}$

The first and second radii of curvature correspond, respectively, to the Earth’s meridional and prime-vertical radii of curvature.

Geometrically, the second fundamental form gives the distance from to the plane tangent at .

Combined radii of curvature[edit]

Azimuthal[edit]

The Earth’s azimuthal radius of curvature, along an Earth normal section at an azimuth (measured clockwise from north) α and at latitude φ, is derived from Euler’s curvature formula as follows:^[14]^: 97

${displaystyle R_{mathrm {c} }={frac {1}{{dfrac {cos ^{2}alpha }{M}}+{dfrac {sin ^{2}alpha }{N}}}},.}$

Non-directional[edit]

It is possible to combine the principal radii of curvature above in a non-directional manner.

The Earth’s Gaussian radius of curvature at latitude φ is:^[14]

${displaystyle R_{mathrm {a} }(varphi )={frac {1}{sqrt {K}}}={frac {1}{2pi }}int _{0}^{2pi }R_{mathrm {c} }(alpha ),dalpha ,={sqrt {MN}}={frac {a^{2}b}{(acos varphi )^{2}+(bsin varphi )^{2}}}={frac {a{sqrt {1-e^{2}}}}{1-e^{2}sin ^{2}varphi }},.}$

Where K is the Gaussian curvature, ${displaystyle K=kappa _{1},kappa _{2}={frac {det ,B}{det ,A}}}$ .

The Earth’s mean radius of curvature at latitude φ is:^[14]^: 97

${displaystyle R_{mathrm {m} }={frac {2}{{dfrac {1}{M}}+{dfrac {1}{N}}}},!}$

Global radii[edit]

The Earth can be modeled as a sphere in many ways. This section describes the common ways. The various radii derived here use the notation and dimensions noted above for the Earth as derived from the WGS-84 ellipsoid;^[6] namely,

Equatorial radius: a = (6378.1370 km)

Polar radius: b = (6356.7523 km)

A sphere being a gross approximation of the spheroid, which itself is an approximation of the geoid, units are given here in kilometers rather than the millimeter resolution appropriate for geodesy.

Nominal radius[edit]

In astronomy, the International Astronomical Union denotes the nominal equatorial Earth radius as ${displaystyle {mathcal {R}}_{mathrm {eE} }^{mathrm {N} }}$ , which is defined to be 6,378.1 km (3,963.2 mi).^[1]^: 3 The nominal polar Earth radius is defined as ${displaystyle {mathcal {R}}_{mathrm {pE} }^{mathrm {N} }}$ = 6,356.8 km (3,949.9 mi). These values correspond to the zero Earth tide convention. Equatorial radius is conventionally used as the nominal value unless the polar radius is explicitly required.^[1]^: 4
The nominal radius serves as a unit of length for astronomy.
(The notation is defined such that it can be easily generalized for other planets; e.g., ${displaystyle {mathcal {R}}_{mathrm {pJ} }^{mathrm {N} }}$ for the nominal polar Jupiter radius.)

Arithmetic mean radius[edit]

Equatorial (a), polar (b) and arithmetic mean Earth radii as defined in the 1984 World Geodetic System revision (not to scale)

In geophysics, the International Union of Geodesy and Geophysics (IUGG) defines the Earth’s arithmetic mean radius (denoted R₁) to be^[2]

$R_{1}={frac {2a+b}{3}},!$

The factor of two accounts for the biaxial symmetry in Earth’s spheroid, a specialization of triaxial ellipsoid.
For Earth, the arithmetic mean radius is 6,371.0088 km (3,958.7613 mi).^[15]

Authalic radius[edit]

Earth’s authalic radius (meaning «equal area») is the radius of a hypothetical perfect sphere that has the same surface area as the reference ellipsoid. The IUGG denotes the authalic radius as R₂.^[2]
A closed-form solution exists for a spheroid:^[16]

${displaystyle R_{2}={sqrt {frac {a^{2}+{frac {b^{2}}{e}}ln {left({frac {1+e}{b/a}}right)}}{2}}}={sqrt {{frac {a^{2}}{2}}+{frac {b^{2}}{2}}{frac {tanh ^{-1}e}{e}}}}={sqrt {frac {A}{4pi }}},,}$

where e² = a² − b²/a² and A is the surface area of the spheroid.

For the Earth, the authalic radius is 6,371.0072 km (3,958.7603 mi).^[15]

The authalic radius $R_{2}$ also corresponds to the radius of (global) mean curvature, obtained by averaging the Gaussian curvature, , over the surface of the ellipsoid. Using the Gauss–Bonnet theorem, this gives

${displaystyle {frac {int K,dA}{A}}={frac {4pi }{A}}={frac {1}{R_{2}^{2}}}.}$

Volumetric radius[edit]

Another spherical model is defined by the Earth’s volumetric radius, which is the radius of a sphere of volume equal to the ellipsoid. The IUGG denotes the volumetric radius as R₃.^[2]

${displaystyle R_{3}={sqrt[{3}]{a^{2}b}},.}$

For Earth, the volumetric radius equals 6,371.0008 km (3,958.7564 mi).^[15]

Rectifying radius[edit]

Another global radius is the Earth’s rectifying radius, giving a sphere with circumference equal to the perimeter of the ellipse described by any polar cross section of the ellipsoid. This requires an elliptic integral to find, given the polar and equatorial radii:

${displaystyle M_{mathrm {r} }={frac {2}{pi }}int _{0}^{frac {pi }{2}}{sqrt {{a^{2}}cos ^{2}varphi +{b^{2}}sin ^{2}varphi }},dvarphi ,.}$

The rectifying radius is equivalent to the meridional mean, which is defined as the average value of M:^[16]

${displaystyle M_{mathrm {r} }={frac {2}{pi }}int _{0}^{frac {pi }{2}}!M(varphi ),dvarphi ,.}$

For integration limits of [0,π/2], the integrals for rectifying radius and mean radius evaluate to the same result, which, for Earth, amounts to 6,367.4491 km (3,956.5494 mi).

The meridional mean is well approximated by the semicubic mean of the two axes,^{[citation needed]}

${displaystyle M_{mathrm {r} }approx left({frac {a^{frac {3}{2}}+b^{frac {3}{2}}}{2}}right)^{frac {2}{3}},,}$

which differs from the exact result by less than 1 μm (4×10⁻⁵ in); the mean of the two axes,

${displaystyle M_{mathrm {r} }approx {frac {a+b}{2}},,}$

about 6,367.445 km (3,956.547 mi), can also be used.

Topographical radii[edit]

The mathematical expressions above apply over the surface of the ellipsoid.
The cases below considers Earth’s topography, above or below a reference ellipsoid.
As such, they are topographical geocentric distances, R_t, which depends not only on latitude.

Topographical extremes[edit]

Maximum R_t: the summit of Chimborazo is 6,384.4 km (3,967.1 mi) from the Earth’s center.
Minimum R_t: the floor of the Arctic Ocean is 6,352.8 km (3,947.4 mi) from the Earth’s center.^[17]

Topographical global mean[edit]

The topographical mean geocentric distance averages elevations everywhere, resulting in a value 230 m larger than the IUGG mean radius, the authalic radius, or the volumetric radius. This topographical average is 6,371.230 km (3,958.899 mi) with uncertainty of 10 m (33 ft).^[18]

Derived quantities: diameter, circumference, arc-length, area, volume [edit]

Earth’s diameter is simply twice Earth’s radius; for example, equatorial diameter (2a) and polar diameter (2b). For the WGS84 ellipsoid, that’s respectively:

2a = 12,756.2740 km (7,926.3812 mi),
2b = 12,713.5046 km (7,899.8055 mi).

Earth’s circumference equals the perimeter length. The equatorial circumference is simply the circle perimeter: C_e=2πa, in terms of the equatorial radius, a. The polar circumference equals C_p=4m_p, four times the quarter meridian m_p=aE(e), where the polar radius b enters via the eccentricity, e=(1−b²/a²)^0.5; see Ellipse#Circumference for details.

Arc length of more general surface curves, such as meridian arcs and geodesics, can also be derived from Earth’s equatorial and polar radii.

Likewise for surface area, either based on a map projection or a geodesic polygon.

Earth’s volume, or that of the reference ellipsoid, is V = 4/3πa²b. Using the parameters from WGS84 ellipsoid of revolution, a = 6,378.137 km and b = 6356.7523142 km, V = 1.08321×10¹² km³ (2.5988×10¹¹ cu mi).^[19]

Published values[edit]

This table summarizes the accepted values of the Earth’s radius.

Agency	Description	Value (in meters)	Ref
IAU	nominal «zero tide» equatorial	6378100	^[1]
IAU	nominal «zero tide» polar	6356800	^[1]
IUGG	equatorial radius	6378137	^[2]
IUGG	semiminor axis (b)	6356752.3141	^[2]
IUGG	polar radius of curvature (c)	6399593.6259	^[2]
IUGG	mean radius (R₁)	6371008.7714	^[2]
IUGG	radius of sphere of same surface (R₂)	6371007.1810	^[2]
IUGG	radius of sphere of same volume (R₃)	6371000.7900	^[2]
IERS	WGS-84 ellipsoid, semi-major axis (a)	6378137.0	^[6]
IERS	WGS-84 ellipsoid, semi-minor axis (b)	6356752.3142	^[6]
IERS	WGS-84 ellipsoid, polar radius of curvature (c)	6399593.6258	^[6]
IERS	WGS-84 ellipsoid, Mean radius of semi-axes (R₁)	6371008.7714	^[6]
IERS	WGS-84 ellipsoid, Radius of Sphere of Equal Area (R₂)	6371007.1809	^[6]
IERS	WGS-84 ellipsoid, Radius of Sphere of Equal Volume (R₃)	6371000.7900	^[6]
	GRS 80 semi-major axis (a)	6378137.0
	GRS 80 semi-minor axis (b)	≈6356752.314140
	Spherical Earth Approx. of Radius (R_E)	6366707.0195	^[20]
	meridional radius of curvature at the equator	6335439
	Maximum (the summit of Chimborazo)	6384400	^[17]
	Minimum (the floor of the Arctic Ocean)	6352800	^[17]
	Average distance from center to surface	6371230±10	^[18]

History[edit]

The first published reference to the Earth’s size appeared around 350 BC, when Aristotle reported in his book On the Heavens^[21] that mathematicians had guessed the circumference of the Earth to be 400,000 stadia. Scholars have interpreted Aristotle’s figure to be anywhere from highly accurate^[22] to almost double the true value.^[23] The first known scientific measurement and calculation of the circumference of the Earth was performed by Eratosthenes in about 240 BC. Estimates of the accuracy of Eratosthenes’s measurement range from 0.5% to 17%.^[24] For both Aristotle and Eratosthenes, uncertainty in the accuracy of their estimates is due to modern uncertainty over which stadion length they meant.

Around 100 BC, Posidonius of Apamea recomputed Earth’s radius, and found it to be close to that by Eratosthenes,^[25] but later Strabo incorrectly attributed him a value about 3/4 of the actual size.^[26] Claudius Ptolemy around 150 AD gave empirical evidence supporting a spherical Earth,^[27] but he accepted the lesser value attributed to Posidonius. His highly influential work, the Almagest,^[28] left no doubt among medieval scholars that Earth is spherical, but they were wrong about its size.

By 1490, Christopher Colombus believed that traveling 3,000 miles west from the west coast of the Iberian peninsula would let him reach the eastern coasts of Asia.^[29] However, the 1492 enactment of that voyage brought his fleet to the Americas. The Magellan expedition (1519–1522), which was the first circumnavigation of the World, soundly demonstrated the sphericity of the Earth,^[30] and affirmed the original measurement of 40,000 km (25,000 mi) by Eratosthenes.

Around 1690, Isaac Newton and Christiaan Huygens argued that Earth was closer to an oblate spheroid than to a sphere. However, around 1730, Jacques Cassini argued for a prolate spheroid instead, due to different interpretations of the Newtonian mechanics involved.^[31] To settle the matter, the French Geodesic Mission (1735–1739) measured one degree of latitude at two locations, one near the Arctic Circle and the other near the equator. The expedition found that Newton’s conjecture was correct:^[32] the Earth is flattened at the poles due to rotation’s centrifugal force.

Notes[edit]

^ For details see figure of the Earth, geoid, and Earth tide.
^ There is no single center to the geoid; it varies according to local geodetic conditions.
^ In a geocentric ellipsoid, the center of the ellipsoid coincides with some computed center of Earth, and best models the earth as a whole. Geodetic ellipsoids are better suited to regional idiosyncrasies of the geoid. A partial surface of an ellipsoid gets fitted to the region, in which case the center and orientation of the ellipsoid generally do not coincide with the earth’s center of mass or axis of rotation.
^ The value of the radius is completely dependent upon the latitude in the case of an ellipsoid model, and nearly so on the geoid.
^ This follows from the International Astronomical Union definition rule (2): a planet assumes a shape due to hydrostatic equilibrium where gravity and centrifugal forces are nearly balanced.^[3]
^ East–west directions can be misleading. Point B, which appears due east from A, will be closer to the equator than A. Thus the curvature found this way is smaller than the curvature of a circle of constant latitude, except at the equator. West can be exchanged for east in this discussion.
^ N is defined as the radius of curvature in the plane that is normal to both the surface of the ellipsoid at, and the meridian passing through, the specific point of interest.

References[edit]

^ ^a ^b ^c ^d ^e ^f Mamajek, E. E; Prsa, A; Torres, G; et al. (2015). «IAU 2015 Resolution B3 on Recommended Nominal Conversion Constants for Selected Solar and Planetary Properties». arXiv:1510.07674 [astro-ph.SR].
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j Moritz, H. (1980). Geodetic Reference System 1980, by resolution of the XVII General Assembly of the IUGG in Canberra.
^ IAU 2006 General Assembly: Result of the IAU Resolution votes Archived 2006-11-07 at the Wayback Machine
^ Satellites Reveal A Mystery Of Large Change In Earth’s Gravity Field , Aug. 1, 2002, Goddard Space Flight Center.
^ NASA’s Grace Finds Greenland Melting Faster, ‘Sees’ Sumatra Quake, December 20, 2005, Goddard Space Flight Center.
^ ^a ^b ^c ^d ^e ^f ^g ^h «WGS84RPT.tif:Corel PHOTO-PAINT» (PDF). Retrieved 2018-10-17.
^ «Info» (PDF). earth-info.nga.mil. Archived from the original (PDF) on 2020-08-04. Retrieved 2008-12-31.
^ «Equatorial Radius of the Earth». Numerical Standards for Fundamental Astronomy: Astronomical Constants : Current Best Estimates (CBEs). IAU Division I Working Group. 2012. Archived from the original on 2016-08-26. Retrieved 2016-08-10.
^ ^a ^b Christopher Jekeli (2016). Geometric Reference Systems in Geodesy (PDF). Ohio State University, Columbus, Ohio. Retrieved 13 May 2023.
^ Bowring, B. R. (October 1987). «Notes on the curvature in the prime vertical section». Survey Review. 29 (226): 195–196. doi:10.1179/sre.1987.29.226.195.
^ Bomford, G. (1952). Geodesy. OCLC 489193198.
^ Christopher Jekeli (2016). Geometric Reference Systems in Geodesy (PDF). Ohio State University, Columbus, Ohio. Retrieved 13 May 2023.
^ ^a ^b ^c Lass, Harry (1950). Vector and Tensor Analysis. McGraw Hill Book Company, Inc. pp. 71–77. ISBN 9780070365209.
^ ^a ^b ^c Torge, Wolfgang (2001). Geodesy. ISBN 9783110170726.
^ ^a ^b ^c Moritz, H. (March 2000). «Geodetic Reference System 1980». Journal of Geodesy. 74 (1): 128–133. Bibcode:2000JGeod..74..128.. doi:10.1007/s001900050278. S2CID 195290884.
^ ^a ^b Snyder, J.P. (1987). Map Projections – A Working Manual (US Geological Survey Professional Paper 1395) p. 16–17. Washington D.C: United States Government Printing Office.
^ ^a ^b ^c «Discover-TheWorld.com – Guam – POINTS OF INTEREST – Don’t Miss – Mariana Trench». Guam.discover-theworld.com. 1960-01-23. Archived from the original on 2012-09-10. Retrieved 2013-09-16.
^ ^a ^b Frédéric Chambat; Bernard Valette (2001). «Mean radius, mass, and inertia for reference Earth models» (PDF). Physics of the Earth and Planetary Interiors. 124 (3–4): 234–253. Bibcode:2001PEPI..124..237C. doi:10.1016/S0031-9201(01)00200-X. Archived from the original (PDF) on 30 July 2020. Retrieved 18 November 2017.
^ Williams, David R. (2004-09-01), Earth Fact Sheet, NASA, retrieved 2007-03-17
^ Phillips, Warren (2004). Mechanics of Flight. John Wiley & Sons, Inc. p. 923. ISBN 0471334588.
^ Aristotle. On the Heavens. Vol. Book II 298 B. Retrieved 5 November 2017.
^
Drummond, William (1817). «On the Science of the Egyptians and Chaldeans, Part I». The Classical Journal. 16: 159.
^
Clarke, Alexander Ross; Helmert, Friedrich Robert (1911). «Earth, Figure of the» . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 8 (11th ed.). Cambridge University Press. pp. 801–813.
^
«Eratosthenes, the Greek Scientist». Britannica.com. 2016.
^ Posidonius, fragment 202
^ Cleomedes (in Fragment 202) stated that if the distance is measured by some other number the result will be different, and using 3,750 instead of 5,000 produces this estimation: 3,750 x 48 = 180,000; see Fischer I., (1975), Another Look at Eratosthenes’ and Posidonius’ Determinations of the Earth’s Circumference, Ql. J. of the Royal Astron. Soc., Vol. 16, p. 152.
^ Thurston, Hugh (1994). Early astronomy. New York: Springer-Verlag New York. p. 138. ISBN 0-387-94107-X.
^ «Almagest – Ptolemy (Elizabeth)». projects.iq.harvard.edu. Retrieved 2022-11-05.
^ John Freely, Before Galileo: The Birth of Modern Science in Medieval Europe (2013), ISBN 978-1468308501
^ Nancy Smiler Levinson (2001). Magellan and the First Voyage Around the World. Houghton Mifflin Harcourt. ISBN 978-0-395-98773-5. Retrieved 31 July 2010.
^ Cassini, Jacques (1738). Méthode de déterminer si la terre est sphérique ou non (in French).
^ Levallois, Jean-Jacques (1986). «La Vie des sciences». Gallica. pp. 277–284, 288. Retrieved 2019-05-22.

External links[edit]

Merrifield, Michael R. (2010). « $R_{oplus }$ The Earth’s Radius (and exoplanets)». Sixty Symbols. Brady Haran for the University of Nottingham.

Источник

О том, кто, когда и как измерил Землю, мы знаем из дошедших до нас трудов древнегреческого ученого Клеомеда. Клеомед был современником Христа, то есть жил спустя почти три века после Эратосфена, но насчет точности даты первого измерения земного шара можно не беспокоиться. Иного дня для измерения нашей планеты не могло быть, да и метод ее измерения в то время мог быть только одним — по длине тени гномона (вертикального шеста солнечных часов) в полдень 19 июня. Именно этот день в III веке до н. э. был днем летнего солнцестояния.

Ход мысли Эратосфена Клеомед восстановил по своему разумению, но и тут было трудно ошибиться, потому что это была единственно возможная логика ученого того времени. Прежде всего, для Эратосфена, который занимал пост хранителя Александрийской библиотеки, главного научного учреждения Древней Греции, шарообразность Земли была не предположением, а фактом. Это экспериментально доказали греческие ученые еще за сто лет до Эратосфена.

Эратосфен исходил из двух допущений. Во-первых, он считал, что Александрия в дельте Нила, где он проводил измерения, и город Сиен (Асуан) в верховьях Нила находятся на одном меридиане. Во-вторых — что Сиен находится под тропиком Рака, то есть в полдень дня летнего солнцестояния вертикальный шест в Сиене не отбрасывает вообще никакой тени, он строго перпендикулярен Солнцу. Оставалось измерить длину тени вертикального шеста (гномона) в солнечных часах в Александрии в полдень 19 июня, что и сделал Эратосфен.

По длине тени можно определить угол, под которым шест направлен к Солнцу в зените. Угол оказался равен 1/50 от всего круга солнечных часов (360 градусов). Расстояние от Александрии до Сиена было известно — 5000 стадиев. Дальше все сводилось к геометрии, в которой греки были сильны. Если дуга окружности Земли в 1/50 ее длины равна 5 тыс. стадиев, то вся окружность Земли равна 250 тыс. стадиев (43 тыс. км). А радиус Земли у Эратосфена получился равным 6287 км в наших мерах длины.

Современные измерения дают окружность нашей планеты по меридиану 40 008 км, радиус — 6371 км. Точность измерений Эратосфена была почти абсолютная. Небольшие расхождения связаны с погрешностями его допущений. Александрия и Асуан лежат не на одном меридиане, Асуан на 2,5 градуса западнее. Кроме того, Асуан лежит все-таки не под тропиком Рака, а на полградуса севернее.

Сергей Петухов

Источник

Содержание

Радиус земли. Как впервые измерили радиус земли.
Радиус земли в м. Какой радиус Земли?
Радиус Марса. Размеры Марса
Как Эратосфен измерил радиус земли. Греческий астроном Эратосфен первым вычислил радиус Земли: любопытные факты
Как измерили радиус земли сообщение 7 класс. Как древний грек измерил радиус Земли (3 фото)
Видео Опровержение вычислений радиуса Земли Эратосфеном
Диаметр Земли и другие космические параметры
Радиус Луны. Как в древней Греции астрономы рассчитывали расстояние до Луны
Радиус Солнца. Размеры Солнца: масса, диаметр, радиус

Размеры Солнца
Диаметр
Радиус
Сравнение размеров небесных тел
Масса Солнца, её измерение и сравнение

Радиус земли. Как впервые измерили радиус земли.

Древние египтяне заметили, что во время летнего солнцестояния солнце освещает дно глубоких колодцев в сиене (ныне Асуан), а в Александрии — нет. У Эратосфена Киренского (276 год до н. э. -194 год до н. э. ) появилась гениальная идея — использовать этот факт для измерения окружности и радиуса земли. В день летнего солнцестояния в Александрии он использовал скафис — чашу с длинной иглой, при помощи которого можно было определить под каким углом солнце находится на небе.

Итак, после измерения угол оказался 7 градусов 12 минут, то есть 1/50 окружности. Стало быть сиена отстоит от александрии на 1/50 окружности земли. Расстояние между городами считалось равным 5, 000 стадиям, следовательно окружность земли равнялась 250, 000 стадиям, а радиус тогда 39, 790 стадиев.

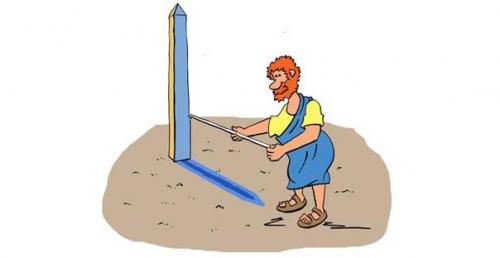
Неизвестно каким стадием пользовался Эратосфен. Лишь в том случае, если греческим (178 метров), то его радиус земли равнялся 7, 082 км, если египетским, то 6, 287 км. Современные измерения дают для усреднённого радиуса земли величину 6, 371 км. В любом случае, точность для тех времён потрясающая.

Радиус земли в м. Какой радиус Земли?

Полярный радиус Земли — малая полуось эллипсоида Красовского, равная 6 356 863 м.

Экваториальный радиус Земли — большая полуось эллипсоида Красовского, равная 6 378 245 м.

Средний радиус Земли — 6 371 302 м.

История измерения радиуса Земли

Эраторсфен. Еще древние египтяне заметили, что во время летнего солнцестояния Солнце освещает дно глубоких колодцев в Сиене (ныне Асуан), а в Александрии — нет. У Эратосфена Киренского (276 год до н. э.—194 год до н. э.) появилась гениальная идея — использовать этот факт для измерения окружности и радиуса Земли. В день летнего солнцестояния в Александрии он использовал скафис — чашу с длинной иглой, при помощи которого можно было определить под каким углом Солнце находится на небе.
Итак, после измерения угол оказался 7 градусов 12 минут, то есть 1/50 окружности. Стало быть Сиена отстоит от Александрии на 1/50 окружности Земли. Расстояние между городами считалось равным 5 тыс. стадиев, следовательно окружность Земли равнялась 250 тыс. стадиев, а радиус тогда 39,8 тыс. стадиев.
Неизвестно каким стадием пользовался Эратосфен. Если греческим (178 метров), то его радиус Земли получался 7,08 тыс. км, если египетским, то 6,3 тыс. км. Современные измерения дают для усреднённого радиуса Земли величину 6,371 км. В любом случае, точность для тех времён потрясающая.

Радиус Марса. Размеры Марса

определяются не одной числовой характеристикой. Ученые обозначают его размер несколькими параметрами. Первый параметр – радиус. Его величина составляет 3 389,5 километров. Второй – окружность, которая численно равна 21 344 километра. Далее следует объем – 6,083·1010 км³. Последним параметром является масса Марса, которая равна 3,33022·1023 кг.

Для сравнения, диаметрсоставляет 53% от диаметра Земли. На первый взгляд это немного, но его величина сравнима с общей площадью суши на. Объем Марса составляет 15% от объема Земли, а масса – 11%. Из приведенных данных видно, что Марс небольшая планета, он в 2 раза меньше Земли и по величине – 7 планета в.

Сравнение размеров Земли, Марса и Луны

Несмотря на свой небольшой размер и отсутствие на нем жизни, у Марса много интересных особенностей. Самая высокая гора Солнечной системы –– находится на Красной планете. Марсианская– самая глубокая. Сотни тысяч кратеров покрывают поверхность Красной планеты. Северный полярный бассейн – крупнейшая из известных равнин, а равнина Эллада, размер которой 2100 км – глубочайшая на планете и третья по величине в Солнечной системе.

Экстремальные топографические особенности Красной планеты дополняют не менее экстремальные погодные условия. Марс – холодная планета. Средняя температура поверхности составляет 470С ниже нуля. Летом в районе экватора температура днем может подняться до +200С, а ночью упасть до -900С. Такие перепады температуры в 1100С вызывают сильнейшие ураганы, достигающие скорости торнадо. Они поднимают с поверхности Марса пыль, и тогда начинается пыльная буря. Астрономы наблюдали на Марсе бури, которые охватывали всю планету всего за несколько дней.

По мнению ученых, Марс в начале развития Солнечной системы был гораздо больших размеров. Размеры планеты уменьшились в результате внешнего воздействия, например столкновения с каким-то космическим телом, которое вызвало образование Северного полярного бассейна. Куски поверхности, разрушенной взрывом, преодолев гравитационное поле Марса, были выброшены в комическое пространство.

Итак, не только размеры Марса могут представлять интерес. О Красной планете можно узнать еще много интересного, все зависит от нашего с вами желания. Много интересного можно узнать и о других планетах –и

Как Эратосфен измерил радиус земли. Греческий астроном Эратосфен первым вычислил радиус Земли: любопытные факты

Точность измерения Эратосфена для тех времён была просто удивительная

Эратосфен Киренский (276 год до н.э. — 194 год до н.э.) — греческий математик, астроном, географ и поэт.

19 июня 240 года до н.э. Эратосфен использовал скафис (чашу с длинной иглой), с помощью которой можно было определить под каким углом Солнце находится на небе. Это был день летнего солнцестояния в Александрии.

Неудовлетворенный познаниями, приобретёнными в Александрии, Эратосфен отправился в Афины, где так тесно сблизился со школой Платона, что обыкновенно называл себя платоником.

Результатом изучения наук в этих обоих центрах древнегреческого просвещения была очень разносторонняя, почти энциклопедическая эрудиция Эратосфена; он писал, кроме сочинений по математике, астрономии, геодезии, географии и хронологии, ещё трактаты «о добре и зле», о комедии и др.

Царь Птолемей III Эвергет тотчас же после смерти Каллимаха вызвал Эратосфена из Афин и поручил ему заведование великой Александрийской библиотекой. Эрастофен — автор многих трудов по математике, астрономии, геодезии, географии. Один из интересных фактов жизни Эратосфена – вычисление радиуса Земли.

Древние египтяне заметили, что во время летнего солнцестояния Солнце освещает дно глубоких колодцев в Сиене (ныне Асуан), а в Александрии — нет. Эратосфен использовал этот факт для измерения окружности и радиуса Земли.

После измерения угол оказался 7 градусов 12 минут, то есть 1/50 окружности. Поэтому Сиена отстает от Александрии на 1/50 окружности Земли. Расстояние между городами равнялось 5,000 стадиям, следовательно окружность Земли равнялась 250,000 стадий, а радиус тогда был 39,790 стадий.

Неизвестно какими стадиями пользовался Эратосфен. Если греческими (178 метров), то его радиус земли — 7,082 км, а если египетскими — 6,287 км.

Современные измерения дают для средний радиус Земли — 6,371 км.

В любом случае, точность измерения для тех времён просто удивительная!

Эратосфен прожил удивительную, насыщенную и долгую жизнь. На протяжении нескольких десятилетий оставался бессменным архивариусом Александрийской библиотеки. Он до последнего боготворил и больше всего на свете любил книги, источник знаний и ярчайших открытий. В старости, отстраненный от должности, ослепший и немощный, довел себя до крайней нищеты и уморил себя голодом в 194 г. до н.э.

Как сообщал портал «Знай.uа», астрономы открыли систему, в которой находятся сразу три землеподобные планеты. Более того, ученые обнаружили систему с двумя суперземлями.

Астрономам уже известно около 500 землеподобных планет. Проблема в том, что большинство из них либо слишком горячие, либо, наоборот, холодные, поэтому ученые продолжают поиск планет, похожих на Землю.

Как измерили радиус земли сообщение 7 класс. Как древний грек измерил радиус Земли (3 фото)

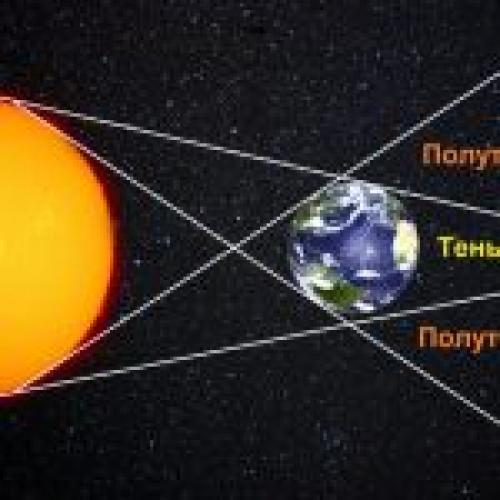
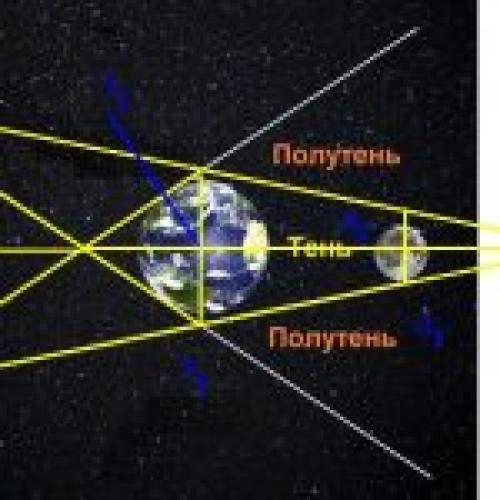
Древние греки, наблюдая за лунными затмениями, обнаружили, что Земля отбрасывает круглую тень на Луну. Таким образом они поняли, что наша планета круглая. В те же времена египтяне провели такое наблюдение, которое заключалось в том, что во время летнего солнцестояния, Солнце освещает дно даже самых глубоких колодцев.

В те времена (240 лет до нашей эры) жил известный греческий математик, астроном, географ и поэт — Эратосфен Киренский. Он получал свое образование в Александрии, но неудовлетворенный тем образованием, отправился в Афины, где учился в платоновской школе, и впоследствии стал называть себя платоником.
После получения образования, имея почти энциклопедические познания, Эратосфен начал свою научную деятельность, впоследствии став известным, благодаря своим работам. Так, в один прекрасный момент, царь Птолемей III пригласил Эратосфена из Афин в Александрию заведовать великой Александрийской библиотекой.

Одно из самых величайших открытий Эратосфена — вычисление радиуса Земли. Посчитал он радиус благодаря колодцам и знанию о том, что Земля круглая. Во время солнцестояния в Александрии Эратосфен замерил при помощи чаши с длинной иглой под каким углом находится Солнце по отношению к Земле в Сиене. После измерения угол оказался 7 градусов 12 минут, то есть 1/50 окружности. Стало быть Сиена отстоит от Александрии на 1/50 окружности Земли, то есть — в 5000 стадиях, следовательно окружность Земли равнялась 250000 стадиям, а радиус тогда 39790 стадиев.
Согласно подсчетам Эратосфен получил значение 6287 км, которое отличается от истинного значения всего на менее чем на 100 км.

Видео Опровержение вычислений радиуса Земли Эратосфеном

Диаметр Земли и другие космические параметры

Каждый из нас изучал в школе много предметов: физику, химию, биологию, математику и другие. В этот список зачастую включалась и астрономия. Это интересная наука, рассказывающая нам про разные космические величины (расстояние от нашей планеты до Солнца, диаметр Земли, массу луны и иные), вселенские явления (черные дыры, звездопады, затмения и т. д.).

Согласитесь, что все это – очень важная и познавательная информация о том, что нас окружает. Но если кто-нибудь спросит нас о том, каков диаметр планеты Земля, мы вряд ли сможем правильно ответить. К сожалению, все, что мы учили в школе, имеет свойство постепенно забываться, если знания не поддерживать. Эта статья поможет возобновить некоторую «космическую» информацию.

Диаметр Земли

Считается, что этот показатель нашей планеты начал изучаться еще до Нашей эры. Знаменитый античный ученый-астроном Эратосфен, используя расстояние между городами и угол падения солнечных лучей, смог вычислить длину окружности нашей планеты, а потом – радиус и диаметр Земли. Так, средний показатель данной величины составляет примерно 12 756 километров. Согласитесь, что это достаточно много. Слово «средний» здесь употребляется, потому что Земля не имеет форму шара (но это и не эллипс, о котором в свое время так много говорили).

Это своеобразная вытянутая к полюсам форма, которую в настоящее время имеют обыкновение называть геоидом. Из-за такой «деформации» диаметр Земли по экватору отличается от соответствующего показателя по нулевому меридиану (вторая величина немного больше).

Другие важные параметры голубой планеты

Земля имеет очень большую и богатую историю, большую часть которой она хранит в себе и о которой, к сожалению, нам вряд ли доведется узнать. Нашей планете уже более четырех с половиной миллиардов лет. За это время она претерпела большое количество изменений. Земля является частью Солнечной системы и вращается по орбите вокруг ее центра – нашего светила. Расстояние до него от третьей планеты – примерно сто пятьдесят миллионов километров. Земля имеет всего один естественный спутник – всем известную Луну, которая оказывает значительное влияние на приливы на голубой планете. Длина экватора составляет примерно 40 076 километров, что почти на 44 километра больше длины меридиана (именно поэтому в зависимости от места измерения и меняется диаметр Земли).

Живая планета

Действительно, Земля в настоящее время является единственным изученным (местными учеными) местом во Вселенной, где есть живые организмы, которые появились здесь почти четыре миллиарда лет назад. Они обитают как на суше, так и в воде. А вода на нашей планете занимает более семидесяти процентов. Кроме наличия организмов, Земля также имеет свою жизнь. Она проявляется в движении тектонических плит: происходят извержения вулканов, сильные и слабые землетрясения. Это подтверждает тот факт, что наша Земля не останавливается в своем развитии и теперь. Никто не знает о том, какие еще сюрпризы подготовил нам дом людей – живая голубая планета.

Радиус Луны. Как в древней Греции астрономы рассчитывали расстояние до Луны

Расстояние от Земли до Луны

Луна стала первым небесным телом, до которого удалось рассчитать расстояние от Земли. Считается, что первыми это сделали астрономы в Древней Греции.

Измерить расстояние до Луны пытались с незапамятных времен – первым это попытался сделать Аристарх Самосский. Он оценил угол между Луной и Солнцем в 87 градусов, поэтому вышло, что Луна ближе Солнца в 20 раз (косинус угла равного 87 градуса равен 1/20). Ошибка измерений угла привела к 20-кратной ошибке, сегодня известно, что это отношение на самом деле равно 1 к 400 (угол равен примерно 89.8 градусов). Большая ошибка была вызвана трудностью оценок точного углового расстояния между Солнцем и Луной с помощью примитивных астрономических инструментов Древнего мира. Регулярные солнечные затмения к этому времени уже позволили древнегреческим астрономам сделать вывод о том, что угловые диаметры Луны и Солнца примерно одинаковы. В связи с этим Аристарх сделал вывод, что Луна меньше Солнца в 20 раз (на самом деле примерно в 400 раз).

Для вычисления размеров Солнца и Луны относительно Земли Аристарх использовал другой метод. Речь идет о наблюдениях лунных затмений. К этому времени древние астрономы уже догадались о причинах этих явлений: Луна затмевается тенью Земли.

На схеме выше хорошо видно, что разность расстояний с Земли до Солнца и до Луны пропорциональна разнице между радиусами Земли и Солнца и радиусами Земли и её тени на расстояние Луны. Во времена Аристарха уже удалось оценить, что радиус Луны равен примерно 15 угловым минутам, а радиус земной тени составляет 40 угловых минут. То есть размер Луны получался примерно в 3 раза меньше размера Земли. Отсюда зная угловой радиус Луны можно было легко оценить, что Луна находится от Земли примерно в 40 диаметрах Земли. Древние греки могли лишь приблизительно оценить размеры Земли. Так Эратосфен Киренский (276 – 195 годы до нашей эры) на основе различий в максимальной высоте Солнца над горизонтом в Асуане и Александрии во время летнего солнцестояния определил, что радиус Земли близок к 6287 км (современное значение 6371 км). Если подставить это значение в оценку Аристарха насчет расстояния до Луны, то оно будет соответствовать примерно 502 тысяч км (современное значение среднего расстояния от Земли до Луны составляет 384 тысяч км).

Радиус Солнца. Размеры Солнца: масса, диаметр, радиус

Солнце — это колоссальный раскалённый шар, в центре которого происходит освобождение энергии из водорода. Водород трансформируется в гелий, а излучаемая энергия выделяется в космическое пространство. Люди в древности не зря обожествляли светило. Именно его энергия обеспечивает существование жизни на Земле .

Размеры Солнца

Диаметр

Солнце (Гелиос) — это ближайшая к нашей планете звезда. Она относится к категории «Жёлтых карликов». Подобно другим светилам, Гелиос не имеет прочной поверхности. Его первичным слоем принято считать фотосферу, излучающую энергию. А потому диаметр Солнца — ни что иное, как диаметр его фотосферы.

Измерить масштабы светила можно простым доступным способом. Для эксперимента необходимо тёмное помещение, куда солнечный луч проникает через маленькое отверстие . Плотную белую бумагу достаточно поставить напротив луча, и на поверхности листа появится крошечное изображение Солнца. Чем дальше будет бумага от отверстия, тем больше будет пятно. На расстоянии 107 см его диаметр составит 1 см. При удалении на 214 см возрастёт до 2 см. То есть диаметр настоящего светила в 107 раз меньше расстояния до Земли и составляет 1400000 км.

Учёные смогли определить точный диаметр Солнца в километрах, базируясь на эффекте под названием «Чётки Бейли». Чётками называют красные точки по окружности солнечного диска, которые становятся видимыми во время затмения. С их помощью астрономы точно выделили положение светила и смогли измерить его размеры.

Анализ исторических данных, дополненный регулярным современным мониторингом, показал, что диаметр Солнца подвержен изменениям. Так, в XVII веке светило было на 2 тыс.километров шире нынешнего. Астрономы установили, что звезда расширяется и сжимается в течение 160 минут. За этот же период меняется количество выбрасываемой энергии.

Радиус

Измерения длительности солнечных затмений и наблюдения за перемещением Меркурия и Венеры на фоне солнечного диска позволили учёным вычислить примерный радиус звезды. Он равен 695990 км.

Приборы на борту космических станций дали возможность уточнить расчёты. Исследования проводились методами гелиосейсмологии. При этом рассматривалось движение так называемых f-волн на поверхности Солнца. Этот способ вычислений дал несколько иной результат — на 300 км меньше (695700 км). Выявленная погрешность может иметь серьёзные последствия для изучения Солнца, его состава и активности.

Радиус будет иметь одинаковое значение во всех направлениях, поскольку Гелиос имеет правильную шарообразную форму.

Сравнение размеров небесных тел

Величину солнечного радиуса в астрономии применяют в качестве меры измерения габаритов других космических объектов:

Полярная Звезда имеет 30 солнечных радиусов. Следовательно, она в 30 раз превышает параметры Солнца.
Наша планета выглядит небольшой точкой на фоне главной звезды. Она в 109 раз уступает светилу по размеру.
Зато крупнейшая планета Солнечной системы – Юпитер всего в 9,7 раза меньше Солнца.

Во Вселенной можно обнаружить звезды – гиганты, превосходящие во много раз наше светило . Крупнейшая звезда VY Canis Majoris, по мнению учёных, имеет 2100 диаметров Гелиоса.

Масса Солнца, её измерение и сравнение

Солнце — крупнейшее небесное тело в нашей звёздной системе (99,86% общей массы). На формирование массы солнца потребовалось почти 5 миллиардов лет.

Для измерения массы небесных тел разработаны три научных метода:

Гравиметрический. В этом способе применяют параметры измерений силы тяжести, которая характеризует поверхность измеряемого тела.
Третий закон Кеплера. Практикуется в том случае, если планета обладает, как минимум, одним спутником. Вычисления проводятся с учётом расстояния между планетой и её спутником, а также периода его обращения по орбите. Таким образом выясняется соотношение масс планеты и звезды.
Анализ заметных воздействий , вызываемых движением одних небесных тел относительно движения других.

В первую очередь с помощью геодезического метода выяснили массу нашей планеты. Она, по оценкам, составила 6*1024кг. Затем на основании Третьего закона Кеплера вычислили массу Луны – 73477*1022 кг. И в завершение узнали, чему равна масса Солнца — 19891*1030кг.

Солнечная масса стала абстрактной метрической единицей . Астрономы употребляют её для описания различных космических объектов. Самая гигантская известная звезда, Eta Carinae, оценивается в 150 масс Гелиоса.

Учёные составили прогноз солнечной активности на будущее. Опираясь на наблюдения за другими звёздами, они пришли к выводу, что звезда постепенно израсходует энергию фотосферы. Её размеры небывало расширятся. Ближайшие планеты — Меркурий и Венера будут поглощены. Возможно, что та же участь постигнет и Землю. Солнце преобразуется в Красного гиганта. Вслед за периодом роста последует катастрофическое сжатие. Светило сожмётся примерно до нынешних параметров Земли и будет именоваться Белым карликом .

Источник

Как Эратосфен измерил окружность Земли?

Вычисления окружности

Определение расстояний на земной поверхности

Как вычислили окружность Земли

Introduction[edit]

Physics of Earth’s deformation[edit]

Radius and local conditions[edit]

Extrema: equatorial and polar radii[edit]

Location-dependent radii[edit]

Geocentric radius[edit]

Radii of curvature[edit]

Principal radii of curvature[edit]

Meridional[edit]

Prime vertical[edit]

Polar and equatorial radius of curvature[edit]

Derivation[edit]

Combined radii of curvature[edit]

Azimuthal[edit]

Non-directional[edit]

Global radii[edit]

Nominal radius[edit]

Arithmetic mean radius[edit]

Authalic radius[edit]

Volumetric radius[edit]

Rectifying radius[edit]

Topographical radii[edit]

Topographical extremes[edit]

Topographical global mean[edit]

Derived quantities: diameter, circumference, arc-length, area, volume [edit]

Published values[edit]

History[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Радиус земли. Как впервые измерили радиус земли.

Радиус земли в м. Какой радиус Земли?

Радиус Марса. Размеры Марса

Как Эратосфен измерил радиус земли. Греческий астроном Эратосфен первым вычислил радиус Земли: любопытные факты

Как измерили радиус земли сообщение 7 класс. Как древний грек измерил радиус Земли (3 фото)

Видео Опровержение вычислений радиуса Земли Эратосфеном

Диаметр Земли и другие космические параметры

Радиус Луны. Как в древней Греции астрономы рассчитывали расстояние до Луны

Радиус Солнца. Размеры Солнца: масса, диаметр, радиус

Размеры Солнца

Диаметр

Радиус

Сравнение размеров небесных тел

Масса Солнца, её измерение и сравнение