В наши дни окружность Земли можно измерить с помощью измерительной аппаратуры и спутников. Но можно и не изобретать никаких хитроумных инструментов, как это сделал Эратосфен более 2000 лет назад. Он вычислил размеры Земли, не покидая стен библиотеки, где работал.
Как Эратосфен измерил окружность Земли?
Эратосфен — греческий ученый, живший в египетском городе Александрии с 276 года по 196 год до нашей эры. Работал он в Александрийском мусейоне. Отчасти это был музей, отчасти научный центр того времени.
В музее был ботанический сад, виварий, астрономическая обсерватория и лаборатории. Одни ученые мужи вели научные диспуты в аудитории музея, другие трапезничали и беседовали в триклинии (то есть в столовой).
Интересный факт: греческий ученый Эратосфен вычислил окружность Земли более 2000 лет назад.
Эратосфен заведовал библиотекой мусейона, в которой хранилось около 100 тысяч книг, написанных на свитках папируса (разновидность бумаги, сделанной из волокон растения папируса). Эратосфен интересовался всем на свете. Он изучал философию, историю и естественные науки, был театральным критиком. Многие коллеги по мусейону считали его дилетантом, то есть человеком, который всем интересуется, но ничего не знает по истине глубоко.
От проезжих путешественников Эратосфен услышал о необычном явлении, которое они наблюдали в Сиене, городе, расположенном далеко к югу от Александрии. Путешественники рассказали, что в полдень первого дня лета — в самый продолжительный день в году — в Сиене исчезали тени. Солнце в это время стояло прямо над головой, лучи его падали на землю отвесно вниз. Внимательно вглядываясь в воду водоема, можно было рассмотреть отражение Солнца на дне.
Интересный факт: окружность Земли равна приблизительно 40000 километров.
Эратосфен съездил в Сиену и убедился в этом сам. Вернувшись в Александрию, он обнаружил, что и в самый длительный день года в полдень стены мусейона продолжали отбрасывать тень на землю. Основываясь на этом простом наблюдении, он смог вычислить окружность Земли. Вот как он это сделал.
Вычисления окружности
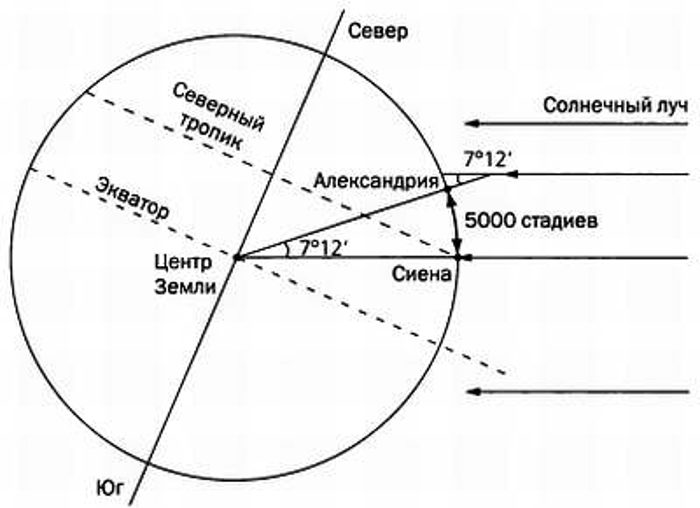
Эратосфен знал, что из – за громадного расстояния от Земли до Солнца, лучи последнего достигают и Сиены и Александрии параллельными лучами. То есть лучи Солнца, падающие на землю в Александрии, параллельны лучам, падающим на землю в Сиене в то же время. Если бы Земля была плоской, то тени исчезали бы на ней повсеместно 21 июня. Но так как, рассуждал он, Земля искривлена, то в Александрии, удаленной от Сиены на 500 миль (1 миля равна 1,609 километра) к северу, местные стены и колонны наклонены по отношению к сиенским стенам и колон нам под некоторым углом.
Итак, в полдень первого дня лета Эратосфен измерил тень, отбрасываемую обелиском, стоявшим неподалеку от мусейона. Зная высоту обелиска, он смог легко вычислить длину линии, соединяющей вершину обелиска и конец тени. Получился воображаемый треугольник. После того как треугольник был «очерчен», оставалось, используя известные к тому времени правила геометрии, вычислить его углы. И Эратосфен их вычислил. Он нашел, что угол отклонения обелиска от солнечного луча составляет чуть больше 7 градусов.
Так как в Сиене вертикальные предметы не отбрасывали тени, то угол между ними и солнечным лучом составлял ноль градусов. Короче, никакого угла не было. Это означало, что Александрия отстоит по земной окружности от Сиены на 7 градусов. Такой угол между городами — это 1/50 часть окружности. Всякая окружность содержит 360 градусов, земная окружность в этом смысле не исключение. Эратосфен умножил расстояние между Сиеной и Александрией — 500 миль — на 50 и получил значение окружности Земли. Оно оказалось равным 25 тысячам миль. Современные ученые, измерившие с помощью высококлассной техники окружность Земли, нашли ее равной 24 894 тысяч миль. Все таки Эратосфен оказался первоклассным ученым, а не дилетантом.
Определение расстояний на земной поверхности
В настоящее время существует целая наука — геодезия, которая занимается определением расстояний на земной поверхности. Геодезисты используют специальные приборы для определения угловых расстояний. Они изучают колебания силы тяжести на нашей планете, чтобы выявить истинную форму Земли. Для вычисления углов используют спутники. Такой спутник перемещается в вершину воображаемого треугольника, два других его угла помещают в заданных точках на земной поверхности.
Как вычислили окружность Земли
Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Как греки Землю измеряли
Время на прочтение
4 мин
Количество просмотров 21K
Пост про расчеты расстояния до Солнца подтолкнул к другому тексту – о вычислении расстояния до Луны (поскольку эта цифра использовалась Аристархом в расчетах, возник вопрос, а откуда он ее взял). Но уже в комментариях ко второму тексту прозвучал следующий вопрос – «А теперь можно про радиус Земли подробнее?»
Спрашивали – отвечаем. Ну и чтобы «два раза не вставать», начну даже не с радиуса, а с того, как греки пришли к выводу, что Земля имеет форму шара, а не диска или сундука (как утверждал позже ученый византиец Козьма Индикоплов).
Этим вопросом озаботились именно греки, в более древних цивилизациях (Вавилон, Египет) небо изучали, и довольно тщательно, пытались предсказать движение небесных тел, а вот вопросом формы Земли не заморачивались.
Трудно сказать, кто из греков первым озвучил идею о том, что Земля – это шар, наиболее распространена версия, что Пифагор. Но самый старый письменный трактат с этим утверждением, дошедший до нас («О движущейся сфере»), принадлежит другому математику – Автолику из Питаны, родившемуся лет на двести позже Пифагора. Правда, это вообще, самый старый античный математический трактат, дошедший до нас. И уже в нем Землю называют сферой. Но там это было подано как некая данность, т.е. Автолик был не первым, кто озвучил эту идею.
А затем его современник, великий Аристотель в трактате «О небе» подробно обосновал это утверждение. В основном объяснения были философского характера (сферическая Земля – неуничтожимый центр космоса и т.п.). Но был и ряд вполне конкретных доказательств. Прежде всего – результаты наблюдений за лунными затмениями: у них всегда бывает дугообразная ограничивающая линия. «Раз Луна затмевается потому, что её заслоняет Земля, то причина такой формы – окружность Земли, и Земля шарообразна», — делает вывод Аристотель.
Еще более интересный вывод сделал он из наблюдений за звездами. Для начала философ отметил, что в Египте и в Македонии имеются заметные наблюдателю различия в расположении звезд. И вывел: «Из этого ясно не только то, что Земля круглой формы, но и то, что эта сфера невелика: иначе столь незначительные перемещения не вызывали бы столь быстрых изменений».
Ну а дальше, поскольку с формой Земли образованная часть греков определилась, равно как и с тем, что размеры ее не так уж велики, напрашивался следующий шаг – измерить Землю.
Перед тем как перейдем к процессу и его результатам, отмечу один нюанс. Мерили греки, как я уже говорил в стадиях, а нюанс в том, что это сейчас километр он и в Африке километр. А тогда системы СИ не было. Всякий стадий составляет 100 пар шагов или 600 ступней, но шаги и ступни в разных системах мер могли несколько различаться: было несколько вариантов стадиев, от 172 до 185 метров (а еще вавилонский вариант стадия, но он нам здесь не интересен). Часто приходится гадать, каким стадием пользовался тот или иной автор. Поэтому, когда мы переводим результаты в привычные километры, то, конечно, рискуем ошибаться. Но – в пределах 6-7%. Для астрономии немало, для истории вопроса – терпимо.
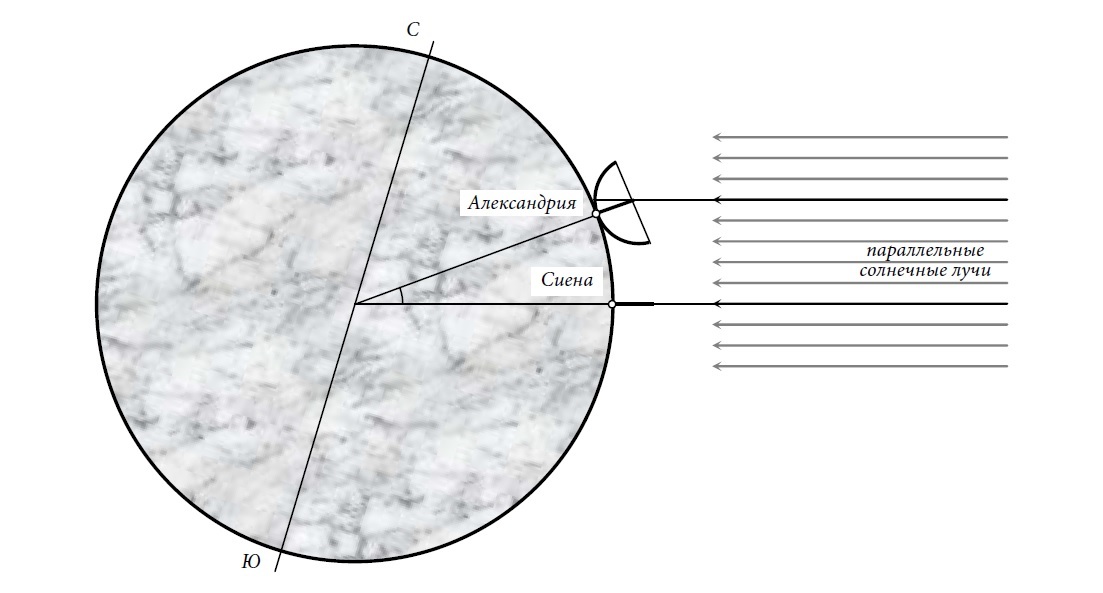
Теперь собственно о том, как греки Землю измеряли. Известны два исследования, проделанных с этой целью. Первое осуществил Эратосфен в III веке до нашей эры, второе – Посидоний сто с небольшим лет спустя. В обоих случаях греки применили схожий подход, разница была в деталях. Смысл его в следующем: и Солнце, и звезды доступны одновременному наблюдению в разных местах на Земле, но поскольку расстояние до них явно во много раз больше размеров самой Земли, все лучи света, приходящие от них к нам мы можем считать параллельными.
Эратосфен измерил высоту Солнца над горизонтом в полдень летнего солнцестояния в Александрии и в Сиене (Асуане). Почему там? А еще до него, древние египтяне заметили, что во время летнего солнцестояния Солнце освещает дно глубоких колодцев в Сиене (ныне Асуан), а в Александрии – нет. Будь Земля плоской, рассуждал Эратосфен, этого не могло бы быть (мы помним – лучи параллельны), но она круглая, т.е. искривлена. А Сиена и Александрия находятся на одном меридиане (считал он) на расстоянии 5000 стадиев друг от друга. Значит, стены в Александрии наклонены под некоторым углом по отношению к стенам в Сиене, поэтому в полдень солнцестояния они продолжают отбрасывать некоторую тень.
Эратосфен измерил тень от одного александрийского обелиска, зная также его высоту, он «построил треугольник из обелиска и его тени» и вычислил, что угол отклонения обелиска от солнечного луча составляет чуть больше 7 градусов. Это означало, что Александрия отстоит по земной окружности от Сиены на 7 градусов. Такой угол – 1/50 часть окружности и одновременно упомянутые 5000 стадиев. Значит общая длина окружности 250 000 стадиев, заключил Эратосфен. А рассчитывать радиус, зная длину окружности, греки умели.
Сегодня мы знаем, что расчеты Эратосфена имели ряд серьезных погрешностей: Александрия и Сиена расположены не на одном меридиане, поэтому разница между их параллелями меньше, само это расстояние тоже было измерено приблизительно, со слов караванщиков, да и углы этих городов по направлению к солнечным лучам он измерил с ошибкой. И все же, ему удалось получит результат очень близкий к современным данным (6 371 км). Правда, в зависимости от того, какими стадиями он считал, если греческими, то да, его ответ — 6 916 км, а если стадиями египетских фараонов (дело было в Египте и расстояние могло быть указано в них), то его ответ — 8 397 км — намного больше реального.
Впрочем, Посидоний напутал еще больше. Но он и считал не по тени от Солнца, а по расположению звезды Канопус на небе Александрии и греческого острова Родос, которые разделяли те же 5000 стадий. Но эти точки тоже лежали не на одном меридиане, плюс морские расстояния греки измеряли с гораздо меньшей точностью. В итоге, по его расчетам Земля получилась чуть ли не на треть меньше, чем у Эратосфена.
Да, греки ошибались в расчетах, но главное они сделали – придумали метод, как можно измерить размер Земли, не покидая ее поверхности. Дальше дело было за совершенствованием географических данных и измерительных приборов. Ну а греки не остановились и придумали как рассчитать расстояние до Луны и до Солнца.
О том, кто, когда и как измерил Землю, мы знаем из дошедших до нас трудов древнегреческого ученого Клеомеда. Клеомед был современником Христа, то есть жил спустя почти три века после Эратосфена, но насчет точности даты первого измерения земного шара можно не беспокоиться. Иного дня для измерения нашей планеты не могло быть, да и метод ее измерения в то время мог быть только одним — по длине тени гномона (вертикального шеста солнечных часов) в полдень 19 июня. Именно этот день в III веке до н. э. был днем летнего солнцестояния.
Ход мысли Эратосфена Клеомед восстановил по своему разумению, но и тут было трудно ошибиться, потому что это была единственно возможная логика ученого того времени. Прежде всего, для Эратосфена, который занимал пост хранителя Александрийской библиотеки, главного научного учреждения Древней Греции, шарообразность Земли была не предположением, а фактом. Это экспериментально доказали греческие ученые еще за сто лет до Эратосфена.
Эратосфен исходил из двух допущений. Во-первых, он считал, что Александрия в дельте Нила, где он проводил измерения, и город Сиен (Асуан) в верховьях Нила находятся на одном меридиане. Во-вторых — что Сиен находится под тропиком Рака, то есть в полдень дня летнего солнцестояния вертикальный шест в Сиене не отбрасывает вообще никакой тени, он строго перпендикулярен Солнцу. Оставалось измерить длину тени вертикального шеста (гномона) в солнечных часах в Александрии в полдень 19 июня, что и сделал Эратосфен.
По длине тени можно определить угол, под которым шест направлен к Солнцу в зените. Угол оказался равен 1/50 от всего круга солнечных часов (360 градусов). Расстояние от Александрии до Сиена было известно — 5000 стадиев. Дальше все сводилось к геометрии, в которой греки были сильны. Если дуга окружности Земли в 1/50 ее длины равна 5 тыс. стадиев, то вся окружность Земли равна 250 тыс. стадиев (43 тыс. км). А радиус Земли у Эратосфена получился равным 6287 км в наших мерах длины.
Современные измерения дают окружность нашей планеты по меридиану 40 008 км, радиус — 6371 км. Точность измерений Эратосфена была почти абсолютная. Небольшие расхождения связаны с погрешностями его допущений. Александрия и Асуан лежат не на одном меридиане, Асуан на 2,5 градуса западнее. Кроме того, Асуан лежит все-таки не под тропиком Рака, а на полградуса севернее.
Сергей Петухов
From Wikipedia, the free encyclopedia
For modern definitions and measurements, see Earth radius.
Earth’s circumference is the distance around Earth. Measured around the Equator, it is 40,075.017 km (24,901.461 mi). Measured around the poles, the circumference is 40,007.863 km (24,859.734 mi).[1]
Measurement of Earth’s circumference has been important to navigation since ancient times. The first known scientific measurement and calculation was done by Eratosthenes, by comparing altitudes of the mid-day sun at two places a known north–south distance apart.[2] He achieved a great degree of precision in his computation.[3] Treating the Earth as a sphere, its circumference would be its single most important measurement.[4] Earth deviates from spherical by about 0.3%, as characterized by flattening.
In modern times, Earth’s circumference has been used to define fundamental units of measurement of length: the nautical mile in the seventeenth century and the metre in the eighteenth. Earth’s polar circumference is very near to 21,600 nautical miles because the nautical mile was intended to express one minute of latitude (see meridian arc), which is 21,600 partitions of the polar circumference (that is 60 minutes × 360 degrees). The polar circumference is also close to 40,000 kilometres because the metre was originally defined to be one ten millionth (i.e., a kilometre is one ten thousandth) of the arc from pole to equator (quarter meridian). The accuracy of measuring the circumference has improved since then, but the physical length of each unit of measure had remained close to what it was determined to be at the time, so the Earth’s circumference is no longer a round number in metres or nautical miles.
History[edit]
Posidonius[edit]
Posidonius calculated the Earth’s circumference by reference to the position of the star Canopus. As explained by Cleomedes, Posidonius observed Canopus on but never above the horizon at Rhodes, while at Alexandria he saw it ascend as far as 7+1⁄2 degrees above the horizon (the meridian arc between the latitude of the two locales is actually 5 degrees 14 minutes). Since he thought Rhodes was 5,000 stadia due north of Alexandria, and the difference in the star’s elevation indicated the distance between the two locales was 1/48 of the circle, he multiplied 5,000 by 48 to arrive at a figure of 240,000 stadia for the circumference of the earth.[5] It is generally thought[by whom?] that the stadion used by Posidonius was almost exactly 1/10 of a modern statute mile.[citation needed] Thus Posidonius’s measure of 240,000 stadia translates to 24,000 mi (39,000 km), not much short of the actual circumference of 24,901 mi (40,074 km).[5] Strabo noted that the distance between Rhodes and Alexandria is 3,750 stadia, and reported Posidonius’s estimate of the Earth’s circumference to be 180,000 stadia or 18,000 mi (29,000 km).[6] Pliny the Elder mentions Posidonius among his sources and—without naming him—reported his method for estimating the Earth’s circumference. He noted, however, that Hipparchus had added some 26,000 stadia to Eratosthenes’s estimate. The smaller value offered by Strabo and the different lengths of Greek and Roman stadia have created a persistent confusion around Posidonius’s result. Ptolemy used Posidonius’s lower value of 180,000 stades (about 33% too low) for the earth’s circumference in his Geography. This was the number used by Christopher Columbus in order to underestimate the distance to India as 70,000 stades.[7]
Eratosthenes[edit]
Illustration showing a portion of the globe showing a part of the African continent. The sun beams shown as two rays hitting earth at Syene and Alexandria. Angle of sun beam and the gnomons (vertical sticks) is shown at Alexandria which allowed Eratosthenes’ estimate of the circumference of Earth.
The measure of Earth’s circumference is the most famous among the results obtained by Eratosthenes,[8] who estimated that the meridian has a length of 252,000 stadia, with an error on the real value between −2.4% and +0.8% (assuming a value for the stadion between 155 and 160 metres;[3] the exact value of the stadion remains a subject of debate to this day; see stadion).
Eratosthenes described his technique in a book entitled On the measure of the Earth, which has not been preserved; what has been preserved is the simplified version described by Cleomedes to popularise the discovery.[9] Cleomedes invites his reader to consider two Egyptian cities, Alexandria and Syene (modern Assuan):
- Cleomedes assumes that the distance between Syene and Alexandria was 5,000 stadia (a figure that was checked yearly by professional bematists, mensores regii).[10]
- He assumes the simplified (but inaccurate) hypothesis that Syene was precisely on the Tropic of Cancer, saying that at local noon on the summer solstice the Sun was directly overhead. Syene was actually north of the tropic by something less than a degree.
- He assumes the simplified (but inaccurate) hypothesis that Syene and Alexandria are on the same meridian. Syene was actually about 3 degrees of longitude east of Alexandria.
According to Cleomedes’ On the Circular Motions of the Celestial Bodies, around 240 BC, Eratosthenes calculated the circumference of the Earth in Ptolemaic Egypt.[11] Using a vertical rod known as a gnomon and under the previous assumptions, he knew that at local noon on the summer solstice in Syene (modern Aswan, Egypt), the Sun was directly overhead, as the gnomon cast no shadow. Additionally, the shadow of someone looking down a deep well at that time in Syene blocked the reflection of the Sun on the water. Eratosthenes then measured the Sun’s angle of elevation at noon in Alexandria by measuring the length of another gnomon’s shadow on the ground.[12] Using the length of the rod, and the length of the shadow, as the legs of a triangle, he calculated the angle of the sun’s rays.[13] This angle was about 7°, or 1/50th the circumference of a circle; assuming the Earth to be perfectly spherical, he concluded that its circumference was 50 times the known distance from Alexandria to Syene (5,000 stadia, a figure that was checked yearly), i.e. 250,000 stadia.[14] Depending on whether he used the «Olympic stade» (176.4 m) or the Italian stade (184.8 m), this would imply a circumference of 44,100 km (an error of 10%) or 46,100 km, an error of 15%.[14] A value for the stadion of 157.7 metres has even been posited by L.V. Firsov, which would give an even better precision, but is plagued by calculation errors and false assumptions.[15] In 2012, Anthony Abreu Mora repeated Eratosthenes’s calculation with more accurate data; the result was 40,074 km, which is 66 km different (0.16%) from the currently accepted polar circumference.[13]
Measure of Earth’s circumference according to Cleomedes’ simplified version, based on the approximation that Syene is on the Tropic of Cancer and on the same meridian as Alexandria
Eratosthenes’ method was actually more complicated, as stated by the same Cleomedes, whose purpose was to present a simplified version of the one described in Eratosthenes’ book. Pliny, for example, has quoted a value of 252,000 stadia.[16]
The method was based on several surveying trips conducted by professional bematists, whose job was to precisely measure the extent of the territory of Egypt for agricultural and taxation-related purposes.[3] Furthermore, the fact that Eratosthenes’ measure corresponds precisely to 252,000 stadia (according to Pliny) might be intentional, since it is a number that can be divided by all natural numbers from 1 to 10: some historians believe that Eratosthenes changed from the 250,000 value written by Cleomedes to this new value to simplify calculations;[17] other historians of science, on the other side, believe that Eratosthenes introduced a new length unit based on the length of the meridian, as stated by Pliny, who writes about the stadion «according to Eratosthenes’ ratio».[3][16]
Aryabhata[edit]
Around AD 525, the Indian mathematician and astronomer Aryabhata wrote Aryabhatiya, in which he calculated the diameter of earth to be of 1,050 yojanas. The length of the yojana intended by Aryabhata is in dispute. One careful reading gives an equivalent of 14,200 kilometres (8,800 mi), too large by 11%.[18] Another gives 15,360 km (9,540 mi), too large by 20%.[19] Yet another gives 13,440 km (8,350 mi), too large by 5%.[20]
Islamic Golden Age[edit]
Around AD 830, Caliph Al-Ma’mun commissioned a group of Muslim astronomers led by Al-Khwarizmi to measure the distance from Tadmur (Palmyra) to Raqqa, in modern Syria. They calculated the Earth’s circumference to be within 15% of the modern value, and possibly much closer. How accurate it actually was is not known because of uncertainty in the conversion between the medieval Arabic units and modern units, but in any case, technical limitations of the methods and tools would not permit an accuracy better than about 5%.[21]
Diagram showing how al-Biruni was able to calculate the Earth’s circumference by measuring the dip of the horizon from a point at a known height.
A more convenient way to estimate was provided in Al-Biruni’s Codex Masudicus (1037). In contrast to his predecessors, who measured the Earth’s circumference by sighting the Sun simultaneously from two locations, al-Biruni developed a new method of using trigonometric calculations, based on the angle between a plain and mountain top, which made it possible for it to be measured by a single person from a single location.[21] From the top of the mountain, he sighted the dip angle which, along with the mountain’s height (which he determined beforehand), he applied to the law of sines formula. This was the earliest known use of dip angle and the earliest practical use of the law of sines.[22] However, the method could not provide more accurate results than previous methods, due to technical limitations, and so al-Biruni accepted the value calculated the previous century by the al-Ma’mun expedition.[21]
Columbus’s error[edit]
1,700 years after Eratosthenes’s death, Christopher Columbus studied what Eratosthenes had written about the size of the Earth. Nevertheless, based on a map by Toscanelli, he chose to believe that the Earth’s circumference was 25% smaller. If, instead, Columbus had accepted Eratosthenes’s larger value, he would have known that the place where he made landfall was not Asia, but rather a New World.[23]
Historical use in the definition of units of measurement[edit]
In 1617 the Dutch scientist Willebrord Snellius assessed the circumference of the Earth at 24,630 Roman miles (24,024 statute miles). Around that time British mathematician Edmund Gunter improved navigational tools including a new quadrant to determine latitude at sea. He reasoned that the lines of latitude could be used as the basis for a unit of measurement for distance and proposed the nautical mile as one minute or one-sixtieth (1/60) of one degree of latitude. As one degree is 1/360 of a circle, one minute of arc is 1/21600 of a circle – such that the polar circumference of the Earth would be exactly 21,600 miles. Gunter used Snellius’s circumference to define a nautical mile as 6,080 feet, the length of one minute of arc at 48 degrees latitude.[24]
In 1793, France defined the metre so as to make the polar circumference of the Earth 40,000 kilometres. In order to measure this distance accurately, the French Academy of Sciences commissioned Jean Baptiste Joseph Delambre and Pierre Méchain to lead an expedition to attempt to accurately measure the distance between a belfry in Dunkerque and Montjuïc castle in Barcelona to estimate the length of the meridian arc through Dunkerque. The length of the first prototype metre bar was based on these measurements, but it was later determined that its length was short by about 0.2 millimetres because of miscalculation of the flattening of the Earth, making the prototype about 0.02% shorter than the original proposed definition of the metre. Regardless, this length became the French standard and was progressively adopted by other countries in Europe.[25] This is why the polar circumference of the Earth is actually 40,008 kilometres, instead of 40,000.
See also[edit]
- Earth radius
- Spherical Earth
- Nautical mile
References[edit]
- ^ Humerfelt, Sigurd (26 October 2010). «How WGS 84 defines Earth». Archived from the original on 24 April 2011. Retrieved 29 April 2011.
- ^ Ridpath, Ian (2001). The Illustrated Encyclopedia of the Universe. New York, NY: Watson-Guptill. p. 31. ISBN 978-0-8230-2512-1.
- ^ a b c d Russo, Lucio (2004). The Forgotten Revolution. Berlin: Springer. p. 273–277.
- ^ Shashi Shekhar; Hui Xiong (12 December 2007). Encyclopedia of GIS. Springer Science & Business Media. pp. 638–640. ISBN 978-0-387-30858-6.
- ^ a b Posidonius, fragment 202
- ^ Cleomedes (in Fragment 202) stated that if the distance is measured by some other number the result will be different, and using 3,750 instead of 5,000 produces this estimation: 3,750 x 48 = 180,000; see Fischer I., (1975), Another Look at Eratosthenes’ and Posidonius’ Determinations of the Earth’s Circumference, Ql. J. of the Royal Astron. Soc., Vol. 16, p.152.
- ^ John Freely, Before Galileo: The Birth of Modern Science in Medieval Europe (2012)
- ^ Russo, Lucio. The Forgotten Revolution. p. 68.
- ^ Cleomedes, Caelestia, i.7.49–52.
- ^ Martianus Capella, De nuptiis Philologiae et Mercurii, VI.598.
- ^ Van Helden, Albert (1985). Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley. University of Chicago Press. pp. 4–5. ISBN 978-0-226-84882-2.
- ^ «Astronomy 101 Specials: Eratosthenes and the Size of the Earth». www.eg.bucknell.edu. Retrieved 19 December 2017.
- ^ a b «How did Eratosthenes measure the circumference of the earth?». 3 July 2012.
- ^ a b «Eratosthenes and the Mystery of the Stades – How Long Is a Stade? – Mathematical Association of America». www.maa.org.
- ^ Donald Engels (1985). The Length of Eratosthenes’ Stade. American Journal of Philology 106 (3): 298–311. doi:10.2307/295030 (subscription required).
- ^ a b Pliny, Naturalis Historia, Book 2, Chapter 112.
- ^ Rawlins, Dennis (1983). «The Eratosthenes-Strabo Nile Map. Is It the Earliest Surviving Instance of Spherical Cartography? Did It Supply the 5000 Stades Arc for Eratosthenes’ Experiment?». Archive for History of Exact Sciences. 26 (3): 211–219. doi:10.1007/BF00348500. S2CID 118004246.
- ^ Kak, Subhash (2010). «Aryabhata’s Mathematics». arXiv:1002.3409 [cs.CR].
- ^ «Journal of the Royal Asiatic Society of Great Britain and Ireland». 1907.
- ^ «The_Aryabhatiya_of_Aryabhata_Clark_1930».
- ^ a b c Mercier, Raymond (1992). «Geodesy». In Harley, J.B.; Woodward, David (eds.). The History of Cartography, Volume 2, Book 1. The University of Chicago Press. pp. 175–188. ISBN 9780226316352.
- ^ Behnaz Savizi (2007), «Applicable Problems in History of Mathematics: Practical Examples for the Classroom», Teaching Mathematics and Its Applications, Oxford University Press, 26 (1): 45–50, doi:10.1093/teamat/hrl009
- ^ Gow, Mary. Measuring the Earth: Eratosthenes and His Celestial Geometry, p. 6 (Berkeley Heights, NJ: Enslow, 2010).
- ^ Marine Insight, Why Nautical Mile and Knot Are The Units Used at Sea?
- ^ Alder, Ken (October 2003). The Measure of All Things: The Seven-Year Odyssey and Hidden Error That Transformed the World. Simon and Schuster. ISBN 978-0-7432-1676-0.
Bibliography[edit]
- Krebs, Robert E.; Krebs, Carolyn A. (2003). «Calculating the Earth’s Circumference». Groundbreaking Scientific Experiments, Inventions, and Discoveries of the Ancient World. Greenwood Publishing Group. p. 52. ISBN 978-0-313-31342-4.
- Nicastro, Nicholas (25 November 2008). Circumference: Eratosthenes and the Ancient Quest to Measure the Globe. St. Martin’s Press. ISBN 978-1-4299-5819-6.
- Gow, Mary (1 July 2009). Measuring the Earth: Eratosthenes and His Celestial Geometry. Enslow Publishing, LLC. ISBN 978-0-7660-3120-3.
- Lowrie, William (20 September 2007). Fundamentals of Geophysics. Cambridge University Press. ISBN 978-1-139-46595-3.
External links[edit]
- Carl Sagan demonstrates how Eratosthenes determined that the Earth was round and the approximate circumference