https://ria.ru/20221116/sechenie-1832065968.html
Гармония во всем: что такое золотое сечение и способы его применения
Золотое сечение: что это такое, пропорции, принцип, применение в архитектуре и строительстве
Гармония во всем: что такое золотое сечение и способы его применения
«Божественная гармония» или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке,… РИА Новости, 16.11.2022
2022-11-16T21:08
2022-11-16T21:08
2022-11-16T21:08
общество
европа
греция
ле корбюзье (шарль-эдуар жаннере-гри)
леонардо да винчи
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21.img.ria.ru/images/07e6/0b/10/1832031636_0:318:3076:2048_1920x0_80_0_0_74519bda270895480ff99027b7b160ec.jpg
МОСКВА, 16 ноя — РИА Новости. «Божественная гармония» или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке, природе, архитектуре, искусстве. Что такое ряд чисел Фибоначчи, принцип расчета и метод построения на основе пропорций – в материале РИА Новости.Золотое сечение»Определенные пропорции повсеместно используются в дизайне и архитектуре, фотографии и очень часто наблюдаются в естественной природе», – говорит Ренат Мансуров, профессиональный фотограф, фотохудожник, лауреат и участник международных фотоконкурсов.История»Первым про золотое сечение писал еще Евклид в “Началах”, которые в свое время были вторые по популярности после Библии. Людям свойственно искать закономерности везде, даже там где их нет, поэтому число “фи” всегда было темой для религиозных спекуляций. Леонардо да Винчи, например, считал, что золотое сечение является выражением божественной сущности Троицы», – комментирует Максим Господинко, диджитал-художник, дизайнер, основатель Spoils.По словам эксперта, про эту пропорцию писал Ян Чихольд, использовал Малевич, Монферран построил по ней Исаакиевский собор.»Но, как мне кажется, острое желание привязать всё мироздание к одному закону больше говорит о людях прошлого, чем о самом мире. Ум человека плохо переносит множественность, неточность моделей и просто хаос. Из этой особенности и происходит когнитивное “удобство”, когда порядок и закономерность всё-таки находятся», – отмечает Максим Господинко.»Впервые термин «золотое сечение» («goldener Schnitt») употребил в эпоху резкого роста европейской секуляризации в примечании ко второму изданию своей «Чистой элементарной математики» в 1835 году доктор философии Мартин Ом. Термин был известен ранее (из текста следует, что Ом не сам его придумал), и в дальнейшем быстро распространился в европейской литературе», – поясняет Сергей Дементьев, эксперт сервиса meta-luxury недвижимости «Душа объекта».Эксперт отмечает, что до Ома это соотношение благодаря трактату монаха францисканца Луки Пачоли, изданному в соавторстве с Леонардо да Винчи, с 1509 года именовали в Европе «божественной пропорцией» (лат. «Divina Proportione», итал. «Proporzione Divina»).По мнению Сергея Дементьева, «божественная пропорция» («золотое сечение») как известная концепция красоты (еще древнегреческий скульптор Поликлет сформировал альтернативные правила красоты, а в 20-м веке модернист архитектор Ле Корбюзье разработал собственную систему пропорционирования) обязана своему появлению упадку веросознания: Эпоха Возрождения в Европе – именно историческая попытка Ренессанса веросознания в новых его формах через умозрение и затем деятельное воплощение в культуре (художественное творчество, архитектура, строительство, парковый, ландшафтный и интерьерный дизайн и т.д.).Пионеры Возрождения Пачоли и Леонардо да Винчи («Тайная вечеря» и «Мона Лиза» вписаны в геометрические фигуры) обратили свое внимание на античность, где еще в «Началах» Евклид (ок. 300 лет до нашей эры) говорил о делении отрезка в крайнем и среднем отношении («ἄκρος καὶ μέσος λόγος»), полагая, что на числах построено все мироздание, на идеи Витрувия (ок. 80-70 гг. до нашей эры — после 13 г. до нашей эры), изложенные в «Десяти книгах об архитектуре» (лат. «De architectura libri decem») о применении математики к искусству архитектуры.Пропорции золотого сеченияО том, как высчитывать золотые пропорции, рассказал эксперт в сфере фотографии Ренат Мансуров.»Если взять для примера линию и разделить ее на две части так, чтобы длинная соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной, получится золотая пропорция», – поясняет он. К слову, она равна всегда 1,618, и это так называемое число «фи» обозначается греческой буквой φ — от имени древнегреческого скульптора Фидия.Ренат Мансуров отмечает, что в правильном прямоугольнике соотношение сторон соответствует золотому сечению.»Интересен этот прямоугольник тем, что сколько бы ни отрезали от него квадратов, он всегда будет оставлять после себя кусочек с золотым соотношением сторон и так до бесконечности», – говорит Ренат Мансуров.Золотое сечение в математикеИтальянский астроном и математик Фибоначчи вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Эта закономерность известна как ряд Фибоначчи.»Если представить два квадрата, поставленных рядом, потом добавить квадрат с удвоенной стороной, то получится квадрат 2 на 2. Далее добавить по спирали против часовой стрелки сумму двух предыдущих квадратов. Получится квадрат с длинной стороны три квадрата, далее добавить к стороне квадрата предыдущую сторону, получится 5, потом 8 потом 13 и 21, каждое последующее число — это сумма сложения с предыдущим, то есть получается такая последовательность, которую и вывел Фибоначчи: 0,1,1,2,3,5,8,13,21 и т.д.», – поясняет Ренат Мансуров.0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и до бесконечности. А при делении последующего числа на предыдущее получается коэффициент золотого сечения. По мере возрастания чисел соотношение приближается к 1,618. К примеру, числа 3 и 5, их соотношение равно 1,666, а если взять 13 и 21, то получается уже 1,625. Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленное значение 0,62.А если в каждом квадрате построить дугу из одного угла к другому, то получится так называемая спираль Фибоначчи.Правило золотого сеченияНа практике золотое сечение представляет собой пропорцию, соотношение сторон прямоугольника, отрезков определенной длины, других геометрических форм или сопряженных размерных характеристик реальных объектов.Метод золотого сечения»Если построить прямоугольник, используя метод, указанный выше, и встроить в этот прямоугольник линии, используя числа золотого сечения, то получится разграничение прямоугольника несколькими линиями. И если говорить о композиции, то размещая объекты на линиях или их пересечениях, можно максимально выделить эти объекты как смысловые центры, и наоборот, чем дальше от этих точек, тем труднее будет улавливать смысловой центр», – поясняет Ренат Мансуров.Если же совместить спираль Фибоначчи и эту сетку, то получится практически инструкция по использованию золотого сечения в фотографии, живописи и дизайне.Где можно увидеть золотое сечениеЕсли разделить обычное куриное яйцо мысленно пополам в самой широкой его части, то получатся правильные золотые пропорции. Пропорции здания Парфенона в Греции, спирали раковин, пропорции тела человека, спиральные галактики и растения, и еще много всего вокруг.ПриродаПо словам Рената Мансурова, примеров этих золотых чисел и спиралей найти в природе можно множество. «Распределение семян подсолнуха, спиральные раковины, спиральные галактики, соотношения пропорций человеческого тела, и например, если внимательно посмотреть на нераскрытую еловую шишку или ананас с торца, то можно увидеть эти спирали», – отмечает эксперт.Свою точку зрения озвучил Максим Господинко.»У растения есть важная задача — наиболее оптимально расположить свои листья или лепестки, для того чтобы уловить больше солнечного света или просто уместить больше семян. В некоторых случаях есть возможность делать это только по плотной спирали (ананас, еловая шишка, подсолнечник). Кажется, что перед таким растением стоит сложная математическая задача — на какой угол сдвинуть следующую семечку или лепесток, но на самом деле вопрос лишь в том, насколько сильное создается отталкивание от уже существующего элемента.И так складывается, что угол отклонения от предыдущего листка действительно очень близок к отношению «фи», – комментирует эксперт. – Ни одно рациональное отношение не подходит, потому что при повороте под такими углами возникают колонны-лучи с большими дырами, а как мы знаем, семена подсолнечника уложены красивыми спиралями, число которых как раз соответствует числам из ряда Фибоначчи и дыр там никаких нет».По словам Максима Господинко, ряд Фибоначчи можно легко образовать, взяв ноль и единицу, а каждое последующее за ними получить из суммы двух предыдущих. «Моделировать растение конечно не умеет, насколько мне известно, и не знает количества рядов спиралей, а усилие отталкивания следующего элемента регулируется поколениями и естественным отбором, но в итоге приходит именно к “фи”», – отмечает специалист.ЧеловекПропорции золотого сечения прослеживаются и на примере тела человека. К золотой формуле приравнивается абсолютно все: кости, ладони и пальцы, пропорции участков на лице, расстояние вытянутых рук по отношению к телу. Пропорции таковы:ИскусствоМножество произведений искусства и архитектурных шедевров сделаны по принципам золотого сечения. Египетские и пирамиды Майя, греческий Парфенон и так далее. Картины известных художников тоже выполнены с учетом правил золотого сечения.Прослеживаются такие пропорции и в музыкальных произведениях Шуберта, Моцарта, Баха, Шопена и прочих.»Для дизайнера и художника вопрос о золотом сечении стоит лишь в разрезе более широкой темы — пропорционирования. Не каждый использует этот инструмент, хоть и должен, но часто амбициозный художник, схватившись за “божественную истину”, начинает транслировать лишь её, упуская суть художественного высказывания, передачу образа. Пропорция – лишь инструмент и, очевидно, инструмент не должен идти вперёд задачи. Если образ не понят художником, его невозможно передать», – говорит Максим Господинко. Но тем не менее, переоценить важность этой пропорции сложно. Часто чувствительный художник сам интуитивно может расположить элементы в соответствии с “фи”, также оно является достаточно простым инструментом, чтобы создать изящную композицию даже в самых простых вещах.Примеры использования в живописи.Примеры использования золотого сечения в дизайне логотипов.Применение золотого сеченияПримеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений и создании проекта дома, в современном дизайне интерьера при планировании и зонировании пространства, расстановки мебели и даже цветовом оформлении, а также в ландшафтном дизайне при выкладке закрученных дорожек, расположении растений на клумбах и других элементов.Так, к примеру, при строительстве квартир и домов отношение самой большой комнаты к площади всей квартиры равно как 0,62 к 1, меньшее помещение делают с таким же соотношением к площади большей комнаты. Так, кухня – к меньшей комнате, прихожая к кухне, санузел к прихожей, а балкон – к санузлу.Кроме того, с помощью золотого сечения подбирают и цветовое оформление. В интерьере применяют соотношение 10-30-60, основанное на золотом сечении. В пространстве используют три основных цвета: первый – доминирующий, охватывает 60% комнаты (стены и пол). Второй оттенок составляет 30% – мебель. И третий, 10%, приходится на декор.»Существует множество вариантов золотого сечения. Но все они, так или иначе, основаны на числах Фибоначчи. Какие то из них популярны, какие то не очень, но о чем мы говорим сегодня, это то, что выработалось за последние столетия — это явно золотой стандарт, – говорит Ренат Мансуров. – Конечно, нужно понимать, что творчество остается творчеством и отходить от стандарта не возбраняется, но и совсем идти наперекор этим пропорциям не стоит».По мнению эксперта, теория золотого сечения и «божественных пропорций» довольно популярна, но наука не стоит на месте, и сейчас активно исследуются теории восприятия с научной точки зрения. «То, что работает на практике не одно столетие, однозначно должно напоминать каждый раз о том, что эти пропорции проверены временем и сотнями тысяч творческих людей: фотографы, художники, дизайнеры и архитекторы каждый день работают и используют золотые пропорции в своей работе.Высчитывать миллиметры и микроны в надежде сделать ваше творчество золотым, наверное, не стоит, но и забывать о приятных для глаза пропорциях наверняка не нужно», – говорит Ренат Мансуров.Как это делать правильно, каждый решает самостоятельно, существует множество приемов композиции и работы с психологией восприятия, которые вместе могут улучшить работу в разы. «Учитесь правильно и не останавливайтесь в изучении художественных и композиционных приемов, и ваше творчество будет сиять оригинальностью и легкостью восприятия», – советует Ренат Мансуров.Второе золотое сечениеВторое золотое сечение вытекает из основного сечения и дает отношение 44: 56.Максим Господинко отмечает, что золотое сечение – не единственная пропорция, приятная глазу человека, есть “серебряное сечение”. Две величины находятся в «серебряном сечении», если отношение суммы меньшей и удвоенной большей величины к большей то же самое, что и отношение большей величины к меньшей. Также можно отметить, что порядок разлинованной в клетку тетради приятнее полного хаоса чистого листа (если не брать пропорцию самого его формата за порядок).По словам эксперта, пропорция тетрадки в клетку ничем не хуже золотого сечения, но действие на человека она оказывает иное, как будто организуя простейший порядок — один к одному. «Если бы мы использовали такой поворот угла в подсолнухе, то получили бы одну линию семян, в случае с 1/4 — крест. Каждой задаче — свое решение. В случае с растениями им нужно как раз самое иррациональное число. Примечательно, что именно такое число и прослыло божественным», – говорит Максим Господинко.Мифы о золотом сечении»Можно спекулировать на тему того, что где-то в глубине восприятия человека лежит именно закономерность ряда Фибоначчи, вероятно, где-то мы так же решали геометрическую задачу поворота на нужный угол по спирали, может быть, всё живое, так или иначе помнит этот опыт. Но чтобы не очаровываться золотым сечением чрезмерно, можно обратить внимание на любовь человека к зигзагам и орнаментам. Далеко не обязательно строить бабушкин ковёр по “фи”, чтобы на него было приятнее смотреть, чем на голую стену, – считает Максим Господинко. – Оказывается, этот вид визуального комфорта обусловлен строением визуального кортекса человеческого мозга, и такие орнаменты, как мы можем увидеть в традиционных культурах, ложатся в него как недостающий кусочек удобного паззла вместо хаотичного визуального потока внешней среды. Резной наличник лучше голых ставень. Кружева лучше минимализма. Природа лучше асфальта. Потому что экономят ресурсы человека, показывая привычные и близкие формы».
https://ria.ru/20210121/litso-1593906541.html
https://radiosputnik.ria.ru/20220201/piramida-1769426771.html
https://ria.ru/20181111/1532496249.html
европа
греция
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2022
Новости
ru-RU
https://ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
https://cdnn21.img.ria.ru/images/07e6/0b/10/1832031636_345:0:3076:2048_1920x0_80_0_0_d15c886e20acd2d1355969b43de06ca8.jpg
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
общество, европа, греция, ле корбюзье (шарль-эдуар жаннере-гри), леонардо да винчи
Общество, Европа, Греция, Ле Корбюзье (Шарль-Эдуар Жаннере-Гри), Леонардо да Винчи
- Золотое сечение
- История
- Пропорции золотого сечения
- Золотое сечение в математике
- Правило золотого сечения
- Метод золотого сечения
- Где можно увидеть золотое сечение
- Природа
- Человек
- Искусство
- Применение золотого сечения
- Второе золотое сечение
- Мифы о золотом сечении
МОСКВА, 16 ноя — РИА Новости. «Божественная гармония» или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке, природе, архитектуре, искусстве. Что такое ряд чисел Фибоначчи, принцип расчета и метод построения на основе пропорций – в материале РИА Новости.
Золотое сечение
«Определенные пропорции повсеместно используются в дизайне и архитектуре, фотографии и очень часто наблюдаются в естественной природе», – говорит Ренат Мансуров, профессиональный фотограф, фотохудожник, лауреат и участник международных фотоконкурсов.
История
«
«Первым про золотое сечение писал еще Евклид в “Началах”, которые в свое время были вторые по популярности после Библии. Людям свойственно искать закономерности везде, даже там где их нет, поэтому число “фи” всегда было темой для религиозных спекуляций. Леонардо да Винчи, например, считал, что золотое сечение является выражением божественной сущности Троицы», – комментирует Максим Господинко, диджитал-художник, дизайнер, основатель Spoils.
По словам эксперта, про эту пропорцию писал Ян Чихольд, использовал Малевич, Монферран построил по ней Исаакиевский собор.
«Но, как мне кажется, острое желание привязать всё мироздание к одному закону больше говорит о людях прошлого, чем о самом мире. Ум человека плохо переносит множественность, неточность моделей и просто хаос. Из этой особенности и происходит когнитивное “удобство”, когда порядок и закономерность всё-таки находятся», – отмечает Максим Господинко.
«
«Впервые термин «золотое сечение» («goldener Schnitt») употребил в эпоху резкого роста европейской секуляризации в примечании ко второму изданию своей «Чистой элементарной математики» в 1835 году доктор философии Мартин Ом. Термин был известен ранее (из текста следует, что Ом не сам его придумал), и в дальнейшем быстро распространился в европейской литературе», – поясняет Сергей Дементьев, эксперт сервиса meta-luxury недвижимости «Душа объекта».
Эксперт отмечает, что до Ома это соотношение благодаря трактату монаха францисканца Луки Пачоли, изданному в соавторстве с Леонардо да Винчи, с 1509 года именовали в Европе «божественной пропорцией» (лат. «Divina Proportione», итал. «Proporzione Divina»).
По мнению Сергея Дементьева, «божественная пропорция» («золотое сечение») как известная концепция красоты (еще древнегреческий скульптор Поликлет сформировал альтернативные правила красоты, а в 20-м веке модернист архитектор Ле Корбюзье разработал собственную систему пропорционирования) обязана своему появлению упадку веросознания: Эпоха Возрождения в Европе – именно историческая попытка Ренессанса веросознания в новых его формах через умозрение и затем деятельное воплощение в культуре (художественное творчество, архитектура, строительство, парковый, ландшафтный и интерьерный дизайн и т.д.).
Пионеры Возрождения Пачоли и Леонардо да Винчи («Тайная вечеря» и «Мона Лиза» вписаны в геометрические фигуры) обратили свое внимание на античность, где еще в «Началах» Евклид (ок. 300 лет до нашей эры) говорил о делении отрезка в крайнем и среднем отношении («ἄκρος καὶ μέσος λόγος»), полагая, что на числах построено все мироздание, на идеи Витрувия (ок. 80-70 гг. до нашей эры — после 13 г. до нашей эры), изложенные в «Десяти книгах об архитектуре» (лат. «De architectura libri decem») о применении математики к искусству архитектуры.
Пропорции золотого сечения
О том, как высчитывать золотые пропорции, рассказал эксперт в сфере фотографии Ренат Мансуров.
«Если взять для примера линию и разделить ее на две части так, чтобы длинная соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной, получится золотая пропорция», – поясняет он. К слову, она равна всегда 1,618, и это так называемое число «фи» обозначается греческой буквой φ — от имени древнегреческого скульптора Фидия.
Ренат Мансуров отмечает, что в правильном прямоугольнике соотношение сторон соответствует золотому сечению.
«Интересен этот прямоугольник тем, что сколько бы ни отрезали от него квадратов, он всегда будет оставлять после себя кусочек с золотым соотношением сторон и так до бесконечности», – говорит Ренат Мансуров.
Золотое сечение в математике
Итальянский астроном и математик Фибоначчи вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Эта закономерность известна как ряд Фибоначчи.
«Если представить два квадрата, поставленных рядом, потом добавить квадрат с удвоенной стороной, то получится квадрат 2 на 2. Далее добавить по спирали против часовой стрелки сумму двух предыдущих квадратов. Получится квадрат с длинной стороны три квадрата, далее добавить к стороне квадрата предыдущую сторону, получится 5, потом 8 потом 13 и 21, каждое последующее число — это сумма сложения с предыдущим, то есть получается такая последовательность, которую и вывел Фибоначчи: 0,1,1,2,3,5,8,13,21 и т.д.», – поясняет Ренат Мансуров.
0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и до бесконечности. А при делении последующего числа на предыдущее получается коэффициент золотого сечения. По мере возрастания чисел соотношение приближается к 1,618. К примеру, числа 3 и 5, их соотношение равно 1,666, а если взять 13 и 21, то получается уже 1,625. Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленное значение 0,62.
А если в каждом квадрате построить дугу из одного угла к другому, то получится так называемая спираль Фибоначчи.
Правило золотого сечения
На практике золотое сечение представляет собой пропорцию, соотношение сторон прямоугольника, отрезков определенной длины, других геометрических форм или сопряженных размерных характеристик реальных объектов.
Метод золотого сечения
«Если построить прямоугольник, используя метод, указанный выше, и встроить в этот прямоугольник линии, используя числа золотого сечения, то получится разграничение прямоугольника несколькими линиями. И если говорить о композиции, то размещая объекты на линиях или их пересечениях, можно максимально выделить эти объекты как смысловые центры, и наоборот, чем дальше от этих точек, тем труднее будет улавливать смысловой центр», – поясняет Ренат Мансуров.
Если же совместить спираль Фибоначчи и эту сетку, то получится практически инструкция по использованию золотого сечения в фотографии, живописи и дизайне.
Где можно увидеть золотое сечение
Если разделить обычное куриное яйцо мысленно пополам в самой широкой его части, то получатся правильные золотые пропорции. Пропорции здания Парфенона в Греции, спирали раковин, пропорции тела человека, спиральные галактики и растения, и еще много всего вокруг.
Природа
«
По словам Рената Мансурова, примеров этих золотых чисел и спиралей найти в природе можно множество. «Распределение семян подсолнуха, спиральные раковины, спиральные галактики, соотношения пропорций человеческого тела, и например, если внимательно посмотреть на нераскрытую еловую шишку или ананас с торца, то можно увидеть эти спирали», – отмечает эксперт.
Свою точку зрения озвучил Максим Господинко.
«У растения есть важная задача — наиболее оптимально расположить свои листья или лепестки, для того чтобы уловить больше солнечного света или просто уместить больше семян. В некоторых случаях есть возможность делать это только по плотной спирали (ананас, еловая шишка, подсолнечник). Кажется, что перед таким растением стоит сложная математическая задача — на какой угол сдвинуть следующую семечку или лепесток, но на самом деле вопрос лишь в том, насколько сильное создается отталкивание от уже существующего элемента.
И так складывается, что угол отклонения от предыдущего листка действительно очень близок к отношению «фи», – комментирует эксперт. – Ни одно рациональное отношение не подходит, потому что при повороте под такими углами возникают колонны-лучи с большими дырами, а как мы знаем, семена подсолнечника уложены красивыми спиралями, число которых как раз соответствует числам из ряда Фибоначчи и дыр там никаких нет».
По словам Максима Господинко, ряд Фибоначчи можно легко образовать, взяв ноль и единицу, а каждое последующее за ними получить из суммы двух предыдущих. «Моделировать растение конечно не умеет, насколько мне известно, и не знает количества рядов спиралей, а усилие отталкивания следующего элемента регулируется поколениями и естественным отбором, но в итоге приходит именно к “фи”», – отмечает специалист.
Названы знаменитости с идеальными пропорциями лица
Человек
Пропорции золотого сечения прослеживаются и на примере тела человека. К золотой формуле приравнивается абсолютно все: кости, ладони и пальцы, пропорции участков на лице, расстояние вытянутых рук по отношению к телу. Пропорции таковы:
- от плеч до макушки к размеру головы = 1:1.618
- от подбородка до верхней губы и от нее до носа = 1:1.618
- от пупка до макушки к отрезку от плеч до макушки = 1:1.618
- от пупка до колен и от колен до ступней = 1:1.618
Искусство
Пирамида Хеопса – единственное сохранившееся классическое чудо света
Множество произведений искусства и архитектурных шедевров сделаны по принципам золотого сечения. Египетские и пирамиды Майя, греческий Парфенон и так далее. Картины известных художников тоже выполнены с учетом правил золотого сечения.
Прослеживаются такие пропорции и в музыкальных произведениях Шуберта, Моцарта, Баха, Шопена и прочих.
«Для дизайнера и художника вопрос о золотом сечении стоит лишь в разрезе более широкой темы — пропорционирования. Не каждый использует этот инструмент, хоть и должен, но часто амбициозный художник, схватившись за “божественную истину”, начинает транслировать лишь её, упуская суть художественного высказывания, передачу образа. Пропорция – лишь инструмент и, очевидно, инструмент не должен идти вперёд задачи. Если образ не понят художником, его невозможно передать», – говорит Максим Господинко. Но тем не менее, переоценить важность этой пропорции сложно. Часто чувствительный художник сам интуитивно может расположить элементы в соответствии с “фи”, также оно является достаточно простым инструментом, чтобы создать изящную композицию даже в самых простых вещах.
Примеры использования в живописи.
© Public DomainКартина Леонардо Да Винчи «Мона Лиза»
Картина Леонардо Да Винчи «Мона Лиза»
1 из 2
Репродукция картины «Девочка на шаре» 1905 г. работы Пабло Пикассо, выставленная в Государственном музее изобразительных искусств им. А.С. Пушкина.
2 из 2
Картина Леонардо Да Винчи «Мона Лиза»
1 из 2
Репродукция картины «Девочка на шаре» 1905 г. работы Пабло Пикассо, выставленная в Государственном музее изобразительных искусств им. А.С. Пушкина.
2 из 2
Примеры использования золотого сечения в дизайне логотипов.
Логотип социальной сети Twitter на экранах мобильного телефона и компьютера.
1 из 2
Логотип компании Apple на стене фирменного магазине на 5-й авеню в Нью-Йорке.
2 из 2
Логотип социальной сети Twitter на экранах мобильного телефона и компьютера.
1 из 2
Логотип компании Apple на стене фирменного магазине на 5-й авеню в Нью-Йорке.
2 из 2
Применение золотого сечения
Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений и создании проекта дома, в современном дизайне интерьера при планировании и зонировании пространства, расстановки мебели и даже цветовом оформлении, а также в ландшафтном дизайне при выкладке закрученных дорожек, расположении растений на клумбах и других элементов.
Так, к примеру, при строительстве квартир и домов отношение самой большой комнаты к площади всей квартиры равно как 0,62 к 1, меньшее помещение делают с таким же соотношением к площади большей комнаты. Так, кухня – к меньшей комнате, прихожая к кухне, санузел к прихожей, а балкон – к санузлу.
Кроме того, с помощью золотого сечения подбирают и цветовое оформление. В интерьере применяют соотношение 10-30-60, основанное на золотом сечении. В пространстве используют три основных цвета: первый – доминирующий, охватывает 60% комнаты (стены и пол). Второй оттенок составляет 30% – мебель. И третий, 10%, приходится на декор.
«
«Существует множество вариантов золотого сечения. Но все они, так или иначе, основаны на числах Фибоначчи. Какие то из них популярны, какие то не очень, но о чем мы говорим сегодня, это то, что выработалось за последние столетия — это явно золотой стандарт, – говорит Ренат Мансуров. – Конечно, нужно понимать, что творчество остается творчеством и отходить от стандарта не возбраняется, но и совсем идти наперекор этим пропорциям не стоит».
По мнению эксперта, теория золотого сечения и «божественных пропорций» довольно популярна, но наука не стоит на месте, и сейчас активно исследуются теории восприятия с научной точки зрения. «То, что работает на практике не одно столетие, однозначно должно напоминать каждый раз о том, что эти пропорции проверены временем и сотнями тысяч творческих людей: фотографы, художники, дизайнеры и архитекторы каждый день работают и используют золотые пропорции в своей работе.
Реальная Вавилонская башня и первая пирамида: самые старые строения в мире
Высчитывать миллиметры и микроны в надежде сделать ваше творчество золотым, наверное, не стоит, но и забывать о приятных для глаза пропорциях наверняка не нужно», – говорит Ренат Мансуров.
Как это делать правильно, каждый решает самостоятельно, существует множество приемов композиции и работы с психологией восприятия, которые вместе могут улучшить работу в разы. «Учитесь правильно и не останавливайтесь в изучении художественных и композиционных приемов, и ваше творчество будет сиять оригинальностью и легкостью восприятия», – советует Ренат Мансуров.
Второе золотое сечение
Второе золотое сечение вытекает из основного сечения и дает отношение 44: 56.
Максим Господинко отмечает, что золотое сечение – не единственная пропорция, приятная глазу человека, есть “серебряное сечение”. Две величины находятся в «серебряном сечении», если отношение суммы меньшей и удвоенной большей величины к большей то же самое, что и отношение большей величины к меньшей. Также можно отметить, что порядок разлинованной в клетку тетради приятнее полного хаоса чистого листа (если не брать пропорцию самого его формата за порядок).
По словам эксперта, пропорция тетрадки в клетку ничем не хуже золотого сечения, но действие на человека она оказывает иное, как будто организуя простейший порядок — один к одному. «Если бы мы использовали такой поворот угла в подсолнухе, то получили бы одну линию семян, в случае с 1/4 — крест. Каждой задаче — свое решение. В случае с растениями им нужно как раз самое иррациональное число. Примечательно, что именно такое число и прослыло божественным», – говорит Максим Господинко.
Мифы о золотом сечении
«Можно спекулировать на тему того, что где-то в глубине восприятия человека лежит именно закономерность ряда Фибоначчи, вероятно, где-то мы так же решали геометрическую задачу поворота на нужный угол по спирали, может быть, всё живое, так или иначе помнит этот опыт. Но чтобы не очаровываться золотым сечением чрезмерно, можно обратить внимание на любовь человека к зигзагам и орнаментам. Далеко не обязательно строить бабушкин ковёр по “фи”, чтобы на него было приятнее смотреть, чем на голую стену, – считает Максим Господинко. – Оказывается, этот вид визуального комфорта обусловлен строением визуального кортекса человеческого мозга, и такие орнаменты, как мы можем увидеть в традиционных культурах, ложатся в него как недостающий кусочек удобного паззла вместо хаотичного визуального потока внешней среды. Резной наличник лучше голых ставень. Кружева лучше минимализма. Природа лучше асфальта. Потому что экономят ресурсы человека, показывая привычные и близкие формы».
Что такое золотое сечение и правда ли оно повсюду
Спойлер: это лишь красивая математическая легенда.
Что такое золотое сечение
Это соотношение двух неравных чисел, при котором большее так же относится к меньшему, как сумма этих чисел к большему. Золотое сечение равно примерно 1,618, или 1,62, если округлить, и обозначается греческой буквой φ, «фи» — от имени древнегреческого скульптора Фидия. Считается, что он использовал такие пропорции при оформлении Парфенона.
Наиболее известные графические представления золотого сечения — это прямоугольник с соотношением сторон примерно 62:48 и построенная в нём спираль.
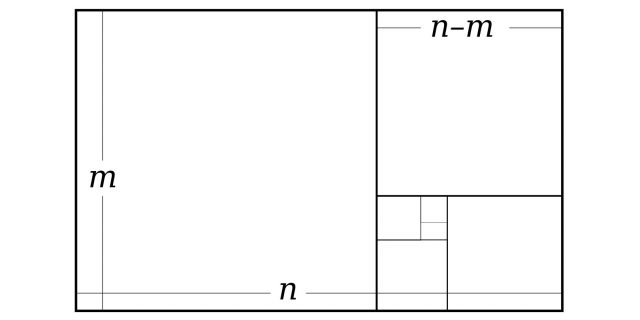
1 / 0
«Золотой прямоугольник» можно разделить на такие же, только меньшего размера. Изображение: Dicklyon / Wikimedia Commons
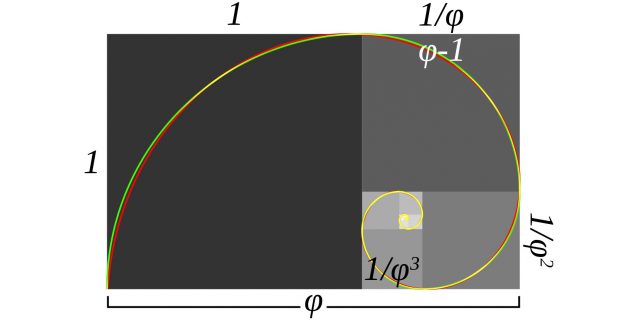
2 / 0
«Золотая спираль» (красная), вписанная в «золотой прямоугольник». Изображение: Silverhammermba & Jahobr / Wikimedia Commons
Золотое сечение тесно связано с числами Фибоначчи. Это ряд чисел, каждое из которых равняется сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Чем дальше продолжается этот ряд, тем ближе соотношение соседних чисел в нём к 1,618. Например, 3/2=1,5; 8/5=1,6, а 34/21= 1,619.
Почему золотое сечение так популярно
Впервые им заинтересовались ещё древнегреческие математики Пифагор и Евклид. Они считали, что на числах построено всё мироздание и с их помощью можно объяснить любой феномен. Неудивительно, что элегантное соотношение так заинтересовало античных мыслителей.
Вслед за ними золотым сечением увлеклись многие выдающиеся учёные и деятели искусства. Например, Леонардо да Винчи, Альбрехт Дюрер, Иоганн Кеплер, Ле Корбюзье, Сальвадор Дали и Ричард Пенроуз.
Его считают «божественной пропорцией»
Название «золотое сечение» придумал немецкий математик XIX века Мартин Ом. До него это соотношение именовали «божественной пропорцией».
Из‑за приписываемых характеристик золотое сечение старались применять как можно чаще. Так, во времена Возрождения это число считалось идеальным способом для выбора размера. «Золотой прямоугольник», например, нередко использовали при создании книг и картин. А линию пояса называли границей золотого сечения человеческого тела.
Некоторые и поныне считают эту пропорцию секретом привлекательности и примером универсальной гармонии, приятной человеческому глазу. Например, о золотом сечении любят говорить пластические хирурги. А ещё это число популярно как никакое другое в математике.
Его можно встретить в природе
Числа Фибоначчи и спирали, подобные золотому сечению, часто обнаруживаются в природе. Например, в количестве лепестков у цветов или форме растений.
Его обнаруживают в произведениях архитектуры и искусства
Например, «божественные пропорции» находят в Парфеноне и египетских пирамидах. Также широко распространено заблуждение, что «Мона Лиза» написана в соответствии с числом φ.
Почему универсальность золотого сечения — миф
Однако при тщательном изучении становится понятно, что эта пропорция не так уж всеобъемлюща.
Божественность золотого сечения преувеличивается
Золотому сечению придают больше значения, чем есть в действительности. Красивые узоры и налёт таинственности сделали из обычного геометрического соотношения математический миф, который, к примеру, очень любят нумерологи.
Чаще всего вещи причисляют к золотому сечению с большими допущениями. Ни о какой точности и математической универсальности в таком случае говорить не приходится. Поэтому при желании можно обнаружить «божественные пропорции» где угодно.
В природе золотое сечение не так уж распространено
Его находят далеко не везде. Например, у маков всегда четыре лепестка, а в ряд Фибоначчи четвёрка не входит. Также нередко встречается четырёхлистный клевер. Раковины морских моллюсков похожи на спираль золотого сечения, но всё-таки другие. У них больше витков, и расстояние между ними меньше. Ни у одного моллюска коэффициент скручивания раковины и близко не равен 1,62. Это видно даже невооружённым глазом:

1 / 0
Спираль морского моллюска. Изображение: Florian Elias Rieser / Wikimedia Commons
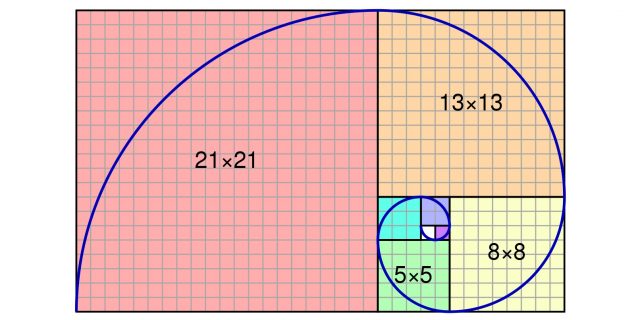
2 / 0
Спираль Фибоначчи, близкая к золотому сечению. Изображение: Jahobr / Wikimedia Commons
В человеческом теле же столько точек, от которых можно производить измерение, что при желании реально найти золотое сечение где угодно. Вот только с большой вероятностью у разных людей «божественную пропорцию» придётся искать в разных местах, так как мы можем сильно отличаться друг от друга.
В искусстве оно тоже встречается не так уж часто
Изучение 565 картин выдающихся художников показало, что в среднем соотношение сторон в работах составляет 1,34. Это явно не дотягивает до золотого сечения. Учёные не находят его даже в произведениях Леонардо да Винчи.
Археологические исследования не подтверждают и того, что древние греки могли использовать золотое сечение при постройке Парфенона. Из более чем 100 памятников древнегреческой архитектуры это число нашлось в пропорциях только четырёх объектов: башни, алтаря, гробницы и надгробия. Не могли пользоваться золотым сечением и древние египтяне, не обладавшие достаточным уровнем технологий, чтобы точно высчитывать пропорции.
Кому золотое сечение может быть полезно на самом деле
Современная математика использует золотое сечение и числа Фибоначчи при описании фракталов — фигур, которые проявляют самоподобие.
Знание о числе φ играет важную роль в изучении хаоса и изменяющихся (динамических) систем. Оно помогает понять, как природа развивается и самоорганизуется.
Также числа Фибоначчи полезны при решении некоторых сложных задач. Например, с помощью этих чисел советский математик Юрий Матиясевич доказал, что не существует универсального алгоритма решения уравнений с как минимум двумя неизвестными.
Читайте также 💆♂️👩🔬
- Продолжите последовательность! 10 мини-задач для разминки мозга
- Как округлять числа
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- Гимнастика для ума: 10 увлекательных задач с числами
- 10 увлекательных задач от советского математика
Число Ф (фи), которое называют золотым сечением или серединой, является одним из самых загадочных терминов в математике и физике. Интересно, что оно часто встречается в повседневной жизни, хотя многие об этом никогда не задумывались. Даже люди, не знакомые с правилом золотого сечения, видят его, сами того не понимая. Проводились эксперименты: испытуемым показывали случайные лица и просили назвать наиболее привлекательные. Таковыми оказывались лица, в которых находили золотые соотношения между различными величинами – шириной лица, глаз, линии бровей, носа. Таким образом, инстинктивно человек видит приближенное к пропорциям, которые считаются идеальными.
Содержание:
- 1 Что такое золотое сечение?
- 2 История золотого сечения
- 3 «Золотые» фигуры
- 4 Золотое сечение в изобразительном искусстве
- 5 Примеры золотого сечения в жизни и в природе
Что такое золотое сечение?
Это пропорция, полученная делением в крайнем и среднем отношении. Также это называют гармоническим делением. Как вычисляется золотая середина? В выражении математическим языком эта величина представляет собой соотношение двух величин a и b, где известно, что а>b, и имеет место такое равенство: a/b=(a+b)/a. Представив, что a и b – это части одного отрезка, можно сказать: отношение меньшей части к большей равно отношению большей части к целому. Золотое сечение обозначают 21-й буквой греческого алфавита – Ф (произносится как «фи»).
Данное число бесконечно, как и Пи, показывающее отношение длины окружности к диаметру. Выглядит оно так: 1.6180339887498948420… Соответственно, округляют Ф до 1,618.
История золотого сечения
У этой величины несколько названий. Среди них – божественная пропорция и асимметричная симметрия. Считается, что в науку метод золотого деления внес Пифагор в VI веке до нашей эры. В свою очередь он узнал об этом у египтян и вавилонян. Ведь то, что они использовали соотношения золотого деления доказывают пропорции пирамид, храмов, барельефов, предметов быта и украшений.
Встречается данное правило и в другой древней архитектуре. Например, пирамида Гизы имеет высоту 146,6 метров, а каждая сторона основания достигает 230,5 метров. Если рассчитать отношение длины стороны к высоте, получаем 1,5717, а это совсем рядом со значением Ф. Греческий скульптор и математик Фидий, живший в V веке до нашей эры с применением правила золотого деления создавал скульптуры для Парфенона. Универсальным связующим звеном математических отношений назвал золотое сечение Платон. А Евклид еще в IV веке до нашей эры увидел золотое сечение в пентаграмме.
С данным понятием непосредственно связана последовательность Фибоначчи. Известный математик создал последовательный ряд чисел, и если взять любые два очередных числа, то их отношение будет очень близко к Ф. При этом по мере возрастания чисел, соотношение всё больше приближается к 1,618. К примеру, если взять 3 и 5, то соотношение равно 1,666, а если 13 и 21, то получается уже 1,625. Равное значению Ф дает отношение 144 и 233.
«Золотые» фигуры
Принцип золотого сечения используется для построения геометрических фигур. И считается, что полученные таким образом фигуры, выглядят наиболее изящными. Это подтверждают многократно проведенные эксперименты. Внимание испытуемых больше привлекают именно такие фигуры.
Самым простым примером является прямоугольник, при вычислении отношения сторон которого получаем значение Ф. Еще один замечательный пример – правильный пятиугольник. Все его диагонали делят друг друга на отрезки, связанные золотой пропорцией, а каждый конец – это золотой треугольник. При вершине такого треугольника образуется угол в 36 градусов, а основание делит боковую сторону в пропорции золотого сечения. Внутри пятиугольника строится пентаграмма.
Древнегреческий ученый Архимед, первым отметил, что если от золотого прямоугольника последовательно отсекать квадраты, соединяя противоположные точки четвертью окружности, получается изящная спираль.
Золотое сечение в изобразительном искусстве
В эпоху Возрождения при создании картин и скульптур великие мастера применяли золотое сечение, чтобы достичь баланс красоты. Наиболее яркими примерами являются творения Леонардо да Винчи. С помощью этого правила художник определял пропорции в работе «Тайная вечеря». Это видно при исследовании размеров стола, стен, элементов интерьера. Также божественная пропорция прослеживается в картинах «Мона Лиза» и «Витрувианский Человек». Такие великие художники, как Микеланджело, Рафаэль, Рембрандт, Сальвадор Дали и другие, использовали золотое сечение при создании своих шедевров.
Примеры золотого сечения в жизни и в природе
Ежедневно мы можем наблюдать идеальные пропорции:
- Грудная и брюшная части тела бабочки соотносятся в золотой пропорции. А при сложенных крыльях это прекрасное создание представляет собой правильный треугольник с равными сторонами.
- У стрекозы длины хвоста и корпуса относятся так же, как общая длина тела к хвосту.
- В пропорциях тела ящерицы также прослеживается данный принцип.
- Большинство яиц птиц можно вписать в золотой прямоугольник.
- Последовательность Фибоначчи видна в развитии растений, в расположении чешуек в шишках, зерен в подсолнухах.
- Спирально растет бараний рог, плетет паутину паук.
- Интересно, что если напугать стадо северных оленей, то животные будут разбегаться по спирали.
- В форме двойной спирали представлена молекула ДНК.
- Цветки разных растений, а также морские звезды имеют форму правильного пятиугольника.
Как видно, примеров с правильными пропорциями в природе и повседневной жизни предостаточно. Не даром золотое сечение называют божественной пропорцией. Вероятно, именно этим правилом руководствовался создатель в процессе заполнения Вселенной живыми и неживыми объектами. То, что соответствует этому правилу, кажется нам наиболее привлекательным.
В мире много интересных вещей, изучение нового делает нас умнее, способствует развитию мозга и мышления. Советуем вам обязательно находить время на познание нового. А чтобы было легче усваивать и запоминать большие объемы информации, рекомендуем тренажеры Викиум. Регулярно используя их для тренировок мозга, вы сможете улучшить память, внимательность, логику и аналитические способности.

Line segments in the golden ratio |
|
| Representations | |
|---|---|
| Decimal | 1.618033988749894…[1] |
| Algebraic form |  |
| Continued fraction |  |
| Binary | 1.10011110001101110111… |
| Hexadecimal | 1.9E3779B97F4A7C15… |
A golden rectangle with long side a and short side b (shaded red, right) and a square with sides of length a (shaded blue, left) combine to form a similar golden rectangle with long side a + b and short side a. This illustrates the relationship
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities 


where the Greek letter phi (




The golden ratio was called the extreme and mean ratio by Euclid,[2] and the divine proportion by Luca Pacioli,[3] and also goes by several other names.[b]
Mathematicians have studied the golden ratio’s properties since antiquity. It is the ratio of a regular pentagon’s diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron.[7] A golden rectangle—that is, a rectangle with an aspect ratio of 
Some 20th-century artists and architects, including Le Corbusier and Salvador Dalí, have proportioned their works to approximate the golden ratio, believing it to be aesthetically pleasing. These uses often appear in the form of a golden rectangle.
Calculation
Two quantities 


One method for finding a closed form for 

Therefore,
Multiplying by 
which can be rearranged to
The quadratic formula yields two solutions:

Because 


History
According to Mario Livio,
Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. … Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.[11]
— The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number
Ancient Greek mathematicians first studied the golden ratio because of its frequent appearance in geometry;[12] the division of a line into «extreme and mean ratio» (the golden section) is important in the geometry of regular pentagrams and pentagons.[13] According to one story, 5th-century BC mathematician Hippasus discovered that the golden ratio was neither a whole number nor a fraction (it is irrational), surprising Pythagoreans.[14] Euclid’s Elements (c. 300 BC) provides several propositions and their proofs employing the golden ratio,[15][c] and contains its first known definition which proceeds as follows:[16]
A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.[17][d]
The golden ratio was studied peripherally over the next millennium. Abu Kamil (c. 850–930) employed it in his geometric calculations of pentagons and decagons; his writings influenced that of Fibonacci (Leonardo of Pisa) (c. 1170–1250), who used the ratio in related geometry problems but did not observe that it was connected to the Fibonacci numbers.[19]
Luca Pacioli named his book Divina proportione (1509) after the ratio; the book, largely plagiarized from Piero della Francesca, explored its properties including its appearance in some of the Platonic solids.[20][21] Leonardo da Vinci, who illustrated Pacioli’s book, called the ratio the sectio aurea (‘golden section’).[22] Though it is often said that Pacioli advocated the golden ratio’s application to yield pleasing, harmonious proportions, Livio points out that the interpretation has been traced to an error in 1799, and that Pacioli actually advocated the Vitruvian system of rational proportions.[23] Pacioli also saw Catholic religious significance in the ratio, which led to his work’s title. 16th-century mathematicians such as Rafael Bombelli solved geometric problems using the ratio.[24]
German mathematician Simon Jacob (d. 1564) noted that consecutive Fibonacci numbers converge to the golden ratio;[25] this was rediscovered by Johannes Kepler in 1608.[26] The first known decimal approximation of the (inverse) golden ratio was stated as «about 
Geometry has two great treasures: one is the theorem of Pythagoras, the other the division of a line into extreme and mean ratio. The first we may compare to a mass of gold, the second we may call a precious jewel.[28]
18th-century mathematicians Abraham de Moivre, Nicolaus I Bernoulli, and Leonhard Euler used a golden ratio-based formula which finds the value of a Fibonacci number based on its placement in the sequence; in 1843, this was rediscovered by Jacques Philippe Marie Binet, for whom it was named «Binet’s formula».[29] Martin Ohm first used the German term goldener Schnitt (‘golden section’) to describe the ratio in 1835.[30] James Sully used the equivalent English term in 1875.[31]
By 1910, inventor Mark Barr began using the Greek letter phi (

The zome construction system, developed by Steve Baer in the late 1960s, is based on the symmetry system of the icosahedron/dodecahedron, and uses the golden ratio ubiquitously. Between 1973 and 1974, Roger Penrose developed Penrose tiling, a pattern related to the golden ratio both in the ratio of areas of its two rhombic tiles and in their relative frequency within the pattern.[36] This gained in interest after Dan Shechtman’s Nobel-winning 1982 discovery of quasicrystals with icosahedral symmetry, which were soon afterward explained through analogies to the Penrose tiling.[37]
Mathematics
Irrationality
The golden ratio is an irrational number. Below are two short proofs of irrationality:
Contradiction from an expression in lowest terms
If φ were rational, then it would be the ratio of sides of a rectangle with integer sides (the rectangle comprising the entire diagram). But it would also be a ratio of integer sides of the smaller rectangle (the rightmost portion of the diagram) obtained by deleting a square. The sequence of decreasing integer side lengths formed by deleting squares cannot be continued indefinitely because the positive integers have a lower bound, so φ cannot be rational.
Recall that:
the whole is the longer part plus the shorter part;
the whole is to the longer part as the longer part is to the shorter part.
If we call the whole 




To say that the golden ratio 










By irrationality of √5
Another short proof – perhaps more commonly known – of the irrationality of the golden ratio makes use of the closure of rational numbers under addition and multiplication. If 

Minimal polynomial
The golden ratio φ and its negative reciprocal −φ−1 are the two roots of the quadratic polynomial x2 − x − 1. The golden ratio’s negative −φ and reciprocal φ−1 are the two roots of the quadratic polynomial x2 + x − 1.
The golden ratio is also an algebraic number and even an algebraic integer. It has minimal polynomial
This quadratic polynomial has two roots, 

The golden ratio is also closely related to the polynomial
which has roots 

Golden ratio conjugate and powers
The conjugate root to the minimal polynomial 
The absolute value of this quantity (

This illustrates the unique property of the golden ratio among positive numbers, that
or its inverse:
The conjugate and the defining quadratic polynomial relationship lead to decimal values that have their fractional part in common with 
The sequence of powers of 




any power of 
As a result, one can easily decompose any power of 


If 
Continued fraction and square root
Approximations to the reciprocal golden ratio by finite continued fractions, or ratios of Fibonacci numbers
The formula 
It is in fact the simplest form of a continued fraction, alongside its reciprocal form:
The convergents of these continued fractions (














This means that the constant 
A continued square root form for 

Relationship to Fibonacci and Lucas numbers
Fibonacci numbers and Lucas numbers have an intricate relationship with the golden ratio. In the Fibonacci sequence, each number is equal to the sum of the preceding two, starting with the base sequence 













The sequence of Lucas numbers (not to be confused with the generalized Lucas sequences, of which this is part) is like the Fibonacci sequence, in-which each term is the sum of the previous two, however instead starts with 













Exceptionally, the golden ratio is equal to the limit of the ratios of successive terms in the Fibonacci sequence and sequence of Lucas numbers:[42]
In other words, if a Fibonacci and Lucas number is divided by its immediate predecessor in the sequence, the quotient approximates 
For example, 

These approximations are alternately lower and higher than 

Closed-form expressions for the Fibonacci and Lucas sequences that involve the golden ratio are:
Combining both formulas above, one obtains a formula for 
Between Fibonacci and Lucas numbers one can deduce 
Indeed, much stronger statements are true:
,
.
These values describe 

Successive powers of the golden ratio obey the Fibonacci recurrence, i.e. 
The reduction to a linear expression can be accomplished in one step by using:
This identity allows any polynomial in 
Consecutive Fibonacci numbers can also be used to obtain a similar formula for the golden ratio, here by infinite summation:
In particular, the powers of 


and so forth.[43] The Lucas numbers also directly generate powers of the golden ratio; for 
Rooted in their interconnecting relationship with the golden ratio is the notion that the sum of third consecutive Fibonacci numbers equals a Lucas number, that is 

Both the Fibonacci sequence and the sequence of Lucas numbers can be used to generate approximate forms of the golden spiral (which is a special form of a logarithmic spiral) using quarter-circles with radii from these sequences, differing only slightly from the true golden logarithmic spiral. Fibonacci spiral is generally the term used for spirals that approximate golden spirals using Fibonacci number-sequenced squares and quarter-circles.
Geometry
The golden ratio features prominently in geometry. For example, it is intrinsically involved in the internal symmetry of the pentagon, and extends to form part of the coordinates of the vertices of a regular dodecahedron, as well as those of a 5-cell. It features in the Kepler triangle and Penrose tilings too, as well as in various other polytopes.
Construction
Dividing a line segment by interior division (top) and exterior division (bottom) according to the golden ratio.
Dividing by interior division
- Having a line segment
construct a perpendicular
at point
with
half the length of
Draw the hypotenuse
- Draw an arc with center
and radius
This arc intersects the hypotenuse
at point
- Draw an arc with center
and radius
This arc intersects the original line segment
at point
Point
divides the original line segment
into line segments
and
with lengths in the golden ratio.
Dividing by exterior division
- Draw a line segment
and construct off the point
a segment
perpendicular to
and with the same length as
- Do bisect the line segment
with
- A circular arc around
with radius
intersects in point
the straight line through points
and
(also known as the extension of
). The ratio of
to the constructed segment
is the golden ratio.
Application examples you can see in the articles Pentagon with a given side length, Decagon with given circumcircle and Decagon with a given side length.
Both of the above displayed different algorithms produce geometric constructions that determine two aligned line segments where the ratio of the longer one to the shorter one is the golden ratio.
Golden angle
When two angles that make a full circle have measures in the golden ratio, the smaller is called the golden angle, with measure 
This angle occurs in patterns of plant growth as the optimal spacing of leaf shoots around plant stems so that successive leaves do not block sunlight from the leaves below them.[44]
Pentagonal symmetry system
Pentagon and pentagram
A pentagram colored to distinguish its line segments of different lengths. The four lengths are in golden ratio to one another.
In a regular pentagon the ratio of a diagonal to a side is the golden ratio, while intersecting diagonals section each other in the golden ratio. The golden ratio properties of a regular pentagon can be confirmed by applying Ptolemy’s theorem to the quadrilateral formed by removing one of its vertices. If the quadrilateral’s long edge and diagonals are 



The diagonal segments of a pentagon form a pentagram, or five-pointed star polygon, whose geometry is quintessentially described by 

Pentagonal and pentagrammic geometry permits us to calculate the following values for 
Golden triangle and golden gnomon
A golden triangle ABC can be subdivided by an angle bisector into a smaller golden triangle CXB and a golden gnomon XAC.
The triangle formed by two diagonals and a side of a regular pentagon is called a golden triangle or sublime triangle. It is an acute isosceles triangle with apex angle 36° and base angles 72°.[45] Its two equal sides are in the golden ratio to its base.[46] The triangle formed by two sides and a diagonal of a regular pentagon is called a golden gnomon. It is an obtuse isosceles triangle with apex angle 108° and base angle 36°. Its base is in the golden ratio to its two equal sides.[46] The pentagon can thus be subdivided into two golden gnomons and a central golden triangle. The five points of a regular pentagram are golden triangles,[46] as are the ten triangles formed by connecting the vertices of a regular decagon to its center point.[47]
Bisecting one of the base angles of the golden triangle subdivides it into a smaller golden triangle and a golden gnomon. Analogously, any acute isosceles triangle can be subdivided into a similar triangle and an obtuse isosceles triangle, but the golden triangle is the only one for which this subdivision is made by the angle bisector, because it is the only isosceles triangle whose base angle is twice its apex angle. The angle bisector of the golden triangle subdivides the side that it meets in the golden ratio, and the areas of the two subdivided pieces are also in the golden ratio.[46]
If the apex angle of the golden gnomon is trisected, the trisector again subdivides it into a smaller golden gnomon and a golden triangle. The trisector subdivides the base in the golden ratio, and the two pieces have areas in the golden ratio. Analogously, any obtuse triangle can be subdivided into a similar triangle and an acute isosceles triangle, but the golden gnomon is the only one for which this subdivision is made by the angle trisector, because it is the only isosceles triangle whose apex angle is three times its base angle.[46]
Penrose tilings
The kite and dart tiles of the Penrose tiling. The colored arcs divide each edge in the golden ratio; when two tiles share an edge, their arcs must match.
The golden ratio appears prominently in the Penrose tiling, a family of aperiodic tilings of the plane developed by Roger Penrose, inspired by Johannes Kepler’s remark that pentagrams, decagons, and other shapes could fill gaps that pentagonal shapes alone leave when tiled together.[48] Several variations of this tiling have been studied, all of whose prototiles exhibit the golden ratio:
- Penrose’s original version of this tiling used four shapes: regular pentagons and pentagrams, «boat» figures with three points of a pentagram, and «diamond» shaped rhombi.[49]
- The kite and dart Penrose tiling uses kites with three interior angles of 72° and one interior angle of 144°, and darts, concave quadrilaterals with two interior angles of 36°, one of 72°, and one non-convex angle of 216°. Special matching rules restrict how the tiles can meet at any edge, resulting in seven combinations of tiles at any vertex. Both the kites and darts have sides of two lengths, in the golden ratio to each other. The areas of these two tile shapes are also in the golden ratio to each other.[48]
- The kite and dart can each be cut on their symmetry axes into a pair of golden triangles and golden gnomons, respectively. With suitable matching rules, these triangles, called in this context Robinson triangles, can be used as the prototiles for a form of the Penrose tiling.[48][50]
- The rhombic Penrose tiling contains two types of rhombus, a thin rhombus with angles of 36° and 144°, and a thick rhombus with angles of 72° and 108°. All side lengths are equal, but the ratio of the length of sides to the short diagonal in the thin rhombus equals
, as does the ratio of the sides of to the long diagonal of the thick rhombus. As with the kite and dart tiling, the areas of the two rhombi are in the golden ratio to each other. Again, these rhombi can be decomposed into pairs of Robinson triangles.[48]
Original four-tile Penrose tiling
Rhombic Penrose tiling
In triangles and quadrilaterals
Odom’s construction
Odom’s construction: AB : BC = AC : AB = φ : 1
George Odom found a construction for 
Kepler triangle
Geometric progression of areas of squares on the sides of a Kepler triangle
An isosceles triangle formed from two Kepler triangles maximizes the ratio of its inradius to side length
The Kepler triangle, named after Johannes Kepler, is the unique right triangle with sides in geometric progression:

These side lengths are the three Pythagorean means of the two numbers 

Among isosceles triangles, the ratio of inradius to side length is maximized for the triangle formed by two reflected copies of the Kepler triangle, sharing the longer of their two legs.[52] The same isosceles triangle maximizes the ratio of the radius of a semicircle on its base to its perimeter.[53]
For a Kepler triangle with smallest side length 
Golden rectangle
To construct a golden rectangle with only a straightedge and compass in four simple steps:
| Draw a square. |
| Draw a line from the midpoint of one side of the square to an opposite corner. |
| Use that line as the radius to draw an arc that defines the height of the rectangle. |
| Complete the golden rectangle. |
The golden ratio proportions the adjacent side lengths of a golden rectangle in 

Golden rhombus
A golden rhombus is a rhombus whose diagonals are in proportion to the golden ratio, most commonly 
The lengths of its short and long diagonals 


Its area, in terms of 

Its inradius, in terms of side 
Golden rhombi feature in the rhombic triacontahedron (see section below). They also are found in the golden rhombohedron, the Bilinski dodecahedron,[57] and the rhombic hexecontahedron.[56]
Golden spiral
The golden spiral (red) and its approximation by quarter-circles (green), with overlaps shown in yellow
A logarithmic spiral whose radius grows by the golden ratio per 108° of turn, surrounding nested golden isosceles triangles. This is a different spiral from the golden spiral, which grows by the golden ratio per 90° of turn.[58]
Logarithmic spirals are self-similar spirals where distances covered per turn are in geometric progression. A logarithmic spiral whose radius increases by a factor of the golden ratio for each quarter-turn is called the golden spiral. These spirals can be approximated by quarter-circles that grow by the golden ratio,[59] or their approximations generated from Fibonacci numbers,[60] often depicted inscribed within a spiraling pattern of squares growing in the same ratio. The exact logarithmic spiral form of the golden spiral can be described by the polar equation with 
Not all logarithmic spirals are connected to the golden ratio, and not all spirals that are connected to the golden ratio are the same shape as the golden spiral. For instance, a different logarithmic spiral, encasing a nested sequence of golden isosceles triangles, grows by the golden ratio for each 108° that it turns, instead of the 90° turning angle of the golden spiral.[58] Another variation, called the «better golden spiral», grows by the golden ratio for each half-turn, rather than each quarter-turn.[59]
In the dodecahedron and icosahedron
| Cartesian coordinates of the dodecahedron : | |
| (±1, ±1, ±1) | |
| (0, ±φ, ±1/φ) | |
| (±1/φ, 0, ±φ) | |
| (±φ, ±1/φ, 0) | |
| A nested cube inside the dodecahedron is represented with dotted lines. |
The regular dodecahedron and its dual polyhedron the icosahedron are Platonic solids whose dimensions are related to the golden ratio. An icosahedron is made of 


For a dodecahedron of side 






While for an icosahedron of side 



The volume and surface area of the dodecahedron can be expressed in terms of 


As well as for the icosahedron:

These geometric values can be calculated from their Cartesian coordinates, which also can be given using formulas involving 


Sets of three golden rectangles intersect perpendicularly inside dodecahedra and icosahedra, forming Borromean rings.[62][55] In dodecahedra, pairs of opposing vertices in golden rectangles meet the centers of pentagonal faces, and in icosahedra, they meet at its vertices. In all, the three golden rectangles contain 

A cube can be inscribed in a regular dodecahedron, with some of the diagonals of the pentagonal faces of the dodecahedron serving as the cube’s edges; therefore, the edge lengths are in the golden ratio. The cube’s volume is 



Other polyhedra are related to the dodecahedron and icosahedron or their symmetries, and therefore have corresponding relations to the golden ratio. These include the compound of five cubes, compound of five octahedra, compound of five tetrahedra, the compound of ten tetrahedra, rhombic triacontahedron, icosidodecahedron, truncated icosahedron, truncated dodecahedron, and rhombicosidodecahedron, rhombic enneacontahedron, and Kepler-Poinsot polyhedra, and rhombic hexecontahedron. In four dimensions, the dodecahedron and icosahedron appear as faces of the 120-cell and 600-cell, which again have dimensions related to the golden ratio.
Other properties
The golden ratio’s decimal expansion can be calculated via root-finding methods, such as Newton’s method or Halley’s method, on the equation 














In the complex plane, the fifth roots of unity 



![{textstyle mathbb {Z} [varphi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c19ab3d8278828be7f591bad1dc4482e4aaac6d)
This also holds for the remaining tenth roots of unity satisfying 
For the gamma function 



When the golden ratio is used as the base of a numeral system (see golden ratio base, sometimes dubbed phinary or 
![{displaystyle mathbb {Z} [varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f984c2710477c64fca0f16a71928134bdb8201)


The golden ratio also appears in hyperbolic geometry, as the maximum distance from a point on one side of an ideal triangle to the closer of the other two sides: this distance, the side length of the equilateral triangle formed by the points of tangency of a circle inscribed within the ideal triangle, is 
The golden ratio appears in the theory of modular functions as well. For 
Then
and
where 







Applications and observations
Architecture
The Swiss architect Le Corbusier, famous for his contributions to the modern international style, centered his design philosophy on systems of harmony and proportion. Le Corbusier’s faith in the mathematical order of the universe was closely bound to the golden ratio and the Fibonacci series, which he described as «rhythms apparent to the eye and clear in their relations with one another. And these rhythms are at the very root of human activities. They resound in man by an organic inevitability, the same fine inevitability which causes the tracing out of the Golden Section by children, old men, savages and the learned.»[70][71]
Le Corbusier explicitly used the golden ratio in his Modulor system for the scale of architectural proportion. He saw this system as a continuation of the long tradition of Vitruvius, Leonardo da Vinci’s «Vitruvian Man», the work of Leon Battista Alberti, and others who used the proportions of the human body to improve the appearance and function of architecture.
In addition to the golden ratio, Le Corbusier based the system on human measurements, Fibonacci numbers, and the double unit. He took suggestion of the golden ratio in human proportions to an extreme: he sectioned his model human body’s height at the navel with the two sections in golden ratio, then subdivided those sections in golden ratio at the knees and throat; he used these golden ratio proportions in the Modulor system. Le Corbusier’s 1927 Villa Stein in Garches exemplified the Modulor system’s application. The villa’s rectangular ground plan, elevation, and inner structure closely approximate golden rectangles.[72]
Another Swiss architect, Mario Botta, bases many of his designs on geometric figures. Several private houses he designed in Switzerland are composed of squares and circles, cubes and cylinders. In a house he designed in Origlio, the golden ratio is the proportion between the central section and the side sections of the house.[73]
Art
Leonardo da Vinci’s illustrations of polyhedra in Pacioli’s Divina proportione have led some to speculate that he incorporated the golden ratio in his paintings. But the suggestion that his Mona Lisa, for example, employs golden ratio proportions, is not supported by Leonardo’s own writings.[74] Similarly, although Leonardo’s Vitruvian Man is often shown in connection with the golden ratio, the proportions of the figure do not actually match it, and the text only mentions whole number ratios.[75][76]
Salvador Dalí, influenced by the works of Matila Ghyka,[77] explicitly used the golden ratio in his masterpiece, The Sacrament of the Last Supper. The dimensions of the canvas are a golden rectangle. A huge dodecahedron, in perspective so that edges appear in golden ratio to one another, is suspended above and behind Jesus and dominates the composition.[74][78]
A statistical study on 565 works of art of different great painters, performed in 1999, found that these artists had not used the golden ratio in the size of their canvases. The study concluded that the average ratio of the two sides of the paintings studied is 







Depiction of the proportions in a medieval manuscript. According to Jan Tschichold: «Page proportion 2:3. Margin proportions 1:1:2:3. Text area proportioned in the Golden Section.»[81]
Books and design
According to Jan Tschichold,
There was a time when deviations from the truly beautiful page proportions

and the Golden Section were rare. Many books produced between 1550 and 1770 show these proportions exactly, to within half a millimeter.[82]
According to some sources, the golden ratio is used in everyday design, for example in the proportions of playing cards, postcards, posters, light switch plates, and widescreen televisions.[83]
Flags
The aspect ratio (width to height ratio) of the flag of Togo was intended to be the golden ratio, according to its designer.[84]
Music
Ernő Lendvai analyzes Béla Bartók’s works as being based on two opposing systems, that of the golden ratio and the acoustic scale,[85] though other music scholars reject that analysis.[86] French composer Erik Satie used the golden ratio in several of his pieces, including Sonneries de la Rose+Croix. The golden ratio is also apparent in the organization of the sections in the music of Debussy’s Reflets dans l’eau (Reflections in Water), from Images (1st series, 1905), in which «the sequence of keys is marked out by the intervals 34, 21, 13 and 8, and the main climax sits at the phi position».[87]
The musicologist Roy Howat has observed that the formal boundaries of Debussy’s La Mer correspond exactly to the golden section.[88] Trezise finds the intrinsic evidence «remarkable», but cautions that no written or reported evidence suggests that Debussy consciously sought such proportions.[89]
Music theorists including Hans Zender and Heinz Bohlen have experimented with the 833 cents scale, a musical scale based on using the golden ratio as its fundamental musical interval. When measured in cents, a logarithmic scale for musical intervals, the golden ratio is approximately 833.09 cents.[90]
Nature
Johannes Kepler wrote that «the image of man and woman stems from the divine proportion. In my opinion, the propagation of plants and the progenitive acts of animals are in the same ratio».[91]
The psychologist Adolf Zeising noted that the golden ratio appeared in phyllotaxis and argued from these patterns in nature that the golden ratio was a universal law.[92] Zeising wrote in 1854 of a universal orthogenetic law of «striving for beauty and completeness in the realms of both nature and art».[93]
However, some have argued that many apparent manifestations of the golden ratio in nature, especially in regard to animal dimensions, are fictitious.[94]
Physics
The quasi-one-dimensional Ising ferromagnet CoNb2O6 (cobalt niobate) has 8 predicted excitation states (with E8 symmetry), that when probed with neutron scattering, showed its lowest two were in golden ratio. Specifically, these quantum phase transitions during spin excitation, which occur at near absolute zero temperature, showed pairs of kinks in its ordered-phase to spin-flips in its paramagnetic phase; revealing, just below its critical field, a spin dynamics with sharp modes at low energies approaching the golden mean.[95]
Optimization
There is no known general algorithm to arrange a given number of nodes evenly on a sphere, for any of several definitions of even distribution (see, for example, Thomson problem or Tammes problem). However, a useful approximation results from dividing the sphere into parallel bands of equal surface area and placing one node in each band at longitudes spaced by a golden section of the circle, i.e. 
The golden ratio is a critical element to golden-section search as well.
Disputed observations
Examples of disputed observations of the golden ratio include the following:
Nautilus shells are often erroneously claimed to be golden-proportioned.
- Specific proportions in the bodies of vertebrates (including humans) are often claimed to be in the golden ratio; for example the ratio of successive phalangeal and metacarpal bones (finger bones) has been said to approximate the golden ratio. There is a large variation in the real measures of these elements in specific individuals, however, and the proportion in question is often significantly different from the golden ratio.[97][98]
- The shells of mollusks such as the nautilus are often claimed to be in the golden ratio.[99] The growth of nautilus shells follows a logarithmic spiral, and it is sometimes erroneously claimed that any logarithmic spiral is related to the golden ratio,[100] or sometimes claimed that each new chamber is golden-proportioned relative to the previous one.[101] However, measurements of nautilus shells do not support this claim.[102]
- Historian John Man states that both the pages and text area of the Gutenberg Bible were «based on the golden section shape». However, according to his own measurements, the ratio of height to width of the pages is
[103]
- Studies by psychologists, starting with Gustav Fechner c. 1876,[104] have been devised to test the idea that the golden ratio plays a role in human perception of beauty. While Fechner found a preference for rectangle ratios centered on the golden ratio, later attempts to carefully test such a hypothesis have been, at best, inconclusive.[105][74]
- In investing, some practitioners of technical analysis use the golden ratio to indicate support of a price level, or resistance to price increases, of a stock or commodity; after significant price changes up or down, new support and resistance levels are supposedly found at or near prices related to the starting price via the golden ratio.[106] The use of the golden ratio in investing is also related to more complicated patterns described by Fibonacci numbers (e.g. Elliott wave principle and Fibonacci retracement). However, other market analysts have published analyses suggesting that these percentages and patterns are not supported by the data.[107]
Egyptian pyramids
The Great Pyramid of Giza (also known as the Pyramid of Cheops or Khufu) has been analyzed by pyramidologists as having a doubled Kepler triangle as its cross-section. If this theory were true, the golden ratio would describe the ratio of distances from the midpoint of one of the sides of the pyramid to its apex, and from the same midpoint to the center of the pyramid’s base. However, imprecision in measurement caused in part by the removal of the outer surface of the pyramid makes it impossible to distinguish this theory from other numerical theories of the proportions of the pyramid, based on pi or on whole-number ratios. The consensus of modern scholars is that this pyramid’s proportions are not based on the golden ratio, because such a basis would be inconsistent both with what is known about Egyptian mathematics from the time of construction of the pyramid, and with Egyptian theories of architecture and proportion used in their other works.[108]
The Parthenon
Many of the proportions of the Parthenon are alleged to exhibit the golden ratio, but this has largely been discredited.[109]
The Parthenon’s façade (c. 432 BC) as well as elements of its façade and elsewhere are said by some to be circumscribed by golden rectangles.[110] Other scholars deny that the Greeks had any aesthetic association with golden ratio. For example, Keith Devlin says, «Certainly, the oft repeated assertion that the Parthenon in Athens is based on the golden ratio is not supported by actual measurements. In fact, the entire story about the Greeks and golden ratio seems to be without foundation.»[111] Midhat J. Gazalé affirms that «It was not until Euclid … that the golden ratio’s mathematical properties were studied.»[112]
From measurements of 15 temples, 18 monumental tombs, 8 sarcophagi, and 58 grave stelae from the fifth century BC to the second century AD, one researcher concluded that the golden ratio was totally absent from Greek architecture of the classical fifth century BC, and almost absent during the following six centuries.[113]
Later sources like Vitruvius (first century BC) exclusively discuss proportions that can be expressed in whole numbers, i.e. commensurate as opposed to irrational proportions.
Modern art
The Section d’Or (‘Golden Section’) was a collective of painters, sculptors, poets and critics associated with Cubism and Orphism.[114] Active from 1911 to around 1914, they adopted the name both to highlight that Cubism represented the continuation of a grand tradition, rather than being an isolated movement, and in homage to the mathematical harmony associated with Georges Seurat.[115] (Several authors have claimed that Seurat employed the golden ratio in his paintings, but Seurat’s writings and paintings suggest that he employed simple whole-number ratios and any approximation of the golden ratio was coincidental.)[116] The Cubists observed in its harmonies, geometric structuring of motion and form, «the primacy of idea over nature», «an absolute scientific clarity of conception».[117] However, despite this general interest in mathematical harmony, whether the paintings featured in the celebrated 1912 Salon de la Section d’Or exhibition used the golden ratio in any compositions is more difficult to determine. Livio, for example, claims that they did not,[118] and Marcel Duchamp said as much in an interview.[119] On the other hand, an analysis suggests that Juan Gris made use of the golden ratio in composing works that were likely, but not definitively, shown at the exhibition.[119][120] Art historian Daniel Robbins has argued that in addition to referencing the mathematical term, the exhibition’s name also refers to the earlier Bandeaux d’Or group, with which Albert Gleizes and other former members of the Abbaye de Créteil had been involved.[121]
Piet Mondrian has been said to have used the golden section extensively in his geometrical paintings,[122] though other experts (including critic Yve-Alain Bois) have discredited these claims.[74][123]
See also
- List of works designed with the golden ratio
- Metallic mean
- Plastic number
- Sacred geometry
- Supergolden ratio
References
Explanatory footnotes
- ^ If the constraint on
and
each being greater than zero is lifted, then there are actually two solutions, one positive and one negative, to this equation.
is defined as the positive solution. The negative solution is
The sum of the two solutions is
, and the product of the two solutions is
.
- ^ Other names include the golden mean, golden section,[4] golden cut,[5] golden proportion, golden number,[6] medial section, and divine section.
- ^ Euclid, Elements, Book II, Proposition 11; Book IV, Propositions 10–11; Book VI, Proposition 30; Book XIII, Propositions 1–6, 8–11, 16–18.
- ^ «῎Ακρον καὶ μέσον λόγον εὐθεῖα τετμῆσθαι λέγεται, ὅταν ᾖ ὡς ἡ ὅλη πρὸς τὸ μεῖζον τμῆμα, οὕτως τὸ μεῖζον πρὸς τὸ ἔλαττὸν.»[18]
- ^ After Classical Greek sculptor Phidias (c. 490–430 BC);[33] Barr later wrote that he thought it unlikely that Phidias actually used the golden ratio.[34]
Citations
- ^ a b c Sloane, N. J. A. (ed.). «Sequence A001622 (Decimal expansion of golden ratio phi (or tau) = (1 + sqrt(5))/2)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^
Euclid. «Book 6, Definition 3». Elements. - ^
Pacioli, Luca (1509). De divina proportione. Venice: Luca Paganinem de Paganinus de Brescia (Antonio Capella). - ^ Livio 2002, pp. 3, 81.
- ^
Summerson, John (1963). Heavenly Mansions and Other Essays on Architecture. New York: W.W. Norton. p. 37.And the same applies in architecture, to the rectangles representing these and other ratios (e.g., the ‘golden cut’). The sole value of these ratios is that they are intellectually fruitful and suggest the rhythms of modular design.
- ^ Herz-Fischler 1998.
- ^ Herz-Fischler 1998, pp. 20–25.
- ^
Strogatz, Steven (2012-09-24). «Me, Myself, and Math: Proportion Control». The New York Times. - ^
Schielack, Vincent P. (1987). «The Fibonacci Sequence and the Golden Ratio». The Mathematics Teacher. 80 (5): 357–358. doi:10.5951/MT.80.5.0357. JSTOR 27965402. This source contains an elementary derivation of the golden ratio’s value. - ^
Peters, J. M. H. (1978). «An Approximate Relation between π and the Golden Ratio». The Mathematical Gazette. 62 (421): 197–198. doi:10.2307/3616690. - ^ Livio 2002, p. 6.
- ^ Livio 2002, p. 4: «… line division, which Euclid defined for … purely geometrical purposes …»
- ^ Livio 2002, pp. 7–8.
- ^ Livio 2002, pp. 4–5.
- ^ Livio 2002, p. 78.
- ^
Hemenway, Priya (2005). Divine Proportion: Phi In Art, Nature, and Science. New York: Sterling. pp. 20–21. - ^ Livio 2002, p. 3.
- ^
Euclid (2007). Euclid’s Elements of Geometry. Translated by Fitzpatrick, Richard. p. 156. ISBN 978-0615179841. - ^ Livio 2002, pp. 88–96.
- ^
Mackinnon, Nick (1993). «The Portrait of Fra Luca Pacioli». The Mathematical Gazette. 77 (479): 130–219. doi:10.2307/3619717. - ^ Livio 2002, pp. 131–132.
- ^
Baravalle, H. V. (1948). «The geometry of the pentagon and the golden section». Mathematics Teacher. 41: 22–31. doi:10.5951/MT.41.1.0022. - ^ Livio 2002, pp. 134–135.
- ^ Livio 2002, p. 141.
- ^
Schreiber, Peter (1995). «A Supplement to J. Shallit’s Paper ‘Origins of the Analysis of the Euclidean Algorithm’«. Historia Mathematica. 22 (4): 422–424. doi:10.1006/hmat.1995.1033. - ^ Livio 2002, pp. 151–152.
- ^
O’Connor, John J.; Robertson, Edmund F. (2001). «The Golden Ratio». MacTutor History of Mathematics archive. Retrieved 2007-09-18. - ^
Fink, Karl (1903). A Brief History of Mathematics. Translated by Beman, Wooster Woodruff; Smith, David Eugene (2nd ed.). Chicago: Open Court. p. 223. (Originally published as Geschichte der Elementar-Mathematik.) - ^
Beutelspacher, Albrecht; Petri, Bernhard (1996). «Fibonacci-Zahlen». Der Goldene Schnitt (in German). Vieweg+Teubner Verlag. pp. 87–98. doi:10.1007/978-3-322-85165-9_6. - ^ Herz-Fischler 1998, pp. 167–170.
- ^ Posamentier & Lehmann 2011, p. 8.
- ^ Posamentier & Lehmann 2011, p. 285.
- ^
Cook, Theodore Andrea (1914). The Curves of Life. London: Constable. p. 420. - ^
Barr, Mark (1929). «Parameters of beauty». Architecture (NY). Vol. 60. p. 325. Reprinted: «Parameters of beauty». Think. Vol. 10–11. IBM. 1944. - ^ Livio 2002, p. 5.
- ^
Gardner, Martin (2001). «7. Penrose Tiles». The Colossal Book of Mathematics. Norton. pp. 73–93. - ^
Livio 2002, pp. 203–209
Gratias, Denis; Quiquandon, Marianne (2019). «Discovery of quasicrystals: The early days». Comptes Rendus Physique. 20 (7–8): 803–816. doi:10.1016/j.crhy.2019.05.009.
Jaric, Marko V. (1989). Introduction to the Mathematics of Quasicrystals. Academic Press. p. x.Although at the time of the discovery of quasicrystals the theory of quasiperiodic functions had been known for nearly sixty years, it was the mathematics of aperiodic Penrose tilings, mostly developed by Nicolaas de Bruijn, that provided the major influence on the new field.
Goldman, Alan I.; Anderegg, James W.; Besser, Matthew F.; Chang, Sheng-Liang; Delaney, Drew W.; Jenks, Cynthia J.; Kramer, Matthew J.; Lograsso, Thomas A.; Lynch, David W.; McCallum, R. William; Shield, Jeffrey E.; Sordelet, Daniel J.; Thiel, Patricia A. (1996). «Quasicrystalline materials». American Scientist. 84 (3): 230–241. JSTOR 29775669. - ^
Martin, George E. (1998). Geometric Constructions. Springer. pp. 13–14. doi:10.1007/978-1-4612-0629-3. - ^
Hailperin, Max; Kaiser, Barbara K.; Knight, Karl W. (1999). Concrete Abstractions: An Introduction to Computer Science Using Scheme. Brooks/Cole. p. 63. - ^
Hardy, G. H.; Wright, E. M. (1960) [1938]. «§11.8. The measure of the closest approximations to an arbitrary irrational». An Introduction to the Theory of Numbers (4th ed.). Oxford University Press. pp. 163–164. - ^ Sizer, Walter S. (1986). «Continued roots». Mathematics Magazine. 59 (1): 23–27. doi:10.1080/0025570X.1986.11977215. JSTOR 2690013. MR 0828417.
- ^
Tattersall, James Joseph (1999). Elementary number theory in nine chapters. Cambridge University Press. p. 28. - ^
Parker, Matt (2014). Things to Make and Do in the Fourth Dimension. Farrar, Straus and Giroux. p. 284. - ^ King, S.; Beck, F.; Lüttge, U. (2004). «On the mystery of the golden angle in phyllotaxis». Plant, Cell and Environment. 27 (6): 685–695. doi:10.1111/j.1365-3040.2004.01185.x.
- ^
Fletcher, Rachel (2006). «The golden section». Nexus Network Journal. 8 (1): 67–89. doi:10.1007/s00004-006-0004-z. - ^ a b c d e
Loeb, Arthur (1992). «The Golden Triangle». Concepts & Images: Visual Mathematics. Birkhäuser. pp. 179–192. doi:10.1007/978-1-4612-0343-8_20. - ^
Miller, William (1996). «Pentagons and Golden Triangles». Mathematics in School. 25 (4): 2–4. JSTOR 30216571. - ^ a b c d
Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. pp. 537–547. - ^
Penrose, Roger (1978). «Pentaplexity». Eureka. Vol. 39. p. 32. (original PDF) - ^
Frettlöh, D.; Harriss, E.; Gähler, F. «Robinson Triangle». Tilings Encyclopedia.Clason, Robert G (1994). «A family of golden triangle tile patterns». The Mathematical Gazette. 78 (482): 130–148. doi:10.2307/3618569.
- ^
Odom, George; van de Craats, Jan (1986). «E3007: The golden ratio from an equilateral triangle and its circumcircle». Problems and solutions. The American Mathematical Monthly. 93 (7): 572. doi:10.2307/2323047. JSTOR 2323047. - ^
Busard, Hubert L. L. (1968). «L’algèbre au Moyen Âge : le «Liber mensurationum» d’Abû Bekr». Journal des Savants (in French and Latin). 1968 (2): 65–124. doi:10.3406/jds.1968.1175. See problem 51, reproduced on p. 98 - ^
Bruce, Ian (1994). «Another instance of the golden right triangle» (PDF). Fibonacci Quarterly. 32 (3): 232–233. - ^ Posamentier & Lehmann 2011, p. 11.
- ^ a b
Burger, Edward B.; Starbird, Michael P. (2005) [2000]. The Heart of Mathematics: An Invitation to Effective Thinking (2nd ed.). Springer. p. 382. - ^ a b
Grünbaum, Branko (1996). «A new rhombic hexecontahedron» (PDF). Geombinatorics. 6 (1): 15–18. - ^
Senechal, Marjorie (2006). «Donald and the golden rhombohedra». In Davis, Chandler; Ellers, Erich W. (eds.). The Coxeter Legacy. American Mathematical Society. pp. 159–177. ISBN 0-8218-3722-2. - ^ a b Loeb, Arthur L.; Varney, William (March 1992). «Does the golden spiral exist, and if not, where is its center?». In Hargittai, István; Pickover, Clifford A. (eds.). Spiral Symmetry. World Scientific. pp. 47–61. doi:10.1142/9789814343084_0002.
- ^ a b Reitebuch, Ulrich; Skrodzki, Martin; Polthier, Konrad (2021). «Approximating logarithmic spirals by quarter circles». In Swart, David; Farris, Frank; Torrence, Eve (eds.). Proceedings of Bridges 2021: Mathematics, Art, Music, Architecture, Culture. Phoenix, Arizona: Tessellations Publishing. pp. 95–102. ISBN 978-1-938664-39-7.
- ^ Diedrichs, Danilo R. (February 2019). «Archimedean, Logarithmic and Euler spirals – intriguing and ubiquitous patterns in nature». The Mathematical Gazette. 103 (556): 52–64. doi:10.1017/mag.2019.7.
- ^ a b Livio (2002, pp. 70–72)
- ^
Gunn, Charles; Sullivan, John M. (2008). «The Borromean Rings: A video about the New IMU logo». In Sarhangi, Reza; Séquin, Carlo H. (eds.). Proceedings of Bridges 2008. Leeuwarden, the Netherlands. Tarquin Publications. pp. 63–70.; Video at «The Borromean Rings: A new logo for the IMU». International Mathematical Union. - ^
Hume, Alfred (1900). «Some propositions on the regular dodecahedron». The American Mathematical Monthly. 7 (12): 293–295. doi:10.2307/2969130. - ^
Coxeter, H.S.M.; du Val, Patrick; Flather, H.T.; Petrie, J.F. (1938). The Fifty-Nine Icosahedra. Vol. 6. University of Toronto Studies. p. 4.Just as a tetrahedron can be inscribed in a cube, so a cube can be inscribed in a dodecahedron. By reciprocation, this leads to an octahedron circumscribed about an icosahedron. In fact, each of the twelve vertices of the icosahedron divides an edge of the octahedron according to the «golden section.
- ^
Muller, J. M. (2006). Elementary functions : algorithms and implementation (2nd ed.). Boston: Birkhäuser. p. 93. ISBN 978-0817643720. - ^
Yee, Alexander J. (2021-03-13). «Records Set by y-cruncher». numberword.org. Two independent computations done by Clifford Spielman. - ^
Horocycles exinscrits : une propriété hyperbolique remarquable, cabri.net, retrieved 2009-07-21. - ^
Berndt, Bruce C.; Chan, Heng Huat; Huang, Sen-Shan; Kang, Soon-Yi; Sohn, Jaebum; Son, Seung Hwan (1999). «The Rogers–Ramanujan Continued Fraction» (PDF). Journal of Computational and Applied Mathematics. 105 (1–2): 9–24. doi:10.1016/S0377-0427(99)00033-3. - ^
Duffin, Richard J. (1978). «Algorithms for localizing roots of a polynomial and the Pisot Vijayaraghavan numbers». Pacific Journal of Mathematics. 74 (1): 47–56. doi:10.2140/pjm.1978.74.47. - ^ Le Corbusier, The Modulor, p. 25, as cited in
Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. Taylor & Francis. p. 316. doi:10.4324/9780203477465. - ^
Frings, Marcus (2002). «The Golden Section in Architectural Theory». Nexus Network Journal. 4 (1): 9–32. doi:10.1007/s00004-001-0002-0. - ^ Le Corbusier, The Modulor, p. 35, as cited in
Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. Taylor & Francis. p. 320. doi:10.4324/9780203477465.Both the paintings and the architectural designs make use of the golden section
- ^
Urwin, Simon (2003). Analysing Architecture (2nd ed.). Routledge. pp. 154–155. - ^ a b c d
Livio, Mario (2002). «The golden ratio and aesthetics». Plus Magazine. Retrieved November 26, 2018. - ^
Devlin, Keith (2007). «The Myth That Will Not Go Away». Retrieved September 26, 2013.Part of the process of becoming a mathematics writer is, it appears, learning that you cannot refer to the golden ratio without following the first mention by a phrase that goes something like ‘which the ancient Greeks and others believed to have divine and mystical properties.’ Almost as compulsive is the urge to add a second factoid along the lines of ‘Leonardo Da Vinci believed that the human form displays the golden ratio.’ There is not a shred of evidence to back up either claim, and every reason to assume they are both false. Yet both claims, along with various others in a similar vein, live on.
- ^
Simanek, Donald E. «Fibonacci Flim-Flam». Archived from the original on January 9, 2010. Retrieved April 9, 2013. - ^
Salvador Dalí (2008). The Dali Dimension: Decoding the Mind of a Genius (DVD). Media 3.14-TVC-FGSD-IRL-AVRO. - ^
Hunt, Carla Herndon; Gilkey, Susan Nicodemus (1998). Teaching Mathematics in the Block. pp. 44, 47. ISBN 1-883001-51-X. - ^
Olariu, Agata (1999). «Golden Section and the Art of Painting». arXiv:physics/9908036. - ^
Tosto, Pablo (1969). La composición áurea en las artes plásticas [The golden composition in the plastic arts] (in Spanish). Hachette. pp. 134–144. - ^
Tschichold, Jan (1991). The Form of the Book. Hartley & Marks. p. 43 Fig 4. ISBN 0-88179-116-4.Framework of ideal proportions in a medieval manuscript without multiple columns. Determined by Jan Tschichold 1953. Page proportion 2:3. margin proportions 1:1:2:3, Text area proportioned in the Golden Section. The lower outer corner of the text area is fixed by a diagonal as well.
- ^
Tschichold, Jan (1991). The Form of the Book. Hartley & Marks. pp. 27–28. ISBN 0-88179-116-4. - ^
Jones, Ronald (1971). «The golden section: A most remarkable measure». The Structurist. 11: 44–52.Who would suspect, for example, that the switch plate for single light switches are standardized in terms of a Golden Rectangle?
Johnson, Art (1999). Famous problems and their mathematicians. Teacher Ideas Press. p. 45.
The Golden Ratio is a standard feature of many modern designs, from postcards and credit cards to posters and light-switch plates.
Stakhov, Alexey P.; Olsen, Scott (2009). «§1.4.1 A Golden Rectangle with a Side Ratio of τ«. The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. World Scientific. p. 20–21.
A credit card has a form of the golden rectangle
Cox, Simon (2004). Cracking the Da Vinci Code. Barnes & Noble. p. 62.
The Golden Ratio also crops up in some very unlikely places: widescreen televisions, postcards, credit cards and photographs all commonly conform to its proportions.
- ^ Posamentier & Lehmann 2011, chapter 4, footnote 12: «The Togo flag was designed by the artist Paul Ahyi (1930–2010), who claims to have attempted to have the flag constructed in the shape of a golden rectangle».
- ^
Lendvai, Ernő (1971). Béla Bartók: An Analysis of His Music. London: Kahn and Averill. - ^ Livio 2002, p. 190.
- ^
Smith, Peter F. (2003). The Dynamics of Delight: Architecture and Aesthetics. Routledge. p. 83. - ^
Howat, Roy (1983). «1. Proportional structure and the Golden Section». Debussy in Proportion: A Musical Analysis. Cambridge University Press. pp. 1–10. - ^
Trezise, Simon (1994). Debussy: La Mer. Cambridge University Press. p. 53. - ^
Mongoven, Casey (2010). «A style of music characterized by Fibonacci and the golden ratio» (PDF). Congressus Numerantium. 201: 127–138.Hasegawa, Robert (2011). «Gegenstrebige Harmonik in the Music of Hans Zender». Perspectives of New Music. Project Muse. 49 (1): 207–234. doi:10.1353/pnm.2011.0000. JSTOR 10.7757/persnewmusi.49.1.0207.
Smethurst, Reilly (2016). «Two Non-Octave Tunings by Heinz Bohlen: A Practical Proposal». In Torrence, Eve; et al. (eds.). Proceedings of Bridges 2016. Jyväskylä, Finland. Tessellations Publishing. pp. 519–522.
- ^ Livio 2002, p. 154.
- ^
Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. Taylor & Francis. pp. 305–306. doi:10.4324/9780203477465.Padovan, Richard (2002). «Proportion: Science, Philosophy, Architecture». Nexus Network Journal. 4 (1): 113–122. doi:10.1007/s00004-001-0008-7.
- ^
Zeising, Adolf (1854). «Einleitung [preface]». Neue Lehre von den Proportionen des menschlichen Körpers [New doctrine of the proportions of the human body] (in German). Weigel. pp. 1–10. - ^
Pommersheim, James E.; Marks, Tim K.; Flapan, Erica L., eds. (2010). Number Theory: A Lively Introduction with Proofs, Applications, and Stories. Wiley. p. 82. - ^
Coldea, R.; Tennant, D.A.; Wheeler, E.M.; Wawrzynksa, E.; Prabhakaran, D.; Telling, M.; Habicht, K.; Smeibidl, P.; Keifer, K. (2010). «Quantum Criticality in an Ising Chain: Experimental Evidence for Emergent E8 Symmetry». Science. 327 (5962): 177–180. arXiv:1103.3694. doi:10.1126/science.1180085. - ^
«A Disco Ball in Space». NASA. 2001-10-09. Retrieved 2007-04-16. - ^
Pheasant, Stephen (1986). Bodyspace. Taylor & Francis. - ^
van Laack, Walter (2001). A Better History Of Our World: Volume 1 The Universe. Aachen: van Laach. - ^
Dunlap, Richard A. (1997). The Golden Ratio and Fibonacci Numbers. World Scientific. p. 130. - ^
Falbo, Clement (March 2005). «The golden ratio—a contrary viewpoint». The College Mathematics Journal. 36 (2): 123–134. doi:10.1080/07468342.2005.11922119. - ^
Moscovich, Ivan (2004). The Hinged Square & Other Puzzles. New York: Sterling. p. 122. - ^
Peterson, Ivars (1 April 2005). «Sea shell spirals». Science News. Archived from the original on 3 October 2012. Retrieved 10 November 2008. - ^
Man, John (2002). Gutenberg: How One Man Remade the World with Word. Wiley. pp. 166–167.The half-folio page (30.7 × 44.5 cm) was made up of two rectangles—the whole page and its text area—based on the so called ‘golden section’, which specifies a crucial relationship between short and long sides, and produces an irrational number, as pi is, but is a ratio of about 5:8.
- ^
Fechner, Gustav (1876). Vorschule der Ästhetik [Preschool of Aesthetics] (in German). Leipzig: Breitkopf & Härtel. pp. 190–202. - ^ Livio 2002, p. 7.
- ^
Osler, Carol (2000). «Support for Resistance: Technical Analysis and Intraday Exchange Rates» (PDF). Federal Reserve Bank of New York Economic Policy Review. 6 (2): 53–68. Archived (PDF) from the original on 2007-05-12.38.2 percent and 61.8 percent retracements of recent rises or declines are common,
- ^
Batchelor, Roy; Ramyar, Richard (2005). Magic numbers in the Dow (Report). Cass Business School. pp. 13, 31.
Popular press summaries can be found in:
Stevenson, Tom (2006-04-10). «Not since the ‘big is beautiful’ days have giants looked better». The Daily Telegraph.
«Technical failure». The Economist. 2006-09-23. - ^
Herz-Fischler, Roger (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. ISBN 0-88920-324-5. The entire book surveys many alternative theories for this pyramid’s shape. See Chapter 11, «Kepler triangle theory», pp. 80–91, for material specific to the Kepler triangle, and p. 166 for the conclusion that the Kepler triangle theory can be eliminated by the principle that «A theory must correspond to a level of mathematics consistent with what was known to the ancient Egyptians.» See note 3, p. 229, for the history of Kepler’s work with this triangle.Rossi, Corinna (2004). Architecture and Mathematics in Ancient Egypt. Cambridge University Press. pp. 67–68.
there is no direct evidence in any ancient Egyptian written mathematical source of any arithmetic calculation or geometrical construction which could be classified as the Golden Section … convergence to
; see also extensive discussion of multiple alternative theories for the shape of the pyramid and other Egyptian architecture, pp. 7–56, and
itself as a number, do not fit with the extant Middle Kingdom mathematical sources
Rossi, Corinna; Tout, Christopher A. (2002). «Were the Fibonacci series and the Golden Section known in ancient Egypt?». Historia Mathematica. 29 (2): 101–113. doi:10.1006/hmat.2001.2334.
Markowsky, George (1992). «Misconceptions about the Golden Ratio» (PDF). The College Mathematics Journal. Mathematical Association of America. 23 (1): 2–19. doi:10.2307/2686193. Retrieved 2012-06-29.
It does not appear that the Egyptians even knew of the existence of
much less incorporated it in their buildings
- ^ Livio 2002, pp. 74–75.
- ^
Van Mersbergen, Audrey M. (1998). «Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic». Communication Quarterly. 46 (2): 194–213. doi:10.1080/01463379809370095. - ^
Devlin, Keith J. (2005). The Math Instinct. New York: Thunder’s Mouth Press. p. 108. - ^
Gazalé, Midhat J. (1999). Gnomon: From Pharaohs to Fractals. Princeton. p. 125. - ^
Foutakis, Patrice (2014). «Did the Greeks Build According to the Golden Ratio?». Cambridge Archaeological Journal. 24 (1): 71–86. doi:10.1017/S0959774314000201. - ^
Le Salon de la Section d’Or, October 1912, Mediation Centre Pompidou - ^
Jeunes Peintres ne vous frappez pas !, La Section d’Or: Numéro spécial consacré à l’Exposition de la «Section d’Or», première année, n° 1, 9 octobre 1912, pp. 1–7 Archived 2020-10-30 at the Wayback Machine, Bibliothèque Kandinsky - ^
Herz-Fischler, Roger (1983). «An Examination of Claims Concerning Seurat and the Golden Number» (PDF). Gazette des Beaux-Arts. 101: 109–112. - ^
Herbert, Robert (1968). Neo-Impressionism. Guggenheim Foundation.[page needed] - ^ Livio 2002, p. 169.
- ^ a b
Camfield, William A. (March 1965). «Juan Gris and the golden section». The Art Bulletin. 47 (1): 128–134. doi:10.1080/00043079.1965.10788819. - ^
Green, Christopher (1992). Juan Gris. Yale. pp. 37–38.Cottington, David (2004). Cubism and Its Histories. Manchester University Press. p. 112, 142.
- ^
Allard, Roger (June 1911). «Sur quelques peintres». Les Marches du Sud-Ouest: 57–64.
Reprinted in
Antliff, Mark; Leighten, Patricia, eds. (2008). A Cubism Reader, Documents and Criticism, 1906–1914. The University of Chicago Press. pp. 178–191. - ^
Bouleau, Charles (1963). The Painter’s Secret Geometry: A Study of Composition in Art. Harcourt, Brace & World. pp. 247–248. - ^ Livio 2002, pp. 177–178.
Works cited
- Herz-Fischler, Roger (1998) [1987]. A Mathematical History of the Golden Number. Dover. ISBN 9780486400075. (Originally titled A Mathematical History of Division in Extreme and Mean Ratio.)
- Livio, Mario (2002). The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. New York: Broadway Books. ISBN 9780767908153.
- Posamentier, Alfred S.; Lehmann, Ingmar (2011). The Glorious Golden Ratio. Prometheus Books. ISBN 9-781-61614-424-1.
Further reading
- Doczi, György (1981). The Power of Limits: Proportional Harmonies in Nature, Art, and Architecture. Boston: Shambhala.
- Hargittai, István, ed. (1992). Fivefold Symmetry. World Scientific. ISBN 9789810206000.
- Huntley, H. E. (1970). The Divine Proportion: A Study in Mathematical Beauty. New York: Dover. ISBN 978-0-486-22254-7.
- Schaaf, William L., ed. (1967). The Golden Measure (PDF). California School Mathematics Study Group Reprint Series. Stanford University. Archived (PDF) from the original on 2015-04-25.
- Scimone, Aldo (1997). La Sezione Aurea. Storia culturale di un leitmotiv della Matematica. Palermo: Sigma Edizioni. ISBN 978-88-7231-025-0.
- Walser, Hans (2001) [Der Goldene Schnitt 1993]. The Golden Section. Peter Hilton trans. Washington, DC: The Mathematical Association of America. ISBN 978-0-88385-534-8.
External links
- Weisstein, Eric W. «Golden Ratio». MathWorld.
- Bogomolny, Alexander (2018). «Golden Ratio in Geometry». Cut-the-Knot.
- Knott, Ron. «The Golden section ratio: Phi». Information and activities by a mathematics professor.
- The Myth That Will Not Go Away, by Keith Devlin, addressing multiple allegations about the use of the golden ratio in culture.
- Spurious golden spirals collected by Randall Munroe
- YouTube lecture on Zeno’s mice problem and logarithmic spirals
Что это? Золотое сечение – это математическая формула, соотношение двух неравных чисел. Его еще называют божественной пропорцией. Правило третей, золотая спираль – всё это визуальное отображения этого универсального правила.
Где используется? Золотое сечение применимо везде, где есть место графике, рисунку, фотографии. Сфера дизайна – не исключение. Конечно, это не единственное правило гармонии, но, пожалуй, самое известное.
В статье рассказывается:
- Что такое золотое сечение
- История золотого сечения
- Золотое сечение Фибоначчи
- Золотое сечение в природе
- Золотое сечение в фотографии
- Золотое сечение в дизайне
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.Бесплатно от Geekbrains
Что такое золотое сечение
Это отношение двух разных по величине чисел, когда большее из них относится к меньшему так же, как и общая их сумма относится к большему. Соотношение золотого сечения равняется около 1,618. Его обозначают греческой литерой Ф (читается как «фи») в честь древнегреческого скульптора Фидия, который применял эти пропорции при создании храма Парфенон.
Одним из популярных способов представления золотого сечения является прямоугольник с соотношением сторон 62 на 48 и построенной внутри спиралью.
История золотого сечения
Согласно истории, данное понятие для научного использования ввел Пифагор, философ и математик Древней Греции. Предполагается, что ученый позаимствовал знание у жителей Египта и Вавилонии.
Если посмотреть на соотношение сторон пирамид, храмов и предметов домашнего обихода у древних египтян, а также на украшения из саркофага царя Тутанхамона, то очевидно, что все они создавались по принципу золотого сечения.
Архитектор из Франции Ле Корбюзье заметил, что рельеф храма египетского правителя Сети I, как и в рельефе изображения царя Рамзеса, тоже создавались по этому правилу. Соотношения золотого деления были обнаружены и в рельефе гробницы, на котором изображен высокопоставленный чиновник Хесира.
Скачать
файл
Жители Древней Греции хорошо владели геометрией. Арифметике, например, они учились по геометрическим фигурам уже в детстве. А квадрат Пифагора и его диагональ служили основой для создания динамических прямоугольников.
Сам термин «золотое сечение» впервые ввел в обиход математик из Германской империи Мартин Ом в 19 веке. До того времени правило имело название «божественная пропорция».
Из-за уникальных свойств она пользовалась большой популярностью. Например, в эпоху Возрождения число 1,618 было идеальным при выборе размера. Его часто применяли для создания картин и книг. А линия талии в то время считалась границей золотого сечения в теле человека.
Многие люди и сегодня уверены, что соблюдение данного правила считается залогом красоты и внешней гармонии. Эту тему активно обсуждают пластические хирурги.
Золотое сечение Фибоначчи
В конце 12 века математик из Италии Леонардо Пизанский, известный по прозвищу Фибоначчи, открыл последовательность чисел, связанных с золотой пропорцией. Суть в том, что если взять любые 2 числа из ряда итальянского математика, то соотношение между ними почти такое же, как на примерах золотого сечения. Особенность последовательности Фибоначчи в том, что каждое новое число всегда равняется сумме 2-х предыдущих. Пример: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д.
По мере увеличения ряда, отношения между числами становится все ближе к 1,618. Разделив, к примеру, 8 на 5, мы получим около 1,6. А соотношение 34 на 21 уже дает 1,619, если округлить. Каждое число ряда является логичным в последовательности Фибоначчи.

Читайте также
Такие соотношения из-за приближения к показателю золотого деления можно использовать при построении золотого прямоугольника. Эта фигура считается одной из самых гармоничных в геометрии, что позволяет применять пропорции Пифагора в любом виде изобразительного искусства.
Золотой прямоугольник тесно связан с золотой спиралью, которая строится методом размещения смежных между собой квадратов по алгоритму Фибоначчи.
Золотое сечение в природе
Пропорции золотого сечения можно наблюдать во всех природных и научных проявлениях. В представленном списке мы рассмотрим наиболее удивительные случаи.
- Лепестки у цветов. Нередки случаи, когда их количество соответствует числовому ряду «Ф». По мнению Дарвина, все лепестки растений располагаются так, чтобы получать как можно больше солнечного света и остальных необходимых для жизни ресурсов.
- Головки у семян. Во многих случаях семена цветов начинают расти посередине головки семени и появляются снаружи, заполняя собой пространство. В качестве примера можно привести семена подсолнуха.
- Шишки у сосен. Семена, находящиеся в их семенных коробочках, произрастают вверх противоположно друг другу по спирали. Расстояние между ними обычно совпадает с соотношениями чисел из последовательности Фибоначчи.
- Ветки у деревьев. На примере их формирования и расщепления также можно заметить правило золотого ряда. То же самое относится и к развитию корневых систем у растений и водорослей.
- Раковины. Большинство из них демонстрируют нам правило золотого сечения. Например, это можно сказать об улитках и наутилусах.
- Спиральные галактики. Млечный Путь содержит в себе несколько рукавов, представленных в виде изогональных спиралей с шагом около 12 градусов. Их форма соответствует форме золотой спирали, при том над каждой такой галактикой можно начертить золотой прямоугольник.
- Ураганы. В большинстве случаев, изнутри они устроены согласно последовательности ряда «фи».
- Пальцы на руках у людей. Все участки пальцев от начала основания и до запястья увеличивается в соотношении по Фибоначчи.
- Тела людей и животных. Расстояние у людей от пупка до пола, а также от темени и до пупка — это яркий пример закона золотого сечения. Помимо человека такую пропорцию можно наблюдать и у других организмов (например, у дельфинов и пчел).
- Молекулы ДНК. Все они содержат соотношение 34 на 21 ангстрем в каждом полном спиральном цикле. А вы уже знаете, что эти цифры — часть ряда Фибоначчи.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Уже скачали 21024
Как мы видим, примеров, где можно увидеть пропорции и соотношения по принципу золотого правила, довольно много. Помимо случаев, описанных выше, 1,618 постоянно встречается в точных науках, биологии и других областях жизни. Поэтому свое альтернативное название — божественное сечение, правило полностью оправдывает. Ведь материальный мир словно был создан по этому закону.
Золотое сечение в фотографии
Гармоническая пропорция напрямую связана с правилом третей — другой неотъемлемой схемой для работы с визуалом. По сути, оно продолжает золотое сечение так же, как, например, фотография рождается из художественного творчества.
Основное различие заключается в соотношении сторон. Так, в принципе третей кадр разделяется на 3 одинаковые части, а в божественной пропорции он делится на 1:0.618:1.
Отсюда следует, что правило третей можно назвать более простой версией золотого сечения, но полностью рабочей.
Например, сегодня большинство камер, в том числе и в смартфонах, имеет разлинованную сетку третей, что позволяет пользователям гармонично выстраивать композицию из фото и видео.
Чем следует руководствоваться при съемке?
- Точки пересечения. Благодаря размещению нужного объекта по линиям, сделать снимок будет намного удобнее.
- Диагональная композиция. Линию можно прочертить самостоятельно из верхнего угла кадра в нижний, а можно использовать объекты, находящиеся в этой последовательности, которые формируют эту линию. Наличие разных диагоналей позволяет получить динамичный кадр. Восходящая, например, из правого нижнего угла в левый верхний придаст фотографии веселое настроение, а нисходящая — грустное.
- Пропорции. Чаще всего это относится к взаимосвязи объектов на нескольких планах снимка. Это тоже вариант золотого сечения, только представленный в соотношении объектов. Например, на заднем плане к большему объекту на переднем плане (либо наоборот).
- Линия горизонта. Когда вы делаете снимок на природе либо в городской инфраструктуре, нужно расположить горизонтальную линию кадра на одной из горизонтальных линий третей. То же самое относится и к общему плану фотографии/видео. Это даст более качественный результат.
- Правило «воздуха». Не забывайте про свободные участки между объектами. Если вы делаете фотографию человека, то оставьте немного пространства от его головы до границы кадра. А в ситуации, когда он смотрит налево, разместите человека по правым точкам пересечения линий (верно и обратное).
Золотое сечение в дизайне
Божественная пропорция делает современный дизайн более упорядоченным. Легкий и быстрый способ использования этого — умножить размер одного элемента на 1,618. Результат покажет, каким должен быть размер следующего объекта.
Только до 1.06
Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы
Список документов:



Чтобы получить файл, укажите e-mail:
Подтвердите, что вы не робот,
указав номер телефона:
Уже скачали 7503
Применение формулы золотого сечения в типографике
Определяющими факторами в данной области являются 3 составляющие: размер шрифта, ширина линии и высота строки. Их необходимо подбирать в правильных пропорциях.
Увеличивая и уменьшая шрифт, а также ширину текста, можно определить, какую высоту следует задать буквам. Установлено, что оптимальным для удобства читателей количеством является 70-80 символов на строку. Когда длина текста превышает этот показатель, его читабельность сильно снижается.
Для примера возьмем текст из 3 строк и определим в нем 3 части: «А», «Б» и «В». Допустим, строка «В» содержит меньше ценной информации, чем «А» и «Б». В связи с этим, текст внутри строки «В» должен иметь шрифт размером 10. Чтобы установить размер контента на строке «Б» (второй по значимости контента), надо умножить 10 на 1,618.
В разработке логотипов
Большинство популярных брендов, например, «Твиттер», «Эппл» и «Пепси», применяют знания божественного сечения, когда создают фирменный логотип.
Поэтому вы тоже можете пользоваться правилом чисел «Ф» при создании сетки. Полученный результат станет вашей опорой в разработке графического рисунка.
Золотое сечение в архитектуре
Зодчие прошлого применяли принцип божественного деления при создании памятников. Мавзолей-мечеть Тадж-Махал, например, относится к одному из 7 чудес света. Когда его возводили, мастера пользовались правилом золотого сечения.
Применение этого знания в современной архитектуре дает возможность добиться баланса между шириной и высотой сооружения. Популярным методом построить гармоничное здание является использование свойств золотого прямоугольника.
Стоит добавить, что золотое сечение дает возможность творить разнообразные формы. При их создании нет необходимости строго следовать прямоугольной структуре. Золотое деление позволяет дизайнерам применять полученные формы как основу для работы.
Разработка проектов и формирование макетов
Чтобы сделать макеты качественными, нужно учесть 2 главные составляющие: отдельные визуальные элементы и как они будут связаны между собой.
Есть много способов формирования макетов. Например — расположение «Z». Оно дает увидеть путь, по которому проходит посетитель на веб странице, а также схему того, как он смотрит на элементы.
Еще одно востребованное правило компоновки — это применение золотой спирали. Она более эффективно, если в дизайне достаточно много элементов, различающихся между собой, но предназначенные для расположения на одном макете. Благодаря использованию правил сечения внимание посетителей ненавязчиво, но эффективно притягивается к середине спирали, в которой можно расположить главный элемент контента.

Читайте также
Некоторые считают, что золотое сечение в большей или меньшей степени присутствует в каждом успешном дизайне. Рассказать о востребованной концепции бывает полезным в общении с заказчиком или когда нужно показать свой проект публично. Действительно ли «божественная пропорция» очень эффективна или это мнение преувеличено? Обсуждение данного вопроса в творческой сфере продолжается и сегодня.






















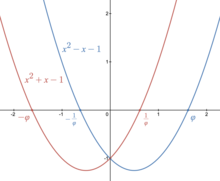





![{displaystyle {begin{aligned}varphi ^{2}&=varphi +1=2.618033dots ,\[5mu]{frac {1}{varphi }}&=varphi -1=0.618033dots .end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff2e5225abf67548cf93c882add3a4b439c4aeb8)

![{displaystyle {begin{aligned}varphi ^{n}&=varphi ^{n-1}+varphi ^{n-3}+cdots +varphi ^{n-1-2m}+varphi ^{n-2-2m}\[5mu]varphi ^{n}-varphi ^{n-1}&=varphi ^{n-2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/048f09b7012c7fbd3d9f32798de6dd5c01acabcd)

![varphi =[1;1,1,1,dots ]=1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95682588ffee3530627c3a7b00ff08bbba6e97d4)
![varphi ^{-1}=[0;1,1,1,dots ]=0+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/165d255e32f4b9af1f9144f15302b147fc3fead2)


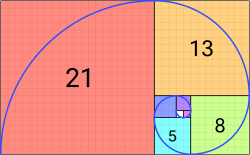
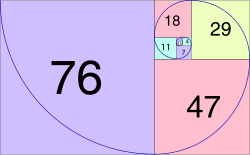








![{displaystyle {begin{aligned}3varphi ^{3}-5varphi ^{2}+4&=3(varphi ^{2}+varphi )-5varphi ^{2}+4\[5mu]&=3[(varphi +1)+varphi ]-5(varphi +1)+4\[5mu]&=varphi +2approx 3.618033.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60ff8508aa117064d60142d447fb0cb58a809848)

![{displaystyle {begin{aligned}varphi ^{0}&=1,\[5mu]varphi ^{1}&=1.618033989...approx 2,\[5mu]varphi ^{2}&=2.618033989...approx 3,\[5mu]varphi ^{3}&=4.236067978...approx 4,\[5mu]varphi ^{4}&=6.854101967...approx 7,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20c9bfd2f9bdc877282b290adc74c88f1dfa63c8)


























![{displaystyle {begin{aligned}{frac {2pi -g}{g}}&={frac {2pi }{2pi -g}}=varphi ,\[8mu]2pi -g&={frac {2pi }{varphi }}approx 222.5^{circ },\[8mu]g&={frac {2pi }{varphi ^{2}}}approx 137.5^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd5f9122b38d09e0cd2992820f27b8587efd167a)


![{displaystyle {begin{aligned}varphi &=1+2sin(pi /10)=1+2sin 18^{circ },\[5mu]varphi &={tfrac {1}{2}}csc(pi /10)={tfrac {1}{2}}csc 18^{circ },\[5mu]varphi &=2cos(pi /5)=2cos 36^{circ },\[5mu]varphi &=2sin(3pi /10)=2sin 54^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c42bbf25d6257a00fad895691aa2c5eb0c6f57a)


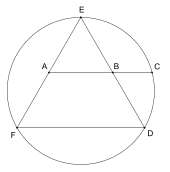
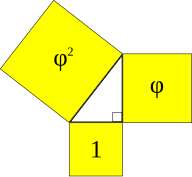
![{displaystyle {begin{aligned}A&={tfrac {s^{2}}{2}}{sqrt {varphi }},\[5mu]theta &=sin ^{-1}{frac {1}{varphi }}approx 38.1727^{circ },\[5mu]theta &=cos ^{-1}{frac {1}{varphi }}approx 51.8273^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f96fa323a2e180a6198f05d33c13e1631854e840)
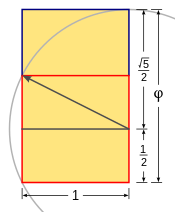
![{displaystyle {begin{aligned}alpha &=2arctan {1 over varphi }approx 63.43495^{circ },\[5mu]beta &=2arctan varphi =pi -arctan 2=arctan 1+arctan 3approx 116.56505^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c5a4321454f4ca1b41b0dbd8f2c6c4afd48467e)
![{displaystyle {begin{aligned}d&={2a over {sqrt {2+varphi }}}=2{sqrt {{3-varphi } over 5}}aapprox 1.05146a,\[5mu]D&=2{sqrt {{2+varphi } over 5}}aapprox 1.70130a.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d00bbc42679ab9e34fdf849ac68de75180cc92c7)
![{displaystyle {begin{aligned}A&=(sin(arctan 2))~a^{2}={2 over {sqrt {5}}}~a^{2}approx 0.89443a^{2},\[5mu]A&={{varphi } over 2}d^{2}approx 0.80902d^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bed70dcf23f16f3f8241aeaf2b56f0897244ff3)






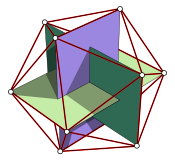

![{displaystyle {begin{aligned}e^{0}+e^{-0}&=2,\[5mu]e^{2pi i/5}+e^{-2pi i/5}&=varphi ^{-1}=-1+varphi ,\[5mu]e^{4pi i/5}+e^{-4pi i/5}&=-varphi .end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec7bcbd2e99aef0874eb163966c3e2dd9424b86)
![{displaystyle {begin{aligned}e^{pi i}+e^{-pi i}&=-2,\[5mu]e^{pi i/5}+e^{-pi i/5}&=varphi ,\[5mu]e^{3pi i/5}+e^{-3pi i/5}&=-varphi ^{-1}=1-varphi .end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9459634b32b6990a97eb560ce696a3bc2e722513)



![{displaystyle {begin{aligned}{Bigl (}varphi +R{{bigl (}e^{-2a}{bigr )}}{Bigr )}{Bigl (}varphi +R{{bigl (}e^{-2b}{bigr )}}{Bigr )}&=varphi {sqrt {5}},\[5mu]{Bigl (}varphi ^{-1}-R{{bigl (}{-e^{-a}}{bigr )}}{Bigr )}{Bigl (}varphi ^{-1}-R{{bigl (}{-e^{-b}}{bigr )}}{Bigr )}&=varphi ^{-1}{sqrt {5}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efa72855991c37845330a894d36b1d91647a265a)