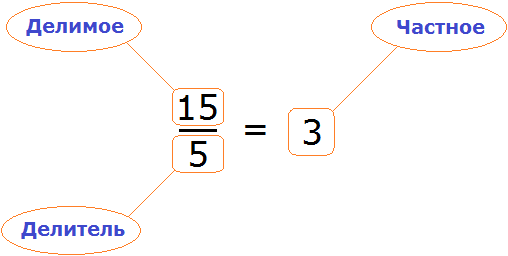
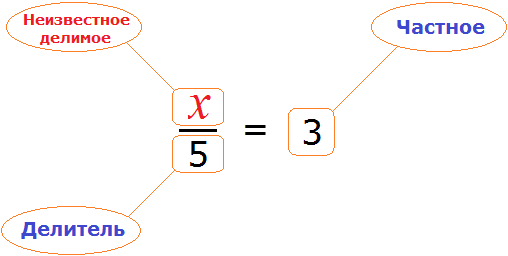
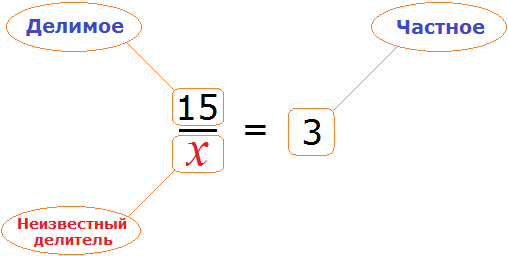
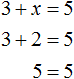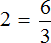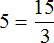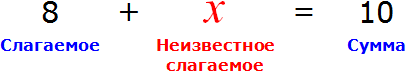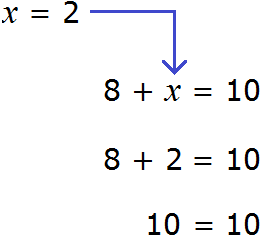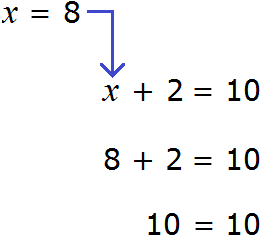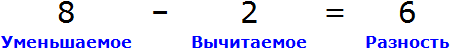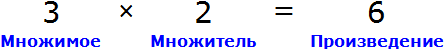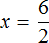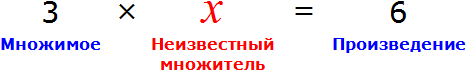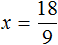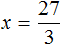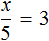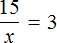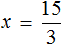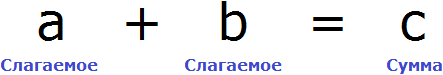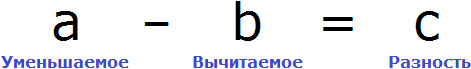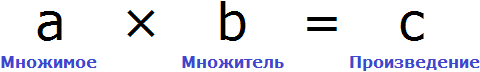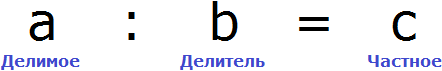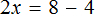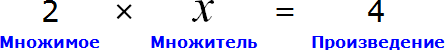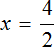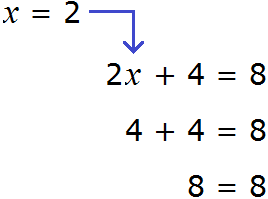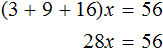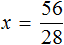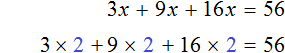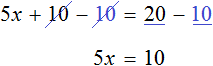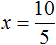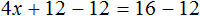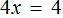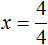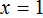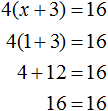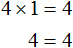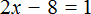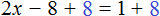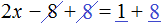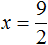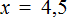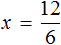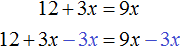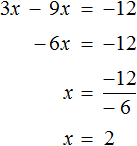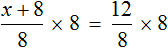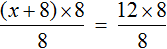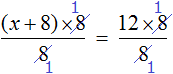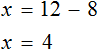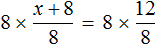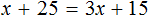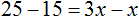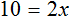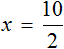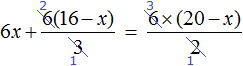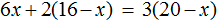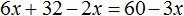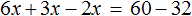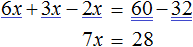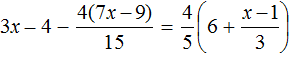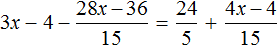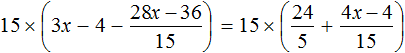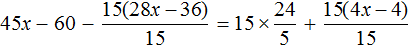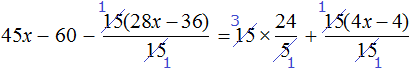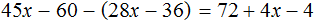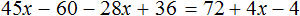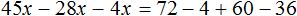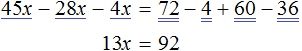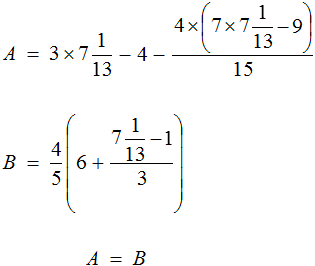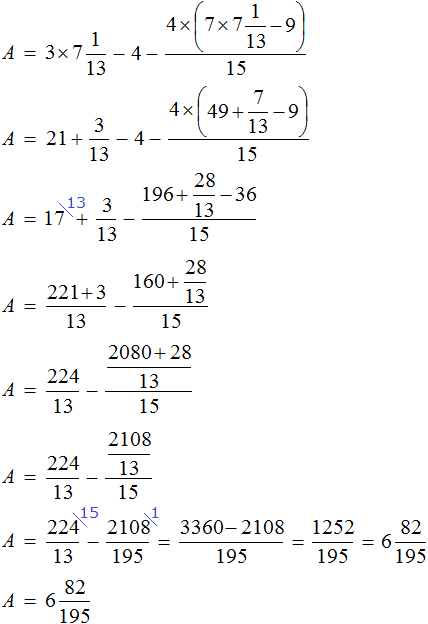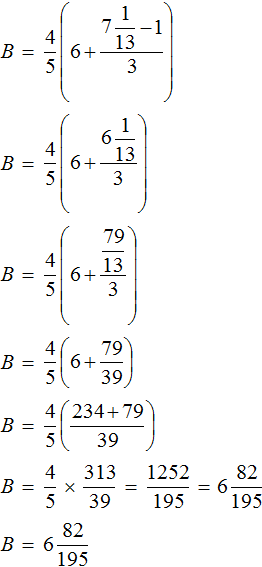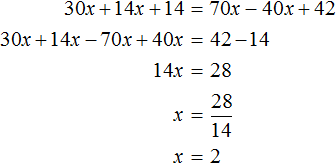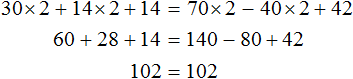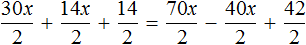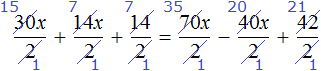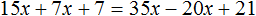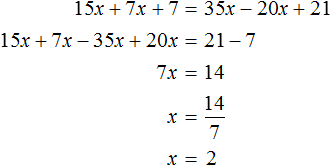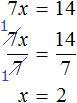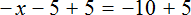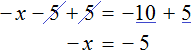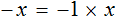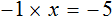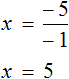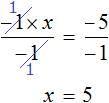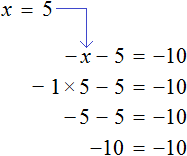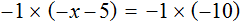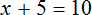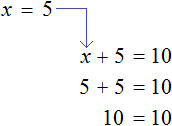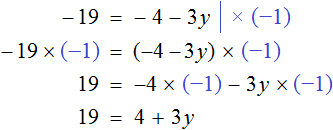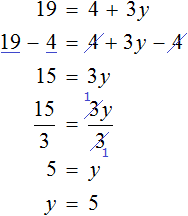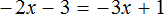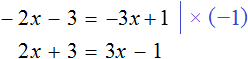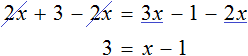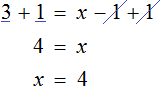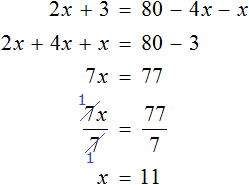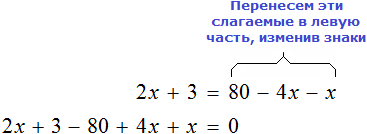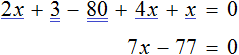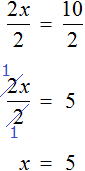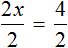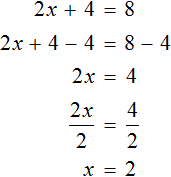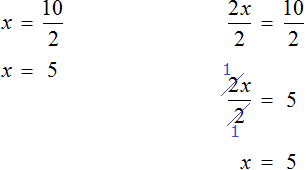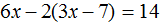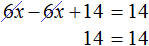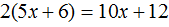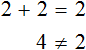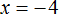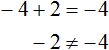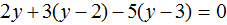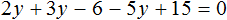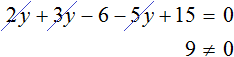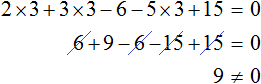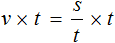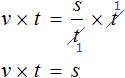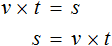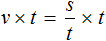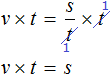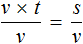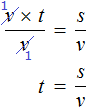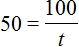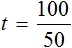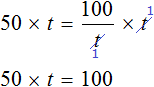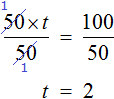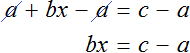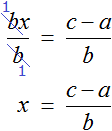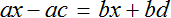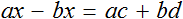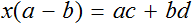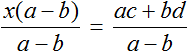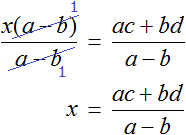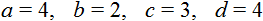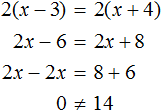«В уравнение» или «в уравнении», как правильно?
«В уравнении» правильно пишется с буквой «и» в окончании предложного падежа. Слово «в уравнение» имеет окончание «е» как форма винительного падежа с предлогом.
Определим, как различать слова «в уравнении» или «в уравнение» по их грамматическим признакам в контексте.
Слова «в уравнение» и «в уравнении» — это падежные формы существительного среднего рода «уравнение». Они имеют один и тот же предлог «в» и звучат одинаково из-за безударного окончания:
- в у равн е́ни е — приставка/корень/суффикс/окончание;
- в у равн е́ни и — приставка/корень/суффикс/окончание.
Чтобы правильно выбрать окончание, обозначенное буквой «е» или «и», определим падежную форму существительного в контексте.
Когда пишется «в уравнение»?
Когда пишется «в уравнение», выясним, если зададим к нему падежный вопрос в предложении:
Вам следует вставить в уравнение неизвестные величины, обозначенные x и y.
Следует вставить (во что?) в уравнение
Рассматриваемое слово имеет форму винительного падежа единственного числа. Как неодушевленное существительное, оно в винительном падеже имеет такое же безударное окончание, как и форме именительного падежа:
(что?) уравне́ни е — (во что?) в уравне́ни е .
Правописание слова «в уравнении»
Чтобы выяснить, почему «в уравнении» пишется окончание «и», укажем, что предлог «в» может использоваться также в форме предложного падежа существительных:
- поставить ударение (в чём?) в сло́в е
- выросло (в чём?) в по́л е
- заметил (в чём?) в окн е́ .
Как видим, в этой падежной форме существительные среднего рода имеют типичное окончание -е, кроме слов, заканчивающихся буквосочетанием -ие. Такие слова склоняются по-особому. В форме предложного падежа с любым предлогом существительные с конечным сочетанием -ие имеют безударное окончание -и :
- созвезд ие — увидим (в чём?) в созве́зди и
- описан ие — узнаешь (при чём?) при описа́ни и
- расстоян ие — поставьте (на чём?) на расстоя́ни и
- измерен ие — расскажете (о чём?) об измере́ни и .
Обратим внимание, что существительное среднего рода «уравнение» также заканчивается буквосочетанием -ие. Посмотрим, как оно изменяется по падежам в единственном числе:
- и. п. (что?) уравне́ни е
- р. п. формула (чего?) уравне́ни я
- д. п. добавлю (к чему?) к уравне́ни ю
- в. п. напишу (что?) уравне́ни е
- т. п. занят (чем?) уравне́ни е м
- п. п. найдем (в чём?) в уравне́ни и
Поупражняемся в определении падежных форм слова «уравнение» и написании окончаний -е или -и.
Примеры
В уравнение с неизвестными величинами подставьте их значения.
Запишите символы величин, входящих в уравнение.
При решении учтите, что в уравнении не проставлены все коэффициенты.
Ученый внес изменения в уравнение, по-своему понимая физику твердого тела.
В уравнении имеется ошибка, которую вам предстоит указать.
Источник статьи: http://russkiiyazyk.ru/orfografiya/pravopisanie/v-uravnenie-ili-v-uravnenii-kak-pravilno.html
«В уравнение» или «в уравнении», как правильно
Определим, как различать слова «в уравнении» или «в уравнение» по их грамматическим признакам в контексте.
Слова «в уравнение» и «в уравнении» — это падежные формы существительного среднего рода «уравнение». Они имеют один и тот же предлог «в» и звучат одинаково из-за безударного окончания:
- в уравне́ние — приставка/корень/суффикс/окончание;
- в уравне́нии — приставка/корень/суффикс/окончание.
«В уравнении» правильно пишется с буквой «и» в окончании предложного падежа. Слово «в уравнение» имеет окончание «е» как форма винительного падежа с предлогом.
Чтобы правильно выбрать окончание, обозначенное буквой «е» или «и», определим падежную форму существительного в контексте.
Когда пишется «в уравнение»?
Когда пишется «в уравнение», выясним, если зададим к нему падежный вопрос в предложении:
Вам следует вставить в уравнение неизвестные величины, обозначенные x и y.
Следует вставить (во что?) в уравнение
Рассматриваемое слово имеет форму винительного падежа единственного числа. Как неодушевленное существительное, оно в винительном падеже имеет такое же безударное окончание, как и форме именительного падежа:
(что?) уравне́ние — (во что?) в уравне́ние.
Слово «в уравнение» правильно пишется с буквой «е» в окончании винительного падежа с предлогом.
Правописание слова «в уравнении»
Чтобы выяснить, почему «в уравнении» пишется окончание «и», укажем, что предлог «в» может использоваться также в форме предложного падежа существительных:
Как видим, в этой падежной форме существительные среднего рода имеют типичное окончание -е, кроме слов, заканчивающихся буквосочетанием -ие. Такие слова склоняются по-особому.
В форме предложного падежа с любым предлогом существительные с конечным сочетанием -ие имеют безударное окончание -и:
- созвездие — увидим (в чём?) в созве́здии
- описание — узнаешь (при чём?) при описа́нии
- расстояние — поставьте (на чём?) на расстоя́нии
- измерение — расскажете (о чём?) об измере́нии.
Обратим внимание, что существительное среднего рода «уравнение» также заканчивается буквосочетанием -ие. Посмотрим, как оно изменяется по падежам в единственном числе:
- и. п. (что?) уравне́ние
- р. п. формула (чего?) уравне́ния
- д. п. добавлю (к чему?) к уравне́нию
- в. п. напишу (что?) уравне́ние
- т. п. занят (чем?) уравне́нием
- п. п. найдем (в чём?) в уравне́нии
Слово «в уравнении» пишется с буквой «и» в безударном окончании предложного падежа существительного «уравнение», заканчивающегося на -ие.
Поупражняемся в определении падежных форм слова «уравнение» и написании окончаний -е или -и.
Примеры
В уравнение с неизвестными величинами подставьте их значения.
Запишите символы величин, входящих в уравнение.
При решении учтите, что в уравнении не проставлены все коэффициенты.
Ученый внес изменения в уравнение, по-своему понимая физику твердого тела.
В уравнении имеется ошибка, которую вам предстоит указать.
Источник статьи: http://sprint-olympic.ru/uroki/russkij-jazyk-uroki/kak-pravilno-pishetsja/264381-v-uravnenie-ili-v-uravnenii-kak-pravilno.html
Уравнение или уровнение как пишется
Склонение существительного «уравнение»
Существительное «уравн е́ ние» (неод.)
| Падеж | Единственное число | Множественное число |
|---|---|---|
| Именительный Кто? Что? |
уравн е́ ние | уравн е́ ния |
| Родительный Кого? Чего? |
уравн е́ ния | уравн е́ ний |
| Дательный Кому? Чему? |
уравн е́ нию | уравн е́ ниям |
| Винительный (неод.) Кого? Что? |
уравн е́ ние | уравн е́ ния |
| Творительный Кем? Чем? |
уравн е́ нием | уравн е́ ниями |
| Предложный О ком? О чём? |
уравн е́ нии | уравн е́ ниях |
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: преграждать — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «уравнение»
Синонимы к слову «уравнение»
Предложения со словом «уравнение»
- Сила тяготения, к примеру, нелинейна – этот технический термин означает, в сущности, что вы не можете решать уравнения движения при помощи красивых формул.
Цитаты из русской классики со словом «уравнение»
Сочетаемость слова «уравнение»
Каким бывает «уравнение»
Значение слова «уравнение»
УРАВНЕ́НИЕ , -я, ср. 1. Действие по знач. глаг. уравнять и состояние по знач. глаг. уравняться. (Малый академический словарь, МАС)
Отправить комментарий
Дополнительно
Значение слова «уравнение»
УРАВНЕ́НИЕ , -я, ср. 1. Действие по знач. глаг. уравнять и состояние по знач. глаг. уравняться.
Предложения со словом «уравнение»
Сила тяготения, к примеру, нелинейна – этот технический термин означает, в сущности, что вы не можете решать уравнения движения при помощи красивых формул.
В итоге начинается решение дифференциальных уравнений гуманитарным способом или сочинение диалогов на языке программирования высокого уровня, а в тяжёлых случаях всё сразу и одновременно.
Второй этап состоит из собственно решения уравнения регрессии и нахождения его параметров.
«В уравнение» или «в уравнении», как правильно
Определим, как различать слова «в уравнении» или «в уравнение» по их грамматическим признакам в контексте.
Слова «в уравнение» и «в уравнении» — это падежные формы существительного среднего рода «уравнение». Они имеют один и тот же предлог «в» и звучат одинаково из-за безударного окончания:
- в уравне́ние — приставка/корень/суффикс/окончание;
- в уравне́нии — приставка/корень/суффикс/окончание.
«В уравнении» правильно пишется с буквой «и» в окончании предложного падежа. Слово «в уравнение» имеет окончание «е» как форма винительного падежа с предлогом.
Чтобы правильно выбрать окончание, обозначенное буквой «е» или «и», определим падежную форму существительного в контексте.
Когда пишется «в уравнение»?
Когда пишется «в уравнение», выясним, если зададим к нему падежный вопрос в предложении:
Вам следует вставить в уравнение неизвестные величины, обозначенные x и y.
Следует вставить (во что?) в уравнение
Рассматриваемое слово имеет форму винительного падежа единственного числа. Как неодушевленное существительное, оно в винительном падеже имеет такое же безударное окончание, как и форме именительного падежа:
(что?) уравне́ние — (во что?) в уравне́ние.
Слово «в уравнение» правильно пишется с буквой «е» в окончании винительного падежа с предлогом.
Правописание слова «в уравнении»
Чтобы выяснить, почему «в уравнении» пишется окончание «и», укажем, что предлог «в» может использоваться также в форме предложного падежа существительных:
- поставить ударение (в чём?) в сло́ве
- выросло (в чём?) в по́ле
- заметил (в чём?) в окне́.
Как видим, в этой падежной форме существительные среднего рода имеют типичное окончание -е, кроме слов, заканчивающихся буквосочетанием -ие. Такие слова склоняются по-особому.
В форме предложного падежа с любым предлогом существительные с конечным сочетанием -ие имеют безударное окончание -и:
- созвездие — увидим (в чём?) в созве́здии
- описание — узнаешь (при чём?) при описа́нии
- расстояние — поставьте (на чём?) на расстоя́нии
- измерение — расскажете (о чём?) об измере́нии.
Обратим внимание, что существительное среднего рода «уравнение» также заканчивается буквосочетанием -ие. Посмотрим, как оно изменяется по падежам в единственном числе:
- и. п. (что?) уравне́ние
- р. п. формула (чего?) уравне́ния
- д. п. добавлю (к чему?) к уравне́нию
- в. п. напишу (что?) уравне́ние
- т. п. занят (чем?) уравне́нием
- п. п. найдем (в чём?) в уравне́нии
Слово «в уравнении» пишется с буквой «и» в безударном окончании предложного падежа существительного «уравнение», заканчивающегося на -ие.
Поупражняемся в определении падежных форм слова «уравнение» и написании окончаний -е или -и.
Примеры
В уравнение с неизвестными величинами подставьте их значения.
Запишите символы величин, входящих в уравнение.
При решении учтите, что в уравнении не проставлены все коэффициенты.
Ученый внес изменения в уравнение, по-своему понимая физику твердого тела.
В уравнении имеется ошибка, которую вам предстоит указать.
«В уравнение» или «в уравнении», как правильно?
«В уравнении» правильно пишется с буквой «и» в окончании предложного падежа. Слово «в уравнение» имеет окончание «е» как форма винительного падежа с предлогом.
Определим, как различать слова «в уравнении» или «в уравнение» по их грамматическим признакам в контексте.
Слова «в уравнение» и «в уравнении» — это падежные формы существительного среднего рода «уравнение». Они имеют один и тот же предлог «в» и звучат одинаково из-за безударного окончания:
Чтобы правильно выбрать окончание, обозначенное буквой «е» или «и», определим падежную форму существительного в контексте.
Когда пишется «в уравнение»?
Когда пишется «в уравнение», выясним, если зададим к нему падежный вопрос в предложении:
Вам следует вставить в уравнение неизвестные величины, обозначенные x и y.
Следует вставить (во что?) в уравнение
Рассматриваемое слово имеет форму винительного падежа единственного числа. Как неодушевленное существительное, оно в винительном падеже имеет такое же безударное окончание, как и форме именительного падежа:
(что?) уравне́ни е — (во что?) в уравне́ни е .
Правописание слова «в уравнении»
Чтобы выяснить, почему «в уравнении» пишется окончание «и», укажем, что предлог «в» может использоваться также в форме предложного падежа существительных:
- поставить ударение (в чём?) в сло́в е
- выросло (в чём?) в по́л е
- заметил (в чём?) в окн е́ .
Как видим, в этой падежной форме существительные среднего рода имеют типичное окончание -е, кроме слов, заканчивающихся буквосочетанием -ие. Такие слова склоняются по-особому. В форме предложного падежа с любым предлогом существительные с конечным сочетанием -ие имеют безударное окончание -и :
- созвезд ие — увидим (в чём?) в созве́зди и
- описан ие — узнаешь (при чём?) при описа́ни и
- расстоян ие — поставьте (на чём?) на расстоя́ни и
- измерен ие — расскажете (о чём?) об измере́ни и .
Обратим внимание, что существительное среднего рода «уравнение» также заканчивается буквосочетанием -ие. Посмотрим, как оно изменяется по падежам в единственном числе:
- и. п. (что?) уравне́ни е
- р. п. формула (чего?) уравне́ни я
- д. п. добавлю (к чему?) к уравне́ни ю
- в. п. напишу (что?) уравне́ни е
- т. п. занят (чем?) уравне́ни е м
- п. п. найдем (в чём?) в уравне́ни и
Поупражняемся в определении падежных форм слова «уравнение» и написании окончаний -е или -и.
Примеры
В уравнение с неизвестными величинами подставьте их значения.
Запишите символы величин, входящих в уравнение.
При решении учтите, что в уравнении не проставлены все коэффициенты.
Ученый внес изменения в уравнение, по-своему понимая физику твердого тела.
В уравнении имеется ошибка, которую вам предстоит указать.
Источник статьи: http://al-shell.ru/articles/uravnenie-ili-urovnenie-kak-pishetsya/
«В уравнение» или «в уравнении», как правильно
Определим, как различать слова «в уравнении» или «в уравнение» по их грамматическим признакам в контексте.
Слова «в уравнение» и «в уравнении» — это падежные формы существительного среднего рода «уравнение». Они имеют один и тот же предлог «в» и звучат одинаково из-за безударного окончания:
- в уравне́ние — приставка/корень/суффикс/окончание;
- в уравне́нии — приставка/корень/суффикс/окончание.
«В уравнении» правильно пишется с буквой «и» в окончании предложного падежа. Слово «в уравнение» имеет окончание «е» как форма винительного падежа с предлогом.
Чтобы правильно выбрать окончание, обозначенное буквой «е» или «и», определим падежную форму существительного в контексте.
Когда пишется «в уравнение»?
Когда пишется «в уравнение», выясним, если зададим к нему падежный вопрос в предложении:
Вам следует вставить в уравнение неизвестные величины, обозначенные x и y.
Следует вставить (во что?) в уравнение
Рассматриваемое слово имеет форму винительного падежа единственного числа. Как неодушевленное существительное, оно в винительном падеже имеет такое же безударное окончание, как и форме именительного падежа:
(что?) уравне́ние — (во что?) в уравне́ние.
Слово «в уравнение» правильно пишется с буквой «е» в окончании винительного падежа с предлогом.
Правописание слова «в уравнении»
Чтобы выяснить, почему «в уравнении» пишется окончание «и», укажем, что предлог «в» может использоваться также в форме предложного падежа существительных:
- поставить ударение (в чём?) в сло́ве
- выросло (в чём?) в по́ле
- заметил (в чём?) в окне́.
Как видим, в этой падежной форме существительные среднего рода имеют типичное окончание -е, кроме слов, заканчивающихся буквосочетанием -ие. Такие слова склоняются по-особому.
В форме предложного падежа с любым предлогом существительные с конечным сочетанием -ие имеют безударное окончание -и:
- созвездие — увидим (в чём?) в созве́здии
- описание — узнаешь (при чём?) при описа́нии
- расстояние — поставьте (на чём?) на расстоя́нии
- измерение — расскажете (о чём?) об измере́нии.
Обратим внимание, что существительное среднего рода «уравнение» также заканчивается буквосочетанием -ие. Посмотрим, как оно изменяется по падежам в единственном числе:
- и. п. (что?) уравне́ние
- р. п. формула (чего?) уравне́ния
- д. п. добавлю (к чему?) к уравне́нию
- в. п. напишу (что?) уравне́ние
- т. п. занят (чем?) уравне́нием
- п. п. найдем (в чём?) в уравне́нии
Слово «в уравнении» пишется с буквой «и» в безударном окончании предложного падежа существительного «уравнение», заканчивающегося на -ие.
Поупражняемся в определении падежных форм слова «уравнение» и написании окончаний -е или -и.
Примеры
В уравнение с неизвестными величинами подставьте их значения.
Запишите символы величин, входящих в уравнение.
При решении учтите, что в уравнении не проставлены все коэффициенты.
Ученый внес изменения в уравнение, по-своему понимая физику твердого тела.
В уравнении имеется ошибка, которую вам предстоит указать.
Читайте также: «На расстояниЕ» или «на расстояниИ» — как правильно писать.
Источник статьи: http://litfest.ru/kak-pisati/yravnenie.html
«В уравнениИ» или «в уравнениЕ», как пишется?
«В уравнении» правильно пишется с буквой «и» в окончании предложного падежа. Слово «в уравнение» имеет окончание «е» как форма винительного падежа с предлогом.
Определим, как различать слова «в уравнении» или «в уравнение» по их грамматическим признакам в контексте.
Слова «в уравнение» и «в уравнении» — это падежные формы существительного среднего рода «уравнение». Они имеют один и тот же предлог «в» и звучат одинаково из-за безударного окончания:
Чтобы правильно выбрать окончание, обозначенное буквой «е» или «и», определим падежную форму существительного в контексте.
Когда пишется «в уравнение»?
Когда пишется «в уравнение», выясним, если зададим к нему падежный вопрос в предложении:
Вам следует вставить в уравнение неизвестные величины, обозначенные x и y.
Следует вставить (во что?) в уравнение
Рассматриваемое слово имеет форму винительного падежа единственного числа. Как неодушевленное существительное, оно в винительном падеже имеет такое же безударное окончание, как и форме именительного падежа:
(что?) уравне́ни е — (во что?) в уравне́ни е .
ВыводСлово «в уравнение» правильно пишется с буквой «е» в окончании винительного падежа с предлогом.
Правописание слова «в уравнении»
Чтобы выяснить, почему «в уравнении» пишется окончание «и», укажем, что предлог «в» может использоваться также в форме предложного падежа существительных:
- поставить ударение (в чём?) в сло́в е
- выросло (в чём?) в по́л е
- заметил (в чём?) в окн е́ .
Как видим, в этой падежной форме существительные среднего рода имеют типичное окончание -е, кроме слов, заканчивающихся буквосочетанием -ие. Такие слова склоняются по-особому. В форме предложного падежа с любым предлогом существительные с конечным сочетанием -ие имеют безударное окончание -и :
- созвезд ие — увидим (в чём?) в созве́зди и
- описан ие — узнаешь (при чём?) при описа́ни и
- расстоян ие — поставьте (на чём?) на расстоя́ни и
- измерен ие — расскажете (о чём?) об измере́ни и .
Обратим внимание, что существительное среднего рода «уравнение» также заканчивается буквосочетанием -ие. Посмотрим, как оно изменяется по падежам в единственном числе:
- и. п. (что?) уравне́ни е
- р. п. формула (чего?) уравне́ни я
- д. п. добавлю (к чему?) к уравне́ни ю
- в. п. напишу (что?) уравне́ни е
- т. п. занят (чем?) уравне́ни е м
- п. п. найдем (в чём?) в уравне́ни и
ВыводСлово «в уравнении» пишется с буквой «и» в безударном окончании предложного падежа существительного «уравнение», заканчивающегося на -ие.
Поупражняемся в определении падежных форм слова «уравнение» и написании окончаний -е или -и.
Примеры
В уравнение с неизвестными величинами подставьте их значения.
Запишите символы величин, входящих в уравнение.
При решении учтите, что в уравнении не проставлены все коэффициенты.
Ученый внес изменения в уравнение, по-своему понимая физику твердого тела.
В уравнении имеется ошибка, которую вам предстоит указать.
Источник статьи: http://sprint-olympic.ru/uroki/russkij-jazyk-uroki/kak-pravilno-pishetsja/168432-v-uravnenii-ili-v-uravnenie-kak-pishetsya.html
«В уравнениИ» или «в уравнениЕ», как пишется?
«В уравнении» правильно пишется с буквой «и» в окончании предложного падежа. Слово «в уравнение» имеет окончание «е» как форма винительного падежа с предлогом.
Определим, как различать слова «в уравнении» или «в уравнение» по их грамматическим признакам в контексте.
Слова «в уравнение» и «в уравнении» — это падежные формы существительного среднего рода «уравнение». Они имеют один и тот же предлог «в» и звучат одинаково из-за безударного окончания:
Чтобы правильно выбрать окончание, обозначенное буквой «е» или «и», определим падежную форму существительного в контексте.
Когда пишется «в уравнение»?
Когда пишется «в уравнение», выясним, если зададим к нему падежный вопрос в предложении:
Вам следует вставить в уравнение неизвестные величины, обозначенные x и y.
Следует вставить (во что?) в уравнение
Рассматриваемое слово имеет форму винительного падежа единственного числа. Как неодушевленное существительное, оно в винительном падеже имеет такое же безударное окончание, как и форме именительного падежа:
(что?) уравне́ни е — (во что?) в уравне́ни е .
ВыводСлово «в уравнение» правильно пишется с буквой «е» в окончании винительного падежа с предлогом.
Правописание слова «в уравнении»
Чтобы выяснить, почему «в уравнении» пишется окончание «и», укажем, что предлог «в» может использоваться также в форме предложного падежа существительных:
- поставить ударение (в чём?) в сло́в е
- выросло (в чём?) в по́л е
- заметил (в чём?) в окн е́ .
Как видим, в этой падежной форме существительные среднего рода имеют типичное окончание -е, кроме слов, заканчивающихся буквосочетанием -ие. Такие слова склоняются по-особому. В форме предложного падежа с любым предлогом существительные с конечным сочетанием -ие имеют безударное окончание -и :
- созвезд ие — увидим (в чём?) в созве́зди и
- описан ие — узнаешь (при чём?) при описа́ни и
- расстоян ие — поставьте (на чём?) на расстоя́ни и
- измерен ие — расскажете (о чём?) об измере́ни и .
Обратим внимание, что существительное среднего рода «уравнение» также заканчивается буквосочетанием -ие. Посмотрим, как оно изменяется по падежам в единственном числе:
- и. п. (что?) уравне́ни е
- р. п. формула (чего?) уравне́ни я
- д. п. добавлю (к чему?) к уравне́ни ю
- в. п. напишу (что?) уравне́ни е
- т. п. занят (чем?) уравне́ни е м
- п. п. найдем (в чём?) в уравне́ни и
ВыводСлово «в уравнении» пишется с буквой «и» в безударном окончании предложного падежа существительного «уравнение», заканчивающегося на -ие.
Поупражняемся в определении падежных форм слова «уравнение» и написании окончаний -е или -и.
Примеры
В уравнение с неизвестными величинами подставьте их значения.
Запишите символы величин, входящих в уравнение.
При решении учтите, что в уравнении не проставлены все коэффициенты.
Ученый внес изменения в уравнение, по-своему понимая физику твердого тела.
В уравнении имеется ошибка, которую вам предстоит указать.
Источник статьи: http://sprint-olympic.ru/uroki/russkij-jazyk-uroki/kak-pravilno-pishetsja/168432-v-uravnenii-ili-v-uravnenie-kak-pishetsya.html
Составить уравнение как пишется
Составить уравнение — значит выразить в математической форме связь между данными (известными) задачи и искомыми (неизвестными) ее величинами. Иногда эта связь, настолько явно содержится в формулировке задачи, что составление уравнения есть просто дословный пересказ задачи, на языке математических знаков.
Пример 1
Петров получил за работу на 160 руб. больше, чем половина суммы, которую получил Иванов. Вместе они получили 1120 руб. Сколько получили за работу Петров и Иванов?
Обозначим через х заработок Иванова. Половина его заработка есть 0,5x ; месячной заработок Петрова 0,5x + 160 вместе они зарабатывают 1120 руб.; математическая запись последней фразы будет
Уравнение составлено. Решая его по раз установленным правилам, находим, заработок Иванова х = 640руб.; заработок же Петрова 0,5x + 160 = 480 (руб.).
Чаще, однако, случается, что связь между данными и искомыми величинами не указывается в задаче прямо; ее нужно установить, исходя из условий задачи. В практических задачах так и бывает почти всегда. Только что приведенный пример носит надуманный характер; в жизни почти никогда подобных задач не встречается.
Для составления уравнения поэтому нельзя дать вполне исчерпывающих указаний. Однако на первых порах полезно руководствоваться следующим. Примем за значение искомой величины (или нескольких величин) какое-нибудь наугад взятое число (или несколько чисел) и поставим себе задачу проверить, угадали ли мы правильное решение задачи или нет. Если мы сумели провести эту проверку и обнаружить либо то, что догадка наша верна, либо то, что она неверна (скорее всего случится, конечно, второе), то мы немедленно можем составить нужное уравнение (или несколько уравнений). Именно, запишем те самые действия, которые мы производили для проверки, только вместо наугад взятого числа введем буквенной знак неизвестной величины. Мы получим требуемое уравнение.
Пример 1
Кусок сплава меди и цинка объемом в 1 дм 3 весит 8,14 кг. Сколько меди содержится в сплаве? (уд. вес меди 8,9 кг/дм 3 ; цинка — 7,0 кг/дм 3 ).
Возьмем наугад число, выражающее искомый объем меди, например 0,3 дм 3 . Проверим, удачно ли мы взяли это число. Так как 1 кг/дм 3 меди весит 8,9 кг, то 0,3 дм 3 весят 8,9 * 0,3 = 2,67 (кг). Объем цинка в сплаве есть 1 — 0,3 = 0,7 (дм 3 ). Вес его 7,0 * 0,7 = 4,9 (кг). Общий вес цинка и меди 2,67+ +4,9 = 7,57 (кг). Между тем вес нашего куска, по условию задачи, 8,14 кг. Догадка наша несостоятельна. Но зато мы немедленно получим уравнение решение которого даст правильный ответ. Вместо наугад взятого числа 0,3 дм 3 обозначим объем меди (в дм 3 ) через х. Вместо произведения 8,9 * 0,3 = 2,67 берем произведшие 8,9 x. Это — вес меди в сплаве. Вместо 1 – 0,3 = 0,7 берем 1 — х; это — объем цинка. Вместо 7,0 * 0,7 = 4,9 берем 7,0 (1 — x); это — вес цинка. Вместо 2,67 + 4,9 берем 8,9х + 7,0 (1 — х); это — общий вес цинка и меди. По условию он равен 8,14 кг; значит, 8,9х +7,0 (1 — x) = 8,14.
Решение этого уравнения дает x = 0,6. Проверку наугад взятого решения можно делать различными способами; соответственно этому можно получить для одной и той же задачи различные виды уравнения; все они, однако, дадут для искомой величины одно и, то же решение, такие уравнения называются равносильными друг другу.
Разумеется, после получения навыков в составлении уравнений нет нужды производить проверку наугад взятого числа: можно для значения искомой величины брать не число, а какую-нибудь букву (х, у и т. д.) и поступать так, как если бы эта буква (неизвестное) была тем числом, проверить которое мы собираемся.
Источник статьи: http://www.maths.yfa1.ru/algebra.php?id=16
Составить уравнение как пишется
Когда химические вещества вступают во взаимодействие, химические связи между их атомами разрушаются и образуются новые, уже в других сочетаниях. В результате одни вещества превращаются в другие.
Рассмотрим реакцию горения метана, происходящую в конфорке газовой плиты:
Молекула метана (CH₄) и две молекулы кислорода (2O₂) вступают в реакцию, образуя молекулу углекислого газа (CO₂) и две молекулы воды (2H₂O). Связи между атомами углерода (С) и водорода (H) в метане, а также между атомами кислорода (O) разрываются, и образуются новые связи между атомами углерода и кислорода в молекуле углекислого газа (CO₂) и между атомами водорода и кислорода в молекуле воды (H₂O).
Картинка даёт наглядное представление о том, что произошло в ходе реакции. Но зарисовывать сложные химические процессы такими схемами неудобно. Вместо этого учёные используют уравнения химических реакций.
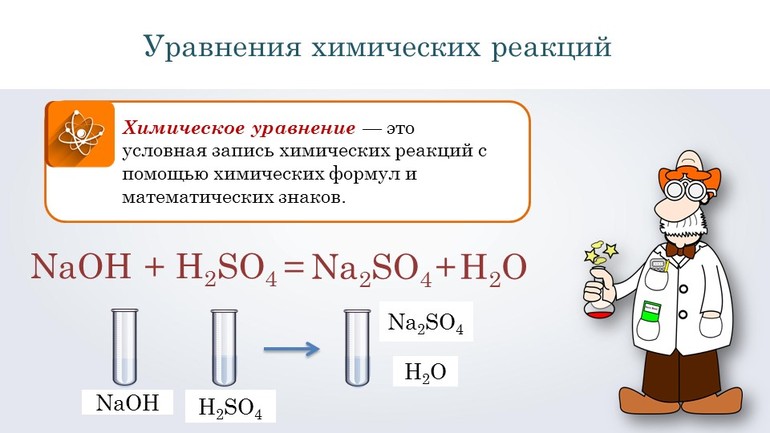
Химическое уравнение — это условная запись химической реакции с помощью формул и символов.
Их записывают в виде схемы, в которой отражён процесс превращения. В левой части располагаются формулы реагентов — веществ, вступающих в реакцию. Завершается уравнение продуктами реакции — веществом или веществами, которые получились в результате.
Новые вещества образуются потому, что изменяются связи между атомами, но сами атомы не возникают из ниоткуда и не исчезают в никуда. На рисунке видно, что атом углерода из состава метана перешёл в состав углекислого газа, атом водорода — в состав воды, а атомы кислорода распределились между молекулами углекислого газа и воды. Число атомов не изменилось.
Согласно закону сохранения массы, общая масса реагентов всегда равна общей массе продуктов реакции. Именно поэтому запись химической реакции называют уравнением.
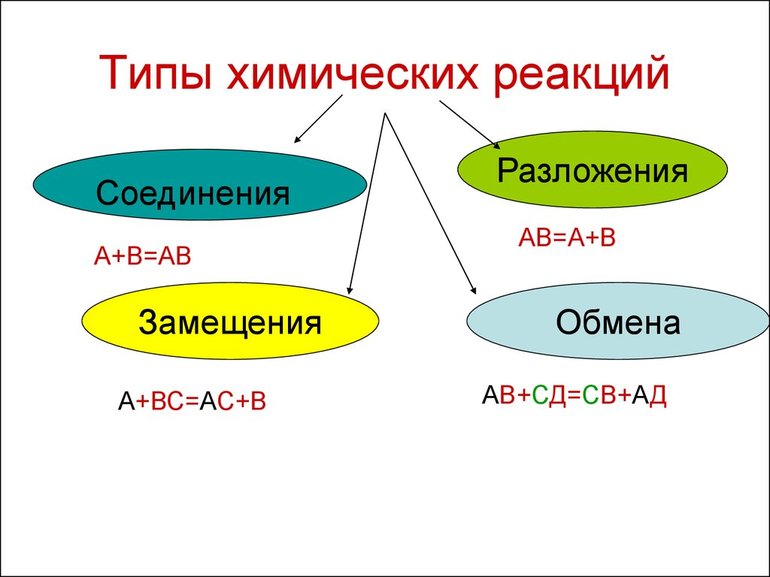
Виды химических реакций
Вещества вступают в реакции по-разному, можно выделить четыре наиболее частых варианта:
- Соединение. Два или несколько реагентов образуют один продукт. В реакцию могут вступать как простые вещества, так и сложные. Например, простые вещества водород и кислород взаимодействуют и образуют сложное — воду:
Сложное вещество негашёная известь соединяется с водой, и образуется новое сложное вещество — гашёная известь:
- Разложение. Обратный процесс: одно вещество распадается на несколько более простых. Например, если нагреть известняк, получаются негашёная известь и углекислый газ:
Стрелка вверх означает, что образовался газ. Он улетучивается и больше не участвует в реакции.
- Замещение. В реакции участвуют два вещества — простое и сложное. Если атомы химического элемента в простом веществе более активны, они замещают атомы одного из менее активных химических элементов в составе сложного вещества.
В примере атомы цинка замещают атомы водорода в составе хлороводорода, и образуется хлорид цинка:
- Обмен. Два сложных вещества обмениваются составными частями, в результате получаются два новых сложных вещества. В такой реакции обязательно образуется вода, газ или осадок.
Стрелка вниз означает, что вещество выпало в осадок, поскольку оно нерастворимо.
Коэффициенты в уравнениях химических реакций
Чтобы составить уравнение химической реакции, важно правильно подобрать коэффициенты перед формулами веществ.
Коэффициент в химических уравнениях означает число молекул (формульных единиц) вещества, необходимое для реакции. Он обозначается числом перед формулой (например, 2NaCl в последнем примере).
Коэффициент не следует путать с индексом (числом под символом химического элемента, например, О₂). Индекс обозначает количество атомов этого элемента в молекуле (формульной единице).
Чтобы узнать общее число атомов элемента в формуле, нужно умножить его индекс на коэффициент вещества. В примере на картинке (2H₂O) — четыре атома водорода и два кислорода.
Подобрать коэффициент — значит определить, сколько молекул данного вещества должно участвовать в реакции, чтобы она произошла. Далее мы расскажем, как это сделать.
Алгоритм составления уравнений химических реакций
Для начала составим схему химической реакции. Например, образование оксида магния (MgO) в процессе горения магния (Mg) в кислороде (O₂). Обозначим реагенты и продукт реакции:
Чтобы схема стала уравнением, нужно расставить коэффициенты. В левой части схемы два атома кислорода, а в правой — один. Уравняем их, увеличив число молекул продукта:
Теперь число атомов кислорода до и после реакции одинаковое, а число атомов магния — нет. Чтобы уравнять их, добавим ещё одну молекулу магния. Когда количество атомов каждого из химических элементов в составе веществ уравнено, вместо стрелки можно ставить равно:
Уравнение химической реакции составлено.
Рассмотрим реакцию разложения. Нитрат калия (KNO₃) разлагается на нитрит калия (KNO₂) и кислород (О₂):
В обеих частях схемы по одному атому калия и азота, а атомов кислорода до реакции 3, а после — 4. Необходимо их уравнять.
Для начала удвоим коэффициент перед реагентом:
Теперь в левой части схемы шесть атомов кислорода, два атома калия и два атома азота. В левой по-прежнему по одному атому калия и азота и четыре атома кислорода. Чтобы уравнять их, в правой части схемы нужно удвоить коэффициент перед нитритом калия.
Снова посчитаем число атомов каждого химического элемента в составе веществ до и после реакции: два атома калия, два атома азота и шесть атомов кислорода. Равенство достигнуто.
Химические уравнения не только позволяют предсказать, что произойдёт при взаимодействии тех или иных веществ, но и помогают рассчитать их количественное соотношение, необходимое для реакции.
Учите химию вместе с домашней онлайн-школой «Фоксфорда»! По промокоду CHEMISTRY892021 вы получите бесплатный недельный доступ к курсам химии за 8 класс и 9 класс.
У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Источник статьи: http://externat.foxford.ru/polezno-znat/wiki-himiya-uravneniya-himicheskih-reakcij
Как составлять ионные уравнения. Задача 31 на ЕГЭ по химии
Достаточно часто школьникам и студентам приходится составлять т. н. ионные уравнения реакций. В частности, именно этой теме посвящена задача 31, предлагаемая на ЕГЭ по химии. В данной статье мы подробно обсудим алгоритм написания кратких и полных ионных уравнений, разберем много примеров разного уровня сложности.
Зачем нужны ионные уравнения
Напомню, что при растворении многих веществ в воде (и не только в воде!) происходит процесс диссоциации — вещества распадаются на ионы. Например, молекулы HCl в водной среде диссоциируют на катионы водорода (H + , точнее, H 3 O + ) и анионы хлора (Cl — ). Бромид натрия (NaBr) находится в водном растворе не в виде молекул, а в виде гидратированных ионов Na + и Br — (кстати, в твердом бромиде натрия тоже присутствуют ионы).
Записывая «обычные» (молекулярные) уравнения, мы не учитываем, что в реакцию вступают не молекулы, а ионы. Вот, например, как выглядит уравнение реакции между соляной кислотой и гидроксидом натрия:
Разумеется, эта схема не совсем верно описывает процесс. Как мы уже сказали, в водном растворе практически нет молекул HCl, а есть ионы H + и Cl — . Так же обстоят дела и с NaOH. Правильнее было бы записать следующее:
H + + Cl — + Na + + OH — = Na + + Cl — + H 2 O. (2)
Это и есть полное ионное уравнение . Вместо «виртуальных» молекул мы видим частицы, которые реально присутствуют в растворе (катионы и анионы). Не будем пока останавливаться на вопросе, почему H 2 O мы записали в молекулярной форме. Чуть позже это будет объяснено. Как видите, нет ничего сложного: мы заменили молекулы ионами, которые образуются при их диссоциации.
Впрочем, даже полное ионное уравнение не является безупречным. Действительно, присмотритесь повнимательнее: и в левой, и в правой частях уравнения (2) присутствуют одинаковые частицы — катионы Na + и анионы Cl — . В процессе реакции эти ионы не изменяются. Зачем тогда они вообще нужны? Уберем их и получим краткое ионное уравнение:
Как видите, все сводится к взаимодействию ионов H + и OH — c образованием воды (реакция нейтрализации).
Все, полное и краткое ионные уравнения записаны. Если бы мы решали задачу 31 на ЕГЭ по химии, то получили бы за нее максимальную оценку — 2 балла.
Итак, еще раз о терминологии:
- HCl + NaOH = NaCl + H 2 O — молекулярное уравнение («обычное» уравнения, схематично отражающее суть реакции);
- H + + Cl — + Na + + OH — = Na + + Cl — + H 2 O — полное ионное уравнение (видны реальные частицы, находящиеся в растворе);
- H + + OH — = H 2 O — краткое ионное уравнение (мы убрали весь «мусор» — частицы, которые не участвуют в процессе).
Алгоритм написания ионных уравнений
- Составляем молекулярное уравнение реакции.
- Все частицы, диссоциирующие в растворе в ощутимой степени, записываем в виде ионов; вещества, не склонные к диссоциации, оставляем «в виде молекул».
- Убираем из двух частей уравнения т. н. ионы-наблюдатели, т. е. частицы, которые не участвуют в процессе.
- Проверяем коэффициенты и получаем окончательный ответ — краткое ионное уравнение.
Пример 1 . Составьте полное и краткое ионные уравнения, описывающие взаимодействие водных растворов хлорида бария и сульфата натрия.
Решение . Будем действовать в соответствии с предложенным алгоритмом. Составим сначала молекулярное уравнение. Хлорид бария и сульфат натрия — это две соли. Заглянем в раздел справочника «Свойства неорганических соединений». Видим, что соли могут взаимодействовать друг с другом, если в ходе реакции образуется осадок. Проверим:
BaCl 2 + Na 2 SO 4 = BaSO 4 ↓ + 2NaCl.
Таблица растворимости подсказывает нам, что BaSO 4 действительно не растворяется в воде (направленная вниз стрелка, напомню, символизирует, что данное вещество выпадает в осадок). Молекулярное уравнение готово, переходим к составлению полного ионного уравнения. Обе соли, присутствующие в левой части, записываем в ионной форме, а вот в правой части оставляем BaSO 4 в «молекулярной форме» (о причинах этого — чуть позже!) Получаем следующее:
Ba 2+ + 2Cl — + 2Na + + SO 4 2- = BaSO 4 ↓ + 2Cl — + 2Na + .
Осталось избавиться от балласта: убираем ионы-наблюдатели. В данном случае в процессе не участвуют катионы Na + и анионы Cl — . Стираем их и получаем краткое ионное уравнение:
Ba 2+ + SO 4 2- = BaSO 4 ↓.
А теперь поговорим подробнее о каждом шаге нашего алгоритма и разберем еще несколько примеров.
Как составить молекулярное уравнение реакции
Должен сразу вас разочаровать. В этом пункте не будет однозначных рецептов. Действительно, вряд ли можно рассчитывать, что я смогу разобрать здесь ВСЕ возможные уравнения реакций, которые могут встретиться вам на ЕГЭ или ОГЭ по химии.
Ваш помощник — раздел «Свойства неорганических соединений». Если вы хорошо знакомы с четырьмя базовыми классами неорганических веществ (оксиды, основания, кислоты, соли), если вам известны химические свойства этих классов и методы их получения, можете на 95% быть уверены в том, что у вас не будет проблем на экзамене с написанием молекулярных уравнений.
Оставшиеся 5% — это некоторые «специфические» реакции, которые мы не сможем перечислить. Не будем лить слез по поводу этих 5%, а вспомним лучше номенклатуру и химические свойства базовых классов неорганических веществ. Три задания для самостоятельной работы:
Упражнение 1 . Напишите молекулярные формулы следующих веществ: оксид фосфора (V), нитрат цезия, сульфат хрома (III), бромоводородная кислота, карбонат аммония, гидроксид свинца (II), фосфат стронция, кремниевая кислота. Если при выполнении задания у вас возникнут проблемы, обратитесь к разделу справочника «Названия кислот и солей».
Упражнение 2 . Дополните уравнения следующих реакций:
- KOH + H 2 SO 4 =
- H 3 PO 4 + Na 2 O=
- Ba(OH) 2 + CO 2 =
- NaOH + CuBr 2 =
- K 2 S + Hg(NO 3 ) 2 =
- Zn + FeCl 2 =
Упражнение 3 . Напишите молекулярные уравнения реакций (в водном растворе) между: а) карбонатом натрия и азотной кислотой, б) хлоридом никеля (II) и гидроксидом натрия, в) ортофосфорной кислотой и гидроксидом кальция, г) нитратом серебра и хлоридом калия, д) оксидом фосфора (V) и гидроксидом калия.
Искренне надеюсь, что у вас не возникло проблем с выполнением этих трех заданий. Если это не так, необходимо вернуться к теме «Химические свойства основных классов неорганических соединений».
Как превратить молекулярное уравнение в полное ионное уравнение
Начинается самое интересное. Мы должны понять, какие вещества следует записывать в виде ионов, а какие — оставить в «молекулярной форме». Придется запомнить следующее.
В виде ионов записывают:
- растворимые соли (подчеркиваю, только соли хорошо растворимые в воде);
- щелочи (напомню, что щелочами называют растворимые в воде основания, но не NH 4 OH);
- сильные кислоты (H 2 SO 4 , HNO 3 , HCl, HBr, HI, HClO 4 , HClO 3 , H 2 SeO 4 , . ).
Как видите, запомнить этот список совсем несложно: в него входят сильные кислоты и основания и все растворимые соли. Кстати, особо бдительным юным химикам, которых может возмутить тот факт, что сильные электролиты (нерастворимые соли) не вошли в этот перечень, могу сообщить следующее: НЕвключение нерастворимых солей в данный список вовсе не отвергает того, что они являются сильными электролитами.
Все остальные вещества должны присутствовать в ионных уравнениях в виде молекул. Тем требовательным читателям, которых не устраивает расплывчатый термин «все остальные вещества», и которые, следуя примеру героя известного фильма, требуют «огласить полный список» даю следующую информацию.
В виде молекул записывают:
- все нерастворимые соли;
- все слабые основания (включая нерастворимые гидроксиды, NH 4 OH и сходные с ним вещества);
- все слабые кислоты (H 2 СO 3 , HNO 2 , H 2 S, H 2 SiO 3 , HCN, HClO, практически все органические кислоты . );
- вообще, все слабые электролиты (включая воду. );
- оксиды (всех типов);
- все газообразные соединения (в частности, H 2 , CO 2 , SO 2 , H 2 S, CO);
- простые вещества (металлы и неметаллы);
- практически все органические соединения (исключение — растворимые в воде соли органических кислот).
Уф-ф, кажется, я ничего не забыл! Хотя проще, по-моему, все же запомнить список N 1. Из принципиально важного в списке N 2 еще раз отмечу воду.
Пример 2 . Составьте полное ионное уравнение, описывающие взаимодействие гидроксида меди (II) и соляной кислоты.
Решение . Начнем, естественно, с молекулярного уравнения. Гидроксид меди (II) — нерастворимое основание. Все нерастворимые основания реагируют с сильными кислотами с образованием соли и воды:
Cu(OH) 2 + 2HCl = CuCl 2 + 2H 2 O.
А теперь выясняем, какие вещества записывать в виде ионов, а какие — в виде молекул. Нам помогут приведенные выше списки. Гидроксид меди (II) — нерастворимое основание (см. таблицу растворимости), слабый электролит. Нерастворимые основания записывают в молекулярной форме. HCl — сильная кислота, в растворе практически полностью диссоциирует на ионы. CuCl 2 — растворимая соль. Записываем в ионной форме. Вода — только в виде молекул! Получаем полное ионное уравнение:
Сu(OH) 2 + 2H + + 2Cl — = Cu 2+ + 2Cl — + 2H 2 O.
Пример 3 . Составьте полное ионное уравнение реакции диоксида углерода с водным раствором NaOH.
Решение . Диоксид углерода — типичный кислотный оксид, NaOH — щелочь. При взаимодействии кислотных оксидов с водными растворами щелочей образуются соль и вода. Составляем молекулярное уравнение реакции (не забывайте, кстати, о коэффициентах):
CO 2 + 2NaOH = Na 2 CO 3 + H 2 O.
CO 2 — оксид, газообразное соединение; сохраняем молекулярную форму. NaOH — сильное основание (щелочь); записываем в виде ионов. Na 2 CO 3 — растворимая соль; пишем в виде ионов. Вода — слабый электролит, практически не диссоциирует; оставляем в молекулярной форме. Получаем следующее:
СO 2 + 2Na + + 2OH — = Na 2+ + CO 3 2- + H 2 O.
Пример 4 . Сульфид натрия в водном растворе реагирует с хлоридом цинка с образованием осадка. Составьте полное ионное уравнение данной реакции.
Решение . Сульфид натрия и хлорид цинка — это соли. При взаимодействии этих солей выпадает осадок сульфида цинка:
Na 2 S + ZnCl 2 = ZnS↓ + 2NaCl.
Я сразу запишу полное ионное уравнение, а вы самостоятельно проанализируете его:
2Na + + S 2- + Zn 2+ + 2Cl — = ZnS↓ + 2Na + + 2Cl — .
Предлагаю вам несколько заданий для самостоятельной работы и небольшой тест.
Упражнение 4 . Составьте молекулярные и полные ионные уравнения следующих реакций:
- NaOH + HNO 3 =
- H 2 SO 4 + MgO =
- Ca(NO 3 ) 2 + Na 3 PO 4 =
- CoBr 2 + Ca(OH) 2 =
Упражнение 5 . Напишите полные ионные уравнения, описывающие взаимодействие: а) оксида азота (V) с водным раствором гидроксида бария, б) раствора гидроксида цезия с иодоводородной кислотой, в) водных растворов сульфата меди и сульфида калия, г) гидроксида кальция и водного раствора нитрата железа (III).
В следующей части статьи мы научимся составлять краткие ионные уравнения и разберем большое количество примеров. Кроме того, мы обсудим специфические особенности задания 31, которое вам предстоит решать на ЕГЭ по химии.
Источник статьи: http://www.repetitor2000.ru/ionnye_uravnenija_01.html
Как решать химические уравнения — схемы и примеры решения для разных реакций
Различные процессы, происходящие с веществами, сопровождаются разрывом и образованием различных связей. Чтобы представить происходящее в понятном виде используют специальные уравнения. С их помощью можно предсказать, что произойдёт при взаимодействии элементов даже без опытов. Это фактически отражение реакций в доступном виде. Существуют определённые правила, позволяющие решать химические уравнения, которые необходимо знать при изучении химии.
Основные термины и понятия
Составление уравнений химических реакций невозможно без знания определённых обозначений, показывающих, как проходит реакция. Объединение атомов, имеющих одинаковый ядерный заряд, называют химическим элементом. Ядро атома состоит из протонов и нейтронов. Первые совпадают с числом атомного номера элемента, а значение вторых может варьироваться. Простейшими веществами называют элементы, состоящие из однотипных атомов.
Любой химический элемент описывается с помощью символов, условно обозначающих структуру веществ. Формулы являются неотъемлемой частью языка науки. Именно на их основе составляют уравнения и схемы. По своей сути они отражают количественный и качественный состав элементов. Например, запись HNO3 сообщает, что в соединении содержится одна молекула азотной кислоты, а оно само состоит из водорода, азота и кислорода. При этом в состав одного моля азотной кислоты входит по одному атому водорода и азота и 3 кислорода.
Символика элементов, условное обозначение, представляет собой химический язык. В значке содержится информация о названии, массовом числе и порядковом номере. Международное обозначение принято, согласно периодической таблице Менделеева, разработанной в начале 1870 года.
Взаимодействующие между собой вещества называются реагентами, а образующиеся в процессе реакции — продуктами. Составление и решение химических уравнений фактически сводится к определению результатов реакций, поэтому просто знать формулы веществ мало, нужно ещё уметь подбирать коэффициенты. Располагаются они перед формулой и указывают на количество молекул или атомов, принимающих участие в процессе. С правой стороны от химического вещества ставится индекс, указывающий место элемента в системе.
Записывают уравнения в виде цепочки, в которой указываются все стадии превращения вещества начиная с левой части. Вначале пишут формулы элементов в исходном состоянии, а затем последовательно их преобразование.
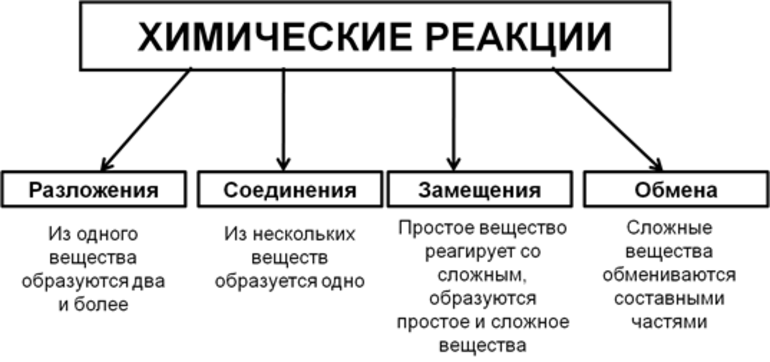
Виды химических реакций
Химические явления характеризуются тем, что из двух и более элементов образуются новые вещества. Уравнения описывают эти процессы. Впервые с объяснениями протекания реакций знакомят в восьмом классе средней образовательной школы на уроках неорганической химии. Ученикам демонстрируют опыты, в которых явно наблюдаются различия в протекании реакций.
Всего существует 4 типа химического взаимодействия веществ:
- Соединение. В реакцию могут вступать 2 простых вещества: металл и неметалл или неметалл и неметалл. Например, алюминий с серой образуют сульфид алюминия. Кислород, взаимодействуя с водородом, превращается в воду. Объединятся могут 2 оксида с растворимым основанием, как оксид кальция с водой: CaO + H2O = Ca (OH)2 или основной оксид с кислотным: CaO + SO3 = CaSO4.
- Разложение. Это процесс обратный реакции соединения: было одно вещество, а стало несколько. Например, при пропускании электрического тока через воду получается водород и кислород, а при нагревании известняка 2 оксида: CaCO3 = CaO + CO2.
- Замещение. В реакцию вступают 2 элемента. Один из них простой, а второй сложный. В итоге образуются 2 новых соединения, при котором атом простого вещества заменяет сложный, как бы вытесняя его. Условие протекания процесса: простое вещество должно быть более активным, чем сложное. Например, Zn + 2HCl = ZnCl2 + H2. Величину активности можно узнать из таблицы ряда электрохимических напряжений.
- Обмен. В этом случае между собой реагируют 2 сложных элемента, обменивающиеся своими составными частями. Условием осуществления такого типа реакции является обязательное образование воды, газа или осадка. Например, CuO + 2HCl = CuCl2 + H2O. Чтобы узнать, смогут ли вещества прореагировать, используют таблицу растворимости.
Основными признаками химических реакций является изменение цвета, выделение газа или образование осадка. Различают их по числу веществ, вступивших в реакцию и образовавшихся продуктов. Правильное определение типа реакции особо важно при составлении химических уравнений, а также определения свойств и возможностей веществ.
Окислительно-восстановительный процесс
Составление большинства реакций сводится к подбору коэффициентов. Но при этом могут возникнуть трудности с установлением равновесия, согласно закону сохранения массы веществ. Чаще всего такая ситуация возникает при решении заданий, связанных с расстановкой количества атомов в уравнениях окислительно-восстановительных процессов.
Под ними принято понимать превращения, протекающие с изменением степени окисления элементов. При окислении происходит процесс передачи атомом электронов, сопровождающийся приобретением им положительного заряда или ионом, после чего он становится нейтральным. При этом также происходит процесс восстановления, связанный с присоединением элементарных частиц атомом.
Для составления уравнений необходимо определить восстановитель, окислитель и число участвующих в реакции электронов. Коэффициенты же подбирают с помощью метода электронно-ионного баланса (полуреакций). Его суть состоит в установлении равенства путём уравнивания количества электронов, отдаваемых одним элементом и принимаемым другим.
Классический алгоритм
В основе решения задач этим методом — закон сохранения массы. Согласно ему, совокупная масса элементов до реакции и после остаётся неизменной. Другими словами, происходит перегруппировка частиц. Если рассматривать решение химического уравнения поэтапно, оно будет состоять из трёх шагов:
- Написания формул элементов, вступающих в реакцию с левой стороны.
- Указания справа формулы образующихся веществ.
- Уравнивания числа атомов с добавлением коэффициентов.
Перед тем как переходить к сложным соединениям, лучше всего потренироваться на простых. Например, нужно составить уравнение, описывающее взаимодействие двух сложных веществ: гидроксида натрия и серной кислоты. При таком соединении образуется сульфат натрия и вода.
Согласно алгоритму, в левой части уравнения необходимо записать реагенты, а в правой продукты реакции: NaOH + H2SO 4 → Na 2SO4 + H2O. Теперь следует уравнять коэффициенты. Начинают с первого элемента. В примере это натрий. В правой части содержится 2 его атома, а в левой один, поэтому необходимо возле реагента поставить цифру 2. Затем нужно уровнять водород. В результате получится выражение: 2 NaOH + H2SO 4 → Na2 SO4 +2H2O.
Ещё одним наглядным примером является процесс реакции тринитротолуола с кислородом. При их взаимодействии образуется: C7H5N3O6 + O2 → CO2 + H2O + N2. Исходя из того, что слева находится нечётное число атомов H и N, а справа чётное, нужно их уравнять: 2C7H5N3O6 + O2 → CO2 + H2O + N2.
Теперь становится понятным, что 14 и 10 атомов углерода и водорода должны образовать 14 долей диоксида и 5 молекул воды. При этом 6 атомов азота превратятся в 3. Итоговое уравнение будет выглядеть как 2C7H5N3O6 + 10,5O2 → 14CO2 + 5H2O + 3N2.
Перед тем как начинать тренировку по составлению уравнений, следует научиться расставлять валентность. Это параметр, равный числу соединившихся атомов каждого элемента. Фактически это способность к соединению. Например, в формуле NH3 валентность атома азота равна 3, а водорода 1.
Решение методом полуреакций
Алгоритм для решения примеров химических уравнений проще рассмотреть на конкретном задании. Пускай необходимо описать процесс окисления пирита азотной кислоты с малой концентрацией: FeS2 + HNO3. Решать этот пример необходимо в следующей последовательности:
- Определить продукты реакции. Так как кислота является сильным окислителем, сера получит максимальную степень оксидации S6+, а железо Fe3+. HNO3 может восстановиться до одного из двух состояний NO2 или NO.
- Исходя из состава ионов и правила, что вещества, переходящие в газовую форму или плохо растворимые, записываются в молекулярном виде, верным будет записать: FeS2 — Fe3+ + 2SO2−4. Гидролизом можно пренебречь.
- В записи уравнивают кислород. Для этого в левую часть добавляют 8 молекул воды, а в правую 16 ионов водорода: FeS2 + 8H20 — Fe3+ + 2SO2−4 + 16H+. Так как заряда в левой части нет, а в правой он равный +15, то серное железо должно будет отдать 15 электронов. Значит, уравнение примет вид: FeS2 + 8H20 — 15e → Fe3+ + 2SO2−4 + 16H+.
- Теперь переходят к реакции восстановления нитрата иона: NO-3 →NO. Для её составления нужно отнять у оксида азота 2 атома кислорода. Делают это путём прибавления к левой части 4 ионов водорода, а правой — 2 молекул воды. В итоге получится: NO-3 + 4H+ → NO + 2H2O.
- Полученную формулу уравнивают добавлением к левой части 3 электронов: NO-3 + 4H+ 3e → NO + 2H2O.
- Объединяют найденные выражения и записывают результат: FeS2 + 8H20 + 5NO-3 + 20H+ → Fe3+ + 2SO2−4 + 16H+ + 5NO + 10H2O.
Уравнение можно сократить на 16H + и 8H2O. В итоге получится сокращённое выражение окислительно-восстановительной реакции: FeS2 + 5NO — 3 + 4 H + = Fe3 + + 2SO 2- 4 + 5NO + 2H2O.
Такой алгоритм считается классическим, но для упрощения понимания лучше использовать способ электронного баланса. Процесс восстановления переписывают как N5+ + 3e → N2+. Степень же окисления составить сложнее. Сере нужно приписать степень 2+ и учесть, что на 1 атом железа приходится 2 атома серы: FeS2 → Fe3++ 2S6+. Запись общего баланса будет выглядеть: FeS2 + 5N5+ = Fe3+ + 2S6+ + 5N2+.
Пять молекул потратятся на окисление серного железа, а ещё 3 на образование Fe (NO3)3. После уравнения двух сторон запись реакции примет вид, аналогичный полученному с использованием предыдущего метода.
Использование онлайн-расчёта
Простые уравнения решать самостоятельно довольно просто. Но состоящие из сложных веществ могут вызвать трудности даже у опытных химиков. Чтобы получить точную формулу и не подбирать вручную коэффициенты, можно воспользоваться онлайн-калькуляторами. При этом их использовать сможет даже пользователь, не особо разбирающийся в науке.
Чтобы расстановка коэффициентов в химических уравнениях онлайн происходила автоматически, нужно лишь подключение к интернету и исходные данные. Система самостоятельно вычислит продукты реакции и уравняет обе стороны формулы. Интересной особенностью таких сайтов является не только быстрый и правильный расчёт, но и описание правил с алгоритмами, по которому выполняются действия.
После загрузки калькулятора в веб-обозревателе единственное, что требуется от пользователя — правильно ввести реагенты в специальные формы латинскими буквами и нажать кнопку «Уравнять». Иногда возникает ситуация, когда запись сделана верно, но коэффициенты не расставляются. Это происходит, если суммы в уравнении могут быть подсчитаны разными способами. Характерно это для реакций окисления. В таком случае нужно заменить фрагменты молекул на любой произвольный символ. Таким способом можно не только рассчитать непонятное уравнение, но и выполнить проверку своих вычислений.
Источник статьи: http://nauka.club/khimiya/khimicheskie-uravneniya.html
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
-
Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
-
Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
-
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Решение задач с помощью уравнений
Тема урока: § 6. Решение задач с помощью уравнений. Приведены все необходимые и достаточные сведения для решения текстовых задач с помощью составления уравнений.
Введение
В школьной математике есть целый кладезь текстовых задач, которые решаются универсальным методом построения уравнения (модели) исходя из условия.
Сам факт того, что огромное количество самых разнообразных задач поддаются решению с помощью составления линейного уравнения, говорит нам, что метод решений является действительно универсальным.
Обычно условия задач удается перевести на математический язык. Полученное уравнение — это следствие перевода нашего условия с русского языка на язык алгебры. Зачастую фактической стороной повествования задачи является описание реальной ситуации, какого либо процесса, события.
Чтобы получить ответ — уравнение нужно решить, полученный корень уравнения будет являться решением, разумеется необходимо еще проверить, не является ли результат противоречивым относительно условия.
Алгоритм решения текстовых задач с помощью уравнений
Для решения задачи с помощью уравнения делают следующие действия:
- Обозначают некоторое неизвестное буквой и, пользуясь условием, составляют уравнение.
- Решают уравнение.
- Истолковывают результат.
Примеры решений
Задача 1.
В мешке было в 3 раза меньше монет, чем в сундуке. После того как из мешка переложили 24 монеты, в сундуке их стало в 7 раз больше, чем в мешке. Сколько было монет в мешке и сколько в сундуке?
Пусть $x$ — количество монет в мешке, а значит в сундуке: $3x$ монет. После того, как из мешка переложили $24$ монеты, в сундуке стало: $3x+24$, а в мешке $x-24$. И если в сундуке их стало в $7$ раз больше чем в мешке, то имеем: $3x+24=7(x-24)$.
Ну вот мы и составили уравнение (математическую модель), осталось решить уравнение относительно $x$ и записать ответ.
Решим полученное уравнение: $3x+24=7(x-24)$. Легко увидеть, что уравнение является линейным (узнать как решаются линейные уравнения можно тут.)
Раскроем скобки в правой части уравнения: $3x+24=7x-7cdot 24$. Перенесём все слагаемые содержащие переменную в правую часть, а всё что не содержит $x$ в левую, получим: $24+7cdot 24=7x-3x$. После упрощения получили $192=4x$, разделим обе части уравнения на коэффициент при неизвестном, т.е на $4$, тогда получим $x=48$.
Осталось истолковать ответ.
За переменную $x$ мы обозначали количество монет в мешке, значит в сундуке в три раза больше т.е $3x$.
Монет в мешке: $48$
Монет в сундуке: $48cdot 3=144$
Задача 2.
Купили 3600 кг муки и высыпали её в три мешка. В первый мешок муки вошло в 3 раза больше, чем во второй, а в третий мешок насыпали 800 кг муки. Сколько муки насыпали в первый и сколько во второй мешок?
Пусть в первый мешок насыпали $3x$ кг муки, тогда во второй мешок насыпали $x$ кг. Если сложим количество кг в каждом мешке, то получим $3600$ кг муки. Имеем: $3x+x+800=3600$, решим уравнение классическим методом.
Все слагаемые содержащие $x$ оставим слева, а всё остальное перенесём в правую часть равенства: $3x+x=3600-800$, упростим обе части; $4x=2800$ поделим обе части равенства на $4$ и получим ответ: $x=700$.
Ответ.
За переменную $x$ мы обозначали количество муки во втором мешке, по условию в первом в три раза больше.
Муки в первом мешке: $700cdot 3=2100$ кг.
Муки во втором мешке: $700$ кг.
Задача 3.
В первом мешке в 4 раза больше картофеля, чем во втором. После того, как из одного мешка взяли 40 кг картофеля, а во второй насыпали ещё 5 кг, в обоих мешках картофеля стало поровну. Сколько килограммов картофеля было во втором мешке.
Пусть во втором мешке $x$ кг картофеля, тогда в первом мешке $4x$ кг. Из первого взяли $40$ кг, тогда в первом стало: $4x-40$. Во второй мешок насыпали $5$ кг и теперь в нём: $x+5$ кг картошки. Нам известно, что после этих изменений количество картофеля в мешках стало поровну, запишем это с помощью линейного уравнения:
Решим это линейное уравнение. Все слагаемые содержащие переменную перенесём влево, а свободные члены вправо и получим:
Избавимся от коэффициента при неизвестном и получим ответ:
Ответ.
За переменную $x$ мы обозначали количество кг картошки во втором мешке, по условию в первом в четыре раза больше.
Картошки в первом мешке: $15cdot 4=60$ кг.
Картошки во втором мешке: $15$ кг.
Задача 4.
По шоссе едут две машины с одной и той же скоростью. Если первая увеличит скорость на 20 км/ч, а вторая уменьшит скорость на 20 км/ч, то первая за 2 часа пройдёт то же самое расстояние, что и вторая за 4 часа. Найдите первоначальную скорость машин.
Пусть машины едут со скоростью $v$ км/ч, тогда после ускорения первой машины её скорость стала: $v+20$ км/ч, а скорость второй машины после замедления стала: $v-20$ км/ч. Нам известно по условию, что после изменения скоростей машин, первая проходит за два часа ровно столько, сколько вторая за четыре, тогда имеем:
По известной нам формуле $S=vt$ ($S$ — расстояние, $v$ — скорость, $t$ — время)
Сократим обе части равенства на $2$, тогда получим: $v+20=2(v-20)$. Раскроем скобки в правой части уравнения и сгруппируем все переменные в правой части равенства.
Ответ.
В качестве неизвестной величины в задаче мы взяли $v$ (первоначальную скорость машин).
Первоначальная скорость машин: $v=60$ км/ч.
Задача 5.
В первую бригаду привезли раствора цемента на 50 кг меньше, чем во вторую. Каждый час работы первая бригада расходовала 150 кг раствора, а вторая – 200кг. Через 3 ч работы в первой бригаде осталось раствора в 1,5 раза больше, чем во второй. Сколько раствора привезли в каждую бригаду?
Пусть во вторую бригаду привезли $x$ кг раствора цемента, тогда в первую бригаду привезли $x-50$ кг. Через 3 часа работы у первой бригады осталось $x-50-3cdot 150$ кг цемента, а у второй $x-3cdot 200$ кг.
По условию известно, что через 3 часа работы в первой бригаде осталось в 1,5 раза больше цемента, чем во второй, тогда имеем:
$$x-50-3cdot 150=1,5(x-3cdot 200)$$
Осталось решить данное уравнение относительно $x$ и истолковать ответ.
Упростим и раскроем скобки в правой части, тогда получим:
Если вам неудобно работать с десятичными дробями, то вы всегда можете их переводить в рациональный вид: $1,5=frac<15><10>=frac<3><2>$.
Запишем с учётом перевода дробей и упростим:
Перенесём слагаемые содержащие переменную в правую сторону, а всё остальное в левую:
Домножим обе части на 2 и получим ответ:
Ответ.
В качестве переменной в задаче мы взяли $x$ (кол-во кг цемента который привезли во вторую бригаду), по условию в первую привезли на 50 кг меньше, а значит $x-50$
Кол-во цемента в первой бригаде: $800-50=750$ кг.
Кол-во цемента во второй бригаде: $800$ кг.
Задачи для самостоятельного решения
По контракту работникам причитается 48 франков за каждый отработанный день, а за каждый неотработанный день с них вычитается по 12 франков. Через 30 дней выяснилось, что работникам ничего не причитается. Сколько дней они отработали в течение этих 30 дней?
Пусть работники отработали $n$ дней, тогда $30-n$ дней они не отработали.
В итоге мы понимаем, что за $n$ рабочих дней они зарабатывают $48n$ франков и с них вычитается за $30-n$ не отработанных дней по $12(30-n)$ франков. Тогда ясно, что: $48n-12(30-n)=0$
Ответ: Рабочие отработали 6 дней.
Кирпич весит фунт и полкирпича. Сколько фунтов весит кирпич?
Пусть целый кирпич весит весит $k$ фунтов, тогда имеем:
1 фунт и половина кирпича = целый кирпич.
Бутылка с пробкой стоит 10 копеек, причем бутылка на 9 копеек дороже пробки. Сколько стоит бутылка без пробки?
Пусть бутылка стоит $b$ копеек, а пробка $p$ копеек, тогда:
$b+p=10$ и $b=p+9$, подставив значение $b$ в первое равенство — получим:
Т.е пробка стоит пол копейки, тогда бутылка $9,5$ копеек.
Ответ: 9,5 копеек стоит бутыка без пробки.
На свитер, шапку и шарф израсходовали 555 г шерсти, причем на шапку ушло в 5 раз меньше шерсти, чем на свитер, и на 5 г больше, чем на шарф. Сколько шерсти израсходовали на каждое изделие?
Пусть на свитер потратили $5x$ г шерсти, тогда на шапку ушло $x$ г и на шарф потребовалось $x-5$ г, имеем:
Ответ: На шапку ушло $80$ г, на свитер $5cdot 80=400$ г, на шарф $80-5=75$ г.
Три пионерских звена собрали для школьной библиотеки 65 книг. Первое звено собрало на 10 книг меньше, чем второе, а третье — 30% того числа книг, которое собрали первое и второе звено вместе. Сколько книг собрало каждое звено?
Пусть второе звено собрало $x$ книг, тогда первое собрало $x-10$ книг, а третье $0,3(2x-10)$, имеем:
$$2x-10+0,3cdot 2x-0,3cdot 10=65$$
$$2x+0,3cdot 2x=65+10+0,3cdot 10$$
Ответ: Первое звено собрало $30-10=20$ книг, второе $30$ книг, третье $0,3(60-10)=15$ книг.
Общие сведения об уравнениях
Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач.
С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.
В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.
Что такое уравнение?
Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.
Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5 .
А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x , значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство.
Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.
Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет
Говорят, что число 2 является корнем или решением уравнения 3 + x = 5
Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.
Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.
Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы.
Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части.
Выразить одно через другое
Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.
Рассмотрим следующее выражение:
Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10
Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.
Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.
Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:
Мы выразили число 2 из равенства 8 + 2 = 10 . Как видно из примера, ничего сложного в этом нет.
При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.
Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8 . Данное равенство можно прочесть так:
2 есть 10 − 8
То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:
Число 2 есть разность числа 10 и числа 8
Число 2 есть разница между числом 10 и числом 8.
Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.
Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:
Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2
Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:
В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно:
Пример 2. Рассмотрим равенство 8 − 2 = 6
Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:
Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6
Пример 3. Рассмотрим равенство 3 × 2 = 6
Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2
Вернем получившееся равенство в первоначальное состояние:
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3
Пример 4. Рассмотрим равенство
Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5
Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:
Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3
Правила нахождения неизвестных
Рассмотрим несколько правил нахождения неизвестных. Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2.
В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой.
Чтобы выразить число 2, мы поступили следующим образом:
То есть из суммы 10 вычли слагаемое 8.
Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x
В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10 , а переменная x берет на себя роль так называемого неизвестного слагаемого
Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10 . Для нахождения неизвестного слагаемого предусмотрено следующее правило:
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10 . Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8
А сейчас, чтобы найти неизвестное слагаемое x , мы должны из суммы 10 вычесть известное слагаемое 8:
Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x
Мы решили уравнение. Значение переменной x равно 2 . Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно:
В результате получается верное числовое равенство. Значит уравнение решено правильно.
Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8.
В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. Чтобы найти неизвестное слагаемое x , нужно из суммы 10 вычесть известное слагаемое 2
Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8.
В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность
Чтобы выразить число 8, мы поступили следующим образом:
То есть сложили разность 6 и вычитаемое 2.
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x
В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого
Для нахождения неизвестного уменьшаемого предусмотрено следующее правило:
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.
Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6 . Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.
А сейчас, чтобы найти неизвестное уменьшаемое x , мы должны к разности 6 прибавить вычитаемое 2
Если вычислить правую часть, то можно узнать чему равна переменная x
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного вычитаемого
Для нахождения неизвестного вычитаемого предусмотрено следующее правило:
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6.
А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6
Вычисляем правую часть и находим значение x
Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3.
В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение
Чтобы выразить число 3 мы поступили следующим образом:
То есть разделили произведение 6 на множитель 2.
Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного множимого.
Для нахождения неизвестного множимого предусмотрено следующее правило:
Чтобы найти неизвестное множимое, нужно произведение разделить на множитель.
Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6 . Произведение 6 мы разделили на множитель 2.
А сейчас для нахождения неизвестного множимого x , нужно произведение 6 разделить на множитель 2.
Вычисление правой части позволяет нам найти значение переменной x
Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x .
В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель:
Чтобы найти неизвестный множитель, нужно произведение разделить на множимое.
Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6 . Тогда для получения числа 2 мы разделили произведение 6 на множимое 3.
А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3.
Вычисление правой части равенства позволяет узнать чему равно x
Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя:
Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель.
Например, решим уравнение 9 × x = 18 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9
Отсюда .
Решим уравнение x × 3 = 27 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3
Отсюда .
Вернемся к четвертому примеру из предыдущей темы, где в равенстве требовалось выразить число 15. В этом равенстве число 15 — это делимое, число 5 — делитель, число 3 — частное.
Чтобы выразить число 15 мы поступили следующим образом:
То есть умножили частное 3 на делитель 5.
Теперь представим, что в равенстве вместо числа 15 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного делимого.
Для нахождения неизвестного делимого предусмотрено следующее правило:
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Что мы и сделали, когда выражали число 15 из равенства . Чтобы выразить число 15, мы умножили частное 3 на делитель 5.
А сейчас, чтобы найти неизвестное делимое x , нужно частное 3 умножить на делитель 5
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Теперь представим, что в равенстве вместо числа 5 располагается переменная x .
В этом случае переменная x берет на себя роль неизвестного делителя.
Для нахождения неизвестного делителя предусмотрено следующее правило:
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Что мы и сделали, когда выражали число 5 из равенства . Чтобы выразить число 5, мы разделили делимое 15 на частное 3.
А сейчас, чтобы найти неизвестный делитель x , нужно делимое 15 разделить на частное 3
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Итак, для нахождения неизвестных мы изучили следующие правила:
- Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
- Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
- Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность;
- Чтобы найти неизвестное множимое, нужно произведение разделить на множитель;
- Чтобы найти неизвестный множитель, нужно произведение разделить на множимое;
- Чтобы найти неизвестное делимое, нужно частное умножить на делитель;
- Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Компоненты
Компонентами мы будем называть числа и переменные, входящие в равенство
Так, компонентами сложения являются слагаемые и сумма
Компонентами вычитания являются уменьшаемое, вычитаемое и разность
Компонентами умножения являются множимое, множитель и произведение
Компонентами деления являются делимое, делитель и частное
В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть.
Пример 1. Найти корень уравнения 45 + x = 60
45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
Вычислим правую часть, получим значение x равное 15
Значит корень уравнения 45 + x = 60 равен 15.
Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить.
Пример 2. Решить уравнение
Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x
В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма.
При этом слагаемое 2x содержит переменную x . После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое:
Теперь применяем правило нахождения неизвестного слагаемого. Вычитаем из суммы известное слагаемое:
Вычислим правую часть получившегося уравнения:
Мы получили новое уравнение . Теперь мы имеем дело с компонентами умножения: множимым, множителем и произведением. 2 — множимое, x — множитель, 4 — произведение
При этом переменная x является не просто множителем, а неизвестным множителем
Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое:
Вычислим правую часть, получим значение переменной x
Для проверки найденный корень отправим в исходное уравнение и подставим вместо x
Получили верное числовое равенство. Значит уравнение решено правильно.
Пример 3. Решить уравнение 3x + 9x + 16x = 56
Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить.
Приведем подобные слагаемые в левой части данного уравнения:
Имеем дело с компонентами умножения. 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
Отсюда x равен 2
Равносильные уравнения
В предыдущем примере при решении уравнения 3x + 9x + 16x = 56 , мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56 . Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.
Уравнения называют равносильными, если их корни совпадают.
Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2 . Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56 , а затем в уравнение 28x = 56 , которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства
Согласно порядку действий, в первую очередь выполняется умножение:
Подставим корень 2 во второе уравнение 28x = 56
Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.
Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56 , которое проще решать.
Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.
Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение
Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.
Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.
Пример 1. Решить уравнение
Вычтем из обеих частей уравнения число 10
Приведем подобные слагаемые в обеих частях:
Получили уравнение 5x = 10 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 10 разделить на известный сомножитель 5.
Отсюда .
Вернемся к исходному уравнению и подставим вместо x найденное значение 2
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение мы вычли из обеих частей уравнения число 10 . В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 2
Пример 2. Решить уравнение 4(x + 3) = 16
Раскроем скобки в левой части равенства:
Вычтем из обеих частей уравнения число 12
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 4x , а в правой части число 4
Получили уравнение 4x = 4 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 4 разделить на известный сомножитель 4
Отсюда
Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12 . В результате получили равносильное уравнение 4x = 4 . Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
Пример 3. Решить уравнение
Раскроем скобки в левой части равенства:
Прибавим к обеим частям уравнения число 8
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 2x , а в правой части число 9
В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 4,5
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение мы прибавили к обеим частям уравнения число 8. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 4,5
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.
Рассмотрим следующее уравнение:
Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство
Получается верное равенство. Значит число 2 действительно является корнем уравнения .
Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.
Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:
Получилось уравнение 12 = 9x − 3x . Приведем подобные слагаемые в правой части данного уравнения:
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда x = 2 . Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.
На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.
Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x
Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.
Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.
Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12 . В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.
Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.
Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.
Пример 1. Решить уравнение
При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.
В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:
Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8
Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:
В результате останется простейшее уравнение
Ну и нетрудно догадаться, что корень этого уравнения равен 4
Вернемся к исходному уравнению и подставим вместо x найденное значение 4
Получается верное числовое равенство. Значит уравнение решено правильно.
При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение . Корень этого уравнения, как и уравнения равен 4. Значит эти уравнения равносильны.
Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение , мы умножили обе части на множитель 8 и получили следующую запись:
От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения на множитель 8 желательно переписать следующим образом:
Пример 2. Решить уравнение
Умнóжим обе части уравнения на 15
В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5
Перепишем то, что у нас осталось:
Раскроем скобки в правой части уравнения:
Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях, получим
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 5
Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15 . Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x . Корень этого уравнения, как и уравнения равен 5 . Значит эти уравнения равносильны.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на 3
В левой части можно сократить две тройки, а правая часть будет равна 18
Останется простейшее уравнение . Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 9
Получается верное числовое равенство. Значит уравнение решено правильно.
Пример 4. Решить уравнение
Умнóжим обе части уравнения на 6
В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:
Сократим в обеих частях уравнениях то, что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки в обеих частях уравнения:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x , сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:
Приведем подобные слагаемые в обеих частях:
Теперь найдем значение переменной x . Для этого разделим произведение 28 на известный сомножитель 7
Вернемся к исходному уравнению и подставим вместо x найденное значение 4
Получилось верное числовое равенство. Значит уравнение решено правильно.
Пример 5. Решить уравнение
Раскроем скобки в обеих частях уравнения там, где это можно:
Умнóжим обе части уравнения на 15
Раскроем скобки в обеих частях уравнения:
Сократим в обеих частях уравнения, то что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки там, где это можно:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:
Приведем подобные слагаемые в обеих частях уравнения:
Найдём значение x
В получившемся ответе можно выделить целую часть:
Вернемся к исходному уравнению и подставим вместо x найденное значение
Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A , а правую часть равенства в переменную B
Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B
Найдем значение выражения, находящегося в переменной А.
Значение переменной А равно . Теперь найдем значение переменной B . То есть значение правой части нашего равенства. Если и оно равно , то уравнение будет решено верно
Видим, что значение переменной B , как и значение переменной A равно . Это значит, что левая часть равна правой части. Отсюда делаем вывод, что уравнение решено правильно.
Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.
Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42 . Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x
Подставим найденное значение 2 вместо x в исходное уравнение:
Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:
Выполним сокращение в каждом слагаемом:
Перепишем то, что у нас осталось:
Решим это уравнение, пользуясь известными тождественными преобразованиями:
Получили корень 2 . Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.
Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14 , нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Этим методом мы тоже будем пользоваться часто.
Умножение на минус единицу
Если обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному.
Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1 .
Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать.
Рассмотрим уравнение . Чему равен корень этого уравнения?
Прибавим к обеим частям уравнения число 5
Приведем подобные слагаемые:
А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения . Это есть произведение минус единицы и переменной x
То есть минус, стоящий перед переменной x, относится не к самой переменной x , а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение на самом деле выглядит следующим образом:
Имеем дело с компонентами умножения. Чтобы найти х , нужно произведение −5 разделить на известный сомножитель −1 .
или разделить обе части уравнения на −1 , что еще проще
Итак, корень уравнения равен 5 . Для проверки подставим его в исходное уравнение. Не забываем, что в исходном уравнении минус стоящий перед переменной x относится к невидимой единице
Получилось верное числовое равенство. Значит уравнение решено верно.
Теперь попробуем умножить обе части уравнения на минус единицу:
После раскрытия скобок в левой части образуется выражение , а правая часть будет равна 10
Корень этого уравнения, как и уравнения равен 5
Значит уравнения и равносильны.
Пример 2. Решить уравнение
В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение . Для этого умнóжим обе части данного уравнения на −1 .
Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.
Так, умножение уравнения на −1 можно записать подробно следующим образом:
либо можно просто поменять знаки всех компонентов:
Получится то же самое, но разница будет в том, что мы сэкономим себе время.
Итак, умножив обе части уравнения на −1 , мы получили уравнение . Решим данное уравнение. Из обеих частей вычтем число 4 и разделим обе части на 3
Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на −1 . Тогда все компоненты поменяют свои знаки на противоположные:
Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые:
Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые:
Приравнивание к нулю
Недавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего.
В качестве примера рассмотрим уравнение . Решим данное уравнение, как обычно — слагаемые, содержащие неизвестные сгруппируем в одной части, а числовые слагаемые, свободные от неизвестных оставим в другой. Далее выполняя известные тождественные преобразования, найдем значение переменной x
Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Приведем подобные слагаемые в левой части:
Прибавим к обеим частям 77 , и разделим обе части на 7
Альтернатива правилам нахождения неизвестных
Очевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных.
К примеру, для нахождения неизвестного в уравнении мы произведение 10 делили на известный сомножитель 2
Но если в уравнении обе части разделить на 2 корень найдется сразу. В левой части уравнения в числителе множитель 2 и в знаменателе множитель 2 сократятся на 2. А правая часть будет равна 5
Уравнения вида мы решали выражая неизвестное слагаемое:
Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении слагаемое 4 можно перенести в правую часть, изменив знак:
Далее разделить обе части на 2
В левой части уравнения сократятся две двойки. Правая часть будет равна 2. Отсюда .
Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее:
В случае с уравнениями вида удобнее делить произведение на известный сомножитель. Сравним оба решения:
Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме.
Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится.
Когда корней несколько
Уравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9 .
В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9) , которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю.
Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0 . Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0 . Несложно догадаться, что корень этого уравнения равен −9 . Проверка показывает, что корень верный:
Пример 2. Решить уравнение
Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2) . А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2) ).
Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули:
Подставляем по-очереди найденные значения в исходное уравнение и убеждаемся, что при этих значениях левая часть равняется нулю:
Когда корней бесконечно много
Уравнение может иметь бесконечно много корней. То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
Пример 1. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14 . Это равенство будет получаться при любом x
Пример 2. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x
Когда корней нет
Случается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение не имеет корней, поскольку при любом значении x , левая часть уравнения не будет равна правой части. Например, пусть . Тогда уравнение примет следующий вид
Пусть
Пример 2. Решить уравнение
Раскроем скобки в левой части равенства:
Приведем подобные слагаемые:
Видим, что левая часть не равна правой части. И так будет при любом значении y . Например, пусть y = 3 .
Буквенные уравнения
Уравнение может содержать не только числа с переменными, но и буквы.
Например, формула нахождения скорости является буквенным уравнением:
Данное уравнение описывает скорость движения тела при равноускоренном движении.
Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения определить расстояние, нужно выразить переменную s .
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении левую и правую часть поменяем местами:
У нас получилась формула нахождения расстояния, которую мы изучали ранее.
Попробуем из уравнения определить время. Для этого нужно выразить переменную t .
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении v × t = s обе части разделим на v
В левой части переменные v сократим на v и перепишем то, что у нас осталось:
У нас получилась формула определения времени, которую мы изучали ранее.
Предположим, что скорость поезда равна 50 км/ч
А расстояние равно 100 км
Тогда буквенное уравнение примет следующий вид
Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t . Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t
либо можно воспользоваться тождественными преобразованиями. Сначала умножить обе части уравнения на t
Затем разделить обе части на 50
Пример 2. Дано буквенное уравнение . Выразите из данного уравнения x
Вычтем из обеих частей уравнения a
Разделим обе части уравнения на b
Теперь, если нам попадется уравнение вида a + bx = c , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться.
Решим уравнение 2 + 4x = 10 . Оно похоже на буквенное уравнение a + bx = c . Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения:
Видим, что второе решение намного проще и короче.
Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0) , поскольку деление на ноль на допускается.
Пример 3. Дано буквенное уравнение . Выразите из данного уравнения x
Раскроем скобки в обеих частях уравнения
Воспользуемся переносом слагаемых. Параметры, содержащие переменную x , сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой.
В левой части вынесем за скобки множитель x
Разделим обе части на выражение a − b
В левой части числитель и знаменатель можно сократить на a − b . Так окончательно выразится переменная x
Теперь, если нам попадется уравнение вида a(x − c) = b(x + d) , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения.
Допустим нам дано уравнение 4(x − 3) = 2(x + 4) . Оно похоже на уравнение a(x − c) = b(x + d) . Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:
Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d . Это позволит нам не ошибиться при подстановке:
Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0) . Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю.
Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d) . В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части:
Пример 4. Дано буквенное уравнение . Выразите из данного уравнения x
Приведем левую часть уравнения к общему знаменателю:
Умнóжим обе части на a
В левой части x вынесем за скобки
Разделим обе части на выражение (1 − a)
Линейные уравнения с одним неизвестным
Рассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным.
Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой».
Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2 (x + 3) = 16 . Давайте решим его.
Раскроем скобки в левой части уравнения, получим 2 x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2 x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x , разделим произведение 10 на известный сомножитель 2. Отсюда x = 5.
Уравнение 2 (x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10 , для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный».
Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b.
Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x . Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.
Если в линейном уравнении a = 0 и b = 0 , то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0 . При любом значении x левая часть будет равна правой части.
Если в линейном уравнении a = 0 и b ≠ 0 , то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5 . Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти.
Если в линейном уравнении a ≠ 0 , и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a
Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3 , и b равно какому-нибудь числу, скажем числу 6 , то уравнение примет вид .
Отсюда .
Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0 . Это то же самое уравнение, что и ax = b , но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0 . Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде.
В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным.
http://reshu.su/algebra/06/
|
Как правильно пишется уравнение или уровнение?Kroket 6 лет назад
НикПетр Ответы на подобные вопросы даёт портал gramota.ru. В данном случае в строке «Проверка слова» пишете «ур*внение» и получаете ответ.
аллаgruz 6 лет назад В данным случае в корне слова следует писать букву -а — не уровнение, а уравнение. Здесь речь идет не о том, что делают рОвным, а о том, что срАвнивают между собой. Проверочные слова — урАвнивать, срАвнивать, рАвные. комментировать
в избранное
ссылка
отблагодарить Правильным будет написать слово уравнение, проверочным словом будет являться — равный, равенство. комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Перейти к содержанию
«Уравнение» или «уровнение» — как правильно?
На чтение 3 мин Просмотров 736 Опубликовано 15.12.2021
Задумываетесь над тем, как пишется общеупотребительное слово «уравнение» или «уровнение»? В корне с чередованием корректно писать гласную букву «а» или «о»? Вспомним ниже правила, которые помогут выбрать нормативный вариант.
Как пишется правильно: «уравнение» или «уровнение»?
Какое правило применяется?
Чтобы понять, в какой части слова возникает орфографическая проблема, поделим его на морфемы. Так, изучаемое существительное состоит из префикса «у», корня «равн», суффикса «ени» и окончания «е». Видим, что сомнительная гласная занимает безударную позицию в корне.
Перед нами чередующиеся корни «равн» / «ровн». Правило гласит, что выбор одной из гласной корня зависит от лексического значения слова. Напишем корень «равн», т.к. анализируемое существительное выражает значение «одинаковый», «равный». В свою очередь, слова с корнем «ровн» означают «гладкий», «прямой».
Примеры предложений
- На контрольной мне попалось очень сложное уравнение.
- Это уравнение Антон не смог решить за три часа.
Как неправильно писать
Правила составления уравнений в математике
Составить уравнение — значит выразить в математической форме связь между данными (известными) задачи и искомыми (неизвестными) ее величинами. Иногда эта связь, настолько явно содержится в формулировке задачи, что составление уравнения есть просто дословный пересказ задачи, на языке математических знаков.
Пример 1
Петров получил за работу на 160 руб. больше, чем половина суммы, которую получил Иванов. Вместе они получили 1120 руб. Сколько получили за работу Петров и Иванов?
Обозначим через х заработок Иванова. Половина его заработка есть 0,5x ; месячной заработок Петрова 0,5x + 160 вместе они зарабатывают 1120 руб.; математическая запись последней фразы будет
( 0,5x + 160 ) + x = 1120.
Уравнение составлено. Решая его по раз установленным правилам, находим, заработок Иванова х = 640руб.; заработок же Петрова 0,5x + 160 = 480 (руб.).
Чаще, однако, случается, что связь между данными и искомыми величинами не указывается в задаче прямо; ее нужно установить, исходя из условий задачи. В практических задачах так и бывает почти всегда. Только что приведенный пример носит надуманный характер; в жизни почти никогда подобных задач не встречается.
Для составления уравнения поэтому нельзя дать вполне исчерпывающих указаний. Однако на первых порах полезно руководствоваться следующим. Примем за значение искомой величины (или нескольких величин) какое-нибудь наугад взятое число (или несколько чисел) и поставим себе задачу проверить, угадали ли мы правильное решение задачи или нет. Если мы сумели провести эту проверку и обнаружить либо то, что догадка наша верна, либо то, что она неверна (скорее всего случится, конечно, второе), то мы немедленно можем составить нужное уравнение (или несколько уравнений). Именно, запишем те самые действия, которые мы производили для проверки, только вместо наугад взятого числа введем буквенной знак неизвестной величины. Мы получим требуемое уравнение.
Пример 1
Кусок сплава меди и цинка объемом в 1 дм 3 весит 8,14 кг. Сколько меди содержится в сплаве? (уд. вес меди 8,9 кг/дм 3 ; цинка — 7,0 кг/дм 3 ).
Возьмем наугад число, выражающее искомый объем меди, например 0,3 дм 3 . Проверим, удачно ли мы взяли это число. Так как 1 кг/дм 3 меди весит 8,9 кг, то 0,3 дм 3 весят 8,9 * 0,3 = 2,67 (кг). Объем цинка в сплаве есть 1 — 0,3 = 0,7 (дм 3 ). Вес его 7,0 * 0,7 = 4,9 (кг). Общий вес цинка и меди 2,67+ +4,9 = 7,57 (кг). Между тем вес нашего куска, по условию задачи, 8,14 кг. Догадка наша несостоятельна. Но зато мы немедленно получим уравнение решение которого даст правильный ответ. Вместо наугад взятого числа 0,3 дм 3 обозначим объем меди (в дм 3 ) через х. Вместо произведения 8,9 * 0,3 = 2,67 берем произведшие 8,9 x. Это — вес меди в сплаве. Вместо 1 – 0,3 = 0,7 берем 1 — х; это — объем цинка. Вместо 7,0 * 0,7 = 4,9 берем 7,0 (1 — x); это — вес цинка. Вместо 2,67 + 4,9 берем 8,9х + 7,0 (1 — х); это — общий вес цинка и меди. По условию он равен 8,14 кг; значит, 8,9х +7,0 (1 — x) = 8,14.
Решение этого уравнения дает x = 0,6. Проверку наугад взятого решения можно делать различными способами; соответственно этому можно получить для одной и той же задачи различные виды уравнения; все они, однако, дадут для искомой величины одно и, то же решение, такие уравнения называются равносильными друг другу.
Разумеется, после получения навыков в составлении уравнений нет нужды производить проверку наугад взятого числа: можно для значения искомой величины брать не число, а какую-нибудь букву (х, у и т. д.) и поступать так, как если бы эта буква (неизвестное) была тем числом, проверить которое мы собираемся.
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
- Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
- Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
- Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Общие сведения об уравнениях
Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач.
С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.
В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.
Что такое уравнение?
Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.
Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5 .
А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x , значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство.
Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.
Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет
Говорят, что число 2 является корнем или решением уравнения 3 + x = 5
Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.
Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.
Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы.
Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части.
Выразить одно через другое
Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.
Рассмотрим следующее выражение:
Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10
Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.
Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.
Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:
Мы выразили число 2 из равенства 8 + 2 = 10 . Как видно из примера, ничего сложного в этом нет.
При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.
Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8 . Данное равенство можно прочесть так:
2 есть 10 − 8
То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:
Число 2 есть разность числа 10 и числа 8
Число 2 есть разница между числом 10 и числом 8.
Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.
Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:
Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2
Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:
В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно:
Пример 2. Рассмотрим равенство 8 − 2 = 6
Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:
Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6
Пример 3. Рассмотрим равенство 3 × 2 = 6
Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2
Вернем получившееся равенство 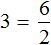
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3
Пример 4. Рассмотрим равенство
Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5
Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:
Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3
Правила нахождения неизвестных
Рассмотрим несколько правил нахождения неизвестных. Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2.
В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой.
Чтобы выразить число 2, мы поступили следующим образом:
То есть из суммы 10 вычли слагаемое 8.
Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x
В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10 , а переменная x берет на себя роль так называемого неизвестного слагаемого
Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10 . Для нахождения неизвестного слагаемого предусмотрено следующее правило:
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10 . Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8
А сейчас, чтобы найти неизвестное слагаемое x , мы должны из суммы 10 вычесть известное слагаемое 8:
Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x
Мы решили уравнение. Значение переменной x равно 2 . Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно:
В результате получается верное числовое равенство. Значит уравнение решено правильно.
Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8.
В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. Чтобы найти неизвестное слагаемое x , нужно из суммы 10 вычесть известное слагаемое 2
Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8.
В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность
Чтобы выразить число 8, мы поступили следующим образом:
То есть сложили разность 6 и вычитаемое 2.
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x
В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого
Для нахождения неизвестного уменьшаемого предусмотрено следующее правило:
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.
Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6 . Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.
А сейчас, чтобы найти неизвестное уменьшаемое x , мы должны к разности 6 прибавить вычитаемое 2
Если вычислить правую часть, то можно узнать чему равна переменная x
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного вычитаемого
Для нахождения неизвестного вычитаемого предусмотрено следующее правило:
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6.
А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6
Вычисляем правую часть и находим значение x
Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3.
В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение
Чтобы выразить число 3 мы поступили следующим образом:
То есть разделили произведение 6 на множитель 2.
Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного множимого.
Для нахождения неизвестного множимого предусмотрено следующее правило:
Чтобы найти неизвестное множимое, нужно произведение разделить на множитель.
Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6 . Произведение 6 мы разделили на множитель 2.
А сейчас для нахождения неизвестного множимого x , нужно произведение 6 разделить на множитель 2.
Вычисление правой части позволяет нам найти значение переменной x
Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x .
В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель:
Чтобы найти неизвестный множитель, нужно произведение разделить на множимое.
Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6 . Тогда для получения числа 2 мы разделили произведение 6 на множимое 3.
А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3.
Вычисление правой части равенства 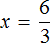
Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя:
Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель.
Например, решим уравнение 9 × x = 18 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9
Отсюда 
Решим уравнение x × 3 = 27 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3
Отсюда 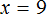
Вернемся к четвертому примеру из предыдущей темы, где в равенстве 
Чтобы выразить число 15 мы поступили следующим образом:
То есть умножили частное 3 на делитель 5.
Теперь представим, что в равенстве 
В этом случае переменная x берет на себя роль неизвестного делимого.
Для нахождения неизвестного делимого предусмотрено следующее правило:
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Что мы и сделали, когда выражали число 15 из равенства 
А сейчас, чтобы найти неизвестное делимое x , нужно частное 3 умножить на делитель 5
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Теперь представим, что в равенстве 
В этом случае переменная x берет на себя роль неизвестного делителя.
Для нахождения неизвестного делителя предусмотрено следующее правило:
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Что мы и сделали, когда выражали число 5 из равенства 
А сейчас, чтобы найти неизвестный делитель x , нужно делимое 15 разделить на частное 3
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Итак, для нахождения неизвестных мы изучили следующие правила:
- Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
- Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
- Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность;
- Чтобы найти неизвестное множимое, нужно произведение разделить на множитель;
- Чтобы найти неизвестный множитель, нужно произведение разделить на множимое;
- Чтобы найти неизвестное делимое, нужно частное умножить на делитель;
- Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Компоненты
Компонентами мы будем называть числа и переменные, входящие в равенство
Так, компонентами сложения являются слагаемые и сумма
Компонентами вычитания являются уменьшаемое, вычитаемое и разность
Компонентами умножения являются множимое, множитель и произведение
Компонентами деления являются делимое, делитель и частное
В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть.
Пример 1. Найти корень уравнения 45 + x = 60
45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
Вычислим правую часть, получим значение x равное 15
Значит корень уравнения 45 + x = 60 равен 15.
Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить.
Пример 2. Решить уравнение
Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x
В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма.
При этом слагаемое 2x содержит переменную x . После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое:
Теперь применяем правило нахождения неизвестного слагаемого. Вычитаем из суммы известное слагаемое:
Вычислим правую часть получившегося уравнения:
Мы получили новое уравнение 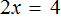
При этом переменная x является не просто множителем, а неизвестным множителем
Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое:
Вычислим правую часть, получим значение переменной x
Для проверки найденный корень отправим в исходное уравнение 
Получили верное числовое равенство. Значит уравнение решено правильно.
Пример 3. Решить уравнение 3x + 9x + 16x = 56
Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить.
Приведем подобные слагаемые в левой части данного уравнения:
Имеем дело с компонентами умножения. 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
Отсюда x равен 2
Равносильные уравнения
В предыдущем примере при решении уравнения 3x + 9x + 16x = 56 , мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56 . Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.
Уравнения называют равносильными, если их корни совпадают.
Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2 . Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56 , а затем в уравнение 28x = 56 , которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства
Согласно порядку действий, в первую очередь выполняется умножение:
Подставим корень 2 во второе уравнение 28x = 56
Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.
Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56 , которое проще решать.
Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.
Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение
Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.
Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.
Пример 1. Решить уравнение
Вычтем из обеих частей уравнения число 10
Приведем подобные слагаемые в обеих частях:
Получили уравнение 5x = 10 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 10 разделить на известный сомножитель 5.
Отсюда 
Вернемся к исходному уравнению 
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 
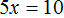

Пример 2. Решить уравнение 4(x + 3) = 16
Раскроем скобки в левой части равенства:
Вычтем из обеих частей уравнения число 12
Приведем подобные слагаемые в обеих частях уравнения:
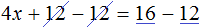
Получили уравнение 4x = 4 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 4 разделить на известный сомножитель 4
Отсюда
Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12 . В результате получили равносильное уравнение 4x = 4 . Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
Пример 3. Решить уравнение
Раскроем скобки в левой части равенства:
Прибавим к обеим частям уравнения число 8
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 2x , а в правой части число 9
В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда
Вернемся к исходному уравнению 
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 
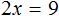

Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.
Рассмотрим следующее уравнение:
Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство
Получается верное равенство. Значит число 2 действительно является корнем уравнения 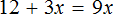
Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.
Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:
Получилось уравнение 12 = 9x − 3x . Приведем подобные слагаемые в правой части данного уравнения:
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда x = 2 . Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.
На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.
Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x
Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.
Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.
Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12 . В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.
Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.
Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.
Пример 1. Решить уравнение
При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.
В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:
Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8
Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:
В результате останется простейшее уравнение
Ну и нетрудно догадаться, что корень этого уравнения равен 4
Вернемся к исходному уравнению 
Получается верное числовое равенство. Значит уравнение решено правильно.
При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение 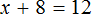

Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение 
От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения 
Пример 2. Решить уравнение
Умнóжим обе части уравнения на 15
В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5
Перепишем то, что у нас осталось:
Раскроем скобки в правой части уравнения:
Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях, получим
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению 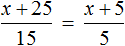
Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15 . Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x . Корень этого уравнения, как и уравнения 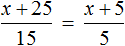
Пример 3. Решить уравнение
Умнóжим обе части уравнения на 3
В левой части можно сократить две тройки, а правая часть будет равна 18
Останется простейшее уравнение 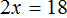
Отсюда
Вернемся к исходному уравнению 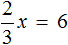
Получается верное числовое равенство. Значит уравнение решено правильно.
Пример 4. Решить уравнение
Умнóжим обе части уравнения на 6
В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:
Сократим в обеих частях уравнениях то, что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки в обеих частях уравнения:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x , сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:
Приведем подобные слагаемые в обеих частях:
Теперь найдем значение переменной x . Для этого разделим произведение 28 на известный сомножитель 7
Вернемся к исходному уравнению 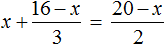
Получилось верное числовое равенство. Значит уравнение решено правильно.
Пример 5. Решить уравнение
Раскроем скобки в обеих частях уравнения там, где это можно:
Умнóжим обе части уравнения на 15
Раскроем скобки в обеих частях уравнения:
Сократим в обеих частях уравнения, то что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки там, где это можно:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:
Приведем подобные слагаемые в обеих частях уравнения:
Найдём значение x
В получившемся ответе можно выделить целую часть:
Вернемся к исходному уравнению и подставим вместо x найденное значение
Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A , а правую часть равенства в переменную B
Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B
Найдем значение выражения, находящегося в переменной А.
Значение переменной А равно 

Видим, что значение переменной B , как и значение переменной A равно 
Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.
Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42 . Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x
Подставим найденное значение 2 вместо x в исходное уравнение:
Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:
Выполним сокращение в каждом слагаемом:
Перепишем то, что у нас осталось:
Решим это уравнение, пользуясь известными тождественными преобразованиями:
Получили корень 2 . Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.
Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14 , нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Этим методом мы тоже будем пользоваться часто.
Умножение на минус единицу
Если обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному.
Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1 .
Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать.
Рассмотрим уравнение 
Прибавим к обеим частям уравнения число 5
Приведем подобные слагаемые:
А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения 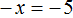
То есть минус, стоящий перед переменной x, относится не к самой переменной x , а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение 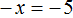
Имеем дело с компонентами умножения. Чтобы найти х , нужно произведение −5 разделить на известный сомножитель −1 .
или разделить обе части уравнения на −1 , что еще проще
Итак, корень уравнения 
Получилось верное числовое равенство. Значит уравнение решено верно.
Теперь попробуем умножить обе части уравнения 
После раскрытия скобок в левой части образуется выражение 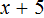
Корень этого уравнения, как и уравнения 
Значит уравнения 
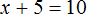
Пример 2. Решить уравнение
В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение 
Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.
Так, умножение уравнения 
либо можно просто поменять знаки всех компонентов:
Получится то же самое, но разница будет в том, что мы сэкономим себе время.
Итак, умножив обе части уравнения 
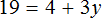
Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на −1 . Тогда все компоненты поменяют свои знаки на противоположные:
Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые:
Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые:
Приравнивание к нулю
Недавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего.
В качестве примера рассмотрим уравнение 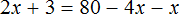
Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Приведем подобные слагаемые в левой части:
Прибавим к обеим частям 77 , и разделим обе части на 7
Альтернатива правилам нахождения неизвестных
Очевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных.
К примеру, для нахождения неизвестного в уравнении 
Но если в уравнении 
Уравнения вида 
Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении 
Далее разделить обе части на 2
В левой части уравнения сократятся две двойки. Правая часть будет равна 2. Отсюда 
Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее:
В случае с уравнениями вида 
Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме.
Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится.
Когда корней несколько
Уравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9 .
В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9) , которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю.
Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0 . Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0 . Несложно догадаться, что корень этого уравнения равен −9 . Проверка показывает, что корень верный:
Пример 2. Решить уравнение
Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2) . А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2) ).
Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули:
Подставляем по-очереди найденные значения в исходное уравнение 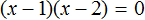
Когда корней бесконечно много
Уравнение может иметь бесконечно много корней. То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
Пример 1. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14 . Это равенство будет получаться при любом x
Пример 2. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x
Когда корней нет
Случается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение 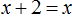
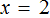
Пусть
Пример 2. Решить уравнение
Раскроем скобки в левой части равенства:
Приведем подобные слагаемые:
Видим, что левая часть не равна правой части. И так будет при любом значении y . Например, пусть y = 3 .
Буквенные уравнения
Уравнение может содержать не только числа с переменными, но и буквы.
Например, формула нахождения скорости является буквенным уравнением:
Данное уравнение описывает скорость движения тела при равноускоренном движении.
Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения 
Умнóжим обе части уравнения 
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении левую и правую часть поменяем местами:
У нас получилась формула нахождения расстояния, которую мы изучали ранее.
Попробуем из уравнения 
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении v × t = s обе части разделим на v
В левой части переменные v сократим на v и перепишем то, что у нас осталось:
У нас получилась формула определения времени, которую мы изучали ранее.
Предположим, что скорость поезда равна 50 км/ч
А расстояние равно 100 км
Тогда буквенное уравнение 
Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t . Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t
либо можно воспользоваться тождественными преобразованиями. Сначала умножить обе части уравнения на t
Затем разделить обе части на 50
Пример 2. Дано буквенное уравнение 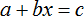
Вычтем из обеих частей уравнения a
Разделим обе части уравнения на b
Теперь, если нам попадется уравнение вида a + bx = c , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться.
Решим уравнение 2 + 4x = 10 . Оно похоже на буквенное уравнение a + bx = c . Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения:
Видим, что второе решение намного проще и короче.
Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0) , поскольку деление на ноль на допускается.
Пример 3. Дано буквенное уравнение 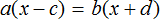
Раскроем скобки в обеих частях уравнения
Воспользуемся переносом слагаемых. Параметры, содержащие переменную x , сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой.
В левой части вынесем за скобки множитель x
Разделим обе части на выражение a − b
В левой части числитель и знаменатель можно сократить на a − b . Так окончательно выразится переменная x
Теперь, если нам попадется уравнение вида a(x − c) = b(x + d) , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения.
Допустим нам дано уравнение 4(x − 3) = 2(x + 4) . Оно похоже на уравнение a(x − c) = b(x + d) . Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:
Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d . Это позволит нам не ошибиться при подстановке:
Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0) . Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю.
Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d) . В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части:
Пример 4. Дано буквенное уравнение 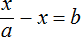
Приведем левую часть уравнения к общему знаменателю:
Умнóжим обе части на a
В левой части x вынесем за скобки
Разделим обе части на выражение (1 − a)
Линейные уравнения с одним неизвестным
Рассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным.
Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой».
Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2 (x + 3) = 16 . Давайте решим его.
Раскроем скобки в левой части уравнения, получим 2 x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2 x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x , разделим произведение 10 на известный сомножитель 2. Отсюда x = 5.
Уравнение 2 (x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10 , для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный».
Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b.
Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x . Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.
Если в линейном уравнении a = 0 и b = 0 , то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0 . При любом значении x левая часть будет равна правой части.
Если в линейном уравнении a = 0 и b ≠ 0 , то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5 . Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти.
Если в линейном уравнении a ≠ 0 , и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a
Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3 , и b равно какому-нибудь числу, скажем числу 6 , то уравнение 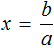
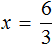
Отсюда 
Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0 . Это то же самое уравнение, что и ax = b , но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0 . Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде.
В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным.
источники:
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij
http://spacemath.xyz/obshhie-svedeniya-ob-uravneniyah/





.jpg)
.jpg)
.jpg)
.jpg)


.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)