Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Как найти радиус окружности хорда
Все основные формулы для определения длины радиуса окружности
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
R — радиус окружности (круга)
D — диаметр, D = 2 R
Формула для определения длины радиуса, если известна площадь круга :
Калькулятор для расчета длины радиуса через площадь
Формула для определения длины радиуса, если известна длина окружности :
Калькулятор для расчета длины радиуса через длину окружности
R — радиус окружности (круга)
h — высота сегмента
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :
Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Отрезки и прямые, связанные с окружностью. Теорема о бабочке
Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства |
| Окружность |  |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Радиус
Отрезок, соединяющий центр окружности с любой точкой окружности
Хорда
Отрезок, соединяющий две любые точки окружности
Диаметр
Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности
Касательная
Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания
Секущая
Прямая, пересекающая окружность в двух точках
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Радиус
Отрезок, соединяющий центр окружности с любой точкой окружности
Хорда
Отрезок, соединяющий две любые точки окружности
Диаметр
Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности
Касательная
Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания
Секущая
Прямая, пересекающая окружность в двух точках
Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  |
Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  |
Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  |
У равных дуг равны и хорды. |
| Параллельные хорды |  |
Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды
Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды
Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности
Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины
Большая из двух хорд расположена ближе к центру окружности.
Равные дуги
У равных дуг равны и хорды.
Параллельные хорды
Дуги, заключённые между параллельными хордами, равны.
Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема |
| Пересекающиеся хорды |  |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Касательные, проведённые к окружности из одной точки
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
| Пересекающиеся хорды |
 |
| Касательные, проведённые к окружности из одной точки |
 |
| Касательная и секущая, проведённые к окружности из одной точки |
 |
| Секущие, проведённые из одной точки вне круга |
 |
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Касательные, проведённые к окружности из одной точки
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга
Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
Все основные формулы для определения длины радиуса окружности
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
R — радиус окружности (круга)
D — диаметр, D = 2 R
Формула для определения длины радиуса, если известна площадь круга :
Калькулятор для расчета длины радиуса через площадь
Формула для определения длины радиуса, если известна длина окружности :
Калькулятор для расчета длины радиуса через длину окружности
R — радиус окружности (круга)
h — высота сегмента
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :
http://b4.cooksy.ru/articles/kak-nayti-radius-okruzhnosti-horda
http://www-formula.ru/radius-if-known-area
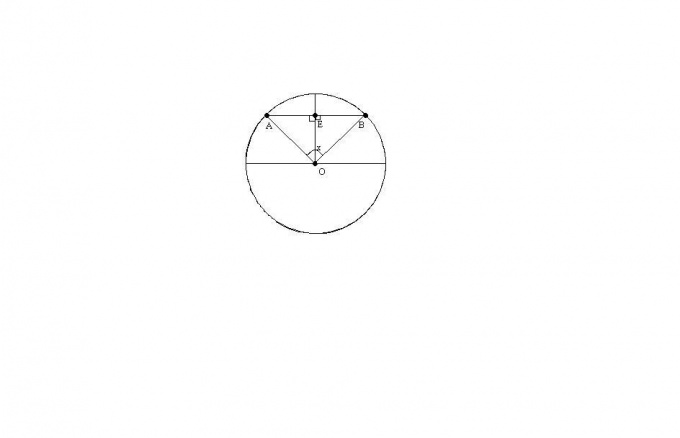
Как найти радиус по хорде
Хорда — это отрезок, соединяющий две точки окружности. Пусть длина хорды известна. Тогда, если также известен угол между радиусами, проведенными в концы хорды, то можно найти и радиус окружности.
Вам понадобится
- Транспортир, линейка.
Инструкция
Пусть известны длина хорды AB и угол AOB между радиусами, проведенными в концы хорды. Найдем по этим данным радиус окружности с центром в точке O.
Треугольник AOB — равнобедренный, так как OA = OB = R. По свойству равнобедренного треугольника высота OE одновременно является его медианой и биссектрисой угла AOB. Обозначим угол AOB за х.
Треугольник AEO — прямоугольный с прямым углом AEO. Так как высота ОЕ также является биссектрисой угла AOB, то угол AOE = x/2. Тогда из прямоугольного треугольника AOE имеем: OA = R = (AB/2)/sin(x/2).
|
Встретил забавную задачу и приглашаю многоуважаемую публику ей поразвлечься… ) Есть окружность. Внутри окружности проведена хорда a, от одного из концов этой хорды проведен внутри окружности под прямым углом отрезок b так, что он не пересекает и не касается окружности. От второго конца отрезка b опять же, под прямым углом, проведен отрезок с, который вторым концом касается окружности. Длина всех отрезков больше нуля. Отрезки a и с лежат в разных полуплоскостях относительно прямой, проходящей через отрезок b. Я не знаю, вроде все по условиям, все как на картинке, честное слово! Мы знаем длины a, b и c. Нужно найти радиус окружности. Можно воспользоваться свойствами хорды, готовыми уравнениями. Точка пересечения двух хорд делит обе хорды в одинаковом соотношении. Используем эту формулу для нахождения отрезка d (cм. рисунок). Когда хорды перпендикулярны то радиус окружности находится по второй формуле. автор вопроса выбрал этот ответ лучшим Тут вспомнил, как мне один раз на практике нужно было найти радиус окружности и были три точки.. Сделано это было простым графическим методом без всяких заумностей.. Просто известно, что радиус в каждой точке окружности перпендикулярен касательной к окружности (которая есть суть производной, но это так, к слову).. Далее, известно, что хорда всегда идёт параллельно касательной (собственно касательная — это хорда сдвинутая на край окружности и касающаяся её в одной точке).. Вот и всё, что нужно.. Без матриц, определителей, систем уравнений, хитроумных формул и построений.. Итак, вот рисунок.. Т. е., мы просто достроили ещё одну хорду (красным цветом), затем каждую хорду поделили пополам и из середины каждой хорды провели линии, перпендикулярные хорде.. Точка пересечения двух линий, перпендикулярных хордам и есть центр окружности.. Теперь из цента мы ставим ногу циркуля и рисуем окружность (можно использовать карандаш на нитке (как пришлось использовать на практике).. Также для построения перпендикуляров использовалась нитка и древний способ построения перпендикуляров.. Деление напополам: сложение отмеренной нитки вдвое.. Всё делается на коленке.. И даже можно использовать на местности для построения окружностей в масштабах сотен метров и более.. Т.е. мы нашли не только радиус, но даже центр окружности и при желании можем с помощью циркуля (или карандаша на нитке) построить искомую окружность.. Именно так на практике мне один раз пришлось искать окружность, причём нужно было знать не только радиус, но расположение центра.. Этот метод наиболее прост, универсален и с помощью его можно искать все параметры окружности.. Если нужно найти радиус с наперёд заданной точностью, то можно использовать метод в моём предыдущем ответе, решение системы из трёх квадратных уравнений, которые описывают нахождение трёх точек, можно решать их не обязательно аналитически, что немного трудоёмко (но не сложно), а используя тот же Маткад.. Кроме того этот аналитический метод может помочь определить не только радиус окружности, но и координаты центра с любой заданной точностью, т.е. все параметры окружности.. Кстати, посткриптум, этот графический метод пришлось придумывать на ходу, поскольку нужно было срочно найти ответ, искать что-то в литературе как найти окружность просто не было времени.. Конечно хорошо знать определитель, которым задаётся дуга окружности через 3 точки.. Как это написал Гр. Роджер.. Можно сделать хитроумные геометрические построения, как сделал родиоил2.. Можно использовать свойства дуги, как попытался это сделать мсб.. Но вот, положим вам на практике нужно быстро определить, тогда нужно искать свойства дуг, определителей?.. Или пыхтеть с построениями? Которые могут быть не очень точны из-за несовершенства инструментария.. Как же поступить? Да как на войне: быстро и эффективно, используя смекалку и минимум средств.. Воспользуемся простыми формулами, которые известны из школы.. И элементами аналитической геометрии (опять это практически школа).. Известно, что уравнение окружности: (x-xo)^2+(y-yo)^2=R^2 где xo, y0, R — соответственно координаты центра и радиус окружности.. Установим первую точку А так, чтобы она находилась в начале координат А(0,0), тогда следующая точка В имеет координаты (0,а), следующая точка С (b, c+a).. Теперь напишем три уравнения одной и той же окружности для трёх точек: (xo)^2+(yo)^2=R^2 (xo)^2+(а-yo)^2=R^2 (b-xo)^2+(с+а-yo)^2=R^2 Получилась система из трёх квадратных уравнений с тремя неизвестными: xo, y0, R.. Значит эта система вполне решается стандартным образом.. Например приравниваем первое и второе уравнение: (xo)^2+(yo)^2=(xo)^2+(а-yo)^2 Тогда всё приводится к уравнению: (yo)^2-(а-yo)^2=0 Упрощаем его и получаем простое линейное уравнение: -2ay0-(а)^2=0 y0=-(а)^2/2a=-a/2 Из него находим первую координату центра.. Затем эту координату подставляем в первое уравнение (которое попроще): (xo)^2+(a/2)^2=R^2 x0=+(-)sqrt(R^2-(a/2)^2) Теперь координаты центра подставляем опять в третье уравнение: (b-R^2-(a/2)^2)^2+(с+а+a/2)^2=R^2 Далее всё приводим, раскрывая скобки, получая уравнение 4-й степени.. Не в каждой школе дают решение уравнения 4-й степени, но это не сложно используя метод Феррари или метод разложения на множетели.. Грустный Роджер 2 года назад Это трёхходовка на аналитическую геометрию. Я расскажу, как она решается, но вычисления вы уж проведите сами… Будем считать, что длины всех трёх отрезков нам известны, и будем для простоты считать, что начало координат находится в точке сопряжения отрезков a, b. Тогда нижний конец отрезка а находится в точке (0, -А) (пусть заглавная буква — это длина соответствующего отрезка), а верхний конец отрезка с находится в точке (В, С). И тогда уравнение окружности, проходящей через три точки с известными координатами, пишется фактически «в одно действие» — через определитель, составленный из координат трёх точек, через которые она проходит: По счастью, при сделанном выше выборе осей координат одна строка определителя получается почти нулевой, и тогда он элементарно превращается в определитель третьего порядка (если знать, что такое минор): Тут, если совсем формально, перед определителем 3 порядка должен стоять минус, но поскольу он равен нулю, то фиг с ним, с минусом… Ну так вот. «Каноническое» уравнение окружности в декартовой системе координат выглядит так: x² + y² + Mx + Ny + K = 0. Если раскрыть определитель, то приравниванием коэффициентов при соответствующих степенях х, у враз получаются выражения для M, N и К. Ну а как только эти величины известны, радиус вычисляется как корень из (M² + N² — 4C). rodleoil2 2 года назад Предлагаю графическое решение Оно поможет найти и математическое решение Чертим линии а,б,с, соблюдая размеры и углы. Чертим одинаковые окружности, чтобы они попарно (одинакового размера рядом) пересекались. на данном чертеже все окружности одинаковые (размеры позволяют). Оранжевые окружности. Проводим линии через пересечения окружностей. Зеленые тонкие линии. Расстояния от точек соприкосновения заданных отрезков «а», «б», а также концов отрезков «а» и «с» и тонких зеленых линий будет радиусом Толстые зеленые линии. Также, легко заметить, что мы проводили тонкие зеленые линии — это серединные перпендикуляры к хордам. При необходимости, математическое решение можно получить работая с размерами отрезков, треугольниками, углами… Но на практике, на чертежах, хватает и графического решения. Грустный Роджер 2 года назад (Продолжение банкета…) Ответ msb натолкнул на забавную мысль: если нужно решить задачу графически, чисто циркулем и линейкой, то хорды b, c вообще на фиг не нужны, потому что есть окружность (это, заметьте, по условию задачки!) и есть хорда в ней. Всё, sapienti sat. На окружности строится ещё одна хорда, лежащая точно напротив хорды а, это делается циркулем и линейкой (проводятся два перпендикуляра к концам отрезка, фигня вопрос…), это нам даёт прямоугольник, вписанный в окружность. Собсно, всё, радиус отсюда определяется на раз. Но и это ещё не конец! Можно не строить этот прямоугольник. Можно построить два перпендикуляра — один к середине хорды a, второй — к середине отрезка, образованного лежащими на окружности концами хорд b, c. Точка их пересечения даст центр окружности. Никольский 2 года назад Фигура АВСD — описанная равнобедренная трапеция (см. рисунок), где а — верхнее основание трапеции, f — нижнее основание трапеции, k — боковая сторона трапеции, m — диагональ трапеции. k и m вычисляются из прямоугольных треугольников, f=2с + а Р — полупериметр треугольника АСD. Р = (m + k + f)/2 Есть формула, по которой вычисляется радиус окружности описанной равнобедренной трапеции: R = (kmf)/(4(sqrt(P(P-k)(P-m)(P-f))) Выражая k, m, f через а, в, с, получим (даже не буду пытаться) конечную формулу. Если знать конкретные числовые значения а, в, с, то найти R можно с помощью калькулятора. Геометрические задачи решаются графически. Здесь много лишних данных. Достаточно продлить отрезок b до пересечения с окружностью и соединить линией эту точку пересечения с точкой пересечения отрезка a c окружностью. Это будет диаметр окружности, который только остается разделить пополам с помощью циркуля и линейки и измерить. Знаете ответ? |
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
Регистрация: 28.08.2009
Казань
Сообщений: 357
Вопроса два.
1). Известны две величины. Это длинна дуги окружности и длинна хорды, соединяющей концы этой дуги. Нужно вычислить радиус.
2). Известны две величины. Это длинна хорды и длинна отрезка, перпендикулярно соединяющего середину хорды с краем окружности. Нужно опять вычислить радиус.
А то у меня формула что-то грешит совсем.
Регистрация: 11.07.2009
Зеленоград
Сообщений: 596
по п.2
R=((Х/2)*2+О*2)/2О , где Х-хорда, О-отрезок, * степень
2О-это 2 умножить на отрезок, О*2- это отрезок в квадрате
Регистрация: 28.08.2009
Казань
Сообщений: 357
Что-то у меня не получается…
Простой пример для проверки: самая длинная хорда — это проходящая через центр окружности и равная ее диаметру. Соответственно обозначенный отрезок в этом случае, будет равняться половине диаметру, то есть равен радиусу. Допустим хорда равна 100см, отрезок 50см… значит радиус по формуле тоже должен быть 50см, а тут 127,5см выходит
Регистрация: 03.01.2008
Днепропетровск
Сообщений: 521
Регистрация: 29.10.2005
Москва
Сообщений: 5260
Keramamaster написал :
Что-то у меня не получается…
2О — это удвоенная длина отрезка, а не число 20
((100/2)*2 + 50*2)/100=(2500 + 2500)/100 = 50
Регистрация: 28.08.2009
Казань
Сообщений: 357
sergeyX написал :
Ваша задача.
Спасибо конечно, но мне, чайнику, проблематично интерпретировать эти формулы под вычисление именно радиуса.
Может вас не затруднит написать её в формате R(радиус)=»бла-бла-бла»
Регистрация: 11.07.2009
Зеленоград
Сообщений: 596
Лида написал :
2О — это удвоенная длина отрезка, а не число 20
ну да, это очевидно, простая теореме Пифагора, там чисел нет, только неизвестные, могу развернуть, но автор не просил.
2О-это 2 умножить на отрезок.
Регистрация: 28.08.2009
Казань
Сообщений: 357
Лида, вы заслуженный гений России!
Простите за жадность, но может еще формулу подкинете? вычисления R по длине дуги и хорды?
Регистрация: 11.07.2009
Зеленоград
Сообщений: 596
Keramamaster не усложняйте жизнь, длина дуги вещь не точная,т.е. сантиметром на полу ее не измеришь, сама задача п.1 имеет решение через тригометрическиую функцию синус , оно вам надо?
Регистрация: 28.08.2009
Казань
Сообщений: 357
Vegazzz написал :
не усложняйте жизнь, длина дуги вещь не точная,т.е. сантиметром на полу ее не измеришь,
Согласен, но это с легкостью можно сделать с помощью курвиметра, по любой криволинейной поверхности.
Vegazzz написал :
сама задача п.1 имеет решение через тригометрическиую функцию синус
Мне нужна конечная формула, ее можно ввести в excel, а он сам посчитает что и как на основе всего двух данных: хорды и дуги.
Vegazzz написал :
оно вам надо?
Не только мне, но и всем тем, кто хочет радовать свой глаз точностью воплощения дизайн-проектов.
Регистрация: 11.07.2009
Зеленоград
Сообщений: 596
Keramamaster,постараюсь вечерком формулу начертить, только и вы колитесь, а то как мозаинки-проф.секркт, проф.секрет…, для вас плитка очевидно…, а я как баран сижу в своих мыслях и проблемах.
Не принимайте всерьез-конечно это шутка!
Регистрация: 04.04.2007
Новосибирск
Сообщений: 1451
1). Известны две величины. Это длинна дуги окружности и длинна хорды, соединяющей концы этой дуги. Нужно вычислить радиус.
Пусть g — длина дуги окружности, x — длина хорды.
Приближенная формула для радиуса:
R = sqrt( g*g*g / (24 * (g — x)) ),
где sqrt — взять квадратный корень.
Точная формула или будет страшной, или ее вообще не выразить аналитически.
Эта приближенная формула дает погрешность в сторону увеличения радиуса.
2). Известны две величины. Это длинна хорды и длинна отрезка, перпендикулярно соединяющего середину хорды с краем окружности. Нужно опять вычислить радиус.
Пусть y — длина отрезка, x — длина хорды.
R = (x*x + 4*y*y) / (8*y)
Это точная формула, её уже здесь приводили.
Замечание такое по русскому языку:
длинна — прилагательное (краткое), то же самое, что ‘длинная’
длина — существительное
Можно написать «длина длинна», это будет что-то в стиле рассказов для детей Толстого,
но «длинна длинна» — это как-то по-папуасски.
Регистрация: 28.08.2009
Казань
Сообщений: 357
И почему Нобель обделил своей премией матеметиков? Такой аццкий головняк эти формулы!
Спасибо всем! Только неужели в формулу для вычисления по окружности не надо вставлять число «Пи»? Может погрешность уменьшится?
Vegazzz написал :
…я как баран сижу в своих мыслях и проблемах.
Vegazzz, персонально благодарствую.
все когда-то случается впервые, скоро и у вас найдется индивидуальное решение
Регистрация: 28.08.2009
Казань
Сообщений: 357
ssrr написал :
Замечание такое по русскому языку:
длинна — прилагательное (краткое), то же самое, что ‘длинная’
длина — существительное
О чудо-форум! искал одно, а получил комплект! математику+русский. Низкий поклон
Регистрация: 11.07.2009
Зеленоград
Сообщений: 596
C-длина окружности
L-хорда
a-угол в радианах от ценра между двумя R до концов хорды.
*-умножение
R*a = C формула длины дуги , отсюда следует R=C/a
R*sin(a/2) = L/2
данные формулы составляют систему уравнений, решаем, делим второе на первое, получаем
(sin(a/2))/a=L/(2*C).
Это трансцендентное уравнение относительно угла a.
sin(a/2) = (L/C) * (a/2)
в правой части волна sin, в левой прямая с коэффициентом отношения хорды к дуге, т.е L/С , в точке пересечения графиков получаем значение a-угла в радианах, которое надо поставить в формулу
R=C/a
и получить ответ на поставленную задачу.
Хорда лежит в пределах между D-диаметром и верхушкой окружности, т.е.
(2/пи)*С (больше равно) L (меньше равно) C , отсюда
2/пи (больше равно) L/C (меньше равно) 1
Регистрация: 28.08.2009
Казань
Сообщений: 357
ЁмоЁ! Vegazzz, вы поломали мой нежный мозг
Ребус какой-то. Как бы это все привести в формат R=»бла-бла-бла»?
Ну честно, не силен я в пифагоровской науке
Регистрация: 11.07.2009
Зеленоград
Сообщений: 596
после поставленной задачи в 3час21мин, между своим делом порешал это до 5час31мин, читал ночь ссылку, которую дал позже sergeyX -вполне гуд!!, нарисовал свой ответ
sin(a/2) = (L/C) * (a/2), а затем R=C/a другого не вижу, если только на месте поверхность разрисовать — построить касательные к точкам хорды, провести перепендикуляры, точки пересечения, которых дадут центр, или другие рис. изобразить, тут возможно есть еще варианты, надо в инете посмотреть.
Регистрация: 29.10.2005
Москва
Сообщений: 5260
Keramamaster написал :
Ребус какой-то. Как бы это все привести в формат R=»бла-бла-бла»?
А всё потому, что Вы не даёте общей картины: что есть и что надо получить на выходе. Может, Вам совсем не длину дуги и хорды надо мерить, а что-то совсем другое. У меня, например, в голове не складывается прикладное применение этой задачи. Что это за окружность, доступа к которой нет (иначе можно было бы просто измерить диаметр), а есть лишь некий выступающий полупенёк (именно пенёк, а не часть трубы, иначе как Вы измерили расстояние до хорды?)? Причём не просто пенёк, а целый лес разновеликих полупеньков, поскольку Вам нужна некая формула для общего случая, чтоб быстренько обсчитывать все эти пеньки
Регистрация: 11.07.2009
Зеленоград
Сообщений: 596
Лида написал :
Что это за окружность, доступа к которой нет
догадываюсь, что керамомастер рисует большую дугу на полу, центр у нее неизвестно где, но надо найти, что бы более точно вывести кривулю, а затем сделать шаблон для плиточек .
Регистрация: 28.08.2009
Казань
Сообщений: 357
Vegazzz написал :
догадываюсь, что керамомастер рисует большую дугу на полу, центр у нее неизвестно где, но надо найти.
Часто такое было — центр окружности у соседей за стеной
Сейчас отдыхаю, но пока есть время, использую его для теоретичеких подкреплений для будущей практики.
Регистрация: 11.07.2009
Зеленоград
Сообщений: 596
Keramamaster написал :
Часто такое было — центр окружности у соседей за стеной
во как!!это в мою копилку знаний в плане плитки.
Регистрация: 29.10.2005
Москва
Сообщений: 5260
Keramamaster написал :
Часто такое было — центр окружности у соседей за стеной
А как же Вы тогда будете его использовать? И что толку от радиуса, который некуда приложить?
Регистрация: 29.10.2005
Москва
Сообщений: 5260
Vegazzz написал :
догадываюсь, что керамомастер рисует большую дугу на полу, центр у нее неизвестно где
А откуда известно в таком случае, что это именно окружность, а не некая кривуля?
Регистрация: 11.07.2009
Зеленоград
Сообщений: 596
Хороший вопрос про радиус, может еще один проф.секрет откроем!!!
Регистрация: 29.10.2005
Москва
Сообщений: 5260
Keramamaster написал :
Сейчас отдыхаю, но пока есть время, использую его для теоретичеких подкреплений для будущей практики.
Так и не поделитесь общей постановкой задачи? Тут ведь вот в чём дело — Вы уже для себя выбрали численный метод для её решения, а теперь просите помощи для реализации именно Вашего численного метода. А кто Вам сказал, что он единственно возможный? Надо начинать с выбора метода, а потом уже приводить выбранный метод к неким формулам.
Регистрация: 08.10.2007
Новокубанск
Сообщений: 2329
Vegazzz написал :
догадываюсь, что керамомастер рисует большую дугу на полу, центр у нее неизвестно где, но надо найти, что бы более точно вывести кривулю, а затем сделать шаблон для плиточек .
Эта задача элементарно решается компьютерными программами Архикад или Автокад,,где рисуются сплайнами кривые по всей поверхности по которой надо вывести(можно задавать радиусы,а можно просто рисовать нужную кривую) и которую визуально можно видеть и корректировать,программа сама пересчитывает и выдает координаты,но лучше затем просто распечатать на принтере 1:1 и получите на выходе готовый шаблон.А в случае гидрорезки просто скинуть файл в формате DWG в фирму производящую гидрорезку и они в точности по Вашим чертежам произведут резку(со всеми ошибками,если их допустить,или без оных,если их не нет).А снятие размеров и дальнейший их перерасчет по формулам-это тупиковый путь,потому,что ошибки которые будут накапливаться при снятии размеров приведут к таким погрешностям,что без ручной доводки затем не обойтись.Это,если для этой цели использовать(ну в случае плитки).
Регистрация: 28.08.2009
Казань
Сообщений: 357
Vegazzz написал :
во как!!это в мою копилку знаний в плане плитки.Лида написал :
А как же Вы тогда будете его использовать? И что толку от радиуса, который некуда приложить?
Вот пример из моей практики. Тут и центр окружности за стенкой, и кривуля
Регистрация: 29.10.2005
Москва
Сообщений: 5260
Keramamaster написал :
Тут и центр окружности за стенкой, и кривуля
А где гарантия, что первая — тоже не кривуля? 

Регистрация: 28.08.2009
Казань
Сообщений: 357
Лида написал :
А где гарантия, что первая — тоже не кривуля?
До меня поработали одни из лучших штукатуров. Сколько плитку после них не ложил, все углы в ноль сходились. Им доверял как себе и даже больше. Большая редкость.
А вообще вы правы, не нужна мне длина окружности, ну или не скоро понадобится.
Спасибо.
Регистрация: 29.10.2005
Москва
Сообщений: 5260
Keramamaster написал :
До меня поработали одни из лучших штукатуров. Сколько плитку после них не ложил, все углы в ноль сходились. Им доверял как себе и даже больше. Большая редкость.
Ну, кривулей я назвала не кривую стену в смысле её качества, а ту линию, которую создаёт эта идеально отштукатуренная стена 

















































