Как по двум координатам найти третью сторону - Исправление недочетов и поиск решений вместе с Examum.ru

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

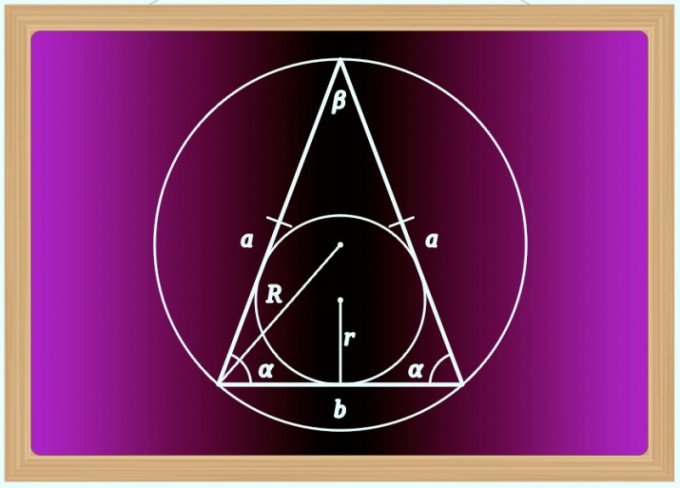
3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Как найти третью сторону треугольника — формулы и расчеты

В геометрии первая фигура, которую школьники начинают изучать, это треугольник. Он является одним из самых распространенных и простых замкнутых объектов. Знание свойств фигуры и необходимых теорем позволяет решать разные задачи о том, как найти третью сторону треугольника на плоскости.

Фигура из шести элементов

Под геометрическим элементом полагают какой-либо объект, который имеет определенную меру и является составляющей частью некоторой фигуры. Например, для сферы основными образующими элементами являются радиус и центр.

Как известно, треугольник — это фигура, которая состоит из трех отрезков и такого же количества вершин. При этом все отрезки попарно пересекаются. Из определения фигуры следует, что ее образуют два типа элементов, общее количество которых составляет 6:

сторона (3);
вершина (3).

Обычно треугольник обозначают большими латинскими буквами, например, ABC, PQM и так далее. Каждая буква — это название вершины (точка пересечения двух отрезков). AB, BC и CA, которые являются длинами сторон, принято обозначать маленькими латинскими буквами по названию противоположных им вершин, то есть c, a и b, соответственно.

Дополнительные отрезки

Несмотря на всю простоту построения фигуры, она обладает большим количеством дополнительных элементов, которые ее могут определять. Среди них самыми важными являются следующие:

Медиана — отрезок, который соединяет вершину и середину противоположной стороны. Таких отрезков в треугольнике три. Все они пересекаются в одной точке, которая является центром масс фигуры. Эта точка делит каждую медиану в отношении 2:1, начиная от вершины. Каждый из трех названных отрезков делит треугольник на две аналогичных фигуры равной площади.

Биссектриса — отрезок, который отличается от медианы тем, что он делит пополам соответствующий угол.

Высота — перпендикуляр, который из вершины опускается на сторону фигуры. Его удобно использовать при вычислении площади или при определении его углов через тригонометрические выражения. Для некоторых типов треугольников высота может совпадать со стороной (катет в прямоугольной фигуре).

Радиусы вписанной и описанной окружностей. Эти замкнутые симметричные кривые можно провести для любого треугольника. Указанные радиусы однозначно определяются через стороны и углы фигуры.

Средняя линия — это соединяющий две середины сторон отрезок. Его особенность заключается в том, что он всегда параллелен третьей стороне и равен половине ее длины.

Виды треугольников

Разработана достаточно развитая классификация рассматриваемых фигур. Главными ее пунктами являются значения углов треугольника и взаимоотношение между его отрезками. Так, если в фигуре все углы острые, то она называется остроугольной. Если же один из углов больше 90 °, то треугольник полагается тупоугольным. Чаще всего в задачах рассматривают следующие виды:

Основные свойства и понятия

Треугольник является одной из самых изученных фигур в геометрии. Для него известны многие теоремы, которые с успехом используются при решении задач. Существует два основных свойства фигуры, которые следуют из характеристик евклидового пространства:

Равенство суммы трех углов 180 °, то есть A + B + C = 180 °. Этот факт доказал еще Евклид в своем знаменитом труде «Элементы». По этой причине треугольник не может содержать больше одного прямого или тупого внутреннего угла.

Если известны три отрезка a, b и c такие, что выполняется равенство a + b = c, то из них составить треугольник невозможно. Это фундаментальное свойство говорит о том, что для всякого типа рассматриваемой фигуры сумма длин ее двух любых сторон всегда больше длины третьей.

Помимо названных свойств, следует знать о треугольнике еще такое понятие, как подобие. Его суть состоит в том, что одна из рассматриваемых фигур является точной копией в миниатюре другой. Для подобных треугольников все углы равны попарно, а все три стороны относятся соответственно попарно друг к другу с одним и тем же коэффициентом подобия.

Еще одной полезной характеристикой рассматриваемой фигуры является ее качество (CT). Вычисляется оно по следующей формуле:

CT = (a + b — c)*(b + c — a)*(c + a — b)/(a*b*c).

Величина CT лежит в пределах от 0 до 1. Она показывает степень близости фигуры к равностороннему, то есть к наиболее симметричному объекту. Если CT 0,5, то фигура характеризуется, как имеющая хорошее качество.

Величина CT применяется для алгоритмов, которые разделяют какую-либо изучаемую геометрическую поверхность на сетку треугольников. Если в этой сетке генерируется много низкокачественных фигур, то будет велика ошибка аппроксимации рассматриваемой величины.

Важные теоремы

Знание теорем для рассматриваемой фигуры позволяет понять, как найти сторону, зная 2 стороны треугольника. Прежде всего применяются две базовые теоремы:

Синусов. Как известно, синус — это тригонометрическая функция, которая вводится в прямоугольном треугольнике и определяет отношение противолежащего углу катета к гипотенузе. Теорема синусов для фигуры произвольного типа устанавливает следующее математическое взаимоотношение между отрезками и углами: a/sinA = b/sinB = c/sinC. Это означает, что вычислить длину любой стороны можно, если известен еще какой-нибудь отрезок и два угла.

Косинусов. Как и синус, косинус тоже является тригонометрической функцией, которая определяет отношение катета прилежащего к гипотенузе прямоугольной фигуры. Теорему косинусов удобно записать в виде следующего математического выражения: c 2 = a 2 + b 2 — 2*a*b*cosC. С помощью этого равенства можно найти 3 сторону треугольника по 2 сторонам известным и углу между ними.

К этим двум теоремам следует добавить еще два важных равенства, которые связаны с именами древнегреческих философов.

Первое выражение базируется на знаменитой теореме Пифагора, которая устанавливает связь между длинами двух катетов (меньшие стороны) и гипотенузы (большая сторона) в треугольнике с прямым углом. Если гипотенузу обозначить буквой c, тогда будет выполняться следующее равенство:

Если известные любые две стороны, то для определения третьей достаточно взять под квадратный корень соответствующую сумму или разницу квадратов.

Вторая из дополнительных теорем носит название философа Аполлония Пергского. Соответствующее ей математическое выражение выглядит так:

a 2 + b 2 = ½*c 2 + 2*Mc 2 .

Здесь Mc — это медиана, проведенная к стороне c из вершины C. Это равенство также называют в математике теоремой медианы.

Примеры решения задач

После того как изучены и рассмотрены основные понятия, свойства и теоремы для различного рода треугольников, можно переходить к решению геометрических задач. Поскольку для этого требуется в большинстве случаев знать значения тригонометрических функций, рекомендуется воспользоваться либо соответствующими таблицами, либо инженерным калькулятором.

Задачи школьного курса с треугольниками, как правило, не являются сложными. Они решаются благодаря однократному применению какого-либо свойства или теоремы.

Квадрат и его диагональ

Пусть дан квадрат, сторона которого составляет 11 см. Необходимо определить половину длины его диагонали.

Эту геометрическую задачу проще всего решить, если увидеть, что две смежные стороны исходной фигуры и ее диагональ образуют прямоугольный треугольник, который к тому же является равнобедренным. Каждая из равных сторон в нем имеет длину 11 см и является катетом. Диагональ c — это гипотенуза. Применяя пифагорову теорему, можно получить следующее равенство:

c = (11 2 + 11 2 )^0,5 ≈ 15,556 см.

Поскольку половина диагонали в два раза меньше гипотенузы, то искомым ответом на задачу будет число c/2 ≈ 7,778 см.

Две высоты и угол

Дан треугольник ABC. Известно, что при вершине C угол составляет 37 °. Из вершин A и B проведены высоты к сторонам этого треугольника, их длины составляют h1 = 10 см и h2 = 8 см, соответственно. Необходимо узнать длину стороны фигуры, которая лежит против угла C.

Из условия задачи можно найти длины сторон AC и BC. Для этого следует увидеть, что каждая из высот с двумя другими сторонами треугольника образует прямоугольную фигуру. Воспользовавшись тригонометрическими равенствами, можно получить следующие результаты:

AC = h1/sinC = 10/sin (37 °) ≈ 16,616 см;
BC = h2/sinC = 8/sin (37 °) ≈ 13,293 см.

Против угла C лежит сторона AB, которую следует найти. Получается, что известны две стороны треугольника (AC и BC) и угол между ними. Остается применить теорему косинусов, чтобы получить ответ:

AB = (AC 2 + BC 2 — 2*AC*BC*cosC)^0,5 = (16,616 2 + 13,293 2 — 2* 16,616 * 13,293 *cos (37 °))^0,5 ≈ 10 см.

Полученный результат свидетельствует о том, что высота h1 совпадает со стороной AB с рассчитанной точностью, то есть исходный треугольник являлся прямоугольным.

Таким образом, для нахождения стороны треугольника, если известны две другие его стороны или иные отрезки, следует воспользоваться теоремами. Основными из них являются теорема косинусов и синусов, а также Пифагора и Аполлония.

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Источник

Наличие двух равных сторон в треугольнике позволяет назвать его равнобедренным, а эти стороны — боковыми. Если они заданы координатами в двух- или трехмерной ортогональной системе, вычисление длины третьей стороны — основания — сведется к нахождению длины отрезка по его координатам. Знания же только размеров боковых сторон недостаточно для расчета длины основания, нужны какие-либо дополнительные сведения о треугольнике.

Инструкция

При наличии в исходных данных координат, определяющих боковые стороны, у вас нет необходимости вычислять их длины или углы фигуры. Рассмотрите отрезок между двумя несовпадающими точками — они определяют координаты основания равнобедренного треугольника. Для вычисления его размеров найдите разницу между координатами вдоль каждой из осей, возведите ее в квадрат, сложите два (для двухмерного пространства) или три (для трехмерного) полученных значения и извлеките из результата квадратный корень. Например, если сторона AB задана координатами точек A(3;5) и B(10;12), а сторона BC координатами точек B(10;12) и С(17;5), рассматривать нужно отрезок между точками A и C. Его длина составит AC = √((3-17)²+(5-5)²) = √((-14)² + 0²) = √196 = 14.

Если о треугольнике известно, что он не только имеет две одинаковых стороны заданной длины (a), но и является прямоугольным, это означает, что вам известен третий параметр — величина угла между боковыми сторонами. Угол в 90° не может не лежать между боковыми сторонами, так как в прямоугольном треугольнике к основанию (гипотенузе) всегда прилегают только острые (меньшие 90°) углы. Для вычисления длины третьей стороны (b) в этом случае просто умножьте длину боковой стороны — катета — на корень из двойки: b = a*√2. Эта формула вытекает из теоремы Пифагора: квадрат гипотенузы (в случае равнобедренного треугольника — основания) равен сумме квадратов катетов (боковых сторон).

Если угол (β) между боковыми сторонами отличается от прямого и его величина дана в условиях вместе с длинами этих сторон (a), используйте для нахождения длины основания (b), например, теорему косинусов. Применительно к равнобедренному треугольнику вытекающее из нее равенство можно преобразовать таким образом: b² = a² + a² — 2*a*a*cos(β) = 2*a² — 2*a²*cos(β) = 2*a²*(1-cos(β)) = 2*a²*sin(β). Тогда окончательную формулу расчетов можно записать так: b = a*√(2*sin(β)).

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Как составить уравнение сторон треугольника по координатам его вершин?

Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.

Пример.

Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)

Составить уравнения сторон треугольника.

Решение:

1) Составим уравнение прямой AB, проходящей через 2 точки A и B.

Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:

$[left{ begin{array}{l} 1 = k cdot ( - 5) + b; \ - 4 = k cdot 7 + b; \ end{array} right. Rightarrow k = - frac{5}{{12}};b = - frac{{13}}{{12}}.]$

Таким образом, уравнение стороны AB

$[y = - frac{5}{{12}}x - frac{{13}}{{12}}.]$

2) Прямая BC проходит через точки B(7;-4) и C(3;7):

$[left{ begin{array}{l} - 4 = k cdot 7 + b; \ 7 = k cdot 3 + b; \ end{array} right. Rightarrow k = - frac{{11}}{4};b = frac{{61}}{4}.]$

Отсюда уравнение стороны BC —

$[y = - frac{{11}}{4}x + frac{{61}}{4}.]$

3) Прямая AC проходит через точки A(-5;1) и C(3;7):

$[left{ begin{array}{l} 1 = k cdot ( - 5) + b; \ 7 = k cdot 3 + b; \ end{array} right. Rightarrow k = frac{3}{4};b = frac{{19}}{4}.]$

Уравнение стороны AC —

$[y = frac{3}{4}x + frac{{19}}{4}.]$

Источник

Как найти длину стороны треугольника по координатам

Геометрические задачи любого уровня высокого уровня сложности предполагают наличия у человека умения решать элементарные задачи. В противном случае возможность получения требуемого результата значительно снижается. Помимо процесса практически интуитивного нащупывания правильного способа, ведущего к нужному вам итогу, вы с необходимостью должны уметь рассчитывать площади, знать большое количество вспомогательных теорем, свободно проводить вычисления в координатной плоскости.

Воспользуйтесь формулой для вычисления длины отрезка, если в вашей задаче в явном виде заданы координаты вершин . Для этого проделайте ряд простых шагов. Сперва вычислите разницу между координатами соответствующих точек по оси абсцисс и оси ординат. Полученные результаты возведите в квадрат и суммируйте. Квадратный корень из результирующей величины и будет искомой длиной отрезка.

Проанализируйте все данные задачи, если отсутствуют данные для простого решения задачи. Выпишите отдельно все, что перечислено в условии. Обратите внимание на тип описываемого треугольника. Если он прямоугольный, то вам достаточно знать координаты двух вершин: длину третьей стороны вы сможете найти, воспользовавшись формулой Пифагора. Также упрощается ситуация при работе с равнобедренным или равносторонним треугольниками.

Обращайте внимание на некоторые характерные элементы условия, которые содержат в себе подсказку. К примеру, в тексте может быть упомянуто, что вершина треугольника лежит на одной из осей (что уже дает вам информацию об одной из координат), проходит через начало координат. Все это важно выписать, чтобы обладать полной информацией.

Не забывайте о формулах, позволяющих выразить стороны треугольника через другие его элементы, а также о существующих пропорциональных отношениях. К числу минимальных вспомогательных уравнений, которые вам пригодятся, относятся формулы для нахождения высоты, медианы и биссектрисы треугольников. Кроме того, запомните, что две стороны треугольника находятся в таком же отношении друг к другу, как и отрезки, на которые разбивает биссектриса, проведенная к третьей его стороне.

Будьте готовы к тому, что если вы используете в решении те или иные формулы или теоремы, вас могут попросить доказать их или описать процедуру вывода.

Источник

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник