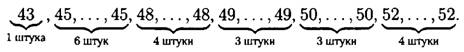Цель:
-
определение
общего размаха -
выбор
интервала группирования разрядов -
определение
границы разрядов. -
выполнить
самостоятельную работу с применением
навыков первичной статистической
обработки
1.
Построение распределения сгруппированных
частот, как правило, происходит в 4 этапа.
1
этап
– Определение размаха внутри всей
выборки. Он вычисляется пол формуле:
Р
= (Max
оценка
– Min
оценка)
+ 1
Если
применить к нашему случаю, т.е. к данным,
предоставленным в таблице 1 и таблице
2, то размах будет следующим: (112 – 44) + 1
= 69
2.Следующий
этап в построении распределения
сгруппированных частот
2
этап
– Выбор интервала группирования
разрядов. Интервал представляет собой
ширину разрядов, по которым должно быть
не больше 15 и не меньше 12 разрядов.
Меньше
12 искажает результат, более 15 затрудняет
работу с таблицей. Для того чтобы
вычислить интервал необходимо размах
поделить на 12, затем на 15 и найти целое
среднее значение между ними. По следующей
формуле:
И
=
– округлить до целого
В
нашем случае, исходя из наших данных,
определение интервала выглядит так:
И=
=
= 5,1. Округляем
до 5ти. Таким образом, в нашем примере
интервал группирования разрядов равен
5ти.
3.Следующий
этап в построении распределения
сгруппированных частот
3 этап
— Определение
границы разрядов необходимо начинать
с величины, которая является самой
низкой, и которая бы делилась на разрядный
интервал без остатка. Если данная низкая
величина не делится на разрядный интервал
без остатка, то выбирается ближайшее к
ней число, котрое делится на разрядный
интервал без остатка, но при этом данная
низкая величина должна попасть в
интервальный ряд.
И
делим на разряды до тех пор, пока не
будет охвачена самая высокая оценка
Таблица
3
|
Границы |
Подсчет |
f |
|
110 |
| |
1 |
|
105 |
||| |
3 |
|
100 |
|| |
2 |
|
95 |
|||| |
4 |
|
90 |
||| |
3 |
|
85 |
| |
1 |
|
80 |
|||||| |
6 |
|
75 |
|||| |
4 |
|
70 |
|||| |
4 |
|
65 |
||| |
3 |
|
60 |
| |
1 |
|
55 |
||| |
3 |
|
50 |
| |
1 |
|
45 |
| |
1 |
|
40 |
| |
1 |
В
нашем случае самой низкой оценкой
является 44, но она не делится на 5 без
остатка, поэтому необходимо выбрать
ближайшую цифру к 44, которая бы делилась
на 5 без остатка. Это может быть 40 либо
45. Если мы начнем с 45, то следующий
интервал начнется с 50 (45+5), а наш интервал
закончится 49. Следовательно оценка 44
не попадает в интервал 45-49, значит,
начинаем с 40.
4
этап
– Тубулирование. Заносим в таблицу
получившийся интервальный ряд.
Подсчитываем частоту (количество) данных
величин (оценок), попавших в каждый
интервал и получившееся число заносим
в колонку «частота». Из таблицы 3 видно,
что при окончательном табулировании
наших данных ведется подсчет для каждой
оценки, затем суммируется и полученное
число заносится в колонку «частота».
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
The grouped frequency table is a statistic method to organize and simplify a large set of data in to smaller «groups.» When a data consists of hundreds of values, it is preferable to group them in a smaller chunks to make it more understandable. When grouped frequency table is created, scientists and statistician can observe interesting trends in the data.
The main purpose of the grouped frequency table is to find out how often each value occurred within each group of the entire data. The group frequency distribution is essentially a table with two columns. The first column titled «Groups» represents all possible «grouping» of the data and the second column titled «Frequency» represents how frequent each value occurred within each group.
-
Rearranging the data in Step 2 will make it easy to create a distribution table. Always rearrange the data. You can use an Excel spreadsheet to rearrange the data by first entering the random data and then clicking on the «Sort Ascending» button.
Collect the data by writing it on a piece of paper. For example, let’s say we have data that consists of following 12 values: 16, 17, 18, 19, 10, 11, 13, 14, 17, 11, 12 and 15.
Rearrange the data so that it starts with the smallest number and ends with the highest number. In this example, this data will be rearranged as follows: 10,11,11,12,13,14,15,16,17,17,18 and 19.
Find the highest and lowest value and deduct lowest value from the highest value. In this example, we will deduct lowest value of «10» from the highest value of «19». Result is 19-10 = 9.
Determine the number of groups. Most of the data has between five to 10 groups. It is your decision to choose the number of groups for your data. In this example, since we have only 12 values, we will choose a total of five groups.
Determine the width of group interval. Width simply means number of values per group. The width of group is obtained by dividing Step 3 by Step 4. In this example, divided «9» by «5.» The result is 1.8 or 9/5 = 1.8. Round up 1.8 to 2. With this step we determined that there will be only two values per group.
Create two columns. Title first column as «Groups.» The first column represents all five groups of your data. Title second column as «Frequency.» The second column represents «how frequent» each value occurred per group.
Create all five groups for the first column of groups. Since the width of each group is «2,» in our example, the first group will be 10-11. This first group has two values; first value is 10 and second value is 11. Continue to create all five groups. All five groups will be as follows:
10-11 12-13 14-15 16-17 18-19
Determine the frequencies for all five groups by tallying the data. In our example, first group is 10-11, tally and see how many values fall under this group. You can see that under the first group of 10-11, three values (10,11,11) fall in. You will write three under the «Frequency Column.» Continue to tally for the remaining four groups. After you complete all five groups and tally its frequencies, your frequency table is complete.
Final Table will look like this:
Groups Frequency 10-11 3
12-13 2 14-15 2 16-17 3 18-19 2
Tips
Дата публикации: 09 апреля 2017.
Урок и презентация на тему: «Математическая статистика, элементы статистики»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:
Математическая статистика, элементы статистики (PPTX)
Статистика, введение
Темой сегодняшнего урока будет математическая статистика.
Этот предмет занимается статистикой, используя различные математические методы. Математическая статистика — это самостоятельно развивающийся раздел математики, в котором существуют и свои уникальные способы решения различных задач.
Так чем же занимается и для чего нужна математическая статистика?
Предположим, что у учеников девятых классов измерили рост. Как представить полученные данные? Можно записать их в строчку друг за другом, можно разделить данные по классам, можно попробовать создать таблицу. Все эти способы довольно громоздки и неудобны. Будет сложно извлечь информацию из такого набора чисел. А теперь представьте, что измерили рост учеников девятых классов всех школ в городе. Количество измерений может перевалить за тысячу.
Математическая статистика занимается обработкой данных и представлением их в виде удобном для восприятия. Это только одна из задач статистики. Построение прогнозов и оценок; применение различных методов исследования; достоверность проведенных испытаний и многое другое — вот чем занимается статистика.
Как же обрабатывает информацию статистика?
- Данные измерений упорядочивают и группируют.
- Составляют таблицы распределений данных.
- По таблицам строят графики распределений.
- В итоге создается паспорт измерений, в котором собраны числовые характеристики полученной информации.
Давайте рассмотрим эти пункты.
Упорядочивание и группировка данных
Первое, что необходимо сделать при анализе данных, определить рамки, в которых находится исследователь. Выбираются наименьшее и наибольшее допустимые значения, которые могут не совпадать с полученными данными. Например, при измерении роста учеников, шансов, что кто-то будет ниже 140 сантиметров и выше 200 сантиметров очень мало. Если найдется такой вариант, то данные статистики можно подкорректировать.
При измерении роста могут получиться числа: 140,150,160,170,180,190,200 – это общий ряд данных, которые принято располагать в порядке возрастания. Общий ряд данных может быть и другим, например: 140,145,150,155,160,…,190,195,200. Как представить общий ряд данных зависит от конкретной задачи.
Пример. Составить общий ряд данных, включающих:
а) месяцы рождения одноклассников,
б) годов рождения родственников и друзей,
в) буквы, с которых начинается слово.
Решение.
а) Всего месяцев 12, если их перечислить по цифрам, то получим общий ряд: 1,2,3,4,5,6,7,8,9,10,11,12.
б) Шанс, что кто-то из родственников старше 100 лет — мал, а что, кто-то родился в этом году — есть. Тогда общий ряд годов рождения можно составить так: 1910,1911,1912,…, 2009,2010,2011,2012,2013,2014.
в) Слово может начинаться с любой буквы алфавита, кроме ь, ы, ъ. Тогда возможны 30 вариантов, если их представить численным рядом, то получим: 1,2,3,4,…,28,29,30.
Понятие «общий ряд» не является строгим, в примере б) мы могли начать ряд с 1900 года, ряд так же назывался «общим».
При проведении эксперимента данные из общего ряда могут не встретиться. Вернемся к нашему примеру б) и рассмотрим конкретный случай.
Вова назвал года рождения родственников: 1935,1937,1960,1965,1980,1981,1997,2005.
Общий ряд представлял собой последовательность: 1910,1911,1912,…,2009,2010,2011,2012,2013,2014.
У Вовы встретились конкретные измерения, которые называются «вариантой измерения».
Варианта измерения – это возможный вариант проведенного измерения.
Если все варианты измерений перечислить по порядку, то получится ряд данных измерения.
Для нашего примера составим таблицу:
Пример. Выписать ряд, состоящий из букв, которые встречаются в словах: мама, папа, брат, сестра, бабушка, дедушка, тетя, дядя.
Решение. Ряд будет выглядеть так: а, б, д, е, к, м, п, р, с, т, у, ш, я. Встретились 13 букв из 33.
Некоторые буквы встречаются несколько раз, например, буква а – девять раз, другие – реже.
Определение. Если среди всех данных конкретного измерения одна из вариант встретилась ровно к раз, то число к называют кратностью измерения.
В этом примере буква а имеет кратность — 9.
Запишем кратности для каждой из букв:
Далее варианты нужно сгруппировать. Создадим сгруппированный ряд данных:
а,а,а,а,а,а,а,а,а,б,б,б,д,д,д,д,е,е,е,к,к,м,м,п,п,р,р,с,с,т,т,т,т,у,у,ш,шя,я,я.
Число повторений каждой варианты равно кратности варианты.
Составление таблицы распределения данных
Если сложить все кратности, получится количество всех данных измерения или объем измерения. Объем измерения равен количеству букв встречающихся в наших словах. Для проверки всегда складывают кратности, сумма должна равняться количеству элементов измерения.
Далее вычисляют частоту варианты.
Частота варианты=Кратность варианты/Объем измерения.
Составим таблицу частот измерений:
Сумма всех частот всегда равна единице, так как это сумма всех дробей с одинаковым знаменателем, а сумма всех числителей как раз и равна знаменателю. Для удобства, часто переводят частоты в проценты от объема измерения. Составим таблицу еще одну таблицу, каждую частоту в новой строке помножим на 100.
Графическое представление данных
Давайте построим графики функций распределения по таблицам. Договоримся, что вместо букв будем использовать цифры 1,2,3,…,13.
Тогда наша таблица примет вид:
По оси абсцисс отложим цифры, соответствующие буквам, а по оси ординат – значения частот появления варианта. Графическое изображение имеющейся информации – график распределения частот.
Таблица значений:
График распределения частот:
График распределения частот также называют полигоном распределения.
Давайте построим график распределения частот процентов. Его тоже называют полигоном распределения процентов.
Таблица значений.
Полигон распределения процентов:
Даже не большая по объему данных задача, представляет собой довольно таки утомительную процедуру подсчета и составления таблиц и графиков распределений.
Числовые характеристики данных измерения
Наши данные обладают уникальными числовыми характеристиками. Давайте определим некоторые из них.
Разность между максимальной и минимальной вариантой называют размахом измерения.
На наших графиках — это область определения (разность крайнего правого значения и крайнего левого значения на оси абсцисс). В нашем примере размах равен $13-1=12$.
Варианта, которая встречается чаще других, называется модой. В нашем примере это буква а или число 1, в зависимости от обозначения.
Если у нас есть таблица распределения частот, то в строчке частот ищем наибольшее число, и смотрим, какому варианту оно соответствует. На графике, это точка в которой достигается максимальное значение.
Наиболее важная характеристика – среднее значение (среднее арифметическое или просто среднее).
Чтобы найти среднее значение нужно:
а) Просуммировать все данные измерения.
б) Полученную сумму разделить на количество вариантов.
Для нашего примера найдем среднее значение:
$frac{1*9+2*3+3*4+4*3+5*2+6*2+7*2+8*2+9*2+10*4+11*2+12*2+13*3}{40}=5,775$.
Среднее значение можно найти другим способом:
а) Каждую варианту умножить на ее частоту.
б) Сложить получившиеся значения.
Подсчитаем этим способом:
1*0,225+2*0,075+3*0,1+4*0,075+5*0,05+6*0,05+7*0,05+8*0,05+9*0,05+10*0,1+11*0,05+12*0,05+13*0,075=5,775.
Давайте рассмотрим еще один пример.
На экзамене по математике 25 учеников 9 класса получили такие оценки:
5,4,3,3,5,4,3,3,4,4,5,5,2,2,5,5,5,3,3,4,5,5,4,3,2.
а) Составить общий ряд данных. Упорядочить и сгруппировать.
б) Составить таблицы распределения и распределения частот.
в) Построить графики распределения и распределения частот.
г) Найти среднее, моду, размах.
Решение.
Возможны такие оценки: 1,2,3,4,5 – общий ряд данных.
В нашем примере встречаются оценки: 2,3,4,5 – ряд данных, все числа в ряде – варианты измерений.
Составим сгруппированный ряд: 2,2,2,3,3,3,3,3,3,3,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5.
б) Объем измерения равен 25, так как 25 оценок выставлено.
Составим таблицу:
в) Нарисуем графики:
Полигон распределения данных:
Полигон распределения частот:
Полигон распределения частот процентов:
Все графики похожи между собой, различия только в масштабе оси ординат.
г)Найдем среднее значение:
$2*0,12+3*0,28+4*0,24+5*0,36=0,24+0,84+0,96+1,8=3,81$.
Мода: чаще всего встречается оценка пять, она и будет модой.
Размах: $5-2=3$.
Задачи статистики для самостоятельного решения
1.На экзамене по математике 50 учеников 9 класса получили такие оценки:
5,3,4,4,5,4,3,2,4,3,5,1,2,3,5,4,5,3,3,4,5,5,4,3,1,3,4,5,4,3,2,2,1,4,4,5,5,4,4,5,3,3,3,2,1,5,4,3,2,5.
а) Составить общий ряд данных. Упорядочить и сгруппировать.
б) Составить таблицы распределения и распределения частот.
в) Построить графики распределения и распределения частот.
г) Найти среднее, моду, размах.
3. Графическое представление информации.Распределение данных измерения рационально задавать в табличном виде. Однако нам известно, что и для функций есть табличный способ их задания. Таблицы являются связующим звеном. С их помощью осуществляется переход от распределения данных к функциям и графикам.
График распределения выборки является графическим представлением информации. Согласно табличным сведениям из примеров выше отметим точки, у которых абсциссы — это номер варианта, а ординаты — кратность. Соединяем отрезками полученные точки:
Пример:
Получили многоугольник или полигон распределения данных. Собственно, polygon и переводится как «многоугольник».
Чтобы представить большой объём информации в графическом виде, можно использовать гистограммы или столбчатые диаграммы.
Пример:

4. Числовые характеристики данных измерения.
У любого из нас имеются не только данные о рождении, но и ряд иных свойств и качеств.
Такие измерения имеют свои числовые характеристики.
Размах измерения — это разность между максимальной и минимальной вариантами.
Мода измерения — вариант, который в измерении встречался чаще других.
Медиана — число, стоящее в середине сгруппированного ряда.
Среднее значение — среднее арифметическое, или просто среднее. Для нахождения среднего значения нужно:
1) вычислить сумму всех данных измерения;
2) полученную сумму разделить на количество данных.
Рядом данных называют результаты измерения, перечисленные в порядке их получения. Каждый из результатов называется вариантой измерения.
Например, результаты написания контрольной работы по математике для класса из 20 человек можно представить в виде следующего ряда данных: 3, 4, 4, 5, 3, 4, 3, 3, 3, 5, 5, 4, 5, 4, 5, 3, 3, 3, 4, 3. Эту же информацию можно представить в
виде таблицы:
Кратность варианты — количество её повторений в ряду данных. В нашем ряду оценка «3» появилась 9 раз, поэтому её кратность равна 9.
Понятно, что таблица распределения отображает данные более наглядно и компактно.
Числовые характеристики данных
Объём измерения — количество всех данных этого измерения. Одна из наиболее важных характеристик варианты — это её частота. Частота варианты показывает долю этой
варианты в ряду распределения. Она вычисляется по формуле:
частота =кратность варианты/объём измерения
В нашем примере частота варианты «4» равна .
Это означает, что оценка 4 составляет 0,3 всех полученных оценок.
Размах измерения — разность между максимальной и минимальной вариантами этого измерения. В нашем примере максимальная варианта равна 5, минимальная — 3, значит, размах равен .
Мода измерения — варианта, которая в измерении встретилась чаще других. В приведённом выше примере чаще всех встретилась оценка 3, значит, она и будет модой этого распределения.
Медиана распределения — это центральное число в упорядоченном ряду данных, если в ряду нечётное количество чисел, или полусумма двух центральных, если в ряду чётное количество чисел.
Например, для ряда распределения 1, 2, 3, 6, 9, объём измерения которого равен 5, медианой распределения будет третье число этого ряда, то есть 3.
Для ряда распределения 7, 3, 2, 1 с объёмом измерения, равным 4, медианой будет полусумма двух центральных чисел данного ряда, то есть число, равное .
Для нахождения медианы распределения необходимо
1. Упорядочить ряд распределения по возрастанию или по убыванию: .
2. Если объём измерения нечётный, то есть , то получим следующую ситуацию:
В этом случае медианой является число .
3. Если объём измерения чётный, то есть , то имеем
В этом случае медианой является число — .
Среднее ряда (среднее арифметическое) — сумма всех чисел ряда, делённая на их количество. Если имеется таблица распределения, то можно
1) умножить каждую варианту на её кратность;
2) просуммировать полученные значения;
3) разделить результат на объём измерения. Например, для ряда распределения 2, 4, б, 8, у которого объём измерения равен 4, среднее значение равно
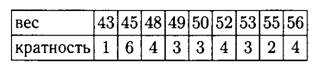
Задача 1. Даны результаты измерения веса школьников 9 класса: 55, 53, 56, 48, 45, 56, 49, 52, 53, 49, 50, 56, 45, 52, 56, 45, 45, 48, 55, 52, 43, 48, 52, 49, 50, 45, 48, 45, 50, 53.
а) Постройте таблицу распределения данных.
б) Найдите объём измерения.
в) Найдите размах ряда.
г) Найдите частоту появления каждого веса в указанном ряду.
д) Найдите медиану, моду и среднее указанного ряда.
Решение.
а) Наименьшее число в ряду — 43, оно встречается в ряду один раз, значит, его кратность равна 1. Следующее по величине — число 45, оно встречается шесть раз, значит, его кратность равна 6. Далее 48, оно встречалось 4 раза, значит, его кратность равна 4.
Продолжая аналогично, заполним таблицу:
б) Найти объём измерения можем несколькими способами.
1- й способ.
Посчитаем количество чисел в ряду, получим 30.
2- й способ.
Сложим кратности всех вариант:
Ответ: 30.
в) Наибольшее значение в ряду 56, наименьшее — 43, значит, размах равен
Ответ: 13.
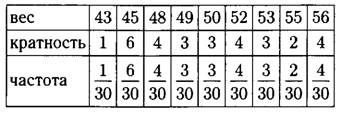
г) Для каждой варианты делим её кратность на объём измерения (на 30), результаты пишем в таблицу.
д) В данном ряду 30 чисел, значит, медиана равна полусумме 15-го и 16-го чисел в упорядоченном ряду.
Как видно из такой записи чисел, от 43 до 49 — 14 чисел, значит, 15-ое и 16-ое числа равны 50, и значит, медиана равна
Мода — то значение, которое встречается чаще всех, то есть то, у которого больше кратность. Из таблицы распределения находим, что наибольшую кратность имеет число 45, значит, мода равна 45.
Для нахождения среднего необходимо найти сумму всех чисел ряда и разделить ее на количество этих чисел. Сумму можно найти просто складывая подряд все числа ряда. А можно поступить иначе: каждую варианту умножить на её кратность и сложить полученные результаты. Имеем:
.
Осталось разделить полученную сумму на количество всех чисел: .
Ответ: медиана: 50; мода: 45; среднее: 50,1.
Задача 2. Пятерых учеников попросили подсчитать, сколько времени (в минутах) они тратят на дорогу от дома до школы. Получили следующие результаты: 5,15,10,15,20.
1) На сколько среднее значение этого ряда меньше его размаха?
2) На сколько мода этого ряда больше медианы?
3) Найдите процентную частоту значения 10.
Решение.
1) Среднее ряда: , размах:
. Искомое значение равно
.
Ответ: 2.
2) Найдём медиану. Расположим числа в порядке возрастания: 5, 10, 15, 15, 20. Медианой этого набора будет третье число в упорядоченном ряду, то есть 15.
В данном ряду число 15 встретилось 2 раза, остальные — по одному разу. Мода ряда равна 15. Мода и медиана этого ряда равны, значит, ответ 0.
Ответ: 0.
3) Кратность значения 10 равна 1, объём измерения равен 5 (всего 5 чисел). Частота значения 10 равна , процентная частота равна
.
Ответ: 20.
Задача 3. Имеется 4 группы породистых котов. Для некоторого соревнования отбирают котов с длиной шерсти не менее 8 см.
Известно следующее:
1) в первой группе наибольшая длина шерсти равна 10 см;
2) во второй группе средняя длина шерсти равна 8 см;
3) в третьей группе мода длины шерсти равна 8 см;
4) в четвёртой группе медиана длины шерсти равна 9 см.
В какой из групп хотя бы половина котов гарантированно подходит по длине шерсти?
Решение.
1) Из того, что наибольшая длина шерсти равна 10 см, не следует никакой другой информации, то есть ничего не можем сказать про остальных котов этой группы.
2) Рассмотрим для примера группу котов с длиной шерсти 7 см, 7 см и 10 см. Среднее равно , но в этой группе нет половины котов, удовлетворяющих требованиям.
3) Рассмотрим для примера группу котов с шерстью длиной 8 см, 8 см, 7 см, б см, 5 см. Мода равна 8, но опять же нет половины котов, удовлетворяющих требованиям.
4) Если медиана равна 9 см, то есть половина котов с шерстью меньшей или равной длины и половина — с большей или равной длины. Значит, в этой группе найдётся половина котов с шерстью длиной не менее 8 см.
Ответ: 4.
Задача 4. По статистике автозавода из 1000 машин в среднем 20 бракованных. Сколько бракованных машин следует ожидать, если завод собирается выпустить 300 500 машин?
Решение.
Если из 1000 машин 20 бракованных, то частота появления бракованной машины равна . То есть доля бракованных машин будет равна 0,02, тогда из 300 500 машин будет
бракованных.
Ответ: 6010.