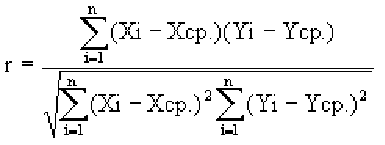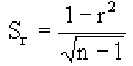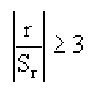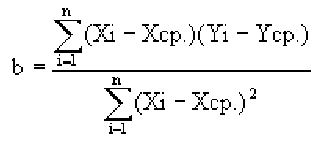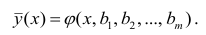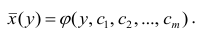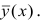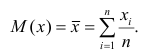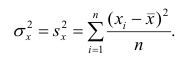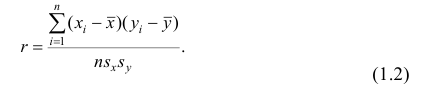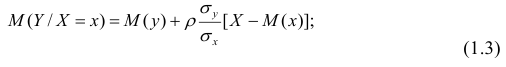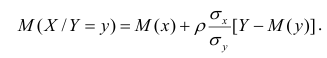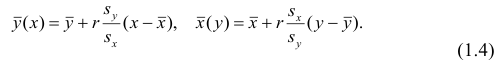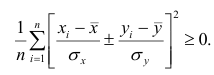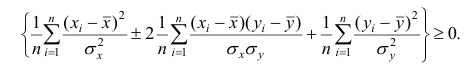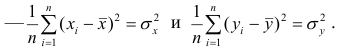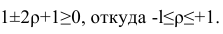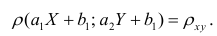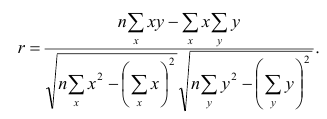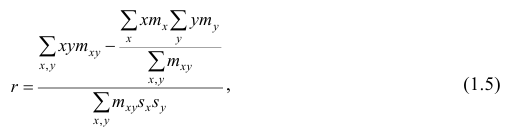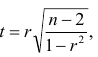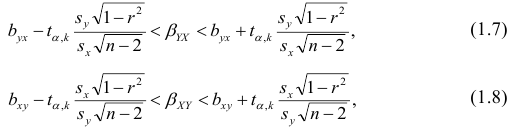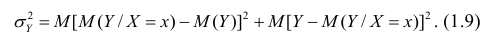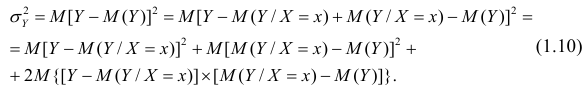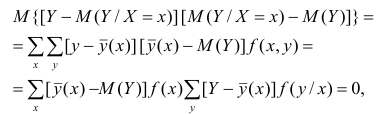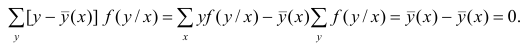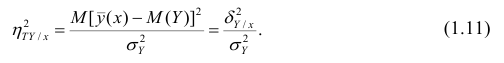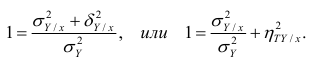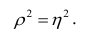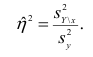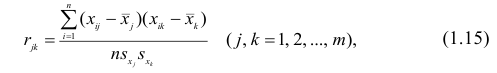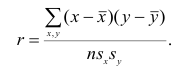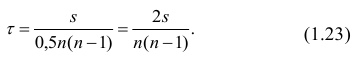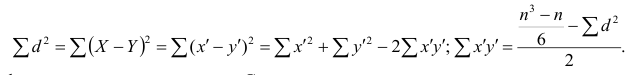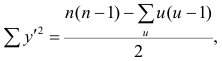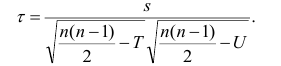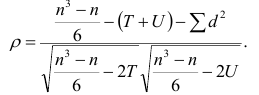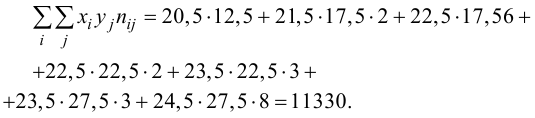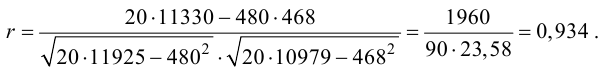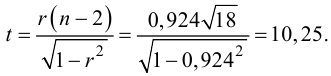Все курсы > Оптимизация > Занятие 3
Как мы уже говорили, исследуя изменения случайных величин, мы зачастую обнаруживаем, что между этими изменениями существует взаимосвязь (bivariate relationship, association).
Откроем ноутбук к этому занятию⧉
Возьмем вот такой простой набор данных.
|
toy_df = pd.DataFrame({ ‘a’:[1, 4, 5, 6, 9], ‘b’:[2, 3, 5, 6, 8], ‘c’:[6, 5, 4, 3, 2], ‘d’:[7, 4, 3, 4, 6] }) toy_df |
Посмотрим на распределения величин с помощью boxplot.
|
plt.figure(figsize = (8, 6)) sns.boxplot(data = toy_df) plt.show() |
Очевидно, распределения отличаются друг от друга, однако пока что мы мало можем сказать об этих распределениях или их взаимосвязи.
Начнем с расчета дисперсии.
Дисперсия
Дисперсия (variance) показывает изменение переменной относительно среднего значения. Приведем формулу для расчета дисперсии генеральной совокупности.
$$ sigma^2 = frac{sum (x_i-mu)^2}{N} $$
где $mu$ — среднее генеральной совокупности из $ x_i $ элементов, а $N$ — ее размер. Дисперсию выборки мы рассчитываем немного иначе.
$$ s^2 = frac{sum (x_i-bar{x})^2}{n-1} $$
В данном случае деление на $n-1$, а не на $n$ называется поправкой Бесселя (Bessel’s correction). Зачем нужна такая поправка? Оказывается, можно показать, что сумма квадратов расстояний, то есть числитель формулы, до среднего генсовокупности (population mean) будет всегда больше, чем сумма квадратов расстояний до выборочного среднего (sample mean).
Как следствие, если при расчете выборочной дисперсии делить на $n$, то мы будем постоянно недооценивать дисперсию генсовокупности. Поправка с делением на $ n-1 $ увеличит дисперсию выборки и сделает ее несмещенной оценкой (unbiased estimation) дисперсии генеральной совокупности.
Приведем основные выводы для показателя дисперсии.
- Большая дисперсия показывает, что значения далеки от среднего и далеки друг от друга
- Дисперсия не может быть отрицательной
- Нулевая дисперсия означает, что все элементы выборки или генеральной совокупности идентичны
Замечу, что далее мы в большинстве случаев будем приводить формулы и вычислять именно выборочные показатели.
Найдем дисперсию для переменной a.
|
# применим формулу дисперсии к первому столбцу (np.square(toy_df[‘a’] — toy_df[‘a’].mean())).sum() / (toy_df.shape[0] — 1) |
Дисперсию для каждой переменной можно измерить с помощью функции np.var() библиотеки Numpy.
|
# рассчитаем дисперсию по столбцам с делением на n — 1 np.var(toy_df, ddof = 1) |
|
a 8.5 b 5.7 c 2.5 d 2.7 dtype: float64 |
Точно такой же результат можно получить с помощью метода .var() библиотеки Pandas.
|
# ddof = 1 можно не указывать, это параметр по умолчанию toy_df.var() |
|
a 8.5 b 5.7 c 2.5 d 2.7 dtype: float64 |
Параметр ddof означает Delta Degrees of Freedom (дельта степеней свободы) и указывает на размер поправки при расчете дисперсии выборки. Соответственно ddof = 1 как раз использует деление на $n-ddof = n-1$. Как мы видим, дисперсия переменной a существенно больше, чем, например, переменной d.
Показатель дисперсии представляет собой квадрат измеряемых нами величин. Для понимания величины отклонения это не очень удобно. В этом смысле лучше подойдет среднее квадратическое отклонение.
Среднее квадратическое отклонение
Среднее квадратическое отклонение (СКО, standard deviation) как раз вычисляется как корень из дисперсии.
$$ sigma = sqrt{sigma^2} $$
$$ s = sqrt{s^2} $$
Рассчитаем СКО для первого столбца.
|
np.sqrt((np.square(toy_df[‘a’] — toy_df[‘a’].mean())).sum() / (toy_df.shape[0] — 1)) |
Мы также можем использовать функцию np.std() библиотеки Numpy и метод .std() библиотеки Pandas.
|
# для расчета СКО будем также делить на n — 1 np.std(toy_df, ddof = 1) |
|
a 2.915476 b 2.387467 c 1.581139 d 1.643168 dtype: float64 |
|
# опять же, этот параметр установлен по умолчанию, и его можно не указывать toy_df.std() |
|
a 2.915476 b 2.387467 c 1.581139 d 1.643168 dtype: float64 |
Теперь перейдем к изучению взаимосвязи между переменными. Одним из способов измерения взаимосвязи является ковариация.
Ковариация
Ковариация (covariance) измеряет направление изменения двух переменных. Другими словами она позволяет понять как изменится одна из двух переменных при изменении второй.
Построим три точечные диаграммы (scatter plots) для переменных a и b, b и c, и c и d соответственно.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# создадим сетку 1 х 3 с подграфиками для каждой из пар переменных f, (pair1, pair2, pair3) = plt.subplots(nrows = 1, ncols = 3, figsize = (12, 4), constrained_layout = True) # в первый подграфик поместим точечную диаграмму переменных a и b pair1.scatter(toy_df[‘a’], toy_df[‘b’]) pair1.set_title(‘a vs. b’, fontsize = 14) pair1.set(xlabel = ‘a’) pair1.set(ylabel = ‘b’) # во второй — b и c pair2.scatter(toy_df[‘b’], toy_df[‘c’]) pair2.set_title(‘b vs. c’, fontsize = 14) pair2.set(xlabel = ‘b’) pair2.set(ylabel = ‘c’) # в третий — c и d pair3.scatter(toy_df[‘c’], toy_df[‘d’]) pair3.set_title(‘c vs. d’, fontsize = 14) pair3.set(xlabel = ‘c’) pair3.set(ylabel = ‘d’) plt.show() |
На первом и втором графике мы видим линейную взаимосвязь. Приведем формулу для ее измерения.
$$ Cov_{x, y} = frac{sum (x_i-bar{x})(y_i-bar{y})}{n-1} $$
Как вы видите, ковариация представляет собой сумму произведений отклонений переменных от своего среднего значения, усредненную на количество наблюдений ($n-1$).
Рассчитаем ковариацию a и b с помощью Питона.
|
((toy_df[‘a’] — toy_df[‘a’].mean()) * (toy_df[‘b’] — toy_df[‘b’].mean())).sum() / (toy_df.shape[0] — 1) |
Если использовать функцию np.cov() библиотеки Numpy или метод .cov() библиотеки Pandas, то мы получим так называемую ковариационную матрицу (covariance matrix).
|
# для расчета по столбцам нужно использовать параметр rowvar = False np.cov(toy_df, ddof = 1, rowvar = False) |
|
array([[ 8.5 , 6.75, -4.5 , -1. ], [ 6.75, 5.7 , -3.75, -0.55], [-4.5 , -3.75, 2.5 , 0.5 ], [-1. , -0.55, 0.5 , 2.7 ]]) |
По диагонали указана дисперсия, вне диагонали — ковариация любых двух переменных.
Переменные a и b имеют положительную ковариацию, с увеличением a увеличивается и b. Переменные b и c — отрицательную, переменные c и d демонстрируют нулевую или близкую к нулевой ковариацию.
Интересно, что если переменные независимы (между ними нет взаимосвязи) — ковариация будет равна нулю, при этом обратное не обязательно верно. Если ковариация равна нулю, взаимосвязь может быть, просто она нелинейна (возможно именно такая взаимосвязь существует между c и d).
Недостатком ковариации является то, что она измеряет только направление, но не силу взаимосвязи. Если мы умножим значения обеих переменных, например, на три, то ковариация, исходя из формулы выше, увеличится в девять раз (поскольку как x, так и y каждой пары переменных умножаются на три), при этом очевидно сила взаимосвязи никак не изменится.
|
# умножим данные на три, рассчитаем ковариацию # и разделим на ковариационную матрицу исходного датасета, # чтобы посмотреть масштаб изменения (toy_df * 3).cov() / toy_df.cov() |
Этот недостаток исправляет коэффициент корреляции.
Корреляция
Корреляция (correlation) между двумя переменными (случайными величинами) измеряет не только направление, но и силу взаимосвязи.
Параметрические и непараметрические тесты
Прежде чем перейти к различным коэффициентам корреляции несколько слов про разделение статистических тестов или методов на параметрические и непараметрические.
Параметрические методы (parametric methods) основываются на допущении (assumption) или предпосылке о том, как распределена генеральная совокупность, из которой взята изучаемая выборка. Например, статистический тест может предполагать, что данные имеют нормальное распределение.
Непараметрические методы (non-parametric) таких допущений соответственно не предполагают.
На практике это означает, что если допущения параметрического теста не выполняются, его результат нельзя считать достоверным. Для непараметрического теста такое ограничение отсутствует.
Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона (Pearson correlation coefficient) — это параметрический тест, который строится на основе расчета ковариации двух переменных, разделенного на произведение СКО каждой из них.
$$ r_{pearson} = frac{Cov_{x, y}}{s_x s_y} $$
Деление на произведение СКО $(s_x s_y)$ выражает любой коэффициент ковариации в единицах этого произведения (нормализует его). Как следствие, мы получаем возможность сравнения коэффициентов корреляции, а значит измерения не только направления, но и силы взаимосвязи.
Коэффициент корреляции всегда находится в диапазоне от $-1$ до $1$.
Значения, приближающиеся к 1 указывают на сильную положительную линейную корреляцию. Близкие к −1 — на сильную отрицательную линейную корреляцию. Околонулевые значения означают отсутствие линейной корреляции.
Посмотрим на график возможных вариантов корреляции данных, приведенный на занятии вводного курса.
Библиотека Numpy предлагает нам функцию np.corrcoef() для создания корреляционной матрицы (correlation matrix) коэффициента Пирсона.
|
# для расчета корреляции по столбцам используем параметр rowvar = False np.corrcoef(toy_df, rowvar = False).round(2) |
|
array([[ 1. , 0.97, -0.98, -0.21], [ 0.97, 1. , -0.99, -0.14], [-0.98, -0.99, 1. , 0.19], [-0.21, -0.14, 0.19, 1. ]]) |
В Pandas мы можем воспользоваться методом .corr().
|
# параметр method = ‘pearson’ используется по умолчанию, # его можно не указывать toy_df.corr(method = ‘pearson’).round(2) |
Корреляция переменной с самой собой равна единице, что и отражают значения на главной диагонали матрицы. Кроме того, очевидно, что величина X также коррелирует с Y, как Y c X.
Продемонстрируем также, что изменение масштаба данных не отразится на коэффициенте корреляции.
|
# умножим значения датасета на два и снова рассчитаем коэффициент Пирсона (toy_df * 2).corr().round(2) |
Особенности коэффициента Пирсона
Несколько важных замечаний.
Замечание 1. Ни ковариация, ни корреляция не устанавливают причинно-следственной связи (correlation does not imply causation). Например, мы можем наблюдать существенную корреляцию между потреблением мороженого и продажами кондиционеров, при этом изменения в обеих переменных могут быть вызваны третьей, на рассматриваемой нами переменной, в частности, температурой воздуха.
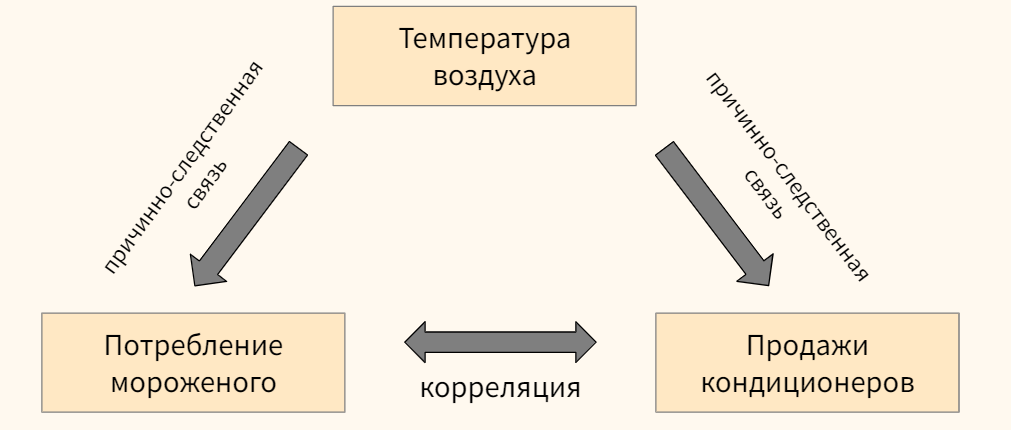
Кроме того в некоторых случаях корреляция может быть чистой случайностью.
Замечание 2. Коэффициент корреляции Пирсона измеряет взаимосвязь (1) количественных переменных и (2) предполагает, что обе переменные имеют нормальное распределение (это и есть упомянутое выше допущение (assumption) параметрического теста).
Замечание 3. Как и в случае с ковариацией, отсутствие линейной корреляции не означает отсутствие взаимосвязи. Возможно взаимосвязь есть, но она нелинейна.
Замечание 4. Более того, на коэффициент корреляции существенное влияние оказывают выбросы (outliers).
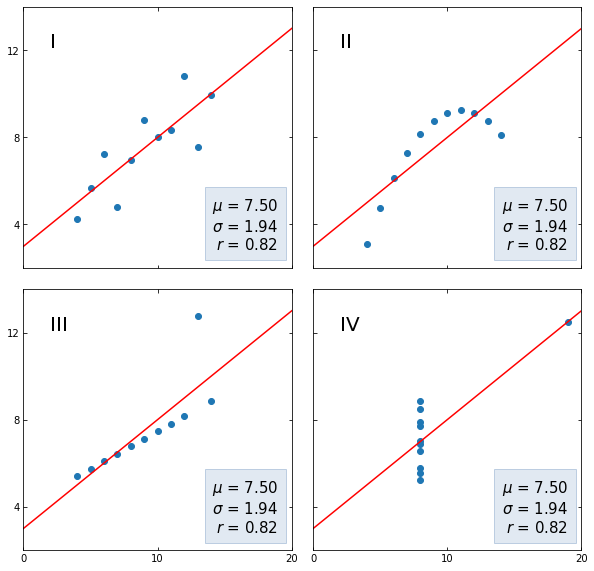
Последние два замечения хорошо иллюстрируются квартетом Энскомба (Anscombe’s quartet), набором небольших датасетов (кстати, встроенных в сессионное хранилище Google Colab) с совершенно разными распределениями x и y, но одинаковым средним арифметическим и СКО переменной y, а также одинаковым коэффициентом корреляции Пирсона.
Вначале получим необходимые данные.
|
# загрузим данные в формате json из сессионного хранилища, # преобразуем в датафрейм и посмотрим на первые три строки anscombe = pd.read_json(‘/content/sample_data/anscombe.json’) anscombe.head(3) |
|
# разобьем данные на четыре части по столбцу Series series_by_group = [x for _, x in anscombe.groupby(‘Series’)] # отдельно получим названия каждой из четырех частей labels = anscombe.Series.unique() labels |
|
array([‘I’, ‘II’, ‘III’, ‘IV’], dtype=object) |
|
# создадим пустой словарь datasets = {} # в цикле пройдемся по названиям и значениям переменных x и y каждой из частей for label, series in zip(labels, series_by_group): # каждое название части станет ключом словаря, а переменные x и y — значениями datasets[label] = (list(series.X.round(2)), list(series.Y.round(2))) # выведем содержимое словаря с помощью функции pprint() from pprint import pprint pprint(datasets) |
|
{‘I’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5], [8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.81, 5.68]), ‘II’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5], [9.14, 8.14, 8.74, 8.77, 9.26, 8.1, 6.13, 3.1, 9.13, 7.26, 4.74]), ‘III’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5], [7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.42, 5.73]), ‘IV’: ([8, 8, 8, 8, 8, 8, 8, 19, 8, 8, 8], [6.58, 5.76, 7.71, 8.84, 8.47, 7.04, 5.25, 12.5, 5.56, 7.91, 6.89])} |
Теперь выведем каждый из четырех датасетов на графиках.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
# создадим сетку подграфиков 2 х 2 fig, axs = plt.subplots(2, 2, sharex = True, sharey = True, figsize = (10, 10), gridspec_kw = {‘wspace’: 0.08, ‘hspace’: 0.08}) # определим границы осей и отметки на осях x и y axs[0, 0].set(xlim = (0, 20), ylim = (2, 14)) axs[0, 0].set(xticks = (0, 10, 20), yticks = (4, 8, 12)) # пройдемся по подграфикам, а также ключам и значениям словаря datasets for ax, (label, (x, y)) in zip(axs.flat, datasets.items()): # выведем название (номер) группы ax.text(0.1, 0.9, label, fontsize = 20, transform = ax.transAxes, va = ‘top’) ax.tick_params(direction = ‘in’, top = True, right = True) # построим точечные диаграммы ax.scatter(x, y) # обучим модель линейной регрессии slope, intercept = np.polyfit(x, y, deg = 1) # выведем график линейной регрессии x_vals = np.linspace(0, 20, num = 1000) y_vals = intercept + slope * x_vals ax.plot(x_vals, y_vals, ‘r’) # рассчитаем среднее арифметическое, СКО и корреляцию Пирсона stats = (f‘$\mu$ = {np.mean(y):.2f}n’ f‘$\sigma$ = {np.std(y):.2f}n’ f‘$r$ = {np.corrcoef(x, y)[0][1]:.2f}’) # создадим отформатированное пространство на графике bbox = dict(boxstyle = ‘square’, pad = 0.5, fc = ‘#c5d4e6’, ec = ‘#89a8cc’, alpha = 0.5) # и выведем в нем рассчитанные выше статистические показатели ax.text(0.95, 0.07, stats, fontsize = 15, bbox = bbox, transform = ax.transAxes, horizontalalignment = ‘right’) plt.show() |
- Как мы видим, на первом графике прослеживается линейная корреляция без каких-либо сюрпризов;
- Во втором наборе данных у нас нелинейная зависимость, силу которой мы не смогли отразить с помощью коэффициента Пирсона;
- В третьем наборе коэффициент корреляции находится под сильным влиянием выброса;
- В четвертом, корреляция по сути отсутствует и тем не менее одного наблюдения оказывается достаточно для появления достаточно сильной корреляции.
Помимо ограничений коэффициента корреляции, эти наборы данных демонстрируют в целом важность визуальной оценки данных.
Коэффициент Пирсона как скалярное произведение векторов
Распишем формулу корреляции более подробно (см. формулы ковариации, дисперсии и СКО).
$$ r_{pearson} = frac{ frac{sum (x_i-bar{x})(y_i-bar{y})}{n-1} }{ sqrt {frac{sum (x_i-bar{x})^2}{n-1} frac{sum (y_i-bar{y})^2}{n-1} } } $$
Упростим выражение.
$$ r_{pearson} = frac{ sum (x_i-bar{x})(y_i-bar{y}) } { sqrt {sum (x_i-bar{x})^2} sqrt{ sum (y_i-bar{y})^2 } } $$
Теперь давайте представим случайные величины X и Y в форме векторов
$$ textbf{x} = [x_1, x_2, x_3,…, x_n] $$
$$ textbf{y} = [y_1, y_2, y_3,…, y_n] $$
со средними значениями $ bar{x} $ и $ bar{y} $. Затем определим новые векторы $ textbf{x}^c $ и $ textbf{y}^c $, в которых из значений $x_i$ и $y_i$ вычтем соответствующие средние значения.
$$ textbf{x}^c = [x_1-bar{x}, x_2-bar{x}, x_3-bar{x},…, x_n-bar{x}] $$
$$ textbf{y}^c = [y_1-bar{x}, y_2-bar{x}, y_3-bar{y},…, y_n-bar{y}] $$
Обратим внимание, что (1) числитель (1) в формуле коэффициента корреляции представляет собой покомпонентное умножение векторов с последующим сложением произведений (то есть скалярное произведение).
Знаменатель (2) же представляет собой покомпонентное умножение и сложение произведений векторов самих на себя. Как мы узнаем на курсе линейной алгебры, корень из скалярного произведение вектора на самого себя есть длина этого вектора. Приведем пример для вектора $ textbf{x} $
$$ sqrt { textbf{x}^2 } = sqrt { textbf{x} cdot textbf{x} } = || textbf{x} || $$
Исходя из этих двух соображений, перепишем формулу расчета коэффициента Пирсона.
$$ r_{pearson} = frac { textbf{x}^c cdot textbf{y}^c }{|| textbf{x}^c || cdot || textbf{y}^c || } $$
Это формула косинусного сходства двух векторов. Другими словами, коэффициент корреляции равен косинусу угла между двумя векторами данных. Рассчитаем корреляцию через косинусное сходство с помощью Питона.
|
# возьмем данные первой группы квартета Энскомба x = np.array([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5]) y = np.array([8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.81, 5.68]) # вычтем из каждого значения x и y соответствующее среднее арифметическое xc = x — np.mean(x) yc = y — np.mean(y) # используем формулу косинусного сходства и округлим результат np.round(np.dot(xc, yc)/(np.linalg.norm(xc) * np.linalg.norm(yc)), 2) |
Как уже было сказано, у коэффициента Пирсона есть ряд ограничений, в частности, он выявляет только линейную взаимосвязь количественных переменных. В этой связи рассмотрим коэффициент Спирмена.
Коэффициент ранговой корреляции Спирмена
Коэффициент ранговой корреляции Спирмена (Spearman’s Rank Correlation Coefficient) хорошо измеряет постоянно возрастающую или постоянно убывающую (монотонную) зависимость двух переменных, а также подходит для работы с категориальными порядковыми данными.
Это непараметрический тест, который не предполагает каких-либо допущений о распределении генеральной совокупности.
Монотонная зависимость
Напомню, что функция или зависимость называется монотонной (monotonic), если на заданном интервале ее производная (градиент) не меняет знака (то есть всегда имеет неотрицательное или неположительное значение). Приведем пример.
Рассмотрим взаимосвязь площади (area) и цены (price) квартиры.
|
# поместим данные площади и цены квартиры в датафрейм flats = pd.DataFrame({ ‘area’ :[78, 90, 74, 69, 63, 57, 72, 67, 83], ‘price’ :[9.1, 9.0, 8.9, 8.2, 6.0, 5.8, 8.7, 7.5, 9.2] }) flats |
Выведем эти данные с помощью точечной диаграммы (scatter plot).
|
plt.figure(figsize = (8, 6)) plt.scatter(flats.area, flats.price) plt.xlabel(‘Площадь, кв. м.’, fontsize = 15) plt.ylabel(‘Цена, млн. руб.’, fontsize = 15) plt.grid() plt.show() |
Рассчитаем коэффициент корреляции Пирсона.
|
# применим метод .corr() с параметром method = ‘pearson’ # выведем одно из значений корреляционной матрицы с помощью .iloc[0, 1] и округлим результат flats.corr(method = ‘pearson’).iloc[0, 1].round(2) |
Достаточно высокий уровень корреляции. При этом, как мы видим, зависимость нелинейна и возможно коэффициент Пирсона не до конца уловил силу взаимосвязи. Как нам преодолеть ограничение линейности?
Обратите внимание, прежде чем построить график, Питон упорядочил значения площади (ось x). Упорядочил, то есть присвоил им ранг (порядковый номер) от первого до, в данном примере, девятого. В каком случае значения цены (ось y) будут также возрастать? Только в случае если их ранги мало отличаются от рангов значений площади квартиры.
Коэффициент корреляции Спирмена как раз считает степень отличия рангов двух переменных.
Приведем формулу.
$$ r_{spearman} = frac{6 sum d_i^2 }{n(n^{2}-1)} $$
Вычислим коэффициент Спирмена с помощью Питона. Вначале присвоим каждому значению в обоих столбцах ранг (порядковый номер), предварительно упорядочив значения по убыванию.
|
# для этого используем метод .rank() с параметром ascending = False flats[‘area_rank’] = flats.area.rank(ascending = False) flats[‘price_rank’] = flats.price.rank(ascending = False) flats |
Таким образом площади дома в 90 квадратных метров и цене в 9,2 миллона рублей будет присвоен ранг 1. Теперь мы можем вычислить разницу рангов для каждого из наблюдений и возвести ее в квадрат.
|
# вычтем из рангов площади ранги цены flats[‘diff’] = flats[‘area_rank’] — flats[‘price_rank’] # возведем разницу в квадрат flats[‘diff_sq’] = np.square(flats[‘diff’]) flats |
Выполним оставшиеся вычисления в соответствии с приведенной выше формулой.
|
# поместим количество наблюдений в переменную n n = flats.shape[0] # применим формулу для расчета коэффициента Спирмена 1 — ((6 * flats[‘diff_sq’].sum()) / (n * (n**2 — 1))) |
Рассчитаем корреляцию Спирмена с помощью метода .corr() библиотеки Pandas с параметром method = ‘spearman’.
|
flats[[‘area’, ‘price’]].corr(method = ‘spearman’).iloc[0, 1].round(2) |
Как мы видим, этот коэффициент гораздо лучше уловил монотонную нелинейную зависимость двух переменных.
Также замечу, что коэффициент корреляции Спирмена менее чувствителен к выбросам, находящимся на «краях» обеих выборок, потому что опять же учитывает не само значение, а присвоенный ему ранг.
Категориальные порядковые данные
Как уже было сказано, помимо количественных значений коэффициент Спирмена способен измерить направление и силу взаимосвязи категориальных порядковых значений (categorical ordinal data).
Это могут быть оценки уровня удовлетворености клиента (очень понравилось, понравилось, не понравилось), размеры, выраженные категорией (S, M, L, …) и так далее.
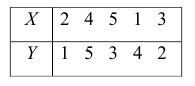
В качестве примера рассмотрим оценку собственного самочувствия по шкале от 1 до 10, которую пациенты поставили себе до и после нового метода лечения.
|
# создадим датафрейм с данными о самочувствии treatment = pd.DataFrame( [ [3, 2], [4, 3], [2, 1], [1, 5], [6, 7], [7, 6], [5, 4] ], columns = [‘Before’, ‘After’]) treatment |
|
# выведем данные на графике plt.figure(figsize = (8, 6)) plt.scatter(treatment.Before, treatment.After) plt.xlabel(‘Before’, fontsize = 15) plt.ylabel(‘After’, fontsize = 15) plt.grid() plt.show() |
По всей видимости корреляция должна быть меньше, чем в предыдущем примере. Приступим к измерениям. Сделать это на самом деле очень просто, потому что порядковые значения уже сами по себе представляют собой ранги. Остается только найти квадрат их разности и применить формулу коэффициента корреляции.
|
# найдем квардрат разницы рангов treatment[‘diff’] = treatment[‘Before’] — treatment[‘After’] treatment[‘diff_sq’] = np.square(treatment[‘diff’]) treatment |
|
# применим формулу коэффициента корреляции Спирмена n = treatment.shape[0] round(1 — ((6 * treatment[‘diff_sq’].sum()) / (n * (n**2 — 1))), 2) |
Остается сравнить с методом .corr() библиотеки Pandas.
|
treatment[[‘Before’, ‘After’]].corr(method = ‘spearman’).iloc[0, 1].round(2) |
Обратите внимание, ни в количественных данных, ни в порядковых у нас не было повторяющихся или совпадающих наблюдений. В случае совпадающих наблюдений (tied ranks), то есть когда значения x или y повторяются, расчет коэффициента корреляции Спирмена также возможен, но немного усложняется.
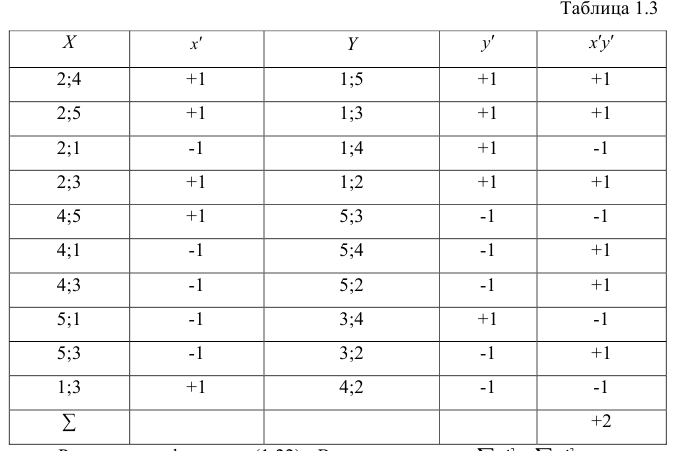
Коэффициент ранговой корреляции Кендалла
Коэффициент ранговой корреляции Кендалла (еще говорят тау Кендалла или тау-коэффициент, Kendall’s $tau$ rank correlation coefficient), как и метод Спирмена, может применяться для измерения силы взаимосвязи количественных и порядковых категориальных переменных и подходит для анализа нелинейных зависимостей. Это также непараметрический тест.
Смысл и методику расчета коэффициента Кендалла легко понять на примере. Вновь возьмем данные о самочувствии до и после лечения.
|
# вернем датафрейм к исходному виду treatment = treatment[[‘Before’, ‘After’]] treatment |
Теперь рассмотрим две пары наблюдений, например, под индексом 0 и 1.
Мы видим, что в столбце Before значения наблюдения 0 меньше, чем значение наблюдения 1 (потому что 3 < 4). То же самое можно наблюдать в столбце After (2 < 3). Такая пара наблюдений называется конкордантной (concordant). Конкордантной будет и пара наблюдений, где оба значения в первом наблюдении больше обоих значений во втором. К ним относятся, например, пары 1 и 2 (где 4 > 2, а 3 > 1).
Если же описанные выше условия не выполняются, то такая пара наблюдений будет называться дискордантной (discordant). К таким наблюдениям относятся, например, наблюдения 4 и 5 (6 > 7, но 7 < 6).
Отнесем каждую из пар нашего датасета к одному из этих классов.
|
# 0 # 1 C # 2 C C # 3 D D D # 4 C C C C # 5 C C C C D # 6 C C C D C C # 0 1 2 3 4 5 6 |
Получилось 16 конкордантных (C) и 5 дискордантных (D) пар. Их общее количество очевидно равно 21. Это значение удобно посчитать по формуле сочетаний.
$$ C(n, r) = frac{n!}{(n-r)! r!} rightarrow C(7, 2) = frac{7!}{(7-2)! 2!} = 21 $$
где n — количество наблюдений, а r равно двум, потому что мы ищем сочетания пар элементов. Можно воспользоваться и упрощенной формулой.
$$ C(r) = frac{(n cdot (n-1))}{2} rightarrow C(7) = frac{7 cdot (7-1)}{2} = 21 $$
|
# найдем количество парных сочетаний с помощью Питона n = 7 pairs = (7 * (7 — 1)) // 2 pairs |
Так вот, коэффициент корреляции Кендалла показывает соотношение конкордантных и дискордантных пар по следующей формуле.
$$ tau = frac{text{concordant pairs}-text{discordant pairs}}{text{total pairs}}$$
Применим ее к нашему датасету.
|
concordant = 16 discordant = pairs — concordant np.round((concordant — discordant) / pairs, 2) |
Точно такого же результата можно добиться с помощью метода .corr() библиотеки Pandas.
|
treatment.corr(method = ‘kendall’).iloc[0, 1].round(2) |
Смысл этого коэффициента в следующем.
Чем больше доля конкордантных пар, тем больше схожих рангов, а значит сильнее взаимосвязь между переменными.
Коэффициент неопределенности
Определение и понятие симметричности теста
Коэффициент неопределенности (uncertainty coefficient) или U Тиля (Theil’s U) позволяет оценить взаимосвязь между двумя категориальными признаками, например, X и Y. Формально он определяется как значение X при условии данного Y.
$$U(x|y)$$
Более того, в отличие от некоторых других тестов, он несимметричен (asymmetric), что позволяет узнать зависит ли Y от X, так же как X от Y.
$$U(y|x) neq U(x|y)$$
Понятие симметричности теста легко представить на следующем простом примере.
Очевидно, что мы легко можем предсказать Y зная X, а вот зная Y мы можем меньше сказать про X (обратите внимание, что категории в X не совпадают для двух категорий в Y).
Используем этот несложный датасет для дальнейших расчетов.
|
# возьмем две категориальные переменные со следующими значениями x = np.array([‘q’, ‘t’, ‘q’, ‘n’, ‘n’, ‘c’]) y = np.array([‘A’, ‘A’, ‘A’, ‘B’, ‘B’, ‘B’]) |
Как рассчитывается
Условная энтропия
U Тиля основывается на понятии условной энтропии (condition entropy), которая позволяет измерить объем информации, необходимый для описания значений переменной X с помощью переменной Y.
$$ S(X|Y) = -sum p(x,y) logfrac{p(x,y)}{p(y)} $$
Теоретическое обоснование формул условной энтропии и энтропии выходит за рамки сегодняшнего занятия. Мы сосредоточимся на расчете и практическом применении каждой из них.
Рассчитаем условную энтропию с помощью Питона. Вначале нам необходимо рассчитать частоту классов категориальных переменных. Для этого прекрасно подойдет класс Counter модуля collections.
|
# импортируем класс Counter модуля collections from collections import Counter |
Посмотрим, сколько раз встречаются классы переменной Y.
|
# найдем частоту классов переменной y y_counts = Counter(y) y_counts |
|
Counter({‘A’: 3, ‘B’: 3}) |
Далее возьмем каждую пару значений X и Y и рассчитаем, сколько раз встречается каждая из них.
|
# возьмем каждую пару значений X и Y с помощью функций zip() и list() list(zip(x, y)) |
|
[(‘q’, ‘A’), (‘t’, ‘A’), (‘q’, ‘A’), (‘n’, ‘B’), (‘n’, ‘B’), (‘c’, ‘B’)] |
|
# рассчитаем их частоту xy_counts = Counter(list(zip(x, y))) xy_counts |
|
Counter({(‘A’, ‘q’): 2, (‘A’, ‘t’): 1, (‘B’, ‘n’): 2, (‘B’, ‘c’): 1}) |
Теперь найдем общее количество значений.
|
total_counts = len(x) total_counts |
В соответствии с формулой выше нам нужно найти вероятность Y ($p(y)$) и вероятность X при условии Y ($p(x,y)$). Для расчета $p(y)$ мы пройдемся по ключам словаря xy_counts и посмотрим в словаре y_counts сколько раз встречается второй элемент каждого ключа.
|
# пройдемся по ключам xy_counts for xy in xy_counts.keys(): # (выведем ключ для наглядности) print(xy) # и посмотрим в y_counts сколько раз встречается второй элемент каждого кортежа print(y_counts[xy[1]]) |
|
(‘q’, ‘A’) 3 (‘t’, ‘A’) 3 (‘n’, ‘B’) 3 (‘c’, ‘B’) 3 |
Мы видим, что категория A и категория B в нашем случае встречаются по три раза. Остается разделить частоту каждой категории на общее количество элементов.
|
# найдем p(y) разделив каждую частоту на общее количество элементов for xy in xy_counts.keys(): print(y_counts[xy[1]] / total_counts) |
Выполним похожее упражнение для того, чтобы найти $p(x,y)$.
|
# снова пройдемся по парам значений for xy in xy_counts.keys(): # (выведем эти пары для наглядности) print(xy) # выведем частоту каждой пары (на этот раз именно пары, а нее ее второго элемента) print(xy_counts[xy]) # и рассчитаем вероятность print(xy_counts[xy] / total_counts) |
|
(‘q’, ‘A’) 2 0.3333333333333333 (‘t’, ‘A’) 1 0.16666666666666666 (‘n’, ‘B’) 2 0.3333333333333333 (‘c’, ‘B’) 1 0.16666666666666666 |
|
# для дальнейшей работы нам понадобится модуль math import math |
Теперь остается подставить $p(y)$ и $p(x,y)$ в формулу.
|
# объявим переменную для условной энтропии cond_entropy = 0.0 # в цикле снова пройдемся по парам значений for xy in xy_counts.keys(): # найдем p(y) p_y = y_counts[xy[1]] / total_counts # и p(x,y) p_xy = xy_counts[xy] / total_counts # подставим их в формулу и просуммируем результат # (мы использовали логарифм с основанием два, но можно использовать, например, и натуральный логарифм) cond_entropy += p_xy * math.log(p_y / p_xy, 2) cond_entropy |
Поместим этот код в функцию.
|
# поместим код в функцию def conditional_entropy(x, y, log_base: float = 2): y_counts = Counter(y) xy_counts = Counter(list(zip(x, y))) total_counts = len(x) cond_entropy = 0.0 for xy in xy_counts.keys(): p_xy = xy_counts[xy] / total_counts p_y = y_counts[xy[1]] / total_counts cond_entropy += p_xy * math.log(p_y / p_xy, log_base) return cond_entropy |
|
# вновь рассчитаем условную энтропию conditional_entropy(x, y) |
Убедимся в несимметричности объема информации, содержащегося в X относительно Y и в Y относительно X, поменяв переменные местами.
|
conditional_entropy(y, x) |
Здесь становится очевидным важный факт.
Если условная энтропия равна нулю, это значит, что с помощью переменной Y мы можем полностью описать переменную X (в нашем примере наоборот). При этом, чем выше условная энтропия, тем меньше информации об X содержится в переменной Y.
Теперь рассмотрим второй компонент формулы коэффициента неопределенности.
Энтропия
Энтропия (entropy) случайной величины рассчитывается по следующей формуле.
$$ S(X) = -sum p(x)log{p(x)} $$
Это значение тем выше, чем менее вероятным является каждый из исходов испытания. Например, энтропия бросания игральной кости будет выше, чем подбрасывания монеты. В первом случае вероятность каждого исхода равна 1/6, во втором 1/2.
Убедимся в этом с помощью функции entropy() модуля stats библиотеки scipy.
|
# импортируем модуль stats библиотеки scipy import scipy.stats as st # рассчитаем энтропию бросания кости и подбрасывания монеты st.entropy([1/6, 1/6, 1/6, 1/6, 1/6, 1/6], base = 2), st.entropy([1/2, 1/2], base = 2) |
Выполним расчет вручную. Вначале найдем вероятность каждого из значений случайной величины $p(x)$.
|
# найдем частоту каждого элемента в X x_counts = Counter(x) # их общее количество total_counts = len(x) # разделим каждую частоту на общее количество элементов p_x = list(map(lambda n: n / total_counts, x_counts.values())) # выведем результат print(p_x) |
|
[0.3333333333333333, 0.16666666666666666, 0.3333333333333333, 0.16666666666666666] |
Теперь подставим это значение в формулу и найдем энтропию.
|
# объявим переменную для условной энтропии entropy = 0.0 # подставим каждую вероятность в формулу и просуммируем for p in p_x: entropy += —p * math.log(p, 2) # выведем результат entropy |
Проверим правильность результата с помощью функции библиотеки scipy().
|
st.entropy(p_x, base = 2) |
Также объявим соответствующую функцию.
|
# объявим функцию def entropy(x, log_base: float = 2): x_counts = Counter(x) total_counts = len(x) p_x = list(map(lambda n: n / total_counts, x_counts.values())) entropy = 0.0 for p in p_x: entropy += —p * math.log(p, 2) return entropy |
|
# проверим результат entropy(x) |
Замечу, что условная энтропия S(X|Y) равна энтропии случайной величины S(X), если величины X и Y независимы.
$$ S(X|Y) = S (X) iff X ⫫ Y $$
Из этого следует, что самое большее условная энтропия может быть равна энтропии этой переменной (в случае, если Y никак не объясняет X).
$$ S(X) leq S(X|Y) $$
Все это важно для расчета коэффициента неопределенности.
U Тиля
Приведем и обсудим формулу.
$$ U(X|Y) = frac{S(X)-S(X|Y)}{S(X)} $$
Зачем рассчитывать не только условную энтропию, но и энтропию случайной величины? Дело в том, что так мы можем не просто измерять «объяснимость» переменной X с помощью Y, но и сравнивать между собой условную энтропию любых категориальных переменных.
Арифметически, чем ниже условная энтропия, тем ближе значение показателя к единице. Чем она выше, тем коэффициент неопределенности ближе к нулю.
Таким образом, U Тиля всегда находится в диапазоне от 0 до 1. При этом, ноль означает, что переменная Y не несет никакой информации относительно переменной X, единица — что переменная Y содержит всю необходимую информацию.
Рассчитаем U Тиля с помощью Питона.
|
# сразу объявим функцию def ucoef(x, y, log_base = 2): # найдем условную энтропию S(X,Y) s_xy = conditional_entropy(x, y, log_base) # энтропию S(X) s_x = entropy(x, log_base) # подставим эти значения в формулу u = (s_x — s_xy) / s_x # выведем результат return u |
Найдем коэффициент неопределенности для X и Y.
Кроме того, убедимся, что X полностью объясняет Y.
Обратите внимание, что коэффициент не может принимать отрицательных значений. Это логично, потому что строго говоря в случае категориальных переменных мы измеряем не корреляцию (направление и силу взаимного изменения, correlation), а степень взаимосвязи (association) между двумя переменными, которая либо есть (и может доходить до единицы), либо ее нет (равна нулю).
Точечно-бисериальная корреляция
Точечно-бисериальная корреляция (point-biserial correlation) позволяет оценить взаимосвязь между количественной переменной и дихотомической (выраженной двумя значениями) качественной переменной. Например, нам может быть важно оценить связь возраста (X) и выживаемости пассажиров «Титаника» (Y, классы 0 и 1). Приведем формулу.
Формула
$$ r_{pb} = frac{M_1-M_0}{s_n} sqrt{frac{n_1 n_0}{n^2}} $$
В данном случае мы делим наблюдения на две группы, в первую группу попадут наблюдения, относящиеся к классу 0, во вторую — к классу 1. Для каждой группы мы считаем средние значения ($M_0$ и $M_1$) и делим их разность на среднее квадратическое отклонение всех значений в переменной X ($s_n$).
Под корнем находится произведение относительного размера двух групп ($n_0$ и $n_1$ — это размеры групп, $n$ — общее число наблюдений).
Коэффициент точечно-бисериальной корреляции находится в диапазоне от $-1$ до $1$ и интерпретируется так же, как и коэффициент корреляции Пирсона.
Выше приведена формула для генеральной совокупности. Если нам доступна лишь выборка, формула выглядит следующим образом.
$$ r_{pb} = frac{M_1-M_0}{s_{n-1}} sqrt{frac{n_1 n_0}{n(n-1)}} $$
СКО ($s_{n-1}$) в этом случае также рассчитывается по формуле для выборки. Приведем пример.
Пример расчета на Питоне
Подгрузим датасет о вине из библиотеки sklearn. На основе свойств вин нам предлагается спрогнозировать один из трех классов вина (классы 0, 1 и 2). Так как нам нужна дихотомическая переменная, удалим наблюдения, относящиеся к классу 2.
|
# из модуля datasets библиотеки sklearn импортируем датасет о вине from sklearn import datasets data = datasets.load_wine() # превратим его в датафрейм wine = pd.DataFrame(data.data, columns = data.feature_names) # добавим целевую переменную wine[‘target’] = data.target # оставим только классы 0 и 1 wine = wine[wine.target != 2] # убедимся, что в целевой переменной осталось только два класса np.unique(wine.target) |
Найдем корреляцию между целевой переменной и содержанием пролина (proline).
|
# оставим только интересующие нас столбцы wine = wine[[‘proline’, ‘target’]] wine.head(3) |
Теперь напишем функцию для расчета точечно-бисериальной корреляции (будем использовать формулу для выборки).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# объявим функцию для расчета точечно-бисериальной корреляции # функция будет принимать два параметра: количественную и качественную переменные def pbc(continuous, binary): # преобразуем количественную переменную в массив Numpy continuous_values = np.array(continuous) # классы качественной переменной превратим в нули и единицы binary_values = np.unique(binary, return_inverse = True)[1] # создадим две подгруппы количественных наблюдений # в зависимости от класса дихотомической переменной group0 = continuous_values[np.argwhere(binary_values == 0).flatten()] group1 = continuous_values[np.argwhere(binary_values == 1).flatten()] # найдем средние групп, mean0, mean1 = np.mean(group0), np.mean(group1) # а также длины групп и всего датасета n0, n1, n = len(group0), len(group1), len(continuous_values) # рассчитаем СКО количественной переменной std = continuous_values.std() # подставим значения в формулу return (mean1 — mean0) / std * np.sqrt( (n1 * n0) / (n * (n—1)) ) |
Применим эту функцию для нахождения корреляции между пролином и классом вина.
|
pbc(wine[‘proline’], wine[‘target’]) |
Для расчета корреляции мы также можем воспользоваться функцией из библиотеки Scipy.
|
# импортируем модуль stats из библиотеки scipy from scipy import stats # передадим данные в функцию и выведем первый результат[0] stats.pointbiserialr(wine[‘proline’], wine[‘target’])[0] |
Небольшие различия связаны с тем, что функция библиотеки Scipy использует формулу для генеральной совокупности.
Что интересно, математически коэффициент точечно-бисериальной корреляции дает тот же результат, что и коэффициент корреляции Пирсона.
|
# сравним в корреляцией Пирсона wine.corr().iloc[0,1] |
Пояснения к коду
Сделаем пояснения к приведенному коду. Упростим пример и предположим, что нам нужно рассчитать, есть ли зависимость между количеством сна и результатом экзамена.
|
# количество сна в часах поместим в массив Numpy sleep = np.array([6, 8, 9, 7]) # результат будет записан с помощью двух категорий pass и fail exam = [‘pass’, ‘fail’, ‘pass’, ‘fail’] |
Для расчета точечно-бисериальной корреляции нам нужно разделить данные о сне в зависимости от результата экзамена на две группы. В первую очередь, преобразуем строковые значения переменной exam в числа. Для этого, в частности, мы можем использовать функцию np.unique() с параметром return_inverse = True.
|
exam_encoded = np.unique(exam, return_inverse = True) exam_encoded |
|
(array([‘fail’, ‘pass’], dtype='<U4′), array([1, 0, 1, 0])) |
Вторым результатом [1] будут числовые значения категорий. Теперь используем функцию np.argwhere(), чтобы найти индексы тех, кто сдал экзамены и тех, кто не сдал.
|
# функция выводит индексы элементов, соответствующих заданному условию fail_index = np.argwhere(exam_encoded[1] == 0) pass_index = np.argwhere(exam_encoded[1] == 1) |
|
# студенты, провалившие тест, должны быть на втором и четвертом местах fail_index |
|
# сдавшие — на первом и третьем pass_index |
Остается убрать второе измерение массивов.
|
fail_index, pass_index = fail_index.flatten(), pass_index.flatten() |
|
(array([1, 3]), array([0, 2])) |
Теперь используем индексы для группировки часов сна в зависимости от результатов экзамена.
|
sleep[fail_index], sleep[pass_index] |
|
(array([8, 7]), array([6, 9])) |
Теперь мы можем легко посчитать нужные метрики и подставить их в формулу точечно-бисериальной корреляции.
Корреляционное отношение
Корреляционное отношение (correlation ratio) выявляет взаимосвязь между количественной переменной и категориальной переменной с любым количеством категорий. Смысл этой метрики лучше всего понять на простом примере из Википедии⧉.
Простой пример
Предположим, что у нас есть результаты экзаменов по трем предметам (алгебре, геометрии и статистике), и нам нужно понять, есть ли взаимосвязь между предметом и поставленными оценками. Взглянем на данные:
- алгебра: 45, 70, 29, 15, 21 (5 оценок)
- геометрия: 40, 20, 30, 42 (4 оценки)
- статистика: 65, 95, 80, 70, 85, 73 (6 оценок)
Шаг 1. Найдем средние значения внутри каждой группы и общее среднее всех наблюдений.
- алгебра: 36
- геометрия: 33
- статистика: 78
- общее среднее: 52
Шаг 2. Теперь найдем, насколько наблюдения в каждой из групп отличаются от группового среднего. Возведем результаты в квадрат для того, чтобы положительные и отрицательные значения не взаимоудалялись, и сложим их. Например, для алгебры сумма квадратов отклонений от среднего будет равна
$$ (36-45)^2+(36-70)^2+(36-29)^2+(36-15)^2+(36-21)^2 = 1959 $$
Для геометрии — 308, для статистики — 600. Сложим внутригрупповые отклонения от среднего и получим $1959+308+600=2860$
Сумма квадратов отклонений всех наблюдений от общего среднего составит 9640.
Шаг 3. Теперь выясним, какую долю в общей дисперсии составляет внутригрупповая дисперсия. Для этого разделим 2860 на 9640.
$$ frac{2860}{9640} approx 0,29668 $$
Соответственно доля не объясненных внутригрупповой дисперсией отклонений (ее принято обозначать греческой буквой $eta$, «эта») составляет
$$ eta^2 = 1-frac{2860}{9640} approx 0,70332 $$
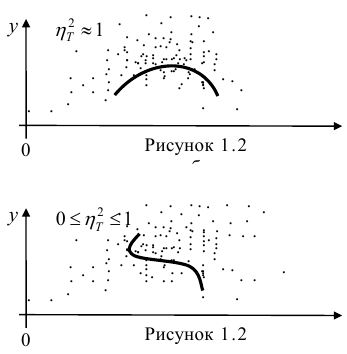
Логично предположить, что чем выше доля не объясненных внутригрупповыми отклонениями дисперсии (чем выше $eta^2$), тем большую важность имеет дисперсия между группами. Другими словами, тем важнее отклонения между предметами, а не между оценками внутри каждого предмета.
Значит, чем выше $eta^2$, тем теснее связь между категориями и количественными оценками.
Шаг 4. Извлечем корень из получившегося значения для того, чтобы вернуться к исходным единицам измерения.
$$ eta = sqrt{0,70332} approx 0,83864 $$
Подведем итог. Корреляционное отношение изменяется от 0 до 1. Если показатель равен нулю, общая дисперсия объясняется исключительно внутригрупповыми отклонениями и связи между качественной и количественной переменными нет. Если показатель равен единице, общая дисперсия полностью объясняется только дисперсией между группами и связь между переменными велика.
Можно также сказать, что если $eta$ равна нулю, то внутригрупповые средние одинаковы, если $eta$ равна единице, все значения в каждой из категорий должны быть одинаковы (например, все студенты по алгебре должны получить одинаковую оценку и т.д.).
Еще один способ расчета
Для расчета корреляционного отношения можно также найти взвешенные по количеству элементов квадраты отклонений общего среднего от внутригрупповых средних. Для примера выше арифметика выглядит следующим образом
$$ 5(36-52)^2+4(33-52)^2+6(78-52)^2 = 6780 $$
Обратите внимание, это то же самое, что и $9640-2860=6780$, то есть сумма отклонений, не объясняемых внутригрупповой дисперсией. Таким образом,
$$ eta^2 = frac{6780}{9640} approx 0,70332 $$
$$ eta = sqrt{0,70332} approx 0,83864 $$
Остается написать функцию для расчета корреляционного отношения на Питоне.
Код на Питоне
Используем те же данные, что и в примере выше.
|
# создадим датафрейм с результатами экзаменов по трем предметам test = pd.DataFrame({ # используем список с названиями предметов ‘subject’ : [‘algebra’] * 5 + [‘geometry’] * 4 + [‘stats’] * 6, # и соответствующими оценками ‘score’ : [45, 70, 29, 15, 21, 40, 20, 30, 42, 65, 95, 80, 70, 85, 73 ] }) |
Вначале возьмем значения оценок, рассчитаем сумму квадратов отклонений от среднего значения, а также закодируем категориальные переменные числами. Для этого как и ранее в случае точечно-бисериальной корреляцией используем функцию np.unique() с параметров return_inverse = True.
|
# возьмем значения оценок values = np.array(test.score) # и рассчитаем сумму квадратов отклонений от среднего значения ss_total = np.sum((values.mean() — values) ** 2) # закодируем категории предметов числами cats = np.unique(test.subject, return_inverse = True)[1] cats |
|
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2]) |
Теперь применим первый вариант расчета корреляционного отношения.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# объявим переменную для внутригрупповой дисперсии ss_ingroups = 0 # в цикле, состоящем из количества категорий for c in np.unique(cats): # вычленим группу оценок по каждому предмету group = values[np.argwhere(cats == c).flatten()] # найдем суммы квадратов отклонений значений от групповых средних # и сложим эти результаты для каждой группы ss_ingroups += np.sum((group.mean() — group) ** 2) # найдем долю внутригрупповой дисперсии и вычтем ее из единицы eta_squared = 1 — ss_ingroups/ss_total # найдем корень из предыщущего значения eta = np.sqrt(eta_squared) # это и будет корреляционное отношение eta |
Напомню, что использование функции np.argwhere() мы уже рассмотрели ранее на этом занятии. Рассчитаем по второму варианту.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# объявим переменную для межгрупповой дисперсии ss_betweengroups = 0 # в цикле, состоящем из количества категорий, for c in np.unique(cats): # вычленим группу оценок по каждому предмету group = values[np.argwhere(cats == c).flatten()] # для каждой группы # найдем взвешенный по количеству элементов в группе # квадрат отклонения группового среднего от общего среднего # и сложим результаты ss_betweengroups += len(group) * (group.mean() — values.mean()) ** 2 # найдем долю межгрупповой дисперсии eta_squared = ss_betweengroups/ss_total # найдем корень из предыщущего значения eta = np.sqrt(eta_squared) # это и будет корреляционное отношение eta |
Мы готовы написать функции.
|
# вариант 1 def correlation_ratio1(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() — values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_ingroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_ingroups += np.sum((group.mean() — group) ** 2) return np.sqrt(1 — ss_ingroups/ss_total) |
|
# проверим результат correlation_ratio1(test.score, test.subject) |
|
# вариант 2 def correlation_ratio2(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() — values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_betweengroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_betweengroups += len(group) * (group.mean() — values.mean()) ** 2 return np.sqrt(ss_betweengroups/ss_total) |
|
# проверим результат correlation_ratio2(test.score, test.subject) |
Подведем итог
Для удобства, давайте обобщим, какие методы и когда можно использовать.
- Если речь идет о двух количественных переменных мы можем использовать:
- коэффициент Пирсона, если речь идет о выявлении линейной зависимости
- коэффициенты Спирмена и Кендалла, если требуется оценить нелинейную взаимосвязь
- В случае двух категориальных переменных, подойдут:
- уже упомянутые коэффициенты Спирмена и Кендалла для порядковых категорий, а также
- коэффициент неопределенности Тиля
- Когда перед нами одна количественная и одна категориальная переменные, мы можем рассчитать:
- точечно-бисериальный коэффициент корреляции, в случае, если категориальная переменная имеет дихотомическую шкалу; или
- корреляционное отношение в случае множества категорий
Вопросы для закрепления
Вопрос. Чем параметрические тесты отличаются от непараметрических?
Посмотреть правильный ответ
Ответ: параметрический тест показывает корректный результат, если данные, на которых он основывается соответствуют определенным критериям или допущениям, для непараметрического теста такие критерии отсутствуют.
При этом обратите внимание, отсутствие допущений не отменяет ограничения на применение тестов только к определенным типам данных. Например, метод Спирмена, как уже было сказано, не подойдет для выявления немонотонной зависимости.
Вопрос. При расчете коэффициента корреляции Пирсона, что дает деление ковариации на произведение СКО двух переменных $s_x s_y$?
Посмотреть правильный ответ
Ответ: таким образом мы выражаем любую ковариацию как долю от произведения двух СКО и, как следствие, можем измерять силу взаимосвязи двух переменных и сравнивать коэффициенты корреляции между собой.
Вопрос. Что такое симметричность и несимметричность корреляционного метода?
Посмотреть правильный ответ
Ответ: симметричный метод покажет одинаковую силу взаимосвязи переменной X с переменной Y, и переменной Y с переменной X даже если в действительности взаимосвязь не одинаковая; несимметричный метод покажет разную корреляцию X с Y и Y с X, если такое различие действительно существует.
Полезные ссылки
- Библиотека dython⧉. Прямые ссылки на документацию⧉ и исходный код⧉ функций.
Корреляция показывает степень совместного изменения двух признаков. При этом, как уже было сказано, в корреляционном анализе нет зависимых и независимых переменных. Они эквивалентны.
Количественным предсказанием одной переменной (зависимой) на основании другой (независимой) занимается регрессионный анализ.
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Дискретной называют двумерную величину, составляющие которой дискретны.
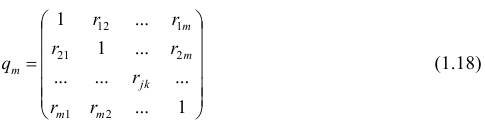
Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Закон
распределения дискретной двумерной случайной величины может быть задан:
а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;
б) аналитически, например в виде функции распределения.
Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность
, надо просуммировать
вероятности столбца
. Аналогично сложив
вероятности строки
получим вероятность
.
Пусть
составляющие
и
дискретны и имеют соответственно следующие
возможные значения:
;
.
Условным распределением составляющей
при
(j сохраняет одно и то же
значение при всех возможных значениях
) называют совокупность
условных вероятностей:
Аналогично
определяется условное распределение
.
Условные
вероятности составляющих
и
вычисляют соответственно по формулам:
Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Ковариация (корреляционный момент)
Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки
.
Ковариацию
(корреляционный момент) можно найти по формуле:
Свойства ковариации
Свойство 1.
Ковариация двух независимых случайных величин равна нулю.
Свойство 2.
Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.
Свойство 3.
Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.
Коэффициент корреляции
Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.
Формула коэффициента корреляции:
Две
случайные величины
и
называют коррелированными, если их коэффициент
корреляции отличен от нуля.
и
называют некоррелированными величинами, если
их коэффициент корреляции равен нулю
Свойства коэффициента корреляции
Свойство 1.
Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.
Свойство 2.
Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.
Свойство 3.
Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Линейная регрессия
Рассмотрим
двумерную случайную величину
, где
и
– зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины
в виде линейной функции величины
:
где
и
– параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.
Линейная
средняя квадратическая регрессия
на
имеет вид:
Коэффициент
называют
коэффициентом регрессии
на
, а прямую
называют
прямой среднеквадратической регрессии
на
.
Аналогично
можно получить прямую среднеквадратической регрессии
на
:
Смежные темы решебника:
- Двумерная непрерывная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Задача 1
Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.
Требуется:
—
определить одномерные законы распределения случайных величин X и Y;
— найти
условные плотности распределения вероятностей величин;
—
вычислить математические ожидания mx и my;
—
вычислить дисперсии σx и σy;
—
вычислить ковариацию μxy;
—
вычислить коэффициент корреляции rxy.
| xy | 3 | 5 | 8 | 10 | 12 |
| -1 | 0.04 | 0.04 | 0.03 | 0.03 | 0.01 |
| 1 | 0.04 | 0.07 | 0.06 | 0.05 | 0.03 |
| 3 | 0.05 | 0.08 | 0.09 | 0.08 | 0.05 |
| 6 | 0.03 | 0.04 | 0.04 | 0.06 | 0.08 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Задана
дискретная двумерная случайная величина (X,Y).
а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X; в) построить регрессию случайной величины X на Y; г) найти коэффициент ковариации; д) найти
коэффициент корреляции.
| Y | X | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 30 | 0.05 | 0.03 | 0.02 | 0.01 | 0.01 |
| 40 | 0.03 | 0.02 | 0.02 | 0.04 | 0.01 |
| 50 | 0.05 | 0.03 | 0.02 | 0.02 | 0.01 |
| 70 | 0.1 | 0.03 | 0.04 | 0.03 | 0.01 |
| 90 | 0.1 | 0.04 | 0.01 | 0.07 | 0.2 |
Задача 3
Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.
|
x y |
1 | 2 | 3 |
| 1.5 | 0.03 | 0.02 | 0.02 |
| 2.9 | 0.06 | 0.13 | 0.03 |
| 4.1 | 0.4 | 0.07 | 0.02 |
| 5.6 | 0.15 | 0.06 | 0.01 |
Задача 4
Двумерная
случайная величина (X,Y) распределена по закону
| XY | 1 | 2 |
| -3 | 0,1 | 0,2 |
| 0 | 0,2 | 0,3 |
| -3 | 0 | 0,2 |
Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.
Задача 5
Случайные
величины ξ и η имеют следующий совместный закон распределения:
P(ξ=1,η=1)=0.14
P(ξ=1,η=2)=0.18
P(ξ=1,η=3)=0.16
P(ξ=2,η=1)=0.11
P(ξ=2,η=2)=0.2
P(ξ=2,η=3)=0.21
1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.
2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).
3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}
4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.
Задача 6
Дан закон
распределения двумерной случайной величины (ξ,η):
| ξ=-1 | ξ=0 | ξ=2 | |
| η=1 | 0,1 | 0,1 | 0,1 |
| η=2 | 0,1 | 0,2 | 0,1 |
| η=3 | 0,1 | 0,1 | 0,1 |
1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания Mξ,
Mη и дисперсии Dξ, Dη
2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).
3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?
4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти Mγ и Dγ.
Задача 7
Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.
| XY | 1 | 2 | 4 |
| -2 | 0,25 | 0 | 0,25 |
| 1 | 0 | 0,25 | 0 |
| 3 | 0 | 0,25 | 0 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 8
Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.
| YX | -1 | 1 |
| -1 | 0,4 | 0,1 |
| 1 | 0,2 | 0,3 |
Задача 9
Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:
| X=-3 | X=0 | X=1 | |
| Y=-2 | 0,3 | ? | 0,1 |
| Y=1 | 0,1 | 0,1 | 0,2 |
Задача 10
Совместный
закон распределения пары
задан таблицей:
| xh | -1 | 0 | 1 |
| -1 | 1/12 | 1/4 | 1/6 |
| 1 | 1/4 | 1/12 | 1/6 |
Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.
Задача 11
Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции rxy?
| X | 20 | 25 | 30 | 35 |
| P | 0.1 | 0.1 | 0.4 | 0.4 |
и
Задача 12
Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):
| XY | 0 | 1 | 2 |
| -1 | ? | 0,1 | 0,2 |
| 1 | 0,1 | 0,2 | 0,3 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:
| ξη | -1 | 1 | 2 |
| 0 | 1/7 | 2/7 | 1/7 |
| 1 | 1/7 | 1/7 | 1/7 |
Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?
Задача 14
Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.
| XY | 2,3 | 2,9 | 3,1 | 3,4 |
| 0,2 | 0,15 | 0,15 | 0 | 0 |
| 2,8 | 0 | 0,25 | 0,05 | 0,01 |
| 3,3 | 0 | 0,09 | 0,2 | 0,1 |
Задача 15
Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.
| xy | 1 | 4 |
| -10 | 0,1 | 0,2 |
| 0 | 0,3 | 0,1 |
| 20 | 0,2 | 0,1 |
Задача 16
Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:
а) законы
распределения ее компонент и их числовые характеристики;
b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.
с)
ковариацию и коэффициент корреляции случайных величин X и Y;
d) составить матрицу ковариаций и матрицу корреляций;
e) вероятность попадания в область, ограниченную линиями y=16-x2 и y=0.
f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.
| XY | -1 | 0 | 1 | 2 |
| -1 | 0 | 1/6 | 0 | 1/12 |
| 0 | 1/18 | 1/9 | 1/12 | 1/9 |
| 2 | 1/6 | 0 | 1/9 | 1/9 |
Задача 17
Совместный
закон распределения случайных величин X и Y задан таблицей:
|
XY |
0 |
1 |
3 |
|
0 |
0,15 |
0,05 |
0,3 |
|
-1 |
0 |
0,15 |
0,1 |
|
-2 |
0,15 |
0 |
0,1 |
Найдите:
а) закон
распределения случайной величины X и закон распределения
случайной величины Y;
б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.
Задача 18
Известен
закон распределения двумерной случайной величины (X,Y).
а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);
б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;
в)
построить поле распределения и линию регрессии Y по X и X по Y;
г)
вычислить корреляционный момент (коэффициент ковариации) μxy и
коэффициент корреляции rxy.
|
|
5 | 20 | 35 |
| 100 | — | — | 0.05 |
| 115 | — | 0.2 | 0.15 |
| 130 | 0.15 | 0.35 | — |
| 145 | 0.1 | — | —- |
Пусть имеется п
наблюдений двумерной величины
При большом числе опытов одно и то же
значение
может приниматься
раз случайной величиной
,
а случайная величина
может принимать значение
соответственно
раз. В выборке одна и та же пара
может наблюдаться
раз. Изображение точек
на плоскости называетсякорреляционным
полем.
Выборку двумерной случайной величины
удобно занести в таблицу 8.2.1., эта таблица
называется корреляционной.
Таблица
8.2.1.
|
|
|
|
|||
|
|
|
… |
|
||
|
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
… |
… |
… |
… |
… |
… |
|
|
|
|
… |
|
|
|
|
|
|
… |
|
п |
Значения случайных
величин
и
представлены в вариационных рядах.
В таблице 8.2.1.
представлены следующие данные:
В корреляционной
таблицу значения
ип
сразу не даются, их легко вычислить. По
данным корреляционной таблицы находятся
условные средние
Предположим, что
уравнение регрессии
на
линейно:
Задача состоит в
нахождении оценок величин
и
.
При использовании данных корреляционной
таблицы формулы вычисления основных
оценок примут вид:
Приведем оценку
коэффициента корреляции случайных
величин
и
где
и
являются оценками среднеквадратических
отклонений.
В параграфе 8.1
было приведено выборочное линейное
уравнение регрессии
на
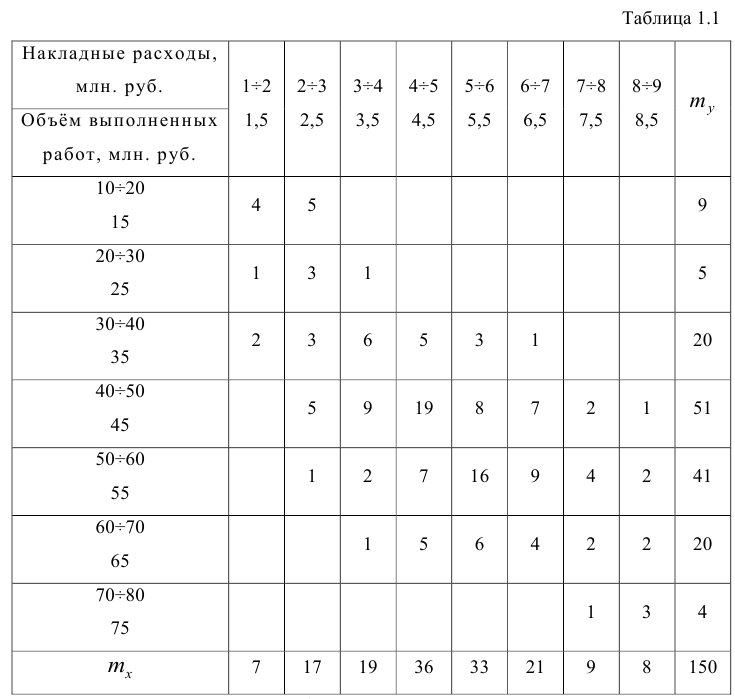
Пример
1. Найти
выборочное уравнение линейной регрессии
на
по данным, приведенным в корреляционной
таблице:
|
|
|
||||||
|
5 |
10 |
15 |
20 |
25 |
30 |
|
|
|
10 |
4 |
6 |
10 |
||||
|
20 |
2 |
8 |
10 |
||||
|
35 |
10 |
2 |
8 |
20 |
|||
|
40 |
5 |
8 |
2 |
15 |
|||
|
50 |
10 |
5 |
15 |
||||
|
|
4 |
8 |
8 |
15 |
20 |
15 |
70 |
Найдем оценки
математических ожиданий случайных
величин
и
:
Найдем оценки
дисперсий
,
Определим оценку
корреляционного момента:
Найдем выборочные
коэффициент корреляции:
,
Запишем выборочное
уравнение линейной регрессии
на
Вопросы и задачи к части 3.
-
Дать определение
случайного процесса. -
Найти математическое
ожидание и дисперсию случайного процесса
,
где
— случайная величина, причем
-
Известно, что
корреляционная функция случайного
процесса
равна
Найти корреляционную функцию случайного
процесса
-
Дать определение
цепи Маркова. -
Какие цепи Маркова
называются однородными? -
Как задается
однородная цепь Маркова? -
Дана матрица
перехода однородной цепи Маркова:
,
— случайная величина, причем
равна
Найти корреляционную функцию случайного
Найти матрицу
перехода за три шага.
-
Дана матрица
перехода однородной цепи Маркова
Какие состояния
будут несущественными, сообщающимися,
поглощающими? Будет ли цепь Маркова
неразложимой?
-
Задано совместное
распределение случайных величин
:
:|
|
|
||
|
1 |
2 |
4 |
|
|
3 |
0,1 |
0,3 |
0,05 |
|
5 |
0,2 |
0,2 |
0,15 |
Найти
-
Задано совместное
распределение случайных величин
|
|
|
||
|
0 |
3 |
5 |
|
|
1 |
0,05 |
0,1 |
0,15 |
|
2 |
0,2 |
0,2 |
0,1 |
|
4 |
0,05 |
0,01 |
0,14 |
Записать закон
распределения условного математического
ожидания
и закон распределения условной дисперсии
Найти генеральный корреляционный
коэффициент детерминации.
-
Дать определение
функции регрессии. -
Сформулировать
условие корреляционной зависимости
случайных величин. -
Какие случайные
величины называются не корреляционными:
условие отсутствия корреляционной
зависимости. -
Какие задачи
решаются с помощью дисперсионного
анализа? -
При каких условиях
проверяется нулевая гипотеза о равенстве
групповых средних? -
Проведено 20
испытаний, из них 5 – на первом уровне
фактора, 5 – на втором, 6 – на третьем и
4 – на четвертом. Методом дисперсионного
анализа при уровне значимости 0,01
проверить гипотезу о равенстве групповых
дисперсий. Предполагается, что выборки
извлечены из нормальных генеральных
совокупностей:Номер
опыта
Уровень
фактора Ф
1
50
60
58
60
2
55
53
60
60
3
22
59
58
61
4
54
56
61
59
5
49
52
60
6
59
-
В трех филиалах
одного из банков были организованы три
уровня различных услуг для клиентов.
После этого в течение шести месяцев
измерялся объем вкладов
.
Проверить нулевую гипотезу о влиянии
организации услуг на объемы вкладов
при уровне значимости
Предполагается, что выборки извлечены
из нормальных генеральных совокупностей
с одинаковыми дисперсиями.Номер
опытаУровень
фактора Ф1
10
16
16
2
15
16
18
3
15
25
28
4
17
22
27
5
20
30
34
6
16
28
40
-
Получена выборка
двумерной случайной величины
.
Предполагается, что выборки извлечены
|
|
10 |
18 |
25 |
27 |
30 |
32 |
33 |
35 |
|
|
15 |
20 |
28 |
31 |
30 |
39 |
42 |
48 |
Найти выборочное
уравнение регрессии
на
.
Найти выборочный коэффициент корреляции.
-
Найти выборочное
уравнение линейной регрессии
на
на основании корреляционной таблицы.
на
на основании корреляционной таблицы.|
|
|
||||
|
2 |
3 |
4 |
5 |
6 |
|
|
15 |
3 |
10 |
5 |
||
|
25 |
6 |
3 |
3 |
||
|
35 |
9 |
7 |
|||
|
40 |
8 |
6 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Корреляционный анализ:
Связи между различными явлениями в природе сложны и многообразны, однако их можно определённым образом классифицировать. В технике и естествознании часто речь идёт о функциональной зависимости между переменными x и у, когда каждому возможному значению х поставлено в однозначное соответствие определённое значение у. Это может быть, например, зависимость между давлением и объёмом газа (закон Бойля—Мариотта).
В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияния каждого из которых ничтожно, а число их велико. В этом случае связь теряет свою однозначность и изучаемая физическая система переходит не в определённое состояние, а в одно из возможных для неё состояний. Здесь речь может идти лишь о так называемой статистической связи. Статистическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения. Следовательно, для изучения статистической зависимости нужно знать аналитический вид двумерного распределения. Однако нахождение аналитического вида двумерного распределения по выборке ограниченного объёма, во-первых, громоздко, во-вторых, может привести к значительным ошибкам. Поэтому на практике при исследовании зависимостей между случайными переменными X и У обычно ограничиваются изучением зависимости между одной из них и условным математическим ожиданием другой, т.е. 
Вопрос о том, что принять за зависимую переменную, а что — за независимую, следует решать применительно к каждому конкретному случаю.
Знание статистической зависимости между случайными переменными имеет большое практическое значение: с её помощью можно прогнозировать значение зависимой случайной переменной в предположении, что независимая переменная примет определенное значение. Однако, поскольку понятие статистической зависимости относится к осредненным условиям, прогнозы не могут быть безошибочными. Применяя некоторые вероятностные методы, как будет показано далее, можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.
Введение в корреляционный анализ
Связь, которая существует между случайными величинами разной природы, например, между величиной X и величиной Y, не обязательно является следствием прямой зависимости одной величины от другой (так называемая функциональная связь).
В некоторых случаях обе величины зависят от целой совокупности разных факторов, общих для обеих величин, в результате чего и формируется связанные друг с другом закономерности. Когда связь между случайными величинами обнаружена с помощью статистики, мы не можем утверждать, что обнаружили причину происходящего изменения параметров, скорее мы лишь увидели два взаимосвязанных следствия.
Например, дети, которые чаще смотрят по телевизору американские боевики, меньше читают. Дети, которые больше читают, лучше учатся. Не так-то просто решить, где тут причины, а где следствия, но это и не является задачей статистики.
Статистика может лишь, выдвинув гипотезу о наличии связи, подкрепить ее цифрами. Если связь действительно имеется, говорят, что между двумя случайными величинами есть корреляция. Если увеличение одной случайной величины связано с увеличением второй случайной величины, корреляция называется прямой.
Например, количество прочитанных страниц за год и средний балл (успеваемость). Если, напротив рост одной величины связано с уменьшением другой, говорят об обратной корреляции. Например, количество боевиков и количество прочитанных страниц. Взаимная связь двух случайных величин называется корреляцией, корреляционный анализ позволяет определить наличие такой связи, оценить, насколько тесна и существенна эта связь. Все это выражается количественно.
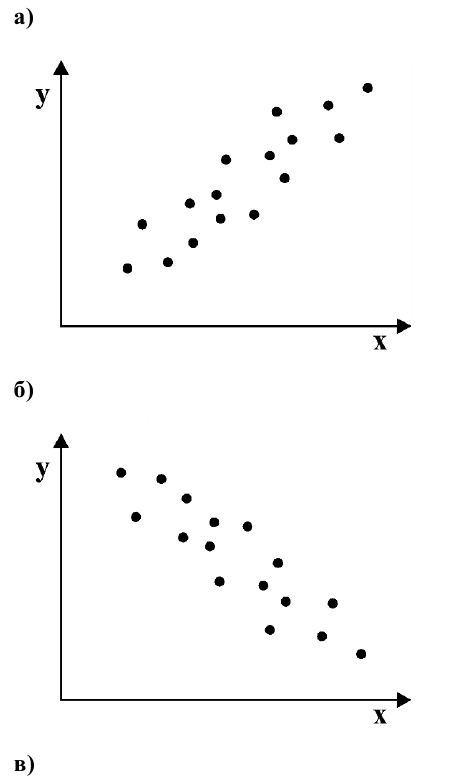
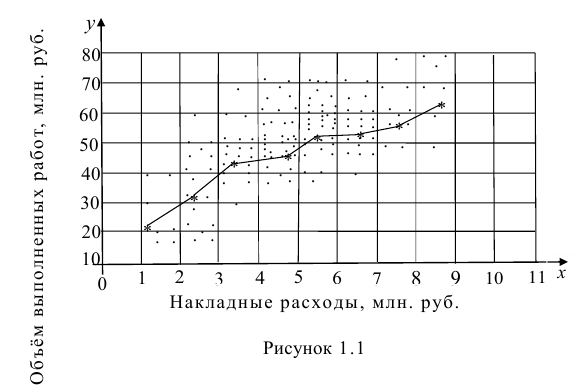
Как определить, есть ли корреляция между величинами? В большинстве случаев, это можно увидеть на обычном графике. Например, по каждому ребенку из нашей выборки можно определить величину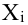 
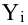
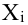
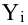
(число страниц) и 
(средний балл годовой оценки), и записать эти данные в виде таблицы. Построить оси X и Y, а затем нанести на график весь ряд точек таким образом, чтобы каждая из них имела определенную пару координат (,) из нашей таблицы. Поскольку мы в данном случае затрудняемся определить, что можно считать причиной, а что следствием, не важно, какая ось будет вертикальной, а какая горизонтальной.
Если график имеет вид а), то это говорит о наличии прямой корреляции, в случае, если он имеет вид б) — корреляция обратная. Отсутствие корреляции тоже можно приблизительно определить по виду графика — это случай в).
С помощью коэффициента корреляции можно посчитать насколько тесная связь существует между величинами.
Пусть, существует корреляция между ценой и спросом на товар. Количество купленных единиц товара в зависимости от цены у разных продавцов показано в таблице: 
Видно, что мы имеем дело с обратной корреляцией. Для количественной оценки тесноты связи используют коэффициент корреляции: 
Коэффициент r мы считаем в Excel, с помощью функции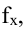 
далее статистические функции, функция KOPPEЛ. По подсказке программы вводим мышью в два соответствующих поля два разных массива (X и Y). В нашем случае коэффициент корреляции получился r = -0,988.
Надо отметить, что чем ближе к 0 коэффициент корреляции, тем слабее связь между величинами. Наиболее тесная связь при прямой корреляции соответствует коэффициенту r, близкому к +1. В нашем случае, корреляция обратная, но тоже очень тесная, и коэффициент близок к -1.
Что можно сказать о случайных величинах, у которых коэффициент имеет промежуточное значение? Например, если бы мы получили r = 0,65. В этом случае, статистика позволяет сказать, что две случайные величины частично связаны друг с другом. Скажем на 65% влияние на количество покупок оказывала цена, а на 35% — другие обстоятельства. И еще одно важное обстоятельство надо упомянуть.
Поскольку мы говорим о случайных величинах, всегда существует вероятность, что замеченная нами связь — случайное обстоятельство. Причем вероятность найти связь там, где ее нет, особенно велика тогда, когда точек в выборке мало, а при оценке Вы не построили график, а просто посчитали значение коэффициента корреляции на компьютере. Так, если мы оставим всего две разные точки в любой произвольной выборке, коэффициент корреляции будет равен или +1 или -1. Из школьного курса геометрии мы знаем, что через две точки можно всегда провести прямую линию. Для оценки статистической достоверности факта обнаруженной Вами связи полезно использовать так называемую корреляционную поправку: 
Связь нельзя считать случайной, если: 
В то время как задача корреляционного анализа — установить, являются ли данные случайные величины взаимосвязанными, цель регрессионного анализа — описать эту связь аналитической зависимостью, т.е. с помощью уравнения. Мы рассмотрим самый несложный случай, когда связь между точками на графике может быть представлена прямой линией. Уравнение этой прямой линии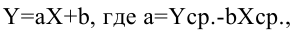 
Зная уравнение прямой, мы можем находить значение функции по значению аргумента в тех точках, где значение X известно, a Y — нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для b и r видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.
Определение формы связи. Понятие регрессии
Определить форму связи — значит выявить механизм получения зависимой случайной переменной. При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.).
Условное математическое ожидание 
случайной переменной К, рассматриваемое как функция х, т.е. 
, называется
функцией регрессии случайной переменной Y относительно X (или функцией регрессии Y по X). Точно так же условное математическое ожидание
случайной переменной X, т.е. 
называется функцией регрессии случайной переменной X относительно Y (или функцией регрессии X по Y).
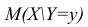
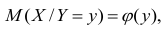
На примере, дискретного распределения найдём функцию регрессии.
Функция регрессии имеет важное значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией условного распределения.
Несмотря на важность понятия функции регрессии, возможности её практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид двумерного распределения (X, Y). Только в этом случае можно точно определить вид функции регрессии, а затем оценить параметры двумерного распределения. Однако для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объема, по которой нужно найти вид двумерного распределения (X, Y), а затем вид функции регрессии. Это может привести к значительным ошибкам, так как одну и ту же совокупность точек
на плоскости можно одинаково успешно описать с помощью различных функций. Именно поэтому возможности практического применения функции регрессии ограничены. Для характеристики формы связи при изучении зависимости используют понятие кривой регрессии.
Кривой регрессии Y по X (или Y на А) называют условное среднее значение случайной переменной У, рассматриваемое как функция определенного класса, параметры которой находят методом наименьших квадратов по наблюдённым значениям двумерной случайной величины (х, у), т.е.
Аналогично определяется кривая регрессии X по Y (X на Y):
Кривую регрессии называют также эмпирическим уравнением регрессии или просто уравнением регрессии. Уравнение регрессии является оценкой соответствующей функции регрессии.
Возникает вопрос: почему для определения кривой регрессии
используют именно условное среднее
Функция у(х) обладает одним замечательным свойством: она даёт наименьшую среднюю погрешность оценки прогноза. Предположим, что кривая регрессии — произвольная функция. Средняя погрешность прогноза по кривой регрессии определяется математическим ожиданием квадрата разности между измеренной величиной и вычисленной по формуле кривой регрессии, т.е. 
. Естественно потребовать вычисления такой кривой регрессии, средняя погрешность прогноза по которой была бы наименьшей. Таковой является
Это следует из свойств минимальности рассеивания около центра распределения
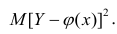
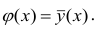
Если рассеивание вычисляется относительно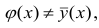
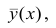
то средний квадрат отклонения увеличивается. Поэтому можно сказать, что кривая регрессии, выражаемая как 
минимизирует среднеквадратическую погрешность прогноза величины Y по X.
Основные положения корреляционного анализа
Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. С помощью этих методов решают разные задачи; требования, предъявляемые к исследуемым переменным, в каждом методе различны.
Основная задача корреляционного анализа — выявление связи между случайными переменными путём точечной и интервальной оценки парных коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации, оценки частных коэффициентов корреляции. Корреляционный анализ позволяет также оценить функцию регрессии одной случайной переменной на другую.
Предпосылки корреляционного анализа следующие:
- 1) переменные величины должны быть случайными;
- 2) случайные величины должны иметь совместное нормальное распределение.
Рассмотрим простейший случай корреляционного анализа — двумерную модель. Введём основные понятия и опишем принцип проведения корреляционного анализа. Пусть X и Y — случайные переменные, имеющие совместное нормальное распределение. В этом случае связь между X и Y можно описать коэффициентом корреляции p;. Этот коэффициент определяется как ковариация между X и Y, отнесённая к их среднеквадратическим отклонениям:
(1.1)
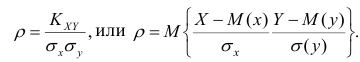
Оценкой коэффициента корреляции является выборочный коэффициент корреляции r. Для его нахождения необходимо знать оценки следующих параметров: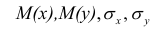 
. Наилучшей оценкой
математического ожидания является среднее арифметическое, т.е.
Оценкой дисперсии служит выборочная дисперсия, т.е.
Тогда выборочный коэффициент корреляции
Коэффициент р называют также парным коэффициентом корреляции, а r— выборочным парным коэффициентом корреляции.
При совместном нормальном законе распределения случайных величин X и Y, используя рассмотренные выше параметры распределения и коэффициент корреляции, можно получить выражение для условного математического ожидания, т. е, записать выражение для функции регрессии одной случайной величины на другую. Так, функция регрессии Y на X имеет вид:
функция регрессии X на Y — следующий вид:
Выражения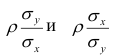
— называют коэффициентами регрессии.
Подставив в (1.3) соответствующие оценки параметров, получим уравнения регрессии, график которых — прямая линия, проходящая через точку 
Запишем уравнение регрессии у на х и х на у:
Таким образом, в корреляционном анализе на основе оценок параметров двумерной нормальной совокупности получаем оценки тесноты связи между случайными переменными и можем оценить регрессию одной переменной на другую. Особенностью корреляционного анализа является строго линейная зависимость между переменными. Это обусловливается исходными предпосылками. На практике корреляционный анализ можно применять для обработки наблюдений, сделанных на предприятиях при нормальных условиях работы, если случайные изменения свойства сырья или других факторов вызывают случайные изменения свойств продукции.
Свойства коэффициента корреляции
Коэффициент корреляции является одним из самых распространенных способов измерения связи между случайными переменными. Рассмотрим некоторые свойства этого коэффициента.
Теорема 1. Коэффициент корреляции принимает значения на интервале (-1, +1).
Доказательство. Докажем справедливость утверждения для случая дискретных переменных. Запишем явно неотрицательное выражение:
Возведём выражение под знаком суммы в квадрат:
Первое и третье из слагаемых равны единице, поскольку из определения дисперсии следует, что 
Таким образом, окончательно получаем
Если коэффициент корреляции положителен, то связь между переменными также положительна и значения переменных увеличиваются или уменьшаются одновременно. Если коэффициент корреляции имеет отрицательное значение, то при увеличении одной переменной уменьшается другая.
Приведём следующее важное свойство коэффициента корреляции: коэффициент корреляции не зависит от выбора начала отсчёта и единицы измерения, т. е. от любых постоянных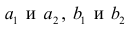 
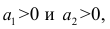
таких, что
т.е.
Таким образом, переменные X и У можно уменьшать или увеличивать в а раз, а также вычитать или прибавлять к значениям X и У одно и то же число b. В результате величина коэффициента корреляции не изменится.
Если коэффициент корреляции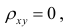 
то случайные переменные некоррелированы. Понятие некоррелированности не следует смешивать с понятием независимости, независимые величины всегда некоррелированы. Однако обратное утверждение невероятно: некоррелированные величины могут быть зависимы и даже функционально, однако эта связь не линейная.
Выборочный коэффициент корреляции вычисляют по формуле (1.2). Имеется несколько модификаций этой формулы, которые удобно использовать при той или иной форме представления исходной информации. Так, при малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по формуле
Если информация имеет вид корреляционной таблицы (см. п 1.5), то удобно пользоваться формулой
где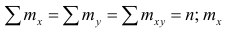
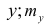
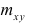
— суммарная частота наблюдаемого значенияпризнака х при всех значениях 
— суммарная частота наблюдаемого значения признака упри всех значениях х; 
— частота появления пары признаков (x, у).
Из формулы (1.2) очевидно, что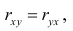 
т.е. величина выборочного коэффициента корреляции не зависит от порядка следования переменных, поэтому обычно пишут просто r.
Поле корреляции. Вычисление оценок параметров двумерной модели
На практике для вычисления оценок параметров двумерной модели удобно использовать корреляционную таблицу и поле корреляции. Пусть, например, изучается зависимость между объёмом выполненных работ (у) и накладными расходами (x). Имеем выборку из генеральной совокупности, состоящую из 150 пар переменных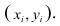 
Считаем, что предпосылки корреляционного анализа выполнены.
Пару случайных чисел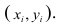 
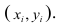
можно изобразить графически в виде точки с координатами
. Аналогично можно изобразить весь набор пар случайных чисел (всю выборку). Однако при большом объёме выборки это затруднительно. Задача упрощается, если выборку упорядочить, т.е. переменные сгруппировать. Сгруппированные ряды могут быть как дискретными, так и интервальными.
По осям координат откладывают или дискретные значения переменных, или интервалы их изменения. Для интервального ряда наносят координатную сетку. Каждую пару переменных из данной выборки изображают в виде точки с соответствующими координатами для дискретного ряда или в виде точки в соответствующей клетке для интервального ряда. Такое изображение корреляционной зависимости называют полем корреляции. На рис. 1.1 изображено поле корреляции для выборки, состоящей из 150 пар переменных (ряд интервальный).
Если вычислить средние значения у в каждом интервале изменения х [обозначим их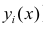 
)], нанести эти точки на рис. 1.1 и соединить между собой, то получим ломаную линию, по виду которой можно судить, как в среднем меняются у в зависимости от изменения х. По виду этой линии можно также сделать предположение о форме связи между переменными. В данном случае ломаную линию можно аппроксимировать прямой линией, так как она достаточно хорошо приближается к ней. По выборочным данным можно построить также корреляционную табл. 1.1.
Корреляционную таблицу, как и поле корреляции, строят по
сгруппированному ряду (дискретному или интервальному). Табл. 1.1 построена на основе интервального ряда. В первой строке и первом столбце таблицы помещают интервалы изменения х и у и значения середин интервалов. Так, например, 1,5 — середина интервала изменения *=1-2,15— середина интервала изменения у= 10-20. В ячейки, образованные пересечением строк и столбцов, заносят частоты попадания пар значений (л у) в соответствующие интервалы по х и у. Например, частота 4 означает, что в интервал изменения у от 10 до 20 попало 4 пары наблюдавшихся значений. Эти частоты обозначают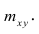 
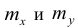
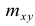
В 9-й строке и 10-м столбце находятся значения 
— суммы 
по соответствующим столбцу и строке.
Как будет показано в дальнейшем, корреляционно таблицей удобно пользоваться при вычислении коэффициентов корреляций и параметров уравнений регрессии.
Корреляционная таблица построена на основе интервального ряда, поэтому для оценок параметров воспользуемся формулами гл. 1 для вычисления средней арифметической и дисперсии. Имеем:
(1.6)
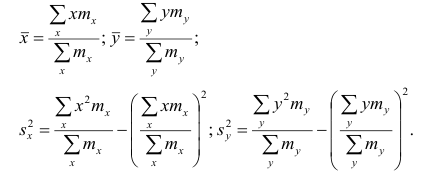
Проверка гипотезы о значимости коэффициента корреляции
На практике коэффициент корреляции р обычно неизвестен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции r.
Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин X и Y. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции г, т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу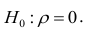 
. Предполагается наличие двумерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют
которая имеет распределение Стьюдента с k=n-2
степенями свободы. Для проверки нулевой гипотезы по уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (t-распределение; см. табл. 1 приложения) критическое значение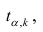 
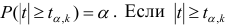
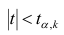
удовлетворяющее условию
, то нулевую гипотезу об отсутствии корреляционной связи между переменными X и Y следует отвергнуть. Переменные считают зависимыми. При
нет оснований отвергать нулевую гипотезу.
В случае значимого выборочного коэффициента, корреляции есть смысл построить доверительный интервал для коэффициента корреляций р. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции r.
Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику:
где r=thz — гиперболический тангенс от z.
Распределение статистики z хорошо аппроксимируется нормальным распределением с параметрами
В этом, случае доверительный интервал для римеетвид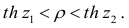
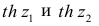
Величины 
находят по таблицам по следующим значениям:
где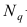 
— нормированная функция Лапласа для q % доверительного интервала (см. табл. 2 приложений значение функции 
Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля, а интервальные оценки для них можно получить по следующим формулам:
где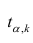 
имеет распределение Стьюдента с k=n—2 степенями свободы.
Корреляционное отношение
На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается величиной не случайной, или признаки не имеют совместного нормального распределения. Однако статистическая зависимость между ними существует. Для изучения связи между признаками в этом случае существует общий показатель зависимости признаков, основанный на показателе изменчивости — общей (или полной) дисперсии.
Полной называется дисперсия признака относительно его математического ожидания. Так, для признака Y это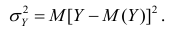 
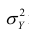
Дисперсию 
можно разложить на две составляющие, одна из которых характеризует влияние фактора X на Y, другая — влияние прочих факторов.
Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. Представим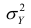 
в следующем виде:
Первое слагаемое обозначим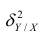
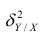
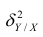
Это дисперсия функции регрессии относительно математического ожидания признака (в данном случае признака У);.она измеряет влияние признака X на Y. Второе слагаемое обозначим
. Это дисперсия признака Y относительно функции регрессии. Её называют также средней из условных дисперсий или остаточной дисперсией 
измеряет влияние на Y прочих факторов.
Покажем, что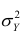 
действительно можно разложить на два таких слагаемых:
Для простоты полагаем распределение дискретным. Имеем 
так как при любом х справедливо равенство
Третье слагаемое в равенстве (1.10) равно нулю, поэтому равенство (1.9) справедливо. Поскольку второе слагаемое в равенстве (1.9) оценивает влияние признака X на Y, то его можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оценивать в единицах общей дисперсии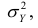 
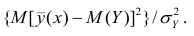
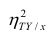
т.е. рассматривать отношение
. Эту величину обозначают 
и называют теоретическим корреляционным отношением. Таким образом,
Разделив обе части равенства (1.9) на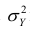 
получим
Из последней формулы имеем
Поскольку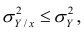 
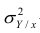
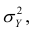
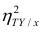
так как 
— составная часть 
то из равенства (1.12) следует, что значение 
всегда заключено между нулем и единицей.
Все сделанные выводы справедливы и для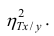 
Из равенства (1.12)
следует, что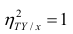 
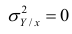
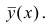
только тогда, когда 
, т.е. отсутствует влияние прочих факторов и всё распределение сконцентрировано на кривой регрессии 
. В этом случае между Y и X существует функциональная зависимость.
Далее, из равенства (1.12) следует, что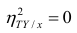 
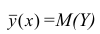
тогда и только тогда, когда
= const, т.е. линия регрессии У по X — горизонтальная прямая, проходящая через центр распределения. В этом случае можно сказать, что переменная У не коррелирована с X (рис. 1.2,а, б, в).
Аналогичными свойствами обладает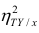
— показатель тесноты связи между X и У.
Часто используют величину
Считают, что она не может быть отрицательной. Значения величины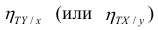 
также могут находиться лишь в пределах от нуля до единицы. Это очевидно из формулы (1.13).
Значения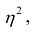
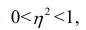
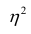
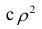
лежащие в интервале
являются показателями тесноты группировки точек около кривой регрессии независимо от её вида (формы связи). Корреляционное отношение 
связано 
следующим образом: 
В случае линейной зависимости между переменными 
Разность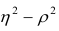
может быть использована как показатель нелинейности связи между переменными.
При вычислении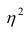 
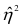
по выборочным данным получаем выборочное корреляционное отношение. Обозначим его
. Вместо дисперсий в этом случае используются их оценки. Тогда формула (1.12) принимает вид
Понятие о многомерном корреляционном анализе
Частный коэффициент корреляции. Основные понятия корреляционного анализа, введенные для двумерной модели, можно распространить на многомерный случай. Задачи и предпосылки корреляционного анализа были сформулированы в п. 1.3. Однако если при изучении взаимосвязи переменных по двумерной модели мы ограничивались рассмотрением парных коэффициентов корреляции, то для многомерной модели этого недостаточно. Многообразие связей между переменными находит отражение в частных и множественных коэффициентах корреляции.
Пусть имеется многомерная нормальная совокупность с m признаками 
В этом случае взаимозависимость между признаками
можно описать корреляционной матрицей. Под корреляционной матрицей будем понимать, матрицу, составленную из парных коэффициентов корреляции (вычисляются по формуле (1,1)):
где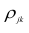 
— парные коэффициенты корреляции; m — порядок матрицы.
Оценкой парного коэффициента корреляции является выборочный парный коэффициент корреляции, определяемый по формуле (1.2), однако для m признаков формула (9.2) принимает вид
где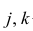 
— порядковые номера признаков.
Как и в двумерном случае, для оценки коэффициента корреляции необходимо оценить математические ожидания и дисперсии. В многомерном корреляционном анализе имеем т математических ожиданий и m дисперсий, а также m(m—1)/2 парных коэффициентов корреляции. Таким образом, нужно произвести оценку 2m+m(m—1)/2 параметров.
В случае многомерной корреляции зависимости между признаками более многообразны и сложны, чем в двумерном случае. Одной корреляционной матрицей нельзя полностью описать зависимости между признаками. Введём понятие частного коэффициента корреляции l-го порядка.
Пусть исходная совокупность состоит из т признаков. Можно изучать зависимости между двумя из них при фиксированном значении l признаков из m-2 оставшихся. Рассмотрим, например, систему из 5 признаков. Изучим зависимости между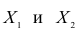 
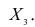
при фиксированном значении признака 
В этом случае имеем частный коэффициент корреляции первого порядка, так как фиксируем только один признак.
Рассмотрим более подробно структуру частных коэффициентов корреляции на примере системы из трёх признаков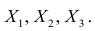 
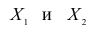
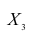
. Эта система позволяет изучить частные коэффициенты корреляции только первого порядка, так как нельзя фиксировать больше одного признака. Частный коэффициент корреляции первого порядка для признаков
при фиксированном значении 
выражается через парные коэффициенты
корреляции и имеет вид
Частный коэффициент корреляции, так же как и парный коэффициент корреляции, изменяется от —1 до +1, В общем виде, когда система состоит из m признаков, частный коэффициент корреляции l-го порядка может быть найден из корреляционной матрицы. Если 1=m—2, то рассматривается матрица порядка m, при
— подматрица порядкаl+2, составленная из элементов матрицы 
, которые отвечают индексам коэффициента частной
корреляции. Например, корреляционная матрица системы из пяти признаков имеет вид
Для определения частного коэффициента корреляции второго порядка, например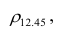
следует использовать подматрицу четвертого порядка,
вычеркнув из исходной матрицы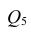 
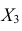
третью строку и третий столбец, так как признак 
не рассматривают.
В общем виде формулу частного коэффициента корреляции l-го порядка (1=m—2) можно записать в виде
где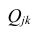 
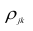
— алгебраические дополнения к элементу 
корреляционной
матрицы 
— алгебраические дополнения к элементам 
и ркк корреляционной матрицы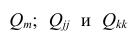 
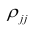
Очевидно, что выражение (1.16) является частым случаем выражения (1.17), в чём легко убедиться, рассмотрев корреляционную матрицу
Оценкой частного коэффициента корреляции l-го порядка является выборочный частный коэффициент корреляции l-го порядка. Он вычисляется на основе корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции:
Формула выборочного частного коэффициента корреляции имеет вид
где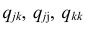 
— алгебраические дополнения к соответствующим элементам матрицы (1.18).
Частный коэффициент корреляции l-го порядка, вызволенный на основе п наблюдений над признаками, имеет такое же распределение, что и парный коэффициент корреляции, вычисленный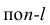 
наблюдениям. Поэтому значимость частных коэффициентов корреляции оценивают так же, как и в п. 1.6.
Множественный коэффициент корреляции
Часто представляет интерес оценить связь одного из признаков со всеми остальными. Это можно сделать с помощью множественного, или совокупного, коэффициента корреляции
где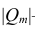 
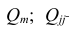
—определитель корреляционной матрицы
—алгебраическое
дополнение к элементу 
Квадрат коэффициента множественной корреляции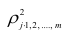 
называется
множественным коэффициентом детерминации. Коэффициенты множественной корреляции и детерминации — величины положительные, принимающие значения в интервале
Оценками этих
коэффициентов являются выборочные множественные коэффициенты корреляции и детерминации, которые обозначают соответственно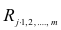 
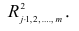
и
Формула для вычисления выборочного множественного коэффициента корреляции имеет вид
где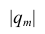 
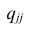
—определитель корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции; 
алгебраическое дополнение к элементу 
Многомерный корреляционный анализ позволяет получить оценку функции регрессии — уравнение регрессии. Коэффициенты в уравнении регрессии можно найти непосредственно через выборочные парные коэффициенты корреляции или воспользоваться методом многомерной регрессии, который мы рассмотрим в вопросе 2.7. В этом случае все предпосылки регрессионного анализа оказываются выполненными и, кроме того, связь между переменными строго линейна.
Ранговая корреляция
В некоторых случаях встречаются признаки, не поддающиеся количественной оценке (назовём такие признаки объектами). Попытаемся, например, оценить соотношение между математическими и музыкальными способностями группы учащихся. «Уровень способностей» является переменной величиной в том смысле; что он варьирует от одного индивидуума к другому. Его можно измерить, если выставлять каждому индивидууму отметки. Однако этот способ лишен объективности, так как разные экзаменаторы могут выставить одному и тому же учащемуся разные отметки. Элемент субъективизма можно исключить, если учащиеся будут ранжированы. Расположим учащихся по порядку, в соответствии со степенью способностей и присвоим каждому из них порядковый номер, который назовем рангом. Корреляция между рангами более точно отражает соотношение между способностями учащихся, чем корреляция между отметками.
Тесноту связи между рангами измеряют так же, как и между признаками. Рассмотрим уже известную формулу коэффициента корреляции
Пусть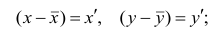 
тогда, учитывая,
что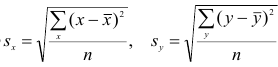
,можно записать
В зависимости от того, что принять за меру различия между величинами 
можно получить различные коэффициенты связи между рангами. Обычно используют коэффициент корреляции рангов Кэнделла 
и коэффициент корреляции рангов Спирмэна р.
Введём следующую меру различия между объектами: будем считать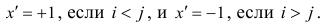 
Поясним сказанное на примере. Имеем две последовательности:
Рассмотрим отдельно каждую из них. В последовательности X первой паре элементов —2; 4 припишем значение +1, так как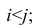
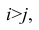
второй паре 2; 5 также припишем значение +1, третьей паре 2; 1 припишем значение —1, поскольку 
и т.д. Последовательно перебираем все пары, причём каждая пара должна быть учтена один раз. Так, если учтена пара 2; 1, то не следует учитывать пару 1; 2. Аналогичные действия проделаем с последовательностью У, причём порядок перебора пар должен в точности повторять порядок перебора пар в последовательности X. Результаты этих действий представим в виде табл. 1.3.
Рассмотрим формулу ( 1 .22). В нашем случае
и равна
количеству пар, участвовавших в переборе. Каждая пара встречается только один раз, поэтому их общее количество равно числу сочетаний из n по 2, т.е.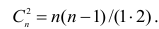
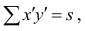
Обозначая 
получаем формулу коэффициента корреляции рангов Кэнделла:
Теперь рассмотрим другую меру различия между объектами. Если обозначить через 
средний ранг последовательности X, через 
— средний ранг последовательности Т, то
Поскольку ранги последовательности X и Y есть числа натурального ряда, то их сумма равна 
а средний ранг 
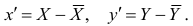
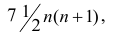
Тогда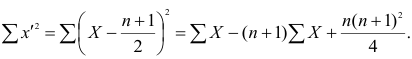
Сумма
чисел натурального ряда равна
Тогда 
Введём новую величину d, равную разности между рангами: d=X—Y, и определим через неё величину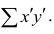
. Имеем:
Коэффициент корреляции рангов Спирмэна
У коэффициентов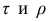 
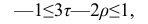
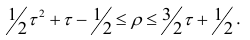
разные масштабы, они отличаются шкалами измерений. Поэтому на практике нельзя ожидать, что они совпадут. Чаще всего, если значения обоих коэффициентов не слишком, близки к 1, p; по абсолютной величине примерно на 50% превышает
Выведены неравенства, связывающие
Например, при больших n можно пользоваться следующим приближённым соотношением: 
или
Коэффициент p легче рассчитать, однако с теоретической точки зрения больший интерес представляет коэффициент
При вычислении коэффициента корреляций рангов Кэнделла для подсчёта s можно использовать следующий приём: одну из последовательностей упорядочивают так, чтобы её элементы были числами натурального ряда; соответственно изменяют и другую последовательность. Тогда сумму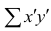
можно подсчитывать лишь по последовательности К, так как все 
равны +1.
Если нельзя установить ранговое различие нескольких объектов, говорят, что такие объекты являются связанными. В этом случае объектам приписывается средний ранг. Например, если связанными являются объекты 4 и 5, то им приписывают ранг 4.5; если связанными являются объекты 1, 2, 3, 4 и 5, то их средний ранг (1+2+3+4+5)/5=3. Сумма рангов связанных объектов должна быть равна сумме рангов при ранжировании без связей. Формулы коэффициентов корреляции для 
в этом случае также можно вывести из формулы обобщённого коэффициента корреляции, только знаменатель выражения (1.21) в этом случае не равен n(n—1)/2. Если / последовательных членов связаны, то все оценки, относящиеся к любой вобранной из них паре, равны нулю; число таких пар t(t—1), Следовательно,
Соответственно для другой последовательности
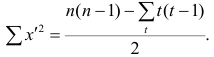
где t и u—число связанных пар в последовательностях.
Обозначая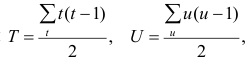 
получаем
Аналогично находим выражение для р. Только в этом случае
, где е и г — число связанных пар в
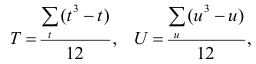
последовательностях, а
Если имеется несколько последовательностей, то возникает необходимость определить общую меру согласованности между ними. Такой мерой является коэффициент копкордации.
Пусть ь — число последовательностей, т — количество рангов в каждой последовательности. Тогда коэффициент конкордации
где d — фактически встречающееся отклонение от среднего значения суммы рангов одного объекта.
Коэффициент корреляции рангов может быть использован для быстрого оценивания взаимосвязи между признаками, не имеющими нормального распределения, и полезен в тех случаях, когда признаки поддаются ранжированию, но не могут быть точно измерены.
Пример:
Для данных табл. 13 найти выборочный коэффициент корреляции, проверить его значимость на уровне 
Решение. Для вычислений составим таблицу. Находим суммы
и заносим их в таблицу. Вычислим
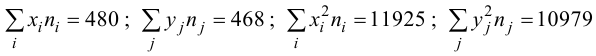
Подставляя полученные значения сумм в (8), найдем выборочный коэффициент корреляции
Проверим значимость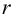 
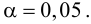
на уровне 
Для этого вычислим статистику
По таблице распределения П6 Стьюдента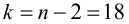 
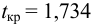
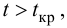
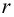
находим критическое значение 
Так как 
то считаем 
значимым.
Пример:
Для данных табл. 13 найти корреляционное отношение 
Для вычисления эмпирического корреляционного отношения найдем групповые средние 
Тогда
Вычисляем корреляционное отношение
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
- Регрессионный анализ