Содержание
- Понятие о поверхности второго порядка
- Общее уравнение поверхности второго порядка, основные определения
- Цилиндрические и конические поверхности
- Исследование формы поверхностей второго порядка методом сечений
- Поверхности второго порядка
- Сфера и ее уравнение
- Цилиндрические поверхности
- Цилиндры второго порядка
- Эллипсоид
- Гиперболоиды
- Параболоиды
- Конические поверхности
- Поверхность вращения
- Как построить график функции
- Трехмерные графики функции
- Принципы и способы построения графика функции
Понятие о поверхности второго порядка
Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению.
Общее уравнение поверхности второго порядка, основные определения
Поверхностью второго порядка называется множество точек пространства 


где 



Уравнение (10.27) называют общим уравнением поверхности второго порядка. Вид поверхности и ее расположение относительно координатных плоскостей зависит от значений параметров в (10.27).
Если не существует ни одной точки 
Поверхность называется вырожденной, если ее общее уравнение описывает точку, одну или две плоскости. К примеру:
уравнение точки в
уравнения двух плоскостей, параллельных
уравнения двух биссекторных плоскостей.
При изучении поверхностей второго порядка решаются две взаимно обратные основные задачи:
- по известным геометрическим свойствам точек поверхности составить уравнение соответствующей поверхности;
- по известным уравнением поверхности установить геометрические свойства ее точек.
Примером решения первой основной задачи является построение уравнения сферы (9.2). Уравнение других важнейших поверхностей рассматриваются ниже.
Цилиндрические и конические поверхности
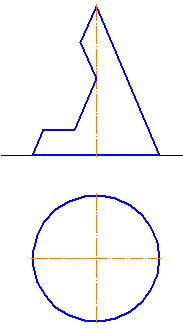
Цилиндрической поверхностью, или просто цилиндром, называется поверхность, образованная движением прямой, перемещается параллельно самой себе вдоль фиксированной линии (кривой). Подвижную прямую называют образующей, а фиксированную кривую — направляющей цилиндрической поверхности. Направляющей может быть любая сомкнутая или разомкнутая линия.
Цилиндром второго порядка называется цилиндрическая поверхность, направляющей которой является кривая второго порядка: эллипс (круг), гипербола, парабола. Название цилиндра определяется названием его направляющей. Если образующая параллельна одной из координатных осей, а направляющая лежит в плоскости, перпендикулярной этой оси, то уравнение цилиндра совпадает с уравнением направляющей. При геометрической интерпретации изображается, как правило, часть поверхности между двумя плоскостями, перпендикулярными образующей.
К примеру:
уравнения эллиптического цилиндра (рис. 10.9 а)
уравнения гиперболического цилиндра (рис. 10.9 б)
уравнения параболического цилиндра (рис. 10.9 в).
Рис. 10.9
Отсутствие переменной 
в уравнениях следует считать равными нулю. Например, уравнение параболического цилиндра можно записать в виде: 
Если в уравнениях эллипса и гиперболы положить 
Конической поверхностью, или конусом, называется поверхность, образованная движением прямой, проходящей через заданную точку, вдоль фиксированной кривой. Подвижную прямую называют образующей, заданную точку — вершиной, а фиксированную кривую — направляющей конуса. Если образующей является кривая второго порядка, то поверхность называется конусом второго порядка.
На рис. 10.10 изображен конус второго порядка, определяется уравнением
Рис. 10.10
с вершиной в начале координат, направляющей которого является эллипс

Поверхность симметрична относительно начала координат, а координатные плоскости является ее плоскостями симметрии. Множество точек поверхности с неотъемлемыми (неположительные) аппликатами называется верхней (нижней) полостью конуса.
Если направляющей конуса является круг 
Эллипс, парабола, гипербола — кривые второго порядка — можно получить сечением прямого кругового конуса плоскостями, которые не проходят через его вершину (рис. 10.11).
А именно:
- если плоскость пересекает только одну полость конуса и непараллельных одной из его образующих, то кривой сечения является эллипс;
- в частном случае — круг;
- если секущая плоскость параллельна одной из образующих конуса, то результат сечения — парабола;
- если плоскость сечения пересекает обе полости конуса, то кривой сечения является гипербола.
Рис. 10.11
Исследование формы поверхностей второго порядка методом сечений
Приведенные выше уравнения поверхностей второго порядка складывались по геометрическим свойствам их точек в соответствии с определений поверхностей. Для решения обратной задачи (по данным уравнением поверхности определить ее вид) применяется метод сечений, суть которого заключается в следующем:
- анализируют поверхность, устанавливая за ее уравнением линии пересечения (сечения) данной поверхности координатными плоскостями параллельными им;
- синтезируют определенные на предыдущем шаге геометрические свойства поверхности, что позволяет представить вид поверхности и изобразить ее.
Продемонстрируем применение метода сечений к исследованию уравнения эллиптического параболоида:
Если:






то есть сечением поверхности плоскостями, параллельными 
(рис. 10.12);
- установим линию пересечения поверхности с плоскостью
:
Это уравнение параболы, расположенной в плоскости 

Рис. 10.12
Аналогично осуществляется построение параболоида 

Поверхностью вращения называется поверхность, для которой каждый из ее сечений плоскостью, перпендикулярной одной из координатных осей или произвольной оси 
прямой, проходящей через начало координат, а цилиндр — прямой, параллельной оси 
Уравнения поверхностей, симметричные относительно координатных осей или / и координатных плоскостей, называют каноническими, или стандартными.
В заключение отметим, что приведенные сведения используются при изучении интегрирования функций двух переменных и является фундаментом для более глубокого изучения теории поверхностей второго порядка.
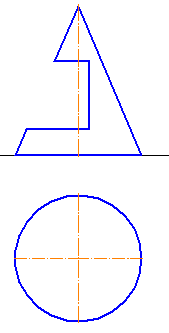
Далее в таблице 10.1 приводятся канонические уравнения и изображения важнейших поверхностей второго порядка.
Важнейшие поверхности второго порядка Таблица 10.1
Поверхности второго порядка
Определение. Поверхности второго порядка называют геометрическое место точек пространства, декартовые координаты которых удовлетворяют уравнению второй степени.
Сфера и ее уравнение
Сферой называют геометрическое место точек пространства, равноудаленное от заданной точки — центра сферы.
- Если центром сферы является точка
а радиус
тогда уравнение сферы будет:
- Если центр сферы находится в начале координат
и радиус
тогда уравнение сферы будет:
Цилиндрические поверхности
Поверхность называется цилиндрической, если она образуется прямой (образующая), параллельно к заданной прямой
и которая проходит через заданную линию
(направляющая линия). Пример цилиндрической линии изображен на рис. 2.24
Если образующая цилиндрической поверхности параллельна оси 



Уравнение 


Цилиндры второго порядка
- Эллиптичным цилиндром называется поверхность (рис. 2.25), каноничное уравнение которой имеет вид:
Если 
- Гиперболичным цилиндром называется поверхность, уравнение которой имеет вид (рис. 2.26):
- Параболическим цилиндром называется поверхность, каноничное уравнение которой имеет вид (рис. 2.27):
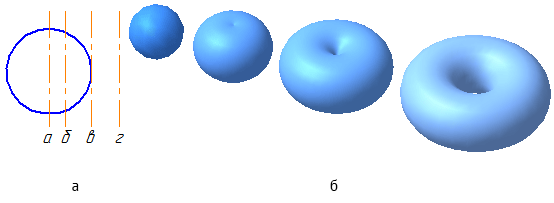
Эллипсоид
Эллипсоидом называется поверхность, каноничное уравнение которой имеет вид (рис. 2.28):
Отрезки
— называются полуосями эллипсоида.
Гиперболоиды
- Однополосным гиперболоидом (рис. 2.29) называется поверхность, каноническое уравнение которой имеет вид :
- Двуполостный гиперболоид. Двуполостным гиперболоидом (рис. 2.30) называется поверхность, каноничное уравнение которой имеет вид:
Параболоиды
Конические поверхности
конической поверхностью называется поверхность, которая описана прямой, что проходит через точку — вершину конуса — и что
пересекает заданную линию — направляющую конуса.
Уравнение конуса (рис. 2.33) второго порядка имеет вид:
Поверхность вращения
Пусть в плоскости 

Тогда чтобы получить уравнение поверхности, что образована вращением линии 




Аналогично правила будут иметь место и по отношению к поверхностям, которые образуют обращение плоских линий около других координатных осей.
Примеры:
Примеры решения задач:
Задача 2.126
Обозначить координаты центра сферы и ее радиус:
Решение. Предоставим заданное уравнение в виде (2.43), для этого:
- объединяем в группы члены, которые содержат одноименные координаты;
- выделим в группах полные квадраты. Получим:
Соизмеряя с (2.43), получим
Следует, центр сферы — точка 
Задача 2.127
Эллипс с полуосями 5 и 3 вращается около своей большей оси. которая совпадает с началом координат. Сложить уравнение поверхности, что описывает эллипс при вращении.
Решение. Сложим каноническое уравнение эллипса с центром в начале координат, который размещен в плоскости
чтобы получить уравнение поверхности, которая образована вращением в плоскости 
необходимо в уравнении эллипса заменить 
Получим эллипсоид вращения, который протянул вдоль оси
или
Задача 2.128
Сложим уравнение конуса с вершиной в начале координат и направляющей:
Решение. Канонические уравнения образующих, что проходят через вершину 

Исключим 







или
Задача 2.129
Какие поверхности обозначаются уравнениями:
Решение. Каждое из уравнений содержит только две переменные 


- круг,
- эллипс,
- параболу,
- гиперболу.
В пространстве же каждое из них обозначается цилиндрическую поверхность с образующими, что параллельны оси 

— уравнение прямого углового цилиндра;
— уравнение эллиптического цилиндра;
— уравнение параболического цилиндра;
— уравнение гиперболичного цилиндра.
Задача 2.130
Гипербола с полуосями 3 и 4 вращается около своей мнимой оси, которая совпадает с осью
Центры гиперболы совпадает с началом координат. Сложить уравнение поверхности, которое получим при вращении гиперболы.
Решение. Сложим каноничное уравнение гиперболы с центром в начале координат, что находятся в плоскости
Чтобы сложить уравнение поверхности, образованной вращением гиперболы, что находится в уравнение гиперболы вместо
подставить
или
Следует, получим однополосный гиперболоид вращения:
Как построить график функции
Трехмерные графики функции
Построить графики (в том числе и трехмерные) можно также, используя следующий сервис. Например, построить график функцииcosx + esinx+x3. Записываем как cos(x)+exp((sin(x)+x^3)) и нажимаем кнопку Построить график.
Чтобы построит два графика в одних координатах, например, y=3x-1, y=x2-2x+5, указываем: 3*x-1,x^2-2*x+5. Также можно задать пределы отображения по оси X (ось абсцисс).
Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3).
f(x)=Пределы по x = ..
Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3).
Также можно начертить график по точкам. Необходимо вставить данные для X (первый столбец) и Y (второй и последующие столбцы). <текстареа name=»TEXTEXCEL» rows=»10″ class=»form-control»>
Построение графика функции в Excel осуществляется в два этапа:
- На первом этапе при заданном интервале [a;b] и шаге h рассчитываются значения функции y=f(x).
- На втором этапе с помощью инструмента ExcelМастер диаграмм строится визуализация рассчитанных значений.
Чтобы построить трехмерный график в Excel, необходимо указать функцию f(x,y), пределы по x и y и шаг сетки h.
f(x,y)=x= .. y= .. h=
Принципы и способы построения графика функции
График любой функции можно построить прямыми вычислениями значения функции y=f(x) и методом дифференциального исчисления.
- При прямом вычислении значений функции y=f(x) необходимо задать интервал [a;b] вычислений и шаг h. Получается таблица, по которой можно построить график.
Например, определим для функции y=x*e2x/3+4 интервал [-3;7], на котором будем отображать найденные точки. Чем меньше шаг h, тем точнее график функции (другими словами, тем точнее аппроксимация). Например, при h=2 количество точек для построения равно N=(7-(-3))/2+1=6 (-3; -1; 1; 3; 5; 7), а при h=0.1 уже N=(7-(-3))/0.1+1=101. - Построение графика функции методом дифференциального исчисления предполагает схематичное построение, используя свойства функции.
| Автор | Сообщение | ||
|---|---|---|---|
|
|||
|
Member Статус: Не в сети |
Нужна программа для построения поверхности в координатах x,y,z . Так же программа должна выводить хотя бы примерное уравнение полученной поверхности. как пример http://xmages.net/show.php/1175872_13.png.html . Помогите плиз… |
| Реклама | |
|
Партнер |
|
holmes2007 |
|
|
Junior Статус: Не в сети |
Обычно в Маткаде можно строить поверхность, если есть z=f(x,y) |
|
w1zzard |
|
|
Member Статус: Не в сети |
вся сложность в том, что функции нету. построить саму поверхность не проблема, проблема в поиске уравнения этой самой поверхности holmes2007 писал(а): Обычно в Маткаде можно строить поверхность, если есть z=f(x,y) проблема состоит в том, что этой зависимости нет. Есть только набор точек, по которой строится поверхность, похожая на приведенную в примере. |
|
holmes2007 |
|
|
Junior Статус: Не в сети |
В Маткаде вроде можно по точкам. А еще есть программа Advanced Grapher |
|
w1zzard |
|
|
Member Статус: Не в сети |
holmes2007 писал(а): В Маткаде вроде можно по точкам. А еще есть программа Advanced Grapher Если бы вы посмотрели пример, то проблемы в построении самой поверхности нету. Есть проблема нахождения функциональной зависимости вида Z=f(x,y) — где f(x,y) -либо полином n-ной степени, либо еще какая-нибудь зависимость. |
|
w1zzard |
|
|
Member Статус: Не в сети |
H(CHCl11B11) писал(а): Спасибо! Жду еще варианты, если можно. А то не совсем получается. тут же будет использоваться по осям х и у концентрации, а по z будет откладываться например электропроводность, плотность и т.д. Следовательно будут очень разные зависимости (не всегда полиномы) |
|
w1zzard |
|
|
Member Статус: Не в сети |
ну статистика может такое, но она начинает интерполировать данный график, что мне не нужно ибо иногда он заходит за границу существования исследуемого объекта. |
|
H(CHCl11B11) |
|
|
Member Статус: Не в сети |
w1zzard писал(а): тут же будет использоваться по осям х и у концентрации, а по z будет откладываться например электропроводность, плотность и т.д. Следовательно будут очень разные зависимости (не всегда полиномы) Абсолютно не имеет никакого значения что откладывать по осям. Многочлен по определению может интерполировать любую функцию, чем больше точек — тем ближе к ней. w1zzard писал(а): ну статистика может такое, но она начинает интерполировать данный график, что мне не нужно ибо иногда он заходит за границу существования исследуемого объекта. не путайте интерполяцию и экстраполяцию. Границы задаются при построении поверхностей. И вообще если не нужна гладкая (интерполированная) поверхность, можно ведь построить по точкам. |
|
w1zzard |
|
|
Member Статус: Не в сети |
Нужно уравнение полученной по точкам поверхности. Построение самой поверхности не проблема. Программ для построения поверхностей по точкам тьма. А чтобы они при этом еще и уравнение данной поверхности давали, пока не видел, но узнал что маткад в состоянии помочь. Поэтому и спросил, может кто знает каким образом в маткаде такое возможно написать. |
—
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Лаборатория
Новости
Содержание:
Уравнения поверхности и линии в пространстве
Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если
— уравнение поверхности Р (рис. 189), то при М(х, у, z)
Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.
Пример (уравнения координатных плоскостей):
Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,
х = 0
— уравнение координатной плоскости Oyz. Аналогично,
— соответственно уравнения координатных плоскостей Oxz и Оху.
Формула 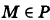
В более общем случае
— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные
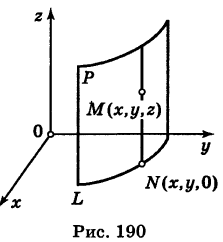
Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.
Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 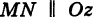
Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).
Пусть
— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,
является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.
Пример (уравнение эллиптического цилиндра):
Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение
В частности, при а = b получаем уравнение кругового цилиндра
Линию L в пространстве можно задать как пересечение двух данных поверхностей 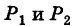

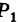
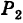
Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:
являющихся уравнениями поверхностей, определяющих данную линию.
Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки 
Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.
Определение: Уравнениями линии в пространстве 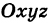
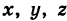
Пример (уравнения координатных осей):
Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому
— уравнения оси Ох. Аналогично,
— уравнения осей Оу и Oz соответственно.
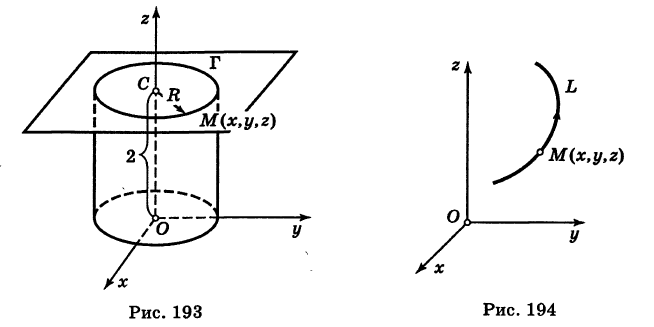
Пример:
Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).
Решение:
Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть
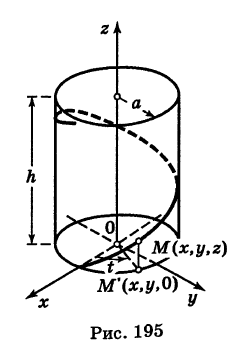
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем
где 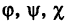
Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.
- Заказать решение задач по высшей математике
Пример:
Написать уравнения винтовой линии радиуса а и шага 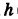
Решение:
Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.
Приняв за параметр 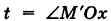
Для определения коэффициента пропорциональности b положим 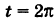
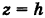
Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем
Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости 
Текущую точку 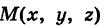
(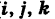
где
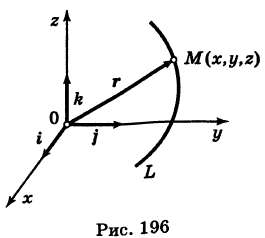
— так называемая вектор-функция скалярного аргумента t.
В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).
Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).
Пример:
Какой геометрический образ соответствует уравнению
Решение:
Из уравнения (8) получаем 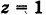
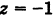
Пример:
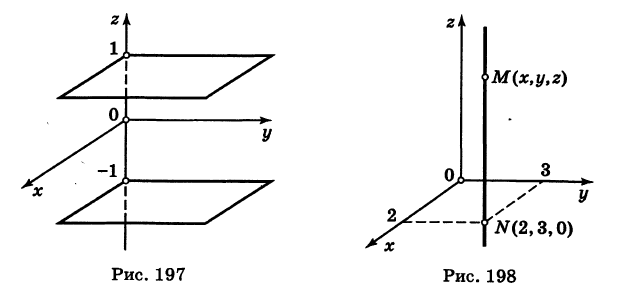
Какой геометрический образ соответствует паре уравнений
Решение:
Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).
- Общее уравнение плоскости
- Угол между плоскостями
- Понятие о производной вектор-функции
- Криволинейные интегралы
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка
- Полярные координаты
- Непрерывность функции
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
7.1. Поверхности. Образование и задание поверхности на чертеже
Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с проектированием, конструированием и изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации проектно-конструкторского процесса и воспроизведения сложных поверхностей. Способы формообразования и отображения поверхностей составляют основу инструментальной базы трехмерного моделирования современных систем автоматизированного проектирования.
Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z)— многочлен n-ой степени и трансцендентные (F(x,y,z)— трансцендентная функция.
Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек её пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).
Поверхность можно рассматривать, как совокупность последовательных положений l1,l2… линии l перемещающейся в пространстве по определенному закону (Рисунок 7.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму — изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в виде одной линии или целого семейства линий (m, n, p…).
Подвижную линию принято называть образующей (li), неподвижные – направляющими (m). Такой способ образования поверхности принято называть кинематическим.
Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несёт на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество линий конгруэнтных профилю резца.
Рисунок 7.1 — Кинематическая поверхность
По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая.
Линейчатые поверхности в свою очередь разделяют на развертывающиеся, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся.
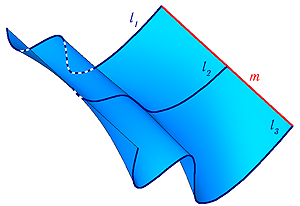
Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Такие поверхности носят название циклические (Рисунок 7.2).
Рисунок 7.2 — Циклическая поверхность
Если группировать поверхности по закону движения образующей линии, то большинство встречающихся в технике поверхностей можно разделить на:
- поверхности вращения;
- винтовые поверхности;
- поверхности с плоскостью параллелизма;
- поверхности параллельного переноса.
Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).
Для графического изображения поверхности на чертеже используется её каркас.
Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности.
Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом.
Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.
Различают две части определителя: геометрическую и алгоритмическую.
Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.
Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.
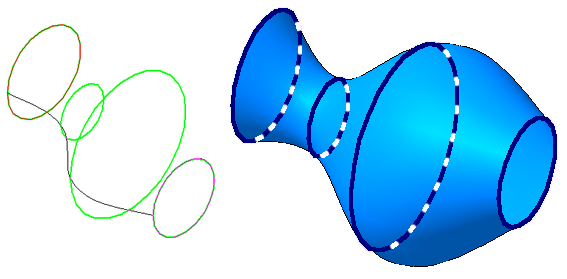
Например, циклическая поверхность, каркас которой состоит из восьмиугольников (Рисунок 7.3), может быть задан следующим образом:
- Геометрическая часть определителя: три направляющих l, m, n.
- Алгоритмическая часть: выбираем плоскость α; находим точки А, В, С, в которых α пересекает соответственно направляющие l, m, n. Строим восьмиугольник, определяемый тремя найденными точками. Переходим к следующей плоскости и повторяем построение
Рисунок 7.3 –Образование циклической поверхности
7.2. Поверхности вращения
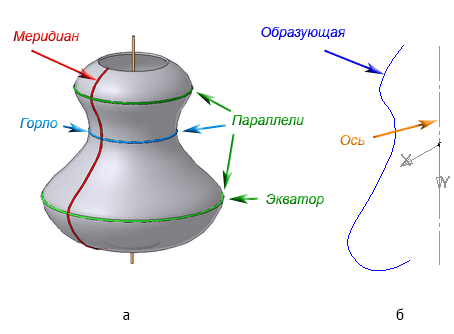
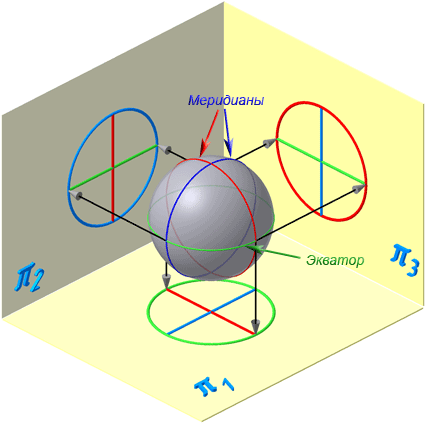
Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).
Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.
Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.
Рисунок 7.4 – Образование поверхностей вращения
Рисунок 7.5 – Элементы поверхности вращения
Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости, перпендикулярной оси вращения. Эти окружности называются параллелями (Рисунок 7.5).
Наименьшая параллель называется горлом, наибольшая – экватором.
Линия пересечения поверхности вращения плоскостью, проходящей через ось, называется меридианом.
Линия пересечения поверхности вращения плоскостью, проходящая через ось, параллельно фронтальной плоскости проекций, называется главным меридианом.
7.3. Цилиндрическая поверхность
Цилиндрическая поверхность образуется движением прямой линии, которая в любом своём положении параллельна данному направлению и пересекает криволинейную направляющую (Рисунок 7.6).
Цилиндр – геометрическое тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими все образующие данной поверхности.
Взаимно параллельные плоские фигуры, ограниченные цилиндрической поверхностью, называются основаниями цилиндра.
Если нормальное сечение (плоскость сечения перпендикулярна образующим) имеет форму окружности, то цилиндрическая поверхность называется круговой.
Если образующие цилиндрической поверхности перпендикулярны к основаниям, то цилиндр называется прямым, в противном случае – наклонным.
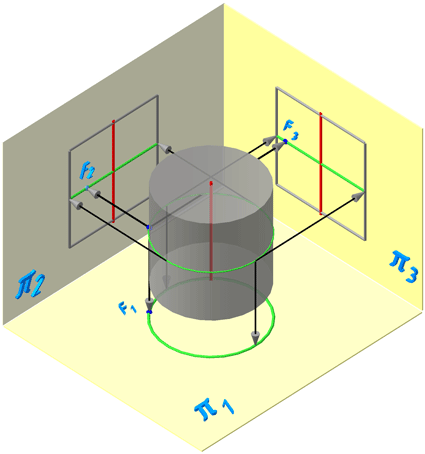
Рассмотрим проецирование прямого кругового цилиндра и принадлежащей ему точки F.
Условимся, что фронтальная проекция точки F – невидима (Рисунок 7.6).
Рисунок 7.6 – Проецирование цилиндра на плоскости проекций
Горизонтальная и профильная проекции точки F будут видимы.
При определении видимости, образующие, которые находятся на части, обращённой к наблюдателю и обозначенной на π1 сплошной зелёной линией – на плоскости проекции π2 видны, а которые находятся на части, обозначенной толстой штриховой линией – видны на π3.
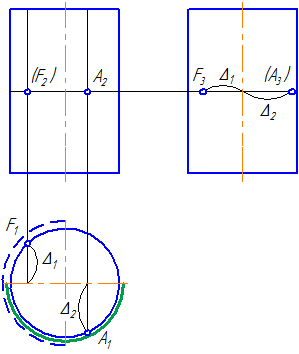
Пусть точка А на π2 видима (Рисунок 7.7). Тогда на π1 она будет видима, а на π3 невидима.
Рисунок 7.7 – Эпюр прямого кругового цилиндра и принадлежащих ему точек
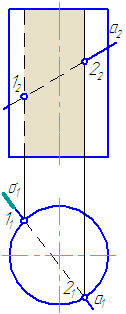
7.4. Пересечение прямой с поверхностью прямого кругового цилиндра
Для построения точек пересечения прямой линии с поверхностью прямого кругового цилиндра не требуется дополнительных построений. На горизонтальной плоскости проекций точки пересечения (1 и 2) находятся сразу. Фронтальные проекции строим по линиям связи.
Но в общем случае, алгоритм решения рассмотрим на следующем упражнении.
Рисунок 7.8 – Пересечение прямой с поверхностью прямого кругового цилиндра
Упражнение
Заданы: прямой круговой цилиндр с осью вращения, перпендикулярной плоскости проекций π1 и прямая а общего положения (Рисунок 7.8).
Построить точки пересечения прямой а с поверхностью цилиндра.
Решение:
Для построения точек пересечения прямой с поверхностью цилиндра необходимо:
- Заключить прямую во вспомогательную секущую плоскость частного положения σ (горизонтально-проецирующую).
- Построить фигуру пересечения поверхности цилиндра горизонтально-проецирующей плоскостью: результат пересечения — четырехугольник (на π2 условно заштрихован).
- Найти точки «входа» и «выхода» прямой: на пересечении её фронтальной проекции с фронтальными проекциями сторон четырёхугольника (они же — проекции образующей цилиндра);
Прямая а пересекается со сторонами сечения в двух точках – 1 и 2.
Определим видимость участков прямой: очевидно, что между точками 1-2 прямая невидима, а на плоскости проекций π2 будет ещё невидим участок прямой от точки 1 до левой крайней образующей.
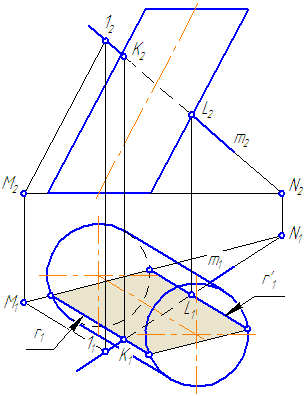
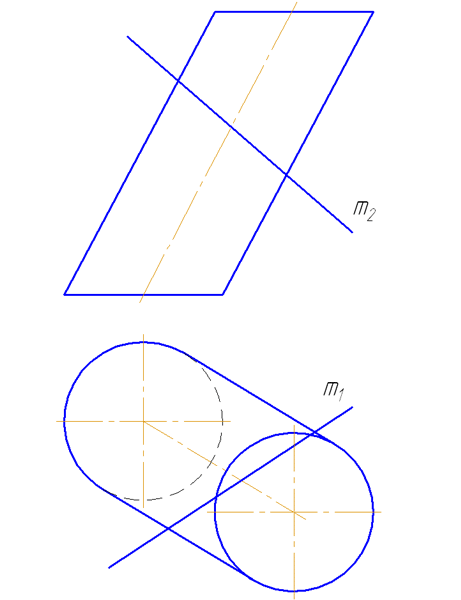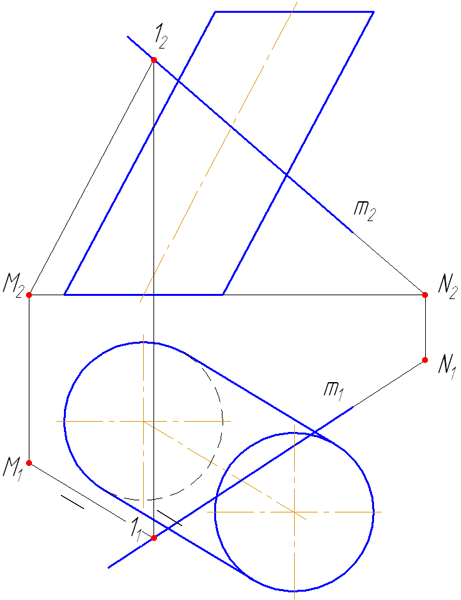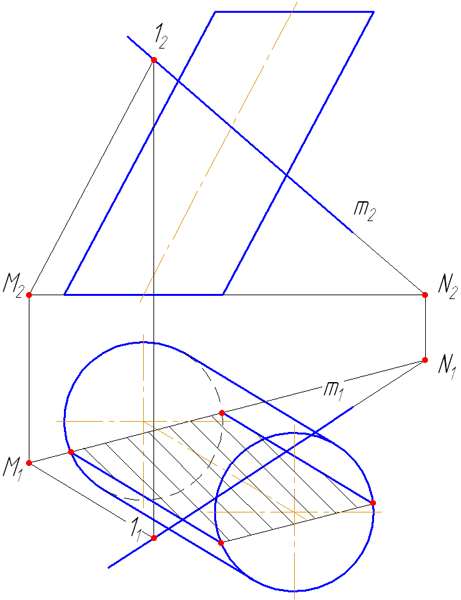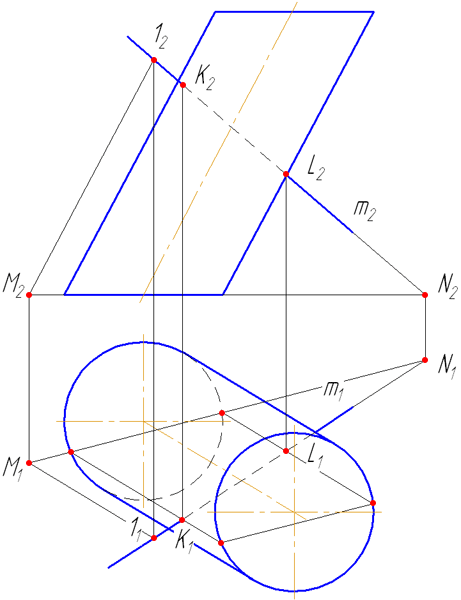
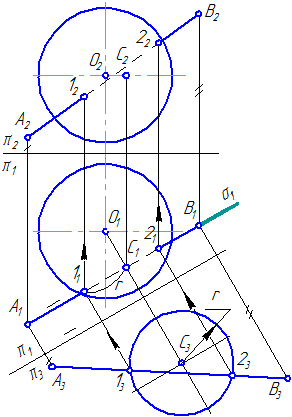
7.5. Пересечение прямой с поверхностью наклонного цилиндра
Упражнение
Заданы: наклонный круговой цилиндр с осью вращения, наклонной к плоскости проекций π1 и прямая mобщего положения (Рисунок 7.9).
Построить точки пересечения прямой mс поверхностью цилиндра.
Решение:
Для построения точек пересечения прямой с поверхностью цилиндра необходимо:
Рисунок 7.9 – Пересечение прямой с наклонным цилиндром
- Заключить прямую m во вспомогательную плоскость σ, дающую в сечении наиболее простую фигуру – четырехугольник (σ параллельна оси цилиндра или образующим). Эту плоскость зададим двумя пересекающимися прямыми m∩(1M);
- Построить горизонтальный след плоскости σ (прямую пересечения σ с плоскостью проекций π1) как проходящую через горизонтальные следы прямых m и (1M) (точки пересечения прямых с плоскостью проекций π1 (основания)) – (MN);
- Найти точки пересечения MN с окружностью основания цилиндра. Через эти точки провести образующие r, по которым плоскость σ пересекает боковую поверхность цилиндра:
На анимации ниже представлена последовательность построения точек пересечения прямой с наклонным цилиндром.
7.6. Сферическая поверхность
Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.
Шаром называется тело, ограниченное сферической поверхностью.
Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).
Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.
Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.
Рисунок 7.10 – Проецирование сферической поверхности
Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой.
Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек
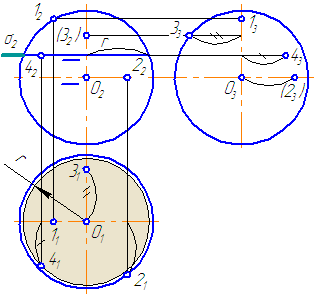
Упражнение
Заданы: сферическая поверхность тремя проекциями (Рисунок 7.11) и фронтальные проекции точек 1, 2, 3, 4.
Необходимо построить горизонтальные и профильные проекции заданных точек.
Решение.
- Проанализируем их расположение на поверхности сферы. Точки 1, 2, 3 лежат на очерковых образующих сферы.
- Точка 1 принадлежит главному меридиану (очерковой окружности на π2), проекция которого на π1 совпадает с проекцией горизонтальной оси, на π3 – с проекцией вертикальной оси.
- Недостающие проекции точки 1 находим посредством линий проекционной связи. Все проекции точки 1 видимы.
- Рассмотрим положение точки 2. Точка 2 принадлежит экватору (очерковой окружности на π1), проекции которого на π2 и π3 совпадают с проекцией горизонтальной оси. Горизонтальная проекция точки 2 строится посредством линии проекционной связи, для построения профильной проекции необходимо измерить расстояние, отмеченное дугой, и отложить его по линии связи от точки О3 вправо. Профильная проекция точки 2 невидима.
- Точка 3 принадлежит очерковой окружности на π3, которая также является меридианом, проекции которого на π2 и π1 совпадают с проекцией вертикальной оси. Профильная проекция точки строится посредством линии проекционной связи. Для построения горизонтальной проекции точки 3 необходимо расстояние, отмеченное на π3 двумя засечками, отложить на π1 вверх от точки О1. Горизонтальная и профильная проекции точки 3 видимы.
- Для построения проекций точки 4 необходимо ввести вспомогательную секущую плоскость (зададим плоскость σ//π1 и σ⊥π2). Плоскость σ пересекает поверхность сферы по окружности радиусом r. На π1 строим данное сечение и по линии проекционной связи находим 41. Для построения профильной проекции необходимо расстояние, отмеченное засечкой, отложить по линии проекционной связи на π3 вправо от оси. Все проекции точки 4 видимы.
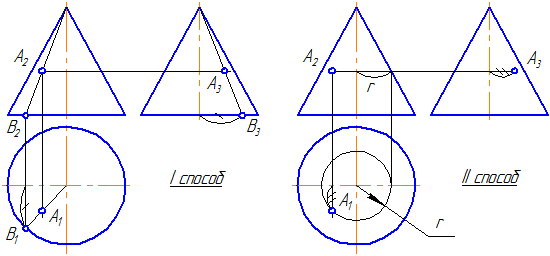
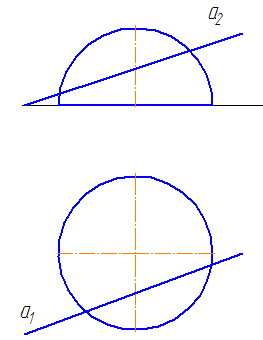
7.7. Пересечение прямой с поверхностью сферы
Упражнение
Заданы: сфера и прямая общего положения АВ.
Найти: точки пересечения прямой с поверхностью сферы (точки «входа» и «выхода»).
Чтобы найти точки пересечения прямой с поверхностью сферы необходимо:
- Заключить прямую во вспомогательную плоскость, пересекающую поверхность сферы так, чтобы получались простые фигуры (например, круг, ограниченный окружностью);
- Построить фигуру пересечения сферы вспомогательной плоскостью;
- Найти общие точки прямой и контура фигуры (окружность): так как прямая и окружность лежат в одной плоскости, то они, пересекаясь, образуют точки, общие для прямой и сферы, которые и будут являться искомыми точками (Рисунок 7.12).
Решение
- Через прямую проводим плоскость σ. Пусть σ⊥π1 и пересекает сферу по окружности радиусом r. С – центр окружности сечения ОС⊥σ:
Рисунок 7.12 – Пересечение прямой с поверхностью сферы
- Введём π3⊥π1 и π3//σ1. Построим проекцию окружности сечения на π3 и проекцию А3В3.
- Находим точки их пересечения 12 и 23.
- Определим видимость участков прямой.
- На π1 точки 1 и 2 находятся на переднем полушарии, следовательно, на π2 они видимы.
7.8. Коническая поверхность
Коническая поверхность образуется движением прямой линии (образующей), которая в любом своем положении проходит через неподвижную точку и пересекает криволинейную направляющую (имеет две полости).
Тело, ограниченное замкнутой конической поверхностью вершиной и плоскостью, называется конусом.
Плоская фигура, ограниченная конической поверхностью, называется основанием конуса.
Часть конической поверхности, ограниченная вершиной и основанием, называется боковой поверхностью конуса.
Если основание конуса является кругом, то конус называется круговым.
Если вершина конуса расположена на перпендикуляре к основанию, восстановленному из его центра, то конус называется прямым круговым.
Перемещая точку A» — можно изменять диаметр основания конуса;
перемещая точку O’ — можно менять положение точки на поверхности конуса.
Рисунок 7.13 – Принадлежность точки конической поверхности
Рассмотрим вопрос принадлежности точки А поверхности конуса.
Дана фронтальная проекция точки А и она видима (Рисунок 7.13).
1 способ. Для построения ортогональных проекций точки, расположенной на поверхности конуса, построим проекции образующей, проходящей через данную точку. При таком положении точки А все её проекции – видимы.
2 способ. Точка А лежит на параллели конуса радиусом r. На π1 строим проекцию окружности (параллели) и по линии проекционной связи находим А1. По двум проекциям точки строим третью.
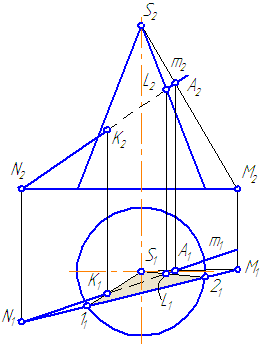
7.9. Пересечение прямой с поверхностью конуса
Пусть задан прямой круговой конус и прямая общего положения m (Рисунок 7.14). Найти точки «входа» и «выхода» прямой с поверхностью конуса.
- Через прямую m проводим вспомогательную секущую плоскость σ, дающую в сечении наиболее простую фигуру.
- Применение в качестве вспомогательной секущей плоскости проецирующей плоскости в данном случае нецелесообразно, так как в сечении получится кривая второго порядка, которую нужно строить по точкам.
Наиболее простая фигура – треугольник. Для этого секущая плоскость σ должна пройти через вершину S. Плоскость зададим с помощью двух пересекающихся прямых σ=SM∩MN или, что, то же самое, (σ=SM∩m).
- Возьмем на прямой m точку А и соединим её с вершиной. Прямая SA пересечёт плоскость основания в точке М.
- Построим горизонтальные проекции этих объектов.
- Продлим фронтальную проекцию прямой m до пересечения с плоскостью основания в точке N.
Рисунок 7.14 – Построение точек пересечения прямой с поверхностью конуса
- Построим её горизонтальную проекцию.
- Соединим точки M1N1, на пересечении с окружностью основания получим точки 1 и 2.
- Строим треугольник сечения конуса плоскостью σ, соединив точки 1 и 2 с вершиной S.
- На пересечении образующих 1-S и 2-S с прямой m получим искомые точки K и L.
- Определим видимость прямой относительно поверхности конуса.
На анимации ниже представлена последовательность построения точек пересечения прямой с поверхностью конуса.
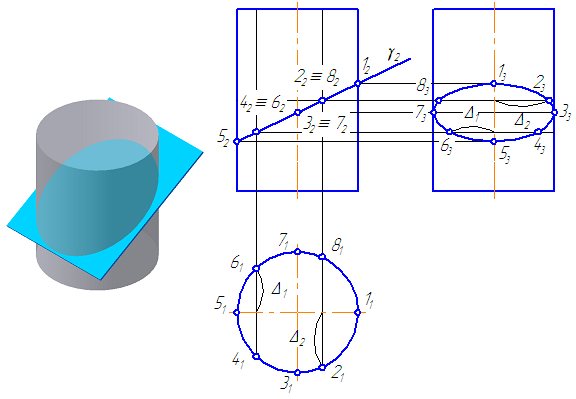
7.10. Пересечение цилиндра плоскостью
Пусть плоскость сечения γ – фронтально-проецирующая (Рисунок 7.15).
- Если плоскость сечения γ параллельна оси цилиндра, то она пересекает цилиндр по четырехугольнику.
- Если плоскость сечения γ перпендикулярна оси цилиндра, то она пересекает цилиндр по окружности.
- Если плоскость сечения γ не параллельна и не перпендикулярна оси цилиндра в сечении эллипс.
Рассмотрим алгоритм построения сечения – эллипс (Рисунок 7.15):
Рисунок 7.15 – пересечение цилиндра плоскостью
- Находим и строим характерные точки (точки, не требующие дополнительных построений) – в нашем случае, точки принадлежащие крайним образующим – 1, 3, 5, 7. Одновременно с этим, данные точки определяют величину большой и малой оси эллипса.
- Для построения участка эллипса необходимо построить не менее 5-ти точек (так как лекальная кривая второго порядка определяется как минимум пятью точками). Для построения точек 2, 4, 6, 8 возьмем на π1 произвольно расположенные образующие цилиндра, которые проецируются на данную плоскость проекции в точки.
- Построим вторые проекции данных образующих. Из точек пересечения вторых проекций образующих с проекцией плоскости сечения γ проводим линии связи к π3. Для построения третьей проекции, например, точки 6 измеряем расстояние Δ1 и откладываем его по соответствующей линии связи на π3. Симметрично ей, относительно оси вращения, строим точку 4. Аналогично строятся другие точки.
7.11. Пересечение сферы плоскостью
Плоскость пересекает поверхность сферы всегда по окружности. Задачу пересечения плоскости со сферой мы рассматривали при решении задачи построения точек пересечения прямой с поверхностью сферы (см. выше).
7.12. Пересечение конуса плоскостью
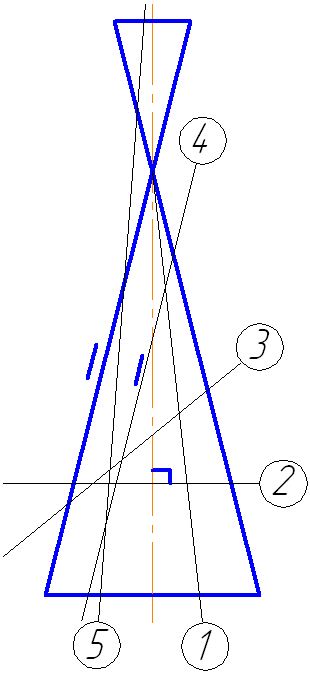
Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π2 (Рисунок 7.16).
Рисунок 7.16
- Если плоскость проходит через вершину (1) – в сечении две образующие и прямая пересечения с плоскостью основания.
- Если плоскость перпендикулярна оси вращения конуса (2) – в сечении окружность.
- Если плоскость не параллельна ни одной образующей (пересекает все образующие (3)) – в сечении эллипс.
- Если плоскость параллельна одной образующей конуса – в сечении парабола (на примере – плоскость сечения (4) параллельна крайней образующей конуса).
- Если плоскость параллельна двум образующим (пересекает обе полости конической поверхности (5)) – в сечении гипербола (рисунок 7.17).
Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса
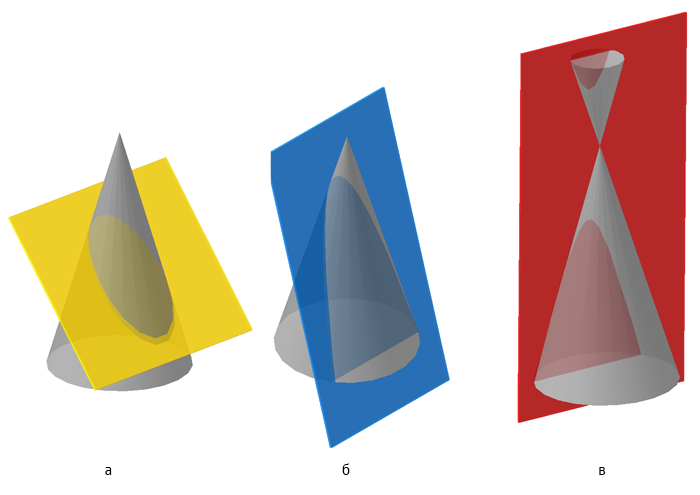
Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.
Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)
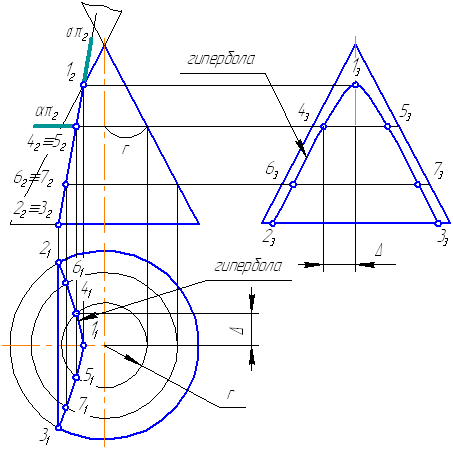
Рассмотрим пример построения сечения конической поверхности плоскостью.
Рисунок 7.19 – Построение пересечения конической поверхности плоскостью
Пусть задана секущая проецирующая плоскость σ⊥π2 (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.
- Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.
- Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π2 и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π1. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π1 и π3 совпадают с линиями проекционной связи.
- На пересечении этих двух сечений на плоскости проекций π1 строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.
- Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.
- Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.
На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.
7.13. Задачи для самостоятельной работы
1. Достроить проекции сферы с заданным вырезом (Рисунок 7.20).
Рисунок 7.20
2-3. Построить три проекции конуса с призматическим отверстием (Рисунки 7.21, 7.22).
Рисунок 7.21
Рисунок 7.22
4. Построить точки «входа» и «выхода» прямой при пересечении её с поверхностью полусферы (Рисунок 7.23).
Рисунок 7.23
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
3 способ. Использование функции CreateMesh() . Встроенная функция в MathCAD для построения графика поверхности. Создает массив, представляющий х-, у- и z-координаты параметрической поверхности, заданной функцией F(). Создает сетку на поверхности определенной функции F() с параметрами , заданными аргументами.
M=CreateMesh (F, x0, x1, y0, y1, xgrid, ygrid, fmap),
F— функция,
x0, x1, y0, y1 – диапазон изменения переменных x и y,
xgrid, ygrid – количество точек переменной х и количество точек переменной y (размеры сетки переменных), количество точек можно задать один раз.
fmap – векторная функция от трех аргументов, задающая преобразование координат, определяет систему координат: декартову, сферическую или цилиндрическую. Если параметр присутствует, то график будет построен в указанной системе координат. Для графика в декартовой системе этот аргумент можно не вводить.
Имеются две встроенные графические функции, которые могут использоваться в аргументах fmap: sph2xyz и syl2xyz.
cyl2xyz – функция преобразования координат из цилиндрической системы в декартову;
ph2xyz – функция преобразования координат из сферической системы в декартову.
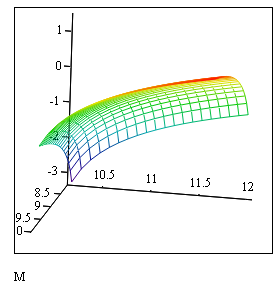
На pис.3.26 показано построение графика функции примера с применением CreateMesh() . Указаны границы изменения x – от 8,2 до 10, границы изменения y, – от 10,2 до 12 количество точек сетки – 20 для x и для y. График строится от значений x и y.
Рис.
3.26.
Листинг построения графика поверхности примера 3.10 с использованием функции CreateMesh()
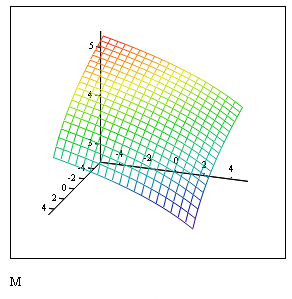
Если не указать параметры сетки, функция CreateMesh по умолчанию создает сетку на поверхности с диапазоном изменения переменных от -5 до 5 и с сеткой 20×20 точек. M=CreateMesh (W) (Рис.3.27).
Рис.
3.27.
Листинг построения графика поверхности примера 3.10 с использованием функции CreateMesh() (параметры по умолчанию)
Построение поверхности, заданной параметрически
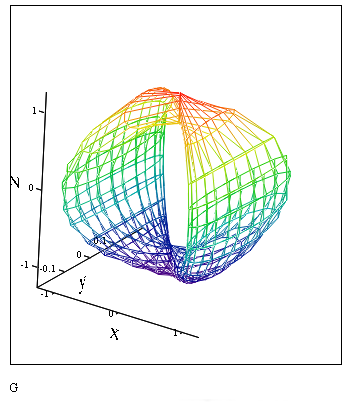
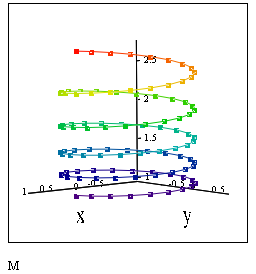
При построении трехмерных поверхностей и объемных фигур можно использовать параметрическое задание описывающих их функций. При этом все три координаты задаются как функции от двух параметров u и v – X(u,v), Y(u,v), Z(u,v). Поверхности задаются значениями координат всех точек. При этом в шаблоне графики указываются три матрицы, хранящие массивы этих координат, X, Y Z.
Пример 3.11
На pис.3.28 показано построение объемной фигуры по точкам. (50 точек). Фигура задана параметрически, параметры – углы 

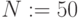
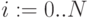
Рис.
3.28.
Листинг примера. 3.11. Поверхность задана параметрически
Построение поверхности, заданной в векторной параметрической форме
Поверхность может быть задана в векторной форме. В этом случае функция вводится в виде матрицы, элементы которой – функции параметров, как и сама поверхность. На pис.3.27 показано построение объемной фигуры примера 3.11, заданной в виде матрицы от параметров — углов 

Рис.
3.29.
Листинг примера. 3.11. Функция задана в векторной параметрической форме
3.3.2. 3D точечный график
Трехмерный график можно представить в виде пространственной кривой. Пространственные кривые задаются, как правило, параметрически, и параметр является непрерывной действительной величиной. Рассмотрим два способа построения.
Пример 3.12
Построить пространственную кривую, у которой координаты определены следующим образом: 


1 способ. Кривая в пространстве задается аналогично параметрическому заданию поверхности (пример 3.11).
- Задать значения параметра t в виде ранжированной переменной, для t выбирается номер точки (0-100).
- Определить координаты x, y, z как индексированные переменные параметра t.
- Вызвать командой с панели Графика Graph / 3D Scatter Plot (график 3D точечный), в шаблон занести имена матриц в скобках (Рис.3.28).
- Настроить график в окне форматирования.
На графике показаны максимальные минимальные значения
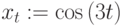

Рис.
3.30.
Листинг примера 3.12. Параметрическое задание кривой
2 способ. (Рис.3.31). Векторная форма. Функция задается в виде матрицы-вектора. Для построения графика используется функция CreateSpace()
CreateSpace (R , t0, t1, tgrid, fmap): встроенная функция , создающая массив представляющий х-, у- и z-координаты параметрической пространственной кривой, заданной функцией R() ; и сетку точек на кривой, определенной функцией R() с параметрами , заданными аргументами ,
t0 и t1 – диапазон изменения параметровй, tgrid – размер сетки переменной, fmap – функция отображения аналогично функции CreateMesh() (необязательный параметр). Аргумент t выбирается из указанного интервала: t0=0 t1=10, сетка tgrid=100 точек. Создает сетку точек на кривой.
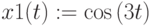

Рис.
3.31.
Листинг примера 3.12. Векторное задание кривой. Использование CreateSpace()
Основные итоги
Представлены методы построения графиков функций одной переменной и двух переменных в различных системах координат. На многих примерах показаны различные варианты задания функции, определяющие график: обычным образом (аргументы –скаляры), параметрически, а также в виде матриц и ранжированных переменных. Рассмотрены различные способы построения: автоматическое построение, с построением сетки, с использованием функций CreateMesh() и CreateSpace(). Описаны способы форматирования и настройки графика.
Задания для самостоятельного выполнения
- Построить в декартовых координатах на одном шаблоне графики функций:
,
,
,
.
- Выбрать пределы изменения x и функции автоматически.
- Изменить пределы: для x и для функций, установить линии сетки, изменить вид кривых (различные линии, маркеры, толщину и т.д.), ввести легенду
- Построить график функции Y. Использовать условную функцию.
- Построить график – область определения функции
, в области вещественных чисел, где функция не существует, принять z=0
- Построить график функции
для табулированных значений x, [-10;10] с шагом=0.5. Показать значения x y. Показать точки на графике.
- Построить график функции
для 20 точек табулированных значений x, [-10;10] с шагом=1. Аргумент и функцию ввести как индексные переменные
и
Показать значения
и
. Показать точки на графике. Ввести линию x=0 в точке особенности как риску.
- Построить графики и вычислить площадь плоской фигуры, ограниченной линиями
и
:
а),
б),
- Построить графики кривых, заданных параметрически. Оформить. Показать линии сетки.
а)и
для t на интервале
с шагом =0.01.
б)b
для t на интервале [-20;20].
- Построить в полярных координатах на одном графике : архимедову спираль
, логарифмическую спираль
, кардиоду
, (параметры задайте сами).
меняется с шагом 0,1 в пределах:
- Построить в полярных координатах
,
,
меняется с шагом 0,01 в пределах:
.
- Показать область определения функции
. Построить график в полярных координатах. В области вещественных чисел, где функция не существует, принять R=0,5.
- Построить график в полярных координатах функции
,
,
меняется от 0 до 8
с шагом 0.05.
- Построить графики поверхности функции:
. Параметры a и b введите сами. Показать максимальные и минимальные значения, ввести линии сетки.
а) в общем виде,
б) с помощью сетки и индексированных переменных, по 30 точкам. Пределы: для x : 0 – 5, для y: 0-1,8.
в) с помощью функции CreateMesh() - Построить график
. Показать максимальные и минимальные значения.
- Построить фигуру, заданную параметрически, с помощью сетки по 30 точкам , N=30.
Параметры – углыи
. Угол
меняется с шагом
, угол
с шагом
:
,
.
,
,
.
Ввести индексы для углови
как ранжированные переменные
Ввести углыи
как индексные переменные
Построить матрицы X , Y и Z как двумерные индексные переменные - Построить область определения функций:
,
.
Ключевые термины
Graph — панель графики.
Formatting Currently Selected X-Y Plot – окно форматирования двумерного графика.
trace — опция форматирования, позволяющая ет точно определить значение функции в любой точки графика.
if(cond, x, y) — условная функция.
параметрическое задание функции — устанавливается зависимость (x,y) точки плоскости от значения параметра t.
полярный график — график функции r(q), заданной в полярных координатах, где полярный радиус r зависит от полярного угла q.
3-D Plot Format — окно форматирования трехмерного графика.
CreateMesh () — встроенная функция в MathCAD, создающая массив, представляющего х-, у- и z-координаты поверхности, заданной функцией F(); и сетку на поверхности определенной функции F() с параметрами , заданными аргументами.
CreateSpace ()— встроенная функция в MathCAD создающая массив представляющий х-, у- и z-координаты параметрической пространственной кривой, заданной функцией R() ; и сетку точек на кривой, определенной функцией R() с параметрами , заданными аргументами .
Surface Plot — опция панели Graph для построения графика поверхности
3D Scatter Plot — опция панели Graph для построения 3-D точечного графика.





















 :
:



 а радиус
а радиус  тогда уравнение сферы будет:
тогда уравнение сферы будет:
 и радиус
и радиус  тогда уравнение сферы будет:
тогда уравнение сферы будет: 













 — называются полуосями эллипсоида.
— называются полуосями эллипсоида.






































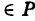
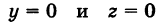
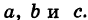

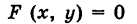
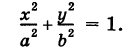

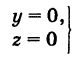
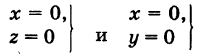
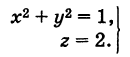
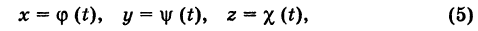
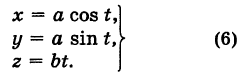

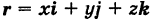


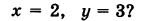
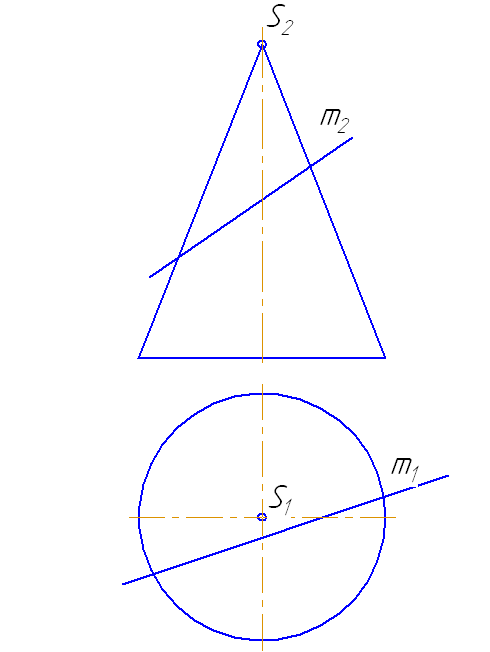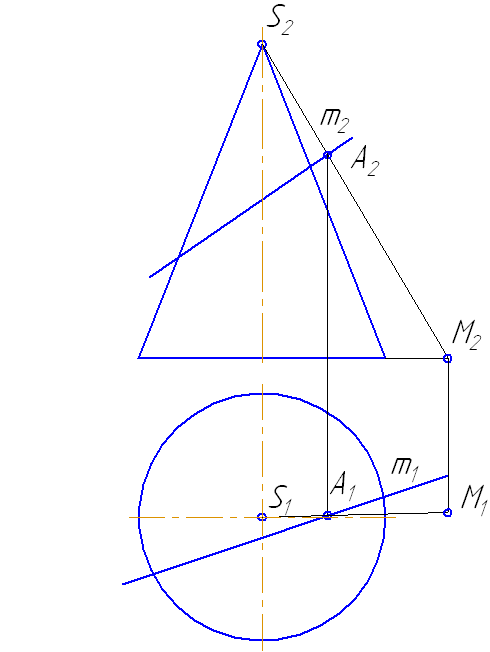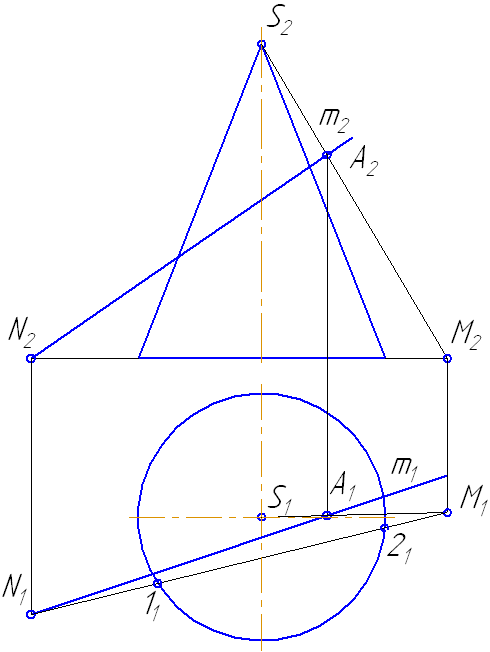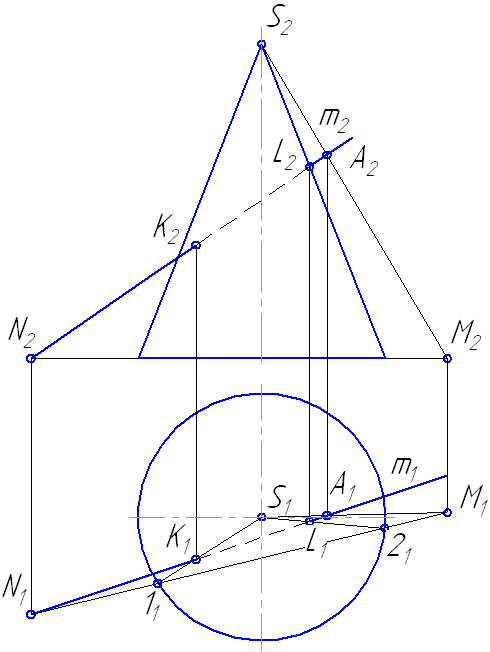

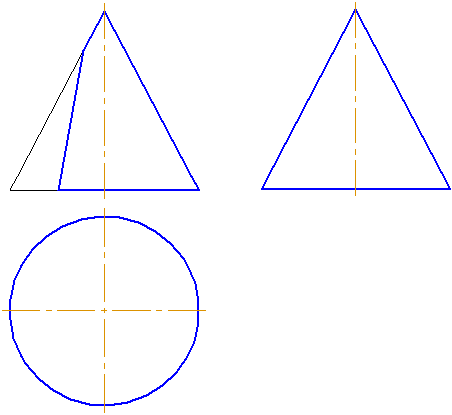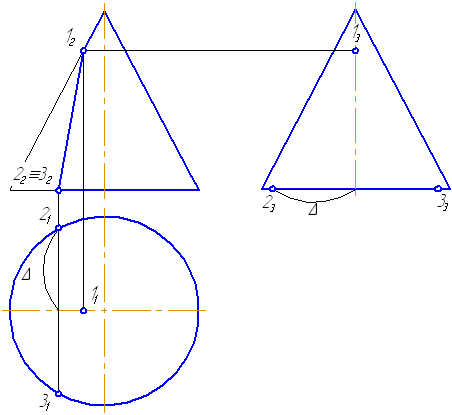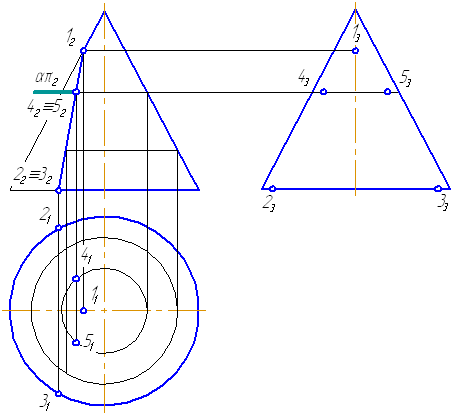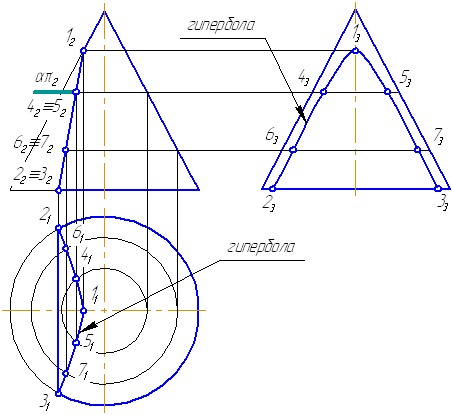
![W(x,y):=ln[(x-8)(y-10)]](https://intuit.ru/sites/default/files/tex_cache/0fdde979008294565c4bce2e6b0e35ad.png)
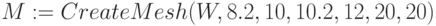
![W1(x,y):=ln[(x-8)(y-10)]](https://intuit.ru/sites/default/files/tex_cache/bde19a4e1389d485cacb387c39c66c52.png)

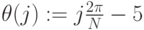

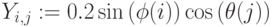
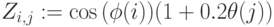

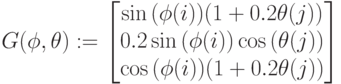
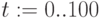
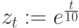


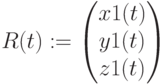

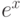 ,
, 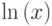 ,
,  ,
, 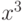 .
.
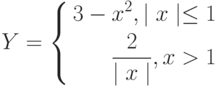
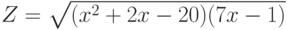 , в области вещественных чисел, где функция не существует, принять z=0
, в области вещественных чисел, где функция не существует, принять z=0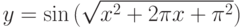 для табулированных значений x, [-10;10] с шагом=0.5. Показать значения x y. Показать точки на графике.
для табулированных значений x, [-10;10] с шагом=0.5. Показать значения x y. Показать точки на графике.  для 20 точек табулированных значений x, [-10;10] с шагом=1. Аргумент и функцию ввести как индексные переменные
для 20 точек табулированных значений x, [-10;10] с шагом=1. Аргумент и функцию ввести как индексные переменные  и
и 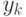 Показать значения
Показать значения 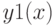 и
и  :
: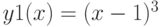 ,
, 
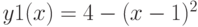 ,
, 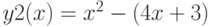
 и
и 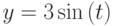 для t на интервале
для t на интервале ![[{0;3frac{pi}{2}}]](https://intuit.ru/sites/default/files/tex_cache/f261bfab3030470c281699e172a53d5d.png) с шагом =0.01.
с шагом =0.01.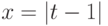 b
b 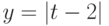 для t на интервале [-20;20].
для t на интервале [-20;20]. 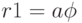 , логарифмическую спираль
, логарифмическую спираль  , кардиоду
, кардиоду 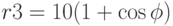 , (параметры задайте сами).
, (параметры задайте сами). 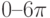
 ,
,  ,
,  меняется с шагом 0,01 в пределах:
меняется с шагом 0,01 в пределах: 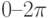 .
.  . Построить график в полярных координатах. В области вещественных чисел, где функция не существует, принять R=0,5.
. Построить график в полярных координатах. В области вещественных чисел, где функция не существует, принять R=0,5.  ,
,  ,
, 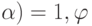 меняется от 0 до 8
меняется от 0 до 8  с шагом 0.05.
с шагом 0.05.  . Параметры a и b введите сами. Показать максимальные и минимальные значения, ввести линии сетки.
. Параметры a и b введите сами. Показать максимальные и минимальные значения, ввести линии сетки.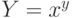 . Показать максимальные и минимальные значения.
. Показать максимальные и минимальные значения.  и
и  . Угол
. Угол  , угол
, угол  :
: ,
, .
. ,
,  ,
, 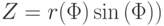 .
.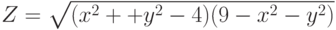 ,
, 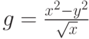 .
.