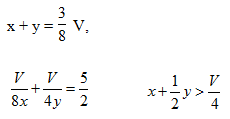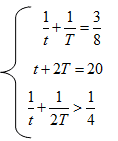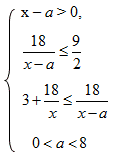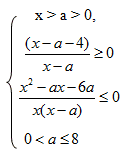Цель: показать способы решения задач с помощью неравенств.
- На выпускных экзаменах по математике часто предлагают задачи, в которых условие задано в форме некоторого текста, как правило, без формул и даже без буквенных обозначений неизвестных. Для решения таких задач на основе условий, предъявленных в тексте, требуется составить уравнения (неравенства) или систему уравнений (неравенств), а затем решить их. Интерес к таким задачам вполне понятен, они способствуют развитию логического мышления, умения самостоятельно проводить небольшие исследования.
- Текстовые задачи отличаются большим разнообразием содержания и могут существенно различаться по уровню сложности. Стандартные текстовые задачи, в которых условия записываются в виде уравнений, число которых равно числу неизвестных, обычно не вызывают особых затруднений, хотя и здесь могут встретиться непредвиденные сложности. Что же касается «нестандартных» по содержанию задач, то при их решении часто возникают трудности, объяснимые именно их непривычностью, необходимостью анализировать, рассуждать, а не просто формально решать системы уравнений или неравенств.
Приведу несколько советов, полезных при решении текстовых задач на составление уравнений и неравенств:
- Внимательно, может быть не один раз, прочитайте условие задачи с тем, чтобы стало понятно ее содержание.
- Часто бывает полезно сделать рисунок с отмеченными на нем числовыми данными.
- При очередном прочтении задачи нужно постепенно вводить неизвестные, при необходимости отмечая их размерности. При этом буквенные обозначения неизвестных должны быть удобны, например, вызывать ассоциации со стандартными обозначениями в физике, химии и т.д. Выбор неизвестных должен быть, в первую очередь, удобен для математической записи условий задачи, а не ориентирован на ее вопрос.
- При очередном прочтении задачи нужно записывать связи между известными и неизвестными величинами в виде уравнений и неравенств.
- Перед решением системы уравнений или неравенств нужно определить искомую величину, имея ввиду, что часто из полученной системы требуется найти только одну неизвестную или некоторую комбинацию неизвестных, что может быть сделано далеко не всегда.
- Если система допускает несколько решений, то проверить каждое из них. Чтобы учащиеся привыкли к задачам, требующих составления неравенств, я предлагаю им на уроке простые задачи. Их можно использовать для проверки теоретического материала, устного счета и т. д. Например:
Задача. Одно из натуральных чисел на 4 меньше другого. Причем квадрат меньшего из чисел не больше, чем удвоенное второе число. Найдите меньшее число из данных чисел.
- Что надо сделать, чтобы ответить на вопрос задачи? (Построить ее математическую модель.)
х2 ≤2(х + 4). - Что представляет математическая модель этой задачи? (Неравенство).
- Что такое неравенство?
- Какие виды неравенств вы знаете? (Линейные неравенства, квадратные неравенства, рациональные неравенства, неравенства, содержащие знак модуля).
- Что называется решением неравенства? (Значение переменной х, которое обращает неравенство f(x) >0 в верное числовое неравенство, называют решением неравенства).
- Что значит решить неравенство? (Решить неравенство, значит найти все его решения или доказать, что их нет).
- Какие правила используют при решении неравенств? (Правила равносильных преобразований).
- К какому виду относится данное неравенство? (Квадратное)
- Какие методы решения квадратных неравенств вы знаете? Решите полученное неравенство.
Текстовые задачи традиционно вызывают затруднения у школьников, многим из которых не удается правильно составить уравнение или неравенство по условию задачи. Учителю математики в такой ситуации почти невозможно организовать самостоятельную работу школьников, постоянно нуждающихся в указаниях и подсказках. Поэтому на уроках я предлагаю таким ученикам карточки с задачами, которые сопровождаются указаниями, следуя которым даже слабый ученик сможет получить правильный ответ, а для сильных учеников предусмотрены дополнительные вопросы. Например:
Задача. Сплав олова и меди, масса которого 16 кг, содержит 55% олова. Сколько килограммов олова нужно добавить, чтобы повысить содержание олова в сплаве до 60%?
Решение.
Обозначив искомую массу олова буквой х, выразите:
а) сколько килограммов олова было в сплаве сначала;
б) сколько килограммов олова стало в сплаве после добавления;
в) массу полученного сплава;
г) отношение массы олова к массе полученного сплава.
Запишите уравнение, решите его и ответьте на вопрос задачи.
Дополнительные вопросы.
- Какова масса меди, содержащейся в сплаве?
- Сколько килограммов меди следовало бы добавить в первоначальный сплав, чтобы содержание меди составило 50%?
Задачи на уроке предлагаются по нарастающему уровню сложности, самые трудные можно предложить на факультативных занятиях.
Задача 1.
Две трубы, действуя вместе в течение одного часа, наполняют водой 3/8 бассейна. Если сначала первая труба наполнит одну восьмую часть бассейна, а затем вторая при выключенной первой доведет объем до 3/8 бассейна, то на это потребуется 2,5 часа, если первую трубу включить на час, а вторую – на полчаса, то они наполнят бассейн более чем на четверть. За какое время наполняет бассейн каждая труба?
Ход решения.
1. Составление математической модели.
х л/час – производительность первой трубы;
у л/час – производительность второй трубы;
V л – объем бассейна.
Тогда условие задачи можно записать следующим образом
t = V/x, T = V/y. Тогда систему можно переписать так
Математическая модель готова.
2. Работа с математической моделью.
1) Из второго уравнения имеем t = 20 – 2T.
2) Подставляем в первое уравнение, получаем уравнение относительно T
3T2 — 34 T + 80 = 0.
Корни данного уравнения: T = 8 или T = 10/3.
3) Тогда решениями данной системы первых двух уравнений являются
Последнему неравенству системы удовлетворяет лишь первое решение.
3. Ответ на вопрос задачи.
Первая труба заполнит бассейн за 4 часа, а вторая – за 8 часов.
Ответ: 4 часа, 8 часов.
Задача 2.
Из города А в 9 часов утра выехал велосипедист и двигался с постоянной скоростью 12 км/ч. Спустя 2 часа вслед за ним из А выехал мотоциклист, который при начальной скорости 22 км/ч двигался равнозамедленно, так, что за час его скорость уменьшается на 2 км/ч. Автомобилист, едущий им навстречу в город А с постоянной скоростью 50 км/ч, сначала встретил мотоциклиста, а потом велосипедиста. Успеет ли автомобилист к 19 часам этого дня прибыть в город А?
Ход решения.
1. Составление математической модели.
По условию задачи автомобилист встретит сначала мотоциклиста, а затем велосипедист. Следовательно, мотоциклист некоторый участок пути пройдет впереди велосипедиста. Именно на этом участке пути произойдут их встречи с автомобилистом. Найдем этот участок.
Пусть х ч – время, отсчитываемое от 9 часов утра, тогда
12х км – путь пройденный велосипедистом,
км – путь пройденный мотоциклистом.
Приравнивая эти два пути, найдем соответствующие значения х, при которых мотоциклист и велосипедист обгонят друг друга.
12 х =
2. Работа с математической моделью
12 х =
t2 – 14t + 48 = 0,
t1 = 6, t2 = 8.
3. Ответ на вопрос задачи.
Следовательно, мотоциклист обгонит велосипедиста в 15 часов дня на расстоянии 72 км от города А, а затем велосипедист обгонит мотоциклиста в 17 часов на расстоянии 96 км от города А. Итак, автомобилист, двигающийся со скоростью50 км/ч, ранее 17 часов был на расстоянии менее 96 км от города А, следовательно, он успеет к 19 часам прибыть в город А.
Ответ. Успеет.
Задача 3.
Из пункта А в пункт В, расстояние между которыми равно 18 км, в 8 часов выходит пешеход, в 11 часов выезжает велосипедист. Известно, что пешеход прибыл в пункт В не позже, чем в 12 часов 30 минут, а велосипедист прибыл в пункт В не позже пешехода. Считая скорости пешехода и велосипедиста постоянными, определить скорость велосипедиста, если она не более, чем на 8 км/ч превышает скорость пешехода.
Ход решения.
1. Составление математической модели.
Необычность условий этой задачи состоит в том, что на их основе нельзя составить ни одного уравнения, а решение сводится к рассмотрению системы неравенств.
х км/ч – скорость велосипедиста,
а км/ч – разность скоростей велосипедиста и пешехода,
(х – а) км/ч – скорость пешехода. Тогда получим
2. Работа с математической моделью.
Из второго неравенства, учитывая первое, получим
х ≥ а + 4.
Рассмотрим третье неравенство.
Корни квадратного трехчлена х2 – ах – 6а
есть
х1,2 =

Применяя метод интервалов с учетом первого неравенства, получим
a < x <
Объединяя результаты, имеем, что значение х должно удовлетворять следующему неравенству
а + 4 ≤ х ≤
Чтобы существовали такие значения х, необходимо и достаточно, чтобы выполнялось неравенство
а + 4 ≤ х ≤
или
а + 8 ≤
,
откуда а ≥ 8.
Учитывая, что по условию а ≤ 8, получим, что а = 8. При этом последнее неравенство для х дает
откуда х = 12.
3. Ответ на вопрос задачи.
Скорость велосипедиста 12 км/ч.
Ответ: 12 км/ч
Задача 4.
На реке, скорость течения которой равна 4 км/ч, в направлении её течения расположены пристани А, В, С, причем расстояние от А до В вдвое меньше, чем расстояние от В до С. От пристани В в один и тот же момент по направлению к пристани С отправлены плот (плывущий относительно берегов со скоростью течения реки) и катер. Дойдя до пристани С, катер разворачивается и движется по направлению к пристани А. Найти все значения собственной скорости катера (т. е. скорости катера в стоячей воде), при которых катер приходит в пункт А не раньше, чем плот приходит в пункт С.
Ход решения:
1. Составление математической модели.
Пусть х км/ч – скорость катера в стоячей воде,
у км — расстояние от пристани А до пристани В.
ч – время движения катера из В в С,
— время движения катера из В в С и обратно из С в А против течения.
По условию
2. Работа с математической моделью.
Применим метод интервалов, учитывая, что x > 4.

Получим, что 4 < x ≤ 12.
3. Ответ на вопрос задачи.
Собственная скорость движения катера в стоячей воде должна быть в интервале (4; 12] км/ч.
Ответ: (4; 12] км/ч.
Задачи такого типа можно использовать при организации математических боев, математических рингов и других уроков обобщения знаний.
Презентация.
автор: Лобанова Людмила Викторовна
учитель математики МБОУ СОШ №2 Барабинского района Новосибирской области
«Текстовые задачи на решение неравенств и их систем в целых числах»
Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа №2 Барабинского района Новосибирской области
Исследовательская работа по математике
«Текстовые задачи на решение неравенств
и их систем в целых числах»
Выполнила:
ученица 8 «б» класса
Семениченко Алина
Руководитель:
учитель математики
высшей квалификационной категории
Лобанова Людмила Викторовна
Содержание:
- Цель и задачи……………………………………………..стр. 3
- Введение…………………………………………………..стр. 4
- Виды и методы решения задач…………………………..стр. 5-8
- Практическая часть………………………………………..стр. 9-11
- Примеры задач из сборника по подготовке к ЕГЭ………стр. 12
- Заключение…………………………………………………стр. 13
- Литература…………………………………………………стр. 14
Цель и задачи:
Цель: рассмотреть решение текстовых задач с помощью неравенств в целых числах.
Задачи:
– закрепить умения и навыки решать неравенства и системы неравенств;
– разобрать некоторые нестандартные приемы решения задач;
– научиться различать, видеть основные приемы, подходы решения неравенств и систем и применять их в традиционных и нетрадиционных примерах и задачах;
– воспитывать чувство уверенности в себе, своих силах.
Введение.
В задачах на составление уравнений и неравенств, их называют ещё текстовыми задачами, как правило, речь идёт о конкретных ситуациях из практической деятельности. Известно, что исторически долгое время математические знания передавались из поколения в поколение в виде списка задач практического содержания вместе с их решениями. При решении задач выписываются соотношения, представляющие собой математическую модель описанной в задаче практической ситуации. Таким образом, текстовые задачи позволяют проверить не только навыки в решении уравнений и неравенств, но и умение описывать с помощью математических соотношений реальные события. Решение таких задач способствует развитию логического мышления, умению самостоятельно проводить небольшие исследования. Этим и объясняется тот факт, что задачи на составление уравнений и неравенств являются непременным элементом вариантов вступительных экзаменов.
Виды и методы решения задач
Текстовая задача — это описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения.
Текстовые задачи отличаются большим разнообразием содержания и могут существенно различаться по уровню сложности. Стандартные текстовые задачи, в которых условия записываются в виде уравнений, число которых равно числу неизвестных, обычно не вызывают особых затруднений, хотя и здесь могут встретиться непредвиденные сложности. Что же касается «нестандартных» по содержанию задач, то при их решении часто возникают трудности, объяснимые именно их непривычностью, необходимостью анализировать, рассуждать, а не просто формально решать системы уравнений или неравенств.
Все текстовые задачи по методике решения можно подразделить на основные виды:
– текстовые задачи группы vts (задачи на движение, на производительность, на цену – количество, стоимость, на перевозку груза и заполнение ёмкостей);
– процентносодержащие текстовые задачи и задачи на доли (задачи на проценты и доли, задачи с экономическим содержанием);
– текстовые задачи на прогрессии (применение формул арифметической и геометрической прогрессий и свойств этих последовательностей);
– текстовые задачи на целые числа (использование кратности чисел и запись чисел через сумму поразрядных произведений и через неполное частное и остаток);
– текстовые задачи на оптимизацию (решение задач с помощью неравенств и элементов математического анализа).
Методика алгебраического способа решения текстовых задач (с помощью уравнений и неравенств).
Основные моменты:
| Этап | Цель | Форма записи |
| 1.Арифметическая краткая запись условий задачи. | Осмысление задачи. | Схематический чертёж или таблица всех известных и неизвестных данных задачи |
| 2. Алгебраическая краткая запись условий задачи. | Удачно выбрать переменную и выразить все неизвестные величины задачи через неё. | такая, как и на 1этапе, но только вместо знаков “?” везде записать выражения с переменной. |
| 3.Составление и решение уравнения или неравенства (системы уравнений или неравенств). | Опираясь на условия задачи составить уравнение или неравенство ( систему уравнений или неравенств ) и найти его (её) решение. | Уравнение или неравенство, система уравнений или неравенств. |
| 4.Анализ решения уравнения или неравенства (системы уравнений или неравенств). | Из всех найденных решений уравнений или неравенств (систем уравнений или неравенств) выбрать те, которые подходят по смыслу задачи и, по мере необходимости, довычислить искомую величину. | Провести проверку решения, причём проверять нужно соответствие полученного ответа условию задачи, а не составленным уравнениям. |
| 5.Ответ. | Записать правильный ответ, удовлетворяющий всем описанным условиям задачи и отвечающий на её “главный вопрос”. |
Немного остановлюсь подробнее на этапах:
1 этап. Арифметическая краткая запись условий задачи.
Важно помнить: этот этап может отсутствовать, если решение задачи элементарно или она не особо усложнена условиями. На этом этапе решения задачи происходит понимание или осмысление её текста. Намного облегчает этот процесс умение правильно “увязать” все известные и неизвестные величины в таблицу данных задачи или составить чертёж. Неизвестные величины удобно обозначать знаком “?”, а “главный вопрос” задачи для того, чтобы потом на последних этапах не запутаться и правильно найти “Ответ”, так как в некоторых задачах, содержащих неявный вопрос искомую величину приходится довычислять.
Значительно облегчает решение и делает задачу более понятной введение обозначений, общепринятых в физике, химии, геометрии, алгебре, экономике и так далее. Например: V,t,s-скорость, время, расстояние (длина пути или отрезка); р,V,m-плотность вещества, объём тела, масса тела; W,t,V–производительность, время работы, объём работы; a,b,P,S–две стороны прямоугольника, его периметр, его площадь; А0,р,n,An-первоначальная величина, процент её увеличения, количество увеличений, конечная величина после увеличения А0 на р процентов n раз; MА,СА,M–масса вещества А в растворе или в смеси, концентрация вещества А в растворе или смеси (доля), масса раствора или смеси; mn=10m+n–запись двузначного числа, где m,n–цифры.
Схематический чертёж оказывает большую помощь в задачах “на движение”. Он позволяет увидеть динамику движения, а также учесть все характерные ситуации–встречи, остановки, повороты и тому подобное.
2 этап. Алгебраическая краткая запись условий задачи.
Обычно, этот этап в оформлении задачи начинается с фразы “Пусть х ед.-…,тогда…”,
не следует пытаться обойтись небольшим числом неизвестных. Наоборот, чем больше неизвестных, тем легче составлять уравнения или неравенства.
Выбирая неизвестные, мы создаём математическую модель ситуации, описанной в условии задачи, точнее, набор переменных представляет собой список параметров, определяющих эту модель, поэтому все они должны быть независимы, и все соотношения должны следовать лишь из конкретных условий задачи.
При введении переменных, следует руководствоваться принципом наибольшего удобства математической записи условий задачи, при этом искомая величина может не входить в их число. Часто имеет место ситуация, когда составленная по условию задачи система уравнений не позволяет однозначно определить неизвестные, однако, искомая величина, являющаяся некоторой комбинацией введенных неизвестных, находится однозначно. В большинстве задач “главный вопрос” подсказывает выбор переменной.
3 этап. Составление и решение уравнения или неравенства (системы уравнений или неравенств).
Обычно этот этап в оформлении задачи начинается словами “По условию задачи (выписать условия из текста задачи), значит,…(запись уравнения или неравенства).”
При составлении математической модели необходимо учитывать ОДЗ переменной (переменных) помня условия существования уравнения или неравенства (системы уравнений или неравенств). Для составления уравнения или неравенства (системы уравнений или неравенств) из текста задачи выбираем условие (условия), которое позволяет увязать известные и неизвестные данные задачи в формулы: S=vt-вычисление длины пути, пройденного телом; m=pV-вычисление массы тела; V=Wt-вычисление объёма работы; S=ab–вычисление площади прямоугольника.
В простейших ситуациях мы получаем уравнение (неравенство) с одной переменной или систему уравнений (неравенств), в которой число уравнений (неравенств) совпадает с числом неизвестных. Но, если число уравнений (неравенств) оказалось меньше числа неизвестных и при этом использованы все условия задачи, то надо попытаться выразить то, что нужно найти, через введенные неизвестные. В корректной задаче, если все условия использованы, то нужное неизвестное или нужная комбинация неизвестных обязательно найдётся.
4 этап. Анализ решения уравнения или неравенства (системы уравнений или неравенств).
Обычно этот этап в оформлении задачи начинается фразой “По смыслу задачи х, должна быть величиной… (натуральной, положительной, целой, принадлежащей промежутку и так далее), (проверка на выполнение условий задачи по смыслу найденного значения переменной)=>(значение х) –постороннее решение ( если смысловое условие не выполнено) или (значение х)–(записать пояснение к найденной величине, если смысловое условие выполнено).”
Не каждое решение уравнения может являться решением задачи. Для любой текстовой задачи полезно провести проверку её решения, причём проверять нужно соответствие полученного ответа условию задачи, а не составленным уравнениям.
Практическая часть.
ЗАДАЧА 1.
Прибывших на парад солдат планировали построить так, чтобы в каждом ряду стояло по 24 человека. Но в действительности не все прибывшие смогли участвовать в параде, и их перестроили так, что число рядов стало на 2 меньше, а число человек в ряду на 26 больше нового числа рядов. Если бы все солдаты участвовали в параде, то их можно было бы построить так, чтобы число рядов было равно числу человек в ряду. Сколько солдат прибыло на парад?
РЕШЕНИЕ:
Пусть первоначально предполагаемое число рядов- n, тогда число прибывших солдат равно 24n. После перестроения число рядов стало равным n-2, а число человек в ряду – соответственно n+24. Очевидно, что число солдат после перестроения явно меньше числа прибывших первоначально. Итак, число прибывших: 24n; число солдат после перестроения (n-2)*(n+24). Составим неравенство: 24n >(n-2)*(n+24)
Получили: n2 – 2n – 48< 0
D=196, n1=8; n2= -6, n ϵ (0;8), n=1;2;3;4;5;6;7
Решая его, получаем, что число рядов лежит в интервале (-6;8). Число рядов может быть целым и положительным. Следовательно, круг решений ограничен от 1 до 7. Учитывая, что число человек в ряду, после перестроения, рано числу рядов,
т.е. x2=24n,x= 2. Единственное число, удовлетворяющее этому условию n=6, а соответствующее число солдат равно 144.
Ответ: 144
ЗАДАЧА 2.
Бригады рабочих получали спецодежду со склада по 2 комплекта на каждого человека. Каждая бригада получала на 20 комплектов больше, чем было бригад. Если бы бригад было на 4 больше и каждой выдавали по 12 комплектов, то одежды на всех не хватило бы. Сколько комплектов спецодежды было на складе?
РЕШЕНИЕ: Пусть было x бригад и n рабочих в каждой бригаде. Тогда число комплектов на каждую бригаду будет 2n, что на 20 больше, чем число бригад, т.е. 2n=x+20.
Если бы бригад было x+4, и каждая получила по 12 комплектов, то общее количество спецодежды было бы 12(x+4) и превысило бы их количество на складе: 12*(x+4) > 2nx .
Это равносильно неравенству: 12*(x+4)>x*(x+20)
X2+8x-48<0
D=256, x1=-12, x2=4, x ϵ (-12;4)
Условию задачи удовлетворяют лишь три числа: 1,2,3.
Далее из 2n=x+20 получаем, что x= 2n – 20, т.е. x – четное число, т.е. бригад 2 штуки. Итак, 2n – 20 =2, n=11, а число комплектов спецодежды будет равно 2nx= 2*11*2 = 44.
Ответ: 44.
ЗАДАЧА 3.
Токарю необходимо сделать 90 деталей, а ученику – 35. Первые 30 деталей токарь делал с производительностью, вдвое большей, производительности ученика. Остальные 60 деталей он делал, повысив производительность ещё на 2 детали. Токарь свою работу закончит не раньше ученика, чем на 1 час. Однако, если бы токарь и первые 30 деталей делал с такой же производительностью, как оставшиеся 60, то он закончил бы работу не раньше чем через 30 минут после ученика. Какова производительность ученика?
РЕШЕНИЕ:
За x дет/ч примем производительность ученика. Тогда ученик затратил времени ч. Первые 30 деталей токарь делал с производительностью 2x , а остальные 60 с производительностью (2x+2),т.е. он затратил времени + ч. По условию, токарь свою работу закончит не раньше ученика, чем на 1 час. Известно, что при производительности (2x+2) на 90 деталей токарь закончит работу не раньше, чем через 30 минут после ученика. Получим систему неравенств:
+ – ≥ 1 ;
– ≥
Условию удовлетворяет единственное значение x = 5. Ответ: 5.
ЗАДАЧА 4.
Планы выплат. За выполнение малярных работ, Эрику может быть выплачена заработная плата одним из двух способов:
План A: $250 плюс $10 в час;
План B: $20 в час.
В каком из случаев выгоднее воспользоваться планом выплат A или B.
РЕШЕНИЕ:
Предположим, что работа занимает n часов. Для каких значений n план B лучше для Эрика? Предположим, что работа отнимет 20 часов. Тогда n = 20, и согласно плану A, Эрик заработает $250 + $10.20, или $250 + $200, или $450. Его заработок согласно плану B составит $20.20, или $400. Это показывает, что план A лучше для Эрика, если он будет работать 20 часов. Подобным образом, если он будет работать 30 часов, тогда n= 30, и согласно плану A, Эрик заработает $250 + $10.30, или $250 + $300, или $550. При плане B, он заработает $20.30, или $600, поэтому план B лучше в этом смысле.
Чтобы определить все значения n, для которых план B является лучшим для Эрика, составим и решим неравенство.
20n > 250 + 10n
10n > 250
n > 25
Проверка.
Для n = 25 выплаты согласно плану A составят: $250 + $10.25, или $250 + $250, или $500, и выплаты согласно плану B составят $20.25, или $500. То есть, для работы длительностью менее 25 часов, доход одинаков для каждого плана в разделе Понимание задачи мы видели, что согласно плану B выплаты больше для работы, которая занимает больше 30-и часов. Так как 30 > 25, это обеспечивает частичную проверку результата, но мы не можем проверить все значения n.
Вывод:
Для значений n, больше чем 25 часов, план B является лучшим.
Примеры задач из сборника по подготовке к ЕГЭ.
ЗАДАЧА 1.
Высота над землей подброшенного вверх мяча меняется по закону h(t)=1+11t-5t2 ,
где h- высота в метрах, t- время в секундах, прошедшее с момента броска.
Сколько секунд мяч будет находиться на высоте не менее 3 метров?
РЕШЕНИЕ:
Составим и решим неравенство:
1+11t-5t2 ≥3
-5t2+11t+1-3≥0
-5t2+11t -2≥0
-5t2+11t -2=0
D=81, D>0, 2 действительных корня: t1=0,2 ; t2 =2; tϵ [0,2;2]. Для ответа на вопрос необходимо найти ∆t. ∆t=2-0,2=1,8
Ответ: 1,8
ЗАДАЧА 2.
Зависимость объема спроса q (тыс. руб.) на продукцию предприятия-монополиста от цены p (тыс.руб.) задается формулой q=85-5p . Выручка предприятия за месяц r (в тыс.руб.) вычисляется по формуле r(p) = q*p. Определите наибольшую цену p , при которой месячная выручка r(p) составит не менее 300 тыс.руб. Ответ приведите в тыс.рублей.
РЕШЕНИЕ:
Составим и решим неравенство: (85-5p)p≥300
-5p2 +85p-300≥0
-5p2 +85p-300=0
D=49, D>0, 2 действительных корня:p1 =5; p2 =12; pϵ [5;12]. Наибольшая цена p=12.
Ответ: 12
Заключение:
Решение задач занимает в математическом образовании огромное место. Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала.
Задачи выполняют очень важную функцию в курсе математики — они являются полезным средством развития логического мышления, умения проводить анализ и синтез, обобщать, абстрагировать и конкретизировать, раскрывать связи, существующие между рассматриваемыми явлениями.
Считаю, что поставленной цели: рассмотреть решения текстовых задач с помощью неравенств, добилась.
В ходе работы закрепила умения и навыки решать неравенства и системы неравенств, разобрала некоторые нестандартные приемы решения задач. Убедилась, что решение задач способствует воспитанию терпения, настойчивости, воли. В процессе работы я расширила рамки школьной программы и испытала чувство удовлетворенности от приложенного труда.
Литература:
- Бродский И.Л., Видус А.М. , Коротаев А.Б. Сборник текстовых задач по математике для профильных классов.- М.: АРКТИ, 2004
- Иванов М.А. Математика без репетитора. 800 задач с ответами и решениями для абитуриентов Учебное пособие. – М.: Издательский центр «Вентана – Граф», 2002г.
- Лурье М.В., Александров Б.И. Задачи на составление уравнений. Учебное руководство. – М.: Наука. Главная редакция физико-математической литературы, 1990г.
- Садовничий Ю.В. Математика. Конкурсные задачи по алгебре с решениями. Часть 6. Решение текстовых задач. (серия < В помощь абитуриенту>). Учебное пособие.- 3-е изд., стер. – М.: Издательский отдел УНЦ ДО, 2003г.
- Семёнов А.Л., Ященко И.В. Математика: типовые экзаменационные варианты. М .-Издательство «Национальное образование», 2013.
Тезисы к работе «Текстовые задачи на решение неравенств и их систем в целых числах».
Цель: рассмотреть решение текстовых задач с помощью неравенств в целых числах. Задачи: закрепить умения и навыки решать неравенства и системы неравенств; разобрать некоторые нестандартные приемы решения задач; научиться различать, видеть основные приемы, подходы решения неравенств и систем и применять их в традиционных и нетрадиционных примерах и задачах; воспитывать чувство уверенности в себе, своих силах.
В задачах на составление уравнений и неравенств, как правило, речь идёт о конкретных ситуациях из практической деятельности. Известно, что исторически долгое время математические знания передавались из поколения в поколение в виде списка задач практического содержания вместе с их решениями.
Решение таких задач способствует развитию логического мышления, умению самостоятельно проводить небольшие исследования. Этим и объясняется тот факт, что задачи на составление уравнений и неравенств являются непременным элементом вариантов вступительных экзаменов.
Текстовая задача — это описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения.
Текстовые задачи отличаются большим разнообразием содержания и могут существенно различаться по уровню сложности.
Решение задач занимает в математическом образовании огромное место. Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала.
Для успешной сдачи ГИА и ЕГЭ необходимо внимательно разобрать и глубоко усвоить теоретический материал, получить твердые и прочные навыки в решении задач. Залог успеха на экзаменах – систематическая самостоятельная работа в течение всего оставшегося до экзаменов времени. Математику нельзя выучить за день или за неделю – только планомерные длительные занятия сделают экзаменационные задачи и вопросы простыми и легкими. И хотя предлагаемая вашему вниманию статья не может заменить учебник, она должна помочь устранить некоторые пробелы в знаниях и предостережет вас от возможных ошибок.
1. При решении задач, в которых используются процентные соотношения, важно правильно определить количество, принимаемое за 100%.
Пример 1.
За смену двое рабочих изготовили вместе 72 детали. После того, как первый рабочий повысил производительность труда на 15%, а второй – на 25%, они вдвоем изготовили 86 деталей. Сколько деталей за смену стал изготавливать каждый рабочий после повышения производительности труда?
Неправильное решение.
Введем обозначения. Пусть x – число деталей, изготавливаемых за смену первым рабочим после повышения производительности труда, а y – число деталей, изготавливаемых за смену вторым рабочим после повышения производительности труда.
Тогда (x – 0,15x) – число деталей, изготавливаемых за смену первым рабочим до повышения производительности труда; (y – 0,25y) – число деталей, изготавливаемых за смену вторым рабочим до повышения производительности труда.
Решаем систему уравнений:
{x + y = 86,
{0,85x + 0,75y = 72.
Имеем:
{x = 75,
{y = 11.
Неправильный ответ: (75; 11).
Правильное решение.
Введем обозначения: x – число деталей, изготавливаемых за смену первым рабочим до повышения производительности труда; y – число деталей, изготавливаемых за смену вторым рабочим до повышения производительности труда.
Тогда: (x + 0,15x) – число деталей, изготавливаемых за смену первым рабочим после повышения производительности труда; (y + 0,25y) – число деталей, изготавливаемых за смену вторым рабочим после повышения производительности труда.
Решаем систему уравнений:
{x + y = 72,
{1,15x + 1,25y = 86.
Имеем:
{x = 40,
{y = 32.
Следовательно,
{1,15x = 46.
{1,25y = 40.
Правильный ответ: (46; 40).
2. При решении задач, в которых используются отношения частей, важно правильно определить количество, принимаемое за единицу.
Пример 2.
Имеется два сплава золота и серебра. В первом сплаве количество этих металлов находится в отношении 2 : 3, а во втором – 3 : 7. В каком отношении нужно взять указанные сплавы, чтобы получить новый сплав, в котором золото и серебро были бы в отношении 5 : 11?
Правильное решение.
Введем обозначения:
x – необходимое количество первого сплава;
y – необходимое количество второго сплава.
Из условия следует, что в первом сплаве 2/5 части золота и 3/5 части серебра, а во втором сплаве – 3/10 части золота и 7/10 части серебра. Тогда в новом сплаве будет (2/5 x + 3/10 y) золота и (3/5 x + 7/10 y) серебра. Следовательно,
(2/5 x + 3/10 y) : (3/5 x + 7/10 y) = 5 : 11.
После упрощения получим, что 7x = y или x/y = 1/7.
Правильный ответ: 1/7.
3.
Пример 3.
Расстояние между городами А и В равно 100 км. Из А в В отправляются одновременно два автомобиля. Скорость первого автомобиля на 10 км/ч больше скорости второго, и в пути он делает остановку на 50 мин. В каких пределах может меняться скорость первого автомобиля при условии, что он прибывает в город В не позже второго автомобиля?
Правильное решение.
Введем обозначения:
x км/ч – скорость первого автомобиля, тогда (x – 10) км/ч – скорость второго автомобиля.
100/(x – 10) ч – время, в течение которого второй автомобиль находится в пути, а (100/x + 5/6) ч – время, в течение которого первый автомобиль находится в пути.
Из условия следует, что
(100/x + 5/6) ≤ 100/(x – 10). После упрощения получим:
(x2 – 10x – 1200) / (x(x – 10)) ≤ 0.
В итоге имеем: x > 0 и 10 < x ≤ 40.
Правильный ответ: (10; 40].
4.
Пример 4.
По двум улицам к перекрестку движутся две машины с постоянными скоростями 50 км/ч и 60 км/ч. Считая, что улицы пересекаются под прямым углом, и зная, что в некоторый момент времени машины находятся на расстоянии соответственно 2 км и 3 км от перекрестка, установите, через какое время расстояние между ними будет наименьшим.
Правильное решение.
Через x часов расстояние между машинами будет S = √((3 – 60x2) + (2 – 50x2)) (рис. 1). 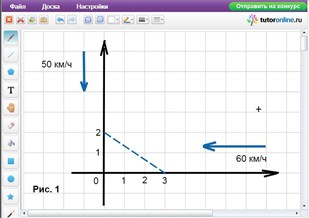
S1(x) = (3 – 60x2) + (2 – 50x2), найдем его минимум из уравнения
S1‘(x) = 0 или ((3 – 60x2) + (2 – 50x2))’ = 0, откуда
610x = 28, x = 14/305.
Правильный ответ: x = 14/305 ч.
5.
Пример 5.
Сумма цифр двузначного числа равна 12. Если к искомому числу прибавить 36, то получим число, записанное с помощью тех же цифр, но расположенных уже в обратном порядку. Найдите это число.
Правильное решение.
Пусть xy – искомое число (x – первая цифра, y – вторая цифра). Тогда xy = 10x + y.
Согласно условию, x + y = 12 и xy + 36 = 10x + y + 36 = yx = 10y + x.
Таким образом, получили систему уравнений:
{ x + y = 12,
{ 9x – 9y = -36.
Решая данную систему, получим, что x = 4 и y = 8.
Правильный ответ: Исходное число 48.
Запомните, самостоятельное решение даже одной задачи принесет гораздо больше пользы, чем разбор готовых решений пусть и нескольких задач. Поэтому всегда пытайтесь решить пример самостоятельно, а только потом, в случае необходимости, воспользуйтесь указанием или разберите правильное решение задачи, если оно у вас имеется.
Остались вопросы? Не знаете, как решать задачи?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
- Альфашкола
- Уроки по математике
- Неравенства
- Примеры неравенств в текстовых задачах.
Примеры неравенств в текстовых задачах. — онлайн урок
В уроке разобраны различные неравенства задачи. Часто условие задачи так записано, что для ее решения требуется составить уравнение или неравенство. На уроке будем рассматривать линейные неравенства задачи. Самое главное в этом уроке — это текстовые задачи по математике на составление неравенств. Рассмотрим различные квадратичные неравенства задачи.
Отзывы:
Прекрасный Преподаватель, хороший подход к новым ученикам
Очень грамотный репетитор. С математикой на ты)
Грамотный и интересный преподаватель.
Похожие уроки
Методические особенности решения текстовых задач с
использованием неравенств и оценок
А.А. ЧУГУНОВА, к.п.н., старший преподаватель СКГУ
им. Козыбаева
Н.А. КЛИМЕНКО, учитель школы №1 г. Петропавловска
При обучении математике задачи имеют большое и многостороннее значение. Решая математическую задачу, человек познает много нового: знакомится с новой ситуацией, описанной в задаче, с применением математической теории к ее решению, познает новый метод решения или новые теоретические разделы математики, необходимые для решения задачи, и т. д. Иными словами, при решении математических задач человек приобретает математические знания, повышает свое математическое образование. При овладении методом решения некоторого класса задач у человека формируется умение решать такие задачи, а при достаточной тренировке - и навык, что тоже повышает уровень математического образования.
Основная задача современного учителя
математики не создание у учащихся механического применения полученных навыков,
а умения их применения в нестандартных ситуациях.
Обучение учащихся решению текстовых задач методом
уравнений или систем уравнений занимает в курсе алгебры довольно большое место.
Значение этих задач в том, что это – простейшая, но достаточно четкая модель
применения математики к изучению действительности. В ней содержатся три
характерных для любых случаев использования математических моделей момента:
перевод реальной задачи на математический язык, исследование внутри модели и
сопоставление результата с исходной задачей. Но все ли задачи решаются с
использованием уравнений и их систем? На конкурсных экзаменах, особенно в
последние годы, попадаются такие задачи, которые с помощью одних только
уравнений решить нельзя. Это так называемые задачи с неопределенным условием
(на самом деле эта неопределенность только кажущаяся). Для их решения
необходимо использовать не только уравнения, но и неравенства, системы
неравенств, а иногда и некоторые дополнительные условия, явно не указанные в задаче.
Во многих текстовых задачах однозначное решение можно найти только в том
случае, если учесть неравенства, вытекающие из условий. В ряде задач только с
помощью неравенств удается получить дополнительные соотношения и тем самым
найти решение. Наконец, существуют текстовые задачи, рассчитанные на умение
составлять не только уравнения, но и неравенства, и с их помощью получать
ответы на поставленные в задачах вопросы.
Весь процесс решения задачи, вслед за
Д. Пойа [3], разобьем на четыре этапа: 1) анализ задачи; 2) поиск решения
задачи; 3) осуществление плана решения; 4) оценка решения задачи.
I
этап.
Анализ и собственная запись условий задачи. Анализ чертежа если он необходим и
построен.
а) установление объекта наблюдения (исследования);
б) выделение процессов, подлежащих рассмотрению;
в) выделение величин, входящих в каждый процесс;
г) уяснение функциональной зависимости между
величинами и составление формул этой зависимости;
д) схематическая запись условий задачи с обозначением
неизвестных величин.
II этап. Выявление
оснований для составления неравенства или системы неравенств. Введение
неизвестных величин и установление взаимосвязей между ними и другими данными
задачи. Составление неравенства (системы).
III этап. Решение
неравенства (системы).
IV этап. Смысловой
анализ решения задачи. Проверка расчетов и обоснования. Запись ответа. Анализ
решения задачи. Комментирование решения задачи. Возвращение к решению задачи
(ретроспективный подход) с целью уяснения и уточнения идей и методов решения
задачи, упрощения расчетов. Выяснение возможностей обобщения. Установление
общих правил для решения подобных задач. Поиск более рациональных приемов
решения задач.
Исходя из специфики реализации учебной деятельности
при решении текстовых задач, выделяется система действий, адекватная структуре
учебной деятельности, которая должна включать в себя:
−
действия
по принятию или самостоятельной постановке учебной задачи, а также следующие
учебные действия по ее решению: выделение основного отношения, реализованного
на предметной области задачи; моделирование основного отношения в предметной
области, графической, буквенной форме; составление системы частных задач,
имеющих общий способ решения; построение модели поиска решения задачи;
−
осуществление
действий контроля за выполнением действий по решению учебной задачи;
−
оценка
результата решения принятой задачи.
Раскроем методику обучения решению текстовых задач на
конкретных примерах.
Задача 2.1.1 Одно
из натуральных чисел на 4 меньше другого. Причем квадрат меньшего из чисел не
больше, чем удвоенное второе число. Найдите меньшее число из данных чисел.
1.
Что надо сделать, чтобы ответить на вопрос задачи? (Построить
ее математическую модель.)
.
2.
Что представляет математическая модель этой задачи? (Неравенство).
3.
Что такое неравенство?
4.
Какие виды неравенств вы знаете? (Линейные неравенства,
квадратные неравенства, рациональные неравенства, неравенства, содержащие знак
модуля).
5.
Что называется решением неравенства? (Значение переменной
х, которое обращает неравенство f(x) >0 в верное числовое неравенство,
называют решением неравенства).
6.
Что значит решить неравенство? (Решить неравенство, значит
найти все его решения или доказать, что их нет).
7.
Какие правила используют при решении неравенств? (Правила
равносильных преобразований).
8.
К какому виду относится данное неравенство? (Квадратное)
9.
Какие методы решения квадратных неравенств вы знаете? Решите
полученное неравенство.
Текстовые задачи традиционно вызывают
затруднения у школьников, многим из которых не удается правильно составить
уравнение или неравенство по условию задачи. Учителю математики в такой ситуации
почти невозможно организовать самостоятельную работу школьников, постоянно
нуждающихся в указаниях и подсказках. Поэтому на уроках целесообразно
предложить таким ученикам карточки с задачами, которые сопровождаются
указаниями, следуя которым даже слабый ученик сможет получить правильный ответ,
а для сильных учеников предусмотрены дополнительные вопросы. Например:
Задача 2.1.2 Сплав
олова и меди, масса которого 16 кг, содержит 55% олова. Сколько килограммов
олова нужно добавить, чтобы повысить содержание олова в сплаве до 60%?
Решение:
Обозначив искомую массу олова буквой х, выразите:
а)
сколько килограммов олова было в сплаве сначала;
б)
сколько килограммов олова стало в сплаве после добавления;
в)
массу полученного сплава;
г)
отношение массы олова к массе полученного сплава.
Запишите уравнение, решите его и ответьте на вопрос задачи.
Дополнительные вопросы.
1.
Какова масса меди, содержащейся в сплаве?
2.
Сколько килограммов меди следовало бы добавить в первоначальный сплав,
чтобы содержание меди составило 50%?
Задачи на уроке предлагаются по
нарастающему уровню сложности, самые трудные можно предложить на факультативных
занятиях.
Приведу несколько советов, полезных при
решении текстовых задач на составление неравенств:
1.
Внимательно, может быть не один раз, прочитайте условие задачи с
тем, чтобы стало понятно ее содержание.
2.
Часто бывает полезно сделать рисунок с отмеченными на нем
числовыми данными.
3.
При очередном прочтении задачи нужно постепенно вводить
неизвестные, при необходимости отмечая их размерности. При этом буквенные
обозначения неизвестных должны быть удобны, например, вызывать ассоциации со
стандартными обозначениями в физике, химии и т.д. Выбор неизвестных должен
быть, в первую очередь, удобен для математической записи условий задачи, а не
ориентирован на ее вопрос.
4.
При очередном прочтении задачи нужно записывать связи между
известными и неизвестными величинами в виде уравнений и неравенств.
5.
Перед решением системы уравнений или неравенств нужно определить
искомую величину, имея ввиду что часто из полученной системы требуется найти
только одну неизвестную или некоторую комбинацию неизвестных, что может быть
сделано далеко не всегда.
6.
Если система допускает несколько решений, то проверить каждое из
них. Чтобы учащиеся привыкли к задачам, требующих составления неравенств,
предложить им на уроке простые задачи. Их можно использовать для проверки
теоретического материала, устного счета и т. д.
Рассмотрим поэтапное решение задачи.
Задача 2.1.3 По плану бригада должна
выполнить заказ за 10 дней. Но фактически она перевыполняла норму на 27 деталей
в день и за 7 дней работы не только выполнила предусмотренное планом задание,
но и изготовила сверх плана 54 детали. Сколько деталей в день должна была
изготовить бригада по плану ?
АНАЛИЗ ТЕКСТА ЗАДАЧИ. После прочтения текста задачи
анализ может быть проведен посредством рассмотрения следующих вопросов (самими
учащимися или с помощью учителя):
1. За сколько дней бригада должна выполнить заказ по
плану?
2. За сколько дней бригада фактически выполнила заказ?
3. Почему бригада выполнила заказ раньше намеченного
срока?
4. Сколько деталей изготовила бригада сверх плана?
5. Какие величины содержатся в задаче?
6. Как связаны между собой производительность труда,
время и объем выполненной работы? (Учитель может конкретизировать этот вопрос,
исходя из возможностей учащихся.)
7. Сколько различных ситуаций можно выделить в задаче?
8. Какие величины, входящие в условие и вопрос задачи,
неизвестны?
9. Какая величина в задаче является искомой?
10. Решалась ли раньше задача, похожая на эту?
В итоге первого этапа работы над задачей с учетом
основного отношения выполняется запись текста задачи. Табличная форма записи на
первых этапах обучения решению текстовых задач наиболее эффективна, потому что
умение учащегося оформить соответствующую таблицу 2.1.2 говорит о том, принял
он задачу или нет. Заметим, что существуют и другие формы записи.
Таблица 2.1.2
|
Величины |
Ситуация |
||
|
По плану |
Фактически |
||
|
Производительность |
? 10 ? |
На 27 |
|
|
Время |
|||
|
Объем |
На 54 |
||
Для выяснения связи между значениями одной и той же
величины перед учащимися ставятся соответствующие вопросы, например:
1. В каком случае производительность труда бригады
была выше?
2. На сколько деталей в день бригада перевыполняла
норму?
Правильный ответ на первый вопрос позволяет поставить
в таблице соответствующий знак неравенства между неизвестными значениями
одноименной величины. Ответ на второй вопрос позволяет записать: «На 27» (в
указанном в таблице месте). Полученная запись позволяет учащимся
актуализировать часть условия задачи: производительность бригады,
предусмотренная планом, на 27 деталей в день меньше фактической. Аналогично
поступают при выяснении связи между неизвестными значениями другой величины. В
данном случае сравнивается плановый и фактический объем работы.
ПОИСК СПОСОБА РЕШЕНИЯ ЗАДАЧИ. На этом этапе
обсуждается стратегия решения задачи. Затем вводится обозначение искомой или
другой неизвестной величины в зависимости от выбранной учителем совместно с
учащимися стратегии. Далее, пользуясь установленными зависимостями между
значениями одноименных величин и основным отношением, реализованным в задаче
(т.е зависимостью между величинами), на основе табличной записи текста задачи
заполняется таблица 2.1.3 поиска решения задачи:
Таблица 2.1.3
|
Величины |
Ситуация |
||
|
По плану |
Фактически |
||
|
Производительность |
х < х + 27 10 10х |
На 27 |
|
|
Время |
|||
|
Объем выполненной |
На 54 |
||
Исходя из модели поиска решения, выписывается
неравенство на 54, с помощью которого
составляется уравнение или уравнение
.
ОСУЩЕСТВЛЕНИЕ ПЛАНА РЕШЕНИЯ ЗАДАЧИ. Отсюда
естественно вытекает план решения задачи, который включает в себя поиск решения
(способ получения уравнения) и решение полученного уравнения. Заметим, что
табличная форма записи деятельности учащихся по составлению уравнения не требует
повторного ее описания. Поэтому на третьем этапе процесса решения текстовой
задачи остается решить полученное уравнение, выполнить проверку решения и
записать ответ.
Имеем уравнение: .
Решим его:
Данное уравнение имеет один корень – число 45. Но
решение задачи не может заканчиваться решением уравнения, необходимо проверить,
удовлетворяет ли полученный корень уравнения условию и требованию задачи. В
связи с этим необходимо сделать проверку корня уравнения по смыслу задачи.
Здесь возможны два способа письменного оформления проверки корней уравнения.
Первый способ состоит в том, что по найденному
значению х по порядку вычисляются значения входящих в задачу величин.
При этом проверяется, удовлетворяют ли эти величины смысловым ограничениям.
Если все найденные значения величин им удовлетворяют, то корень уравнения дает
решение задачи. С этой целью воспользуемся моделью поиска решения задачи. По
смыслу данной задачи все входящие в нее величины должны принимать положительные
значения. Проверим, выполняется ли это для найденного значения х = 45:
х = 45
Положительное число.
х + 27 = 45 + 27 = 72
Положительное число.
(х + 27) ∙ 7 = 72 ∙ 7 = 504 Положительное
число.
10х = 10 ∙ 45 = 450 Положительное
число.
504 – 450 = 54 Положительное
число, являющееся данным.
Следовательно, значение х = 45 удовлетворяет
условию задачи, т.е. является ее решением.
Ответ: бригада должна
изготовить в день по плану 45 деталей.
Второй способ письменного оформления проверки корней
уравнения по смыслу задачи на использование неравенства с одной переменной.
Сущность проверки остается при этом прежней, а способ оформления состоит в
следующем. Совместно с уравнением, составленным по тексту задачи,
рассматриваются смысловые ограничения для значений величин, входящих в задачу.
Следует иметь в виду, что даже нахождение области определения не снимает
вопроса о том, удовлетворяет ли найденное значение корня полученного уравнения
условию и требованию задачи. Дело в том, что количество ограничений,
определяющее эту область, может оказаться большим и некоторые ограничения могут
быть незамечены (например, целочисленность корня в данной задаче). Получают
систему:

или
Видим, что значение х = 45 удовлетворяет
двойному неравенству и, следовательно, является решением задачи. Множество
целочисленных значений х, удовлетворяющих двойному неравенству, является
областью допустимых по смыслу задачи значений искомой величины.
ИЗУЧЕНИЕ (АНАЛИЗ) НАЙДЕННОГО РЕШЕНИЯ. Перед учащимися
в соответствии с содержанием этого этапа процесса решения задачи ставятся
вопросы следующего типа:
1. Какова главная идея решения данной задачи?
2. Нельзя ли указать другие способы решения данной
задачи?
3. Почему рассмотренный способ решения является
рациональным?
Заметим, что для данной задачи все возможные пути
поиска ее решения не выявляют другого способа, т.е. эта задача имеет постоянную
структуру.
Естественно, что при последовательном формировании
умений решать текстовые задачи методика обучения претерпевает определенные
изменения: отпадает необходимость применять табличную форму записи текста
задачи и поиска ее решения, сам этот процесс станет более свернутым.
Задача 2.1.4 В провинции Х фермер перевозит
початки кукурузы в мешках по 40 кг в грузовике, масса которого без груза равна
4500 кг. Какое количество мешков может находиться в грузовике, чтобы он мог
переехать через ручей по мосту, выдерживающему груз в 7 т [8]?
Решение: Пусть в грузовике находится х мешков
с кукурузой, тогда масса груза равна 40х кг. Число мешков, которое можно
перевозить на грузовике, должно удовлетворять неравенству
отсюда
Ответ: не более
62 мешков.
Задача 2.1.5 Прибывших на парад солдат
планировали построить так, чтобы в каждом ряду стояло по 24 человека. Но в
действительности не все прибывшие смогли участвовать в параде, и их перестроили
так, что число рядов стало на 2 меньше, а число человек в ряду на 26 больше
нового числа рядов. Если бы все солдаты участвовали в параде, то их можно было
бы построить так, чтобы число рядов было равно числу человек в ряду. Сколько
человек прибыло на парад [10]?
Решение: Обозначим первоначально
предполагавшееся число рядов за п, тогда число прибывших солдат равно 24п.
После перестроения число рядов стало равным (п – 2), а число человек в
ряду – соответственно (п + 24). И вот тут-то возникают вопросы: «Как
составить уравнение, ведь неизвестно число бывших солдат? Имеет ли вообще задача
однозначное решение?». Оказывается, имеет.
Начнем с очевидного: число солдат после перестроения
явно меньше, чем число прибывших первоначально. Зная, что число солдат после
перестроения равно , составим неравенство
.
Оно равносильно следующему неравенству
Решая его, получим, что число рядов лежит в интервале
(-6;8).
Внимательно вчитываемся в условие, мы еще не все
использовали. Число рядов может быть только целым и положительным. Уже это
условие ограничивает круг решений интервалом (0;8), т.е. всего семью целыми
числами от 1 до 7.
А если учесть еще и последнее предложение о
перестроении роты квадратом (число человек в ряду равно числу рядов), то
нетрудно сообразить, что из первоначального числа солдат (24п) должен
извлекаться квадратный корень. Единственное число, удовлетворяющее этому
условию, это число 6, а соответствующее число солдат равно 144.
Ответ: 144.
Так, внимательно вчитываясь в условие, находим единственное
решение, не составляя уравнений.
И все-таки, почему же этот
материал труден для учащихся? Разрозненные указания учителей по решению задач
быстро забываются учениками, они не приобретают навыков решения текстовых
задач. Без конкретной программы деятельности учащихся, без алгоритмов, системы
приемов поиска решения задачи трудно организовать процесс решения задач,
поэтому необходимы «ускорители» для приобретения навыков решения: иллюстрация,
схемы, таблицы, дополнительные символы, условные знаки, стрелки, способствующие
более конкретному наглядному представлению об отношениях между частями задачи,
связях между величинами, порядке этих связей. Это позволяет стимулировать у
учащихся развитие наглядно-действенного мышления и на основе его в дальнейшем –
образного мышления. Поиск решения текстовой задачи путем составления таблицы
дает возможность охватить взором отношения между элементами всей задачи.
Задачи для самостоятельного
решения:
Задача 1.
Две трубы, действуя вместе в течение
одного часа, наполняют водой 3/8 бассейна. Если сначала первая труба наполнит
одну восьмую часть бассейна, а затем вторая при выключенной первой доведет
объем до 3/8 бассейна, то на это потребуется 2,5 часа, если первую трубу
включить на час, а вторую – на полчаса, то они наполнят бассейн более чем на
четверть. За какое время наполняет бассейн каждая труба?
Задача 2.
Из пункта А в пункт В, расстояние между
которыми равно 18 км, в 8 часов выходит пешеход, в 11 часов выезжает
велосипедист. Известно, что пешеход прибыл в пункт В не позже, чем в 12 часов
30 минут, а велосипедист прибыл в пункт В не позже пешехода. Считая скорости
пешехода и велосипедиста постоянными, определить скорость велосипедиста, если
она не более, чем на 8 км/ч превышает скорость пешехода.
Задача 3.
На реке, скорость течения которой равна 4
км/ч, в направлении её течения расположены пристани А, В, С, причем расстояние
от А до В вдвое меньше, чем расстояние от В до С. От пристани В в один и тот же
момент по направлению к пристани С отправлены плот (плывущий относительно
берегов со скоростью течения реки) и катер. Дойдя до пристани С, катер
разворачивается и движется по направлению к пристани А. Найти все значения
собственной скорости катера (т. е. скорости катера в стоячей воде), при которых
катер приходит в пункт А не раньше, чем плот приходит в пункт С.