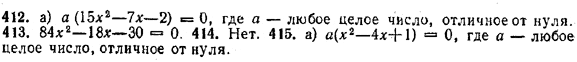Как по заданным корням составить квадратное уравнение по его корням

Уведомление

Cookie

• Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
• Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
• Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.

Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax 2 + c = 0, при b = 0;
• ax 2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax 2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.

Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x 2 = 0.

1. Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

Как решить уравнение ax 2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:

• перенесем c в правую часть: ax 2 = — c,
• разделим обе части на a: x 2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.

Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:

• не имеет корней при — c/а 0.

В двух словах

Пример 1. Найти решение уравнения 8x 2 + 5 = 0.

Перенесем свободный член в правую часть:

Разделим обе части на 8:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.

Как решить уравнение ax 2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0

Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.

Решить линейное уравнение:

0,5x = 0,125,
х = 0,125/0,5

Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x₁) (x − x₂).

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b 2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b 2 −4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.

1. Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x 2 = 0.

Произведем равносильные преобразования. Умножим обе части на −1

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x 2 — х = 0.

Преобразуем уравнение так, чтобы появились множители

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x 2 — 10 = 39.

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.

Найдем дискриминант по формуле

D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112

Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b 2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней:

2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>

Для удобства вычислений обозначим выражение n 2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n 2 — ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n 2 — ac;
• если D₁ 0, значит можно найти два действительных корня по формуле

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>

Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

Теорема Виета

Приведенное квадратное уравнение и его корни

Приведенным квадратным уравнением называется уравнение вида:

Для корней $x_1$ и $x_2$ приведенного квадратного уравнения (при $D ge 0$) справедливо следующее:

$$ x_1+x_2 = -b, quad x_1 x_2 = c $$

$$ x_1 = -6, x_2 = 1, quad x_1+x_2 = -5, quad x_1 x_2 = -6 $$

Теорема Виета

Для корней $x_1$ и $x_2$ квадратного уравнения $ax^2+bx+c = 0$ (при $D ge 0$) справедливо следующее:

$$ ax^2+bx+c = a(x-x_1 )(x-x_2 ) $$

$$ 2x^2+5x-3 = 2 left(x-frac<1> <2>right)(x+3) $$

$$ x_1 = frac<1><2>, x_2=-3, quad x_1+x_2=-frac<5><2>, quad x_1 x_2 = — frac<3> <2>$$

Примеры

Пример 1. Составьте квадратное уравнение по его корням:

Искомое уравнение: $x^2-3x-10 = 0$

Искомое уравнение: $x^2-3,5x-2 = 0$

$$ left(x-frac<1> <3>right) left(x-frac<1> <2>right) = x^2- left(frac<1><3>+frac<1> <2>right)x+frac<1> <3>cdot frac<1> <2>= x^2-frac<5> <6>x+frac<1> <6>$$

Искомое уравнение: $x^2-frac<5> <6>x+frac<1> <6>= 0 или 6x^2-5x+1 = 0$

$г) frac<3><5>$ — один корень

$$ left(x-frac<3> <5>right)^2 = x^2-2 cdot frac<3> <5>x+ left(frac<3> <5>right)^2 = x^2-frac<6> <5>x+frac<9><25>$$

Искомое уравнение: $x^2-frac<6> <5>x+ frac<9> <25>= 0$ или $25x^2-30x+9 = 0$

Пример 2. Один из корней уравнения $x^2+bx-21 = 0$ равен 3. Найдите другой корень и коэффициент b.

По теореме Виета можем записать:

Получаем: второй корень равен -7, уравнение имеет вид $x^2+4x-21 = 0$.

Ответ: $x_2$ = -7, b = 4

Пример 3. Один из корней уравнения $x^2+3x+c = 0$ равен 12. Найдите другой корень и коэффициент c.

По теореме Виета можем записать:

$$ <left< begin x_2+12 = -3 \ 12x_2 = c end right.> Rightarrow <left< begin x_2 = -15 \ c = 12 cdot (-15) = -180 end right.> $$

Получаем: второй корень равен -15, уравнение имеет вид $x^2+3x-180 = 0$.

Ответ: $x_2$ = -15, c = -180

Пример 4*. Дано уравнение $x^2+5x-7 = 0$ с корнями $x_1$ и $x_2$.

Не решая его, постройте уравнение:

а) с корнями $y_1 = frac<1>, y_2 = frac<1>$

По теореме Виета для корней исходного уравнения получаем:

Для корней искомого уравнения можем записать:

$$ y^2-frac<5> <7>y-frac<1> <7>= 0 iff 7y^2-5y-1 = 0 $$

б) с корнями $y_1 = frac ,y_2 = frac $

Для корней искомого уравнения можем записать:

$$ y^2+frac<39> <7>y+1 = 0 iff 7y^2+39y+7 = 0 $$

КВАДРАТНЫЙ ТРЕХЧЛЕН  III

§ 55. Составление квадратного уравнения по заданным корням

Предположим, что нам нужно составить квадратное уравнение, корнями которого были бы числа x₁ и x₂. Очевидно, что в качестве  искомого  уравнения   можно  выбрать  уравнение

a(х — x₁)(х — x₂) = 0,                      (1)

где а — любое отличное от нуля действительное число. С другой стороны, как было показано в § 54, каждое квадратное уравнение с корнями x₁ и x₂ можно записать в виде (1).

Таким образом, формула (1) полностью решает поставленную выше задачу. Из всех квадратных уравнений корни x₁ и x₂ имеют уравнения вида (1) и только, они.

Пример. Составить квадратное уравнение, корни которого равны  1  и — 2.

Ответ.   Корни 1 и —2 имеют все квадратные уравнения вида

а(х — 1)(х + 2) = 0,

или

ах² + ах — 2а = 0,

где а — любое отличное от нуля действительное число. Например,   при   а = 1   получается   уравнение

х² + х — 2 = 0.

Упражнения

411.  Составить квадратное уравнение, корнями которого были бы  числа:

а) 2 и — 3;    б) — 1 и — 5;      в) ¹/₄ и ¹/₆;    г) — ¹/₂ и — ¹/₃ .

412.  Составить квадратное уравнение с целыми коэффициентами так, чтобы его корни были равны:

а) — ¹/₅   и  ²/₃;    б) ⁴/₇  и 5;    в) — ³/₂  и  ²/₉;    г) — ³/₁₀  и — ²/₅.

413.   Составить квадратное уравнение с целыми  коэффициентами, корни которого равны ⁵/₇ и — ¹/₂, а сумма всех коэффициентов равна 36.

414.  Могут ли  корнями  квадратного уравнения с натуральными коэффициентами   быть  числа ⁶/₅ и — ¹/₇?

415.  Составить квадратное уравнение с целыми  коэффициентами, если известно, что один из его корней равен:

а) 2 + √3 ;       б) 3 —√2 .

ОТВЕТЫ

Составьте квадратное уравнение по его корням 5 и 3

По теореме Виета сумма корней квадратного уравнения равна коэффициенту при x с обратным знаком, то есть:

Также, по теореме Виета произведение корней квадратного уравнения равно свободному члену, то есть:

По условию x₁ = 5 и x₂ = 3.

Следовательно, квадратное уравнение с корнями x₁ = 5 и x₂ = 3 имеет вид:

Нам нужно составить квадратное уравнение по его корням. Корни равны 5 и 3.

Решать задание будем по алгоритму

• вспомним определение полного квадратного уравнения и приведенного квадратного уравнения;
• вспомним теорему Виета;
• найдем коэффициента уравнения, используя теорему Виета;
• запишем уравнение;
• сделаем проверку — решим полученное уравнение.

Определение квадратного уравнения и теорема Виета

Квадратным уравнением называется уравнение вида ax ^2 + bx + c = 0;

где a, b — коэффициенты, а с — свободный член. Так же обязательно должно выполняться условие, что коэффициента a не равен нулю (a ≠ 0).

Если в уравнении ax^2 + bx + c = 0, коэффициент a = 1, то уравнение называется полным приведенное квадратное уравнение.

Мы в ответе получим уравнение с коэффициентом а = 1, то есть приведенное квадратное уравнение.

Теорема Виета для приведенного квадратного уравнения.

Сумма корней уравнения равна коэффициенту b с противоположным знаком.

А произведение корней уравнения равно свободному члену уравнения с.

Находим коэффициенты для нашего уравнения

Корни уравнения имеют значения x1 = 5; x2 = 3.

При условии, что уравнение приведенное, то есть а = 1, находим коэффициенты b и c.

Как составить квадратное уравнение по его корням

КВАДРАТНЫЙ ТРЕХЧЛЕН III

§ 55. Составление квадратного уравнения по заданным корням

Предположим, что нам нужно составить квадратное уравнение, корнями которого были бы числа x₁ и x₂. Очевидно, что в качестве искомого уравнения можно выбрать уравнение

a(х — x₁)(х — x₂) = 0, (1)

где а — любое отличное от нуля действительное число. С другой стороны, как было показано в § 54, каждое квадратное уравнение с корнями x₁ и x₂ можно записать в виде (1).

Таким образом, формула (1) полностью решает поставленную выше задачу. Из всех квадратных уравнений корни x₁ и x₂ имеют уравнения вида (1) и только, они.

Пример. Составить квадратное уравнение, корни которого равны 1 и — 2.

Ответ. Корни 1 и —2 имеют все квадратные уравнения вида

а(х — 1)(х + 2) = 0,

ах 2 + ах — 2а = 0,

где а — любое отличное от нуля действительное число. Например, при а = 1 получается уравнение

х 2 + х — 2 = 0.

Упражнения

411. Составить квадратное уравнение, корнями которого были бы числа:

а) 2 и — 3; б) — 1 и — 5; в) 1 /₄ и 1 /₆; г) — 1 /₂ и — 1 /₃ .

412. Составить квадратное уравнение с целыми коэффициентами так, чтобы его корни были равны:

413. Составить квадратное уравнение с целыми коэффициентами, корни которого равны 5 /₇ и — 1 /₂, а сумма всех коэффициентов равна 36.

414. Могут ли корнями квадратного уравнения с натуральными коэффициентами быть числа 6 /₅ и — 1 /₇?

415. Составить квадратное уравнение с целыми коэффициентами, если известно, что один из его корней равен:

Теорема Виета

Приведенным квадратным уравнением называется уравнение вида:

Для корней $x_1$ и $x_2$ приведенного квадратного уравнения (при $D ge 0$) справедливо следующее:

$$ x_1+x_2 = -b, quad x_1 x_2 = c $$

$$ x_1 = -6, x_2 = 1, quad x_1+x_2 = -5, quad x_1 x_2 = -6 $$

Теорема Виета

Для корней $x_1$ и $x_2$ квадратного уравнения $ax^2+bx+c = 0$ (при $D ge 0$) справедливо следующее:

$$ ax^2+bx+c = a(x-x_1 )(x-x_2 ) $$

$$ 2x^2+5x-3 = 2 left(x-frac right)(x+3) $$

$$ x_1 = frac, x_2=-3, quad x_1+x_2=-frac, quad x_1 x_2 = — frac $$

Примеры

Пример 1. Составьте квадратное уравнение по его корням:

Искомое уравнение: $x^2-3x-10 = 0$

Искомое уравнение: $x^2-3,5x-2 = 0$

$$ left(x-frac right) left(x-frac right) = x^2- left(frac+frac right)x+frac cdot frac = x^2-frac x+frac $$

Искомое уравнение: $x^2-frac x+frac = 0 или 6x^2-5x+1 = 0$

$г) frac$ — один корень

$$ left(x-frac right)^2 = x^2-2 cdot frac x+ left(frac right)^2 = x^2-frac x+frac$$

Искомое уравнение: $x^2-frac x+ frac = 0$ или $25x^2-30x+9 = 0$

Пример 2. Один из корней уравнения $x^2+bx-21 = 0$ равен 3. Найдите другой корень и коэффициент b.

По теореме Виета можем записать:

Получаем: второй корень равен -7, уравнение имеет вид $x^2+4x-21 = 0$.

Ответ: $x_2$ = -7, b = 4

Пример 3. Один из корней уравнения $x^2+3x+c = 0$ равен 12. Найдите другой корень и коэффициент c.

По теореме Виета можем записать:

$$ x_2+12 = -3 \ 12x_2 = c end right.> Rightarrow x_2 = -15 \ c = 12 cdot (-15) = -180 end right.> $$

Класс: 8
«Б»                      Предмет: Алгебра                          Дата:
_______

Урок
№ 64        Тема: «Составление
квадратного трехчлена по  его корням»

Цели
урока: научить составлять
квадратный трехчлена по  его корням.

Задачи
урока:

Обучающая: повторить
понятие квадратного трехчлена и его корней; формировать умение составлять квадратный трехчлена по  его корням.

Развивающая:
развитие логического мышления, познавательных интересов.

Воспитательная: воспитание  организованности,
дисциплинированности, аккуратности, усидчивости.

Тип
урока: урок изучения нового
материала и первичного закрепления

Методы и приемы: словесный, наглядный, практический.

Материально-техническое  обеспечение: дидактический материал.

План
урока:                                                                                                                        

I.     
Организационный
момент

II.     
Актуализация  знаний

III.     
Первичное усвоение новой учебной информации

IV.     
Осознание и осмысление

V.     
Закрепление

VI.     
Информация о домашнем задании

VII.     
Подведение итогов урока

Ход урока

І.
Организационный момент

— Здравствуйте ребята, тема сегодняшнего урока: «Составление квадратного трехчлена по  его корням». Цели данного урока: научится составлять квадратный трехчлена по  его корням.

Приветствие, проверка готовности учащихся к уроку, сообщение темы и цели урока и требований к уроку.

ІІ. Актуализация  знаний

— Давайте вспомним пройденный материал —  Разложите на множители выражение: —  а) Х2— 9;       б) Х2 – 9Х; —  Найдите корень уравнения: —  а) Х2— 9 = 0;  б) Х2 – 9Х = 0;  в) Х2 – 6Х + 9 = 0

Ребята отвечают на вопросы учителя.

ІІІ. Первичное усвоение
новой учебной информации

§  54 . Разложение  квадратного   трехчлена  на линейные множители

В этом
параграфе мы рассмотрим следующий вопрос: в каком случае  квадратный  трехчлен  ax²  + bx + c можно
представить в   виде   произведения

(a₁x + b₁)
(a₂x + b₂)

двух
линейных  относительно х множителей  с действительными
коэффициентами     a₁, b₁, a₂, b₂     (a₁ =/=0, a₂ =/=0) ?

1.
 Предположим, что данный  квадратный   трехчлен  ax²  + bx + c  представим
в виде

ax²  + bx
+ c  = (a₁x
+ b₁) (a₂x + b₂).
                  (1)

Правая
часть формулы (1) обращается в нуль при  х =  —  b₁/ a₁ и х = —  b₂/ a₂  (a₁иa₂ по условию не равны нулю). Но
в таком случае числа  —  b₁/ a₁ и  —  b₂/ a₂  являются
корнями уравнения

ax²  + bx + c = 0.

Следовательно,
дискриминант  квадратного   трехчлена  ax²  + bx + c должен  быть  неотрицательным.

2.
 Обратно,   предположим,   что
  дискриминант  D = b² — 4ас квадратного трехчлена ax²  + bx + c  неотрицателен.
 Тогда этот  трехчлен  имеет
действительные корни x₁
и x₂.
Используя  теорему Виета,  получаем:

ax²  + bx + c  = а (x² + ^b/_a х + ^c/_a)
= а [x² — (x₁ + x₂) х + x₁x₂]
=

= а [(x²— x₁x ) — (x₂x — x₁x₂)]
= а [х (х — x₁)
— x₂(х — x₁)
=

= a(х — x₁)(х — x₂).

Итак,

ax²  + bx + c = a(х — x₁)(х — x₂),
                (2)

где x₁ и x₂ — корни  трехчлена  ax²  + bx + c. Коэффициент а можно отнести к любому из двух
линейных множителей,  например,

a(х — x₁)(х — x₂)
= (aх — ax₁)(х — x₂).

Но это
означает, что в рассматриваемом случае  квадратный   трехчлен  ax²  + bx + c представим в
виде произведения двух линейных множителей с действительными коэффициентами.

Объединяя
результаты, полученные в пунктах 1 и 2, мы приходим к следующей теореме.

Теорема.  Квадратный   трехчлен  ax²  + bx + c тогда и тoлько
тогда можно представить в виде произведения двух линейных множителей с
действительными коэффициентами,

ax²  + bx + c = (aх — ax₁)(х — x₂),

когда
дискриминант этого  квадратного   трехчлена  неотрицателен
(то есть когда этот  трехчлен  имеет
действительные корни).

Пример
1.
  Разложить на линейные множители 6x² — х —1.

Корни
этого  квадратного   трехчлена  равны x₁ = ¹/₂  и x₂ = — ¹/₃.

Поэтому
по формуле (2)

6x² — х —1 = 6 (х — ¹/₂)(х + ¹/₃)
= (2х — 1) (3x + 1).

Пример
2.
 Разложить на линейные множители x² + х + 1. Дискриминант
   этого     квадратного      трехчлена     отрицателен:

D = 1² — 4•1•1 = — 3 <
0.

Поэтому
данный   квадратный   трехчлен   на линейные множители с
действительными  коэффициентами   не раскладывается.

Упражнения

Разложить
  на   линейные   множители   следующие
 выражения (№ 403 — 406):

403. 6x² —
7х + 2.
                 405. x² — х + 1.

404.
  2x² —
7ах + 6а².
            406. x² — 3ах + 2а² — аb— b².

Предположим,
что нам нужно  составить  квадратное уравнение, корнями которого
были бы числа x₁ и x₂. Очевидно,
что в качестве искомого уравнения можно выбрать уравнение

a(х — x₁)(х — x₂)
= 0,
                     (1)

где а — любое отличное от нуля
действительное число. С другой стороны, как было показано в § 54, каждое
квадратное уравнение с корнями x₁
и x₂ можно
записать в виде (1).

Таким
образом, формула (1) полностью решает поставленную выше задачу. Из всех квадратных
уравнений корни x₁ и x₂ имеют
уравнения вида (1) и только, они.

ІV.Осознание и осмысление

Пример. Составить квадратное уравнение,
корни которого равны  1  и — 2.

Ответ.
  Корни 1 и —2 имеют все квадратные уравнения вида

а(х — 1)(х + 2) = 0,

или

ах² + ах — 2а = 0,

где а — любое отличное от нуля
действительное число. Например,   при   а = 1   получается
  уравнение

х² + х — 2 = 0.

V. Закрепление

Упражнения

1.
 Составить квадратное уравнение, корнями которого были бы  числа:

а) 2 и
— 3;    б) — 1 и — 5;      в) ¹/₄ и ¹/₆;
   г) — ¹/₂ и
— ¹/₃ .

2.
 Составить квадратное уравнение с целыми коэффициентами так, чтобы его
корни были равны:

а) — ¹/₅   и
 ²/₃;    б) ⁴/₇  и
5;    в) — ³/₂
 и  ²/₉;
   г) — ³/₁₀  и — ²/₅.

3.
  Составить квадратное
уравнение с целыми  коэффициентами, корни которого равны ⁵/₇ и — ¹/₂, а сумма
всех коэффициентов равна 36.

Решение:
(х-5/7)(х-1/2)=0    х²-17/14х+5/14=0    14х²-17х+5=0  
14+17+5=36

4.
 Могут ли  корнями  квадратного уравнения с натуральными коэффициентами
  быть  числа ⁶/₅ и
— ¹/₇?

Решение:
(х-6/5)(х+1/7)=0      35х²-37х-6=0  (да)

5.
 Составить
квадратное уравнение с целыми  коэффициентами, если известно, что один из
его корней равен:

а) 2 +
√3 ;       б) 3
—√2   

в)
√3-5

Решение

Второй корень будет сопряжён первому, т. е.   x₁ =
√3−5; x₂ = −√3−5.
Ищем квадратное уравнение в виде x² + ax + b =
0,
тогда по теореме Виета    a = −(_x1+x2)
= −2•(−5) = 10,   b = x1•x2 = (−5)²−(√3)² = 22.
ОТВЕТ: x²+10x+22 = 0.

Решить №3,№5 на стр.97-98 проверь себя, дополнительно №242
(1,2).

VI.Информация о домашнем задании

 №228, №234+ Повторить пройденную
тему§12.

VII.Подведение итогов
урока

Давайте
теперь подведем итоги урока :

Учитель благодарит за урок и объявляет оценки.