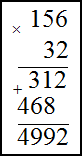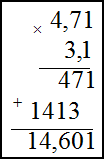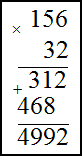Содержание
Определение действия умножение, компоненты произведения
Переместительный и сочетательный закон умножения
Особые случаи умножения
Умножение однозначных чисел
Умножение многозначного числа на однозначное
Умножение в столбик многозначного и однозначного чисел
Особые случаи умножения многозначных чисел
Общее правило умножения многозначных чисел
Умножение в столбик многозначных чисел
Некоторые особенности записи умножения в столбик
Изменение произведения при изменении сомножителей
Умножение числа на произведение и произведения на число
Распределительный закон умножения (умножение суммы на число)
Я сперва покажу на примере, для чего нужно умножение, а после дам определение умножения и подробно расскажу об этом действии.
Допустим, мы хотим купить 14 тетрадей по 22 рубля каждая. Планируя покупку, нам нужно знать, сколько мы заплатим за всю покупку?
Чтобы ответить на этот вопрос, нам нужно сложить стоимость каждой тетради, которую мы хотим купить. А, так мы запланировали покупку 14 тетрадей, тогда мы складываем 22 рубля 14 раз, то есть, находим сумму 14 слагаемых, каждое из которых равно 22:
22+22+22+22+22+22+22+22+22+22+22+22+22+22=308 (то есть, 308 рублей).
Если размер и количество одинаковых слагаемых небольшие, мы без особого труда можем найти их сумму. Но что же делать, если слагаемые многозначные и их количество велико?
Для ускорения подсчетов используется действие умножения.
Умножение – это арифметическое действие сложения определенного количества одинаковых слагаемых.
Действие умножение – это частный случай действия сложение.
Когда нам нужно сложить несколько одинаковых слагаемых, мы, вместо утомительного вычисления суммы одинаковых чисел, умножаем это слагаемое на количество его повторений. Если взять наш пример, то мы слагаемое 22 умножаем на количество – 14.
Еще раз: умножить 22 на 14 – это означает, что нам нужно сложить 14 чисел, каждое из которых равно 22.
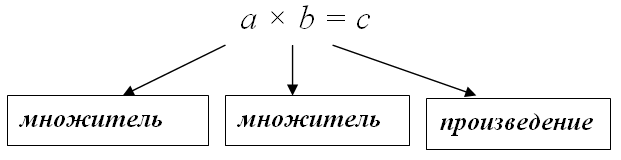
Число, которое является повторяющимся слагаемым, называется множимое (то, что множится, умножается).
Число, которое указывает на количество одинаковых слагаемых, называется множитель.
Множимое и множитель имеют общее название – сомножители.
Результат действия умножения называется произведением.
Так, в нашем примере мы складываем цену одной тетради (22 рубля) столько раз, сколько тетрадей хотим купить (14 штук). Значит, 22 – это множимое, 14 – это множитель. Стоимость покупки, полученная в результате умножения 22 на 14 (308 рублей) – это произведение.
На записи действие умножения обозначается точкой (∙) или косым крестом (x), которые ставятся между сомножителями. В отдельных случаях допускается обозначение звездочкой (*). Результат действия умножение, то есть, найденное произведение записывается в виде равенства. Если, к примеру, нужно умножить 22 на 14, то записать это действие и его результат можно так:
22 ∙14=308,
или
22x14=308,
или
22*14=308.
При записи от руки действие умножение принято обозначать при помощи точки, косой крест используется в основном при печати, а звездочка – в компьютерном наборе. Но даже и во время компьютерного набора грамотнее использовать точку или косой крест (букву х).
Прочитать действие умножения и результат можно такими способами:
- двадцать два умножить на четырнадцать будет триста восемь;
- двадцать два, умноженное на четырнадцать, равно триста восемь;
- двадцать два на четырнадцать – триста восемь;
- произведение двадцати двух и четырнадцати равно триста восемь.
Компоненты действия умножение для двух сомножителей:
Компоненты умножения для трех сомножителей и более:

Основные свойства умножения
Поскольку действие умножение является частным случаем действия сложение, то основные свойства сложения распространяются и на умножение.
Действие умножение, как и сложение, можно выполнить всегда, и при этом получается единственный результат этого действия.
Законы умножения и их следствия
Умножение обладает такими основными свойствами, называемые законами умножения, из которых вытекают остальные свойства и следствия:
- переместительный закон умножения;
- сочетательный закон умножения.
Переместительный закон умножения.
Произведение двух или нескольких сомножителей от изменения их порядка не меняется.
Это значит, что значение произведения не зависит от порядка перемножения сомножителей, то есть, от порядка выполнения действия умножение.
Для двух сомножителей мы можем записать переместительный закон умножения в общем виде так:
ab=ba.
Допустим, нам нужно подсчитать количество отделений в шкафу (рис. 1).
Рисунок 1.
В верхнем ряду их 5, в среднем и нижнем тоже по 5 отделений. Нетрудно посчитать, что всего во всех рядах их: 5+5+5=15, или 5 ∙3=15.
Но эти же самые отделения можно считать и по вертикали, по столбцам: в первом их 3, во втором тоже 3, в третьем, четвертом и пятом столбцах их также по 3 штуки. То есть, в каждом столбце по 3 отделения. Всего столбцов 5, поэтому: 3+3+3+3+3=15, или 3 ∙5=15.
Это означает, что 5 ∙3=3 ∙5.
Это свойство также верно для трех и более сомножителей.
К примеру, нам нужно подсчитать количество отделений в двух одинаковых шкафах (рис. 2).
Рисунок 2.
В первом шкафу количество отделений, как мы уже выяснили, можно узнать, умножив количество отделений в одном ряду на количества рядов: 5 ∙3.
Во втором шкафу количество отделений точно такое же (5 ∙3), поскольку два шкафа полностью одинаковые.
Общее количество отделений в двух шкафах можно найти, сложив количество отделений в каждом шкафу: 5 ∙3+5 ∙3.
Выражение 5 ∙3 – это не что иное, как повторяющееся слагаемое, поэтому мы можем заменить эту сумму произведением, умножив слагаемое 5 ∙3 на количество его повторений, то есть, на 2:
5 ∙3+5 ∙3 =5 ∙3 ∙2.
Найдя результаты левой и правой части этого равенства, мы убедимся, что они одинаковые, а значит, мы произвели замену суммы произведением верно:
15+15=15 ∙2,
30=30.
Но количество отделений в одном шкафу мы также можем найти, умножив количество рядов на количество отделений в одном ряду: 3∙5. Тогда в двух шкафах у нас будет:
3 ∙5+3 ∙5=3 ∙5 ∙2,
15+15=15 ∙2,
30=30.
Значит, 5 ∙3 ∙2=3 ∙5 ∙2=30.
Также мы можем сразу умножить количество шкафов на количество отделений в одном шкафу. Тогда мы получим: 2 ∙5 ∙3=30 или 2 ∙3 ∙5=30, в зависимости от того, каким способом мы посчитали, сколько отделений содержит один шкаф.
Поэтому, для трех сомножителей переместительный закон умножения в общем виде выглядит так:
abc=acb=bac=bca=cab=cba.
Сочетательный закон умножения.
Результат умножения трех и более чисел не изменяется, если любые из этих сомножителей заменить их произведением.
Следовательно, мы можем группировать множители между собой каким угодно образом, и выполнять действие умножения с этими группами.
В общем виде для трех сомножителей сочетательный закон умножения можно выразить так:
abc=a(bc)=(ab)c=b(ac).
Этот закон можно назвать следствием переместительного закона умножения.
Действительно, согласно переместительному закону, мы можем перенести множители, стоящие в конце выражения a ∙b ∙c ∙d, в его начало, и объединить их в одну группу (c ∙d) ∙a∙b, то есть, найти их произведение c∙d. А так как при изменении порядка сомножителей, результат действия умножение не изменяется, то и изменение порядка групп сомножителей одного произведения, также не влияют на результат.
Так, при подсчете количества отделений в двух шкафах на рисунке 2, мы можем сперва найти число отделений в одном шкафу, а потом умножить результат на 2:
(5 ∙3) ∙2=15 ∙2=30,
или
(3 ∙5) ∙2=15 ∙2=30,
а можем сперва найти общее количество рядов отделений в обоих шкафах, а после умножить их на количество отделений в ряду:
(3 ∙2) ∙5=6 ∙5=30.
Как видите, результат во всех случаях одинаковый.
Особые случаи умножения: умножение единицы и нуля
Если в произведении двух чисел один из сомножителей единица, то произведение равно второму сомножителю:
a ∙1=1 ∙a=a.
Действительно, при умножении любого числа на 1, мы берем это число 1 раз, а значит, получаем только это число.
А при умножении единицы на любое число (например, 1∙7) мы находим сумму семи единиц, то есть, то количество единиц, из которых состоит данное число. Следовательно, сумма этих единиц равна самому данному числу:
1+1+1+1+1+1+1=7.
Если в произведении любого количества сомножителей одним из сомножителей является нуль, то и произведение равно нулю:
a∙b∙0=0∙a∙b=a∙0∙c=0.
Так, при умножении любого числа на 0, мы берем это число 0 раз, то есть, не берем ни разу. А если ничего не брать, то ничего и не получится.
А при умножении нуля на любое число, мы находим сумму нулей, которая, как вам известно, равна 0.
Умножение однозначных чисел
Умножение двух однозначных натуральных чисел a и b – это нахождения суммы b слагаемых, каждое из которых равно числу a, и при этом a и b являются натуральными числами.
Если a и b – числа, находящиеся в самом начале натурального ряда, то найти такую сумму особого труда не составляет: 1 ∙2=1+1=2. Но если взять числа, которые замыкают первый десяток, например, 8 и 9, то для вычисления 8 ∙9, а именно, суммы 8+8+8+8+8+8+8+8+8=72, то в этом случае вычисление результата потребует от нас определенного времени.
Для облегчения вычисления, были посчитаны результаты умножения всех однозначных чисел друг на друга, и сведены в специальные таблицы умножения.
Умножение однозначных чисел – это основа быстрого и точного вычисления произведений любых чисел, поэтому очень важно знать на память все таблицы умножения.
Умножение многозначного числа на однозначное
Допустим, нам нужно умножить 985 на 4. Умножить 985 на 4 – это сложить 4 раза число 985, то есть, 985+985+985+985. Мы можем представить каждое из слагаемых 985 в виде суммы его разрядных слагаемых, а именно: 900+80+5. Получится такое выражение:
900+80+5+900+80+5+900+80+5+900+80+5.
Воспользуемся законами сложения и сгруппируем одинаковые слагаемые этого выражения вместе:
900+900+900+900+80+80+80+80+5+5+5+5,
(900+900+900+900)+(80+80+80+80)+(5+5+5+5).
Суммы в скобках мы можем заменить на произведение одинаковых слагаемых и числа этих слагаемых в каждых скобках:
900 ∙4+80 ∙4+5 ∙4.
Таким образом, чтобы умножить многозначное число на однозначное, достаточно умножить это однозначное число на количество единиц в каждом разряде многозначного числа, и сложить полученные результаты.
Умножение в столбик многозначного числа на однозначное
Удобно и быстро умножить многозначное число на однозначное, и при этом не запутаться в расчете помогает запись вычисления в столбик.
Для этого пишем множимое 985, и под цифрой его разряда единиц записываем множитель 4. Проводим под множителем горизонтальную черту, ставим между сомножителями знак умножения (точку или косой крест), и получаем такую запись:
4 раза по 5 единиц – это будет 20 единиц, то есть, 2 десятка и 0 простых единиц. Поэтому, пишем под чертой в разряде единиц 0, а 2 десятка запоминаем или записываем маленькую цифру 2 над разрядом десятков множимого 985:
4 раза по 8 десятков – это 32 десятка. Прибавим к ним 2 десятка, которые получились после умножения однозначного числа на единицы, получим 32 десятка, то есть, 3 сотни и 2 десятка. Цифру 2 пишем под чертой в разряде десятков, а над разрядом сотен множимого 975 (в уме) ставим маленькую цифру 3:
4 раза по 9 сотен – это 36 сотен. Прибавим к ним 3 сотни, которые держим в уме, получаем 39 сотен, или 3 тысячи и 9 сотен. Значит, пишем под горизонтальной чертой в разряде сотен цифру 9 и, поскольку в множимом 985 нет ни одной тысячи, то сразу запишем в результате под чертой цифру 3 в разряде тысяч:
Умножение многозначных чисел
Прежде чем рассказать, как в общем случае умножить одно многозначное число на другое, я расскажу о двух частных случаях умножения многозначных чисел:
- умножение на число, которое начинается на единицу, и заканчивается любым количеством нулей;
- умножение на число, которое начинается на любые, отличные от нуля, цифры, и заканчивается одним или несколькими нулями.
Умножение на число, состоящее из единицы и любого количества нулей
Пусть необходимо умножить 327 на 10. Это означает, что мы должны 10 раз взять (сложить) число 327. Известно, что если мы возьмем (сложим) одну единицу 10 раз, то мы получим 1 десяток, значит, взяв 327 единиц 10 раз, у нас будет 327 десятков, то есть, 3270 единиц. Значит:
327 ∙10 =3270
Рассмотрим еще один пример. Умножим 327 на 100, то есть, 100 раз возьмем (сложим) число 327. Если единицу повторить 100 раз, получится 100 единиц, или одна сотня. Значит, 327 единиц, повторенные 100 раз, дадут нам 327 сотен, что можно записать так: 32700.
327 ∙100 =32700
Итак, чтобы умножить какое-нибудь число на другое, которое начинается на единицу, и заканчивается любым количеством нулей, достаточно к концу первого числа дописать столько нулей, сколько содержится во втором числе.
Умножение на число, которое начинается цифрами, и заканчивается любым количеством нулей
Например, умножим то же самое число 327, но уже на 20. Это означает, что мы должны сложить одно и то же число 327 друг с другом 20 раз:
327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327.
Воспользуемся сочетательным законом умножения, и представим эти слагаемые в виде 10 одинаковых групп, каждая из которых содержит два слагаемых 327:
(327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327).
Сумму в скобках мы можем, согласно определению действия умножение, заменить на произведение, поскольку слагаемые суммы у нас одинаковые. Получим следующее:
(327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2).
Но здесь мы опять видим, что выражение состоит из десяти одинаковых слагаемых, каждое из которых представляет собой произведение. Значит, мы и это выражение можем представить в виде произведения:
(327 ∙2) ∙10.
Рассмотрим другой пример: 764 ∙300.
Здесь нам нужно найти сумму 300 чисел, каждое из которых – это число 764. Эти 300 слагаемых мы группируем в 100 групп, в каждой из которых содержится 3 слагаемых 764. Можем ли мы узнать, какое число единиц содержит каждая из 100 групп? Да, можем. Для этого нам нужно найти сумму трех слагаемых 764, или просто 764 умножить на 3.
764 ∙3 =2292.
Зная, сколько единиц содержится в одной группе и количество этих одинаковых групп, мы можем найти, сколько единиц находится во всех этих группах. Групп у нас 100, значит, мы находим сумму 100 слагаемых, каждое из которых – это найденное нами число 2292. То есть, 2292 умножаем на 100. Для этого достаточно просто приписать справа к числу 2292 два нуля:
2292 ∙100 =229200.
Итак, чтобы умножить какое-нибудь число на другое, начинающееся любыми цифрами и заканчивающееся нулями, достаточно умножить первое число на число, образованное первыми цифрами второго, а к результату приписать справа столько нулей, сколько их было в конце второго числа.
Иными словами: нужно от второго числа отбросить нули в конце, умножить получившиеся числа, а к результату приписать справа столько нулей, сколько изначально отбросили.
Общее правило умножения чисел
Допустим, необходимо найти произведение двух многозначных чисел 2834 и 168. Это означает, что нам нужно сложить 168 одинаковых чисел, каждое из которых равно 2834:
Количество слагаемых (168) мы можем разложить на разрядные слагаемые (100+60+8) и согласно сочетательному закону сложения сгруппировать их следующим образом: сто слагаемых плюс шестьдесят слагаемых плюс восемь слагаемых.
Исходя из определения умножения, выражения в скобках мы можем представить не в виде суммы большого количества слагаемых, а как сумму произведений:
Таким образом, чтобы умножить два многозначных числа, достаточно последовательно умножить одно из этих чисел на количество единиц каждого из разрядов второго числа, и сложить полученные результаты.
Частное произведение – это число, полученное после умножения одного из сомножителей на количество единиц какого-либо разряда другого сомножителя.
Умножение в столбик многозначных чисел
При записи действия умножения в столбик сомножители располагаются друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел; под множителем проводим горизонтальную черту, и ставим между сомножителями знак действия умножения:
Далее, умножаем множимое 2834 последовательно на количество единиц каждого разряда множителя справа налево, то есть, начиная с младшего разряда.
Умножаем 2834 на 8 единиц, получается 22672 единиц. Результат умножения, то есть, первое частное произведение, записываем под горизонтальной чертой.
Далее, нам нужно умножить множимое на 6 десятков; для этого умножаем 2834 на 6, а к результату приписываем 0, получается 170040.
В частных произведениях обычно не пишут (опускают) нули в конце числа для упрощения записи. При этом следует не забывать, что, первую полученную цифру частного произведения нужно писать в том разряде, цифру которого мы умножаем на множимое.
В нашем случае это выглядит так. Цифра 6, которую мы умножаем на множимое 2834, находится в числе 168 в разряде десятков, то есть, обозначает количество десятков. Следовательно, первую полученную цифру частного произведения нужно записать в разряде десятков, потому что сейчас мы именно количество десятков умножаем на множимое.
Итак, 6 ∙4 =24, значит мы пишем в строке под первым частным произведением в разряде десятков цифру 4, а 20 десятков, то есть, 2 сотни, запоминаем. Дальше считаем и записываем так же, как и любое другое умножение многозначного и однозначного чисел. После нахождения второго частного произведения, у нас получилась такая запись:
Теперь умножаем множимое на 1 сотню. Для этого достаточно умножить 2834 на 1 и приписать справа два нуля, получится 283400. Но в записи мы нули не пишем, поэтому начинаем писать третье частное произведение с разряда сотен.
Нам осталось только сложить три полученные частные произведения.
Итак, результат умножения 2834 ∙168 = 476112.
Некоторые особенности записи умножения в столбик
При записи нахождения произведения двух чисел в столбик существуют некоторые особенности, которые помогают сократить запись и упростить наглядность вычисления. Все они являются следствием свойств умножения.
Если у первого сомножителя количество цифр, составляющих его, меньше, чем у второго, то удобно при записи в столбик поменять сомножители местами, записав число с большим количеством цифр первым. Например, произведение 284 ∙12093 находят как 12093 ∙284. Это делается, чтобы избавиться от необходимости находить много частных произведений.
Если в множителе некоторые цифры являются нулями, то можно не записывать соответствующие промежуточные произведения, которые, что очевидно, будут равняться также нулю. При этом промежуточное произведение, полученное от умножения следующей значащей цифры (то есть, отличной от нуля) на множимое, начинают записывать с разряда, соответствующего положению этой значащей цифры. Например:
Если один из сомножителей представляет собой число, которое оканчивается любым количеством нулей, то мы записываем сомножители в столбик так, как будто этих нулей нет, находим произведение, мысленно отбросив эти нули, а потом к получившемуся после умножения числу приписываем отброшенные нули и получаем окончательный результат.
Если оба сомножителя – это числа, оканчивающиеся любым количеством нулей, то мы записываем их в столбик так, как будто этих нулей нет, а после нахождения произведения чисел без нулей, приписываем к ним столько нулей, сколько их было изначально.
Попробуйте самостоятельно доказать справедливость этого утверждения. Пишите в комментариях, получилось ли это у вас или нет.
Изменение произведения чисел при изменении его сомножителей
Чтобы понять, что происходит с произведением чисел при изменении одного или нескольких сомножителей, нужно вспомнить, что действие умножения – это частный случай действия сложения, а также переместительный и сочетательный законы сложения.
Если увеличить один из сомножителей в несколько раз, произведение также увеличится в это же число раз.
Рассмотрим пример 18 ∙2. Увеличив второй сомножитель, к примеру, в 3 раза, мы получим другое выражение: 18 ∙6.
Действительно:
18 ∙2 =36
18 ∙6 =108.
Если мы увеличим 36 в 3 раза, то мы получим как раз 108.
По-другому и быть не может, и вот почему.
Первое произведение представляет собой сумму двух слагаемых:
18+18.
Второе произведение – это сумма шести таких же слагаемых:
18+18+18+18+18+18.
Если мы, воспользовавшись сочетательным законом умножения, сгруппируем эти слагаемые по 2, то получим следующее:
(18+18)+(18+18)+(18+18).
Как видите, у нас получилось 3 одинаковых слагаемых, каждый из которых равен первому произведению. А это значит, что полученное произведение состоит из трех, которые были даны изначально, то есть, в 3 раза больше начального. Что и требовалось доказать.
Для второго сомножителя справедливость этого свойства доказывается на основе переместительного закона умножения.
Если уменьшить один из сомножителей в несколько раз, произведение также уменьшится в это же число раз.
Попробуйте самостоятельно доказать правильность этого свойства. Пишите в комментариях, получилось ли это у вас?
Если увеличить один из сомножителей в несколько раз, а второй в это же число раз уменьшить, то произведение при этом не поменяется.
Действительно, при увеличении одного из сомножителей произведение увеличивается, а при уменьшении другого сомножителя произведение уменьшается. Поэтому, если увеличить одно и одновременно уменьшить другое число, то эти изменения компенсируют друг друга, и произведение останется неизменным:
32 ∙8 =256,
Увеличим первый сомножитель в 4 раза, а второй во столько же раз уменьшим:
128 ∙2 =256.
Теперь уменьшим первый сомножитель произведения 32 ∙8 в 4 раза, а второй уменьшим в это же число раз:
8 ∙32 =256.
Умножение произведения на число и числа на произведение
Если необходимо умножить произведение на число, нужно любой сомножитель этого произведения умножить на данное число, а результат умножить последовательно на оставшиеся сомножители.
(a ∙b ∙c) ∙d =(a ∙d) ∙b ∙c =(b ∙d) ∙a ∙c =(c ∙d) ∙a ∙b
Действительно, пусть требуется найти результат (7 ∙9 ∙2) ∙5. Мы можем сперва вычислить произведение в скобках (оно равно 126), а потом умножить его на 5 (результат 630). А можем, чтобы быстрее вычислить результат в уме, сперва умножить 5 на 2, чтобы получить круглое число 10, и потом легко вычислить ещё два произведения, воспользовавшись частными правилами умножения, описанными выше:
10 ∙7 =70 (просто приписываем к семерке нуль),
70 ∙9 =630 (находим по таблице умножения 7 ∙9 =63 и приписываем в конце нуль).
То есть, мы видим, что (7 ∙9 ∙2) ∙5 = (5 ∙2) ∙7 ∙9.
Когда я пишу «находим по таблице умножения», это означает, что мы вспоминаем эту строку из таблицы, а не ищем её там на самом деле. Таблицу умножения нужно знать наизусть!
Если необходимо умножить число на произведение, нужно умножить данное число на любой сомножитель, а результат умножить на оставшиеся сомножители.
a ∙(b ∙c ∙d) =(a ∙b) ∙c ∙d =(a ∙c) ∙b ∙d =(a ∙d) ∙b ∙c.
Рассмотрим такой пример: 6 ∙(3 ∙5 ∙2). Если найти значение произведения в скобках (30), а потом умножить на него число 6, результатом будет 180. А можно сначала умножить число 6 на 5 (будет 30), а потом результат умножить с остальными сомножителями:
30 ∙3 =90,
90 ∙2 =180.
Оба эти свойства являются очевидными следствиями переместительного и сочетательного законов умножения.
Распределительный закон умножения (умножение суммы на число)
Когда мы рассматривали умножение многозначного и однозначного чисел, мы раскладывали число 975 на его разрядные слагаемые (900+70+5), а потом умножали на 4 отдельно каждое это слагаемое. Аналогично можно поступать при умножении числа на любую сумму.
Например, найдем произведение суммы 5+2+4+9 и числа 3. Это означает, что нужно найти такую сумму:
(5+2+4+9)+(5+2+4+9)+ (5+2+4+9).
Все эти слагаемые представляют собой одну сумму чисел, сгруппированных в определенные группы. Запишем их без скобок:
5+2+4+9+5+2+4+9+5+2+4+9,
а затем, используя переместительный и сочетательный законы сложения, сгруппируем одинаковые слагаемые:
(5+5+5)+(2+2+2)+(4+4+4)+(9+9+9).
Основываясь на определении действия умножение, так как мы имеем в каждых скобках одинаковые слагаемые, переписываем это выражение следующим образом:
5 ∙3+2 ∙3+4 ∙3+9 ∙3.
Распределительный закон умножения: для умножения суммы на любое число, необходимо каждое слагаемое этой суммы умножить на данное число, а затем сложить полученные произведения.
Согласно переместительному закону умножения, это свойство справедливо и при умножении числа на сумму.
Для умножения числа на сумму, необходимо умножить данное число на каждое слагаемое этой суммы, а результаты полученных произведения сложить.
(a+b+c+d)∙z =z∙(a+b+c+d) =a ∙z+b ∙z+c ∙z+d ∙z.
Название распределительный происходит от того, что действие умножения на сумму распределяется между каждым из слагаемых этой суммы.
Содержание
- Что значит найдите значение произведения
- Что такое произведение чисел (онлайн калькулятор на умножение)
- Определение произведения чисел
- Свойства произведения чисел
- Умножение или произведение натуральных чисел, их свойства.
- Умножение натурального числа.
- Переместительный закон умножения.
- Сочетательный закон умножения.
- Умножение любого натурального числа на единицу.
- Умножение любого натурального числа на нуль.
- Что такое произведение чисел
- Определение произведения чисел
- Свойства произведения чисел
- Числа. Произведение чисел. Свойства умножения.
- Свойства умножения чисел.
- Числовые и буквенные выражения
- Числовые выражения: что это
- Буквенные выражения
- Выражения с переменными
Что значит найдите значение произведения
Что такое произведение чисел (онлайн калькулятор на умножение)

Давайте наверное начнем с банальных вещей. Когда у нас появляется много чего-то, то довольно сложно это хранить даже в виде информации. Нам каким-то образом это приходится компактно сокращать. Вот скажем у нас появилось более чем две пары носков в шкафу, а точнее пусть их будет 15. Как нам из записать на бумаге. Да, конечно, мы можем взять и записать 2+2+2. и так далее, пока не перечислим цифру два, с которой ассоциируется одна из пар носков на их количество, то есть на 15. Но это ведь право не удобно, особенно если представить, что речь идет не только о наших носках в шкафу, но и о случае их хранения в магазине! И здесь проще записать словами так. У нас две пары носков взято какое-то количество раз!
Вот, здесь где-то и образуется эта самая магия перехода от обычной суммы к произведению, когда мы подразумеваем, что берем какое-то число какое-то количество раз. Самое время дать определение.
Определение произведения чисел
Произведение двух чисел это есть не что иное, как взятое одно из чисел в количестве другого числа.
Еще раз! Если произведение будет С, то номинальное значение одного из чисел пусть а, взятое в количестве b раз и будет этим произведением. Можно записать скажем так
С=а1+а2+а3+а4. +аb где 1,2,3,4. b будут индексом указывающим на то, какое это число а по порядку и не более того!
Пример Найти произведение чисел:
Свойства произведения чисел
Коммутативность: n⋅m=m⋅n
Ассоциативность: (n⋅m)⋅k=n⋅(m⋅k)
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
Пример Найти произведение чисел удобным способом:
1) 5⋅17⋅2 ; 2) 7⋅2⋅15⋅5
Решение. По свойства умножения имеем:
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.
Пример Найти произведение чисел
1) 156⋅32 ; 2) 4,71⋅3,1
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое, полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в столбик
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором — один, значит, в ответе нужно отделить справа три знака:
Побалуемся с произведением!?
Цифра которую будем брать N раз (множитель)
А чему равно это самое N раз?(множитель)
Источник
Умножение или произведение натуральных чисел, их свойства.
Умножение натурального числа.
Разберем понятие умножение на примере:
Туристы находились в пути три дня. Каждый день они проходили одинаковый путь по 4200 м. Какое расстояние они прошли за три дня? Решите задачу двумя способами.
Решение:
Рассмотрим задачу подробно.
В первый день туристы прошли 4200м. Во-второй день тот же самый путь прошли туристы 4200м и в третий день – 4200м. Запишем математическим языком:
4200+4200+4200=12600м.
Мы видим закономерность число 4200 повторяется три раза, следовательно, можно сумму заменить умножением:
4200⋅3=12600м.
Ответ: туристы за три дня прошли 12600 метров.
Рассмотрим пример: 
Чтобы нам не писать длинную запись можно записать ее в виде умножения. Число 2 повторяется 11 раз поэтому пример с умножением будет выглядеть так:
2⋅11=22
Подведем итог. Что такое умножение?
Умножение – это действие заменяющее повторение n раз слагаемого m.
Запись m⋅n и результат этого выражения называют произведением чисел, а числа m и n называют множителями.
Рассмотрим сказанное на примере:
7⋅12=84
Выражение 7⋅12 и результат 84 называются произведением чисел.
Числа 7 и 12 называются множителями.
В математике есть несколько законов умножения. Рассмотрим их:
Переместительный закон умножения.
Мы отдали по два яблока 5 своим друзьям. Математически запись будет выглядеть так: 2⋅5.
Или мы отдали по 5 яблок двум своим друзьям. Математически запись будет выглядеть так: 5⋅2.
В первом и втором случаем мы раздадим одинаковое количество яблок равное 10 штукам.
Если мы умножим 2⋅5=10 и 5⋅2=10, то результат не поменяется.
Свойство переместительного закона умножения:
От перемены мест множителей произведение не меняется.
m⋅n=n⋅m
Сочетательный закон умножения.
Рассмотрим на примере:
(2⋅3)⋅4=6⋅4=24 или 2⋅(3⋅4)=2⋅12=24 получим,
(2⋅3)⋅4=2⋅(3⋅4)
(a⋅b) ⋅c=a⋅(b⋅c)
Свойство сочетательного закона умножения:
Чтобы число умножить на произведение двух чисел, можно его сначала умножить на первый множитель, а затем полученное произведение умножить на второй.
Меняя несколько множителей местами и заключая их в скобки, результат или произведение не изменится.
Эти законы верны для любых натуральных чисел.
Умножение любого натурального числа на единицу.
Рассмотрим пример:
7⋅1=7 или 1⋅7=7
a⋅1=a или 1⋅a=a
При умножении любого натурального числа на единицу произведением будет всегда тоже число.
Умножение любого натурального числа на нуль.
6⋅0=0 или 0⋅6=0
a⋅0=0 или 0⋅a=0
При умножении любого натурального числа на нуль произведение будет равно нулю.
Вопросы к теме “Умножение”:
Что такое произведение чисел?
Ответ: произведением чисел или умножение чисел называется выражение m⋅n, где m – слагаемое, а n – число повторений этого слагаемого.
Для чего нужно умножение?
Ответ: чтобы не писать длинное сложение чисел, а писать сокращенно. Например, 3+3+3+3+3+3=3⋅6=18
Что является результатом умножения?
Ответ: значение произведения.
Что означает запись умножения 3⋅5?
Ответ: 3⋅5=5+5+5=3+3+3+3+3=15
Если умножить миллион на нуль, чему будет равно произведение?
Ответ: 0
Пример №1:
Замените сумму произведением: а) 12+12+12+12+12 б)3+3+3+3+3+3+3+3+3
Ответ: а)12⋅5=60 б) 3⋅9=27
Пример №2:
Запишите в виде произведения: а) а+а+а+а б) с+с+с+с+с+с+с
Решение:
а)а+а+а+а=4⋅а
б) с+с+с+с+с+с+с=7⋅с
Задача №1:
Мама купила 3 коробки конфет. В каждой коробке по 8 конфет. Сколько конфет купила мама?
Решение:
В одной коробке 8 конфет, а у нас таких коробок 3 штуки.
8+8+8=8⋅3=24 конфеты
Ответ: 24 конфеты.
Задача №2:
Учительница рисования сказала приготовить своим восемью ученикам по семь карандашей на урок. Сколько всего карандашей вместе было у детей?
Решение:
Можно посчитать суммой задачу. У первого ученика было 7 карандашей, у второго ученика было 7 карандашей и т.д.
7+7+7+7+7+7+7+7=56
Запись получилась неудобная и длинная, заменим сумму на произведение.
7⋅8=56
Ответ 56 карандашей.
Источник
Что такое произведение чисел
Определение произведения чисел
Произведение $p$ чисел $a_<1>, a_<2>, dots, a_$ есть результат умножения этих чисел: $p=a_ <1>cdot a_ <2>cdot ldots cdot a_$ . В частности, если умножаются два числа $a$ и $b$, то
Задание. Найти произведение чисел:
1) 1.2$cdot 3$ ; 2) 4$cdot 5 cdot 13$
Ответ.
$4 cdot 5 cdot 13=260$
Свойства произведения чисел
- Коммутативность: $n cdot m=m cdot n$
Ассоциативность: $(n cdot m) cdot k=n cdot(m cdot k)$
На основании этих свойств можем заключить, что при перестановке множителей значение произведения не меняется.
Что такое произведение чисел не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Найти произведение чисел удобным способом:
1) 5$cdot 17 cdot 2$ ; 2) 7$cdot 2 cdot 15 cdot 5$
Решение. По свойства умножения имеем:
$$5 cdot 17 cdot 2=(5 cdot 2) cdot 17=10 cdot 17=170$$
$$7 cdot 2 cdot 15 cdot 5=(7 cdot(2 cdot 15)) cdot 5=(7 cdot 30) cdot 5=210 cdot 5=1050$$
Ответ.
$5 cdot 17 cdot 2=170$
$7 cdot 2 cdot 15 cdot 5=1050$
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.
Задание. Найти произведение чисел
1) 156$cdot 32$ ; 2) $4,71 cdot 3,1$
Решение. Запишем умножаемые числа в столбик. Далее умножим сначала единицы второго числа на первое, полученное произведение запишем под чертой. Затем аналогично умножим десятки второго числа на первое. Результат запишем под первым произведением только на один разряд левее. В конце найдем сумму полученных произведений по правилу сложения в столбик
Умножение десятичных дробей во втором примере производится следующим образом: не обращая внимания на запятые, дроби перемножаются как целые числа; в получившемся произведении отделяют справа число знаков, равное сумме чисел знаков после запятой у сомножителей. В нашем случае в первом сомножителе два знака после запятой, во втором — один, значит, в ответе нужно отделить справа три знака:
Источник
Числа. Произведение чисел. Свойства умножения.
Умножение — одно из четырёх основных арифметических действий, бинарная математическая операция, в которой один аргумент складывается столько раз, сколько показывает другой.
Произведение чисел m и n — это сумма n слагаемых, каждое из этих слагаемых = m.
Выражение типа m • n, и значение такого выражения называется произведение чисел m и n. Числа m и n называются множителями.
Если устное умножение чисел затруднительно используют умножение в столбик. В столбик можно умножать большие натуральные числа или десятичные дроби.
Свойства умножения чисел.
1. Коммутативность:
При перестановке множителей местами, значение произведения остается без изменений. Это переместительное свойство умножения.
где, 3 и 4 — множители, а 12 — произведение.
2. Ассоциативность:
В произведении 3-х и больше множителей при перестановке этих множителей либо изменения последовательности выполнения умножения результат остается одинаковым.
(6 • 2) • 3 = 12 • 3 = 36 или 6 • (2 • 3) = 6 • 6 = 36 .
3. Дистрибутивность:
4. Произведение всякого натурального числа и единицы, будет соответствовать этому числу.
Произведение всякого натурального числа и нуля, = 0.
Выражения с буквенными множителями записывают так:
вместо 8 • x пишут 8x , вместо a • b пишут ab.
Кроме того, не используют знак умножения и перед скобками,
2 • (a + b) записывают как 2(а + b),
(x + 2) • (y + 3) записывают как (x + 2)(y + 3) ,
Источник
Числовые и буквенные выражения
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
- 23 + 5 = 28
- 5 — 2 = 3
- 52 * 3 = 156
- 28 : 7 = 4
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
- (5 * 3) — (5 * 2) = 5
- 6 : (7 — 4) = 2
- (45 + 45) : 9 = 10
- 11 * (5 * 5) = 275
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
- Сначала выполняется действие, записанное в скобках.
- Затем выполняется деление/умножение.
- В последнюю очередь выполняется сложение/вычитание.
Пример 1. Найдите значение числового выражения: 3 * (2 + 
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
(6 + 7) * (13 + 2) = 195
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
- Сначала находим значение первого выражения:
6 + 8 = 14
Затем находим значение второго выражения:
2 * 2 = 4
Сравниваем получившиеся результаты:
14 больше 4
14 > 4
6 + 8 > 2 * 2
Пример 2. Сравните следующие числовые выражения:
5 * (12 — 2) — 7 и (115 + 9) — (7 — 3)
- Находим значение первого выражения, соблюдая порядок выполнения арифметических действий:
12 — 2 = 10
5 * 10 = 50
50 — 7 = 43
5 * (12 — 2) — 7 = 43
Затем находим значение:
115 + 9 = 124
7 — 3 = 4
124 — 4 = 120
Сравниваем полученные результаты:
43 меньше 120
43
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
- Сначала следует прочитать его полностью.
- Затем оно записывается.
- Третьим шагом идет подстановка значения неизвестного в выражение.
- А затем производится вычисление, согласно очередности выполнения арифметических действий.
Пример 1. Найдите значение выражения: 5 + x.
- Читаем: найдите сумму числа 5 и x.
- Подставляем вместо неизвестного x число 4.
- Вычисляем: 5 + 4 = 9.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
- Читаем: найдите произведение суммы числа 4 и а и суммы числа 2 и x.
- Подставляем вместо неизвестного a число 2.
- Вычисляем 4 + 2 = 6.
- Подставляем вместо неизвестного x число 5.
- Вычисляем 2 + 5 = 10.
- Находим произведение 6 * 10 = 60.
- Записываем результат: (4 + 2) * (2 + 5) = 60.
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
- Например, в выражении x + a — 8
x — переменная
a — переменная
Если вместо переменных подставить числа, то буквенное выражение x + a — 8 станет числовым выражением. Вот так:
- подставляем вместо переменной x число 5, а вместо переменной a — число 10, получаем 5 + 10 — 8.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
После подстановки значения переменных находим значение x + a — 8 = 5 + 10 — 8 = 7.
Часто можно встретить буквенные выражения, записанные следующим образом:
5x — 4a
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
- Сумма 6 и a.
- Разность 8 и x.
- Сумма x — 2 и 6
- Разность 15 и x — y
- Сумма 45 + 5 и 12 — 6
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: (b — 345) + (180 + x).
Задание три.
Составьте буквенное выражение:
Разность разности 30 и y и разности a и b.
Ответ: (30 — y) — (a — b).
Задание четыре.
Составьте выражение для решения задачи и найдите его значение.
Ролл «Калифорния» стоит 480 рублей — это на 40 рублей меньше, чем ролл «Филадельфия». Сколько будут стоить оба ролла?
Как решаем:
Калифорния — 480 рублей.
Филадельфия — 480 + 40.
Калифорния + Филадельфия = ?
480 + (480 + 40).
Мы помним, что выполнение арифметических действий в числовом выражении имеет строгую последовательность. Сначала — действие в скобках:
480 + 520 = 1 000.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
Маша — 150 видео.
Лена — 150 + 13 видео.
Маша + Лена = ? видео.
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Задание шесть.
Вычислите:
(500 + 300) : a — 15,
при условии, что a = 10.
Подставляем число 10 (значение переменной) вместо переменной
(500 + 300) : 10 — 15
Затем выполняем сначала арифметическое действие в скобках: 500 + 300 = 800.
Затем выполняем деление 800 : 10 = 80.
Выполняем вычитание 80 — 15 = 65.
Ответ: (500 + 300) : 10 — 15 = 65.
Задание семь.
Вычислите:
(270 — 120) * (x — 10),
при условии, что x = 45.
Как решаем: подставляем число 45 (значение переменной) вместо переменной x
(270 — 120) * (45 — 10).
Затем выполняем сначала арифметическое действие в скобках: 270 — 120 = 150.
Выполняем арифметическое действие во вторых скобках: 45 — 10 = 35.
Затем выполняем умножение 150 * 35 = 5 250
Ответ: (270 — 120) * (45 — 10) = 5 250.
Задание восемь.
Вычислите:
(50 * x) — (3 * y)
при условии, что x = 2; y = 10
Подставляем число 2 вместо переменной x
(50 * 2) — (3 * y).
Подставляем число 10 вместо переменной y
(50 * 2) — (3 * 10).
Затем выполняем сначала арифметическое действие в скобках: 50 * 2 = 100.
Выполняем арифметическое действие во вторых скобках: 3 * 10 = 30.
Затем выполняем вычитание 100 — 30 = 70
Источник
Как понять обясните найдите значения произведения чисел.
Если вам необходимо получить ответ на вопрос Как понять обясните найдите значения произведения чисел?, относящийся
к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу.
В категории Математика вы также найдете ответы на похожие вопросы по
интересующей теме, с помощью автоматического «умного» поиска. Если после
ознакомления со всеми вариантами ответа у вас остались сомнения, или
полученная информация не полностью освещает тематику, создайте свой вопрос с
помощью кнопки, которая находится вверху страницы, или обсудите вопрос с
посетителями этой страницы.
Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.
Поиск значения числовых выражений
Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.
Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:
- Числа (целые, дробные и т.д.);
- Знаки: «+», «—», «•» и «÷».
Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.
Пример 1. Решение числового выражения
Задача. Решить:
20 — 2 • 10 ÷ 5 — 4 = ?
Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:
20 — 4 — 4 = ?
Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.
Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.
Ответ. 12
Пример 2. Решение числового выражения
Задача. Решить:
0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?
Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:
0,2 — (— 20) + 10
Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:
0,2 + 20 + 10 = 30,2
Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2
Ответ. 30,2
Находим значение выражения со скобками
Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.
Пример 3. Значение числового выражения со скобками
Задача. Решить:
5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?
Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:
- 7 — 2 • 3 = 7 — 6 = 1
- 6 — 4 = 2
Когда скобки решены, подставляем полученные значения в наш пример:
5 + 1 • 2 ÷ 2
Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:
- 1 • 2 = 2
- 2 ÷ 2 = 1
Упрощенное выражение выглядит следующим образом:
5 + 1 = 6
Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6
Ответ. 6
Значение числового выражения со скобками
Задача. Решить:
4 + (3 + 1 + 4 • (2+3)) = ?
Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:
3 + 1 + 4 • (2+3)
В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:
2 + 3 = 5
Теперь можем подставить определенное значение в общую скобку:
3 + 1 + 4 • 5
Начинаем решение с умножения и далее слева направо:
- 4 • 5 = 20
- 3 + 1 = 4
- 4 + 20 = 24
Далее подставляем полученный ответ вместо большой скобки и получаем:
4 + 24 = 28
Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28
Ответ. 28
Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.
Поиск значения выражения с корнями
Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:
- Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
- Извлекаем корень из числа, которое получили в результате решения обычного примера.
Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.
Значение числового выражения с корнями
Задача. Решить:
√ 2² • 2² • 3² = ?
Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:
√2² • √2² • √3² = ?
Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:
2 • 2 • 3 = 12
Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12
Ответ. 12
Нет времени решать самому?
Наши эксперты помогут!
Находим значение числовых выражений со степенями
Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.
Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].
Задача. Решите:
[ 3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=? ]
Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:
[(a cdot b)^{r}=a^{r} cdot b^{r}]
Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:
[ (3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3} ]
Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:
[ 21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21 ]
Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]
Ответ. 21
Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:
[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]
Ответ. 21
Задача. Решить:
[ 2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6} ]
Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25
Выражения с дробями
Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.
Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.
Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.
Задача. Решить:
[ 6 frac{2}{13}+4 frac{1}{13}=? ]
Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13} ]
Теперь выполняем вычисления в знаменателе и числителе и находим ответ:
[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13} ]
Ответ. [10 frac{3}{13}]
Примеры(2):

Задача. Решить:
[ frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=? ]
Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:
[ frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4} ]
Теперь можем придать нашему первоначальному выражению следующий вид:
[ frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4} ]
Ответ. [-frac{3}{4}].
Выражения с логарифмами
Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.
Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).
В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.
Задача. Решить:
[log _{27} 81+log _{27} 9=?]
Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:
Это позволит нам решить пример следующим образом:

Ответ. 2
Решаем выражения с тригонометрической функцией
Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:
- Синус;
- Косинус;
- Котангенс;
- Тангенс;
- Секанс;
- Косеканс.
Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.
В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.
Задача. Решить:
[ frac{24}{sin ^{2} 127+1+sin ^{2} 217} ]
Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:
sin217 — sin (90 + 127) = cos127
Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1} ]
Вспоминаем, что по тригонометрическому тождеству sin2a+ cos2 a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin2127+ cos2127) преобразуем в единицу и получаем:
[ frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2 ]
Ответ. 2

Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой. Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле.
Задача. Решить:
[ sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=? ]
Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

Теперь по формуле приведения решаем наш пример:
[ sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6 ]
Ответ. — 6.
Общий случай: находим значения выражений с дробями, функциями, степенями и не только
Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:
- Степени;
- Скобки;
- Корни;
- Функции и т.д.
Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.
Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:
- Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
- Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
- Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
- Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.
Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.
Задача. Решить:
[ -frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=? ]
Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:

Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:
[ sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right. ]
Со знаменателем дела обстоят куда проще:
[ ln e^{2}=2 ]
Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:

Теперь остается решить следующее выражение:

Ответ. 27
Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.
Как найти значение выражения числителя дроби, подкорневого значения рационально?
Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.
Правило 1. Когда произведение равно нулю
Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.
Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.
Правило 2. Группировка и вынесение чисел
Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.
Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]
Решение примеров с переменными
Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.
Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:
2x — y = 2 • 2,5 — 2 = 3
При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.
Математика
6 класс
Урок № 26
Произведение целых чисел. Часть 2
Перечень рассматриваемых вопросов:
- На уроке мы научимся формулировать и узнавать свойства умножения.
- Находить квадраты и кубы целых чисел.
- Вычислять значения числовых выражений, содержащих разные действия.
- Выполнять числовые подстановки в буквенные выражения и находить соответствующие им значения.
Тезаурус
Произведение любого целого числа a и нуля равно нулю.
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.
Степенью целого числа a с натуральным показателем n (n > 1) называется произведение n множителей, каждый из которых равен a.
Список литературы
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Мы уже изучали правила умножения целых чисел.
Сегодня рассмотрим свойства произведения целых чисел.
Умножение целых чисел на 0.
Произведение любого целого числа a и нуля равно нулю.
a ∙ 0 = 0
Рассмотрим примеры.
Найдите произведение целого положительного числа 209 и нуля.
Решение:
203 ∙ 0 = 0
Найдите произведение нуля и целого отрицательного числа (– 29).
Решение:
0 ∙ (– 29) = 0
Умножение целого числа на 1
Произведение целого числа и 1 равно cамому числу.
a ∙ 1 = a
Рассмотрим примеры.
Вычислите произведение положительного целого числа 64 и единицы.
Решение:
64 ∙ 1 = 64
Вычислите произведение единицы и отрицательного целого числа (– 475).
Решение:
1 ∙ (– 475) = – 475
Найдите произведение нуля и единицы.
Решение:
0 ∙ 1 = 0
Умножение на (– 1)
При умножении числа на (– 1) меняется только знак, то есть получается число, противоположное a.
a ∙ (– 1) = – a
Законы умножения
Переместительный и сочетательный законы умножения верны для любых целых чисел, и их можно применять для упрощения числовых выражений.
Переместительный закон умножения:
a ∙ b = b ∙ a
Сочетательный закон умножения:
a ∙ (b ∙ c) = (a ∙ b) ∙ c
Умножение или произведение нескольких целых чисел
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.
Вычислим произведение нескольких целых чисел:
9 ∙ (– 14) ∙ 5 ∙ (– 1)
Решение:
9 ∙ (– 14) ∙ 5 ∙ (– 1) = (9 ∙ (– 14)) ∙ 5 ∙ (– 1) = (– 126) ∙ 5 ∙ (– 1) = ((– 126) ∙ 5) ∙ (– 1) = (– 630) ∙ (– 1) = 630
Ответ: 630.
При перемножении целых чисел, результат всегда будет целым числом.
Выводы
1. Если в произведении нечётное количество отрицательных множителей, то произведение будет отрицательным.
2. Если в произведении чётное количество отрицательных множителей, то произведение будет положительным.
Степень целого числа a с натуральным показателем n
Определение: степенью целого числа a с натуральным показателем n (n > 1) называется произведение n множителей, каждый из которых равен a.
a ∙ a ∙ a ∙ a ·…∙ a = an
n множителей
Рассмотрим примеры.
1. Первая степень любого числа равна самому числу.
a1 = a
2. Вторая степень любого числа называется квадратом.
a2 = a ∙ a
3. Третья степень любого целого числа называется кубом.
a3 = a ∙ a ∙ a
Например,
24 = 2 ∙ 2 ∙ 2 ∙ 2 = 16
(– 5)3 = (– 5) ∙ (– 5) ∙ (– 5) = – 125
Итак, мы научились выполнять сложение, вычитание и умножение целых чисел. Рассмотрим, как найти значение выражения, которое содержит такие действия.
42 – 15 ∙ (– 6)
Решение
42 – 15 ∙ (– 6) = 42 – (15 ∙ (– 6)) = 42 – (– 90) = 42 + 90 = 132
Ответ: 132.
Дополнительный материал
Мы изучили правила и свойства умножения целых чисел.
Используя их, решим две задачи.
Задача №1
Чему равно произведение последовательных целых чисел, начинающихся числом (– 200) и оканчивающихся числом 200?
Решение
Между числами (– 200) и 200 находится 0, а любое число, умноженное на 0 равно 0. Поэтому произведение последовательных целых чисел от (– 200) до 200 равно 0.
Ответ: 0.
Задача №2
Чему равно произведение всех целых чисел?
Решение
Целые числа состоят из целых положительных, отрицательных чисел, а также нуля. При умножении любого числа на ноль будет 0. Поэтому произведение всех целых чисел равно 0.
Ответ: 0.
Разбор заданий тренировочного модуля
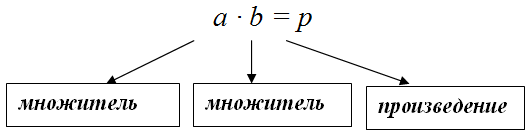
Тип 1. Разместите нужные подписи под изображениями.
Какие законы представлены в формулах?
Законы умножения
- a ∙ b = b ∙ а
- а ∙ (b ∙ с) = (а ∙ b) ∙ с
Варианты ответов:
Сочетательный закон умножения
Переместительный закон умножения
Свойство 0
Для ответа на вопрос задания обратимся к теоретическому материалу сегодняшнего урока.
Правильный ответ:
1. Переместительный закон умножения
2. Сочетательный закон умножения
Тип 2. Вставьте в текст нужные слова.
Чтобы найти … нескольких чисел, нужно найти произведение … чисел, … на третье число и так далее.
Варианты слов для вставки:
произведение
трёх
первого
двух первых
умножить
разделить
сложить
вычесть
Для ответа на вопрос задания обратимся к теоретическому материалу сегодняшнего урока.
Правильный ответ:
Чтобы найти произведение нескольких чисел, нужно найти произведение двух первых чисел, умножить на третье число и так далее.