Если вы когда-либо слышали, что алгоритмы нужно знать всем разработчикам, но что это такое представляете с трудом – вам сюда.
Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
Интересно, хочу попробовать
Для опытных программистов некоторые понятия, в том числе и алгоритмы, настолько фундаментальны, что не возникает даже мыслей о том, что, то или иное определение может оказаться непонятным, сложным или вообще, пугающим, для новичка.
Алгоритм – вызывает ассоциации ни то с логарифмами, ни то с арифметикой.
И это слово действительно пришло из математики и использовалось для описания алгоритма Евклида, который применяется для нахождения наибольшего общего делителя двух целых чисел.
Если говорить нормальным языком, алгоритм – это пошаговая инструкция, где результат прошлого шага строго определен и используется в качестве входных данных для следующего шага.
Однако, поскольку в реальной жизни при написании программы совсем нечасто нужно искать общий делитель у целых чисел, раскладывать на множители и вообще думать о математиках, творивших в 300-е года до н.э., рассмотрим немного более жизненный пример применения алгоритмов.
Давайте представим, что телефонный справочник все еще актуален (да, тот бумажный, если вы их застали). Допустим, мы хотим набрать Николая Должанского. Принимая во внимание, что Николай есть в телефонном справочнике, мы можем найти его номер несколькими различными способами.
Метод полного перебора или линейный/последовательный поиск
Самый простой способ найти что-то в списке – пройти по нему по порядку, сравнивая с искомым значением. То есть:
1. Надежда Александрова –> не подходит
2. Николай Алексеев –> не подходит
…
И так далее, пока вы не найдете наконец Николая Должанского. Вероятно, понадобятся десятки и даже сотни операций сравнения. То есть, если вы захотите поболтать с Ярославом Яковлевым, то это займет порядком больше времени.
Как вы уже поняли, смысл алгоритма линейного поиска заключается в простом переборе значений от начала списка и до конца (или искомого результата). Это брутфорс. Этот алгоритм крайне прост и может возникнуть множество ситуаций, где его использование будет иметь смысл.
Например, если нужно найти телефон приятеля не в целой книге, а, предположим, на клочке бумаги, где помимо его номера всего десяток других записей – пройти список сверху вниз, в этом случае, будет умным решением.
Поиск по частям
У большинства людей просто не хватит терпения перебирать весь справочник. Поэтому они пойдут более прагматичным путем – будут разделять книгу на части.
Процесс деления на части предполагает сначала нахождение основной области, где, предположительно, находится искомое значение. Мы тут все еще ищем Николая Должанского.
Поиск начнем, перелистнув книгу на 30 страниц вперед. Мы увидим, что все фамилии начинаются на «Б». Перейдем еще на 60 вперед и увидим «Г». Достоверно известно, что «Г» находится прямо перед «Д», а значит, Коля где-то рядом и с этого момента мы будем двигаться осторожнее.
Этот алгоритм описывает, как большинство людей ищут что-то в справочниках. Но поскольку мы, люди, часто выбираем неоптимальные пути решения задач, рассмотрим правильный подход к делению на части – бинарный алгоритм поиска.
Бинарный алгоритм поиска
Вот это уже звучит серьезно, да? На самом деле, ничего сложного. Бинарный поиск предполагает, что мы будем делить исходный массив данных пополам, отбрасывать ту часть, где искомого значения быть не может и делить остаток пополам снова, пока область поиска не сократится до минимально возможной.
В терминах телефонной книги, работа будет строиться следующим образом. Наш справочник содержит 400 страниц. Даже если мы все еще ищем Николая Должанского, который находится на 136 странице, мы можем воспользоваться бинарным поиском. Делим книгу пополам и по счастливой случайности попадаем прямо между буквами «М» и «Н» на 199 и 200 страницах соответственно. Мы знаем, что буква «Д» в алфавите находится перед «М», так что справедливо будет утверждение:
Николай Должанский находится на странице между 0 и 199
Ту часть, что начинается с «Н» мы выбрасываем.
Далее, мы делим на две части первые 200 страниц телефонного справочника и видим, что попали мы прямо на страницу с буквой «Г», а «Г», как известно, идет перед «Д». То есть нам снова стал известен неоспоримый факт:
Телефон Николая Должанского находится между 99 и 199 страницами
И вот, стартовав с 400 страниц, мы, всего через две операции сравнения, сократили область поиска на 3/4. Учитывая, что телефон Коли находится на 136 странице, нам предстоит сделать следующие операции:
[99-199] -> [99-149] -> [124-149] -> [124-137] -> [130-137] -> [133-137] -> [135-137] -> [136]
Еще 6 сравнений. Чтобы рассчитать количество операций необходимых для нахождения нужной страницы бинарным поиском, мы можем взять логарифм от количества страниц с основанием 2 и получим:
log2(400) = 8.644
то есть, округлив, в худшем случае – 9 операций сравнения. Рядом с исходным числом страниц, конечно, ерунда. Но давайте поговорим о по-настоящему серьезных книгах. Пусть в нашем справочнике будет не 400, а 4 000 000 страниц. Попробуйте представить, сколько операций сравнения нам потребуется? На самом деле, немного:
log2(4000000) = 21.932
то есть, 22 раза нужно будет провести сравнение частей справочника, прежде, чем 4 000 000 превратятся в 1.
Сравните скорость работы линейного и бинарного алгоритмов поиска для такого количества страниц.
Заключение
В общем, так и со всеми алгоритмами. Изучение алгоритмов – это изучение способов решать проблемы и задачи наиболее оптимальным путем. Алгоритм – это решение, рассмотренное со всех сторон и преобразованное в эдакий todo-list действий, которые нужно совершить, чтобы воспроизвести его.
И отдельная тема, это преобразование алгоритма в код на конкретном языке, ведь в разных языках алгоритмы (особенно поисковые) могут реализовываться по-разному. Иногда, это может быть уже встроенная в язык функция, которая выдаст нужный результат из массива одной строкой, а где-то понадобиться пара-тройка десятков строк.
И, для примера, вот так будет реализован бинарный поиск на Ruby:
def binary_search(target, list)
position = (list.count / 2).floor
mid = list[position]
return mid if mid == target
if(mid < target)
return binary_search(target, list.slice(position + 1, list.count/2))
else
return binary_search(target, list.slice(0, list.count/2))
end
end
puts binary_search(9, [1,2,3,4,5,6,7,8,9,10])
Другие статьи по теме
Изучаем алгоритмы: полезные книги, веб-сайты, онлайн-курсы и видеоматериалы
Что такое алгоритм?! Часть первая
Время на прочтение
13 мин
Количество просмотров 42K
Терзаем вместе основной кирпичик программиста — Алгоритм.
Проблема
Текущее состояние в области программирования — это обучение ремеслу по большей части личной практикой или разборами примеров стороннего кода, с которым по каким-то причинам приходится сталкиваться.
В результате программированию учишься по наитию. Лишь немного в этом труде помогают сборники алгоритмов, прикладных техник и шаблонов проектирования. Общая совокупность предлагаемых ими рецептов выстраивается длинным списком, и его длина грозит каждому из прочитанных приемов быть позабытым (как была забыта 53-яя личная группа в «телеге» до введения разбиения по каталогам). Но даже тот прием, который остался в памяти, чаще всего просто является описанием прикладной задачи, в которой было успешно его использование.
Почему конкретный прием был успешен в задаче-образце? Будет ли он успешен в твоём проекте? Какие признаки проекта дают понять, что использование приёма уместно?
В личном опыте существования в профессии не раз отмечено, что каждый Junior борется с одинаковыми ветряными мельницами и постигает методы создания программ основываясь только на своих ошибках. Но ведь такие ошибки совершили уже очень многие. Почему до сих пор не создана система правил программирования, которая поможет обойти новоиспеченному кораблю-программисту подводные прибрежные камни? Ну, например, объяснение вреда использования метода «Copy-Paste» для развития кода. Если такие правила получится объяснить малым набором причин, их сформировавшим, то это объяснение обеспечит их запоминание и последующее использование в практике, тем самым поможет уклониться от бесчисленных грабель, разложенных тут и там.
Для компактного и полезного набора объяснений нужно:
- систематизировать методы работы с кодом;
- разобрать по группам приёмы работы с алгоритмами, которые являются главной целью написания любого кода;
- выделить простые признаки применения шаблонов проектирования;
- разработать универсальные правила и наборы эффективных способов построения сложных алгоритмов.
Если обобщить, то нужны алгоритмы для написания и развития алгоритмов.
Задуманная серия статей не претендует на полное решение указанной проблемы. Предпринимается небесспорная попытка сделать первый шаг на пути к этому решению. Этот шаг состоит в выделении структуры и свойств главного кирпичика программиста — Алгоритма.
Задача
Сформулируем основную задачу, которую хочется решить. Для этого сначала запишем операции над алгоритмами, которые программист выполняет в ходе написания своего проекта:
- методы синтеза макро-алгоритма из под-алгоритмов (последовательной, параллельной и смешанной группировкой);
- методы структурной трансформации макро-алгоритмов (оптимизационной, специализирующей, стыковочной…);
- методы сохранения и переноса алгоритмов;
- методы синтеза универсального алгоритма из сходных алгоритмов разных областей исполнения;
- методы специализации универсального алгоритма в новой области исполнения;
- методы формирования и развития комплексной системы совместно работающих алгоритмов;
- методы взаимодействия одновременно исполняющихся алгоритмов;
- и другие методы, полный список которых привести сложно, да и нет необходимости.
Рассмотрим существующие на текущий момент варианты значения слова «алгоритм» в поисках подсказок, о том как можно работать с алгоритмами.
Так, например, формулировка «конечная совокупность точно заданных правил решения произвольного класса задач» говорит что есть возможность как-то «точно задать правила» из них собрать «совокупность» и этой совокупностью «решить» некоторый «класс задач».
Сразу возникает масса вопросов к этому определению:
- Что такое правило?
- Как, кому и для кого это правило можно задать?
- Что есть объединение совокупностью?
- Каким образом правила соотносятся с задачей?
- Что формирует класс задачи?
- Определяется ли способ формирования совокупности правилами и задачами?
- …
Другая формулировка «набор инструкций, описывающих порядок действий исполнителя для решения некоторой задачи» говорит что есть «исполнитель», который может выполнять некоторые «действия», и при некотором «порядке» выполнения этих «действий» «решается задача». Вопросов не стало меньше:
- Какова структура набора?
- Какие есть варианты действий и исполнителей?
- Существуют ли минимально возможное действие, минимальный набор необходимых действий?
- Каким образом действия встроены в исполнителя?
- Какие есть способы создания копии исполнителя (например, если исполнитель — человек)?
- Как действия зависят друг от друга в упорядоченном выполнении?
- Что есть задача кроме того, что она выполняется последовательностью действий?
- Как задача соотносится с исполнителем и с действиями?
- Возможно ли использовать решение задачи в качестве действия?
- Какие возможны варианты указания порядка действий?
- Если воспроизведение патефоном записи звуков леса является алгоритмом, то какова структура этой задачи?
- Если репликация ДНК является алгоритмом, то каков её исполнитель?
- Если исполнителем является Машина Тьюринга, то как с её использованием решить механическую задачу, например, воспроизведение звука?
Перечислено много вопросов, но они мало помогают в поиске методов работы с алгоритмом. Поэтому поставим себе меньшую задачу, но тоже очень нам важную. Давайте попробуем сформулировать, что делает алгоритм способом решения наших задач, и какие процессы являются для него «действиями». Даже решение этой «маленькой» задачи оказывается очень объемным для одной статьи, поэтому будем его разбивать на части. И поэтому первую статью серии целиком посвятим только «Действию» и его признакам, которые опущены в указанных выше определениях алгоритма, но являются очень важными для ответов на все заданные вопросы.
Определение алгоритма
Рассмотрим определение алгоритма, говорящее, что он — приводящая к решению задачи последовательность действий. Как программисту мне приходится писать много кода. Этот код состоит из частей. Такими частями являются и функции, и классы, и модули. Когда я пишу текст функции — я занимаюсь написанием алгоритма.
Раньше алгоритм создавали в виде блок схем и полуавтоматически компилировали в машинные коды. Сейчас я избавлен от необходимости быть художником и компилятором для написания программы. Текст моей функции — это запись алгоритма в текстовом виде — его текстовая блок-схема. Здесь можно вспомнить Scratch, где используется визуальное создание блок-схемы алгоритма без написания текста. Способ записи алгоритма сейчас не так важен.
Важно, что в написании алгоритма функции я могу использовать вызовы других функции, которые я или другой программист уже написал до этого момента. Вспоминая фразу «последовательность действий, приводящая к решению задачи», можно отметить, что функции, написанные ранее, являются моими «действиями». То есть «действия» могут быть функциями. Если обобщать, то «действия» могут быть алгоритмами.
Если «действие = алгоритм», то определение можно попробовать переписать рекурсивно «алгоритм — это приводящая к решению задачи последовательность использования существующих алгоритмов». Рекурсивные определение не самое простое, что можно записать в словаре обычного человека. Но для программиста и математика эта форма знакома. Мы умеем с ней работать, и это даёт нам преимущество в рассмотрении разных задач, разбиваемых на подобные себе подзадачи. Так давайте воспользуемся этим преимуществом.
Чтобы разрешить рекурсию нам необходимо найти:
- терминальное условие выхода из рекурсии — минимальное неделимое «действие» (атомарный алгоритм), которое можно использовать в разработке алгоритма;
- способ перехода от текущего уровня рекурсии (набора «действий») к следующему уровню (алгоритму).
Действие
Для начала рассмотрим «действие» и попробуем найти причину, обеспечивающую возможность использования существующего «действия» для создания нового алгоритма.
Этой причиной является возможность повторного использования «действия» с получением тождественного результата. Только тогда разработанный с использованием этого «действия» алгоритм решения некоторой задачи будет одинаково решать эту задачу снова и снова. Мы нащупали важные законы нашего мира, в котором:
- существуют «действия», главным свойством которых является одинаковость результатов их исполнения в разные моменты времени и в разных местах,
- существует возможность создать такую схему использования нескольких «действий», которая сформирует из них новое «действие», которое мы назвали алгоритмом.
Какие признаки «действия» кроме повторимости делают возможным его использование в создании алгоритма? Что является терминальным неделимым «действием»? Чтобы ответить на этот вопрос стоит рассмотреть разные примеры «действий» из нашего опыта. Программисты встречали их много раз. Это и сложение, и умножение, и установка цвета пикселя на экране. Но мы знакомы с ними и вне программирования. Вся наука основывается на повторяемых явлениях.

Рассмотрим, что происходит при выполнении «действия». Например, во время падения яблока с ветки яблони на землю. В этом процессе происходит несколько изменений. Если вспомнить школьную физику и рассмотреть ситуацию в системе отсчета, привязанной к Земле, то сила гравитации вызывает изменение скорости яблока, разгоняя его. При этом в процессе отмечается еще одно важное изменение — уменьшается расстояние между яблоком и Землей.
В рамках примера процесса «Земля-Яблоко» можно отметить у «действия» следующие признаки:
- наличие процесса изменения (расстояния и параметров движения объектов);
- наличие объектов, взаимодействие которых вызывает такие изменения;
- наличие локальности процесса, то есть существование значения расстояния между объектами, с превышением которого их взаимодействие перестает вызывать процесс изменения, что делает невозможным использование «действия» (Земля и гипотетическое яблоко, находящееся вне солнечной системы).
Рассмотрим с этими признаками разные области и процессы, выделяя в них примеры «действий» и контролируя особенности указанных признаков в описании структуры «действия».
Физические процессы
Для физических систем, процессы которых мы наблюдаем в нашем мире, характерные объекты и изменения опираются на фундаментальные взаимодействия и потому их достаточно просто выделить по аналогии с гравитационным взаимодействием Земли и яблока. Например, для системы из протона и электрона или системы двух протонов.
Отдельно от этих простых взаимодействий двух объектов стоят многокомпонентные процессы, например, ядерные реакции (по структуре «действия» близки к химическим процессам, рассматриваемым далее). Сложны и процессы описываемые суммарным взаимодействием большого числа элементов, например, «идеальный газ». Пока отложим их рассмотрение и сосредоточимся на самых простых примерах.
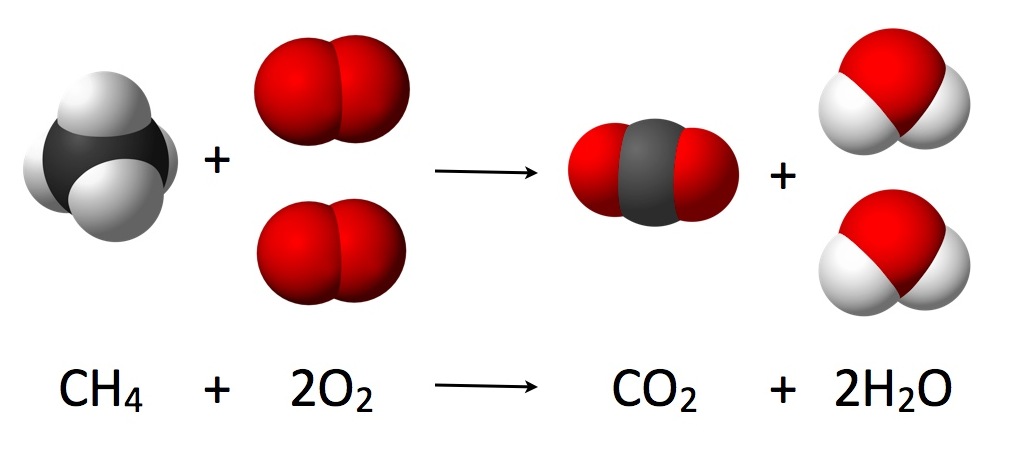
Химические процессы
Перейдем к следующей большой области — химическим процессам. Химические реакции (например, ) по признаку своей повторимости так же являются «действиями». Объектами в них являются атомы и молекулы. Для описания происходящих изменений необходимо немного преобразовать «физические» изменения. Так изменения параметров движения в совокупности дают нам изменение температуры в ходе химической реакции. А среди изменений расстояний между молекулами мы, игнорируя броуновское движение, можем выделить фиксацию расстояния в виде повторимого формирования и разрушения связей между частями взаимодействующих молекул. Локальность для химической реакции тоже существует — это отсутствие реакции при нахождении гидроксида натрия и соляной кислоты в разных пробирках и наличие реакции при соприкосновении веществ. Конечно, в «химической» области «действий» есть особенности не сводящиеся к молекулам, например, фотохимические реакции, где к объектам необходимо добавить фотоны. Самые простые процессы выбраны для рассмотрения намеренно.
Математические процессы
Следующей областью выберем «действия» из известных нам абстрактных алгоритмов. Самые яркие их представители — математические процессы. В этой области есть действительно «сложные случаи», но для этой статьи достаточно хорошо знакомых примеров. Рассмотрим в качестве «действия» достаточно элементарную операцию — сложение. А примером этого «действия» выберем сложение математиком двух целых чисел.
В ситуации с математиком можно выделить много объектов, но с точки зрения «действия» («сложение математиком двух целых чисел»), объекта всего три: это объект «математик», объект «первое число» и объект «второе число». В отличие от всех рассмотренных ранее объектов числа являются обозначениями, то есть виртуальными объектами. И их преобразование в алгоритме более сложно устроено нежели изменение расстояния и параметров движения объектов, как это было для «химических» действий. Подробности такого преобразования — это тема отдельной увлекательной статьи. А в рамках текущей рассмотрим древнего математика, который складывает числа, используя кучки камешков (рим. ‘calculi’), и более «современного» математика, использующего абак. Абстракции таких способов вычисления суммы не так далеко отошли от физических и химических процессов, поэтому структура процессов их «действий» полностью описывается изменениями расстояний и связей.
Интересно, что на примере древнего математика становится понятен смысл слова «сложить», которое отсылает нас к действию «класть» и к фразе «положить вместе».
Сложение и древний математик
Для математика, оперирующего камешками, сумма это «действие» со следующими характеристиками.
Исходные объекты:
- это сам «математик» (он взаимодействует со слагаемыми);
- лежащая отдельно кучка №1, содержащая и связывающая вместе камешки (подобно химическим связям), и обозначающая первое слагаемое;
- лежащая отдельно кучка камешков №2, обозначающая второе слагаемое.
Процессы:
- «математик» подходит к кучкам (физически изменяет расстояние между кучками и собой) и начинает с ними взаимодействие;
- «математик» объединяет две кучки (физически изменяет расстояние между двумя кучками или переносит все камешки одной кучки в другую, возможно, используя «действие» «Перенос по-одному» камешку)
Результирующие объекты:
- сформированная кучка камешков, обозначающая результат (сумму);
- «математик», отошедший от кучки результата и переставший на неё воздействовать.
Сложение и математик-абакист
У математика с абаком ситуация сложнее. Кучки разделены по значению на разрядные борозды.
Можно рассмотреть самый простой абак с двумя разрядами-бороздами. Пусть он будет десятичный. Тогда один камешек на борозде десятков соответствует десяти камешкам на борозде единиц. И 10 — это максимальное количество камешков на борозде единиц. По сравнению с действием первого математика меняется представление слагаемых. И в арсенале математика уже необходимы нескольких готовых «действий».
Действия:
- «Перенос по-одному» из борозды в борозду одинакового уровня (действие, позаимствованное у первого математика);
- «Перенос в десятки», которое необходимо выполнять, если борозда единиц полностью заполняется, тогда из неё убираются все камешки кроме одного, который переносится в борозду десятков.
Исходные объекты:
- это сам «математик» (он взаимодействует со слагаемыми);
- группа камешков №1, лежащих и удерживаемых двумя бороздами (единиц и десятков), и обозначающих первое слагаемое;
- группа камешков №2, лежащих и удерживаемых двумя бороздами (единиц и десятков), и обозначающих второе слагаемое;
Процессы:
- «математик» подходит к группам борозд (физически изменяет расстояние между ними и собой) и начинает с ними взаимодействие;
- «математик» объединяет камешки из двух борозд единиц (физически изменяет расстояние между камешками, разрушает связи со старой бороздой и создает связи с новой) с использованием действий «Перенос по-одному» и «Перенос в десятки»;
- «математик» объединяет камешки из двух борозд десятков с использованием действия «Перенос по-одному»
Результирующие объекты:
- сформированная группа камешков в двух бороздах (единиц и десятков), обозначающая результат (сумму);
- «математик», отошедший от группы камешков результата и переставший на них воздействовать.
Локальность в этих математических «действиях» описывается отсутствием взаимодействия двух слагаемых, находящихся далеко от математика, и запуском процессов сложения когда все три объекта сложения «близко». Повторяемое изменение в математическом «действии» выражается в изменении связей между камнями и удерживающими их локациями (кучками, бороздами).
Сложение и машина Тьюринга
Можно пойти чуть дальше и заменить математика в таких «действиях» на «управляющее устройство» машины Тьюринга. Тогда «ячейки ленты» машины Тьюринга будут содержать слагаемые.

Подробное описание исходных и результирующих состояний объектов, а так же «действий» производящих эти изменения для сложения, исполняемого машиной Тьюринга, оставим за рамками этой статьи. Но упомянем, что перейдя к машине мы снижаем требования к исполнителю «действия», что является главным способом для создания формальных методов работы с алгоритмом. Можно поставить себе целью упрощение каждой составляющей алгоритма до состояния, когда её выполнение можно будет поручить компьютеру. Тогда в определении алгоритма не останется тёмных мест, и многочисленные вопросы, перечисленные в начале, найдут свои ответы. Пока формализован только исполнитель. Скажем спасибо за это Тьюрингу и вспомним про «действие», формализация которого уже на пороге.
Выводы
Соберём всё, что мы отметили рассматривая разные примеры «действия»:
- «действие» можно использовать для создания алгоритма;
- «действие» может быть элементарным;
- «действие» может быть реализовано алгоритмом;
- в «действии» обязательно участвует некоторый объект или группа объектов;
- для группы объектов «действие» происходит только тогда, когда эти объекты «достаточно близко»;
- в действии изменяются связи и параметры объектов (включая параметры их движения);
- «действие» всегда и обязательно должно быть повторимо.
Признак Повторимости помогает нам в создании наших алгоритмов. С его использованием мы из всех процессов выделяем те, что являются «действием» и на их основе создаём новые алгоритмы. Более того этот признак достаточно прост и на основе его формализации можно снизить требования к системе обнаруживающей и создающей «действия» и поручить это нашему компьютеру.
Следующая статья серии (Часть 2) будет посвящена рассмотрению способов, с использованием которых «действия» могут быть сгруппированы в алгоритм. Этих способов достаточно много и есть предпосылки, что их описание не получится уместить в одну статью. Напишем — увидим.
Спасибо Вам за внимание.
Отзывы
Буду очень благодарен за отзывы и предложения, так как они помогают мне скорректировать направление развития работы в области.
Отдельное волнение у меня есть по стилю и форматированию, используемым в статье (кавычки, абзацы, курсив). Напишите, пожалуйста, если у Вас есть замечания к ним. Можно личным сообщением.
Ссылки
- Главная страница и теория работы (GitLab GPL): Проект «Общая теория алгоритмов»
- Вводная статья работы «Разрабатываем теорию алгоритмов как проект с открытым исходным кодом». Пожалуйста, не судите строго эту наивную публикацию «сверх-идеи» устаревшей версии 2019 года.
- Статьи серии «Что такое алгоритм?!»
- №1 «Действие» (текущая)
- №2 «Жизнь»
- №3 «Синтез алгоритма запоминанием»
- №3.1 «Эволюция памяти»
- №3.14 «Обучение»
- №5 «Эволюция поведения»
- №4 «Математика»
- №4.0 «Физика»
- №3.25 «Язык»
- №5.0 «Философия»
- №5.00 «Искусственный интеллект»
- Статьи в хабе «Программирование»:
- Детская сказка программисту на ночь
- Эволюция программного проекта и ООП
- Как не понимать принципы развития архитектуры SOLID
- Все рисунки к статье (кроме заглавного) сформированы сообществом Wikipedia. Лицензия (Creative Commons Attribution-Share Alike 4.0 International)
Основы алгоритмов
С помощью этого хендбука вы научитесь проектировать, оптимизировать, комбинировать и отлаживать алгоритмы — причём без привязки к какому-либо языку программирования. Кроме теории мы собрали и практические задания разного уровня сложности, а также подготовили систему автоматической проверки эффективности алгоритмов — всё это поможет вам закрепить и отточить новые навыки.
Общий прогресс изучения
0 / 48
глав прочитано
0 / 0
задач выполнено
-
1. Введение
-
2. Алгоритмы и сложность
-
3. Техники проектирования алгоритмов
-
4. Решение практических задач по программированию
-
5. Разминка. Последовательные алгоритмы
-
6. Жадные алгоритмы
-
7. Разделяй и властвуй
-
8. Динамическое программирование
-
9. Основные структуры данных
-
10. Графы
#статьи
- 7 дек 2022
-
0
Что такое алгоритмы и какими они бывают
Ты можешь разрабатывать микросервисы и знать все уровни модели OSI, но какой ты программист, если не можешь объяснить ребёнку, что такое алгоритм?
Иллюстрация: Катя Павловская для Skillbox Media
Пишет об истории IT, разработке и советской кибернетике. Знает Python, JavaScript и немного C++, но предпочитает писать на русском.
Ведущий бэкенд-разработчик мобильного приложения «Альфа-Банка».
Иногда совсем простые вопросы о профессии вводят в ступор даже опытных специалистов. Примерно так происходит, когда у разработчика с 5–10-летним стажем спрашивают: «Что такое алгоритм?»
Но для того мы здесь и собрались, чтобы дать понятные ответы на «глупые» вопросы. В этой статье расскажем, что такое алгоритмы, для чего они нужны и какими бывают.
Вы узнаете:
- Что такое алгоритмы
- Для чего их используют
- Какие у них есть свойства
- Что такое псевдокод
- Что такое блок-схемы и как их рисовать
- Примеры линейных, ветвящихся, циклических и рекурсивных алгоритмов и блок-схем
В широком смысле алгоритм — это последовательность действий, которые нужно выполнить, чтобы получить определённый результат.
Слово «алгоритм» произошло от имени персидского математика Абу Абдуллаха аль-Хорезми. В своём труде «Китаб аль-джебр валь-мукабала» учёный впервые дал описание десятичной системы счисления. А наука алгебра получила своё название в честь его книги.
Мы часто пользуемся алгоритмами в повседневной жизни. Например, когда хотим приготовить кофе в капсульной кофемашине, руководствуемся примерно таким алгоритмом:
1. Устанавливаем капсулу.
2. Проверяем уровень воды в специальном отсеке.
3. Если воды недостаточно — доливаем.
4. Ставим чашку под кран кофемашины.
5. Запускаем кофемашину.
6. Выключаем кофемашину, когда чашка наполнилась.
7. Достаём кружку.
Если не перепутать порядок шагов, то с помощью такой инструкции любой сможет порадовать себя чашкой горячего кофе. Достаточно лишь знать, как установить капсулу и включить/выключить кофемашину.
С компьютерами намного сложнее. Им неизвестно, что значит «установить капсулу», «долить воду», «запустить кофемашину» и так далее. Чтобы запрограммировать робота-баристу под определённую модель бытовой техники, алгоритм придётся расписать более детально:
1. Возьми штепсельную вилку шнура питания кофемашины.
2. Вставь штепсельную вилку в розетку.
3. Проверь, есть ли вода в отсеке для воды.
4. Если воды недостаточно:
4.1. Подними крышку отсека.
4.2. Возьми кувшин с водой.
4.3. Лей воду из кувшина в отсек, пока он не заполнится.
4.4. Закрой крышку отсека.
4.5. Поставь кувшин с водой на стол.
5. Открой крышку кофемашины.
6. Возьми из коробки капсулу с кофе.
7. Вставь капсулу в отсек для капсулы.
8. Закрой крышку кофемашины.
9. Поверни рычаг кофемашины вправо.
10. Когда чашка наполнится, поверни рычаг кофемашины влево.
11. Возьми кружку.
12. Принеси кружку хозяину.
Конечно, если мы собираем робота с нуля, то даже такой детализации будет недостаточно. Каждую процедуру ещё нужно будет реализовать на языке программирования (например, на C++ или Python), что само по себе — нетривиальная задача. Тем не менее описание стало более точным и формальным.
C научной точки зрения определение алгоритма, которое мы дали выше, не совсем точное. Ведь не всякую последовательность действий, приводящую к результату, можно назвать алгоритмом.
Алгоритм в информатике — это понятный исполнителю набор правил для решения конкретного множества задач, который получает входные данные и возвращает результат за конечное время.
У алгоритмов есть два замечательных качества: они позволяют эффективно решать задачи и не изобретать решения, которые кто-то уже придумал до нас. Это справедливо как для повседневной жизни, так и для IT.
Представьте, что оформляете загранпаспорт. Если будете всё делать сами и без инструкции, около 40 минут потратите только на выяснение необходимых справок и порядка оформления. Куда проще воспользоваться «Госуслугами», потому что алгоритм там уже составлен — делаете, что вам говорят, и ждёте результат. А ещё проще — обратиться к посреднику, который подготовит все справки и оформит паспорт за неделю.
Это очень бытовой пример, но программирование примерно так и работает. Разработчики изучают алгоритмы, чтобы писать быстрый и эффективный код, — распознают типовую задачу и подбирают для неё оптимальный алгоритм.
Допустим, нужно отсортировать в порядке возрастания числа в списке из 1000 элементов. Можно пройтись по списку 1000 раз: на каждой итерации находить наименьшее число и переставлять его в начало списка. В этом случае общее количество шагов будет равно 1 000 000 — современный компьютер справится с этим за секунду.
А если нужно упорядочить массив из 10 000 000 элементов? Тогда компьютеру придётся выполнить 1014 шагов, что потребует гораздо больше времени. Надо оптимизировать!
Разработчик, не сведущий в computer science, начнёт ломать голову над более эффективным решением. А опытный специалист применит алгоритм быстрой сортировки, который в среднем случае даст «время» 16 × 107 шагов.
Знатоки скажут, что ещё проще было бы воспользоваться библиотечной функцией сортировки (например, sorted() в Python). Тем не менее даже встроенные алгоритмы бывают недостаточно эффективными и разработчикам приходится писать собственные функции для сортировки. Но это уже совсем другая история 🙂
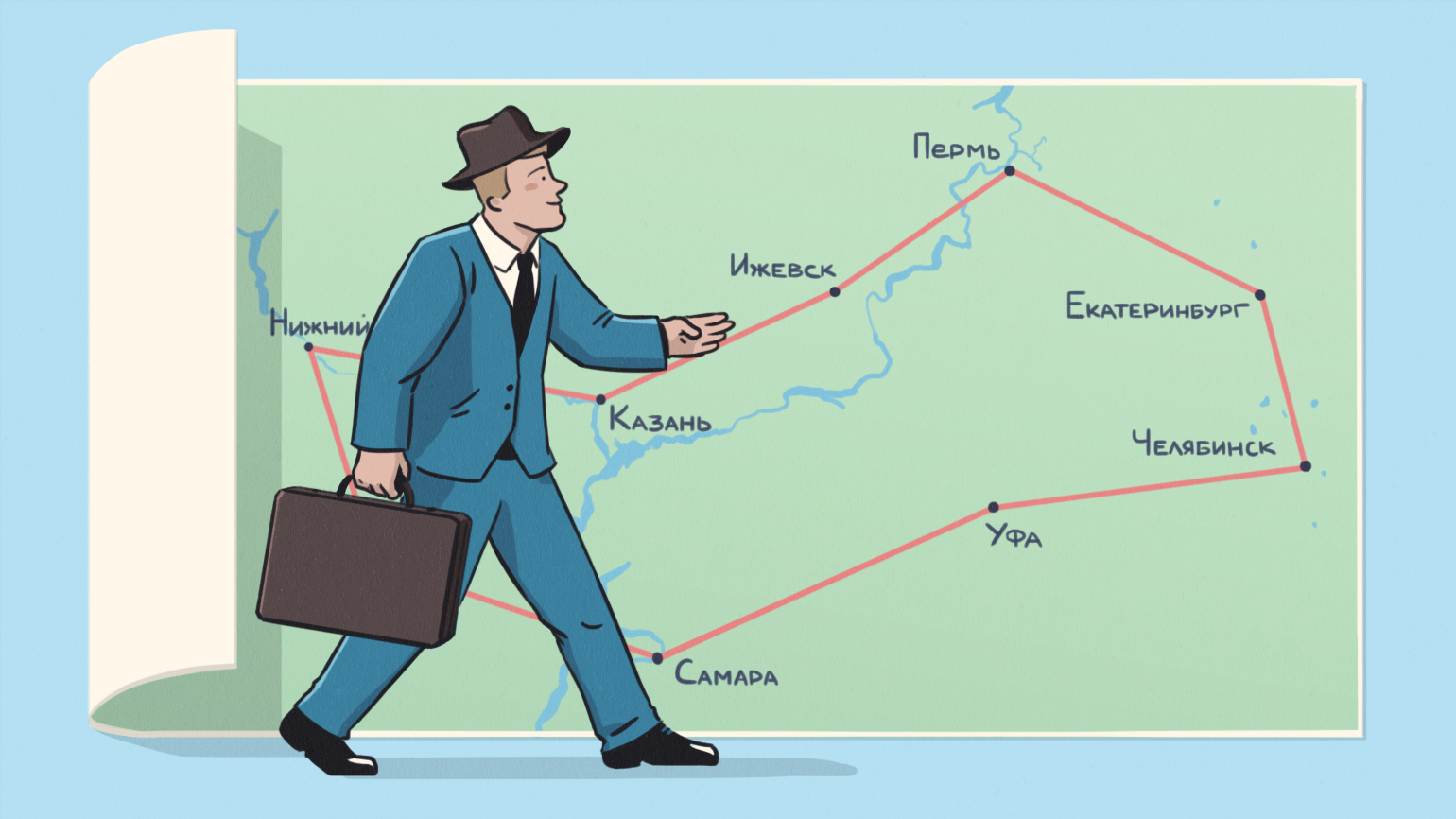
Теперь представьте: вы живёте в XX веке где-нибудь в США и зарабатываете тем, что ездите по городам и продаёте мультимиксеры. Чтобы сэкономить время и деньги, вам нужно придумать кратчайший маршрут, который позволит заехать в каждый город хотя бы один раз и вернуться обратно.
Это знаменитая задача коммивояжёра, для которой практически невозможно подобрать лучшее решение. Простой перебор здесь не поможет. Уже при 10 городах количество возможных маршрутов будет равно 3,6 млн, а при 26 — даже самым мощным компьютерам понадобится несколько миллиардов лет, чтобы перебрать все варианты.
Тем не менее каждый день миллионы устройств решают эту задачу: смартфоны строят маршруты между городами, а маршрутизаторы рассчитывают оптимальный путь для пакетов в сети. Дело в том, что существуют специальные алгоритмы, которые дают неидеальный, но достаточно эффективный результат. И их нужно знать, если вы хотите работать в компаниях, которые создают сложные, интересные проекты.
Информатик и автор классических учебников по программированию Дональд Кнут выделял следующие свойства алгоритмов:
- конечность,
- определённость,
- наличие ввода,
- наличие вывода, или результативность,
- универсальность,
- эффективность.
Рассмотрим каждое подробно.
Конечность. Алгоритм должен решать задачу за конечное число шагов. Необходимость этого критерия очевидна: программа, которая решает задачу бесконечно долго, никогда не приведёт к результату.
Определённость. Исполнитель (компьютер, операционная система) должен однозначно и верно интерпретировать каждый шаг алгоритма.
Наличие ввода. Как и у математической функции, результат работы алгоритма зависит от входных данных. Например, на вход алгоритма сортировки подаётся массив чисел. А функция, рассчитывающая факториал, принимает натуральное число.
Наличие вывода, или результативность. Алгоритм должен выдавать конкретный результат. Например, если мы ищем подстроку в строке и такая подстрока в ней присутствует, то на выходе мы должны получить позицию этой строки. Если такой подстроки нет — алгоритм должен вернуть соответствующее значение, например -1.
Универсальность. Алгоритм должен решать задачи с разными входными данными. Например, хорошая функция для сортировки массивов должна одинаково хорошо справляться с массивами из 10, 100 и 1 000 000 элементов.
Эффективность. Это требование продиктовано ограниченными ресурсами компьютеров. На заре развития вычислительной техники каждая секунда работы процессора, каждый байт памяти были на счету. И хотя современные компьютеры гораздо мощнее своих предшественников, они тоже могут «тормозить» из-за неэффективных алгоритмов.
Представьте, что вы изучили какой-нибудь язык программирования, например Go, и устроились бэкенд-разработчиком в IT-компанию. В вашей команде, помимо бэкендеров, есть фронтенд-разработчики, которые пишут код на JavaScript.
Вы придумали крутой алгоритм, который ускорит работу приложения, и хотите рассказать о нём коллегам. Но как это сделать, если они программируют на другом языке?
Для таких ситуаций есть псевдокод. Он позволяет изложить логику программы с помощью понятных для всех команд, не углубляясь в детали реализации конкретного языка. В учебной литературе алгоритмы описывают в основном с помощью псевдокода.
У псевдокода нет общепринятых стандартов, и авторы используют собственные оригинальные нотации. Хотя часто они заимствуют названия операций из Python, Pascal и Java. Например, код ниже напоминает программу на Python:
int linear_search(int[] arr, int x): if arr is empty: return -1 for i in 0..n: if arr[i] == x: return i return -1
Также псевдокод можно писать на русском языке, как в школьных учебниках по информатике:
ФУНКЦИЯ линейный_поиск(целое[] массив, целое x):
ЕСЛИ массив ПУСТОЙ:
ВЕРНУТЬ -1
ДЛЯ i В ДИАПАЗОНЕ ОТ 0 ДО ДЛИНА(массив):
ЕСЛИ массив[x] РАВНО x:
ВЕРНУТЬ i
ВЕРНУТЬ -1
Главное — чтобы тот, кто читает ваш алгоритм, понял его и воспроизвёл на своём языке программирования.
Если у вас в школе были уроки по информатике, то вы наверняка рисовали и читали блок-схемы. Если нет, то знайте: алгоритмы можно описывать не только словесно, но и графически.
Блок-схемы — это геометрические фигуры, соединённые между собой стрелками. Овалы, прямоугольники, ромбы и другие фигуры обозначают отдельные шаги алгоритма, а стрелки указывают направление потока данных. При этом в каждый блок записывается команда в виде логического или математического выражения.
В таблице ниже представлены основные элементы блок-схем:
Графическое изображение
Значение
Элемент кода в Python
Начало/конец программы
Никак не обозначается
или обозначается как начало функции:
def foo(x): #код
Конец функции обозначается словом return
Ввод/вывод данных
Операторы ввода и вывода:
print("Hello!")
word = input()
Арифметические операции
Арифметические операторы:
100 - 10 25 + 100 6 * 12.0
Условие
Условный оператор:
if n < 5: sum += 10
Цикл со счётчиком
Цикл for:
for k,v in enumerate(arr): print(k, v)
Ввод/вывод в файл
Функции для работы с файлами:
f = open("text.txt", 'r') f.close()
С помощью этого нехитрого набора фигур можно нарисовать схему практически любого алгоритма. Другие фигуры блок-схем вы найдёте в документации к ГОСТ 19.701-90.
Блок-схемы можно рисовать в Microsoft Visio и в Google Docs (Вставка → Рисунок → Новый +). Также есть специальные сервисы: например, облачный Draw.io и десктопные Dia и yEd.
А теперь разберёмся, какими бывают алгоритмы, напишем примеры на Python и нарисуем для них блок-схемы.
По конструкции алгоритмы можно разделить на несколько групп.
В линейных алгоритмах действия идут последовательно, одно за другим. Такие программы — самые простые, но на практике они встречаются редко.
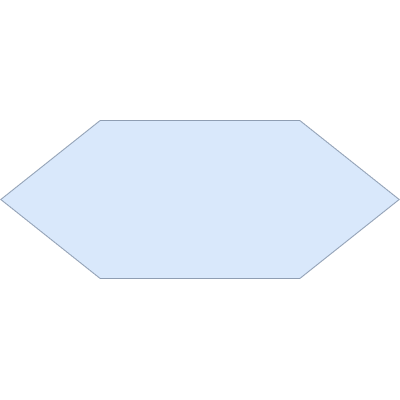
Пример. Напишите программу, которая умножает число, введённое пользователем, на 100 и выводит результат на экран.
Последовательность действий уже изложена в задании: ввести число → умножить на 100 → вывести результат. Переведём это на язык блок-схем:
Ниже приведена реализация алгоритма на языке Python:
x = int(input()) x = x * 100 print(x) >>> 5 >>> 500
В ветвящихся алгоритмах ход программы зависит от значения логического выражения в блоке «Условие». По большому счёту, любое логическое выражение сводится к выбору между истиной (True, «1») или ложью (False, «0»).
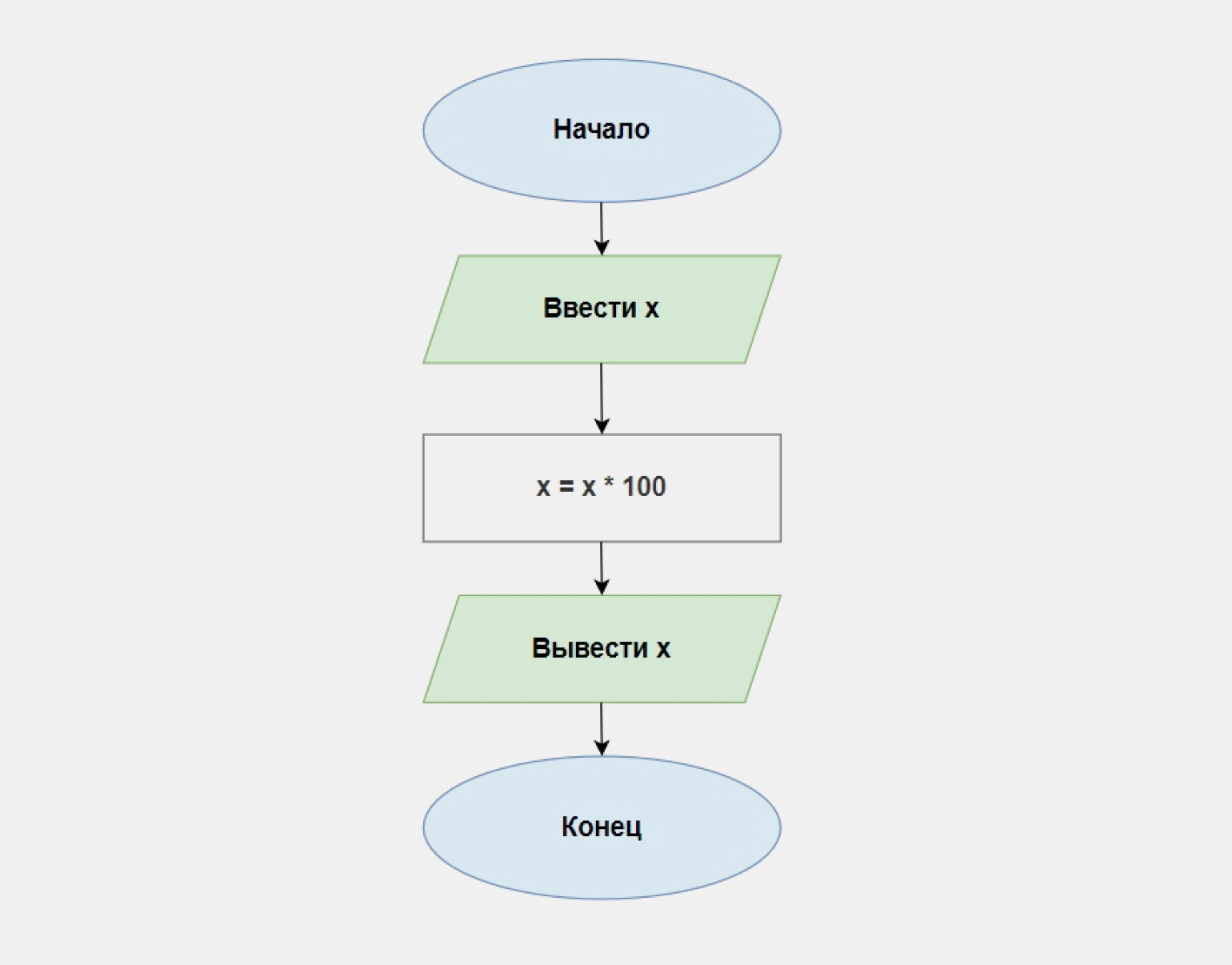
Пример. Напишите программу, которая запрашивает у пользователя возраст. Если он равен или больше 18, программа выводит приветствие, увеличивает значения счётчика посетителей на 1 и прощается, а если меньше — сразу прощается и завершает работу.
Чтобы изобразить ход решения, воспользуемся условным блоком. Во всех схемах его обозначают ромбом с вписанным условием:
То же самое на Python:
visits_counter = 0 answer = int(input("Сколько вам лет? ")) if answer >= 18: print("Добро пожаловать!") visits_counter += 1 else: print("Доступ запрещён")
Когда пользователь вводит 18 или больше, программа выполняет часть кода, которая записана под оператором if. Если же возраст меньше 18, то на экран выводится сообщение «Доступ запрещён» и программа завершает работу.
Такие алгоритмы содержат циклы — наборы действий, которые выполняются несколько раз. Количество повторений может задаваться целым числом или условием. В некоторых случаях, например, в операционных системах и прошивках микроконтроллеров, используются бесконечные циклы.
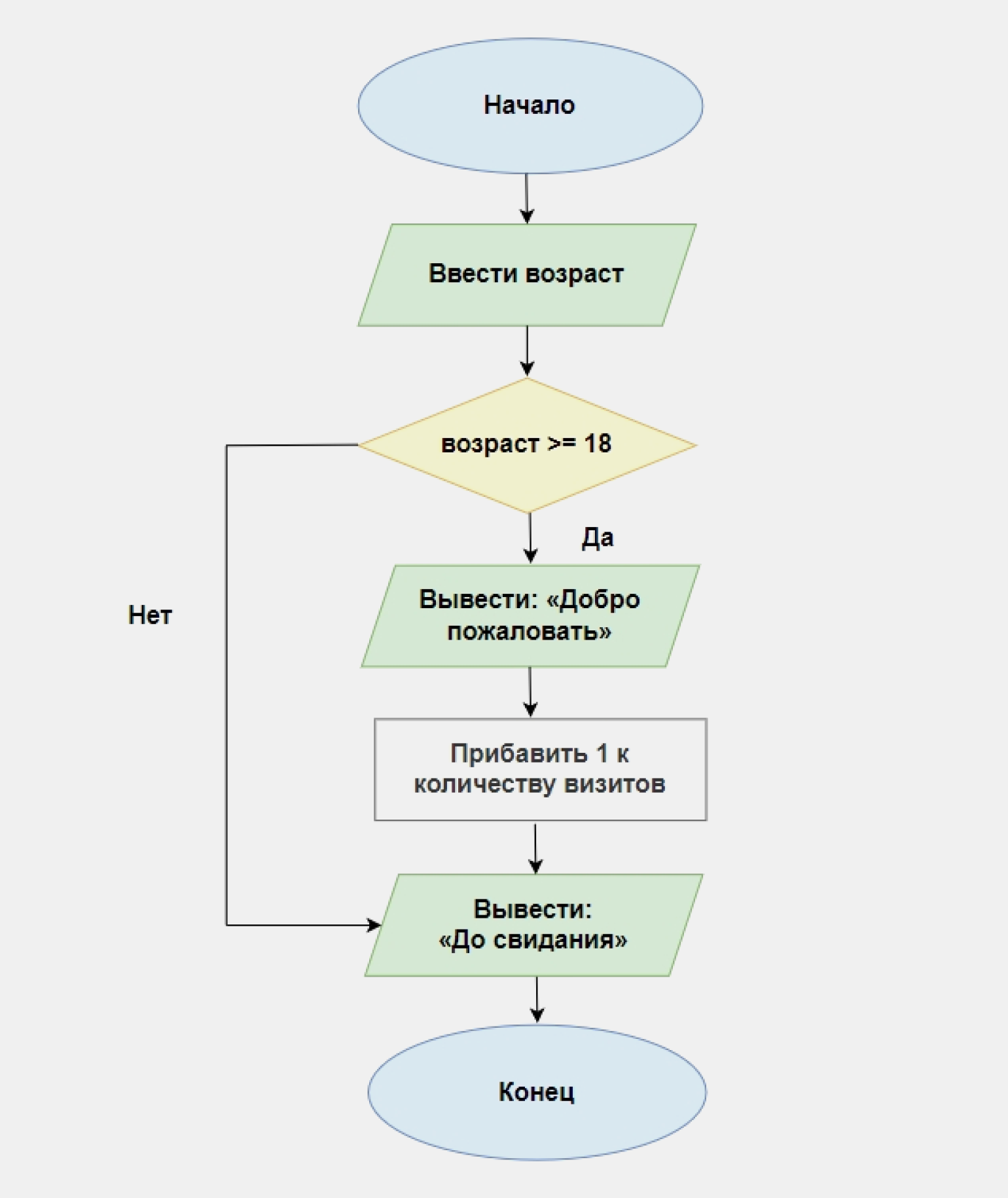
Пример. Напишите программу, которая циклично увеличивает значения счётчика на 1 и на каждом шаге выводит его значение. Когда значение счётчика достигнет 10, программа должна завершиться.
В основе нашего решения будет лежать следующее условие: если значение счётчика меньше 10 — прибавить 1, иначе — завершить работу. Вот как это выглядит в виде блок-схемы:
Переведём это в код на Python. Обратите внимание, что мы не прописываем отдельную ветвь для случая «Нет»:
count = 0 #прибавлять 1 к count, пока count меньше 10 while count < 10: count += 1 print(count) print("Переменная count равна 10!")
Результат работы программы:
1 2 3 4 5 6 7 8 9 10
Рекурсия — это явление, при котором система вызывает саму себя, но с другими входными данными. Такие алгоритмы используют для обхода словарей в глубину, вычисления факториала, расчёта степеней и других практических задач. В целом всё это можно сделать с помощью циклов, но код рекурсивных функций более лаконичен и удобочитаем.
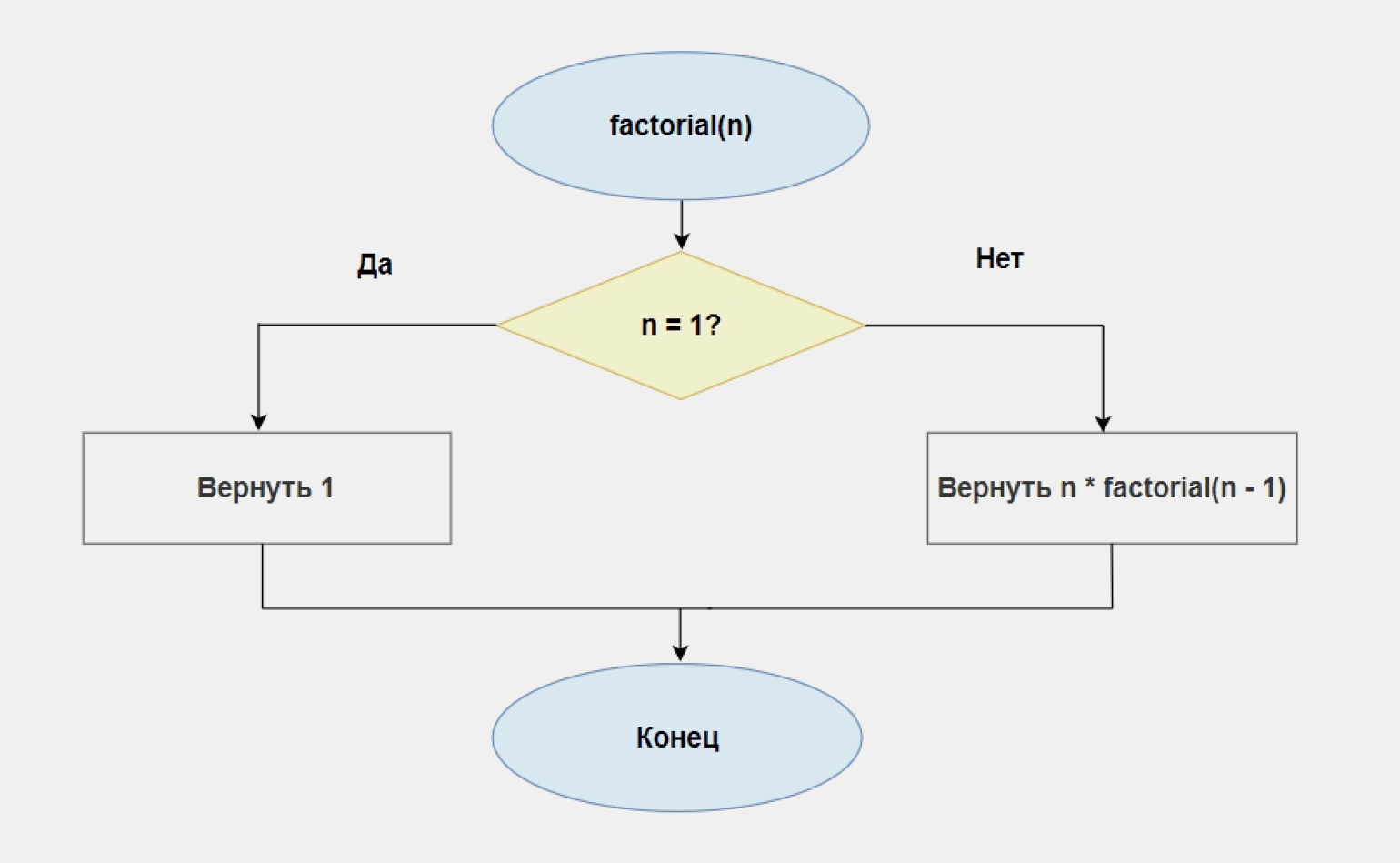
Пример. Пользователь вводит число n. Посчитайте его факториал и выведите результат на экран.
#функция, которая вызывает саму себя def factorial(n): if n == 1: return 1 #когда функция возвращает значение, #она вызывает себя, но с аргументом n - 1 return n * factorial(n - 1)
Вот как выглядит блок-схема рекурсивного алгоритма:
На практике чисто последовательные, условные или циклические алгоритмы встречаются редко, но вместе они позволяют создать решение любой сложности.
Есть и другие классификации алгоритмов. Например, по множеству решаемых задач их можно разделить на численные, поисковые, сортировочные, строковые, сетевые и криптографические. А по точности получаемых результатов — на нормальные и стохастические (вероятностные).
Если хотите изучить алгоритмы более подробно, начните с простых и увлекательных книг по computer science:
- «Грокаем алгоритмы», Адитья Бхаргава;
- «Теоретический минимум по Computer Science», Владстон Фило;
- «Гид по Computer Science», Вильям Спрингер.
Когда познакомитесь с основными алгоритмами и научитесь решать с их помощью стандартные задачи, переходите к более серьёзной литературе. Например, прочитайте Computer Science Роберта Седжвика и «Алгоритмы» Рода Стивенса.
У «Яндекса» есть бесплатные тренировки с разбором алгоритмических задач и распространённых ошибок. А попрактиковаться, закрепить теорию и подготовиться к техническому интервью можно на LeetCode — там есть сотни задач разной сложности и для разных языков программирования.

Научитесь: Профессия Python-разработчик
Узнать больше
Чтобы что-то было сделано компьютером, нужно указать ему, как это сделать. Нужно написать программу с пошаговым объяснением: какие задачи компьютер должен выполнить и каким образом. В этом нам помогают алгоритмы.

Алгоритмы — это набор инструкций, используемых компьютерами для решения тех или иных задач, ведущих к достижению конечной цели.

Знание алгоритмов имеет важнейшее значение для создания и разработки эффективных компьютерных программ. В этой статье я хотел бы поделиться своим опытом изучения алгоритмов в университете и рассказать о том, как он помог мне в учебе и карьере.
Первое знакомство
Я начал программировать, когда ещё учился в средней школе. А первые шаги делал, создавая калькуляторы и светофоры на Visual Basic. Позже освоил HTML и Java. В то время я разрабатывал настольные и веб-приложения. Я просто писал хоть какой код, о внутренней логике и не задумывался.
Поступив в университет на специальность компьютерных наук, на втором курсе я начал изучать структуры данных и алгоритмы. Это был обязательный курс, поэтому его должен был пройти каждый.

Из программиста в разработчики
Изучение структур данных и алгоритмов стало поворотным пунктом в моём понимании компьютерного программирования: теперь я думал больше как инженер-разработчик, а не как программист. Почему я так говорю? Приведу несколько примеров.
Пример 1: алгоритмы сортировки
Представьте, что мы делаем приложение для интернет-магазина. Нам надо, чтобы пользователи могли просматривать товары в порядке возрастания цены. Для этого товары нужно отсортировать по цене. Будь я начинающим программистом, добавил бы цены в массив (или список) с записью их индексов и просто вызвал бы встроенный в массив метод sort(). Что на самом деле происходит внутри метода sort()? Когда я раньше делал приложения, я об этом и понятия не имел.
Алгоритмы сортировки — это одна из базовых тем, которую в первую очередь проходят на курсе по изучению структур данных и алгоритмов в университете.
Различают следующие алгоритмы сортировки:
- сортировка вставками;
- сортировка выбором;
- быстрая сортировка;
- сортировка пузырьком;
- сортировка слиянием.
Изучив различные алгоритмы сортировки, я понял, что для каждой задачи нужен свой алгоритм сортировки. Все алгоритмы сортировки различаются по временной сложности, которая зависит от размера данных. Наибольшее значение имеет их время выполнения при разработке приложений, даже если это всего лишь несколько секунд. Кроме того, я узнал о внутренних алгоритмах сортировки (сортировка элементов на месте) и внешних алгоритмах сортировки (требуют дополнительного пространства для хранения элементов во время сортировки). Всё это заставило меня тщательно обдумывать выбор алгоритмов сортировки для каждого конкретного приложения, принимая во внимание ограничения по времени и памяти.
Пример 2: синтаксический анализ математических выражений
При вводе какого-нибудь математического выражения в калькулятор или в ячейку электронной таблицы, например MS Excel, оно автоматически вычисляется, и мы получаем ответ. Вы когда-нибудь задумывались о том, как это выражение высчитывается? А вот нам пришлось разработать программное обеспечение для работы с электронными таблицами и реализовать парсер выражений. Именно тогда я узнал о популярном алгоритме сортировочной станции. В нём используется очередь для хранения значений и стек для хранения операторов. Я узнал о реальных приложениях, в которых применяются такие структуры данных, как очереди и стеки (изучал их на курсе по структурам данных и алгоритмам), и понял лежащую в их основе логику. Меня так и распирала гордость оттого, что удалось самостоятельно реализовать алгоритм сортировочной станции, хотя таких реализаций тогда было уже полным-полно. 😃
Пример 3: списки, множества и словари
Когда нужно сохранить кучу значений, я применяю списки. Раньше я не задумывался, нужно ли соблюдать очерёдность или нужно ли допускать дубли: просто использовал список для всего подряд. Узнав о том, что, помимо списков, существуют ещё словари и множества, я понял, что всё это можно применять в различных сценариях. Так, сделав правильный выбор в той или иной ситуации и отдав предпочтение, скажем словарю, можно фактически ускорить выполнение кода. Например, если надо проверить принадлежность элемента, гораздо быстрее это будет сделать во множестве или словаре (на это требуется константное время), чем при использовании списка (требуется время, пропорциональное длине списка). Кроме того, список допускает наличие дублей, в то время как множество — нет.
Всё это примеры из моего опыта, иллюстрирующие переход от мышления программиста к мышлению инженера-разработчика. Когда я делал выбор в пользу более подходящей структуры данных или более быстрого алгоритма, происходило значительное улучшение производительности моего кода.
С чего начать?
Изучаем концепции программирования
Прежде чем приступать к изучению алгоритмов, я бы порекомендовал освоить такие понятия программирования, как переменные, функции, классы и особенно понятия объектно-ориентированного программирования (ООП). Это будет вашим фундаментом для понимания более продвинутых концепций из области компьютерных наук.
Осваиваем алгоритмы и их принципы работы
Помимо материалов моего курса, я занимался также по учебнику «Алгоритмы: построение и анализ» Томаса Х. Кормена, Чарльза Э. Лейзерсона, Рональда Ривеста и Клиффорда Штайна. Можно начать с самых азов:
- анализа временной и пространственной сложности;
- терминов “O” большое и “o” малое;
- рекурсии;
- базовых структур данных, таких как массивы, матрицы, связные списки, стеки, очереди, деревья и т. д.;
- основных алгоритмов, таких как алгоритмы поиска и сортировки.
Анализ временной и пространственной сложности — это очень важная тема, которую необходимо освоить, чтобы анализировать алгоритмы. Затем можно перейти к более продвинутым алгоритмам, таким как алгоритмы на графах.
Самое важное — чётко понимать, что происходит внутри алгоритма. Раньше я брал простые примеры и применял алгоритм, чтобы посмотреть, что происходит на каждом его шаге. Проработка примеров помогала мне лучше понять, что происходит в алгоритме, причём мне никогда не приходилось эти алгоритмы запоминать. Если меня попросят написать псевдокод для алгоритма, я смогу легко связать его с примером и проработать его, вместо того чтобы запоминать каждый шаг.
Погружаемся в код с головой
На курсе нам предлагалось реализовать различные структуры данных с нуля, используя основные их операции. Например, двоичные деревья поиска (BST) в C++ с операциями вставки, удаления, поиска, обхода с предварительной выборкой, обхода с отложенной выборкой и обхода с порядковой выборкой. Приходилось создавать класс BST и реализовывать все эти операции в виде функций. Предлагалось даже сравнивать время выполнения определённых операций с различными размерами наборов данных. Это был отличный опыт. Я многому научился благодаря этим занятиям и стал лучше разбираться в операциях. Такой учебный процесс с практическими заданиями помог мне лучше понять концепцию алгоритмов.
Можно начать программировать с языков, поддерживающих ООП. Это легко с очень простыми в освоении языками:
- C++
- Java
- Python
Для новичков один из этих языков будет в самый раз.
Ресурсы для обучения
Онлайн-курсы
Можно заниматься дистанционно на:
- Coursera: специализация «Алгоритмы», специализация «Структуры данных и алгоритмы», «Алгоритмы, часть I», «Алгоритмы, часть II».
- MIT Open Courseware: «Введение в алгоритмы».
- Академия Хана: «Алгоритмы».
- Udacity: «Введение в алгоритмы», «Введение в структуры данных и алгоритмы», «Структуры данных и алгоритмы», «Введение в алгоритмы для студентов», «Вычислимость, сложность и алгоритмы».
- edX: «Алгоритмы: дизайн и анализ, часть 1», «Алгоритмы: дизайн и анализ, часть 2», «Алгоритмы и структуры данных», «Алгоритмы: дизайн и техники», «Алгоритмы: дизайн и анализ», «Графовые алгоритмы».
и многие другие платформы. Для лучшего понимания можно попробовать приведённые там упражнения.
Средства интерактивной визуализации алгоритмов
Кроме того, можно попробовать платформы визуализации алгоритмов:
- Визуализация структуры данных.
- Визуализатор алгоритмов.
- VisuAlgo.
- Визуальное отображение алгоритмов сортировки| Toptal.
- Анимированные алгоритмы.
- Визуализации и визуальное отображение алгоритма.
Они доступны в Интернете и понимают пошаговый механизм работы алгоритмов.

Упражнения на закрепление
Освоив азы, можно переходить к практическим занятиям, закрепляя пройденный материал в упражнениях. Вот платформы, на которых собраны очень хорошие задачи самых разных уровней сложности:
- «Проект Эйлер».
- HackerRank.
- CodeChef.
- Coderbyte.
- Exercism.
- Codewars.
- LeetCode.
Чем больше практики, тем лучше понимание. Закрепление учебного материала в упражнениях — это хороший способ узнать, как изученные теории можно применить в решении задач.
Подводя итоги
Резюмируем статью списком из десяти рекомендаций для тех, кто приступает к изучению алгоритмов:
- Начинайте с изучения основ.
- Сформируйте чёткое понимание того, что происходит в алгоритме.
- Прорабатывайте шаги алгоритма с примерами.
- Обстоятельно разберитесь в анализе сложности.
- Попробуйте самостоятельно реализовывать алгоритмы.
- Записывайте всё важное, чтобы вернуться к этому в будущем.
- Занимайтесь дистанционно на онлайн-курсах платформ для обучения.
- Следите за онлайн-лекциями, опубликованными известными университетами.
- Закрепляйте пройденный материал в упражнениях.
- Если среди упражнений вам попались трудные задачи, не расстраивайтесь. После завершения упражнения можно будет почитать специальную инструкцию и понять, где вы застряли.
Дополнительные материалы для чтения
Если хотите узнать больше о структурах данных и алгоритмах, то можете ознакомиться со следующими статьями:
Заключение
Не забывайте о том, что путь к совершенству — практика!
Надеюсь, для вас эта статья была полезной и познавательной.
Спасибо за внимание.
Читайте также:
- Алгоритмы поиска, которые должен знать каждый специалист по обработке и анализу данных
- Алгоритмы машинного обучения простым языком. Часть 1
- 10 Графовых алгоритмов
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Vijini Mallawaarachchi: How to be Good at Algorithms?