Как правильно найдите площадь трапеции - Исправление недочетов и поиск решений вместе с Examum.ru

{S = dfrac{1}{2} (a + b) cdot h}

Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций — обычная, равнобедренная (равнобокая).

Калькулятор площади трапеции
Площадь трапеции
1. через основания и высоту
2. через среднюю линию и высоту
3. через диагонали и среднюю линию
4. через 4 стороны
5. через диагонали и угол между ними
6. через основания и углы при основании
7. через площади треугольников
8. через диагонали и высоту
9. через радиус вписанной окружности и основания
10. через перпендикулярные диагонали
Площадь равнобедренной (равнобокой) трапеции
1. через основания и высоту
2. через 3 стороны (формула Брахмагупты)
3. через верхнее основание, боковую сторону и угол при нижнем основании
4. через нижнее основание, боковую сторону и угол при нижнем основании
5. через основания и угол
6. через диагонали и угол между ними
7. через боковую сторону, угол при основании и среднюю линию
8. через радиус вписанной окружности и угол при основании
Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
1. через высоту (диаметр вписанной окружности) и угол при основании
2. через основания и угол при основании
3. через основания и радиус вписанной окружности
4. через основания
5. через основания и боковую сторону
6. через основания и среднюю линию
Примеры задач

Площадь трапеции

Трапеция — выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

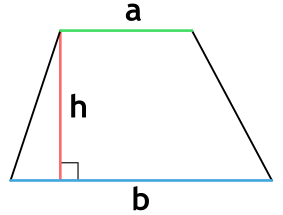
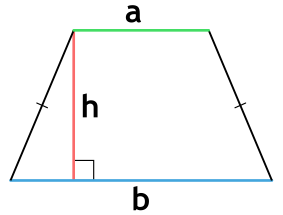
Площадь трапеции через основания и высоту

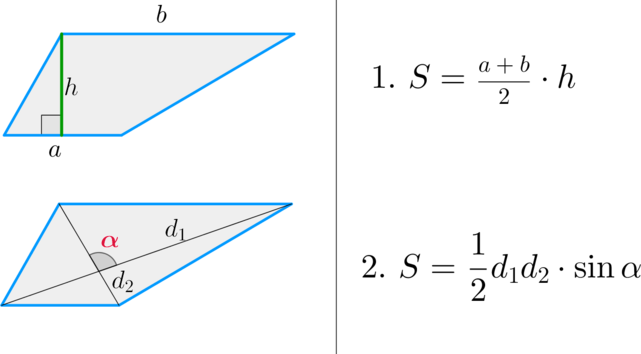
{S = dfrac{1}{2} (a + b) cdot h}

a и b — основания трапеции

h — высота, проведенная к основанию

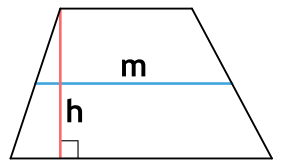
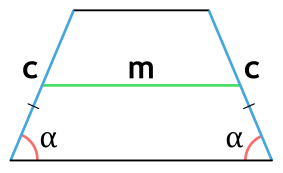
Площадь трапеции через среднюю линию и высоту

{S = m cdot h}

m — средняя линия трапеции

h — высота трапеции

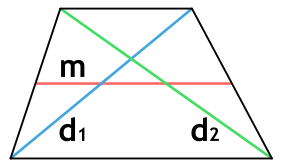
Площадь трапеции через диагонали и среднюю линию

{S = sqrt{p(p-d_1)(p-d_2)(p-2m)}}
{p = dfrac{d_1+d_2+2m}{2}}

d₁ и d₂ — диагонали трапеции

m — средняя линия трапеции

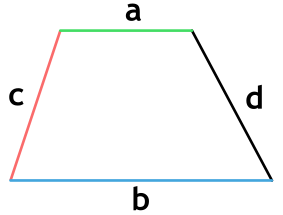
Площадь трапеции через 4 стороны

{S = dfrac{a+b}{2} sqrt{c^2 — {Big( dfrac{(a-b)^2 + c^2 — d^2}{2(a-b)} Big)}^2}}

a, b, c и d — стороны трапеции

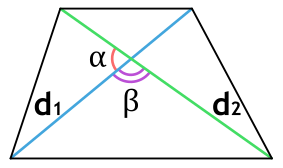
Площадь трапеции через диагонали и угол между ними

{S = dfrac{d_1 cdot d_2}{2}cdot sin(alpha); S = dfrac{d_1 cdot d_2}{2}cdot sin(beta)}

d₁ и d₂ — диагонали трапеции

α или β — угол между диагоналями трапеции

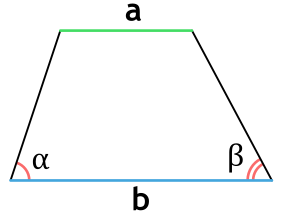
Площадь трапеции через основания и углы при основании

{S = dfrac{b^2 — a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(alpha + beta)}}

a и b — основания трапеции

α или β — прилежащие к основанию трапеции углы

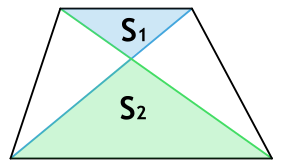
Площадь трапеции через площади треугольников

{S = (sqrt{S_1} + sqrt{S_2})^2}

S₁ и S₂ — площади образованных пересечением диагоналей трапеции треугольников

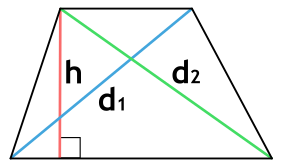
Площадь трапеции через диагонали и высоту

{S = dfrac{sqrt{{d_2}^2-h^2}+sqrt{{d_1}^2-h^2}}{2} cdot h}

d₁ и d₂ — диагонали трапеции

h — высота трапеции

Площадь трапеции через радиус вписанной окружности и основания

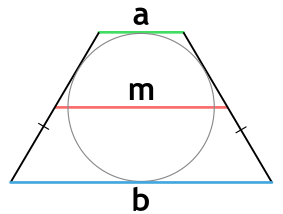
{S = (a+b)cdot r}

a и b — основания трапеции

r — радиус вписанной в трапецию окружности

Площадь трапеции через перпендикулярные диагонали

{S = dfrac{1}{2} cdot d_1 cdot d_2}

d₁ и d₂ — перпендикулярные диагонали трапеции

Площадь равнобедренной (равнобокой) трапеции

Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.

Площадь равнобедренной трапеции через основания и высоту

{S = dfrac{a+b}{2} cdot h}

a и b — основания равнобедренной трапеции

h — высота, проведенная к основанию равнобедренной трапеции

Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)

{S = sqrt{(p-a)(p-b)(p-c)^2}}
{p = dfrac{a+b+2c}{2}}

a и b — основания равнобедренной трапеции

c — боковая сторона равнобедренной трапеции

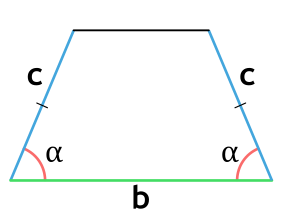
Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании

{S = c cdot sin(alpha) cdot (a+c cdot cos(alpha))}

a — верхнее основание равнобедренной трапеции

c — боковая сторона равнобедренной трапеции

α — прилежащие к нижнему основанию трапеции углы

Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании

{S = c cdot sin(alpha) cdot (b-c cdot cos(alpha))}

b — нижнее основание равнобедренной трапеции

c — боковая сторона равнобедренной трапеции

α — прилежащий к нижнему основанию трапеции угол

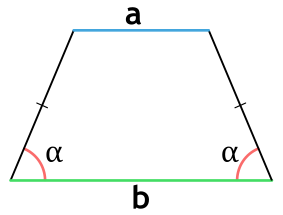
Площадь равнобедренной трапеции через основания и угол

{S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha)}

a и b — основания равнобедренной трапеции

α — прилежащий к основанию трапеции угол

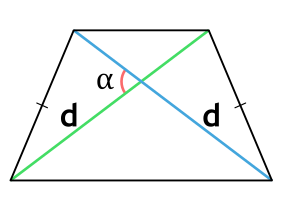
Площадь равнобедренной трапеции через диагонали и угол между ними

{S = dfrac{1}{2}d^2 cdot sin(alpha)}

a — диагональ равнобедренной трапеции

α — угол между диагоналями равнобедренной трапеции

Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию

{S = m cdot c cdot sin(alpha)}

m — средняя линия равнобедренной трапеции

c — боковая сторона равнобедренной трапеции

α — угол при основании равнобедренной трапеции

Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании

{S = dfrac{4r^2}{sin(alpha)}}

r — радиус вписанной окружности

α — угол при основании равнобедренной трапеции

Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность

В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.

Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании

{S = dfrac{h^2}{sin(alpha)}}

h — высота равнобедренной трапеции

α — угол при основании равнобедренной трапеции

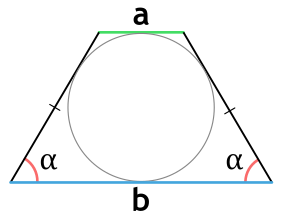
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании

{S = dfrac{a cdot b}{sin(alpha)}}

a и b — основания равнобедренной трапеции

α — угол при основании равнобедренной трапеции

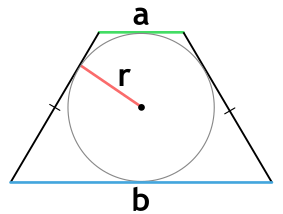
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности

{S = r(a+b); r=dfrac{sqrt{a cdot b}}{2}}

a и b — основания равнобедренной трапеции

r — радиус вписанной окружности

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания

{S = sqrt{a cdot b} cdot dfrac{a+b}{2}}

a и b — основания равнобедренной трапеции

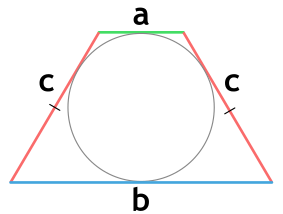
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону

{S = c cdot sqrt{a cdot b}}

a и b — основания равнобедренной трапеции

c — боковая сторона равнобедренной трапеции

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию

{S = m cdot sqrt{a cdot b}}

a и b — основания равнобедренной трапеции

m — средняя линия равнобедренной трапеции

Примеры задач на нахождение площади трапеции

Задача 1

Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.

Решение

Для решения задачи воспользуемся первой формулой.

S = dfrac{1}{2} (a + b) cdot h = dfrac{1}{2} (6 + 9) cdot 5 = dfrac{1}{2} cdot 15 cdot 5 = dfrac{1}{2} cdot 75 = 37dfrac{1}{2} : см^2

Ответ: 37.5 см²

Полученный ответ легко проверить с помощью калькулятора .

Задача 2

Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.

Решение

С решением этой задачи нам поможет вторая формула.

S = m cdot h = 18 cdot 9 = 162 : см^2

Ответ: 162 см²

Воспользуемся калькулятором для проверки результата.

Задача 3

Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.

Решение

Для решения этой задачи нам поможет третья формула.

На первом этапе вычислим p:

p = dfrac{d_1+d_2+2m}{2} = dfrac{10+8+2 cdot 3}{2} = dfrac{10+8+6}{2} = dfrac{24}{2} = 12

А теперь можно вычислить площадь трапеции:

S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-10)(12-8)(12-2 cdot 3)} = sqrt{12 cdot 2 cdot 4 cdot 6} = sqrt{576} = 24 : см^2

Ответ: 24 см²

Осталось проверить полученный ответ.

Задача 4

Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.

Решение

Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.

На первом этапе вычислим p:

p = dfrac{d_1+d_2+2m}{2} = dfrac{17+15+ 2 cdot 4}{2} = dfrac{17+15+8}{2} = dfrac{40}{2} = 20

А теперь можно вычислить площадь трапеции:

S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{20(20-17)(20-15)(20-2 cdot 4)} = sqrt{20 cdot 3 cdot 5 cdot 12} = sqrt{3600} = 60 : см^2

Ответ: 60 см²

Проверка .

Задача 5

Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.

Решение

Еще одна типовая задача. Повторим действия как в задачах выше.

На первом этапе вычислим p:

p = dfrac{d_1+d_2+2m}{2} = dfrac{8+6+ 2 cdot 5}{2} = dfrac{8+6+10}{2} = dfrac{24}{2} = 12

А теперь можно вычислить площадь трапеции:

S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-8)(12-6)(12-2 cdot 5)} = sqrt{12 cdot 4 cdot 6 cdot 2} = sqrt{576} = 24 : см^2

Ответ: 24 см²

Проверка .

Задача 6

Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.

Решение

Для решения этой задачи используем формулу Брахмагупты.

Сначала вычислим p:

p = dfrac{a+b+2c}{2} = dfrac{5+17+2 cdot 10}{2} = dfrac{22+20}{2} = dfrac{42}{2} = 21

А теперь можно вычислить площадь трапеции:

S = sqrt{(p-a)(p-b)(p-c)^2} = sqrt{(21-5)(21-17)(21-10)^2} = sqrt{16 cdot 4 cdot 11^2} = sqrt{16 cdot 4 cdot 121} = sqrt{7744}= 88 : см^2

Ответ: 88 см²

Проверка .

Задача 7

Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.

Решение

Для решения этой задачи воспользуемся формулой.

S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha) = dfrac{1}{2}(8^2-6^2) cdot tg(45°)

Тангенс 45° = 1, продолжим вычисления:

S = dfrac{1}{2}(8^2-6^2) cdot tg(45°) = dfrac{1}{2}(64-36) cdot 1 = dfrac{1}{2} cdot 28 = 14 : см^2

Ответ: 14 см²

Убедиться в правильности решения нам поможет калькулятор .

Источник

Выбирайте формулу в зависимости от известных величин.

1. Как найти площадь трапеции через основания и высоту

Посчитайте сумму оснований трапеции.

Умножьте результат на высоту и поделите на два.

Иллюстрация: Лайфхакер

S – искомая площадь трапеции.
a и b – основания трапеции (её параллельные стороны).
h – высота трапеции.

2. Как вычислить площадь трапеции через высоту и среднюю линию

Просто умножьте высоту трапеции на среднюю линию.

Иллюстрация: Лайфхакер

S – искомая площадь трапеции.
m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
h – высота трапеции.

3. Как найти площадь трапеции через диагонали и угол между ними

Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.

Поделите результат на два.

Иллюстрация: Лайфхакер

S – искомая площадь трапеции.
x и y – диагонали трапеции.
α – любой угол между диагоналями.

4. Как найти площадь трапеции через четыре стороны

Отнимите от большего основания меньшее.

Найдите квадрат полученного числа.

Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.

Поделите полученное число на удвоенную разность оснований.

Найдите квадрат результата и отнимите его от квадрата боковой стороны.

Найдите корень из полученного числа.

Умножьте результат на половину от суммы оснований.

Иллюстрация: Лайфхакер

S – искомая площадь трапеции.
a, b – основания трапеции.
c, d – боковые стороны.

5. Как вычислить площадь равнобедренной трапеции через четыре стороны

Отнимите от большего основания трапеции меньшее и поделите результат на два.

Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.

Найдите корень из результата.

Умножьте полученное число на сумму оснований и поделите на два.

Иллюстрация: Лайфхакер

S — искомая площадь трапеции.
a, b — основания трапеции.
c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).

6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол

Найдите квадрат радиуса и умножьте его на четыре.

Поделите результат на синус известного угла.

Иллюстрация: Лайфхакер

r — радиус вписанной окружности.
α — любой угол трапеции.

Читайте также 📐✏️🎓

8 способов найти длину окружности
8 способов найти периметр треугольника
7 способов найти площадь прямоугольника
Как перевести обычную дробь в десятичную
Как освоить устный счёт школьникам и взрослым

Источник

Загрузить PDF

Трапеция является четырехугольником, у которого две параллельные стороны (основания) имеют разную длину. Формула для вычисления площади трапеции: S = ½(b₁+b₂)h, где b₁ и b₂ — основания, h — высота трапеции. Если известны только боковые стороны правильной трапеции, ее можно разбить на ряд простых фигур, чтобы найти высоту, а затем вычислить площадь.

1
Сложите основания. Основания — это две стороны трапеции, которые параллельны друг другу. Если значения оснований не даны, измерьте их линейкой, а затем сложите полученные значения.^[1]
- Например, если верхнее основание (b₁) равно 8 см, а нижнее (b₂) — 13 см, сумма оснований b = b₁ + b₂ = 8 + 13 = 21 см.
2
Измерьте высоту трапеции. Высота трапеции — это расстояние между параллельными основаниями. Проведите перпендикуляр к основаниям, а затем с помощью линейки измерьте его и запишите найденное значение.^[2]
- Помните, что высота не равна боковым сторонам трапеции. Высота равна боковой стороне трапеции, только если эта сторона перпендикулярна основаниям.
3
Перемножьте сумму оснований и высоту. То есть умножьте значение «b» на значение «h». Результат запишите в квадратных единицах измерения.^[3]
- В нашем примере: 21 x 8 = 147 см².
4
Разделите найденное значение на 2, чтобы найти площадь трапеции. Также найденное значение можно умножить на ½. Результат запишите в квадратных единицах измерения.^[4]
- В нашем примере: S = 147/2 = 73,5 см².
Реклама

1
Разбейте трапецию на 1 прямоугольник и 2 прямоугольных треугольника. Проведите два перпендикуляра из вершин трапеции на нижнее основание. Так вы получите 1 прямоугольник (посередине) и 2 прямоугольных равных треугольника (по бокам).^[5]
- Этот метод можно применить только к правильной трапеции.
2
Найдите основание прямоугольного треугольника. Для этого сначала вычтите верхнее основание из нижнего основания. Теперь найденное значение разделите на 2, чтобы вычислить основание треугольника. На данном этапе вам известны основание и гипотенуза треугольника.^[6]
- Например, если верхнее основание (b₁) трапеции равно 6 см, а нижнее основание (b₂) равно 12 см, основание треугольника равно 3 см (потому что b = (b₂ — b₁)/2 = (12 — 6)/2 = 3 см).
3
Найдите высоту трапеции по теореме Пифагора. Для этого подставьте значения основания и гипотенузы треугольника в формулу A² + B² = C², где A — основание, C — гипотенуза. Найдите значение B, то есть высоту трапеции. Если основание треугольника равно 3 см, а гипотенуза равна 5 см:^[7]
- Подставьте значения: 3² + B² = 5²
- Возведите в квадрат: 9 + B² = 25
- Вычтите 9 из каждой стороны уравнения: B² = 16
- Извлеките квадратный корень из каждой стороны уравнения: B = 4 см
Подсказка: если в уравнении нет идеального квадрата, упростите ответ и оставьте квадратный корень. Например, √32 = √(16)(2) = 4√2.
4
Подставьте значения оснований и высоты в формулу для вычисления площади трапеции. Формула: S = ½(b₁ + b₂)h. Результат запишите в квадратных единицах измерения.^[8]
- Запишите формулу: S = ½(b₁ + b₂)h
- Подставьте значения: S = (6 + 12)(4)
- Упростите выражение и перемножьте числа: S = ½(18)(4)
- Ответ: S = 36 см².
Реклама

Советы

Если вам известна медиана трапеции (отрезок, который соединяет середины боковых сторон трапеции и параллелен основаниям трапеции), умножьте ее на высоту, чтобы найти площадь.^[9]

Об этой статье

Эту страницу просматривали 105 556 раз.

Была ли эта статья полезной?

Источник

Разделы теории

Открыть каталог
Свернуть каталог

Алгебра. Краткий справочник. Формулы

Дроби. Формулы сокращенного умножения

Проценты

Теорема Виета для квадратного и кубического уравнений

Арифметическая прогрессия. Геометрическая прогрессия

Степень. Свойства степеней

Модуль. Корни

Логарифмы. Логарифмические формулы. Свойства логарифмов

Тригонометрические формулы. Таблица углов. Формулы приведения

Тригонометрические формулы. Основное тригонометрическое тождество и следствия

Тригонометрические формулы: синус, косинус, тангенс и котангенс двойного и тройного углов; понижения степени

Тригонометрические формулы суммы и разности углов

Тригонометрические формулы произведения функций

Тригонометрические формулы суммы и разности функций

Тригонометрические формулы вспомогательного аргумента (угла)

Производная. Таблица производных. Связь функции с производной. Касательная. Первообразная

Графики функций. Прямая. Парабола. Функция корня. Тригонометрические функции. Показательная функция. Логарифм

Планиметрия. Краткий справочник. Формулы

Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия

Признаки и свойства параллельных прямых. Теорема Фалеса

Параллелограмм. Свойства и признаки

Ромб. Свойства и признаки

Прямоугольник. Квадрат. Свойства и признаки

Трапеция. Равнобедренная трапеция. Средняя линия трапеции

Теорема Пифагора. Пифагоровы тройки

Основные свойства площадей треугольников

Теорема синусов. Теорема косинусов

Центральные углы. Вписанные углы. Угол между хордами. Угол между секущими. Угол между касательной и хордой

Свойства касательных, секущих и хорд окружности. Радикальная ось

Вписанная окружность (описанный треугольник, описанный четырехугольник)

Описанная окружность (вписанный треугольник, вписанный четырехугольник)

Теорема Вариньона. Теорема Менелая. Теорема Чевы. Теорема Ван-Обеля

Теорема Стюарта. Длина биссектрисы и длина медианы треугольника

Площадь выпуклого четырехугольника

Площадь треугольника. Формула Герона

Площадь параллелограмма

Площадь ромба

Площадь прямоугольника. Площадь квадрата.

Площадь трапеции

Площадь правильного треугольника. Площадь квадрата. Площадь правильного шестиугольника

Длина окружности. Длина дуги. Площадь круга. Площадь сектора

Длина отрезка. Середина отрезка. Координаты вектора. Сложение векторов. Скалярное произведение векторов

Стереометрия. Краткий справочник. Формулы

Справочник с основными фактами стереометрии

Теорема о трех перпендикулярах

Призма. Прямая призма. Правильная призма. Объем призмы

Параллелепипед. Прямоугольный параллелепипед. Объем параллелепипеда

Куб. Объем куба. Диагональ куба. Площадь поверхности куба

Пирамида. Прямоугольная пирамида. Правильная пирамида. Объем пирамиды. Тетраэдр

Цилиндр. Объем цилиндра. Площадь поверхности цилиндра

Конус. Объем конуса. Площадь поверхности конуса

Шар. Объем шара. Сфера. Площадь поверхности сферы

Шаровой слой. Шаровой сектор. Шаровой сегмент.

Векторы. Метод координат. Угол между прямыми, плоскостями. Расстояние от точки до плоскости, между скрещивающимися прямыми

Геометрия на плоскости (планиметрия). Часть I. Подробная теория

Введение в планиметрию. Основные факты о треугольниках

Выпуклый четырехугольник

Параллелограмм

Ромб

Прямоугольник и квадрат

Трапеция

Площади многоугольников

Подобие треугольников. Средняя линия треугольника

Треугольник. Важные факты о высоте, биссектрисе и медиане

Длина дуги окружности. Площадь кругового сектора

Геометрия на плоскости (планиметрия). Часть II. Подробная теория

Начальные сведения о синусе, косинусе, тангенсе и котангенсе

Площади многоугольников. Дополнение

Окружность. Основные теоремы

Окружность: описанная около многоугольника

Окружность: вписанная в многоугольник или угол

Теорема синусов и теорема косинусов

Правильный шестиугольник и его свойства

Векторы. Начальные сведения

Векторы на координатной плоскости

Геометрия на плоскости (планиметрия). Часть III. Важные теоремы для решения задания 16

Метод площадей для решения задач

Окружность. Основные теоремы, связанные с окружностями

Подобие треугольников и пропорциональные отрезки

Задачи на теоремы Менелая, Чевы и Стюарта. Формулы для биссектрисы и медианы

Геометрия в пространстве (стереометрия). Подробная теория

Введение в стереометрию. Параллельность

Перпендикулярность. Углы и расстояния в пространстве

Многогранники. Призма. Параллелепипед. Куб

Пирамида

Поверхности вращения: цилиндр, конус, сфера

Построение сечений

Алгебра. Часть I. Подробная теория: рациональные и десятичные дроби, квадратные корни

Рациональные (обыкновенные) дроби и действия с ними. Простые числа

Десятичные дроби и действия с ними

Квадратный корень. Действия с квадратными корнями. Модуль. Сравнение квадратных корней

Алгебра. Часть II. Простейшие уравнения. Задание 5

Линейные, квадратные и простейшие кубические уравнения. Примеры

Простейшие рациональные уравнения. Примеры

Простейшие иррациональные уравнения. Примеры

Простейшие показательные уравнения (с неизвестной в показателе степени). Примеры

Простейшие логарифмические уравнения. Примеры

Алгебра. Часть III. Тригонометрия. Задания 5 и 13

Введение в тригонометрию

Простейшие тригонометрические уравнения (задание 5) и неравенства

Решение простейших тригонометрических уравнений с помощью аркфункций

Тригонометрические формулы. Их вывод

Основные виды тригонометрических уравнений (задание 13)

Алгебра. Часть IV. Показательные и логарифмические уравнения. Смешанные уравнения. Задание 13

Кубические уравнения. Метод деления в столбик. Примеры *

Некоторые известные типы рациональных уравнений *

Алгебра. Часть V. Неравенства. Задание 15

Рациональные неравенства

Показательные неравенства

Логарифмические неравенства

Метод рационализации

Иррациональные неравенства

Алгебра. Часть VI. Взаимосвязь функции и ее производной. Задание 7

Геометрический смысл производной

Связь производной с монотонностью и точками экстремума функции

Физический смысл производной

Первообразная

Алгебра. Часть VII. Исследование функций с помощью производной. Задание 12

Поиск точек экстремума функции

Поиск наибольшего/наименьшего значения функции

Алгебра. Часть IX. Сложные задачи прикладного характера. Задание 17

Банковский кредит. Аннуитетный платеж

Банковский кредит. Дифференцированный платеж

Банковский вклад

Тренировочные варианты ЕГЭ-2018

Вариант № 1 от 11.11.2017

Вариант № 2 от 27.11.2017

Вариант № 3 от 13.01.2018

Вариант № 4 (вторая часть)

Вариант №5 от 06.04.2018

Вариант №6 от 15.04.2018

Пробные ЕГЭ центра «Школково»

Пробный ЕГЭ 03.04.2017

Пробный ЕГЭ 10.04.2017

Тренировочные варианты. Первая часть.

Тренировочный вариант №1

Тренировочный вариант №2

Тренировочный вариант №3

Тренировочный вариант №4

Тренировочный вариант №5

Тренировочный вариант №6

Тренировочные варианты «Школково». Уровень школьник

Тренировочный вариант №1

Тренировочный вариант №2

Тренировочный вариант №3

Тренировочный вариант №4

Тренировочный вариант №5

Тренировочный вариант №6

Тренировочные варианты «Школково». Уровень составитель ЕГЭ

Тренировочный вариант №1

Тренировочный вариант №2

Тренировочный вариант №3

Тренировочный вариант №4

Тренировочный вариант №5

Тренировочный вариант №6

Тренировочный вариант №7

Тренировочный вариант №8

Тренировочный вариант №9

Тренировочный вариант №10

Тренировочные варианты «Школково». Уровень Максим Олегович

Тренировочный вариант №1

Тренировочный вариант №2

Тренировочный вариант №3

Тренировочный вариант №4

Тренировочный вариант №5

Тренировочный вариант №6

Тренировочный вариант №7

ДВИ в МГУ им. М. В. Ломоносова

Вариант 111, июль 2011 года.

Вариант Москва, июль 2014 года.

Вариант Москва, июль 2015 года.

Вариант Ф22, июль 2015 года.

Вариант КМ-15, июль 2015 года.

Вариант Москва, июль 2017 года.

Реальные варианты ЕГЭ 2015

Основная волна

Резервный день. Задания с развернутым ответом

Досрочная волна

Реальные варианты ЕГЭ 2016

Резервный день. Задания с развернутым ответом

Основная волна

Досрочная волна

Реальные варианты ЕГЭ 2017

Досрочная волна. 31 марта 2017

Официальный пробный ЕГЭ. 21 апреля 2017

Досрочная волна. Резерв. 14 апреля 2017

Основная волна. 2 июня 2017. Вторая часть. Вариант 1

Основная волна. 2 июня 2017. Первая и вторая часть. Вариант 2

Основная волна. 2 июня 2017. Первая и вторая часть. Вариант 3

Основная волна. 2 июня 2017. Первая и вторая часть. Вариант 4

Основная волна. 2 июня 2017. Вторая часть. Вариант 5

Резервная волна. 28 июня 2017. Первая и вторая часть. Вариант 1

Резервная волна. 28 июня 2017. Вторая часть. Вариант 2

Реальные варианты ЕГЭ 2018

СтатГрад. Москва. 11 октября 2017

СтатГрад. Москва. 26 января 2018

Досрочная волна. 30 марта 2018

Досрочная волна. Резервный день. 11 апреля 2018

СтатГрад. Москва. 19-23 апреля 2018

Основная волна. Вариант №1. 1 июня 2018

Кликните, чтобы открыть меню

Главная
>
Площадь трапеции

Площадь трапеции

1. Читай полную теорию

2. Вникай в доказательства

3. Применяй на практике

Факт 1.
(bullet) 1. Площадь трапеции равна произведению полусуммы оснований на высоту.
(bullet) 2. Площадь трапеции равна половине произведения диагоналей на синус угла между ними (как площадь любого выпуклого четырехугольника).

Источник

Определение трапеции

Трапеция — это четырехугольник, в котором две противоположные стороны параллельны.

Онлайн-калькулятор площади трапеции

Введем некоторые понятия, которые в дальнейшем помогут решить задачи, связанные с нахождением площади данной фигуры.

Основания трапеции — это стороны, параллельные друг другу.

Боковые стороны — соответственно, две оставшиеся стороны.

Средняя линия — отрезок, который соединяет центры боковых сторон. Эта линия всегда параллельна основаниям трапеции.

Виды трапеций

Трапеция бывает трех видов:

Равнобедренная – та, у которой боковые стороны равны.
Прямоугольная, у которой два углы прямые, т. е. равны 90 градусам.
Произвольная, которая не относится к двум вышеописанным категориям.

Площадь трапеции можно найти различными способами. Разберем их более подробно и закрепим материал решением простых задач.

Формула площади трапеции по основанию и высоте

Пусть нам дана произвольная трапеция. Чтобы найти ее площадь, воспользуемся следующей формулой:

S=a+b2⋅hS=frac{a+b}{2}cdot h

a,ba, b — основания трапеции;
hh — высота трапеции.

Пример

Найти площадь SS трапеции, в которой известны основания, численно равные 10 (см.) и 8 (см.) и высота, длиной 6 (см.).

Решение

a=8a=8
b=10b=10
h=6h=6

Сразу подставляем числа в имеющуюся у нас формулу и вычисляем искомую величину:
S=a+b2⋅h=8+102⋅6=54S=frac{a+b}{2}cdot h=frac{8+10}{2}cdot 6=54 (см. кв.)

Ответ: 54 см. кв.

Формула площади трапеции по основанию и средней линии

Нужно упомянуть, что средняя линия трапеции равна половине суммы ее оснований. Тем самым, способ нахождения площади через среднюю линию есть не что иное, как способ, аналогичный первому. Поскольку:

l=a+b2,l=frac{a+b}{2},

то:

S=l⋅hS=lcdot h

ll — средняя линия трапеции;
hh — высота.

Пример

Найти площадь трапеции, если известно, что средняя линия равна 5 (см.), а высота трапеции в 2 раза больше её.

Решение

l=5l=5
h=2⋅lh=2cdot l

Найдем высоту трапеции:
h=2⋅5=10h=2cdot 5=10
Площадь:
S=l⋅h=5⋅10=50S=lcdot h=5cdot 10=50 (см. кв.)

Ответ: 50 см. кв.

Формула площади трапеции по всем сторонам

Данный способ подходит для тех случаев, когда в задаче известны все 4 стороны нашей трапеции.

S=a+b2c2−((b−a)2+c2−d22⋅(b−a))2S=frac{a+b}{2}sqrt{c^2-big(frac{(b-a)^2+c^2-d^2}{2cdot(b-a)}big)^2}

Пример

Даны длины всех сторон трапеции. Основания равны 10 (см.) и 5 (см.), боковые стороны: 4 (см.) и 3 (см.). Найти площадь фигуры.

Решение

a=5a=5
b=10b=10
c=4c=4
d=3d=3

Тогда:
S=a+b2c2−((b−a)2+c2−d22⋅(b−a))2=15216−(25+16−910)2=18S=frac{a+b}{2}sqrt{c^2-big(frac{(b-a)^2+c^2-d^2}{2cdot(b-a)}big)^2}=frac{15}{2}sqrt{16-big(frac{25+16-9}{10}big)^2}=18 (см. кв.)

Ответ: 18 см. кв.

Формула площади трапеции через диагонали и угол между ними

S=12⋅d1⋅d2⋅sin⁡(α)S=frac{1}{2}cdot d_1cdot d_2cdotsin(alpha)

d1,d2d_1, d_2 — диагонали трапеции;
αalpha — угол между диагоналями.

Пример

Пусть две диагонали трапеции равны 20 (см.) и 7 (см.) и при пересечении они образуют угол 30 градусов. Найти площадь трапеции SS.

Решение

d1=20d_1=20
d2=7d_2=7
α=30∘alpha=30^{circ}

Площадь:
S=12⋅d1⋅d2⋅sin⁡(α)=12⋅20⋅7⋅sin⁡(30∘)=35S=frac{1}{2}cdot d_1cdot d_2cdotsin(alpha)=frac{1}{2}cdot20cdot 7cdotsin(30^{circ})=35 (см. кв.)

Ответ: 35 см. кв.

Формула площади трапеции через радиус вписанной окружности и угол

Этот случай подходит только для равнобедренной трапеции.

S=4⋅r2sin⁡(α)S=frac{4cdot r^2}{sin(alpha)}

rr — радиус вписанной окружности;
αalpha — угол между основанием и боковой стороной.

Пример

Дан радиус вписанной окружности в трапецию, равный 4 (см.). Угол αalpha равный 90 градусам. Найти площадь трапеции.

Решение

r=4r=4
α=90∘alpha=90^{circ}

По формуле:
S=4⋅r2sin⁡(α)=4⋅16=64S=frac{4cdot r^2}{sin(alpha)}=4cdot 16=64 (см. кв.)

Ответ: 64 см. кв.

Хотите заказать контрольную работу по геометрии? У нас самые низкие цены среди конкурентов!

Тест по теме «Площадь трапеции»

Источник