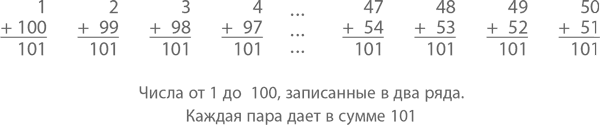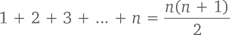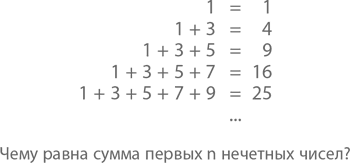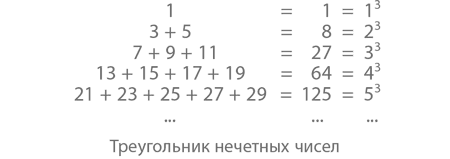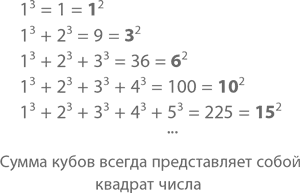Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом.
В чем смысл игры?
Игры такого рода развивают умение выделять закономерности в последовательном ряде элементов. Для этого сначала нужно внимательно рассмотреть задание: сравнить соседние объекты и попробовать определить правило закономерности.
Решить задачу можно с помощью простого счета, обобщения по какому-либо признаку или простого анализа рисунка, текста или схемы.
Как научить ребенка находить закономерности?
Маленьким детям, для решения задач на поиски закономерностей, понадобится только смекалка и воображение. Достаточно лишь объяснить, как можно установить закономерность между звеньями ряда. Если задачу решить не получается, то вместо прямых подсказок следует задать дополнительные вопросы, не раскрывая решение задачи полностью.
В любом случае, пользы будет больше, если ребенок решит, хотя бы одну задачу самостоятельно, нежели взрослый просто расскажет, как её решать.
Рассмотрим способы, которые помогут ребенку понять закономерности и последовательности в заданиях.
Инструкция по решению числовых последовательностей:
- Найти разницу между двумя рядом стоящими числами
- Определить алгоритм построения последовательности
- Применить алгоритм к следующей паре чисел
- Использовать алгоритм для определения следующего числа в ряду
Инструкция по нахождению закономерностей в заданиях с геометрическими фигурами:
- Рассмотреть фигуры и разделить их, на повторяющиеся группы
- Определить какой элемент изменился в группе
- Решить, какая именно фигура отсутствует или является лишней.
Задания для 1 класса
Задание 1
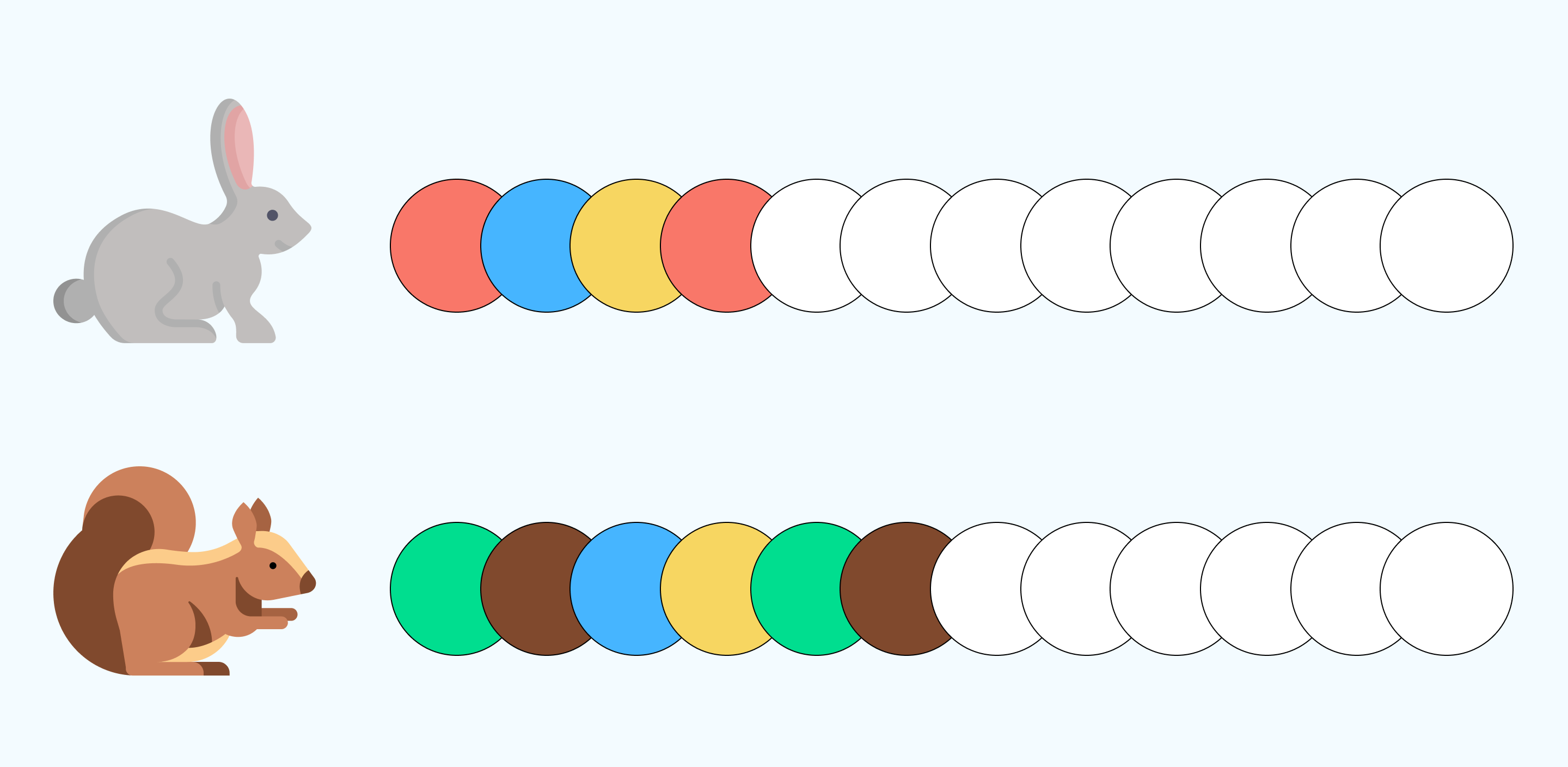
Раскрась дорожки для зайчика и белочки, сохраняя закономерность.
Решение: Белочка и зайчик бегут по разным дорожкам. У каждой дорожки есть своя закономерность. У зайчика повторяется 3 цвета на дорожке: красный, голубой, жёлтый, а у белочки 4: зеленый, коричневый, фиолетовый, жёлтый.
В этом задании можно обратить внимание на то, что обе дорожки состоят из 12 кругов. Но количество повторяющихся цветов разное.
Задание 2
Найди закономерность в ряду геометрических фигур.
Решение: В этом ряду нужно обратить внимание на размеры фигур, а не на цвет и форму. Сначала идет одна большая фигура, а за ней две маленькие, далее они повторяются.
Задание 3
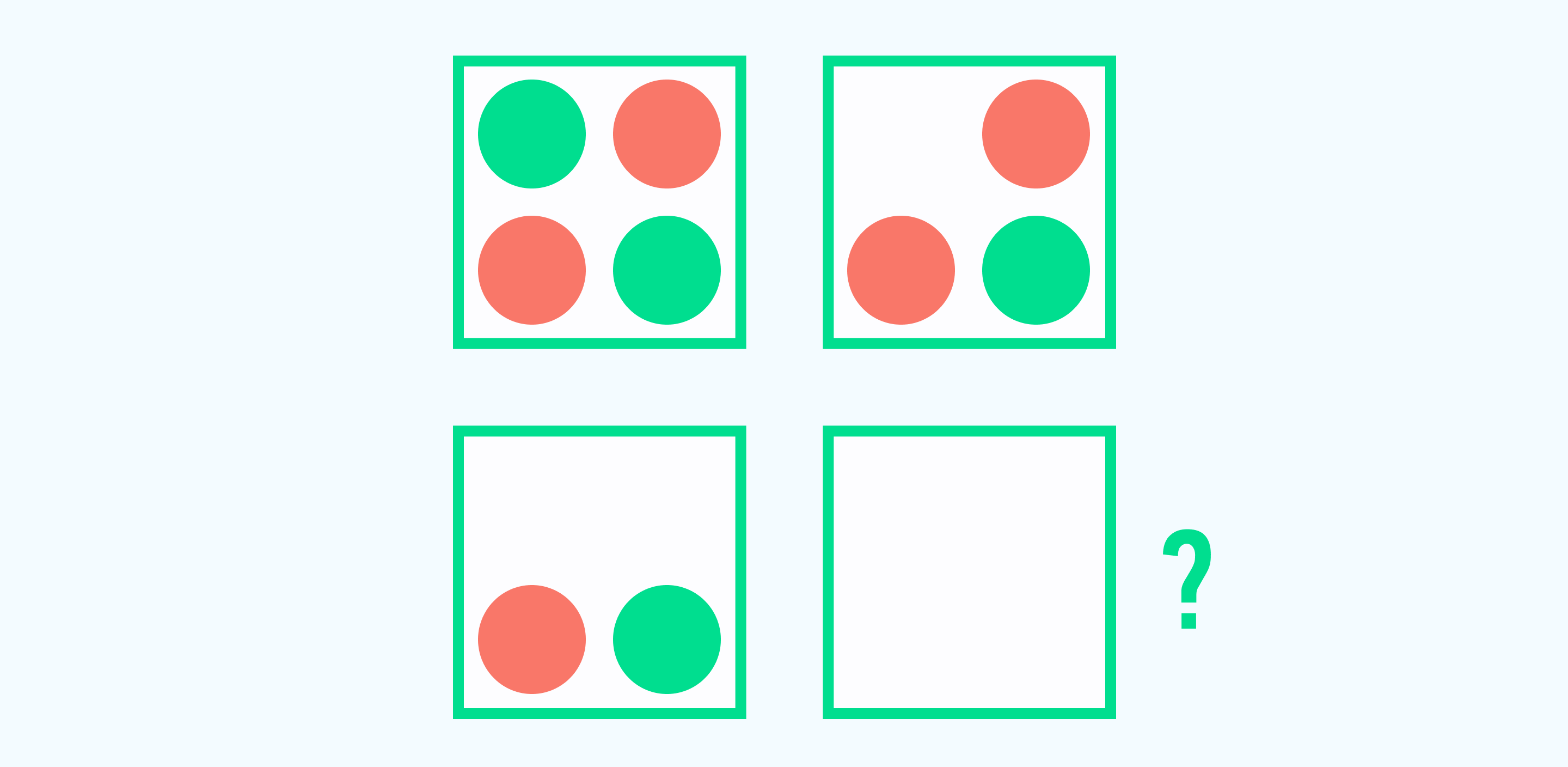
Нарисуйте в четвертом квадрате правильный ответ.
Решение: Рассмотрев внимательно рисунок, мы увидим, что круги в квадратах исчезают по одному, против часовой стрелки. В этой задаче имеет значение только расположение кругов квадрате. Таким образом, в последний квадрат мы должны нарисовать один синий круг в нижнем левом углу.
Задание 4
Соблюдая закономерность, продолжи ряд чисел до 10. Сформулируй правило, которое действует в этой закономерности. Используя это правило, придумай свою закономерность.
- 2, 4, 6,…
Решение: В этом ряду каждая цифра увеличивается на 2 относительно предыдущей – мы вычислили правило для данной закономерности. Значит, чтобы продолжить ряд, мы прибавим к каждой следующей цифре по 2. Ответ будет выглядеть так: 2,4,6,8,10.
Чтобы придумать подобную закономерность, нужно использовать сформулированное выше правило: например, 1,3,5,7,9.
Задания для 2 класса
Задание 1
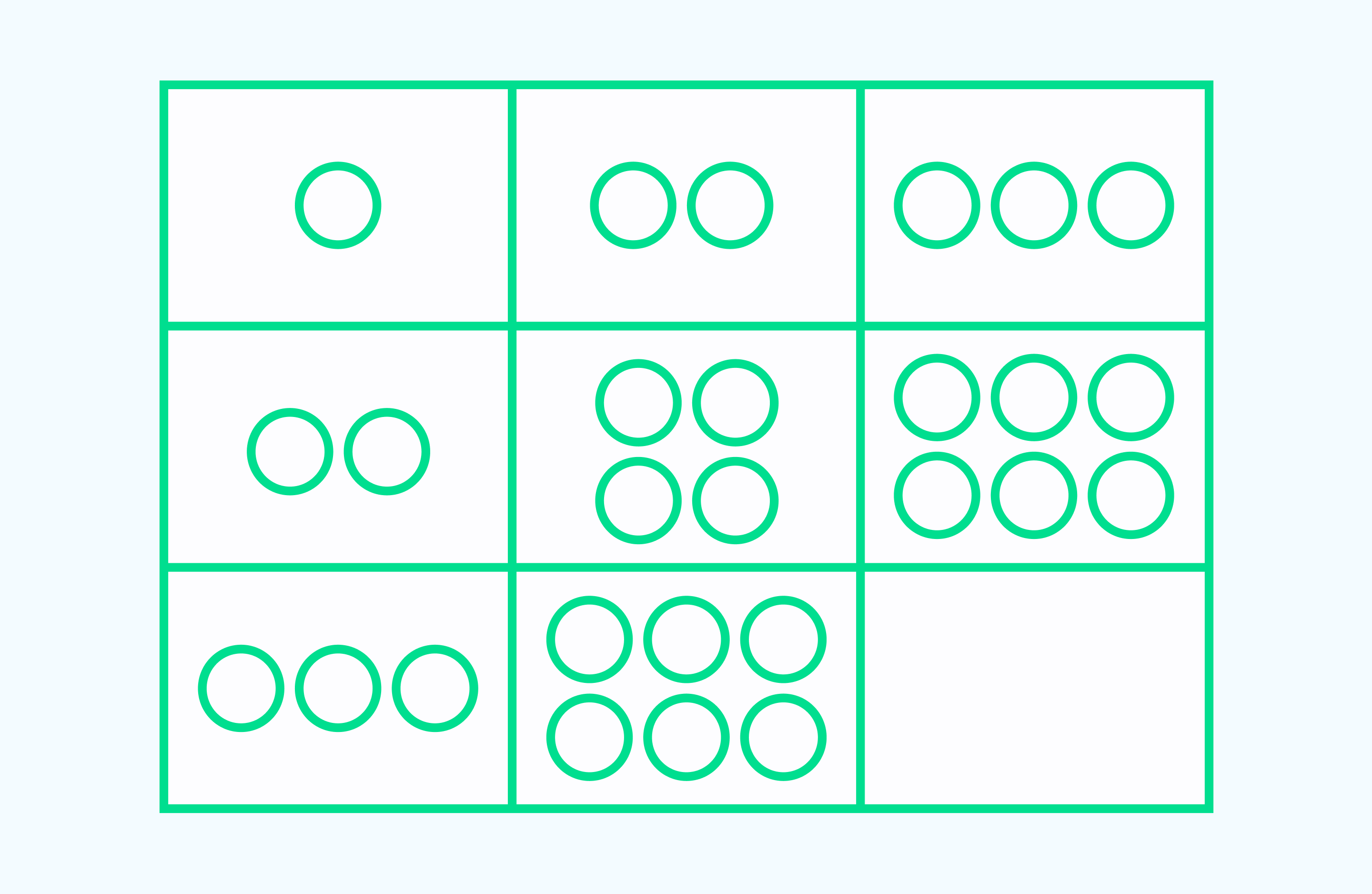
Найди закономерность и в пустом квадрате нарисуй нужное количество кругов.
Решение: В таблице в первом горизонтальном ряду количество кругов увеличивается на 1. Во втором ряду увеличивается на 2. Таким образом, можно предположить, что в третьем ряду количество кругов будет увеличиваться на 3 и ответ будет 9. Можно заметить, что и в вертикальных рядах эта закономерность повторяется.
Задание 2
В цепочке чисел найди закономерность и вставь пропущенные числа
- 95, 90, 85, 80, 75,_, 65,_, _,50
Решение: В цепочке чисел можно выделить пары: 95 -90, 85 – 80 и далее. Каждый раз, в паре, число уменьшается на 5. Значит, после 75 запишем 70, после 65 — 60, а затем 55 .
Задание 3
Найди закономерность и продолжи последовательность.
- 2, 3, 5, 8, …, …, …, …
Решение: В этой цепочке чисел к каждому последующему числу прибавляется предыдущее. 2+3=5+3=8+5=13+8=21+13=34 и далее.
Задание 4
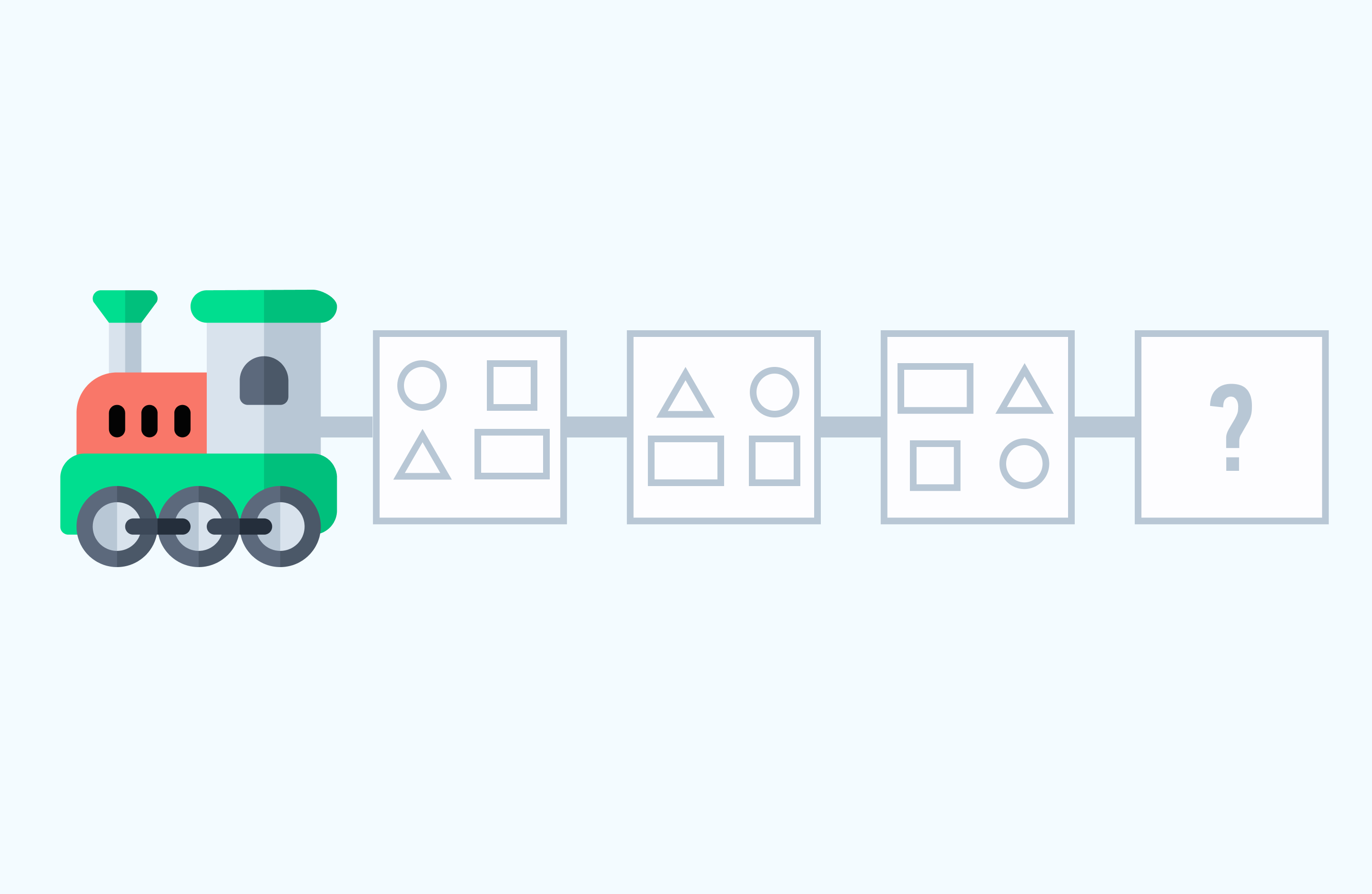
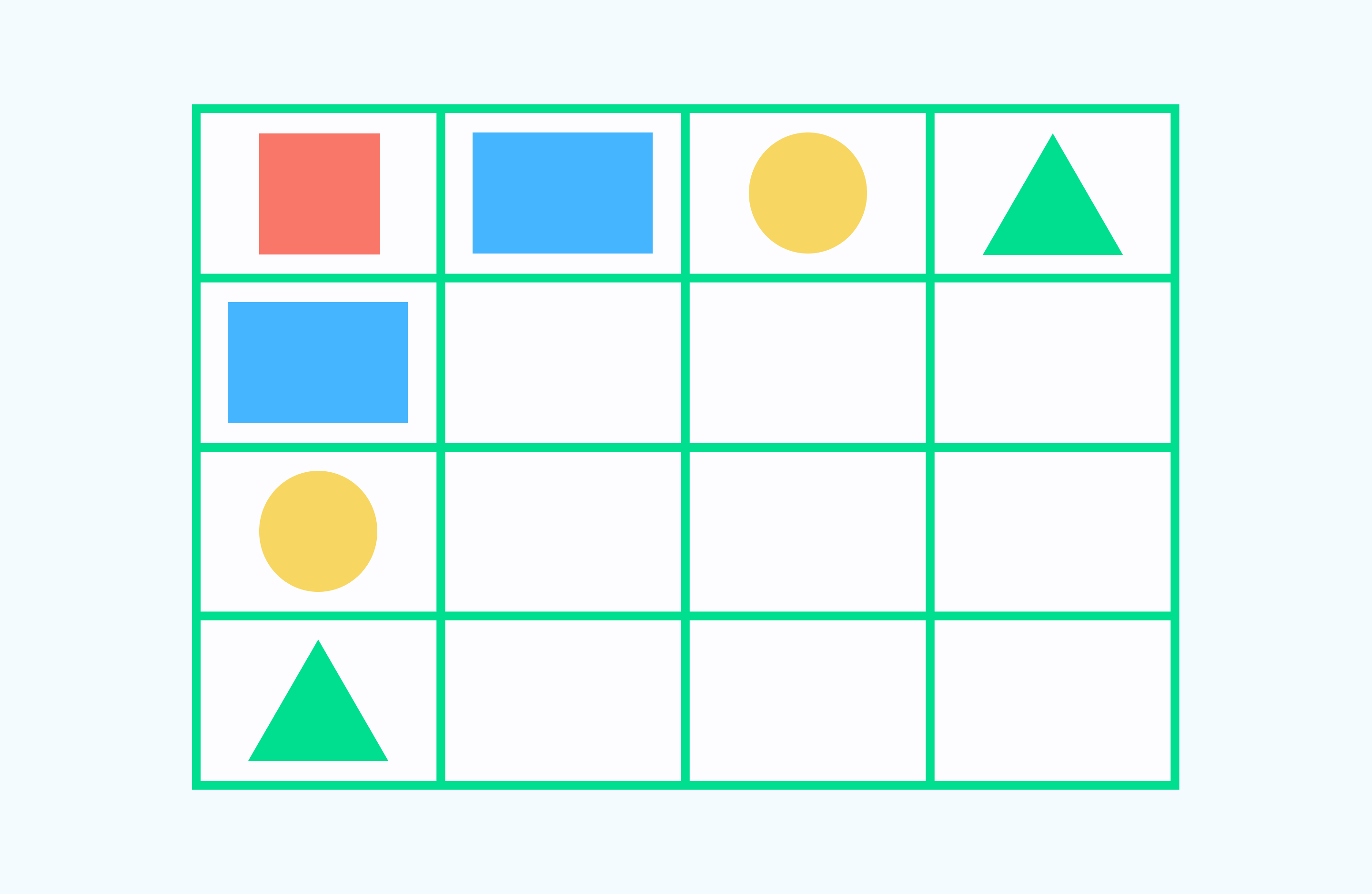
В поезде едут геометрические фигуры. Нарисуйте фигуры, в четвёртом вагоне, соблюдая закономерность их расположения.
Решение: В поезде едут геометрические фигуры: квадрат, треугольник, прямоугольник и круг. В трёх вагонах все места заняты фигурами, в определённом порядке. Расставим их и в четвертом вагоне: Круг в нём будет располагаться в нижнем левом углу, квадрат в верхнем левом, треугольник поедет в правом нижнем, а прямоугольник – в левом верхнем углу.
Задания для 3 класса
Задание 1
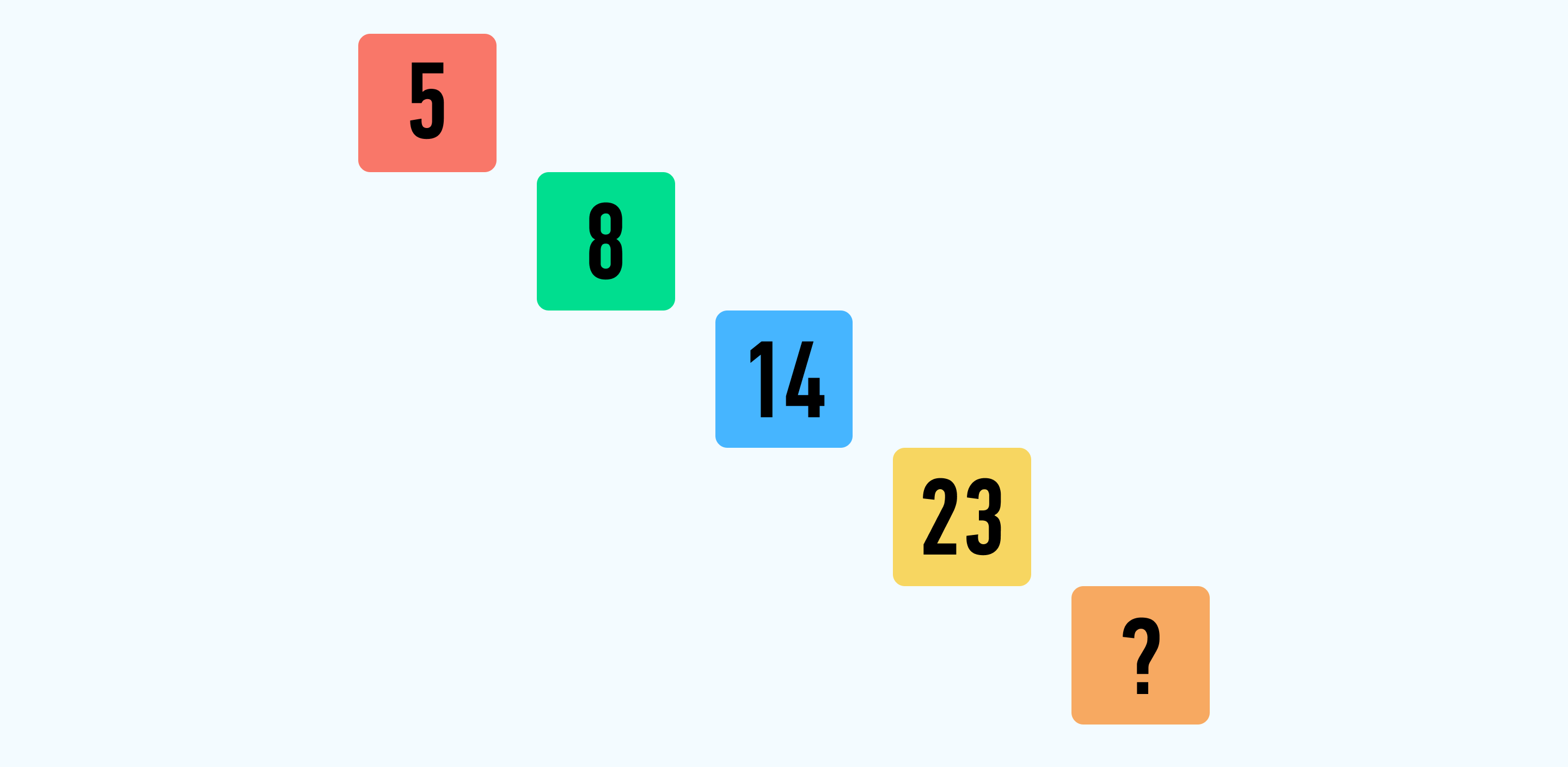
Рассмотрите картинку и найдите закономерность в задаче.
Решение: В таблице мы увидим такую закономерность:
8-5=3, то есть число увеличилось на 3; далее 14-8=6, соответственно, число увеличилось на 6. В последней связке 23-14=9 число увеличилось на 9. Мы делаем вывод, что каждое следующее число увеличивается на предыдущее значение+3. Таким образом, следующее число увеличивается на 9+3=12. 23 + 12 = 35. Ответ: 35.
Задание 2
В пустые клетки вставьте геометрические фигуры, сохраняя закономерность.
Решение: Чтобы выполнить задание, нужно фигуры расставить по порядку, друг за другом, соблюдая последовательность. Значит, после прямоугольника стоит круг, треугольник и квадрат и т. д.
Задание 3
Найди закономерность и продолжи ряды:
- 12, 23, 34, 45, 56…
- 13, 24, 35, 46…
Решение: В этой задаче каждая последующая цифра увеличивается так: десятки на один десяток и единицы на одну единицу. 12=10+2, 23=20+3, 34=30+5 и т. д.
Задание 4
Продолжи ряд, сохраняя закономерность.
- 12, 36, 13, 39, 14, 42, 15,…
Решение: В числовой цепочке выделяем пары чисел. Первая пара:12 и 36. 12×3=36, далее по порядку: 13×3=39. Умножая каждый раз на 3, цифры, следующие по порядку (12,13,14,15…), мы продолжаем последовательный ряд. Ответ: 45.
Задания для 4 класса
Задание 1
Найди ошибку в бусах.
Решение: В первых бусах повторяются квадрат и круг, значит лишний шестой круг. Во вторых бусах, повторяется закономерность: круг, два треугольника, два круга, лишний – восьмой, по счету, круг.
Задание 2
Определите закономерность. Найдите лишнее число.
- 8, 16, 20, 24, 32, 40, 48, 56, 64, 72.
Решение: В этом числовом ряду таблица умножения на 8. Ответ: число 20 – лишнее.
Задание 3
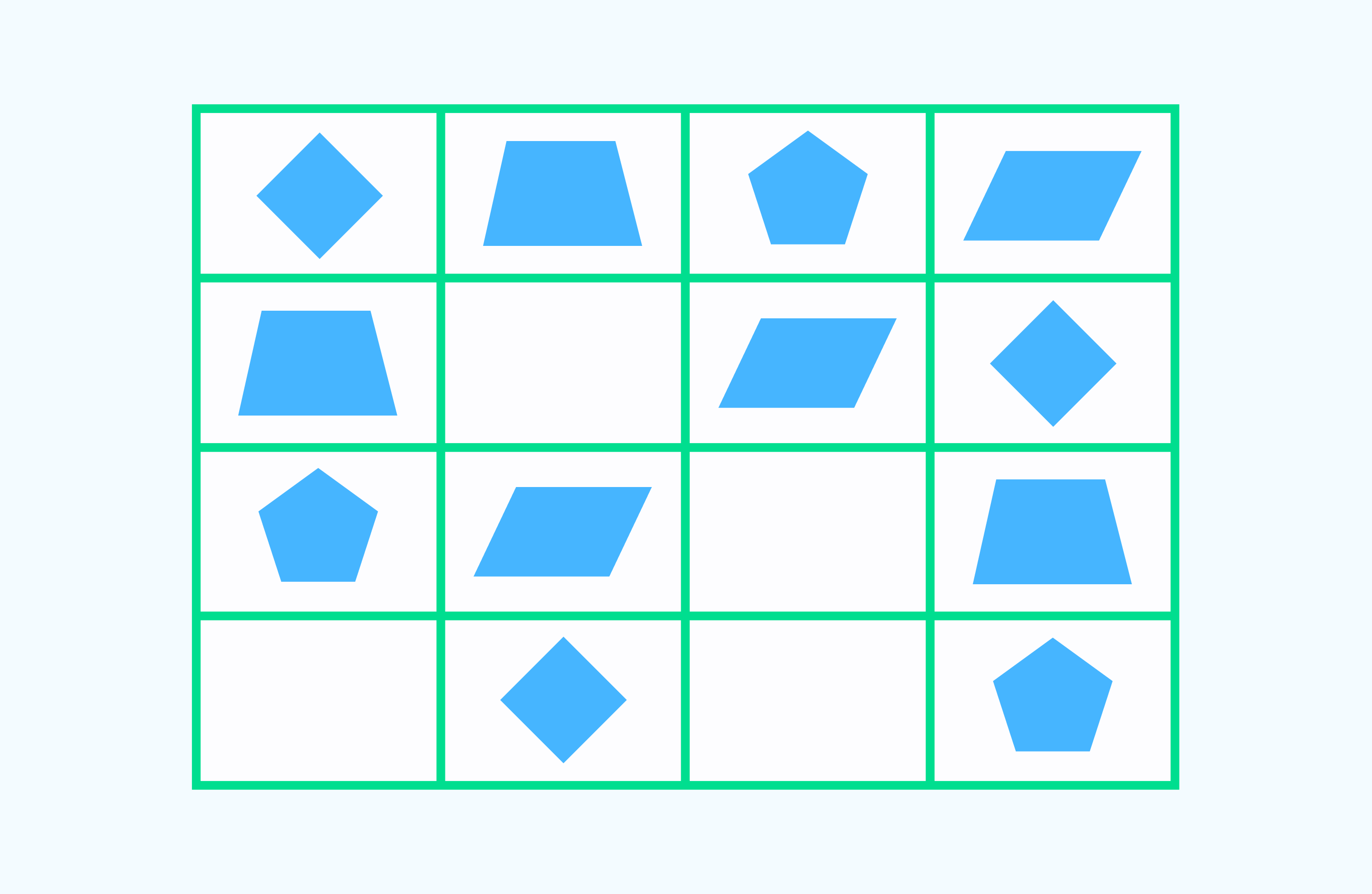
Каких геометрических фигур не хватает? Дорисуй их, соблюдая закономерность в таблице:
Решение: Определить, какой элемент изменился во втором и последующих рядах, можно, выделив последовательность: ромб, трапеция, шестиугольник и параллелограмм. Во втором ряду недостает шестиугольника, в третьем — ромба, в четвертом – параллелограмма и трапеции.


Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Найди закономерность и продолжи ряд
Задачи на поиск закономерностей развивают логическое мышление ребёнка, учат сравнивать,
рассуждать, классифицировать и делать выводы. 3500+ задач с ответами и пояснениями.
Рекомендуем наш курс развития для детей 5-12 лет!
Выберите возраст ребёнка, чтобы начать занятия

На платформе LogicLike.com дети с удовольствием развивают логику
и способности к математике. У нас 3500 занимательных заданий
с ответами и пояснениями!
Как ЛогикЛайк может помочь родителям?
Выберите основную цель занятий
Что такое закономерность в математике?
Математическая закономерность – это определенное правило, по которому в числовом, фигурном
или другом ряду элементов происходит повторение или изменение самих элементов или их свойств в
соответствии с заданным правилом.
Из учебных материалов с картинками и видео,
подготовленных опытными педагогами, ваш ребёнок узнает:
- что собой представляют закономерности, каких видов они
бывают (циклические, возрастающие и убывающие); - с чего начать решение задачи и как понять, в каких
направлениях думать; - как строятся умозаключения о том, какое число, буква или
фигура должны продолжить предложенный ряд.
Рекомендуем взрослым и детям сначала решить несколько заданий вместе. Продолжить
занятия ребёнок может самостоятельно.
В курсе развития мышления LogicLike
есть всё, что вы искали!
Пройдите 3 главы-разминки и откройте доступ к закономерностям и другим
занимательным заданиям на логику.
Задачи типа «Найди закономерность»
Для ознакомления с темой предлагаем несколько примеров заданий по математике на поиск
закономерностей разного уровня сложности.
Задачи для 1 класса
Найди закономерность и продолжи числовой ряд:
Картинки расставили в определённом порядке (в виде закономерности). Подумай,
какой элемент будет следующим.
Догадайся, как нужно раскрасить последние 3 карандаша, чтобы сохранить
закономерность в этом ряду:
Примеры заданий для 2-3 классов
Фигуры разложили в виде закономерности (в определённом порядке). Продолжи
закономерность: выбери подходящий набор фигур.
Какую закономерность можно заметить? Продолжи ряд чисел:
Помоги Алисе найти числовую закономерность и запиши следующие два числа,
которые ее продолжат:

Задача повышенной сложности (математика 4 класс)
Ученики посадили дерево. Его высота составляла 72 см.
Через год дерево выросло до 80 см, через 2 года — до 86 см, через 3 года —
до 90 см.

Какой высоты (в см) будет деревце через 9 лет, если закономерность его роста
не изменится?
Как научить детей находить закономерности?
Объясните понятие закономерности и покажите на конкретных примерах несколько типов
последовательностей. Поясните, как вы рассуждаете, чтобы найти закономерность между числами,
буквами, картинками, любыми элементами ряда.
В видеоуроке по теме «Закономерности» мы на примерах разбираем: что такое возрастающая и
убывающая закономерности, как правильно
решать задачи на поиск закономерностей.
Действуем по такой схеме:
- Внимательно смотрим на ряд чисел, фигур, животных, предметов.
- Пробуем догадаться, на чем основана закономерность – по какому правилу расположены элементы.
- Пробуем определить тип закономерности.
- Проверяем наши предположения одно за другим, чтобы увидеть какое правило соблюдается.
-
Убедившись, что «задуманное» правило соблюдается, мы сможем точно назвать следующие элементы
ряда.
Сразу отметим, что единой универсальной методики для решения задач на числовые ряды нет. Закономерности, по которым числа следуют друг за другом, могут быть самыми разными, и научиться быстро решать такого рода задачи можно только путём практики — прорешав большое количество других задач на ряды.
Рассмотрим самые простые случаи.
Надо продолжить ряд
1) 2 4 6 8 …
В этом случае всё просто — каждое следующее число на 2 больше предыдущего (т.е. это ряд чётных чисел, или арифметическая прогрессия с шагом 2), поэтому следующее число будет 10
2) 4 8 16 32 …
Тут каждое следующее число в 2 раза больше предыдущего (геометрическая прогрессия), поэтому следующим будет число 64
3) 6 11 17 24 …
Этот случай уже чуть сложнее. В этом числовом ряду разница между соседними числами на 1 больше, чем разница между предыдущими
11 — 6 = 5
17 — 11 = 6
24 -17 = 7
Как видим, шаг (разница) между соседними числами каждый раз увеличивается на 1.
Соответственно, после 24 будет число, которое на 8 больше, то есть 32
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Пример 1
Ряд: 18 10 6 4 …
Взглянув на этот ряд, можно достаточно быстро понять, что разница между соседними числами с каждым шагом сокращается в 2 раза
18 – 10 = 8
10 — 6 = 4 (8:4 = 2)
6 – 4 = 2 (4:2 = 2)
Следовательно, следующий шаг — это 2:2 = 1, то есть число будет 4-1 = 3
Пример 2
Ряд: 7 15 31 63
Этот ряд противоположен предыдущему. Тут разница между соседними числами с каждым шагом увеличивается в 2 раза
15 – 7 = 8
31 – 15 = 16 (16:8 = 2)
63 – 31 = 32 (32:16 = 2)
Следующий шаг будет 32∙2 = 64, соответственно, следующее число будет 63 + 64 = 127
Ответ: 127
Пример 3
Ряд: 2 4 8 10 20 22 44 46 92 94
Взглянем на этот ряд подробнее.
4 – 2 = 2
8:4 = 2
10 – 8 =2
20:10 = 2
То есть одно число на 2 больше предыдущего, а следующее — в 2 раза больше предыдущего.
Далее опять — на 2 больше, и потом в два раза больше.
Следующие числа в этом ряду:
22 – 20 = 2
44:22 = 2
46 – 44 = 2
92:46 = 2
94 – 92 = 2
Соответственно, следующее число будет в 2 раза больше, чем 94. Т.е. это будет 94∙2 = 188
Ответ: 188
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример 4
Ряд: 1 2 3 5 7 11 13 17 19
В этом ряду бесполезно искать закономерности, насколько соседние числа отличаются друг от друга. Все числа в этом ряду — простые, то есть без остатка делятся только на 1 и на само себя. Соответственно, следующим в ряду будет следующее после 19 простое число, то есть 23.
После того, как вы поняли, что это ряд простых чисел, то вы поняли, почему иные закономерности в этом ряду искать бесполезно — ведь математики до сих пор не нашли закона, по которому распределяются простые числа, и как можно по формуле (а не путём перебора) найти следующее простое число, зная предыдущие.
Ответ: 23
Дата публикации
02.05.2020
Числовые закономерности
Изучение математики всегда начинается с чисел. Сначала мы учимся выражать количество с помощью букв, цифр или самих предметов. А потом долгие и долгие годы складываем, вычитаем, умножаем, делим и решаем разные арифметические задачи. И за всей этой рутиной часто не видим магию чисел, способную развлечь и удивить любого, кто решится всего лишь заглянуть чуть глубже.
Вот, например, одна хитрость, с которой еще в детстве столкнулся немецкий математик Карл Фридрих Гаусс[2]. Как-то раз на уроке математики учитель попросил класс сложить между собой всей числа от 1 до 100. Вряд ли он хотел развлечь учеников – скорее, отвлечь: заставить заняться чем-нибудь нудным и требующим полного сосредоточения, а самому спокойно сделать другую работу. Представьте себе его удивление, когда через несколько секунд Гаусс вышел к доске и написал ответ – 5050. Хотите знать, как он это сделал? Он просто представил все эти числа в виде двух рядов: верхний – от 1 до 50, нижний – от 51 до 100, причем в нижнем ряду числа шли в обратном порядке, вот так:
Гаусс заметил, что сумма чисел в каждом из 50 столбцов одинаковая – 101, а значит, для того, чтобы получить искомый результат, нужно всего лишь умножить 101 на 50. Так у него и получилось 5050.
Собственно говоря, благодаря такой вот способности – не быстро считать в уме, но заставлять числа плясать под свою дудку – Гаусс и стал одним из величайших математиков XIX столетия. В этой главе мы как раз и поговорим об интересных числовых закономерностях и, конечно, увидим танец чисел. Одни из этих примеров полезны тем, что развивают способности умственного счета, другие – просто красивы.
Только что мы последовали путем гауссовой логики, чтобы получить сумму первой сотни простых чисел. Но что, если нам нужна сумма 17 из них? Или тысячи? Миллиона? Логика Гаусса позволяет подсчитывать сумму первых n чисел, где n – любое нужное вам количество! Некоторым людям легче разобраться с математическими абстракциями, если они могут их визуализировать. К примеру, числа 1, 3, 6, 10 и 15 иногда называют треугольными, потому что, заменив их соответствующим количеством кружков, можно легко сложить треугольники, вроде того, что изображен чуть ниже (конечно, один кружок треугольником можно назвать с очень большой натяжкой, но число 1, несмотря на это, все же считается треугольным). Согласно определению, треугольное число n равняется 1 + 2 + 3 +… + n.
Посмотрите, что произойдет, если мы расположим два треугольника основаниями друг к другу, вот так:
У нас получился прямоугольник из 5 рядов и 6 столбцов – всего 30 кружков. Значит, в каждом из двух наших треугольников была половина общего их количества, то есть по 15 кружков. Мы, это, разумеется, уже знаем, но давайте применим этот же принцип к двум прямоугольникам, количество рядов в которых равно n. Точно так же составим из них прямоугольник с n рядов и n + 1 столбцов. Кружков в нем будет n ? (n + 1) – ну или в более привычной записи – n(n + 1). В результате мы получим формулу, которая позволит нам подсчитывать сумму первых n чисел:
Видите, закономерность, которую мы использовали для сложения первой сотни чисел, вполне применима к любому подобному ряду, сколько бы членов в него ни входило. И если вдруг нам понадобится сложить между собой все числа от 1 до 1 000 000, сделать это можно будет всего за два шага: перемножив 1 000 000 и 1 000 001 и разделив результат пополам.
Разобравшись в одной формуле, вы с легкостью разберетесь и в остальных. Например, если мы удвоим обе части последнего уравнения, получится формула суммы первых n четных чисел:
2 + 4 + 6 +… + 2n = n(n + 1)
А как насчет суммы первых нечетных, спр?сите вы? Давайте посмотрим, что говорят нам числа.
То, что справа – квадраты целых чисел. 1 ? 1; 2 ? 2; 3 ? 3 и т. д. Сложно не заметить следующую закономерность: сумма первых n нечетных чисел равняется n ? n. Или n?. Но что, если это просто совпадение? Чуть позже, в главе 6, мы с вами увидим несколько путей развития этой формулы, но уже и сейчас понятно, что у такой простой закономерности должно быть не менее простое объяснение. Самое мое любимое – методом подсчета кружков: он наглядно показывает, почему числа вроде 25 называются квадратами. Но почему вдруг мы должны складывать первые 5 нечетных чисел с 5?? А просто посмотрите на квадрат размером 5 на 5:
Кружков в нем 5 ? 5 = 25, это очевидно. Но давайте подсчитаем иначе. Начнем с одинокого кружка в левом верхнем углу. Его окружают 3 кружка, потом 5, потом 7 и, наконец, 9. Следовательно,
1 + 3 + 5 + 7 + 9 = 25
И возьми мы квадрат со сторонами n на n, его можно будет легко разбить на n-ное количество L-образных секторов, в каждом из которых будет соответственно 1, 3, 5…., (2n – 1) кружков. Это и есть формула суммы первых n нечетных чисел
1 + 3 + 5 + … + (2n – 1) = n?
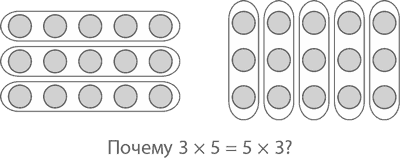
Отступление
Чуть позже мы еще вернемся к методу подсчета кружков (как и к методу решения задачи двумя разными способами), и вы увидите, к каким интересным результатам он может привести в высшей математике. Но и для понимания основ он не менее полезен. Почему, например, 3 ? 5 = 5 ? 3? Уверен, вы никогда даже не задавались таким вопросом: просто однажды в детстве вам сказали, что порядок чисел при умножении абсолютно не важен (математики, кстати, называют это законом коммутативности). Но почему же три пакетика по пять жемчужин – это то же, что и пять пакетиков по три жемчужины? Самый простой способ объяснить этот закон – посчитать кружки в прямоугольнике размером 3 на 5. Считая ряд за рядом, мы видим 3 ряда, в каждом из них 5 кружков, то есть во всем прямоугольнике 3 ? 5 кружков. С другой стороны, мы можем подсчитать столбики, а не ряды: по 3 кружка в каждом из 5 рядов, значит, всего кружков 5 ? 3.
Эта закономерность может привести нас к другой, еще более красивой. Раз уж мы хотим заставить числа танцевать, почему бы не сделать это и с их квадратами?
Взгляните вот на такую пирамидку уравнений:
Какую закономерность вы видите? Подсчитать количество чисел в каждом ряду несложно: 3, 5, 7, 9, 11 и так далее. А дальше неожиданность: первое число каждого ряда – по крайней мере, первых 5 записанных здесь рядов – является квадратом числа. И правда: 1, 4, 9, 16, 25… Почему так получается? Возьмем пятый ряд. Сколько чисел ему предшествуют? Давайте сложим их количество: 3 + 5 + 7 + 9. Прибавим к ним еще единицу, и у нас получится первое число пятого ряда – сумма первых 5 нечетных чисел, которая, как мы уже знаем, равна 5?.
А теперь просчитаем пятое уравнение, ничего к нему не добавляя. Как бы это сделал Гаусс? Если пока не обращать внимания на начальное 25, слева у нас останется 5 чисел, каждое из которых будет ровно на 5 меньше, чем соответствующее ему число справа.
То есть сумма чисел справа будет ровно на 25 больше суммы чисел слева. Но это без учета 25, которые стоят в начале. А с ними у нас получается именно тот результат, который обещан нам знаком равенства. Следуя той же логике и призвав на помощь алгебру, мы докажем, что этот ряд можно продолжать бесконечно.
Отступление
А теперь – специально для тех, кто хотел немного алгебры. Ряду n предшествует количество чисел, равное 3 + 5 + 7 +… + (2n – 1) = n? – 1, поэтому левая сторона нашего уравнения должна начинаться с числа n?, за которым следует n последовательных чисел, от n? + 1 до n? + n. Справа – n последовательных чисел, начиная с n? + n + 1, заканчивая n? + 2n. Если мы временно «забудем» про число n? слева, то увидим, что каждое из n чисел справа на n больше, чем соответствующее ему последовательное число слева. Разница при этом составляет n ? n, то есть n?. Закономерность эта компенсируется начальным n? слева, поэтому-то левая и правая части и равны.
Перейдем к другой закономерности. Как мы уже видели, из нечетных чисел можно составлять квадраты. А теперь посмотрим, что произойдет, если собрать их в один большой треугольник – вроде того, что изображен чуть ниже.
Так отлично видно, что 3 + 5 = 8, а 7 + 9 + 11 = 27, а 13 + 15 + 17 + 19 = 64. Что общего у 1, 8, 27 и 64? Да это же полные кубы чисел! Например, если сложить между собой пять чисел пятого ряда, мы получим:
21 + 23 + 25 + 27 + 29 = 125 = 5 ? 5 ? 5 = 5?
Логика вроде бы подсказывает, что сумма чисел в ряду n будет равна n?. Но насколько верным будет этот вывод? Не простое ли это совпадение? Чтобы лучше понять эту закономерность, посмотрим на числа в середине 1, 3 и 5 рядов. Что мы видим? 1, 9 и 25. То есть квадраты. В середине 2 и 4 рядов чисел нет, но по сторонам центра 2 ряда видим числа 3 и 5, среднее арифметическое которых – 4, а по сторонам центра 4 ряда – 15 и 17 со средним арифметическим 16. Давайте подумаем, как эту закономерность можно использовать.
Снова возьмем 4 ряд. Что мы тут видим? А видим мы, что сумма всех чисел в нем есть 5? – и не нужно к ним ничего добавлять, чтобы заметить: все они симметрично расположены вокруг 25. Так как среднее арифметическое этих чисел – 5?, уравнение преобразуется в 5? + 5? + 5? + 5? + 5? = 5 ? 5?, то есть 5?. То же справедливо и в отношении 4 ряда: среднее арифметическое всех чисел в нем – 4?, их сумма – 4?. Чуть-чуть алгебры (к которой мы здесь не прибегаем), и вы легко сделаете вывод, что среднее арифметическое n чисел ряда n равно n?, а их сумма равна n?, что и требовалось доказать.
Кстати, если уж мы взялись оперировать квадратами и кубами, не могу удержаться, чтобы не указать вам на еще одну закономерность. Что получится, если сложить кубы чисел, начиная с 1??
Подсчитывая сумму кубов, мы получаем 1, 9, 36, 100, 225 и т. д. – числа, которые являются полными квадратами. Но это не любые квадраты, а квадраты 1, 3, 6, 10, 15 и т. д. – треугольных чисел! Мы уже знаем, что они по своей сути являются суммами простых чисел, а значит,
1? + 2? + 3? + 4? + 5? = 225 = 15? = (1 + 2 + 3 + 4 + 5)?
Другими словами, сумма кубов первых n чисел есть квадрат суммы этих самых первых n чисел. Подтвердить это мы пока не можем, но в главе 6 пару доказательств увидим.
Данный текст является ознакомительным фрагментом.