Download Article
Download Article
In order to graph points on the coordinate plane, you have to understand the organization of the coordinate plane and know what to do with those (x, y) coordinates. If you want to know how to graph points on the coordinate plane, just follow these steps.
Things You Should Know
- Start at (0, 0), or the origin, which is in the center of the coordinate plane.
- Move over x units to the right or left. Then, move over y units up or down. Mark the point.
- If you’re working with a linear equation, draw lines connecting points from left to right. For a quadratic equation, connect points with curved lines.
-
1
Understand the axes of the coordinate plane. When you’re graphing a point on the coordinate plane, you will graph it in (x, y) form. Here is what you’ll need to know:[1]
- The x-axis goes left and right, the second coordinate is on the y-axis.
- The y-axis goes up and down.
- Positive numbers go up or right (depending on the axis). Negative numbers go left or down.
-
2
Understand the quadrants on the coordinate plane. Remember that a graph has four quadrants (typically labeled in Roman numerals). You will need to know which quadrant the plane is in.[2]
- Quadrant I gets (+,+); quadrant I is above and to the left of the y-axis.
- Quadrant IV gets (+,-); quadrant IV is below the x-axis and to the right of the y-axis. (5,4) is in quadrant I.
- (-5,4) is in Quadrant II. (-5,-4) is in Quadrant III. (5,-4) is in Quadrant IV.
Advertisement
-
1
Start at (0, 0), or the origin. Just go to (0, 0), which is the intersection of the x and y axes, right in the center of the coordinate plane.[3]
-
2
Move over x units to the right or left. Let’s say you’re working with the set of coordinates (5, -4). Your x coordinate is 5. Since five is positive, you’ll need to move over five units to the right. If it was negative, you would move over 5 units to the left.[4]
-
3
Move over y units up or down. Start where you left off, 5 units to the right of (0, 0). Since your y coordinate is -4, you will have to move down four units. If it were 4, you would move up four units.[5]
-
4
Mark the point. Mark the point you found by moving over 5 units to the right and 4 units down, the point (5, -4), which is in the 4th quadrant. You’re all done.[6]
Advertisement
-
1
Learn how to graph points if you’re working with an equation. If you have a formula without any coordinates, then you’ll have to find your points by choosing a random coordinate for x and seeing what the formula spits out for y. Just keep going until you’ve found enough points and can graph them all, connecting them if necessary. Here’s how you can do it, whether you’re working with a simple line, or a more complicated equation like a parabola:[7]
- Graph points from a line. Let’s say the equation is y = x + 4. So, pick a random number for x, like 3, and see what you get for y. y = 3 + 4 = 7, so you have found the point (3, 7).
- Graph points from a quadratic equation. Let’s say the equation of the parabola is y = x2 + 2. Do the same thing: pick a random number for x and see what you get for y. Picking 0 for x is easiest. y = 02 + 2, so y = 2. You have found the point (0, 2).
-
2
Connect the points if necessary. If you have to make a line graph, draw a circle, or connect all of the points of a parabola or another quadratic equation, then you’ll have to connect the points. If you have a linear equation, then draw lines connecting the points from left to right. If you’re working with a quadratic equation, then connect the points with curved lines.[8]
- Unless you are only graphing a point, you will need at least two points. A line requires two points.
- A circle requires two points if one is the center; three if the center is not included (Unless your instructor has included the center of the circle in the problem, use three).
- A parabola requires three points, one being the absolute minimum or maximum; the other two points should be opposites.
- A hyperbola requires six points; three on each axis.
-
3
Understand how modifying the equation changes the graph. Here are the different ways that modifying the equation changes the graph:[9]
- Modifying the x coordinate moves the equation left or right.
- Adding a constant moves the equation up or down.
- Turning it negative (multiplying by -1) flips it over; if it is a line, it will change it from going up to down or going down to up.
- Multiplying it by another number will either increase or decrease the slope.
-
4
Follow an example to see how modifying the equation changes the graph.[10]
Consider the equation y = x^2 ; a parabola with its base at (0,0). Here are the differences you will see as you modify the equation:- y = (x-2)^2 is the same parabola, except it is graphed two spaces to the right of the origin; its base is now at (2,0).
- y = x^2 + 2 is still the same parabola, except now it is graphed two spaces higher at (0,2).
- y = -x^2 (the negative is applied after the exponent ^2) is an upside down y = x^2; its base is (0,0).
- y = 5x^2 is still a parabola, but it gets larger even faster, giving it a thinner look.
Advertisement
Add New Question
-
Question
How do I graph y=3x?
Substitute the x values on your cartesian plan into your equation, which will give you the corresponding y values. You can then plot it onto your graph.
-
Question
What do the (+,+), (-,-), (+,-), and (-,+) notations indicate on a coordinate graph?
These notations indicate whether the x and y coordinates of a graphed point are positive or negative. You can use this information to determine the graph quadrant in which a point appears. Quadrant I (upper right) is (+,+), quadrant II (upper left) is (-,+), quadrant III (lower left) is (-,-), and quadrant IV (lower right) is (+,-).
-
Question
How do I draw the graph of 3y=2x?
Solve the equation for y; y will equal 2/3 x. Pick several values for x. Multiply each value of x by 2/3 (for example, if x= 2 then y will be 2/3 times 2 or 4/3). Once you have done this for all of your x values, you are ready to graph. Locate your first x value on the horizontal axis and go up to the y value you calculated and make a small dot. Do this for each x value—connect the dots with a smooth line or curve as (in this case, it will be a line).
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If you are making these, you will most likely have to read them too. A good way to remember to go along the x axis first and the y second, is to pretend that you are building a house, and you have to build the foundation (along the x axis) fist before you can build up. This is the same the other way; if you go down, pretend you are making the basement. You still need a foundation, and to start at the top.
-
A good way of remembering which axis is which is to imagine the vertical axis having a small slanted line on it, making it look like a «y».
-
Axes are basically horizontal and negative number lines, with both intersecting at the origin (the origin on a coordinate plane is zero, or where both axes intersect). Everything «originates» from the origin.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To graph a point on the coordinate plane, take a look at your coordinates, which should be two numbers within parenthesis, separated by a comma. The first number is the location of the point on the x-axis, and the second is the location of the number on the y-axis. A positive number means you move to the right on the x-axis or up on the y-axis, while a negative number means you move left on the x-axis and down on the y-axis. For example, to plot (5, -4), move 5 spaces to the right and 4 spaces down. To learn how to graph an equation on the coordinate plane, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 335,636 times.
Did this article help you?
С помощью точечной диаграммы в Excel можно изобразить данные, расположенные в столбцах и строках. График этого типа показывает отношения между числами в нескольких рядах данных или две группы значений как один ряд координат х и у.
Где используется точечная диаграмма
В точечной диаграмме одни значения выводятся вдоль горизонтальной оси Х, другие – вертикальной оси У. Эти числовые значения объединяются в точку. А точки выводятся через неравные промежутки или кластеры.
С помощью точечных диаграмм хорошо сравнивать и отображать научную, статистическую или техническую информацию. Подобные графики рекомендуются при следующих условиях:
- нужно менять масштаб оси Х;
- для горизонтальной оси используется логарифмическая шкала;
- числовые значения расположены неравномерно;
- горизонтальная ось представлена множеством точек;
- необходимо показать данные таблицы, содержащие пары сгруппированных значений, и вывести самостоятельные шкалы точечного графика для иллюстрации дополнительной информации о сгруппированных данных;
- требуется продемонстрировать аналогию между точками в больших наборах данных.
С помощью точечной диаграммы можно сравнивать сразу много точек без учета времени. Сравнение будет тем точнее, чем больше значений будет использовано.
Как построить точечную диаграмму в Excel
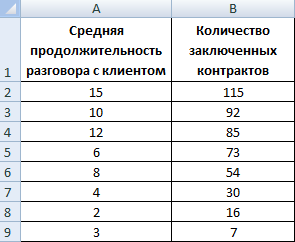
Возьмем примерный набор данных, которые нужно нанести на точечную диаграмму:
- Выделяем значения, которые нужно иллюстрировать с помощью точечной диаграммы. Переходим на вкладку «Вставка». В группе «Диаграммы» находим тип «Точечная».
- Из предлагаемых вариантов выберем «Точечную с маркерами». Она подойдет для сравнения пар значений.
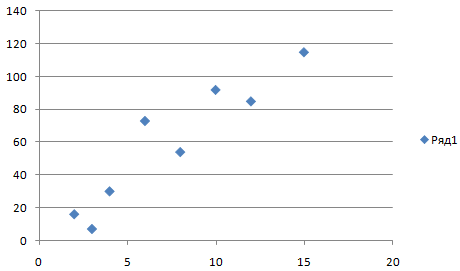
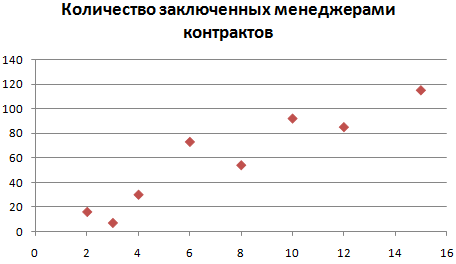
- Получаем диаграмму такого вида:
- Активизируем инструмент «Работа с диаграммами». Для этого нужно щелкнуть мышкой по области диаграммы. Поменяем стиль – сделаем точки красными. Добавим название (на вкладке «Макет») – «Количество заключенных менеджерами контрактов». Чтобы изменить размер шрифта, выделим название и щелкнем правой кнопкой мыши. В контекстном меню выберем поле «Шрифт».
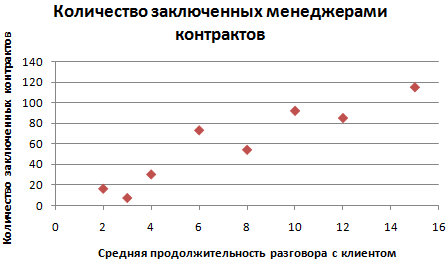
- Зададим названия осей. В одноименной группе на вкладке «Макет» выбираем название для горизонтальной оси («под осью»), вводим нужный текст. Для вертикальной оси – «Повернутое название».
- Вводим название для оси и жмем ВВОД.
Точечная диаграмма отличается от других типов способом отображения показателей по горизонтальной оси. Средняя продолжительность разговора с клиентом из первого столбца показана в виде значений Х. Количество контрактов из второго столбца – в виде значений Y. То есть один набор числовых данных всегда формируется вдоль горизонтальной оси значений. А второй набор – вдоль вертикальной оси, тоже значений.
На пересечении координат – точка данных, которая объединяет два числовых значения. В нашем примере первая точка данных на рисунке представлена значением Y (16, ячейка В8) и значением Х (2, А8). Получилась точечная диаграмма связи показателей.
Подтипы точечной диаграммы
- Мы построили точечную диаграмму с маркерами, которая позволяет сравнивать пары значений. Такой подтип рекомендуется применять, когда много данных (соединительная линия только затруднит восприятие) или нет нужды показывать связь между точками.
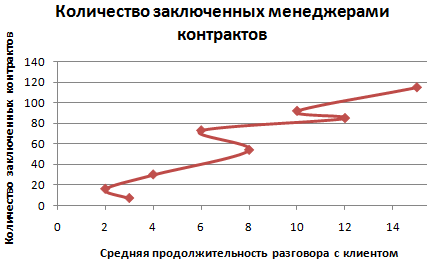
- На точечной диаграмме со значениями, соединенными сглаживающими линиями, точки данных объединены гладкой кривой. Можно делать с маркерами или без. Без маркеров – когда много исходных данных.
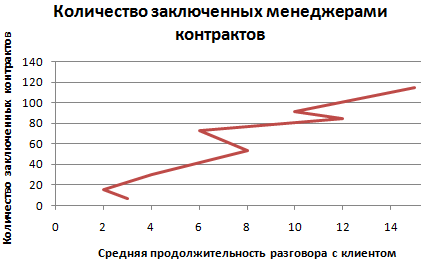
- В диаграмме с прямыми отрезками между точками – прямые соединительные линии. Пользователь может задать с маркерами или без.
Таким образом, числовые значения отображаются на точечной диаграмме в виде единых точек данных. Интервалы могут быть равномерными и неравномерными. Горизонтальная ось – всегда ось значений. Набор параметров для ее шкалы не ограничен (по сравнению с осью категорий).
Точечную диаграмму удобно использовать для демонстрации связи между данными, находящимися в разных рядах. Их можно показать в виде одной последовательности точек.
Построение графиков функций

В данном пособии рассматриваются различные способы построения графиков функций. Приводятся примеры построения графиков различными методами, задания для самостоятельной работы.Пособие рекомендовано для учащихся старших классов и учителей школ, гимназий, лицеев для организации работы, как на уроке, так и на факультативах и дополнительных занятиях по данной теме, а также для подготовки к экзаменам.
Оглавление
Построение графика функции по точкам
Построение графика функции по точкам выполняется в следующем порядке:
1. составляется таблица значений аргумента и функции на основе данной формулы;
2. в выбранной системе координат строятся точки, координатами которых являются соответствующие значения переменных, содержащиеся в таблице;
3. полученные точки соединяются плавной линией.
При задании значений аргумента следует учитывать область определения функции.
Пример 1. Построить график функции у=х (6-х), где — 1 <х <5.
Решение. Функция у=х (6-х) определена на всем указанном интервале. Составим таблицу значений аргумента и функции:
На координатной плоскости отметим полученные точки и соединим их плавной линией.
Получим график функции у=х (6-х) на интервале — 1 <х <5.
При построении графика функции по точкам иногда указывают шаг, т.е. число, через которое выбирается последующее значение аргумента. Чем меньше шаг, тем точнее получается график.
Задание 1. Постойте по точкам график функции…
Пример 2. Постройте график функции у=х2—3, на интервале [ — 4; 4] с шагом 1.
Решение. Функция у=х2—3 определена на всем интервале. Составим таблицу значений. Первое значение аргумента — 4. Следующее с учетом шага — 4+1=-3 и т. д. пока не получим последнее значение 4.
Отметим точки на координатной плоскости и построим график:
Задание 2. Постройте график функции на заданном интервале с указанным шагом…

Смотрите также
Построение графика заданной функции по точкам имеет целью получение точного рисунка нужных размеров, который можно было бы использовать в публикациях, технической документации, презентациях и т.п.
Чтобы получить графическое изображение заданной функции y=f(x)y = f(x) на заданном отрезке [a,b][a, b] в прямоугольной системе координат, необходимо выполнить следующие действия:
- выбрать количество точек для построения nn;
- вычислить шаг табуляции аргумента xx по формуле h=(b–a)/(n–1)h = (b–a) / (n–1);
- найти все nn значений xx, для которых должны быть вычислены значения функции, то есть x1=ax_{1} = a; xi+1=xi+hx_{i+1} = x_{i} + h, i=1,2,…,n–2i = 1,2,…,n–2; xn=bx_{n} = b;
- построить таблицу значений функции, вычислив yi=f(xi)y_{i} = f(x_{i}), i=1,2,…,ni = 1,2,…,n;
| i | 1 | 2 | n–1n – 1 | n |
|---|---|---|---|---|
| xix_i | x1x_1 | x2x_2 | xn–1x_{n–1} | xnx_n |
| yiy_i | y1y_1 | y2y_2 | yn–1y_{n–1} | yny_n |
- вычислить масштабы по осям координат OxO_x и OyO_y по формулам mx=(b–a)/Lxm_{x} = (b – a) / Lx, my=(ymax–ymin)/Lym_{y} = (y_{max} – y_{min}) / L_{y} соответственно, где LxL_x и LyL_y – заданные размеры графика по осям координат, ymaxy_{max} и yminy_{min} – наибольшее и наименьшее значения функции, выбранные из таблицы; значения масштабов следует округлить;
- на поле размером Lx×LyL_{x} × L_{y} изобразить оси координат OxO_x и OyO_y в пределах промежутков [a,b][a, b] и [ymin,ymax][y_{min}, y_{max}] соответственно, на осях проставить масштабные деления, нанести точки графика (xi,yi)(x_{i}, y_{i}) и соединить их плавной линией.
Пример построения графика функции по точкам
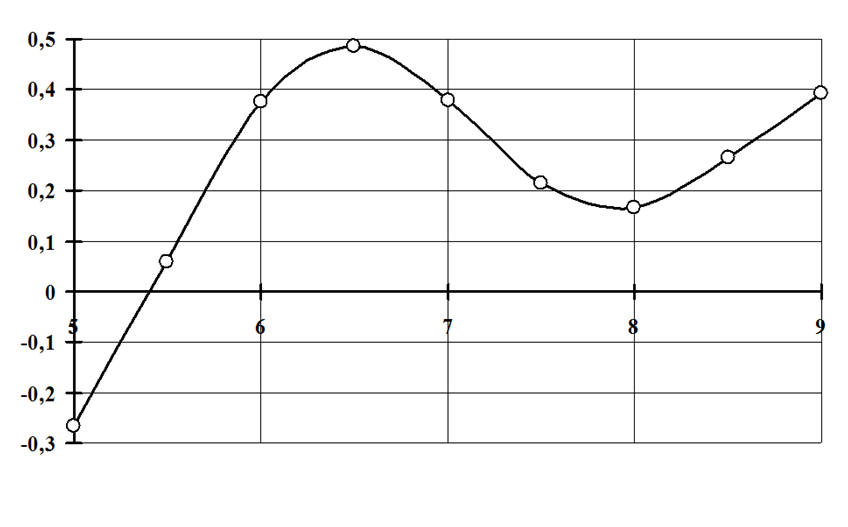
Построим график функции y=(3⋅sinx+x⋅cos2x)/(2⋅ln3x+1)y = (3·sinx + x·cos^2x) / (2·ln^3x +1) на отрезке [5, 9] размером Lx=16L_{x} = 16 см по горизонтали и Ly=7,5L_{y} = 7,5 см по вертикали.
Выбираем количество точек для построения n=9n = 9. Вычисляем шаг табуляции по аргументу x:h=(9–5)/(9–1)=0,5x: h = (9 – 5) / (9 – 1) = 0,5. Находим значения аргумента и строим таблицу значений функции:
| ii | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| xix_i | 5 | 5,5 | 6 | 6,5 | 7 | 7,5 | 8 | 8,5 | 9 |
| yiy_i | -0,265 | 0,059 | 0,375 | 0,485 | 0,378 | 0,214 | 0,165 | 0,266 | 0,392 |
Вычисляем масштабы: mx=(9–5)/16=0,25m_{x} = (9 – 5) / 16 = 0,25 единиц на 1 см (или 1 единица на 4 см) по оси OxO_x; my=(0,485–(–0,265))/7,5=0,1m_{y} = (0,485 – (–0,265)) / 7,5 = 0,1 единиц на 1 см по оси OyO_y.
Выполняем построение графика:
Тест на тему “Построение графика функции по точкам”
Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Декартова система координат
- Функция
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Функция – это отображение элементов множества X на множество Y . При этом каждому элементу x множества X соответствует одно единственное значение y множества Y .
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y .
Если a 0 , прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y .
Если a = 0 , функция принимает вид y = b .
Отдельно выделим график уравнения x = a .
Важно : это уравнение не является функцией так как нарушается определение функции ( функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y ). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y . Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
Парабола
Графиком функции y = a x 2 + b x + c является парабола .
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y .
- Коэффициент b помогает найти x в – координату вершины параболы.
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D > 0 – две точки пересечения.
- Если D = 0 – одна точка пересечения.
- Если D 0 – нет точек пересечения.
Гипербола
Графиком функции y = k x является гипербола .
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.
0″ height=»346″ width=»346″ sizes=»(max-width: 346px) 100vw, 346px» data-srcset=»/wp-content/uploads/2017/01/Гипербола-1.png 346w,/wp-content/uploads/2017/01/Гипербола-1-150×150.png 150w,/wp-content/uploads/2017/01/Гипербола-1-300×300.png 300w,/wp-content/uploads/2017/01/Гипербола-1-176×176.png 176w,/wp-content/uploads/2017/01/Гипербола-1-60×60.png 60w, https://epmat.ru/wp-content/uploads/2017/01/Гипербола-1.png»>
Если k 0, ветви гиперболы проходят через II и IV четверти.
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
Функция y = f ( x ) возрастает на интервале , если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
Функция y = f ( x ) убывает на интервале , если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:
Для того, чтобы найти наибольшее значение функции , находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.
Для того, чтобы найти наименьшее значение функции , находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Построение графиков функций
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
при х ≠ -1.
График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
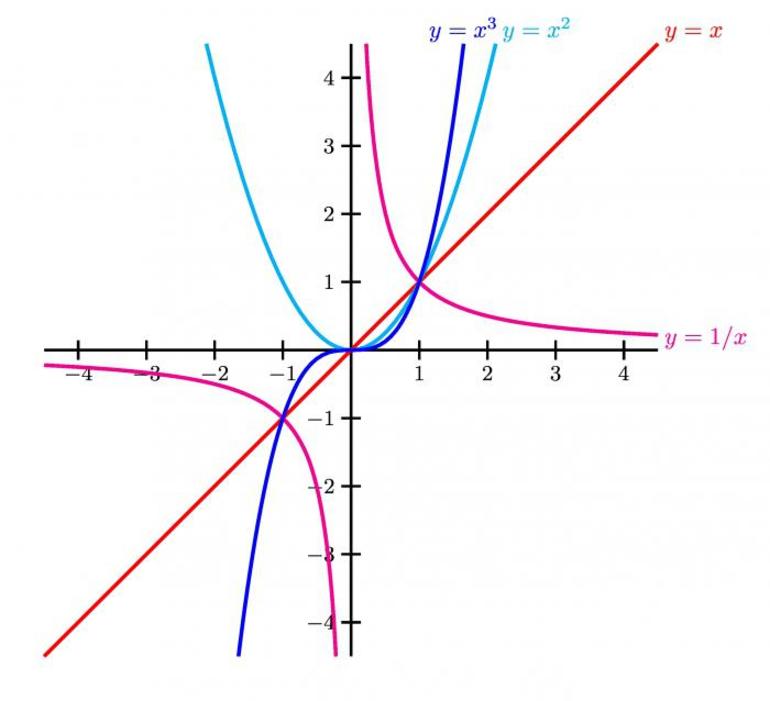
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
Как найти точки пересечения графиков функций — алгоритмы и примеры правила и методики
Общие сведения
Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.
Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.
Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.
Классификация уравнений
Уравнение — тождество, содержащее неизвестные величины (переменные), которые следует найти при помощи определенного алгоритма. Последний зависит от типа выражений. Тождества классифицируются на несколько типов:
Линейными являются уравнения, содержащие единичную степень, т. е. 2t=4. Квадратные — тождества, у которых переменная возведена в квадрат. Они имеют следующий вид: Pt^2+St+U=0, где Р и S — коэффициенты при неизвестных, а U — свободный член.
Кубическое — уравнение вида Ot^3+Pt^2+St+U=0, где O, Р и S — коэффициенты при переменных, а U — константа. Последний вид — равенства, в которых при переменной присутствует четвертая степень (Nt^4+Ot^3+Pt^2+St+U=0).
Равносильные тождества
При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.
Формулировка первого: когда I уравнение равносильно II, то значит, и II равносильно I. Суть транзитивности состоит в том, что если I равносильно II, а II — III, то значит I эквивалентно III. Второе свойство имеет такую формулировку: произведение двух элементов, содержащих переменные, равное нулевому значению, эквивалентно двум выражениям, которые можно приравнять к 0. Математическая запись утверждения имеет такой вид: R(t)*S(t)=0 .
Математические преобразования
Для решения уравнения необходимо выполнить некоторые математические преобразования. Они должны выполняться грамотно, поскольку любая ошибка приводит к образованию ложных корней. Допустимыми операциями являются следующие:
- Правильное раскрытие скобок с учетом алгебраической операции и знаков.
- Упрощение выражения (приведение подобных величин).
- Перенос элементов в любые части равенства с противоположным знаком.
- Возможность прибавлять или вычитать эквивалентные величины.
- Деление и умножение на любые эквивалентные значения, не превращающие тождества в пустое множество.
Специалисты рекомендуют избегать операций, при которых сокращаются неизвестные величины. Следствием этого могут стать ложные корни. Кроме того, делитель не должен иметь значения, при которых его значение равно 0. Последнее условие следует всегда проверять, а при решении ни один корень уравнения не должен соответствовать значению переменной при нахождении окончательных корней.
Иными словами, в выражении (t+2)^2=0 для упрощения можно разделить обе части на (t+2) при условии, что t не равно -2, т. к. [(t+2)^2]/(t+2)=0/(t+2).
Однако при решении (t+2)=0 получается, что t=-2, а это недопустимо. Следовательно, вышеописанный метод не всегда подходит.
Разложение на множители
Для решения уравнений при выполнении математических преобразований могут потребоваться специальные формулы разложения на множители. Их еще называют тождествами сокращенного умножения. К ним относятся следующие:
- Квадрат суммы и разности: (p+r)^2=p^2+2pr+r^2 и (p-r)^2=p^2-2pr+r^2 соответственно.
- Разность квадратов: p^2-r^2=(p-r)(p+r).
В некоторых случаях можно воспользоваться сразу двумя соотношениями, т. е. выделить квадрат суммы, а затем из первого — разность квадратов. Выделение первого осуществляется группировкой посредством скобок в выражении, а затем введение положительного и отрицательного элементов, т. е. s^2+4s-5=s^2+4s+4-4-5=(s^2+4s+4)-4-5=(s+2)^2 -9. Для получения всех элементов формулы «p+r)^2=p^2+2pr+r^2» нужно прибавить, а затем отнять 4. При этом значение равенства не изменится, поскольку 4-4=0.
Следует отметить, что математические преобразования выражения (s+2)^2 -9 не заканчиваются, поскольку его можно представить в виде разности квадратов, т. е. (s+2-9)(s+2+9)=(s-7)(s+11). Кроме того, формулы сокращенного умножения рекомендуется применять при понижении степени.
Методики нахождения точек
Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными. В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида.
Первой и второй степени
Уравнение первой степени, или линейное, решается очень просто. Для этого необходимо перенести переменные величины в одну, а известные — в другую сторону. Методика решения имеет следующий вид:
- Раскрыть скобки и привести подобные коэффициенты.
- Выполнить перенос известных в одну, а неизвестных — в другую часть равенства.
- Произвести необходимые математические преобразования.
- Найти корень.
Сложнее решается квадратное уравнение. Существует несколько способов нахождения его корней:
- Разложить на множители.
- Выделить полный квадрат.
- Найти дискриминант.
- По теореме Виета.
Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).
Однако не всегда можно быстро решить квадратное уравнение при помощи первых двух методов. Еще один вариант — нахождение корней через дискриминант (Д), т. е. дополнительный параметр, позволяющий сразу находить решения. Он находится по следующей формуле: Д=(-S)^2 -4PU.
Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д 3 +St 2 +Ut+V=0 существует еще одна методика нахождения корней. Она имеет следующий вид:
- Уравнение требуется разделить на P.
- Осуществить замену: t=m-(S/(3P)). При этом получается тождество вида m^3 +km+l=0.
- Найти значение коэффициентов по формулам: k=[2S 3 -9PSU+27(P 2 )V] / (27P 3 ) и l=[(3PU-S 2 )/(3P 2 )]. Подставить их во второй пункт и найти промежуточные корни, при помощи которых найти основные значения переменных.
Следует отметить, что важным пунктом методики является правильный выбор выражения замены, а затем верное выполнение математических преобразований.
Пример решения
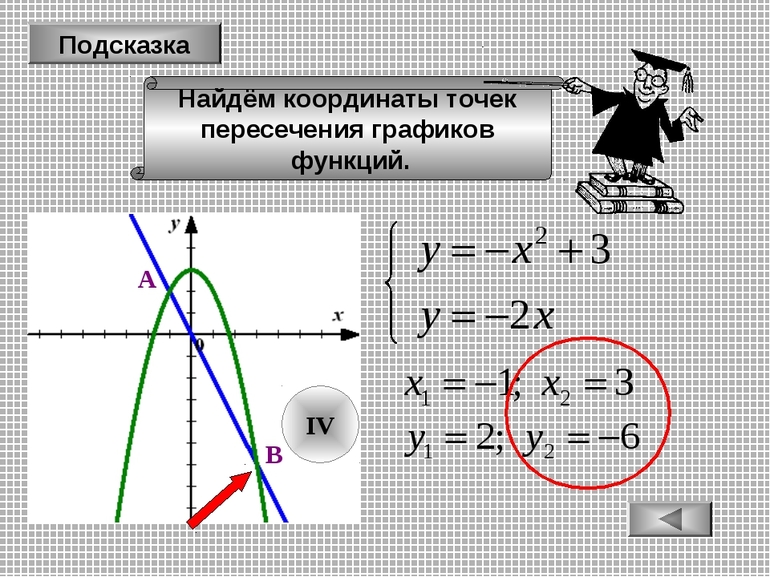
Для закрепления знаний необходимо перейти к практическому решению заданий.Одной из простых задач является следующая: найдите координаты точки пересечения графиков линейных функций z=2t+7 и z=t-1. Решается задача по такому алгоритму:
- Приравнять уравнения: 2t+7=t-1.
- Перенести переменные влево, а константы — вправо: 2t-t=-1-7.
- Привести подобные коэффициенты: t=-8.
- Найти координаты второй составляющей: z=-8-1=-9.
- Искомая точка пересечения: (-8;-9).
В четвертом пункте нужно подставить координату по оси абсцисс в любое из уравнений для получения второй составляющей, необходимой для точки. Следует отметить, что в этой задаче нет необходимости проводить математические преобразования. Однако существуют и более сложные задания, в которых необходимо решать квадратные уравнения, а также раскрывать скобки.
Таким образом, для определения точки пересечения графиков необходимо уметь находить корни уравнения, а также выполнять алгебраические преобразования.
http://skysmart.ru/articles/mathematic/postroenie-grafikov-funkcij
http://nauka.club/matematika/algebra/ochki-peresecheniya-grafikov.html