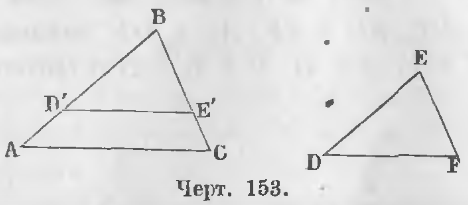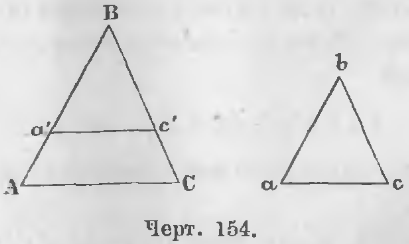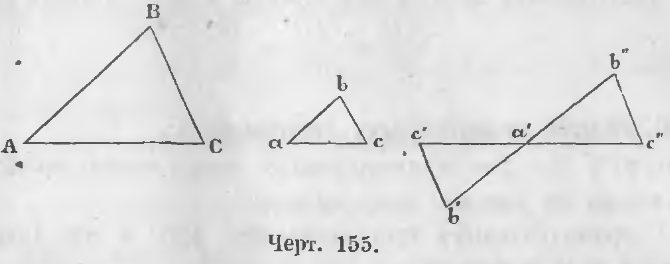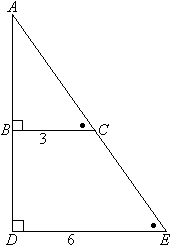Как правильно составить пропорцию в геометрии

Математика

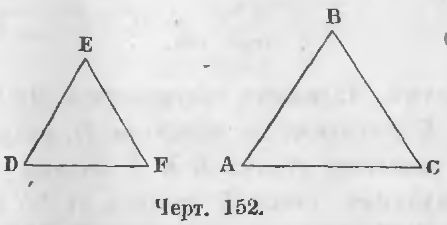
В двух треугольниках, имеющих равные углы, стороны, лежащие против одинаковых углов, называются сходственными (соответственными).

В треугольниках ABC и DEF (черт. 152), в которых

стороны AB и DE, BC и EF, AC и DF, лежащие против равных углов C и F, A и D, B и E будут соответственными сторонами.

Определение подобных треугольников. Подобными называются такие два треугольника, у которых углы равны и сходственные стороны пропорциональны.

Если в двух треугольниках (черт. 152) ABC и DEF углы равны

и соответственные стороны пропорциональны

AB/DE = AC/DF = BC/EF

то треугольники называются подобными.

Подобие обычно выражают знаком ∼.

Подобие двух треугольников изображают письменно:

Случаи подобия треугольников

Теорема 89. (Первый случай подобия.) Два треугольника подобны, если три угла одного равны трем углам другого треугольника.

Дано. В треугольниках ABC и DEF углы равны (черт. 153).

Требуется доказать, что они подобны. Для этого нужно доказать, что их стороны пропорциональны, т. е. удовлетворяют отношениям:

AB/DE = AC/DF = BC/EF

Доказательство. Наложим треугольник DEF на ABC так, чтобы вершина E совпала с вершиной B, сторона ED со стороной AB. По равенству углов B и E сторона EF пойдет по стороне BC. Положим, точка D упадет в D’, а точка F в E’. Треугольник D’BE’ равен треугольнику DEF, следовательно,

Если соответственные углы равны, то D’E || AC.

По теореме 86 имеют место равенства

AC/D’E’ = AB/BD’ = BC/BE’

Так как BD’ = ED, BE’ = EF, D’E’ = DF, то

AC/DF = AB/ED = BC/EF (ЧТД).

Теорема 90 (второй случай подобия). Два треугольника подобны, если они имеют по два равных угла.

Доказательство. Если в двух треугольниках ABC и DEF два угла равны (черт. 153).

то и третьи углы тоже равны, а в таком случае треугольники подобны (теорема 89).

Теорема 91 (третий случай подобия). Два треугольника подобны, если они имеют по равному углу, заключающемуся между пропорциональными сторонами.

Дано. В треугольниках ABC и DEF (черт. 153) углы B и E равны, и стороны, их содержащие, пропорциональны, т. е.

∠B = ∠E и AB/DE = BC/EF.

Требуется доказать, что треугольники подобны.

Доказательство. Совместим угол E с углом B, и отложим BD’ = ED, BE’ = EF, тогда ∆ BD’E’ = ∆ DEF, следовательно,

Так как имеет место пропорция

то сторона D’E’ || AC (теорема 87).

Поэтому ∠D’ = ∠A, ∠C = ∠E’.

т. е. три угла одного равны трем углам другого треугольника.

В этом же случае треугольники ABC и DEF подобны (ЧТД).

Теорема 92 (четвертый случай подобия). Два треугольника подобны, если стороны одного пропорциональны сторонам другого.

Дано. В треугольниках ABC и abc (черт. 154) стороны пропорциональны:

AB/ab = BC/bc = AC/ac (1)

Требуется доказать, что у них углы равны, т. е.

Доказательство. Отложим на стороне BA отрезок Ba’, равный ba, и проведем отрезок a’c’, параллельный AC, тогда будут иметь место отношения:

AB/Ba’ = BC/Bc’ = AC/a’c’

Так как Ba’ = ba, то рядом с этими имеют место отношения:

AB/ab = BC/Bc’ = AC/a’c’ (2)

Сопоставляя отношения (1) и (2), заключаем, что

следовательно, два треугольника a’Bc’ и abc равны, откуда

∠B = ∠b, ∠Ba’c’ = ∠a, ∠Bc’a’ = ∠c

∠A = ∠a’, ∠C = ∠c’, то
B = b, A = a, C = c,

следовательно, углы двух треугольников ABC и abc равны (ЧТД).

Теорема 93 (пятый случай подобия). Два треугольника подобны, если стороны одного параллельны сторонам другого.

Доказательство. Здесь могут быть два случая:

1-й случай. Если углы двух треугольников с параллельными сторонами обращены в одну сторону. В таком случае в двух таких треугольниках ABC и abc (черт. 155) все углы одного соответственно равны углам другого, и, следовательно, треугольники подобны.

2-й случай. Когда углы с параллельными сторонами обращены в разные стороны. Так в треугольниках ABC и a’b’c’ стороны параллельны.

AB || a’b’, AC || a’c’, BC || b’c’.

Углы же между параллельными сторонами обращены в разные стороны.

В таком случае, продолжив стороны a’c’ и a’b’, откладываем на продолжении их части a’b» = a’b’ и a’c» = a’c’.

Треугольники a’b»c» и a’b’c’ равны. Треугольник a’b»c» подобен треугольнику ABC, ибо у него стороны параллельны и углы, направленные в одну сторону, равны, следовательно,

a’b»c», следовательно, ∆ ABC

a’b’c’ и
AB/a’b’ = AC/a’c’ = BC/b’c’

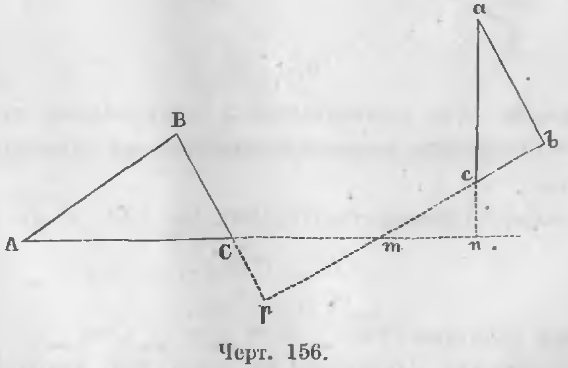
Теорема 94 (шестой случай подобия). Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.

Даны два треугольника ABC и abc (черт. 156), стороны которых перпендикулярны:

ab ⊥ AB, ac ⊥ AC, bc ⊥ BC

Требуется доказать, что треугольники подобны.

Доказательство. Продолжим стороны ac и bc до пересечения их со сторонами AC и BC в точках n и p. Тогда в двух треугольниках mcn и mCp все углы равны, ибо

n = p как прямые

Углы при точке m равны как вертикальные,

а следовательно, и третьи углы равны ∠pCm = ∠mcn.

∠pCm = ∠ACB, ∠mcn = ∠acb

Подобным же образом можно доказать, что A = a, B = b, следовательно, треугольники ABC и abc подобны и имеет место пропорция

AB/ab = AC/ac = BC/bc

Подобие прямоугольных треугольников

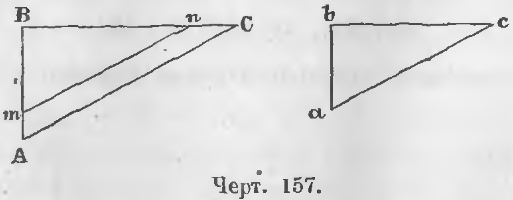
Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.

Требуется доказать, что треугольники ABC и abc подобны.

Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).

Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.

Дано. В прямоугольных треугольниках ABC и abc (черт. 157)

Требуется доказать, что ∠A = ∠a, ∠C = ∠c.

Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:

Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.

Действительно, у них Bm = ab, mn = ac. У равных треугольников и углы равны:

∠m = ∠a = ∠A и ∠n = ∠c = ∠C

следовательно, два треугольника ABC и abc подобны.

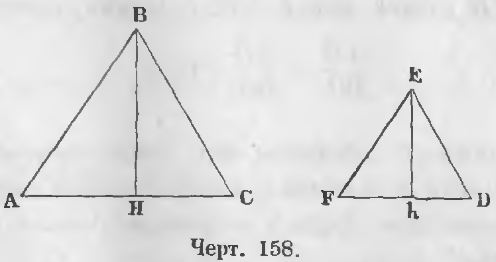
Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.

Даны два подобных треугольника ABC и FED (черт. 158), следовательно,

∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF

и проведены высоты BH и Eh.

Требуется доказать, что AB/FE = BH/Eh.

Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,

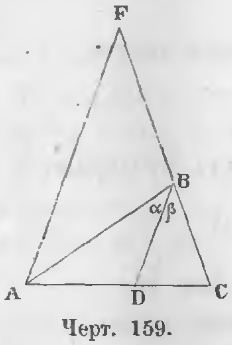
Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.

Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).

∠ABD = ∠DBC или ∠ α = ∠ β

Требуется доказать, что AB/BC = AD/DC.

Доказательство. Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA

∠AFB = ∠ β как соответственные углы,
∠FAB = ∠ α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.

Так как ∠ α = ∠β по условию, то

∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.

Из того, что AF || BD вытекает пропорция:

Заменяя FB равным отрезком AB, получим пропорцию:

Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.

Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:

Требуется доказать, что ∠ α = ∠β .

Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:

Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,

Так как ∠ α = ∠ FAB, ∠β = ∠ AFB, то и

Отношения в прямоугольном треугольнике

Теорема 100. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, среднепропорционален между частями гипотенузы.

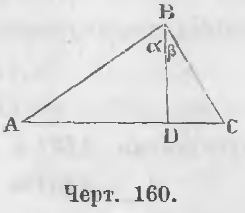
Дано. В треугольнике ABC угол ABC прямой (черт. 160) и BD ⊥ AC.

Требуется доказать, что AD/BD = BD/DC.

Доказательство. Треугольники ABD и BDC подобны, ибо углы при точке D равны как прямые; кроме того из равенств ∠A + ∠ α = d, ∠ α + ∠β = d вытекает

A + α = α + β, или A = β, следовательно и C = α.

Из подобия треугольников ABD и BDC вытекает пропорция

Примечание. Если составляют одно отношение из сторон одного треугольника, то другое отношение составляется из соответственных сторон другого треугольника. При этом рассуждают следующим образом: против стороны AD лежит угол α , которому в подобном треугольнике BCD равен угол C, а против него лежит сходственная сторона BD треугольника BCD и т. д.

Теорема 101. Каждый катет среднепропорционален между целой гипотенузой и отрезком, прилежащим катету.

Доказательство. a) Треугольники ABC и ABD (черт. 160) подобны, ибо ∠ ABC = ∠ADB как прямые, ∠A общий, следовательно,

Из подобия треугольников вытекает пропорция:

b) Треугольники ABC и BCD подобны, ибо ∠ABC = ∠BDC как прямые, ∠C общий, следовательно,

∠A = ∠ β, откуда
DC/BC = BC/AC (b)

Теорема 102. Квадрат гипотенузы равен сумме квадратов катетов.

Из предыдущих пропорций (a) и (b) вытекают равенства:

AB 2 = AD · AC
BC 2 = DC · AC

Складывая их, получим:

AB 2 + BC 2 = AD · AC + DC · AC или
AB 2 + BC 2 = AC (AD + DC) = AC · AC = AC 2 , т. е.
AC 2 = AB 2 + BC 2

a) Гипотенуза равна корню квадратному из суммы квадратов катетов.

b) Катет равен корню квадратному из квадрата гипотенузы без квадрата другого катета.

Теорема 103. Диагональ квадрата несоизмерима с его стороной, или гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетом.

Дано. В квадрате ABCD проведена диагональ AC (черт. 161).

Требуется доказать, что отношение AC/AD есть величина несоизмеримая.

Доказательство. Станем сравнивать больший отрезок AC с меньшим BC по обыкновенным приемам нахождения общей меры, т. е. наложим меньший отрезок на больший, первый остаток на меньший и т. д.

a) Наложим отрезок BC на отрезок AC. Отложив отрезок AE, равный AB или BC, мы видим, что отрезок BC уложился один раз, ибо

Так как AB = BC, то 2BC > AC и BC > ½AC, следовательно, первый остаток EC 2 = AB 2 + BC 2 .

Так как AB = BC, то AC 2 = 2AB 2 , откуда AC = AB √ 2 и AC/AB = √ 2 величина несоизмеримая.

Соотношение между сторонами остроугольного и тупоугольного треугольника

Теорема 104. Квадрат стороны, лежащей против острого угла, равен сумме квадратов прочих двух сторон треугольника без удвоенного произведения основания на отрезок, заключающийся между вершиной острого угла и высотой.

Здесь могут быть два случая: 1) когда перпендикуляр, выражающий высоту, пойдет внутри и 2) когда он пойдет вне треугольника.

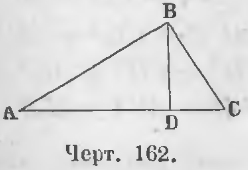
Первый случай. Перпендикуляр BD (черт. 162), опущенный из вершины B на основание AC треугольника ABC, пойдет внутри треугольника.

Требуется доказать, что AB 2 = BC 2 + AC 2 — 2AC · DC.

Доказательство. Для прямоугольного треугольника ABD имеем равенство:

AB 2 = BD 2 + AD 2 (a)
AD = AC — DC, AD 2 = (AC — DC) 2 = AC 2 + DC 2 — 2AC · DC

Из прямоугольного треугольника BDC имеем:

BD 2 = BC 2 — DC 2

Вставляя величины BD 2 и AD 2 в равенство (a), получим:

AB 2 = BC 2 — DC 2 + AC 2 + DC 2 — 2AC · DC, откуда
AB 2 = BC 2 + AC 2 — 2AC · DC (ЧТД).

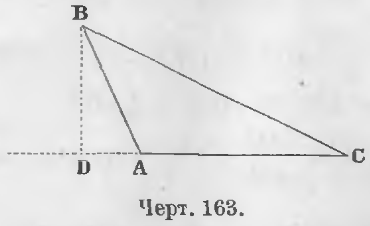
2-й случай. Перпендикуляр BD (черт. 163) лежит вне треугольника ABC.

Доказательство. Из прямоугольного треугольника ABD имеем:

AB 2 = BD 2 + DA 2

Из прямоугольного треугольника BCD имеем:

BD 2 = BC 2 — CD 2

AB 2 = BC 2 — CD 2 + DA 2 .

DA = CD — AC
DA 2 = (CD — AC) 2 = CD 2 + AC 2 — 2CD · AC, то
AB 2 = BC 2 — CD 2 + CD 2 + AC 2 — 2CD · AC, откуда
AB 2 = BC 2 + AC 2 — 2CD · AC (ЧТД).

Теорема 105. Квадрат стороны, лежащей против тупого угла, равен сумме квадратов прочих двух сторон треугольника с удвоенным произведением основания на отрезок его от вершины тупого угла до высоты.

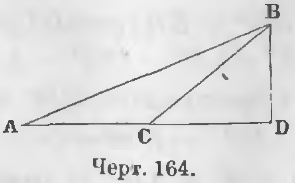
Дано. В тупоугольном треугольнике ABC отрезок CD (черт. 164) есть отрезок, лежащий между вершиной тупого угла и высотой.

Требуется доказать, что

AB 2 = AC 2 + BC 2 + 2AC · CD

Доказательство. Из тупоугольного треугольника ABC имеем:

AB 2 = BD 2 + AD 2 (a)
AD = AC + CD, AD 2 = AC 2 + CD 2 + 2AC · CD

Из прямоугольного треугольника BCD вытекает, что

BD 2 = BC 2 — CD 2

Заменяя AD 2 и BD 2 в равенстве (a), получим:

AB 2 = BC 2 — CD 2 + AC 2 + CD 2 + 2AC · CD

AB 2 = BC 2 + AC 2 + 2AC · CD (ЧТД).

Теорема 106. Сумма квадратов диагоналей равна сумме квадратов всех четырех сторон параллелограмма.

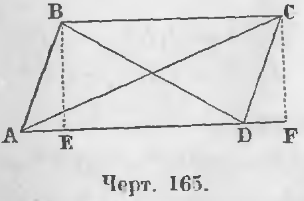
Дан параллелограмм ABCD (черт. 165) и проведены его диагонали AC и BD.

Требуется доказать, что

AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2

Доказательство. Опустив перпендикуляры BE и CF, имеем из косоугольного треугольника ABD равенство:

BD 2 = AB 2 + AD 2 — 2AD · AE (1)

Из тупоугольного треугольника ACD равенство:

AC 2 = CD 2 + AD 2 + 2AD · DF (2)

Отрезки AE и DF равны, ибо прямоугольные треугольники ABE и DCF равны, так как они имеют по равному катету и равной гипотенузе.

Сложив равенства (1) и (2), имеем:

BD 2 + AC 2 = AB 2 + AD 2 + CD 2 + AD 2

Так как AD = BC, то

BD 2 + AC 2 = AB 2 + BC 2 + CD 2 + AD 2 (ЧТД).

Теорема 107. Сумма квадратов двух сторон треугольника равна сумме удвоенного квадрата отрезка, соединяющей вершину с серединой основания, с удвоенным квадратом половины основания.

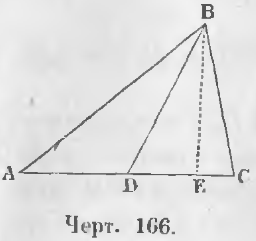
Дано. Соединим вершину B с серединой основания D треугольника ABC так, что AD = DC (черт. 166).

Требуется доказать, что

AB 2 + BC 2 = 2AD 2 + 2BD 2

Доказательство. Проведем высоту BE.

Из прямоугольных треугольников ABE и BCE вытекают равенства:

AB 2 = BE 2 + AE 2
BC 2 = BE 2 + CE 2

Сложив их, находим:

AB 2 + BC 2 = 2BE 2 + AE 2 + CE 2 (a)

Так как AE = AD + DE = CD + DE, CE = CD — DE, то

AE 2 = (CD + DE) 2 = CD 2 + DE 2 + 2CD · DE
CE 2 = (CD — DE) 2 = CD 2 + DE 2 — 2CD · DE

AE 2 + CE 2 = 2CD 2 + 2DE 2 (b)

Заменяя в равенстве (a) сумму AE 2 + CE 2 из равенства (b), имеем:

AB 2 + BC 2 = 2BE 2 + 2CD 2 + 2DE 2 .

Из прямоугольного треугольника BDE видно, что

BE 2 = BD 2 — DE 2

AB 2 + BC 2 = 2BD 2 — 2DE 2 + 2CD 2 + 2DE 2

Подобные треугольники

Определение

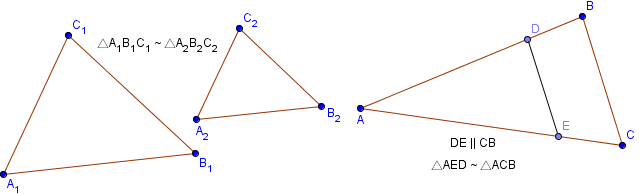
Как правило, два треугольника считаются подобными если они имеют одинаковую форму, даже если они различаются размерами, повернуты или даже перевернуты.

Математическое представление двух подобных треугольников A₁B₁C₁ и A₂B₂C₂ , показанных на рисунке, записывается следующим образом:

Два треугольника являются подобными если:

1. Каждый угол одного треугольника равен соответствующему углу другого треугольника:
∠A₁ = ∠A₂, ∠B₁ = ∠B₂ и∠C₁ = ∠C₂

2. Отношения сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой:
$frac=frac=frac$

3. Отношения двух сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой и при этом
углы между этими сторонами равны:
$frac=frac$ и $angle A_1 = angle A_2$
или
$frac=frac$ и $angle B_1 = angle B_2$
или
$frac=frac$ и $angle C_1 = angle C_2$

Не нужно путать подобные треугольники с равными треугольниками. У равных треугольников равны соответствующие длины сторон. Поэтому для равных треугольников:

Из этого следует что все равные треугольники являются подобными. Однако не все подобные треугольники являются равными.

Несмотря на то, что вышеприведенная запись показывает, что для выяснения, являются ли два треугольника подобными или нет, нам должны быть известны величины трех углов или длины трех сторон каждого треугольника, для решения задач с подобными треугольниками достаточно знать любые три величины из указанных выше для каждого треугольника. Эти величины могут составлять различные комбинации:

1) три угла каждого треугольника (длины сторон треугольников знать не нужно).

Или хотя бы 2 угла одного треугольника должны быть равны 2-м углам другого треугольника.
Так как если 2 угла равны, то третий угол также будет равным.(Величина третьего угла составляет 180 — угол1 — угол2)

2) длины сторон каждого треугольника (углы знать не нужно);

3) длины двух сторон и угол между ними.

Далее мы рассмотрим решение некоторых задач с подобными треугольниками. Сначала мы рассмотрим задачи, которые можно решить непосредственным использованием вышеуказанных правил, а затем обсудим некоторые практические задачи, которые решаются по методу подобных треугольников.

Практические задачи с подобными треугольниками

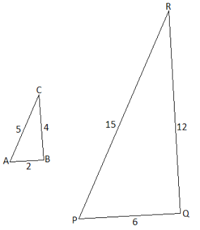
Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными.

Решение:
Так как длины сторон обоих треугольников известны, то здесь можно применить второе правило:

Пример №2: Покажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR.

Решение:
∠A = ∠P и ∠B = ∠Q, ∠C = ∠R(так как ∠C = 180 — ∠A — ∠B и ∠R = 180 — ∠P — ∠Q)

Из этого следует, что треугольники ΔABC и ΔPQR подобны. Следовательно:
$frac=frac=frac$

Пример №3: Определите длину AB в данном треугольнике.

Решение:

∠ABC = ∠ADE, ∠ACB = ∠AED и ∠A общий => треугольники ΔABC и ΔADE являются подобными.

$frac = frac<3> <6>= frac = frac = frac = frac<1> <2>Rightarrow 2times AB = AB + 4 Rightarrow AB = 4$

Пример №4:Определить длину AD (x) геометрической фигуры на рисунке.

Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C.
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.

AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC

Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны.

Следовательно:
$frac = frac<7> <11>= frac = frac<15> Rightarrow CA = frac<15 times 11> <7>= 23.57$
x = AC — DC = 23.57 — 15 = 8.57

Практические примеры

Пример №5: На фабрике используется наклонная конвеерная лента для транспортировки продукции с уровня 1 на уровень 2, который выше уровня 1 на 3 метра, как показано на рисунке. Наклонный конвеер обслуживается с одного конца до уровня 1 и с другого конца до рабочего места, расположенного на расстоянии 8 метров от рабочей точки уровня 1.

Фабрика хочет модернизировать конвеер для доступа к новому уровню, который находится на расстоянии 9 метров над уровнем 1, и при этом сохранить угол наклона конвеера.

Определите расстояние, на котором нужно установить новый рабочий пункт для обеспечения работы конвеера на его новом конце на уровне 2. Также вычислите дополнительное расстояние, которое пройдет продукция при перемещении на новый уровень.

Решение:

Для начала давайте обозначим каждую точку пересечения определенной буквой, как показано на рисунке.

Исходя из рассуждений, приведенных выше в предыдущих примерах, мы можем сделать вывод о том, что треугольники ΔABC и ΔADE являются подобными. Следовательно,

$frac = frac<3> <9>= frac = frac<8> Rightarrow AB = frac<8 times 9> <3>= 24 м$
x = AB — 8 = 24 — 8 = 16 м

Таким образом, новый пункт должен быть установлен на расстоянии 16 метров от уже существующего пункта.

А так как конструкция состоит из прямоугольных треугольников, мы можем вычислить расстояние перемещения продукции следующим образом:

Аналогично, $AC = sqrt = sqrt <24^2 + 9^2>= 25.63 м$
что является расстоянием, которое проходит продукция в данный момент при попадании на существующий уровень.

y = AC — AE = 25.63 — 8.54 = 17.09 м
это дополнительное расстояние, которое должна пройти продукция для достижения нового уровня.

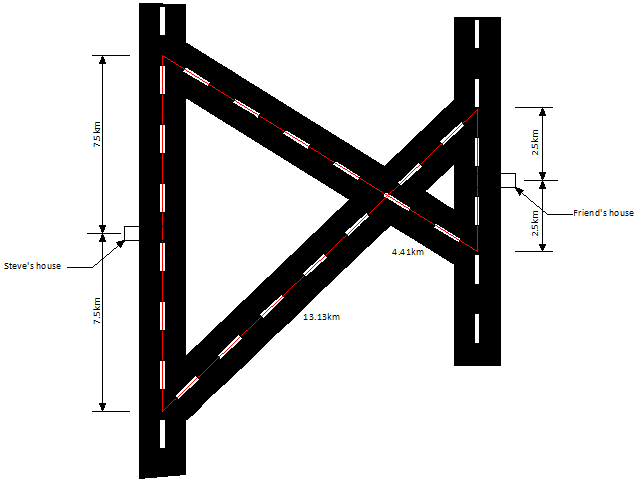
Пример №6: Стив хочет навестить своего приятеля, который недавно переехал в новый дом. Дорожная карта проезда к дому Стива и его приятеля вместе с известными Стиву расстояниями показана на рисунке. Помогите Стиву добраться к дому его приятеля наиболее коротким путем.

Решение:

Дорожную карту можно геометрически представить в следующем виде, как показано на рисунке.

Мы видим, что треугольники ΔABC и ΔCDE подобны, следовательно:
$frac = frac = frac$

В условии задачи сказано, что:

AB = 15 км, AC = 13.13 км, CD = 4.41 км и DE = 5 км

Используя эту информацию, мы можем вычислить следующие расстояния:

Стив может добраться к дому своего друга по следующим маршрутам:

A -> B -> C -> E -> G, суммарное расстояние равно 7.5+13.23+4.38+2.5=27.61 км

F -> B -> C -> D -> G, суммарное расстояние равно 7.5+13.23+4.41+2.5=27.64 км

F -> A -> C -> E -> G, суммарное расстояние равно 7.5+13.13+4.38+2.5=27.51 км

F -> A -> C -> D -> G, суммарное расстояние равно 7.5+13.13+4.41+2.5=27.54 км

Следовательно, маршрут №3 является наиболее коротким и может быть предложен Стиву.

Пример 7:
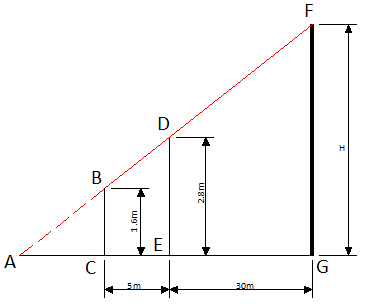
Триша хочет измерить высоту дома, но у нее нет нужных инструментов. Она заметила, что перед домом растет дерево и решила применить свою находчивость и знания геометрии, полученные в школе, для определения высоты здания. Она измерила расстояние от дерева до дома, результат составил 30 м. Затем она встала перед деревом и начала отходить назад, пока верхний край здания стал виден над верхушкой дерева. Триша отметила это место и измерила расстояние от него до дерева. Это расстояние составило 5 м.

Высота дерева равна 2.8 м, а высота уровня глаз Триши равна 1.6 м. Помогите Трише определить высоту здания.

Решение:

Геометрическое представление задачи показано на рисунке.

Сначала мы используем подобность треугольников ΔABC и ΔADE.

$frac = frac<1.6> <2.8>= frac = frac <5 + AC>Rightarrow 2.8 times AC = 1.6 times (5 + AC) = 8 + 1.6 times AC$

$(2.8 — 1.6) times AC = 8 Rightarrow AC = frac<8> <1.2>= 6.67$

Затем мы можем использовать подобность треугольников ΔACB и ΔAFG или ΔADE и ΔAFG. Давайте выберем первый вариант.

Подобные треугольники

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Свойства подобных треугольников

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
• Отношение периметров подобных треугольников равно коэффициенту подобия.
• Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Ratio, Proportion, and Geometric Means

Before you start analyzing similar triangles, you need to pick up a few more algebraic supplies. You’ll be dealing with fractions and ratios a lot in this section, so you might as well brush up on those algebra skills first.

A ratio is a quotient ^a/_b, where b 0. A ratio provides a comparison between the numbers a and b. For example, if a is twice as big as b, then the ratio ^a/_b is ²/₁. The ratio ^a/_b is read “a to b” and is sometimes written in the form a:b.

There are times when you might want to compare three or more items. When that happens, a simple fraction just won’t cut it. You’ll need to use what is called an extended ratio. An extended ratio is written in the form a:b:c (if you are comparing three quantities) or a:b:c:d (if you are comparing four quantities). If you are comparing lots of quantities, just keep adding them on, separating each quantity with a colon.

Eureka!

An extended ratio compares more than two quantities and cannot be expressed as a single fraction.

A proportion is a statement that two ratios are equal. The proportion ^a/_b is read as “a is to b as c is to d.” The first and last terms (a and d) are called the extremes, and the middle terms (b and c) are called the means. There are several useful properties involving proportions, and these properties can be established using algebra.

• Property 1: The Means-Extremes Property. In a proportion, the product of the means equals the product of the extremes. That is, if ^a/_b = ^c/_d (where b 0 and d 0), then a · d = b · c.

This is just an old-fashioned “cross-multiply” step used in algebra to get rid of unwanted denominators when dealing with fractions. You can use the Means-Extremes Property to solve algebraic equations.

• Example 1: Use the Means-Extremes Property to solve for x: ^{x + 1}/₉ = ^{x — 3}/₃.

  Solution: If we apply the Means-Extremes Property to our equation, we have

  3(x + 1) = 9(x 3)

  3x + 3 = 9x 27

  6x = 30

  x = 5

  Example 2: Use the Means-Extremes Property to solve for x: ⁴/_x = ^x/₉.

  Solution: If you apply the Means-Extremes Property to your equation, you have

  36 = x²

  x = ± 36 = ±6.

Now combine these ideas with a problem involving geometry.

• Example 3: Suppose that two complementary angles are in the ratio 2 to 3. Find the measure of each angle.
• Solution: Let one of your angles have measure x and the other angle have measure y. Because your two angles are compementary, x + y = 90º, so y = 90º x. Because the ratio of the angle measurements is 2 to 3, you have the following proportion:
• ^x/_y = ^x/_{90º x} = ²/₃
• You can then use the Means-Extremes Property:
• 3x = 2(90º x)
• 3x = 180º 2x
• 5x = 180º
• x = 36º

Now that you know the measure of one of your angles, you can find the measure of the second angle because the two angles are complementary:

• y = 90º x = 90º 36º = 54º

There are other properties of proportions. You can flip the proportions and mix and match numerators and denominators. Property 2 of proportions provides a list of the changes you can make.

• Property 2: In a proportion, the means or the extremes (or both the means and the extremes) may be interchanged. That is, if ^a/_b = ^c/_d and a, b, c, and d are all non-zero, then ^a/_c = ^b/_d, ^d/_b = ^c/_a and ^d/_c = ^b/_a.

Again, mixing numerators and denominators is not surprising because you’ve been doing this in algebra for years! But there is another property of proportions that might be a bit surprising. You have to be careful when you apply this property because it involves adding or subtracting things.

• Property 3: If ^a/_b = ^c/_d, where b 0 and d 0, then ^{a + b}/_b = ^{c + d}/_d.

To derive this property, start with ^a/_b = ^c/_d, add 1 to both sides and add the fractions.

Now that you have proportions under your belt, you can talk about the geometric mean of two numbers. If you start with a proportion where the two means are identical (and the two extremes may be different), such as ^a/_b = ^b/_d, then b is the geometric mean of a and d. You found the geometric means of the numbers 4 and 9 in Example 2. Although a pair of numbers actually has two geometric means (one positive and the other negative), geometers are only interested in the positive one. After one more example you’ll be ready to apply these algebraic properties to geometry.

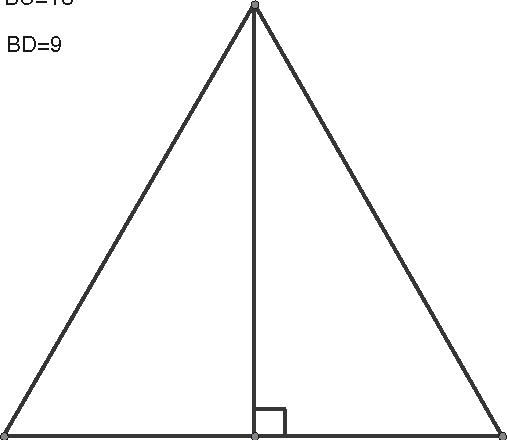
• Example 4: In Figure 13.1, suppose that AD is the geometric mean of BD and DC. If BC = 13 and BD = 9, find AD.

Figure 13.1AD is the geometric mean of BD and DC, BC = 13 and BD = 9.

• Solution: Because AD is the geometric mean of BD and DC, You know that ^BD/_AD = ^AD/_DC. You are given that BD = 9, but you still need to find DC. Using the Segment Addition Postulate, BC = BD + DC. Substituting in for BC and BD gives 13 = 9 + DC, or DC = 4. Now you can substitute the values into the proportion and solve for AD:
• ^BD/_AD = ^AD/_DC
• ⁹/_AD = ^AD/₄
• (AD)² = 36
• AD = 6

Excerpted from The Complete Idiot’s Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.

To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.