Как правильно составить уравнение окружности - Исправление недочетов и поиск решений вместе с Examum.ru

Написать уравнение окружности

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.

Следовательно, уравнение данной окружности

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

Таким образом, уравнение окружности с диаметром AB —

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение

получаем систему уравнений:

Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим

Приравняем правые части 2-го и 3-го уравнений:

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

Следовательно, уравнение окружности, проходящей через три данные точки —

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Уравнение с двумя переменными и его график. Уравнение окружности

п.1. Понятие уравнения с двумя переменными

Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm) – гипербола.

Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.

Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm<frac1x>) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).

п.2. Обобщенные правила преобразования графика уравнения

Пусть F(x; y) = 0 – исходный график некоторой функции

Симметричное отображение относительно оси OY

Симметричное отображение относительно оси OX

Центральная симметрия относительно начала координат

Параллельный перенос графика на a единиц вправо

Параллельный перенос графика на a единиц влево

Параллельный перенос графика на b единиц вниз

Параллельный перенос графика на b единиц вверх

Сжатие графика к оси OY в a раз

Сжатие графика к оси OX в b раз

F(x; by) = 0
0 Например:

Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm <(x-2)^2+(y-1)^2=9>$$

п.4. Примеры

Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm<7>=-frac<2> + 2 > ) – это прямая

б) xy + 4 = 0
Выразим y из уравнения: ( mathrm> ) – это гипербола

в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm=2> )

г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm<5>> ) – это парабола

Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm<5>=-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.

б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.

в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.

г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).

д) (mathrm<frac<|x-1|><2>+2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.

Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.

источники:

http://www.calc.ru/Uravneniye-Okruzhnosti.html

http://reshator.com/sprav/algebra/9-klass/uravnenie-s-dvumya-peremennymi-i-ego-grafik-uravnenie-okruzhnosti/

Источник

Download Article

The equation of a circle gives you the center coordinates and radius, allowing you to represent all of the literally infinite points around the boundary of the circle. But how exactly do you write it? Read on to learn how to write the equation of a circle in standard form, as well as how to convert general form to standard form. Once you’ve got that down, you can try your hand at some sample problems and check your answers. Let’s get started!

Things You Should Know

1
2

The general form of the equation of a circle is ${displaystyle x^{2}+y^{2}+Dx+Ey+F=0}$ . This equation technically has all the same information the standard form has, it’s just expressed differently. Let’s break it down:^[2]

1
2

Plug in values for the radius and center coordinates to complete a standard equation. This is probably the simplest type of problem you’ll have dealing with the equation of a circle. Just place the values where they go in the the standard form ${displaystyle (x-h)^{2}+(y-k)^{2}=r^{2}}$ .^[4]
3

1
2

Move the constant to the other side of the equation. Since the number is moving to the other side of the equation, the sign in front of it changes. So if it was negative on the left side, it’ll be positive on the right side (and vice versa).^[7]
3
4
5
6

Add the numbers to both sides of the equation. Keeping your groups together on the left side of the equation, add your third number to each parenthetical expression. Then, add each of those numbers to the right side of the equation to maintain equality.^[11]
7

Solve the and groups. Now you have what you may recognize as a basic trinomial in each parenthesis. Use the quadratic formula to find the number you need for each parenthetical expression in the standard equation of a circle.^[12]
8

Simplify the right side of the equation. Almost there! Add the numbers on the right side, then square them. The equation you’re left with will be the standard form for the equation of a circle. From here, you can easily determine the center points and radius if you need to graph the circle.^[13]

1
Write the equation of the circle with center and radius .^[14]
- Hint: pay attention to the negative signs in front of the center coordinates.
2
Find the center coordinates of the circle with the equation ${displaystyle (x+5)^{2}+(y+2)^{2}=81}$ .^[15]
- Hint: look at the signs in the parentheses and compare them to the standard form for the equation.
3

Find the center coordinates and radius for the circle ${displaystyle x^{2}+y^{2}+4x+8y-29=0}$ .^[16]

Hint: complete the square twice to convert general form to standard form. Don’t forget that anything you add on the left side you also have to add on the right side.
4

Is ${displaystyle x^{2}+y^{2}+8x+20=0}$ the equation of a circle? Why or why not?^[17]

Hint: a circle can never have a negative radius.

1
2

The center coordinates are . You’re given the equation of the circle ${displaystyle (x+5)^{2}+(y+2)^{2}=81}$ . Since the signs in the parentheses in the standard form are , the signs in this equation tell you that the center coordinates must be negative.^[19]
3
4

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

References

About This Article

Thanks to all authors for creating a page that has been read 1,254 times.

Did this article help you?

Get all the best how-tos!

You’re all set!

Источник

Как составить уравнение окружности

Окружность — совокупность точек, лежащих на расстоянии R от заданной точки (центра окружности). Уравнением окружности в декартовых координатах называется такое уравнение, что для любой точки, лежащей на окружности, ее координаты (x, y) удовлетворяют этому уравнению, а для любой точки, не лежащей на окружности — не удовлетворяют.

Инструкция

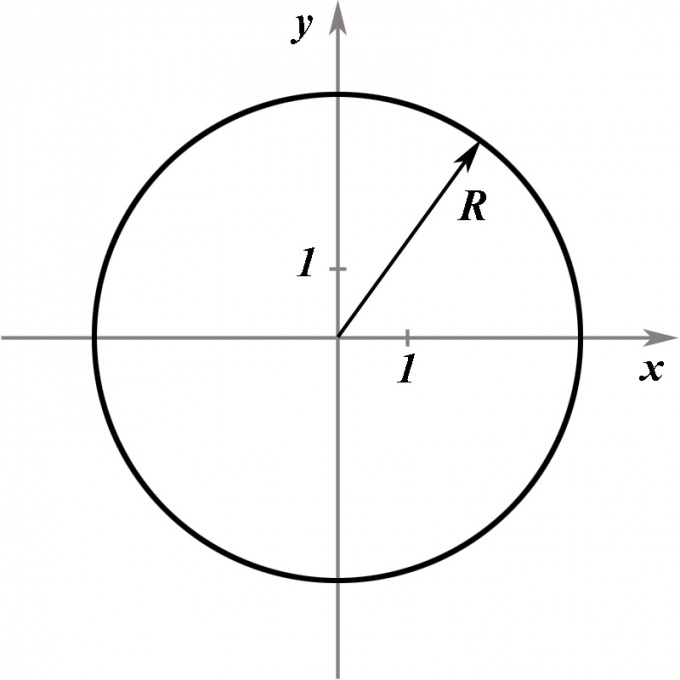
Предположим, что ваша задача — составить уравнение окружности заданного радиуса R, центр которой находится в начале координат. Окружность, по определению — множество точек, находящихся на заданном расстоянии от центра. Это расстояние как раз и равно радиусу R.

Расстояние от точки (x, y) до центра координат равно длине отрезка, соединяющего ее с точкой (0, 0). Этот отрезок вместе с его проекциями на координатные оси составляют прямоугольный треугольник, катеты которого равны x0 и y0, а гипотенуза, по теореме Пифагора, равна √(x^2 + y^2).

Чтобы получить окружность, вам нужно уравнение, определяющее все точки, для которых это расстояние будет равно R. Таким образом:√(x^2 + y^2) = R, а следовательно,
x^2 + y^2 = R^2.

Аналогичным способом составляется уравнение окружности радиусом R, центр которой находится в точке (x0, y0). Расстояние от произвольной точки (x, y) до заданной точки (x0, y0) равно √((x — x0)^2 + (y — y0)^2). Следовательно, уравнение нужной вам окружности будет выглядеть так:(x — x0)^2 + (y — y0)^2 = R^2.

Вам может понадобиться также составить уравнение окружности с центром в точке координат, проходящей через заданную точку (x0, y0). В этом случае радиус искомой окружности не задан в явном виде, и его придется вычислять. Очевидно, он будет равен расстоянию от точки (x0, y0) до начала координат, то есть √(x0^2 + y0^2). Подставляя это значение в уже выведенное уравнение окружности, вы получите:x^2 + y^2 = x0^2 + y0^2.

Если вам предстоит построить окружность по выведенным формулам, то их придется разрешать относительно y. Даже самое простое из этих уравнений при этом превращается в:y = ±√(R^2 — x^2).Знак ± необходим здесь потому, что квадратный корень числа всегда неотрицателен, а это значит, что без знака ± такое уравнение описывает только верхнюю полуокружность.Чтобы построить окружность, удобнее составить ее параметрическое уравнение, в котором обе координаты x и y зависят от параметра t.

Согласно определению тригонометрических функций, если гипотенуза прямоугольного треугольника равна 1, а один из углов при гипотенузе равен φ, то прилежащий к нему катет равен cos(φ), а противолежащий — sin(φ). Таким образом, sin(φ)^2 + cos(φ)^2 = 1 для любого φ.

Предположим, вам дана окружность единичного радиуса с центром в начале координат. Возьмем любую точку (x, y) на этой окружности и проведем от нее отрезок к центру. Этот отрезок образует угол с положительной полуосью x, который может быть равен от 0 до 360° или от 0 до 2π радиан. Обозначая этот угол t, вы получите зависимость:x = cos(t),
y = sin(t).

Эту формулу можно обобщить на случай окружности радиуса R с центром в произвольной точке (x0, y0):x = R*cos(t) + x0,
y = R*sin(t) + y0.

Источники:

уравнение окружности с заданным центром и радиусом

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Решение:

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

$[{(x - a)^2} + {(y - b)^2} = {R^2}]$

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

$[{(x - 5)^2} + {(y - ( - 1))^2} = {7^2},]$

$[{(x - 5)^2} + {(y + 1)^2} = 49.]$

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Решение:

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

$[R = AC = sqrt {{{({x_C} - {x_A})}^2} + {{({y_C} - {y_A})}^2}} ]$

$[R = AC = sqrt {{{(3 - 8)}^2} + {{( - 6 - ( - 3))}^2}} = sqrt {25 + 9} = sqrt {34} ,]$

$[{R^2} = 34.]$

Следовательно, уравнение данной окружности

$[{(x - 8)^2} + {(y + 3)^2} = 34.]$

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Решение:

$[{x_O} = frac{{{x_A} + {x_B}}}{2},{y_O} = frac{{{y_A} + {y_B}}}{2}]$

$[{x_O} = frac{{ - 4 + 6}}{2} = 1,{y_O} = frac{{ - 9 + 5}}{2} = - 2]$

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

$[R = OA = sqrt {{{({x_A} - {x_O})}^2} + {{({y_A} - {y_O})}^2}} ]$

$[R = OA = sqrt {{{( - 4 - 1)}^2} + {{( - 9 - ( - 2))}^2}} = sqrt {25 + 49} = sqrt {74} ,]$

$[{R^2} = 74.]$

Таким образом, уравнение окружности с диаметром AB —

$[{(x - 1)^2} + {(y + 2)^2} = 74.]$

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Решение:

$[{(x - a)^2} + {(y - b)^2} = {R^2},]$

получаем систему уравнений:

$[left{ begin{array}{l} {(4 - a)^2} + {( - 5 - b)^2} = {R^2}\ {(8 - a)^2} + {(3 - b)^2} = {R^2}\ {( - 8 - a)^2} + {(11 - b)^2} = {R^2} end{array} right.]$

$[{(4 - a)^2} + {( - 5 - b)^2} = {(8 - a)^2} + {(3 - b)^2}]$

$[16 - 8a + {a^2} + 25 + 10b + {b^2} = 64 - 16a + {a^2} + 9 - 6b + {b^2}]$

Приравняем правые части 2-го и 3-го уравнений:

$[{(8 - a)^2} + {(3 - b)^2} = {( - 8 - a)^2} + {(11 - b)^2}]$

$[64 - 16a + {a^2} + 9 - 6b + {b^2} = 64 + 16a + {a^2} + 121 - 22b + {b^2}]$

Умножив уравнение

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

$[{(4 + 2)^2} + {( - 5 - 3)^2} = {R^2}]$

$[{(4 + 2)^2} + {( - 5 - 3)^2} = {R^2},]$

получаем R²=100.

Следовательно, уравнение окружности, проходящей через три данные точки —

$[{(x + 2)^2} + {(y - 3)^2} = 100.]$

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

$[{(x - 5)^2} + {(y - 2)^2} = 25.]$

Источник

Прежде всего,
давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что
уравнение с двумя переменными x и y
называется уравнением линии l, если этому уравнению
удовлетворяют координаты любой точки линии l и не
удовлетворяют координаты никакой точки, не лежащей на этой линии.

Сегодня на уроке мы
попробуем по геометрическим свойствам линии найти ее уравнение.

В качестве линии
рассмотрим окружность радиуса с
центром в точке .

Пусть центр
окружности имеет координаты . Возьмем на
окружности произвольную точку . Запишем формулу
расстояния между точками C и M.
Мы знаем, что длина отрезка, который соединяет любую точку на окружности с
центром окружности – это радиус. Поэтому можно записать, что MC
равно r. Возведем MC в квадрат
и получим уравнение MC² = r².
Заменим MC² квадрат на выражение и получим, что если
точка лежит на окружности с радиусом r и центром в
точке C, то координаты этой точки удовлетворяют
уравнению . Если точка не
лежит на окружности, то расстояние от этой точки до центра окружности не равно
радиусу, поэтому координаты таких точек не будут удовлетворять полученному
уравнению. Поэтому можно сказать, что в прямоугольной системе координат уравнение
окружности радиуса r с центром в точке C с координатами имеет вид: .

Задача. Записать
уравнение окружности с радиусом и центром в начале
координат.

Решение.

Начало координат
имеет координаты (0;0). Подставим их в уравнение окружности и получим, что
уравнение окружности с радиусом r и
центром в начале координат имеет вид

Задача. Начертить
окружность, заданную уравнением .

Решение.

Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего,
определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь
давайте определим величину радиуса окружности.

Поскольку в правой
части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо
извлечь квадратный корень из 4. Получим 2.

Значит наша
формула задает окружность с центром в точке с координатами пять три и радиусом
равным двум.

Задача. Начертить
окружность, заданную уравнением .

Решение.

Запишем общее
уравнение окружности и проанализируем исходное уравнение. Прежде всего
определимся с координатами центра окружности.

Это будут числа -4
и 2. Теперь давайте определим величину радиуса окружности.

Задача. Начертить
окружность, заданную уравнением .

Решение. Уравнениями
такого типа описываются окружности с центром в начале координат. Теперь давайте
определим величину радиуса окружности. Поскольку в правой части формулы стоит
квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень
из 9.

Значит наша формула
задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.

Теперь давайте
попробуем решить задачу обратную данным.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Как и в предыдущих
задачах мы начнем с определения координат центра окружности. Сделать это
нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр
окружности имеет координаты (0;0).

Нетрудно заметить,
что радиус окружности равен 4.

Запишем уравнение
окружности и подставим найденные значения.

Ответ: .

Решим еще одну
задачу.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Решение.

– центр окружности

– радиус окружности

Ответ:.

Задача. Составить
уравнение окружности, которая показана на рисунке.

Решение.

– центр окружности

– радиус окружности

Ответ:.

Решая задачи, мы с
вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот
порядок.

Для того, что
бы составить уравнение окружности и построить ее надо:

1. Найти координаты
центра окружности.

2. Найти длину
радиуса этой окружности.

3. Записать уравнение
окружности.

4. Подставить
полученные значения в уравнение окружности.

5. Построить
окружность, если это требуется для решения задачи.

Рассмотрим еще одну
задачу.

Написать уравнение
окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм
имеет координаты шесть три.

Задача. Написать
уравнение окружности с диаметром , если , .

Решение.

Найдем координаты
центра окружности. Центр окружности является серединой диаметра. Воспользуемся
формулами для нахождения координат середины отрезка.

Получим, что центр
окружности имеет координаты .

Теперь определим
радиус окружности. Для этого найдем расстояние от центра окружности до концов
диаметра.

Запишем общее
уравнение окружности и подставим в него найденные значения. Тогда получим, что
уравнение данной окружности имеет вид:

Ответ: .

Подведем итоги
урока.

На сегодняшнем
уроке мы познакомились с формулой, которая задает окружность с центром в точке С
(x₀; y₀)
и радиусом r.

Также мы
познакомились с формулой, которая задает окружность с центром в начале
координат и радиусом r.

Мы рассмотрели
задачи на составление уравнения окружности по рисунку и на построение
окружности по заданному уравнению.

Источник