Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.
Здесь будет калькулятор
Уравнение прямой с угловым коэффициентом
y=kx+by=kx+b,
где kk — угловой коэффициент, а bb — свободный коэффициент.
Уравнения данного вида составляются следующим образом по формуле:
y−y0=k(x−x0)y-y_0=k(x-x_0),
где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.
Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.
Решение
Подставляем значения в формулу:
y−y0=k(x−x0)y-y_0=k(x-x_0)
y−2=1⋅(x−1)y-2=1cdot(x-1)
Приводим подобные слагаемые:
y=x+1y=x+1
Ответ
y=x+1y=x+1
Общее уравнение прямой
Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:
y−x−1=0y-x-1=0
Уравнение прямой по двум точкам
Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},
где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.
Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).
Решение
x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}
x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}
x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}
x−4=−y−12x-4=frac{-y-1}{2}
y+1=2⋅(4−x)y+1=2cdot(4-x)
y=8−2x−1y=8-2x-1
y=−2x+7y=-2x+7
Ответ
y=−2x+7y=-2x+7
Уравнение прямой при помощи точки и вектора нормали
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.
Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).
Решение
x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,
x−7+40−5y=0x-7+40-5y=0
x−5y=−40+7x-5y=-40+7
x−5y=−33x-5y=-33
5y=x+335y=x+33
y=x5+335y=frac{x}{5}+frac{33}{5}
Проверка
Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.
8=75+3358=frac{7}{5}+frac{33}{5}
8=88=8 — верно, ответ правильный.
Ответ
y=x5+335y=frac{x}{5}+frac{33}{5}
Прямая в пространстве
Уравнение прямой, заданной в пространстве имеет такой вид:
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.
Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).
Решение
x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Проверка
Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:
1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.
Такой вид уравнения прямой называется каноническим.
Ответ
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Тест по теме “Составление уравнения прямой”
Правило составления уравнения прямой
Положение
прямой на плоскости относительно системы
координат можно задать различными
способами:
1.
точкой и направлением;
2.
точкой и перпендикулярным прямой
вектором;
3.
двумя точками;
4.
отрезками, которые прямая отсекает на
осях координат.
Во
всех случаях задания прямой обязательно
должна быть известна хотя бы одна точка,
через которую проходит искомая прямая
и дополнительное
условие:
коллинеарности,
перпендикулярности или вторая точка,
принадлежащая прямой.
Правило составления уравнения прямой l , для которой известны координаты точки м1 (х1;у1) и задано какое-либо второе условие, состоит в следующем:
1)
На прямой l
выбирают произвольную точку с текущими
координатами х,у
:
М
( х; у)
.
2)
Находят
координаты вектора, лежащего на прямой
l
и такого, что его начало есть точка М1
(х1;у1),
а конец точка М
( х; у), то
есть вектор
М1М=(
х-х1;у-у1).
3)
Записывают координаты вектора, заданного
дополнительными условиями (коллинеарности,
перпендикулярности, двумя точками), то
есть направляющего или нормального
вектора
.
4).
Используют условие коллинеарности или
перпендикулярности векторов
и М1М.
9.4. Уравнение прямой с угловым коэффициентом
Пусть
дана ось Ох
и прямая l.
О
пределение
9.3. Углом
между осью и прямой называют угол, на
который нужно повернуть ось, чтобы она
совпала с заданной прямой или стала ей
параллельна.
Определение
9.4. Угловым
коэффициентом прямой называется тангенс
угла наклона этой прямой к положительному
направлению оси Ох.
Обозначается так:
.
Выразим из общего уравнения (9.4) при
условии, что
переменную у:
.
Полагая, что
получим:
-уравнение
прямой с угловым коэффициентом,
(9.5)
где
,
а b
– ордината точки пересечения прямой с
осью Oy.
9.5. Уравнение прямой в отрезках
Пусть
прямая не параллельна ни одной из осей
координат и не проходит через точку О.
Тогда она задается уравнением (9.4):
,
где
.
Она (прямая) будет пересекать оси
координат в точках
.
Т.к.
точки
,
то их координаты удовлетворяют уравнению
(9.4). Подставим координаты точки P
и Q:
Для
P:
;

Для
Q:
;
.
Подставляя
полученные A
и В
в (9.4):
.
Разделим всё уравнение на
.
Получим:
— уравнение
прямой в отрезках,
(9.6),
где а
– абсцисса точки пересечения с осью
Ох,
b
– ордината точки пересечения с осью
Оу.
9.6. Уравнение
пучка прямых, проходящих через данную
точку
Пусть
на прямой l
задана точка
.Запишем
уравнение с угловым коэффициентом:
(9.5). Т.к.
,
то её координаты удовлетворяют уравнению:
.
Вычтем из (9.5) соответствующие части
последнего уравнения получим:
— уравнение пучка прямых, (9.7),
проходящих через данную точку
.
9.7. Уравнение
прямой, проходящее через две заданные
точки
Пусть
на прямой даны две точки
.
Запишем уравнение (9.7) для точки А:
, (9.8)
Т.к.
точка
,
то координаты
точки В
удовлетворяют уравнению (9.8):
(9.9)
Считая,
что
.
Поделим (9.8) на (9.9):
— уравнение
прямой, проходящей через две точки
(9.10).
9.8.
Угол между двумя прямыми
Определение
9.5. Углом
между двумя прямыми
будем называть угол, на который нужно
повернуть прямую
,
чтобы она совпала с
или стала ей параллельна.
П
усть
прямые
заданы:
;
;
.
Из
рисунка видно, что
Т.о.,
.
9.9.
Условия параллельности и перпендикулярности
дух прямых
Определение
9.6. Два
вектора, лежащие на одной прямой или на
параллельных прямых называются
коллинеарными.
Три вектора, лежащие в одной плоскости
и параллельные одной плоскости называются
компланарными.
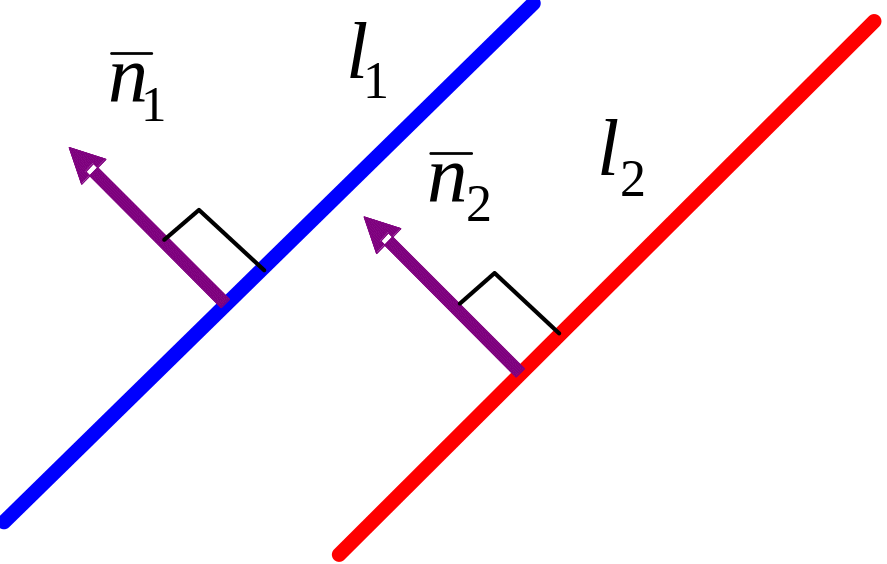
Пусть
даны две прямые
и
.
Обе они имеют нормали с координатами:
.
Теорема
9.1: Две
прямые параллельны тогда и только тогда,
когда коллинеарны их нормальные векторы.
Свойство
коллинеарности двух векторов.
Для
того, чтобы два вектора были коллинеарны,
необходимо и достаточно, чтобы и
координаты были пропорциональны, т.е.:
— условие
параллельности двух прямых.
Е
сли
выполняется условие:
, то прямые совпадают,
т.к. одно уравнение получается из другого
путём умножения на любое число.
Теорема 9.2
.(условие
перпендикулярности двух прямых).
Две прямые перпендикулярны тогда и
только тогда, когда перпендикулярны их
нормальные векторы, т.е.
.
Напомним
определение: скалярным
произведением
двух векторов
называется
число, равное
произведению длин этих векторов на
косинус угла между ними, т.е.
,
т.к.
,
то
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Загрузить PDF
Загрузить PDF
В тригонометрии есть задачи, в которых нужно найти уравнение прямой. При этом даны либо координаты одной точки и угловой коэффициент, либо координаты двух точек, которые лежат на прямой. В любом случае найти уравнение прямой довольно легко, если использовать соответствующие формулы.
-
1
Подставьте значение углового коэффициента «k» в альтернативное уравнение прямой y-y1 = k(x-x1). С помощью этого уравнения, в котором присутствуют координаты точки, которая лежит на прямой, можно найти координаты точки пересечения прямой с осью Oy. Данное значение углового коэффициента «k» подставьте вместо «k» в уравнении y-y1= k(x-x1).[1]
- Например, угловой коэффициент k = 2, тогда уравнение запишется так: y-y1= 2 (x-x1).
-
2
Вместо x1 и y1 подставьте координаты данной точки, чтобы записать окончательное уравнение прямой.[2]
- Например, если дана точка с координатами (4,3), уравнение запишется так: y-3 = 2(x-4).
-
3
Изолируйте «y», чтобы записать уравнение прямой в конечном виде. Чтобы раскрыть скобки, примените свойство дистрибутивности, а затем следуйте определенному порядку выполнения математических операций.
- Раскрыв скобки, вы получите: y-3 = 2x-8.
- Теперь прибавьте 3 к каждой стороне уравнения, чтобы изолировать «y».
- Окончательное уравнение прямой, которая проходит через точку с координатами (4, 3) и имеет угловой коэффициент 2, запишется так: y = 2x-5.
Реклама
-
1
Вычислите угловой коэффициент по формуле k = (y2-y1)/(x2-x1). Вам будут даны две пары координат; каждая пара координат записывается так: (x, y). Первую пару координат обозначьте как (x1, y1), а вторую как (x2, y2). Подставьте числа в формулу k = (y2-y1)/(x2-x1) и вычислите угловой коэффициент k.[3]
- Например, даны две точки с координатами (3,
и (7, 12). Тогда формула запишется так: k = (12-8)/(7-3) = 4/4 = 1. В этом примере угловой коэффициент k = 1.
- Например, даны две точки с координатами (3,
-
2
Подставьте найденное значение углового коэффициента k в стандартное уравнение прямой. Уравнение прямой имеет следующий вид: y = kx + b, где k — угловой коэффициент, b — координата «y» точки пересечения прямой с осью Oy. В уравнение прямой подставьте найденное значение углового коэффициента вместо «k».[4]
- В нашем примере уравнение прямой запишется так: y = 1x + b или y = x + b.
-
3
Вместо «x» и «y» подставьте координаты одной из данных точек, чтобы найти «b». Координаты подставьте в уравнение прямой — вместо «х» подставьте координату «х», а вместо «y» координату «y».[5]
- В нашем примере возьмем точку с координатами (3, 8). Тогда уравнение прямой запишется так: 8 = 1(3) + b.
- Используйте координаты одной из двух данных точек, но никогда не смешивайте координаты сразу двух точек.
-
4
Вычислите «b». Сделайте это, когда в уравнение прямой подставите значения «k», «х» и «у». Изолируйте «b» на одной стороне уравнения, следуя определенному порядку выполнения математических операций.[6]
- В нашем примере уравнение приняло вид 8 = 1(3) + b. Умножьте 1 на 3 и получите 8 = 3 + b. Теперь вычтите 3 из каждой стороны уравнения, чтобы изолировать «b». Вы получите 5 = b, или b = 5.
-
5
Подставьте найденные значения «k» и «b» в уравнение прямой, чтобы записать его в окончательном виде.
- В нашем примере уравнение прямой, которая проходит через точки с координатами (3,
и (7, 12), запишется так: y = 1x + 5 или просто y = x + 5.
Реклама
- В нашем примере уравнение прямой, которая проходит через точки с координатами (3,
Об этой статье
Эту страницу просматривали 31 460 раз.
Была ли эта статья полезной?
Получить уравнение прямой по двум точкам бывает необходимо, когда мы решаем задачи, связанные с анализом различных фигур на плоскости. В этом случае бывает полезно знать уравнение прямой, проходящей через две точки. Например, составляя такое уравнение мы уже знаем – как проходит прямая, с какие углом наклона к осям координат и можем рассчитать расположение прямой по отношению к другим прямым или к фигурам.
Составляем уравнение прямой по двум точкам
Итак, пусть нам даны две точки и
. Наша прямая проходит через две эти точки, давайте получим уравнение этой прямой. Уравнение пучка прямых, проходящих через точку с координатами
имеет вид:
То есть если прямая проходит через две точки и
она – одна из этого пучка прямых, проходящих через точку
и эта прямая имеет определенный коэффициент
. Значит, координаты точки
должны удовлетворять уравнению (1), то есть
.
Находим из (2) :
и подставим в уравнение (1):
.
Преобразовывая уравнение (3) получим:
Это и есть уравнение прямой, проходящей через две точки
и
.
Примечание: если точки и
лежат на прямой, которая параллельна оси
или оси
, то уравнение прямой будет иметь вид
или
соответственно.
Зная координаты любых двух точек прямой, мы всегда сможем определить угловой коэффициент прямой:
Геометрический вывод уравнения прямой
Действительно, давайте нарисуем прямую в системе координат и отметим на прямой две точки
и
, координаты которых известны
и
и отметим на этой прямой произвольную точку
.
Из подобия треугольников и
находим:
Из рисунка видно, что:
,
Таким образом, получаем уравнение прямой по двум точкам:
Задача
Составим уравнение прямой, проходящей через две точки и
.
Решение: Имеем ,
,
,
. Подставим эти значения в уравнение прямой, проходящей через две заданные точки:
Умножим левую и правую части уравнения на 5, получим:
– получившееся уравнение прямой.
Давайте сделаем проверку – если мы все решили правильно, то при подстановке координат точек и
мы получим верное равенство. Итак, подставим сначала координаты точки
:
Теперь координаты точки :
Значит, уравнение прямой мы нашли верно.
Ответ:
Условие прохождения прямой через три заданные точки
Если нам в задаче нужно убедиться, что три точки с заданными координатами лежат на одной прямой, можно рассуждать так:
- Если две точки с заданными координатами образуют прямую, то их координаты удовлетворяют уравнению прямой, проходящей через две точки.
- Если третья точка также лежит на этой прямой, то и ее координаты будут удовлетворять этому уравнению.
Таким образом, если нам даны три точки ,
и
, лежащие на одной прямой, то их координаты будут удовлетворять условию:
Теперь вы легко сможете составить уравнение прямой по двум точкам, а также найти угловой коэффициент прямой и проверить – принадлежит ли третья точка этой прямой.
В данном материале рассмотрим, что такое уравнение прямой. Проанализируем каждый вид данного уравнения. Изучим основные формулы и графики. Применим весь рассмотренный материал на практике, в виде решения задач и уравнений.
Данное уравнение — характеризуется, как уравнение двух переменных значений.
Значения в математики, чаще всего обозначают буквами x и y. Это самое распространенное обозначение, однако можно встретить и другие буквенные обозначения. Например: z, n и другие значения.
Определение прямой линии- фигура, состоящая из множества простых точек. Каждая точка, имеет собственные, определенные координаты, относительно осей абсцисс и ординат.
Уравнение прямой на плоскости — уравнение, характеризующее взаимосвязь координатных значений точек на прямой.
Для решения уравнений необходимо помнить ряд важным математических функций, правил, значений.
Все их мы будем рассматривать подробно в каждом разделе на примерах решения.
Общее уравнение прямой линии системы координат
Рассмотрим соответствующую теорему, которая отражает уравнение прямой на плоскости в системе координат Oxy.
Подробно исследуем следующее уравнение: ax+by+c=0.
Значения х и y, являются переменными данными со значениями.
a и b — действительные простые числа. Обязательное условие, которых неравенство нулю.
Следовательно, прямая линия задается вышеупомянутым уравнением данного вида: ax+by+c=0.
Рассмотрим на примере изученную теорему:
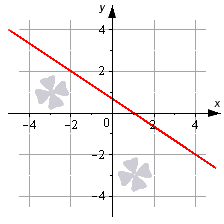
На данном рисунке, мы рассмотрим красную линию и запишем уравнение для нее.
2x+3y-2=0.
Координаты на данной прямой удовлетворяют составленному уравнению.
Уравнение может быть также полным и неполным. Рассмотрим случаи:
- Полное уравнение.
Все действительные числа, имеют любое значение, но не равные нулю. Поэтому такое определение относится к данному типу уравнений.
- Неполное уравнение.
Все числа в уравнении имеют любое значение. Характерно, также значения отрицательных знаков.
Уравнение прямой в отрезках прямой
Для отрезков уравнение будет иметь следующей вид:
[frac{x}{a}+frac{y}{b}=1]
Данные в знаменателе, являются действительными значениями, не равными нулевому значению. Величины действительных данных равняются отрезку. Он отсоединяется линией на оси координат. Протяженность начинает свой отсчет от начала координатной прямой.
Пример:
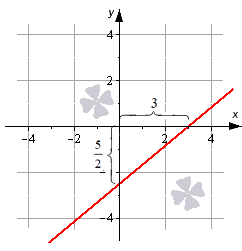
Нужно начертить прямую линию, которая задается формулой.
[frac{x}{3}+frac{y}{-frac{5}{2}}=1]
Обозначим на графике две точки ( 3 ; 0 ) , (0; [-frac{5}{2}]). Далее необходимо их соединить между собой.
Уравнение прямой с угловым коэффициентом
Записываем уравнение вида: [mathrm{y}=mathrm{k} cdot x+b];
x — значение, которое принимается, как переменное;
к — простое действительное число, является показателем углового коэффициента;
b — действительное число.
Угол наклона на плоскости в системе координат — угол, который берет свой отсчет значений от направления с положительным знаком до прямой, которая направлена против хода часовой стрелки.
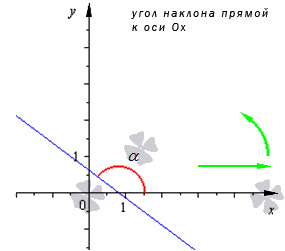
Угол будут считать нулевым, если прямая линии, имеют параллельное расположение относительно оси абсцисс либо совпадает с ней по расположению. Угол принимает значения, согласно интервалу (0, [pi]).
Формула
[text { Формула обозначения коэффициента: } k=operatorname{tg} alpha .]
Угловой коэффициент — значение тангенса угла наклона этой же прямой линии.
В случае, когда прямая линия параллельная другой оси, ординат, то принято считать, что угловой коэффициент не определяется. И соответствует интервалу бесконечности.
График функции будет возрастать, если значение коэффициента имеет положительное значение. Следовательно, убывание будет наблюдаться в противоположном значение, а именно с отрицательным значением.
На графиках показаны значения угловых коэффициентов и угол наклона. Когда есть разное расположение относительно осей.
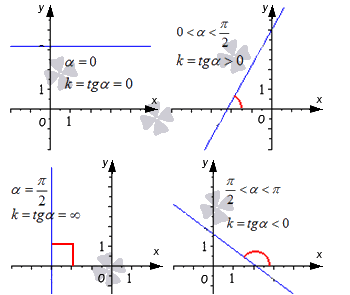
На примерах рассмотрим нахождение углового коэффициента. Для этого из прошлых тем, вспомним определение тангенса и его вычисление.
Пример №1:
Угол наклона прямой равен 120 градусов, относительно оси ох.
Нам нужно определить угловой коэффициент.
Применим известные нам формулы и подставим данные.
[alpha=120^{circ}, mathrm{k}=operatorname{tg} alpha=120=-sqrt{3}]
Следовательно правильный ответ задачи будет равняться [k=-sqrt{3}]
Пример №2:
В этом примере нам уже известно значение углового коэффициента.
Нужно определить угол наклона, относительно прямой. Для этого, нужно обязательно учитывать знак известного коэффициента. Если к>0, следует что угол будет острый и определяться как [alpha=operatorname{arctg} k].
Когда к<0, то угол будет характеризоваться как тупой. его значение определяется функцией: [alpha=pi-operatorname{arctg}|k|].
Например, угловое значение равно 3.
Значение коэффициента является положительным, значит угол будет острый. Вычисляться он будет по формуле: [alpha=operatorname{arctg} k=3]
Ответ задачи: [operatorname{arctg}=3].
Пример №3:
Значение углового коэффициента имеет отрицательное число в виде дроби. И равняется следующему значению: [-frac{1}{sqrt{3}}]
Для определения угла наклона, выполнить следующие действия: обозначим все значения. Угол наклона относительно оси имеет положительное значение. Следовательно формула для решения запишется следующим образом: [mathrm{k}=-frac{1}{sqrt{3}}<0 Rightarrow alpha=pi-operatorname{arctg}|k|].
Подставим данные, которые заданы в условии задания:
[alpha=pi-operatorname{arctg}left|-frac{1}{sqrt{3}}right|=pi-operatorname{arctg} frac{1}{sqrt{3}}=pi-frac{pi}{6}=frac{5 pi}{6} Rightarrow]ответ будет [frac{5 pi}{6}].
Пример №4:
Необходимо определить, относятся ли точки координат к прямой. Они равны: [m_{1}(3 ; 0) text { и } m_{2}(2 ;-2)]. Уравнение прямой задано следующее: [y=frac{1}{3} x-1].
Известные нам значения точек подставляем, в заданное уравнение прямой.
И получаем следующий вид формулы: [0=frac{1}{3} cdot 3-1 Leftrightarrow 0=0]. Так после вычисления, мы получаем равенство, которое считается верным. Можно утверждать, что точка принадлежит прямой.
Далее подставляем значения второй точки в уравнение.
[-2=frac{1}{3} cdot 2-1 Leftrightarrow-2=-frac{1}{3}] следовательно точка [m_{2}] не относится к прямой и не лежит на ней.
Вывод решения: только первая точка относится к прямой и лежит на ней, а вторая равная (2;-2) — нет.
Пример №5:
Нужно найти уравнение прямой, которая проходит через значение точки [m_{1}(4 ; 1)]. Значение углового коэффициента — (-2).
Запишем условие : [x_{1}=4, y_{1}=-1, k=-2]
Следовательно необходимое уравнение прямой равно: [y-y_{1}=k].
[left(x-x_{1}right) text { следовательно } y-(-1)=-2 cdot(x-4) Leftrightarrow y=-2 x+7]
Искомое уравнение: [y=-2 x+7]
Пример №6:
Составить уравнение прямой, проходящей через значение (-2;4). Угол наклона положительного направления равен [frac{3 pi}{4}].
Решение необходимо начать с определения коэффициента угла.
[k=operatorname{tg} alpha frac{3 pi}{4}=-1]
Определив угловое значение, можно составить искомое уравнение вида: [y-y_{1}=k cdotleft(x-x_{1}right) text { из этого следует } y-4=-1 cdot(x-(-2) Leftrightarrow y=-x+2]
Каноническое уравнение прямой на плоскости
Определение канонического уравнения — это уравнение следующего вида [frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}}].
Данное уравнение задает на плоскости в прямоугольной системе прямую линию. Она, в свою очередь проходит через точку [m_{1}(x ; y)], которая имеет вектор направления, обозначающийся как [underline{alpha}=left(alpha_{x} ; a_{y}right)]
Запишем несколько примеров для данного вида уравнения.
[frac{x-2}{sqrt{3}}=frac{y-3}{1}]
Приведенное уравнение — это уравнение прямой для канонического вида. Прямая его будет проходить через значения точек [m_{1}(2 ; 3)]. Вектор направляющий равен [sqrt{3}, 1].
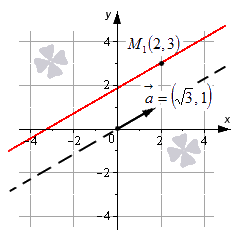
Важные моменты, которые следует помнить, при решении задач с каноническим уравнением.
Отметим следующие важные факты:
- если вектор является прямым и прямая линия проходит через точку, то ее уравнение имеет вид : [frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}}]
- когда вектор прямой по направлению, то любой из векторов может быть направляющим вектором прямой. И уравнение записывается следующим образом: [frac{x-x_{1}}{mu cdot alpha_{x}}=frac{y-y_{1}}{mu cdot alpha_{y}}]
Пример №1:
Прямая в системе координат проходит через точки (2;-4) и вектор направляющий равен (1;-3). Составьте и напишите каноническое уравнение, применяя известные нам данные.
[frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}}]
[x_{1}=2, y_{1}=2, alpha_{x}=1, alpha_{y}=-3]
Следовательно уравнение записывается следующим образом: [frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}} Leftrightarrow frac{x-2}{1}=frac{y-(-4)}{-3} Leftrightarrow frac{x-2}{1}=frac{y+4}{-3}]
[frac{x-x_{1}}{alpha_{x}}=frac{y-y_{1}}{alpha_{y}} Leftrightarrow frac{x-2}{1}=frac{y-(-4)}{-3} Leftrightarrow frac{x-2}{1}=frac{y+4}{-3}] — окончательное искомое уравнение.
Пример №2:
Составить каноническое уравнение, проходящее через точки [sqrt[3]{2} ; quad-frac{1}{7}]
Прямая является параллельной относительно оси координат. Направляющий вектор принимается [underline{j}=(0 ; 1)]. Учитывая значение точек, через которые проходит прямая, записываем уравнение:
[frac{x-sqrt[3]{2}}{0}=frac{y-left(-frac{1}{7}right)}{1} Leftrightarrow frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}]
[text { Ответ: } frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}]
Пример №3:
Составим уравнение, руководствуясь графиком, приведенным ниже.
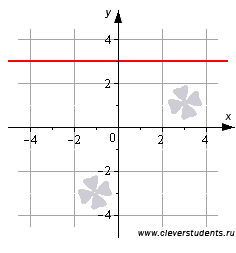
Из рисунка видно, что прямая проходит через точки со значениями (0;3). Расположена параллельно относительно оси x (ось абсцисс). Координатный вектор [underline{i}=(1,0)] — направляющий вектор, для данной системы.
Собрав все данные, преобразовав их. можно записать уравнение:
[frac{x-0}{1}=frac{y-3}{0} Leftrightarrow frac{x}{1}=frac{y-3}{0}]
Нет времени решать самому?
Наши эксперты помогут!
Параметрическое уравнение на плоскости и его характеристики
Уравнение такого типа записываются в следующем виде:
[x=x_{1}+alpha_{x} cdot lambda]
[mathrm{y}=y_{1}+alpha_{y} cdot lambda]
[x_{1} y_{1} alpha_{x} alpha_{y} text { — действительные простые значения. }]
[alpha_{x} alpha_{y} text{ — значения, которые математически возможны равняться нулю.}]
[lambda text { — параметр, значение которого может быть различным. }]
Уравнение параметрического вида предназначено, для установления не очевидного взаимодействия между координатами точек системы. Для определения этого свойства и вводится параметр [lambda].
Пример №1:
Задана система уравнения:
[{x=-3-1 / 2 cdot lambda}]
[{y=3 cdot lambda}]
[{z=2 / 3}]
Необходимо определить все координаты, каждой направляющей системы.
[{x=-3-1 / 2 cdot lambda}]
[{y=3 cdot lambda}]
[{z=2 / 3} Leftrightarrow]
[Leftrightarrow{x=-3-1 / 2 cdot lambda}]
[{y=0+3 cdot lambda}]
[{z=2 / 3+0 cdot lambda}]
Коэффициенты перед значение [lambda] имеют соответствующие значения координат направляющего вектора и равняются: [underline{alpha}=(-1 / 2,3,0)] — для прямой по заданию.
Соответственно запишем все координаты направляющих векторов:
[left(-frac{1}{2} cdot mu, 3 cdot mu, 0 cdot muright)=left(-frac{1}{2} cdot mu, 3 cdot mu, 0 cdot muright), mu in R, mu neq 0 ]
[left(-frac{1}{2} cdot mu, 3 cdot mu, 0 cdot muright), mu in R, mu neq 0]
Пример №2
Составить параметрическое уравнение в пространстве:
[underline{alpha}=left(2 ;-frac{1}{sqrt{3}}, 0right)-text { вектор направляющий.}]
Точки (7, -1, 0) — значения точки на прямой координат.
[x_{1}=7, y_{1}=-1, z_{1}=0, alpha_{x}=2, alpha_{y}=-frac{1}{sqrt{3}}, alpha_{z}=0]
Полученные данные подставляем систему уравнения.
[x=x_{1}+alpha_{x} cdot lambda]
[mathrm{y}=y_{1}+alpha_{y} cdot lambda]
[z=z_{1}+alpha_{z} cdot lambda]
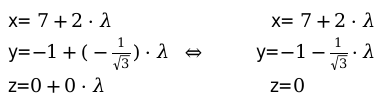
Особые моменты данного типа уравнений:
Имея любое значение [lambda], можно определить три числа (z, y,x).
К примеру точки [M_{1}left(x_{1} text { и так далее }right) text { находятсся в параметрах уравнения в системе. }]
[mathrm{x}=chi_{1}+alpha_{x} cdot lambda]
[mathrm{y}=y_{1}+alpha_{y} cdot lambda]
[z=z_{1}+alpha_{z} cdot lambda]
где значение [lambda]=0.
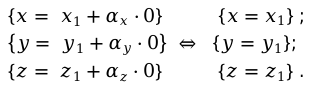
Пример №3:
Любые значения точек находятся на прямой, для определенной заданной системы координат.
[M_{1}(4 ; 3 ;-2)]
[N_{1}(-2 ; 3 ;-1)]
Запишем систему параметрических уравнение:
[x=2+2 cdot lambda]
[y=3 cdot lambda]
[z=-1-lambda]
Поставляя данные первой точки, получаем уравнения:
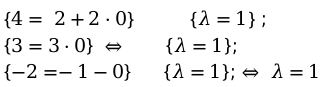
Следовательно значение [lambda=1 text {, для } M_{1}(4 ; 3 ;-2)]. следовательно она находится на прямой координат.
Аналогичные действия проводим для второй координаты точек.
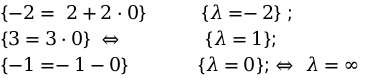
Выполнив вычисления, мы видим, что параметра для [lambda] не существует.
Нормальное уравнение для координатной прямой
Формула
Нормальное уравнение можно выразить в виде уравнения:
[A_{x}+B_{y}+C=0]
Где числа А, В, и C имеют такие значения, что, вектор [underline{n}=(mathrm{A}, quad mathrm{B})] равняется единице, [C leq 0].
Вектор [underline{n}=(mathrm{A}, quad mathrm{B})], будет является нормальным в системе координат.
Так же есть еще один способ записать нормальный вид уравнения, применяя для этого значения тригонометрических функций.
[cos alpha cdot x+cos beta cdot y-rho=0]
[cos alpha cos beta] — это действительные простые числа. Следовательно, они представлены направляющими косинусами. А также нормального вектора и единичной прямой.
Отсюда следует [underline{n}=left(begin{array}{lll} cos alpha & cos beta end{array}right)] равняется равенству: [underline{n}=cos ^{2} alpha+cos ^{2} beta=1]
Значение [rho geq 0]
Данное значение определяет длину расстояния от прямой линии до начала координатной прямой.
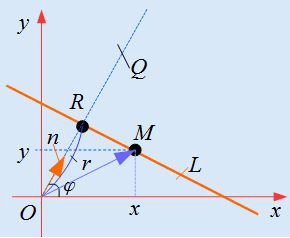
Пример №1:
В задаче имеется уравнение прямой для общего случая.
2x-3y+4=0
Нужно используя вышеуказанное уравнение составить простое уравнение для координатной прямой.
Для начала запишем А=2; В=-3; С=4.
Неизвестное значение t, сможем вычислить из равенства используя известные значения.
[mathrm{t}=pm frac{1}{sqrt{A^{2}+B^{2}}}=pm frac{1}{sqrt{13}}]
t- будет отрицательным значение, так как С>0.
[t=-frac{1}{sqrt{13}}]
Перемножим уравнение:
[frac{2}{sqrt{13}} x+frac{3}{sqrt{13}} y-frac{4}{sqrt{13}}=0]
Вывод решения: [frac{2}{sqrt{13}} x+frac{3}{sqrt{13}} y-frac{4}{sqrt{13}}=0]
Значение [frac{4}{sqrt{13}}] — будет являться, тем самым значение, которое показывает расстояние от начала до прямой координат прямой.
Пример №2.
Определим и составим нужное уравнение имея следующие известные нам данные: угол [varphi=60 text { градусов }]
Расстояние до прямой от начала координат равняется 4.
Используя данные решим задачу.
[cos varphi=cos left(60^{circ}right)=frac{1}{2}]
[sin varphi=sin left(60^{circ}right)=frac{sqrt{3}}{2}]
[frac{1}{2} x+frac{sqrt{3}}{2} y-4=0]
[text { Ответ: } frac{1}{2} x+frac{sqrt{3}}{2} y-4=0]
Пример №3:
Имея данные значения решим задачу согласно задания. Где угол [varphi=90 text { градусов }]
Расстояние до прямой от начала координат равняется 3.
Используя данные решим задачу.
[cos varphi=cos left(90^{circ}right)=0]
[sin varphi=sin left(90^{circ}right)=1]
[1 x+0 y-3=-2]
Ответ: [0 x+-1 y-3=-2] координата не лежит на прямой, так как имеет отрицательное значение.
Выводы по материалу:
Рассмотрев типы уравнения, для прямой в плоскости. Перечислив их категории и основные характеристики. Можно сказать, что это одна из составляющих математики.
В ней переплетаются все основные значения и функции этой технической науки.
Для решения задач, необходимо обладать следующими навыками:
- вспомнить весь изученный материал по работе с тригонометрическими функциями: косинус, синус. тангенс и другие.
- вычисление отрицательных значений и их правила;
- решение уравнений с дробными числами;
- помнить правило возведения числа в степень.
Учитывая все, рекомендации, процесс работы с материалом по данной теме значительно облегчит процесс.






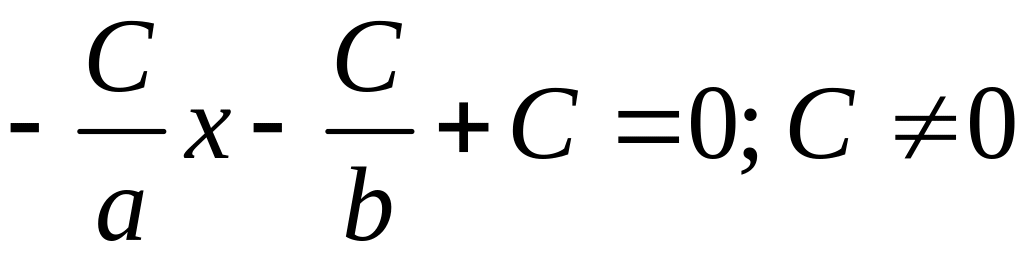





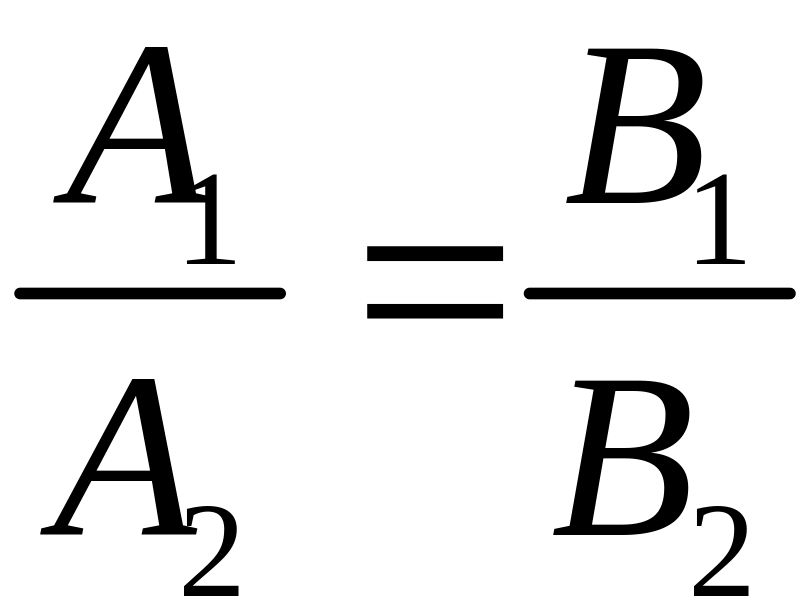

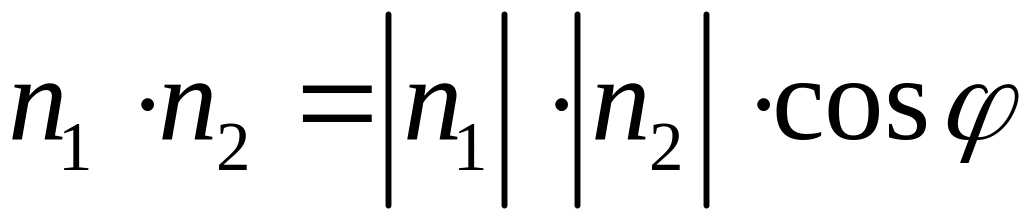




 и (7, 12). Тогда формула запишется так: k = (12-8)/(7-3) = 4/4 = 1. В этом примере угловой коэффициент k = 1.
и (7, 12). Тогда формула запишется так: k = (12-8)/(7-3) = 4/4 = 1. В этом примере угловой коэффициент k = 1.




