Как путем перегибания можно найти центр круга

1. Учебники
2. 5 класс
3. Математика 👍
4. Дорофеев
5. №560

Раздел:

• Глава 7. ТРЕУГОЛЬНИКИ И ЧЕТЫРЕХУГОЛЬНИКИ
• 7.3 Равенство фигур

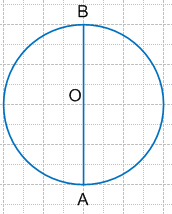
1) Начертите в тетради круг и разделите его отрезком на две равные части. Как называется этот отрезок? Разделите круг на четыре равные части.
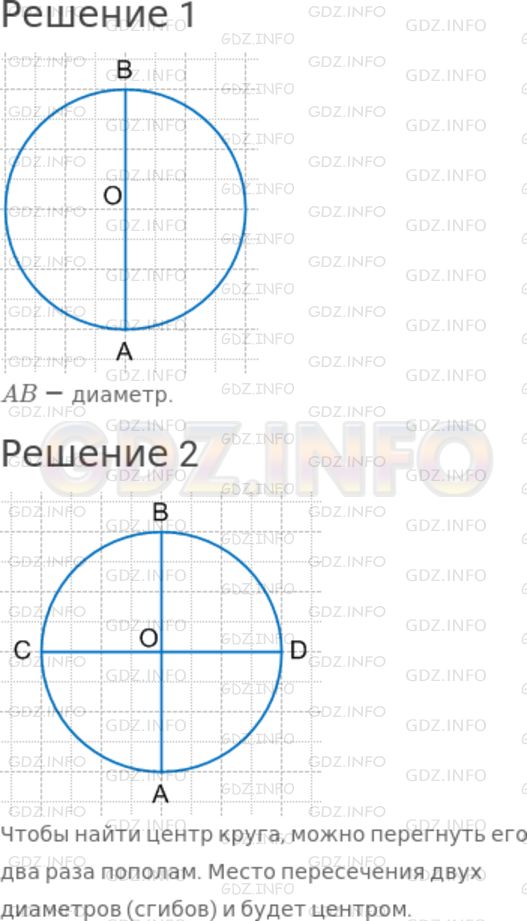
2) Как путем перегибания можно найти центр круга?

Ответы к теме 7.3 Равенство фигур

Задание 556. С помощью кальки найдите на рисунке 7.18 четырехугольник, равный четырехугольнику ABCD.

Решение

Четырехугольнику ABCD равен четырехугольник 2.

Задание 557. 1) У двух многоугольников, изображенных на рисунке 7.19, есть равные элементы. Назовите их. Равны ли эти многоугольники?
2) Верны ли утверждения?
а) Если у двух треугольников углы попарно равны, то равны и сами треугольники.
б) Если у двух четырехугольников стороны попарно равны, то равны и сами четырехугольники.
С помощью рисунка 7.19 опровергните эти утверждения.

Решение

1. а)
AB = EK
AC = DE
∠A = ∠D
∠B = ∠E
Многоугольники не равны.

б)
AB = DC = ON = KM
BC = AD = KO = MN
Многоугольники не равны.

2) а) Неверно, так как длины сторон могут быть разными.
б) Неверно, так как величины углов могут разными.

Задание 558. Начертите в тетради треугольник, равный треугольнику ABC (рис.7.20), но в другом положении, так, чтобы эти треугольники нельзя было совместить, передвигая по листу бумаги.

Решение

Задание 559. 1) Начертите прямоугольник, обозначьте его и проведите одну диагональ. Диагональ разделила прямоугольник на два равных треугольника. Покажите на чертеже и назовите их равные стороны и равные углы.
2) Возьмите вырезанный из бумаги прямоугольник и разрежьте его по диагонали. Сложите из получившихся равных треугольников равнобедренный треугольник.
3) Равнобедренный треугольник ABC (рис. 7.21) разрезали по отрезку BO. Каков вид получившихся треугольников? Из этих треугольников сложили прямоугольник. Нарисуйте его. Какой из сторон треугольника равна диагональ прямоугольника?

Задание 560. 1) Начертите в тетради круг и разделите его отрезком на две равные части. Как называется этот отрезок? Разделите круг на четыре равные части.
2) Как путем перегибания можно найти центр круга?

Решение

1)

AB − диаметр.
2)

Чтобы найти центр круга, можно перегнуть его два раза пополам. Место пересечения двух диаметров (сгибов) и будет центром.

Как путём перегибания можно найти центр круга?