УЛЬЯНОВСКИЙ САЙТ ДЛЯ МАМОЧЕК

Задание в учебнике:
а) Как разрезать фигуру на две части, чтобы можно было составить квадрат?
б) Разрежь её на две части по-другому, чтобы можно было составить прямоугольник, который не является квадратом.
| Решение:
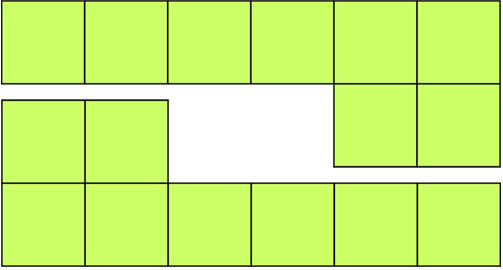
а) Составить из фигуры квадрат. |
 |
 |
 |
 |
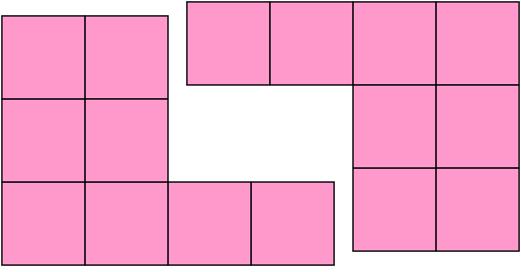
| б) Составить из фигуры прямоугольник. |
 |
 |
 |
 |
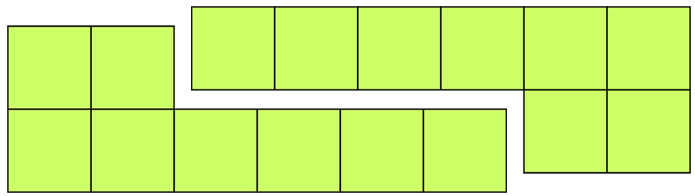
Считаем квадраты, их всего — 16. Тогда, если нам нужно сложить квадрат без «дырки», сторона квадрата должна быть равной — 4. Это возможно, если Г-образную дырку «заполнить одной из частей. Значит там должна быть уголок длиной в 2 клетки и т.д. Короче вот мой ответ на задание а). Разрез я проводил по красным линиям.
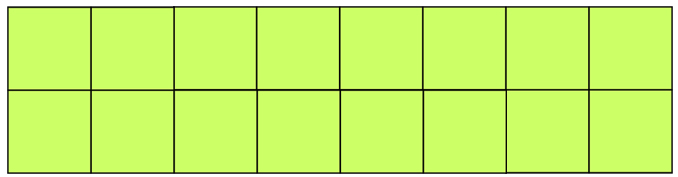
Аналогично, во второй фигуре 25 клеток (без дырки), значит мы должны получить квадрат стороной равной 5. И опять «заполняем пустоты и получаем вот такое решение. Красная клетка на исходном рисунке идет туда где красная клетка на втором рисунке-ответе.
Как разрезать фигуру на две части, чтобы можно было составить квадрат?
Вы открыли страницу вопроса Как разрезать фигуру на две части, чтобы можно было составить квадрат?. Он относится к категории
Математика. Уровень сложности вопроса – для учащихся 1 — 4 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Математика,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.
Светило науки — 52 ответа — 0 раз оказано помощи
Ответ:
Для того, чтобы разделить фигуру на 2 части так, чтобы получился квадрат, нужно выполнить следующие шаги:
Нарисуйте квадрат со стороной, равной длине одной из сторон фигуры.
Проведите диагонали квадрата.
Разрежьте фигуру вдоль одной из диагоналей квадрата так, чтобы получилось две части.
Переверните одну из частей фигуры и поместите ее в квадрат.
Проверьте, что обе части фигуры вместе образуют квадрат.
Важно помнить, что это решение возможно не для всех фигур и может потребовать тщательных вычислений и анализа геометрических свойств фигуры.
Пошаговое объяснение:
Опыт показывает, что при использовании
практических методов обучения удается
сформировать у учащихся ряд мыслительных
приемов, необходимых для правильного вычленения
существенных и несущественных признаков при
ознакомлении с геометрическими фигурами.
развивается математическая интуиция, логическое
и абстрактное мышление, формируется культура
математической речи, развиваются математические
и конструкторские способности, повышается
познавательная активность, формируется
познавательный интерес, развивается
интеллектуальный и творческий потенциал.В
статье приводится ряд практических задач на
разрезания геометрических фигур на части с целью
составить из этих частей новую фигуру. Ученики
работают над заданиями в группах. Затем каждая
группа защищает свой проект.
Две фигуры называются равносоставленными,
если, определённым образом разрезав одну из них
на конечное число частей, можно (располагая эти
части иначе) составить из них вторую фигуру. Итак,
метод разбиения основан на том, что всякие два
равносоставленных многоугольника равновелики.
Естественно поставить обратный вопрос: всякие ли
два многоугольника, имеющих одинаковую площадь,
равносоставлены? Ответ на этот вопрос был дан
(почти одновременно) венгерским математиком
Фаркашем Бойяи (1832г.) и немецким офицером и
любителем математики Гервином (1833г.): два
многоугольника, имеющих равные площади,
равносоставленны.
Теорема Бойяи-Гервина гласит: любой
многоугольник можно так разрезать на части, что
из этих частей удастся сложить квадрат.
Задание 1.
Разрежьте прямоугольник a х 2a на такие
части, чтобы из них можно было составить квадрат.
Решение.
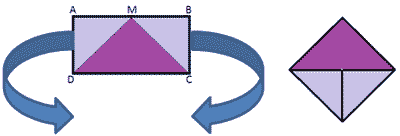
Прямоугольник ABCD разрежем на три части по
линиям MD и MC (М – середина АВ)
Рисунок 1
Треугольник АMD переместим так, чтобы вершина М
совместилась с вершиной С, катет АМ переместится
на отрезок DС. Треугольник МВС переместим влево и
вниз так, что катет МВ наложится на половину
отрезка DС. (Рисунок 1)
Задание 2.
Разрезать равносторонний треугольник на части
так, чтобы из них можно было сложить квадрат.
Решение.
Обозначим данный правильный треугольник АВС.
Необходимо разрезать треугольник АВС на
многоугольники так, чтобы из них можно было
сложить квадрат. Тогда эти многоугольники должны
иметь по крайней мере по одному прямому углу.
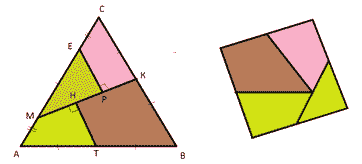
Пусть К – середина СВ, Т – середина АВ, точки М и
Е выберем на стороне АС так, что МЕ=АТ=ТВ=ВК=СК=а,
АМ=ЕС=а/2.
Рисунок 2
Проведем отрезок МК и перпендикулярные к нему
отрезки ЕР и ТН. Разрежем треугольник на части
вдоль построенных линий. Четырехугольник КРЕС
повернем по часовой стрелке относительно
вершины К так, что СК совместится с отрезком КВ.
Четырехугольник АМНТ повернем по часовой
стрелке относительно вершины Т так, что АТ
совместится с ТВ. Треугольник МЕР переместим так,
что в результате получится квадрат. (Рисунок 2)
Задание 3.
Разрезать квадрат на части так, чтобы из них
можно было сложить два квадрата.
Решение.
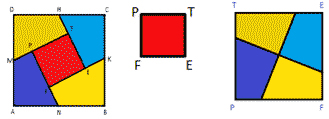
Обозначим исходный квадрат ABCD. Отметим
середины сторон квадрата – точки M, N, K, H. Проведем
отрезки МТ, НЕ, КF и NР – части отрезков МС, НВ, КА и
ND соответственно.
Разрезав квадрат ABCD по проведенным линиям,
получим квадрат PTEF и четыре четырехугольника MDHT,
HCKE, KBNF и NAMP.
Рисунок 3
PTEF – уже готовый квадрат. Из оставшихся
четырехугольников составим второй квадрат.
Вершины A, B, C и D совместим в одну точку, отрезки АМ
и ВК, MD и КС, BN и СН, DH и АN совместятся. Точки Р, Т, Е
и F станут вершинами нового квадрата. (Рисунок 3)
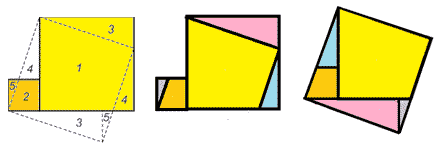
Задание 4.
Из плотной бумаги вырезаны равносторонний
треугольник и квадрат. Разрезать эти фигуры
на многоугольники так, чтобы из них можно было
сложить один квадрат, при этом части должны
полностью его заполнять и не должны
пересекаться.
Решение.
Треугольник разрежем на части и составим из них
квадрат так, как показано в задании 2. Длина
стороны треугольника – 2а. Теперь следует
разделить на многоугольники квадрат так, чтобы
из этих частей и того квадрата, который получился
из треугольника, составить новый квадрат.
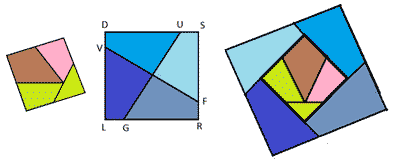
Возьмем квадрат со стороной 2а, обозначим его
LRSD. Проведем взаимно перпендикулярные отрезки UG
и VF так, что DU=SF=RG=LV. Разрежем квадрат на
четырехугольники.
Рисунок 4
Возьмем квадрат, составленный из частей
треугольника. Выложим четырехугольники – части
квадрата так, как показано на рисунке 4.
Задание 5.
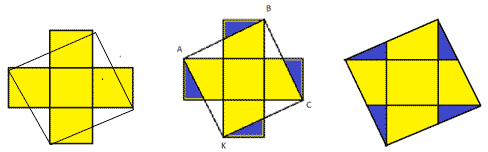
Крест составлен из пяти квадратов: один квадрат
в центре, а остальные четыре прилежат к его
сторонам. Разрезать его на такие части, чтобы из
них можно было составить квадрат.
Решение.
Соединим вершины квадратов так, как показано на
рисунке 5. Отрежем “внешние” треугольники и
переместим их на свободные места внутри квадрата
АВСК.
Рисунок 5
Задание 6.
Перекроить два произвольных квадрата в один.
Решение.
На рисунке 6 показано, как нужно разрезать и
переместить части квадратов.
Рисунок 6
Приложение.