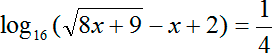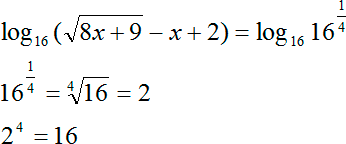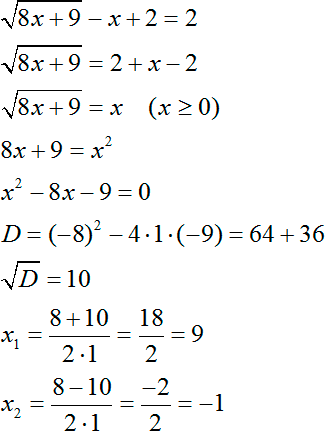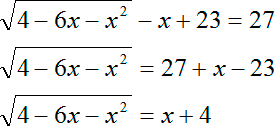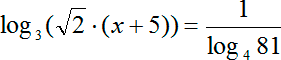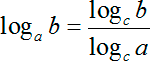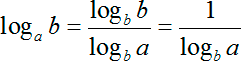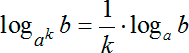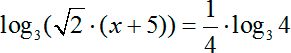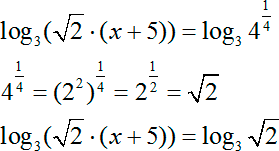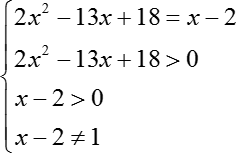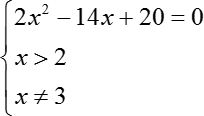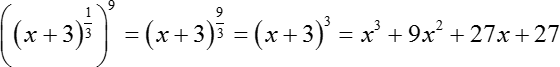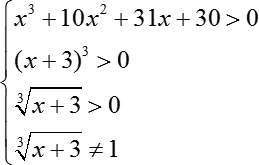Как решать логарифмические уравнения найти корень уравнения

Как решать логарифмические уравнения – подробный разбор

Опубликовано 12.01.2018

Чтобы ответить на вопрос как решать логарифмические уравнения давайте вспомним, что такое логарифм. Логарифм – это показатель степени, в которую нужно возвести основание логарифма, чтобы получить число.

Например,

или число 3 (показатель степени) мы можем записать так  , таким образом 

Основание логарифма всегда положительное число, не равное 1. Число под знаком логарифма – строго больше нуля.

Теперь переходим непосредственно к вопросу – как решать логарифмические уравнения из профильного и из базового ЕГЭ.

Пример 1 Найдите корень уравнения.

согласно определению логарифма:

Все неизвестные переносим в левую часть уравнения (слева от =), а известные – переносим в правую сторону.

Получим:

Делаем проверку:

Ответ:

Пример 2. Найдите корень уравнения.

Здесь для решения данного логарифмического уравнения будем использовать свойство логарифма:

То есть внесем число 3 справа под знак логарифма.

или

Если показатели степени равны, основания степени равны, то равны числа, получаемые в результате, то есть получим

Делаем проверку:

Получаем:

Ответ:

Пример 3. Найдите корень уравнения

Используем следующее свойство логарифма:

Тогда получим:

Делаем проверку:

Ответ:

Пример 4. Найдите корень уравнения.

Используя определение логарифма, получим:

Проверим:

Ответ: .

Таким образом, теперь вы можете составить четкую инструкцию, как решать логарифмические уравнения. Она заключается в следующих шагах:

1. Сделать справа и слева от знака равенства (=) логарифмы по одному основанию, избавившись от коэффициентов перед логарифмами, используя свойства логарифмов.
2. Избавляемся от логарифмов, используя правило потенцирования. Остаются только числа, которые были под знаком логарифма.
3. Решаем получившееся обычное уравнение – как найти корень уравнения смотрите здесь.
4. Делаем проверку
5. Записываем ответ.

( 4 оценки, среднее 5 из 5 )

Как решать логарифмические уравнения

Уравнения, содержащие в том или ином виде логарифмы от некоторого выражения, зависящего от (х), называются логарифмическими.

Давайте сразу же рассмотрим пример, так будет легче всего разобраться.

Пример 1
$$ log_{2}(x)=log_{2}(5)$$

Мы видим слева и справа логарифмы с одинаковыми основаниями, равными (2). Вполне логично предположить, что логарифмы будут равны, если будут равны выражения, стоящие под логарифмом (их называют аргументами) — то есть (х=5). Мы только что решили логарифмическое уравнение!

На самом деле, абсолютно такая же логика применима при решении почти всех логарифмических уравнений — если у нас сравниваются два логарифма с одинаковыми основаниями, то мы можем избавиться от логарифмов, приравнять их аргументы и решить получившееся уравнение.

Пример 2
$$ log_{3}(2x+5)=log_{3}(11) $$

Опять имеем два логарифма с одинаковым основанием (3). Избавляемся от логарифмов, приравнивая аргументы:

$$ 2x+5=11,$$
$$ 2x=6,$$
$$ x=3.$$

Кажется, что все очень просто. Но есть несколько непростых нюансов, которые необходимо обсудить. Давайте посмотрим еще один пример:

Пример 3
$$ log_{2}(1+3x)=log_{2}(2x-3) $$

Смотрим на основания — они одинаковые, значит убираем логарифмы и решаем уравнение:

$$1+3x=2x-3,$$
$$3x-2x=-3-1,$$
$$x=-4.$$

Мы решили уравнение, но я хочу позанудствовать и проверить, действительно ли получившийся корень является корнем исходного уравнения. Для этого подставим его в логарифмическое уравнение:

$$ log_{2}(1+3*(-4))=log_{2}(2*(-4)-3),$$
$$log_{2}(-11)=log_{2}(-11).$$

Мы получили слева и справа два одинаковых логарифма, вот только эти логарифмы НЕ СУЩЕСТВУЮТ, потому что нельзя взять логарифм от отрицательного числа.

Действительно, давайте вспомним определение логарифма (log_{a}b) — это в какую степень нужно возвести (a), чтобы получить (b). При этом определение справедливо не для всех (a) и (b), а только для (a>0), (b>0), (a neq 1). Подробнее про логарифм и его свойства можно почитать здесь.

Значит, с нашим решением что-то не так — мы нашли корень, подставили его в уравнение, но получили логарифм от отрицательного числа, который не существует!

Тут самое время вспомнить про область допустимых значений (ОДЗ). В логарифмах нужно всегда внимательно следить за тем, чтобы не нарушались ограничения, которые вытекают из определения логарифма. Рассмотрим логарифм от некоторой функции:

$$log_{a}f(x)$$

Область допустимых значений (ОДЗ) для него будет задаваться системой неравенств:

$$ begin{cases}
f(x)>0, \
a>0, \
a neq 1.
end{cases}$$

И при решении любых логарифмических уравнений или неравенств всегда первым делом записываем ОДЗ для каждого логарифма в уравнении.
В нашем примере 3, ОДЗ будет выглядеть вот так:

$$ begin{cases}
1+3x>0, \
2x-3>0. \
end{cases}$$

Решаем получившуюся систему

$$ begin{cases}
x>-frac{1}{3}, \
x>frac{3}{2}. \
end{cases}$$

Находим (х), удовлетворяющие одновременно обоим неравенствам, и получаем в итоге ОДЗ:
$$x>frac{3}{2}.$$

Вспоминаем, что решая это уравнение мы получили корень (x=-4), который нашему ОДЗ не удовлетворяет. Поэтому в примере 3 корней нет.

И так, всегда пишем ОДЗ!

Следующая трудность при решении логарифмических уравнений возникает, когда у нас сравниваются логарифмы с разными основаниями:

Пример 4
$$ log_{2}(x)=log_{4}(9).$$

Запишем ОДЗ: (x>0).

У логарифма слева основание (2), а у логарифма справа основание (4). Чтобы воспользоваться способом решения, аналогичным первым трем примерам, необходимо привести логарифмы к одинаковому основанию.

$$ log_{2}(x)=log_{2}(3).$$

Ого, как я такое получил?
Просто воспользовался формулой возведения в степень основания и аргумента логарифма — если возвести в одинаковую степень, то логарифм от этого не поменяется:

$$ log_{a}(b)=log_{a^n}(b^n).$$

В нашем примере возведем основание и аргумент в степень (frac{1}{2}):

$$ log_{4}(9)=log_{4^{frac{1}{2}}}(9^{frac{1}{2}})=log_{2}(3).$$

$$ log_{2}(x)=log_{2}(3).$$

Ну теперь основании у логарифмов одинаковые и можно с чистым сердцем приравнять аргументы, как мы делали до этого.
$$x=3.$$

Кстати, решить уравнение (log_{2}(x)=log_{4}(9))
можно было и по-другому — привести к основанию (4) логарифм, стоящий слева в уравнении:

Опять воспользуемся свойством логарифма:
$$ log_{a}(b)=log_{a^n}(b^n);$$
$$log_{2}(x)=log_{2^2}(x^2)=log_{4}(x^2);$$
Подставим в исходное уравнение наши преобразования:
$$ log_{4}(x^2)=log_{4}(9);$$
Ура, у нас слева и справа логарифмы с одинаковым основанием — вычеркиваем логарифмы:
$$x^2=9;$$
Решаем аккуратно простейшее квадратное уравнение. Не забываем, что у него будет 2 корня!
$$x=pm3;$$

Опа, у нас получилось два корня. А когда мы решали первым способом был один корень! Что за дела?

Вспоминаем, что в самом начале к уравнению мы записывали ОДЗ (х>0). Тогда корень (x=-3) не удовлетворяет ОДЗ. Обратите внимание, что без учета ОДЗ в этом случае, мы бы получили неправильный ответ.

Ответ: (x=3.)

Подробнее про свойства логарифмов можно посмотреть тут. Логарифмические уравнения с разными основаниями встречаются в ЕГЭ регулярно, поэтому важно уметь применять все свойства логарифмов.

Рассмотрим еще один пример.

Пример 5
$$log_{5}(x)=2$$

Как видим, в примере есть только логарифм в левой части равенства, а справа стоит просто число 2. Давайте постараемся привести к такому же виду, как и в прошлых примерах. То есть сделаем так, чтобы справа появился логарифм с основанием 5.

Оказывается, любое число (a) можно представить в виде логарифма с нужным вам основанием (b) по формуле:
$$a=log_{b}(b^a);$$
Эту формулу можно просто запомнить. А въедливым читателям, я бы рекомендовал посидеть и подумать откуда берется данное выражение. Подсказка — оно напрямую вытекает из определения логарифма. Задайте себе вопрос — «В какую степень нужно возвести основание, чтобы получить аргумент?»

И так, воспользуемся формулой и распишем 2-ку:
$$2=log_{5}(5^2);$$
Подставим в уравнение:
$$log_{5}(x)=log_{5}(5^2);$$
Ура, у нас два логарифма с одинаковыми основаниями, теперь можно приравнять подлогарифмические выражения.
$$x=5^2;$$
$$x=25.$$

Пример 6
$$log_{3}(x+2)=0$$

Начинаем с ОДЗ:
$$x+2>0;$$
$$x>-2.$$

Приступаем к решению уравнения. Что делать в случае, когда справа стоит (0)? Ничего страшного в этом нет, действуем по прежнему плану — представим (0) в виде логарифма по нашей формуле:
$$a=log_{b}(b^a);$$
$$log_{3}(x+2)=log_{3}(3^0);$$
Вспоминаем, что любое число в нулевой степени это единица.
$$log_{3}(x+2)=log_{3}(1);$$
$$x+2=1;$$
$$x=-1.$$
Корень удовлетворяет ОДЗ — записываем ответ.
Ответ: (x=-1).

Подведем итоги. В большинстве случаев, для того, чтобы решить простейшее логарифмическое уравнение, необходимо привести логарифмы слева и справа к одинаковому основанию. Затем приравнять подлогарифмические выражения и решить получившееся уравнения. При этом ни в коем случае не забываем про ОДЗ. На ЕГЭ, если вы вдруг запишите в ответ хотя бы один корень, не удовлетворяющий ОДЗ, то вам поставят за это задание 0 баллов.

В общем виде формула для решения логарифмов выглядит так:
$$ log_{a}(f(x))=log_{a}(g(x)) qquad (*)$$
где (a>0) — основание логарифмов, а (f(x)) и (g(x)) — какие-то выражения, зависящие от (x).
$$ begin{cases}
f(x)>0, или \
g(x)>0. \
end{cases}$$
$$f(x)=g(x).$$

Обратите внимание на «или» в ОДЗ. Оказывается можно накладывать условие больше нуля только на одную функцию: либо на f(x), либо на g(x) — смотря какое неравенство вам кажется легче для решения. Дело в том, что если одна из функций будет больше нуля, то и другая автоматически тоже будет будет больше, ведь мы ищем корни, при которых (f(x)=g(x)).

Для того, чтобы закрепить материал, решим еще одно логарифмическое уравнение:

Пример 7
$$2*log_{4}(4+x)=4-log_{2}(x-2);$$

Здесь все несколько сложнее, чем в предыдущих примерах. Для того чтобы представить наше уравнение в виде (*), нужно избавиться от множителя (2) перед первым логарифмом, кроме этого, нам мешается отдельное слагаемое (4), и в придачу ко всем этим неприятностям у логарифмов разные основания!

Но перед тем как решать, запишем ОДЗ:
$$ begin{cases}
4+x>0, \
x-2>0. \
end{cases}$$

$$ begin{cases}
x>-4, \
x>2. \
end{cases}$$

Находим пересечение и в итоге ОДЗ получается:
$$ x>2.$$

Приступаем непосредственно к решению уравнения. Самое главное, нам необходимо привести все логарифмы к одинаковому основанию, и, по возможности, привести к виду (log_{a}f(x)=log_{a}g(x)).
Здесь не обойтись без свойств логарифмов.
Воспользуемся формулой вынесения степени из основания логарифма:
$$log_{a^n}(b)=frac{1}{n}*log_{a}(b)$$
$$log_{4}(4+x)=log_{2^2}(4+x)=frac{1}{2}*log_{2}(4+x)$$

Подставим в уравнение
$$2*frac{1}{2}*log_{2}(4+x)=4-log_{2}(x-2);$$
$$log_{2}(4+x)=4-log_{2}(x-2);$$
Теперь у нас хотя бы логарифмы с одинаковым основанием. Далее преобразуем левую часть уравнения, воспользовавшись формулами:
$$ a=log_{b}(b^a);$$
$$log_{a}(b)-log_{a}(c)=log_{a}(frac{b}{c})$$
$$4-log_{2}(x-2)=log_{2}(2^4)-log_{2}(2-x)=log_{2}(16)-log_{2}(2-x)=log_{2}(frac{16}{2-x});$$
Подставим получившееся выражение в уравнение:
$$log_{2}(4+x)=log_{2}(frac{16}{2-x});$$

Ура, теперь у нас слева и справа в уравнении логарифмы с одинаковым основанием (2).
Избавляемся от логарифмов и решаем:
$$4+x=frac{16}{x-2};$$
Перекинем все налево и приведем к общему знаменателю
$$4+x-frac{16}{x-2}=0;$$
$$frac{(4+x)(x-2)}{x-2}—frac{16}{x-2}=0;$$
$$frac{4x-8+x^2-2x–16}{x-2}=0;$$
$$frac{x^2+2x-24}{x-2}=0;$$
Дробь равна 0, когда числитель равен 0
$$x^2+2x-24=0;$$
$$D=(2^2-4*(-24)=4+96=100;$$
$${x}_{1,2}=frac{-2pm 10}{2};$$
$${x}_{1}=4;$$
$${x}_{2}=-6;$$
Мы получили два корня. Но не забываем про ОДЗ. Выше мы его посчитали и получилось, что (x>2). Значит второй корень не подходит.
Ответ: (x=4).

Логарифмические уравнения с переменным основанием

Рассмотри теперь уравнение, в котором есть, так называемый, логарифм с переменным основанием. То есть логарифм, у которого в основании стоит какое-то выражение, зависящее от (х).

Пример 8
$$log_{1-x}(x^2+3x+1)=1;$$

В основании логарифма стоит ((1-х)), это переменное основание, потому что я могу подставлять различные значения (х) и каждый раз основание логарифма будет разным. Ничего страшного в этом нет, начинаем решать, руководствуясь тем же принципом, что и в предыдущих примерах — стараемся привести обе части уравнения к виду двух логарифмов с одинаковым основанием. Для этого нужно представить (1) справа в виде логарифма с основанием ((1-х)).

Но первым делом выпишем ОДЗ, не забывая накладывать условия и на основание логарифма, так как оно зависит от (х):
$$ begin{cases}
x^2+3x+1>0, \
1-x>0, \
1-xneq1.\
end{cases} qquad (**)$$

Теперь приступаем к решению самого уравнения. Выпишем еще раз формулу, по которой преобразуем правую часть:

$$a=log_{b}(b^a);$$
Где (а=1), а (b=1-x):
$$1=log_{1-x}(1-x)^1=log_{1-x}(1-x);$$
Подставим в уравнение
$$log_{1-x}(x^2+3x+1)=log_{1-x}(1-x);$$

Два логарифма с одинаковым основанием — можем приравнять аргументы:
$$x^2+3x+1=1-x;$$
$$x^2+4x=0;$$
$$x(x+4)=0;$$
$$x=0;$$
$$x=-4.$$
Получили два корня, проверим удовлетворяют ли они ОДЗ, подставив их в (**). Корень (0) не удовлетворяет последнему неравенству в ОДЗ, а ((-4)) удовлетворяет всем условиям.
Ответ: x=-4.

Замена переменной в уравнениях с логарифмами

Разберем еще один частый тип логарифмических уравнений — это уравнения с заменой переменной. Общий принцип заключается в том, чтобы привести все логарифмы в уравнении к одинаковому основанию и одинаковому аргументу, а потом сделать замену.

Проще разобрать на примерах:

Пример 9

$$log^2_{2}(x)+6=5*log_{2}(x)$$

Как и любой пример на логарифмы, начинаем с ОДЗ:

$$x>0.$$

В уравнении один из логарифмов в квадрате, поэтому представить в виде равенства двух логарифмов, как мы делали в предыдущих примерах, не получится. Кроме этого, замечаем, что у нас оба логарифма абсолютно одинаковые (у них одинаковые основания, и одинаковые аргументы).

Попробуем сделать замену:
$$t=log_{2}(x)$$
Тогда наше уравнение после замены примет вид:
$$t^2-5t+6=0;$$
$$D=25-24=1;$$
$$t_{1}=frac{5+1}{2}=3;$$
$$t_{2}=frac{5-1}{2}=1;$$
И сделаем обратную замену, получив два простых логарифмических уравнения:
$$t_{1}=log_{2}(x)=3;$$
$$log_{2}(x)=log_{2}(2^3);$$
$$x=8.$$
$$t_{2}=log_{2}(x)=1;$$
$$log_{2}(x)=log_{2}(2^1);$$
$$x=2.$$
Обязательно, не забываем проверить, удовлетворяют ли корни ОДЗ ((x>0)). Оба корня подходят, записываем ответ.
Ответ: (x=8; , x=2.)

Пример 10
$$ log_{2}left(frac{8}{x}right)-frac{10}{log_{2}(16x)} = 0;$$

Как обычно, начинаем с ОДЗ:
$$ begin{cases}
frac{8}{x}>0, \
log_{2}(16x)neq0,\
16x>0.\
end{cases}$$

Решаем каждое из получившихся неравенств в системе:
$$ begin{cases}
x>0, \
xneqfrac{1}{16},\
x>0.\
end{cases}$$
В итоге ОДЗ будет: (xin(0;frac{1}{16})cup(frac{1}{16};infty)).

Посмотрим теперь на сам пример. Видим два логарифма, у них одинаковые основания, что хорошо. Но функции, стоящие под логарифмами, разные. Постараемся при помощи свойств логарифма сделать одинаковые аргументы, чтобы потом сделать замену.

Воспользуемся формулами суммы и разности логарифмов с одинаковыми основаниями:
$$log_{a}(b*c)=log_{a}(b)+log_{a}(c);$$
$$log_{a}(frac{b}{c})=log_{a}(b)-log_{a}(c);$$
$$log_{2}left(frac{8}{x}right)=log_{2}(8)-log_{2}(x)=3-log_{2}(x);$$
$$log_{2}(16x)=log_{2}(16)+log_{2}(x)=4+log_{2}(x);$$
Подставим наши преобразования в исходное уравнение
$$3-log_{2}(x)-frac{10}{4+log_{2}(x)}=0;$$
Теперь в уравнении все логарифмы одинаковые, модем сделать замену. Пусть (t=log_{2}(x)).
$$3-t-frac{10}{4+t}=0;$$
Приводим к общему знаменателю
$$frac{(3-t)(4+t)-10}{4+t}=0;$$
$$frac{-t^2-t+2}{4+t}=0;$$
Дробь равна нулю, когда числитель равен нулю:
$$-t^2-t+2=0;$$
$$t_{1}=1;$$
$$t_{2}=-2;$$
Делаем обратную замену:
$$t_{1}=log_{2}(x)=1;$$
$$log_{2}(x)=log_{2}(2^1);$$
$$x=2.$$
$$t_{2}=log_{2}(x)=-2;$$
$$log_{2}(x)=log_{2}({2}^{-2});$$
$$x=frac{1}{4}.$$
Сверяем с ОДЗ, видим, что оба корня подходят, записываем ответ.
Ответ: (x=2; , x=frac{1}{4}.)

Пример 11
$$log_{2}(x^2+4x)+log_{0,5}(frac{x}{4})+2=log_{2}(x^2+3x-4)$$

Область допустимых значений:
$$ begin{cases}
x^2+4x>0, \
x^2+3x-4>0,\
x>0.\
end{cases}$$

$$ begin{cases}
x(x+4)>0, \
x>0,\
(x-1)(x+4)>0.\
end{cases}$$

Зеденым цветом показано решение первого неравенства в системе, синим — второго и фиолетовым третьего. Область, которая находится на пересечении сразу всех трех промежутков заштрихована бордовым.

Решаем методом интервалов, и находим пересечение решений всех неравенств в системе:

В итоге получаем ОДЗ: (x>1).

Приступаем к решению самого уравнения. Первым делом приведем все логарифмы к одинаковому основанию (2). Для этого нужно преобразовать только второе слагаемое в уравнении:
$$0,5=frac{1}{2}=2^{-1};$$
$$log_{2}(x^2+4x)+log_{2^{-1}}(frac{x}{4})+2=log_{2}(x^2+3x-4);$$
Вынесем степень из основания, воспользовавшись формулой (log_{a^n}(b)=frac{1}{n}log_{a}(b)).
$$log_{2}(x^2+4x)-log_{2}(frac{x}{4})+2=log_{2}(x^2+3x-4);$$
В первом слагаемом под логарифмом вынесем общий множитель (х). А квадратный многочлен под логарифмом справа разложим на множители при помощи дискриминанта:
$$log_{2}(x(x+4))-log_{2}(frac{x}{4})+2=log_{2}((x-1)(x+4));$$
И опять воспользуемся формулами суммыразности логарифмов:

$$log_{a}(b*c)=log_{a}(b)+log_{a}(c);$$
$$log_{a}left(frac{b}{c}right)=log_{a}(b)-log_{a}(c);$$
$$log_{2}(x)+log_{2}(x+4)-log_{2}(x)+log_{2}(4)+2=log_{2}(x-1)+log_{2}(x+4);$$
Сократим подобные слагаемые и посчитаем (log_{2}(4)=2):
$$4=log_{2}(x-1);$$
$$log_{2}(x-1)=4;$$
$$log_{2}(x-1)=log_{2}(2^4);$$
$$x-1=16;$$
$$x=17.$$
Сверяем корень с ОДЗ — подходит. Записываем ответ.
Ответ: (x=17).

Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.

Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.

.

При этом .

Обратим внимание на область допустимых значений логарифма:

.

Основное логарифмическое тождество:

,

.

Основные формулы для логарифмов:

(Логарифм произведения равен сумме логарифмов)

(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)

Формула перехода к новому основанию:

.

Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.

Все это пригодится нам в решении логарифмических уравнений.

Простейшие логарифмические уравнения

1.Решите уравнение:

Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.

Получаем:

Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при .

Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.

2. Решите уравнение:

В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.

Ответ: -124

3. Решите уравнение:

Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.

;

;

;

4. Решите уравнение:

Область допустимых значений: Значит,

Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.

Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом .

.

Ответ: 21.

5. Решите уравнение:

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: –4.

Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.

6.Решите уравнение: .

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

Запишем решение как цепочку равносильных переходов.

Ответ: 19.

7.Решите уравнение: .

Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.

ОДЗ:

Теперь можно «убрать» логарифмы.

— посторонний корень, поскольку должно выполняться условие .

Ответ:

8. Решите уравнение .

ОДЗ уравнения:

Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.

Вернемся к переменной х:

9.Решите уравнение:

Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.

Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.

«Отбрасываем» логарифмы.

Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену

Вернемся к переменной х. Получим:

. Мы нашли все корни исходного уравнения.

Ответ: .

Логарифмические уравнения могут встретиться вам и в задании №1 Профильного ЕГЭ по математике, и в задании №12. И если в задании №1 нужно решить простейшее уравнение, то в задаче 12 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.

План урока:

Простейшие логарифмические уравнения

Уравнения вида log_a f(x) = log_a g(x)

Уравнения, требующие предварительных преобразований

Логарифмические уравнения с заменой переменных

Логарифмирование уравнений

Переход от логарифмических неравенств к нелогарифмическим

Неравенства вида log_a x < b

Неравенства вида log_a f(x) <log_a g(x)

Простейшие логарифмические уравнения

Рассмотрим уравнение

которое обычно называют простейшим логарифмическим уравнением, его единственным корнем будет число х = а^с.

Задание. Укажите корень логарифмического уравнения

Задание. Решите урав-ние

В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид

Задание. Найдите решение логарифмического уравнения

Задание. Решите урав-ние

Задание. Решите урав-ние

Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания:

Уравнения вида log_af(x) = log_ag(x)

Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов.

Задание. Решите урав-ние

Задание. Найдите корень урав-ния

Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид

С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями.

Задание. Решите урав-ние

Получили квадратное уравнение, которое решаем с помощью дискриминанта:

Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем:

Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4:

Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log₃ (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3).

Ответ: – 3.

Уравнения, требующие предварительных преобразований

Естественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду log_af(x) = log_ag(x).

Задание. Решите урав-ние

с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае:

Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы:

Задание. Решите урав-ние

Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем

Задание. Решите урав-ние

Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log₅ 5. Тогда урав-ние можно преобразовать:

Задание. Решите урав-ние

Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что

Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что

Задание. Решите урав-ние

Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log₂₅x⁴ к основанию 5, используя известную нам формулу

Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы:

Логарифмические уравнения с заменой переменных

Иногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид.

Задание. Решите уравнение методом замены переменной

Задание. Найдите решение уравнения методом замены переменной

Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части:

Логарифмирование уравнений

Ясно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры.

Задание. Укажите корни урав-ния

Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5:

Возвращаемся от переменной t к переменной х:

Переход от логарифмических неравенств к нелогарифмическим

Рассмотрим график логарифмической функции у = log_ax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t<s), то этим двум значениям на оси Оу будет соответствовать числа log_at и log_as, причем окажется, что log_at лежит ниже, чем log_as. Это значит, что log_at<log_as:

Из картинки можно предположить, что неравенства log_at<log_as и t<s равносильны (если а > 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства

Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными.

Задание. Найдите решение логарифмического неравенства

Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 <x< 17 выполняется на промежутке (0; 17)

Ответ: (0; 17).

Задание. Решите нерав-во

Очевидно, что первую часть этого двойного нерав-ва можно просто отбросить, ведь условие 0 < 29 справедливо в любом случае:

Ситуация несколько меняется, когда основание лог-фма оказывается меньше единицы, то есть 0 <а < 1. В таком случае функция у = log_a x уже является не возрастающей, а убывающей. Тогда, если мы отметим на оси Ох такие точки tи s, что t<s, то окажется, что величина log_at будет находиться на оси Оу выше, чем log_as, то есть log_at>log_as:

Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0<а< 1 от логарифмического нерав-ва log_at>log_a s можно перейти к двойному нерав-ву 0 <t<s.

Грубо говоря, при переходе от логарифмического нерав-ва к нелогарифмическому знак нерав-ва сохраняется, если основание лог-фма больше единицы. Но в противном случае знак нерав-ва меняется на противоположный.

Задание. Решите нерав-во

Задание. Решите нерав-во

Неравенства вида log_ax<b

В случае, когда в одной из частей неравенства стоит логарифм, а в другой – обычное число, следует просто заменить число логарифмом, чтобы свести его к уже знакомым неравенствам.

Задание. Решите нерав-во

Решение.

Представим число 0,5 как логарифм с основанием 4. Так как 0,5 = log₄ 2, мы можем переписать нерав-во в виде:

Задание. Решите нерав-во

От него можно перейти к нелогарифмическому нерав-ву. Так как основание логарифмов 1/3 меньше единицы, то знак нерав-ва должен измениться:

Неравенства вида log_af(x) <log_ag(x)

В более сложных случаях в обоих частях неравенства под знаком логарифма находятся выражения с переменными. Алгоритм решения в таком случае остается неизменным – надо перейти к нелогарифмическому нерав-ву и при этом не забыть учесть, что под знаком логарифма может стоять исключительно положительное число.

Задание. Решите нерав-во

Решение. Основание логарифма, число 3, больше единицы, а потому мы можем перейти к такому двойному нерав-ву:

Для удобства дальше запишем его в виде системы неравенств:

Задание. Решите нерав-во

Так как выражения под знаком логарифма должны быть положительны, то мы можем записать сразу два нерав-ва:

Решим отдельно последнее нерав-во, которое является квадратным. Для этого найдем нули квадратичной функции, стоящей в правой части

Таким образом, нерав-во 0 <x²– 45х + 200 имеет решение

Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения:

Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5).

Ответ: (0; 5)⋃(40; 45).

Логарифмическое уравнение: основные формулы и приемы

3 мая 2014

• Скачать тест
• Ответы к тесту

Этим видео я начинаю длинную серию уроков про логарифмические уравнения. Сейчас перед вами сразу три примера, на основе которых мы будем учиться решать самые простые задачи, которые так и называются — простейшие.

Решите:

log_0,5 (3x − 1) = −3

lg (x + 3) = 3 + 2 lg 5

Напомню, что простейшим логарифмическим уравнением называется следующее:

log_a f (x) = b

При этом важно, чтобы переменная х присутствует только внутри аргумента, т. е. только в функции f (x). А числа а и b являются именно числами, а ни в коем случае не функциями, содержащими переменную х.

Основные методы решения

Существует множество способов решения таких конструкций. Например, большинство учителей в школе предлагают такой способ: Сразу выразить функцию f (x) по формуле f (x) = a^b. Т. е. когда вы встречаете простейшую конструкцию, сразу без дополнительных действий и построений можете перейти к решению.

Да, безусловно, решение получится правильным. Однако проблема этой формулы состоит в том, что большинство учеников не понимают, откуда она берется и почему именно букву а мы возводим в букву b.

В результате я часто наблюдаю очень обидные ошибки, когда, например, эти буквы меняются местами. Данную формулу нужно либо понять, либо зубрить, причем второй способ приводит к ошибкам в самые неподходящие и самые ответственные моменты: на экзаменах, контрольных и т. д.

Именно поэтому всем своим ученикам я предлагаю отказаться от стандартной школьной формулы и использовать для решения логарифмических уравнений второй подход, который, как вы уже наверняка догадались из названия, называется канонической формой.

Идея канонической формы проста. Давайте еще раз посмотрим на нашу задачу: слева у нас есть log_a, при этом под буквой a имеется в виду именно число, а ни в коем случае не функция, содержащая переменную х. Следовательно, на эту букву распространяются все ограничения, которые накладываются на основание логарифма. а именно:

1 ≠ a > 0

С другой стороны, из того же самого уравнения мы видим, что логарифм должен быть равен числу b, и вот на эту букву никаких ограничений не накладывается, потому что он может принимать любые значения — как положительные, так и отрицательные. Все зависит от того, какие значения принимает функция f (x).

И вот тут мы вспоминаем наше замечательное правило, что любое число b может быть представлено в виде логарифма по основанию а от а в степени b:

b = log_a a^b

Как запомнить эту формулу? Да очень просто. Давайте запишем следующую конструкцию:

b = b · 1 = b · log_a a

Разумеется, что при этом возникают все ограничения, которые мы записали вначале. А теперь давайте воспользуемся основным свойством логарифма, и внесем множитель b в качестве степени а. Получим:

b = b · 1 = b · log_a a = log_a a^b

В результате исходное уравнение перепишется в следующем виде:

log_a f (x) = log_a a^b → f (x) = a^b

Вот и все. Новая функция уже не содержит логарифма и решается стандартными алгебраическими приемами.

Конечно, кто-то сейчас возразит: а зачем вообще было придумывать какую-то каноническую формулу, зачем выполнять два дополнительных ненужных шага, если можно было сразу перейти от исходной конструкции к итоговой формуле? Да уже хотя бы затем, что большинство учеников не понимают, откуда берется эта формула и, как следствие, регулярно допускают ошибки при ее применении.

А вот такая последовательность действий, состоящая из трех шагов, позволяет вам решить исходное логарифмическое уравнение, даже если вы не понимаете, откуда берется та самая итоговая формула. Кстати, канонической формулой называется именно эта запись:

log_a f (x) = log_a a^b

Удобство канонической формы состоит еще и в том, что ее можно применять для решения очень широкого класса логарифмических уравнений, а не только простейших, которые мы рассматриваем сегодня.

Примеры решения

А теперь давайте рассмотрим реальные примеры. Итак, решаем:

log_0,5 (3x − 1) = −3

Давайте перепишем его следующим образом:

log_0,5 (3x − 1) = log_0,5 0,5⁻³

Многие ученики торопятся и пытаются сразу возвести число 0,5 в степень, которая пришла к нам из исходной задачи. И действительно, когда вы уже хорошо натренируетесь в решении подобных задач, вы можете сразу выполнять этот шаг.

Однако если сейчас вы только приступаете к изучению этой темы, лучше никуда не торопиться, чтобы не допускать обидных ошибок. Итак, перед нами каноническая форма. Имеем:

3x − 1 = 0,5⁻³

Это уже не логарифмическое уравнение, а линейное относительно переменной х. Чтобы решить его, давайте для начала разберемся с числом 0,5 в степени −3. Заметим, что 0,5 — это 1/2.

(1/2) ⁻³ = (2/1)³ = 8

Все десятичные дроби переводите в обычные, когда вы решаете логарифмическое уравнение.

Переписываем и получаем:

3x − 1 = 8
3x = 9
x = 3

Все, мы получили ответ. Первая задача решена.

Вторая задача

Переходим ко второй задаче:

Как видим, это уравнение уже не является простейшим. Уже хотя бы потому, что слева стоит разность, а не один-единственный логарифм по одному основанию.

Следовательно, нужно каким-то образом избавиться от этой разности. В данном случае все очень просто. Давайте внимательно посмотрим на основания: слева стоит число под корнем:

Общая рекомендация: во всех логарифмических уравнениях старайтесь избавиться от радикалов, т. е. от записей с корнями и переходить к степенным функциям, просто потому что показатели этих степеней легко выносятся за знак логарифма и в конечном счета такая запись существенно упрощает и ускоряет вычисления. Вот давайте так и запишем:

Теперь вспоминаем замечательное свойство логарифма: из аргумента, а также из основания можно выносить степени. В случае с основаниями происходит следующее:

log_{a^{k b = 1/k loga b}}

Другими словами, число, которое стояло в степени основания, выносится вперед и при этом переворачивается, т. е. становится обратным числом. В нашем случае стояла степень основания с показателем 1/2. Следовательно, мы можем вынести ее как 2/1. Получим:

5 · 2 log₅ x − log₅ x = 18
10 log₅ x − log₅ x = 18

Обратите внимание: ни в коем случае нельзя избавляться от логарифмов на этом шаге. Вспомните математику 4—5 класса и порядок действий: сначала выполняется умножение, а лишь затем — сложение и вычитание. В данном случае мы из 10 элементов вычитаем один такой же:

9 log₅ x = 18
log₅ x= 2

Теперь наше уравнение выглядит как надо. Это простейшая конструкция, и мы решаем его с помощью канонической формы:

log₅ x = log₅ 5²
x = 5²
x = 25

Вот и все. Вторая задача решена.

Третий пример

Переходим к третьей задаче:

lg (x + 3) = 3 + 2 lg 5

Напомню следующую формулу:

lg b = log₁₀ b

Если вас по каким-либо причинам смущает запись lg b, то при выполнении всех вычислений вы можете записать просто log₁₀ b. С десятичными логарифмами можно работать так же, как и с другими: выносить степени, складывать и представлять любые числа в виде lg 10.

Вот именно этими свойствами мы сейчас и воспользуемся для решения задачи, поскольку она не является простейшей, которую мы записали в самом начале нашего урока.

Для начала заметим, что множитель 2, стоящий перед lg 5, может быть внесен и станет степенью основания 5. Кроме того, свободное слагаемое 3 также представимо в виде логарифма — это очень легко наблюдать из нашей записи.

Судите сами: любое число можно представить в виде log по основанию 10:

3 = log₁₀ 10³ = lg 10³

Перепишем исходную задачу с учетом полученных изменений:

lg (x − 3) = lg 1000 + lg 25
lg (x − 3) = lg 1000 · 25
lg (x − 3) = lg 25 000

Перед нами снова каноническая форма, причем мы получили ее, минуя стадию преобразований, т. е. простейшее логарифмическое уравнение у нас нигде не всплывало.

Именно об этом я и говорил в самом начале урока. Каноническая форма позволяет решать более широкий класс задач, нежели стандартная школьная формула, которую дают большинство школьных учителей.

Ну и все, избавляемся от знака десятичного логарифма, и получаем простую линейную конструкцию:

x + 3 = 25 000
x = 24 997

Все! Задача решена.

Замечание по поводу области определения

Тут бы хотелось привести важное замечание по поводу области определения. Наверняка сейчас найдутся ученики и учителя, которые скажут: «Когда мы решаем выражения с логарифмами, необходимо обязательно помнить, что аргумент f (x) должен быть больше нуля!» В связи с этим возникает логичный вопрос: почему ни в одной из рассмотренных задач мы не требовали, чтобы это неравенство выполнялось?

Не переживайте. Никаких лишних корней в этих случаях не возникнет. И это еще одна замечательная хитрость, которая позволяет ускорить решение. Просто знайте, что если в задаче переменная х встречается лишь в одном месте (а точнее — в одном-единственном аргументе одного-единственного логарифма), и больше нигде в нашем случае нет переменной х, то записывать область определения не нужно, потому что она будет выполняться автоматически.

Судите сами: в первом уравнении мы получили, что 3х − 1, т. е. аргумент должен быть равен 8. Это автоматически означает, что 3х − 1 будет больше нуля.

С тем же успехом мы можем записать, что во втором случае х должен быть равен 5², т. е. он заведомо больше нуля. А в третьем случае, где х + 3 = 25 000, т. е. опять же заведомо больше нуля. Другими словами, область определения выполняется автоматически, но только при условии, что х встречается лишь в аргументе лишь одного логарифма.

Вот и все, что нужно знать для решения простейших задач. Уже одно это правило вместе с правилами преобразования позволит вам решать очень широкий класс задач.

Но давайте будем честными: для того, чтобы окончательно разобраться с этим приемом, чтобы научиться применять каноническую форму логарифмического уравнения, недостаточно просто посмотреть один видеоурок. Поэтому прямо сейчас скачайте варианты для самостоятельного решения, которые прилагаются к данному видеоуроку и начните решать хотя бы одну из этих двух самостоятельных работ.

Времени у вас уйдет буквально несколько минут. А вот эффект от такого обучения будет намного выше по сравнению с тем, если бы вы просто просмотрели данный видеоурок.

Надеюсь, этот урок поможет разобраться вам с логарифмическими уравнениями. Применяйте каноническую форму, упрощайте выражения с помощью правил работы с логарифмами — и никакие задачи вам будут не страшны. А у меня на сегодня все.

Учет области определения

Теперь поговорим об области определения логарифмической функции, а также о том, как это влияет на решение логарифмических уравнений. Рассмотрим конструкцию вида

log_af(x) = b

Такое выражение называется простейшим — в нем лишь одна функция, а числа а и b — это именно числа, а ни в коем случае не функция, зависящая от переменной х. Решается оно очень просто. Достаточно лишь использовать формулу:

b = log_aa^b

Данная формула является одним из ключевых свойств логарифма, и при подстановке в наше исходное выражение мы получим следующее:

log_a f(x) = log_a a^b

Далее, поскольку и слева, и справа стоит логарифмы по одному и тому же основанию, мы избавляемся от них:

f(x) = a^b

Это уже знакомая формула из школьных учебников. У многих учеников наверняка возникнет вопрос: поскольку в исходном выражении функция f(x) стоит под знаком log, на нее накладываются следующие ограничения:

f(х) > 0

Это ограничение действует потому, что логарифм от отрицательных чисел не существует. Так, может быть, вследствие этого ограничения следует ввести проверку на ответы? Быть может, их нужно подставлять в исходник?

Нет, в простейших логарифмических уравнениях дополнительная проверка излишня. И вот почему. Взгляните на нашу итоговую формулу:

f(x) = a^b

Дело в том, что число а в любом случае больше 0 — это требование тоже накладывается логарифмом. Число а является основанием. При этом на число b никаких ограничений не накладывается. Но это и неважно, потому что в какую бы степень мы бы не возводили положительное число, на выходе мы все равно получим положительное число. Таким образом, требование f(х) > 0 выполняется автоматически.

Что действительно стоит проверять, так это область определения функции, стоящей под знаком log. Там могут встречаться довольно непростые конструкции, и в процессе решения за ними обязательно нужно следить. Давайте посмотрим.

Первая задача:

Первый шаг: преобразуем дробь справа. Получим:

Избавляемся от знака логарифма и получаем обычное иррациональное уравнение:

Из полученных корней нас устраивает только первый, так как второй корень меньше нуля. Единственным ответом будет число 9. Все, задача решена. Никаких дополнительных проверок того, что выражение под знаком логарифма больше 0, не требуется, потому что оно не просто больше 0, а по условию уравнения оно равно 2. Следовательно, требование «больше нуля», выполняется автоматически.

Переходим ко второй задаче:

Здесь все то же самое. Переписываем конструкцию, заменяя тройку:

Избавляемся от знаков логарифма и получаем иррациональное уравнение:

Возводим обе части в квадрат с учетом ограничений и получаем:

х + 4 ≥ 0

4 − 6x− x² = (x− 4)²

4 − 6x− x² = x² + 8x + 16

x² + 8x + 16 −4 + 6x + x² = 0

2x² + 14x + 12 = 0 |:2

x² + 7x + 6 = 0

Решаем полученное уравнение через дискриминант:

D = 49 − 24 = 25

x₁ = −1

x₂ = −6

Но x = −6 нас не устраивает, потому что если мы подставим это число в наше неравенство, то получим:

−6 + 4 = −2 < 0

В нашем же случае требуется, чтобы было больше, чем 0 или в крайнем случае равно. А вот x = −1 нам подходит:

−1 + 4 = 3 > 0

Единственным ответом в нашем случае будет x = −1. Вот и все решение. Давайте вернемся в самое начало наших вычислений.

Основной вывод из этого урока: проверять ограничения для функции в простейших логарифмических уравнениях не требуется. Потому что в процессе решения все ограничения выполняются автоматически.

Однако это ни в коем случае не означает, что о проверке можно вообще забыть. В процессе работы над логарифмическим уравнением вполне может перейти в иррациональное, в котором будут свои ограничения и требования к правой части, в чем мы сегодня и убедились на двух различных примерах.

Смело решайте такие задачи и будьте особо внимательные, если в аргументе стоит корень.

Логарифмические уравнения с разными основаниями

Продолжаем изучать логарифмические уравнения и разберем еще два довольно интересных приема, с помощью которых модно решать более сложные конструкции. Но для начала вспомним, как решаются простейшие задачи:

log_af(x) = b

В этой записи а и b являются именно числами, а в функции f(x) должна присутствовать переменная х, и только там, т. е. х должен находиться только в аргументе. Преобразовывать такие логарифмические уравнения мы будем с помощью канонической формы. Для этого заметим, что

b = log_aa^b

Причем a^b— это именно аргумент. Давайте перепишем это выражение следующим образом:

log_a f(x) = log_a a^b

Мы именно этого и добиваемся, чтобы и слева, и справа стоял логарифм по основанию а. В этом случае мы можем, образно говоря, зачеркнуть знаки log, а с точки зрения математики мы можем сказать, что мы просто приравниваем аргументы:

f(x) = a^b

В результате мы получим новое выражение, которое будет решаться намного проще. Давайте применим это правило к нашим сегодняшним задачам.

Итак, первая конструкция:

Прежде всего, отмечу, что справа стоит дробь, в знаменателе которой находится log. Когда вы видите такое выражение, не лишним будет вспомнить замечательное свойство логарифмов:

Переводя на русский язык, это означает, что любой логарифм может быть представлен в виде частного двух логарифмов с любым основанием с. Разумеется, 0 < с ≠ 1.

Так вот: у этой формулы есть один замечательный частный случай, когда переменная с равна переменной b. В этом случае мы получим конструкцию вида:

Именно такую конструкцию мы наблюдаем от знака справа в нашем уравнении. Давайте заменим эту конструкцию на log_ab, получим:

Другими словами, в сравнении с исходным заданием, мы поменяли местами аргумент и основание логарифма. Взамен нам пришлось перевернуть дробь.

Далее осталось привести логарифмы к общему основанию. Заметим, что 81 = 3⁴. В этом случае давайте перепишем все наше логарифмическое уравнение:

Вспоминаем, что любую степень можно выносить из основания по следующему правилу:

Другими словами, коэффициент k, который является степенью основания, выносится как перевернутая дробь. Давайте вынесем ее как перевернутую дробь:

Дробный множитель нельзя оставлять спереди, потому что в этом случае мы не сможем представить данную запись как каноническую форму (ведь в канонической форме перед вторым логарифмом никакой дополнительный множитель не стоит). Следовательно, давайте внесем дробь 1/4 в аргумент в виде степени:

Теперь мы приравниваем аргументы, основания которых одинаковые (а основания у нас действительно одинаковые), и записываем:

x + 5 = 1

x = −4

Вот и все. Мы получили ответ к первому логарифмическому уравнению. Обратите внимание: в исходной задаче переменная х встречается лишь в одном log, причем стоит в его аргументе. Следовательно, проверять область определения не требуется, и наше число х = −4 действительно является ответом.

Теперь переходим ко второму выражению:

lg 56 = lg 2 log₂ 7 − 3lg (x + 4)

Здесь помимо обычных логарифмов, нам придется работать с lg f(x). Как решать такое уравнение? Неподготовленному ученику может показаться, что это какая-то жесть, но на самом деле все решается элементарно.

Внимательно посмотрите на слагаемое lg 2 log₂ 7. Что мы можем о нем сказать? Основания и аргументы log и lg совпадают, и это должно наводить на некоторые мысли. Давайте еще раз вспомним, как выносятся степени из-под знака логарифма:

log_abⁿ = nlog_ab

Другими словами, то, что являлось степенью при числе b в аргументе, становится множителем перед самим log. Давайте применим эту формулу для выражения lg 2 log₂ 7. Пусть вас не пугает lg 2 — это самое обычное выражение. Можно переписать его следующим образом:

lg 2 = log₁₀ 2

Для него справедливы все правила, которые действуют для любого другого логарифма. В частности, множитель, стоящий спереди, можно внести в степень аргумента. Давайте запишем:

Очень часто ученики в упор не видят это действие, потому что нехорошо вносить один log под знак другого. На самом деле ничего криминального в этом нет. Более того, мы получаем формулу, которая легко считается, если помнить важное правило:

Эту формулу можно рассматривать и как определение, и как одно из его свойств. В любом случае, если вы преобразуете логарифмическое уравнение, эту формулу вы должны знать точно так же, как и представление любого числа в виде log.

Возвращаемся к нашей задаче. Переписываем его с учетом того факта, что первое слагаемое справа от знака равенства будет равно просто lg 7. Имеем:

lg 56 = lg 7 − 3lg (x + 4)

Давайте перенесем lg 7 влево, получим:

lg 56 − lg 7 = −3lg (x + 4)

Вычитаем выражения слева, потому что они имеют одно и то же основание:

lg (56/7) = −3lg (x + 4)

Теперь давайте внимательно посмотрим на уравнение, которое мы получили. Оно практически является канонической формой, однако справа присутствует множитель −3. Давайте внесем его в аргумент правого lg:

lg 8 = lg (x + 4)⁻³

Перед нами каноническая форма логарифмического уравнения, поэтому мы вычеркиваем знаки lg и приравниваем аргументы:

(x + 4)⁻³ = 8

x + 4 = 0,5

х = −3,5

Вот и все! Мы решили второе логарифмическое уравнение. При этом никаких дополнительных проверок не требуется, потому что в исходной задаче х присутствовал лишь в одном аргументе.

Перечислю еще раз ключевые моменты этого урока.

Главная формула, которая изучается во всех уроках на этой странице, посвященной решению логарифмических уравнений — это каноническая форма. И пусть вас не пугает то, что в большинстве школьных учебников вас учат решать подобные задачи по-другому. Данный инструмент работает очень эффективно и позволяет решать гораздо более широкий класс задач, нежели простейшие, которые мы изучали в самом начале нашего урока.

Кроме того, для решения логарифмических уравнений полезно будет знать основные свойства. А именно:

1. Формулу перехода к одному основанию и частный случай, когда мы переворачиваем log (это очень пригодилось нам в первой задаче);
2. Формулу внесения и вынесения степеней из-под знака логарифма. Здесь многие ученики зависают и в упор не видят, что выносимая и вносимая степень сама может содержать log f(x). Ничего страшного в этом нет. Мы можем вносить один log по знак другого и при этом существенно упрощать решение задачи, что мы и наблюдаем во втором случае.

В заключении хотел бы добавить, что проверять область определения в каждом из этих случае не требуется, потому что везде переменная х присутствует только в одном знаке log, и при этом находится в его аргументе. Как следствие, все требования области определения выполняются автоматически.

Задачи с переменным основанием

Сегодня мы рассмотрим логарифмические уравнения, которые для многих учеников кажутся нестандартными, а то и вовсе нерешаемыми. Речь идет об выражениях, в основании которых стоят не числа, а переменные и даже функции. Решать такие конструкции мы будем с помощью нашего стандартного приема, а именно через каноническую форму.

Для начала вспомним, как решаются простейшие задачи, в основании которых стоят обычные числа. Итак, простейшей называется конструкция вида

log_af(x) = b

Для решения таких задач мы можем использовать следующую формулу:

b = log_aa^b

Переписываем наше исходное выражение и получаем:

log_a f(x) = log_a a^b

Затем мы приравниваем аргументы, т. е. записываем:

f(x) = a^b

Таким образом мы избавляемся от знака log и решаем уже обычную задачу. При этом полученные при решении корни и будут корнями исходного логарифмического уравнения. Кроме того, запись, когда и слева, и справа стоит по одному и тому же логарифму с одним и тем же основанием, как раз и называется канонической формой. Именно к такой записи мы будем пытаться свести сегодняшние конструкции. Итак, поехали.

Первая задача:

log_{x− 2} (2x² − 13x + 18) = 1

Заменяем 1 на log_{x− 2} (x − 2)¹. Та степень, которую мы наблюдаем у аргумента, это, на самом деле то число b, которое стояло справа от знака равенства. Таким образом, перепишем наше выражение. Получим:

log_{x− 2} (2x² − 13x + 18) = log_{x− 2} (x − 2)

Что мы видим? Перед нами каноническая форма логарифмического уравнения, поэтому мы смело можем приравнять аргументы. Получим:

2x² − 13x + 18 = x− 2

Но на этом решение не заканчивается, потому что данное уравнение не равносильно исходному. Ведь полученная конструкция состоит из функций, которые определены на всей числовой прямой, а наши исходные логарифмы определены не везде и не всегда.

Поэтому мы должны отдельно записать область определения. Давайте не будем мудрить и для начала запишем все требования:

Во-первых, аргумент каждого из логарифмов должен быть больше 0:

2x² − 13x + 18 > 0

x− 2 > 0

Во-вторых, основание должно быть не только больше 0, но и отлично от 1:

x− 2 ≠ 1

В итоге получим систему:

Но вы не пугайтесь: при обработке логарифмических уравнений такую систему можно существенно упростить.

Судите сами: с одной стороны, от нас требуется, чтобы квадратичная функция была больше нуля, а с другой стороны — эта квадратичная функция приравнивается к некому линейному выражению, от которого также требуется, чтобы оно было больше нуля.

В таком случае, если мы требуем, чтобы x− 2 > 0, то автоматически будет выполняться и требование 2x² − 13x + 18 > 0. Поэтому мы можем смело зачеркнуть неравенство, содержащее квадратичную функцию. Таким образом, количество выражений, которое содержится в нашей системе, уменьшится до трех.

Разумеется, с тем же успехом мы могли бы зачеркнуть и линейное неравенство, т. е. вычеркнуть x− 2 > 0 и потребовать, чтобы 2x² − 13x + 18 > 0. Но согласитесь, что решить простейшее линейное неравенство гораздо быстрее и проще, чем квадратичное, пусть даже при условии, что в результате решения всей этой системы мы получим одни и те же корни.

В общем, по возможности старайтесь оптимизировать вычисления. И в случае с логарифмическими уравнениями вычеркивайте самые сложные неравенства.

Давайте перепишем нашу систему:

Вот такая система из трех выражений, с двумя из которых мы, по сути, уже разобрались. Давайте отдельно выпишем квадратное уравнение и решим его:

2x²− 14x + 20 = 0

x²− 7x + 10 = 0

Перед нами приведенный квадратный трехчлен и, следовательно, мы можем воспользоваться формулами Виета. Получим:

(х − 5)(х − 2) = 0

x₁ = 5

x₂ = 2

А теперь возвращаемся к нашей системе и обнаруживаем, что х = 2 нас не устраивает, потому что от нас требуется, чтобы х был строго больше, чем 2.

А вот х = 5 нас вполне устраивает: число 5 больше, чем 2, и при этом 5 не равно 3. Следовательно, единственным решением данной системы будет являться х = 5.

Все, задача решена, в т. ч. с учетом ОДЗ. Переходим ко второму уравнению. Здесь нас ждут более интересные и содержательные выкладки:

Первый шаг: как и в прошлый раз, приводим все это дело к канонической форме. Для этого число 9 мы можем записать следующим образом:

Основание с корнем можно не трогать, а вот аргумент лучше преобразовать. Давайте перейдем от корня в степень с рациональным показателем. Запишем:

Давайте я не буду переписывать все наше большое логарифмическое уравнение, а просто сразу приравняю аргументы:

x³ + 10x² + 31x + 30 = x³ + 9x² + 27x + 27

x² + 4x + 3 = 0

Перед нами вновь приведенный квадратный трехчлен, воспользуемся формулами Виета и запишем:

(х + 3)(х + 1) = 0

x₁ = −3

x₂ = −1

Итак, мы получили корни, но никто нам не гарантировал, что они подойдут к исходному логарифмическому уравнению. Ведь знаки log накладывают дополнительные ограничения (здесь мы должны были бы записать систему, но из-за громоздкости всей конструкции я решил посчитать область определения отдельно).

В первую очередь, вспоминаем, что аргументы должны быть больше 0, а именно:

Это и есть требования, накладываемые областью определения.

Сразу заметим, что поскольку мы приравниваем первые два выражения системы друг к другу, то любое из них мы можем вычеркнуть. Давайте вычеркнем первую, потому что она выглядит более угрожающе, нежели вторая.

Кроме того, заметим, что решением второго и третьего неравенства будут одни и те множества (куб какого-то числа больше нуля, если само это число больше нуля; аналогично и с корнем третьей степени — эти неравенства полностью аналогичны, поэтому одно из них мы можем вычеркнуть).

А вот с третьим неравенством такое не пройдет. Избавимся от знака радикала, стоящего слева, для чего возведем обе части в куб. Получим:

х + 3 ≠ 1

х ≠ −2

Итак, мы получаем следующие требования:

− 2 ≠ x > −3

Какой из наших корней:x₁ = −3 или x₂ = −1 отвечает этим требованиям? Очевидно, что только х = −1, потому что х = −3 не удовлетворяет первому неравенству (ибо неравенство у нас строгое). Итого возвращаясь к нашей задаче, мы получаем один корень: х = −1. Вот и все, задача решена.

Еще раз ключевые моменты данной задачи:

1. Не стесняйтесь применять и решать логарифмические уравнения с помощью канонической формы. Ученики, которые делают такую запись, а не переходят напрямую от исходной задачи к конструкции типа log_af(x) = b, допускают намного меньше ошибок, чем те, которые куда-то спешат, пропуская промежуточные шаги вычислений;
2. Как только в логарифме появляется переменное основание, задача перестает быть простейшей. Следовательно, при его решении необходимо учитывать область определения: аргументы должны быть больше нуля, а основания — не только больше 0, но еще они не должны быть равны 1.

Накладывать последние требования на итоговые ответы можно по-разному. Например, можно решать целую систему, содержащую все требования к области определения. С другой стороны, можно сначала решить саму задачу, а затем вспомнить про область определения, отдельно проработать ее в виде системы и наложить на полученные корни.

Какой способ выбирать при решении конкретного логарифмического уравнения, решать только вам. В любом случае ответ получится один и тот же.

Смотрите также:

1. Квадратные уравнения относительно логарифма
2. Как решать простейшие логарифмические уравнения
3. Сводный тест по задачам B12 (2 вариант)
4. Что такое логарифм
5. Текстовые задачи про рельсы
6. Задача B4: Скачать файл на разной скорости