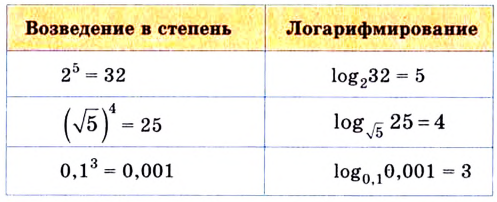
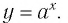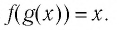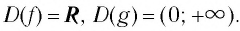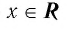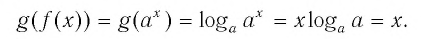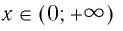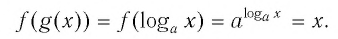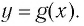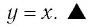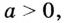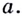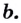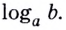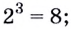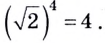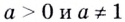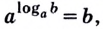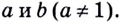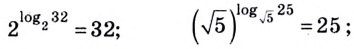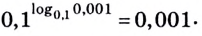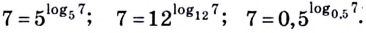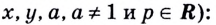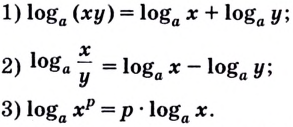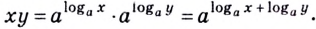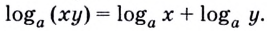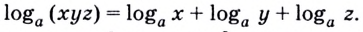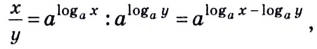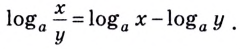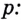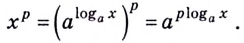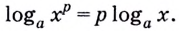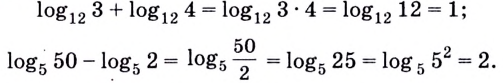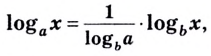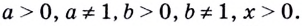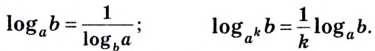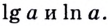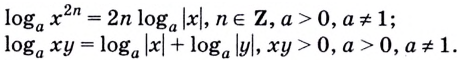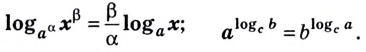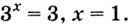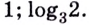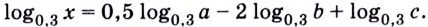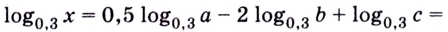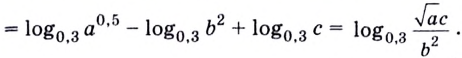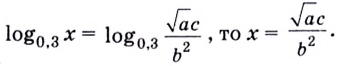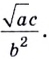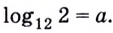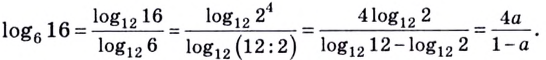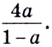Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.
Теперь при помощи этой таблицы введем понятие логарифма.
Логарифм от числа 32 по основанию 2 ((log_{2}(32))) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:
$$ log_{2}(32)=5;$$
Аналогично, глядя в таблицу получим, что:
$$log_{2}(4)=2;$$
$$log_{2}(8)=3;$$
$$log_{2}(16)=4;$$
$$log_{2}(64)=6;$$
$$log_{2}(128)=7.$$
Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.
Теперь дадим определение логарифма в общем виде:
Логарифмом положительного числа (b) по основанию положительно числа (a) называется степень (c), в которую нужно возвести число (a), чтобы получить (b)
$$log_{a}(b)=c;$$
$$a^{c}=b.$$
Будьте внимательны! В первое время обычно путают, что такое основание и то, что стоит под логарифмом (аргумент). Логарифм — это всегда функция, зависящая от двух переменных. Чтобы их не путать, помните определение логарифма – это степень, в которую нужно возвести основание, чтобы получить аргумент.
Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:
$$log_{2}(5)=???$$
Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:
$$log_{2}(5)=2,32192809…$$
Или логарифм шести по основанию 4:
$$log_{4}(6)= 1.2924812…$$
На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!
Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм (log_{4}(6)). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6-ке:
$$ log_{4}(4) lt log_{4}(6) lt log_{4}(16);$$
$$ 1 lt log_{4}(6) lt 2. $$
Значит (log_{4}(6)) принадлежите промежутку от 1 до 2:
$$ log_{4}(6) in (1;2). $$
Как посчитать логарифм
Перед тем, как научиться считать логарифмы, нужно ввести несколько ограничений. Дело в том, что функция логарифма (log_{a}(b)) существует только при положительных значениях основания (a) и аргумента (b). И кроме этого на основание накладывается условие, что оно не должно быть равно (1).
$$ log_{a}(b) quad существует,;при quad a gt 0; ;b gt 0 ;a neq 1.$$
Почему так? Это следует из определения показательной функций. Показательная функция не может быть (0). А основание не равно (1), потому что тогда логарифм теряет смысл – ведь (1) в любой степени это будет (1).
При этих ограничениях логарифм существует.
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.
$$log_{3}(frac{1}{3})=-1;$$
Так как (вспоминайте определение отрицательной степени)
$$3^{-1}=frac{1}{3};$$
Теперь давайте разберем общий алгоритм вычисления логарифмов:
- Во-первых, постарайтесь представить основание и аргумент (то, что стоит под логарифмом) в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
- Разобраться в какую степень (x) нужно возвести основание, чтобы получить аргумент. Когда у вас там и там степени с одинаковым основанием, это сделать довольно просто.
- (x) и будет искомым значением логарифма.
Давайте разберем на примерах.
Пример 1. Посчитать логарифм (9) по основанию (3): (log_{3}(9))
- Сначала представим аргумент и основание в виде степени тройки:
$$ 3=3^1, qquad 9=3^2;$$ - Теперь надо разобраться в какую степень (x) нужно возвести (3^1), чтобы получить (3^2)
$$ (3^1)^x=3^2, $$
$$ 3^{1*x}=3^2, $$
$$ 1*x=2,$$
$$ x=2.$$ - Вот мы и решили:
$$log_{3}(9)=2.$$
Пример 2. Вычислить логарифм (frac{1}{125}) по основанию (5): (log_{5}(frac{1}{125}))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1, qquad frac{1}{125}=frac{1}{5^3}=5^{-3};$$ - В какую степень (x) надо возвести (5^1), чтобы получить (5^{-3}):
$$ (5^1)^x=5^{-3}, $$
$$ 5^{1*x}=5^{-3},$$
$$1*x=-3,$$
$$x=-3.$$ - Получили ответ:
$$ log_{5}(frac{1}{125})=-3.$$
Пример 3. Вычислить логарифм (4) по основанию (64): (log_{64}(4))
- Представим аргумент и основание в виде степени двойки:
$$ 64=2^6, qquad 4=2^2;$$ - В какую степень (x) надо возвести (2^6), чтобы получить (2^{2}):
$$ (2^6)^x=2^{2}, $$
$$ 2^{6*x}=2^{2},$$
$$6*x=2,$$
$$x=frac{2}{6}=frac{1}{3}.$$ - Получили ответ:
$$ log_{64}(4)=frac{1}{3}.$$
Пример 4. Вычислить логарифм (1) по основанию (8): (log_{8}(1))
- Представим аргумент и основание в виде степени двойки:
$$ 8=2^3 qquad 1=2^0;$$ - В какую степень (x) надо возвести (2^3), чтобы получить (2^{0}):
$$ (2^3)^x=2^{0}, $$
$$ 2^{3*x}=2^{0},$$
$$3*x=0,$$
$$x=frac{0}{3}=0.$$ - Получили ответ:
$$ log_{8}(1)=0.$$
Пример 5. Вычислить логарифм (15) по основанию (5): (log_{5}(15))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1 qquad 15= ???;$$
(15) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть:
$$ log_{5}(15).$$
Внимание!
Как понять, что некоторое число (a) не будет являться степенью другого числа (b). Это довольно просто – нужно разложить (a) на простые множители.
$$16=2*2*2*2=2^4,$$
(16) разложили, как произведение четырех двоек, значит (16) будет степенью двойки.
$$ 48=6*8=3*2*2*2*2,$$
Разложив (48) на простые множители, видно, что у нас есть два множителя (2) и (3), значит (48) не будет степенью.
Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.
Десятичный логарифм
На самом деле, все просто. Десятичный логарифм – это любой обыкновенный логарифм, но с основанием 10. Обозначается — (lg(a)).
Пример 6
$$ log_{10}(100)= lg(100)=2;$$
$$log_{10}(1000)=lg(1000)=3;$$
$$log_{10}(10)=lg(10)=1.$$
Натуральный логарифм
Натуральным логарифмом называется логарифм по основанию (e). Обозначение — (ln(x)). Что такое (e)? Так обозначают экспоненту, число-константу, равную, примерно, (2,718281828459…). Это число известно тем, что используется в многих математических законах. Просто запомните, что логарифмы с основанием (e) часто встречаются, и поэтому им придумали специальное название – натуральный логарифм.
Пример 7
$$ log_{e}(e^2)=ln(e^2)=2;$$
$$ log_{e}(e)=ln(e)=1;$$
$$ log_{e}(e^5)=ln(e^5)=5.$$
Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.
У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.
Свойства логарифмов
$$1. ; log_{a}(1)=0;$$
$$2. ; log_{a}(a)=1;$$
$$3. ; log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$4. ; log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$5. ; log_{a}(b^m)= m*log_{a}(b);$$
$$6. ; log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
$$ 7. ; log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0; ; c gt 0; ; c neq 1; $$
$$ 8. ; log_{a}(b)=frac{1}{log_{b}(a)};$$
$$ 9. ; a^{ log_{a}(b)}=b.$$
Давайте разберем несколько примеров на свойства логарифмов.
Пример 8. Воспользоваться формулой (3). Логарифм от произведения – это сумма логарифмов.
$$log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$ log_{3}(12)=log_{3}(3*4)=log_{3}(3)+log_{3}(4)=1+log_{3}(4);$$
$$ log_{3}(2.7)+log_{3}(10)=log_{3}(2.7*10)=log_{3}(27)=3;$$
Пример 9. Воспользоваться формулой (4). Логарифм от частного – это разность логарифмов.
$$ log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$ log_{7}(98)-log_{7}(2)=log_{7}(frac{98}{2})=log_{7}(49)=2;$$
Пример 10. Формула (5,6). Свойства степени.
$$log_{a}(b^m)= m*log_{a}(b);$$
$$log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
Логично, что будет выполняться и такое соотношение:
$$log_{a^m}(b^n)=frac{n}{m}* log_{a}(b);$$
И если (m=n), то:
$$log_{a^m}(b^m)=frac{m}{m}* log_{a}(b);=log_{a}(b)$$
$$log_{4}(9)=log_{2^2}(3^2)=log_{2}(3);$$
Пример 11. Формулы (7,8). Переход к другому основанию.
$$ log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0;c gt 0;c neq 1; $$
$$ log_{a}(b)=frac{1}{log_{b}(a)};$$
$$log_{4}(5)=frac{1}{log_{5}(4)};$$
$$log_{4}(5)=frac{log_{7}(5)}{log_{7}(4)};$$
#статьи
- 6 окт 2022
-
0
Стыдные вопросы о логарифмах: всё, что нужно знать программисту
Объясняем, почему не стоит бояться логарифмов и как их считать в Python.
Иллюстрация: Оля Ежак для Skillbox Media
Журналист, изучает Python. Любит разбираться в мелочах, общаться с людьми и понимать их.
Прежде чем начать обсуждение, давайте немного освежим знания и решим несколько стандартных задачек:
- Чему равен log3 81?
- А lg 2 × lb 10?
- А сумма log216 2 + log216 3?
Если вы легко прорешали все три примера в уме, не пользуясь калькулятором, — можете сразу переходить к заключительной главе. Для тех же, кто слегка подзабыл школьные годы чудесные, — буквально пять минут ликбеза.
По большому счёту, логарифм — это просто перевёрнутая степень. Рассмотрим выражение 23 = 8. В нём:
- 2 — основание степени;
- 3 — показатель степени;
- 8 — результат возведения в степень.
У возведения в степень существует два обратных выражения. В одном мы ищем основание (это извлечение корня), в другом — показатель (это логарифмирование).
Таким образом, выражение 23 = 8 можно превратить в log2 8 = 3.
Закрепляем знания: логарифм — это число, в которое нужно возвести 2 (основание степени), чтобы получить 8 (результат возведения в степень).
Форма записи неинтуитивна, и поначалу можно легко спутать основание со степенью. Чтобы избежать этого, можно использовать следующее правило:
Основание у логарифма, как и у возведения в степень, находится внизу.
Чтобы лучше запомнить структуру записи, посмотрите на эти выражения и постарайтесь понять их смысл:
- log3 9 = 2
- log4 64 = 3
- log5 625 = 4
- log7 343 = 3
- log10 100 = 2
- log2 128 = 7
- log2 0,25 = −2
- log625 125 = 0,75
В общем виде запись logAB читается так: логарифм B по основанию A.
Главная часть любого логарифма — его основание. Именно наличие общего основания у нескольких логарифмических функций позволяет проводить с ними различные операции.
Основанием натурального логарифма является число Эйлера (e) — иррациональное число, приблизительно равное 2,71828.
На всякий случай напомним, что такое иррациональные числа. Так называют числа, которые нельзя записать в виде обыкновенной дроби с целыми числителем и знаменателем. При этом знаменатель не должен быть равен нулю.
Например, 0,333… — рациональное число, потому что его можно записать как 1/3. А вот число Пи или корень из 2 — иррациональны.
Так как натуральные логарифмы часто используются, для них ввели особый способ записи: ln x — это то же самое, что loge x.
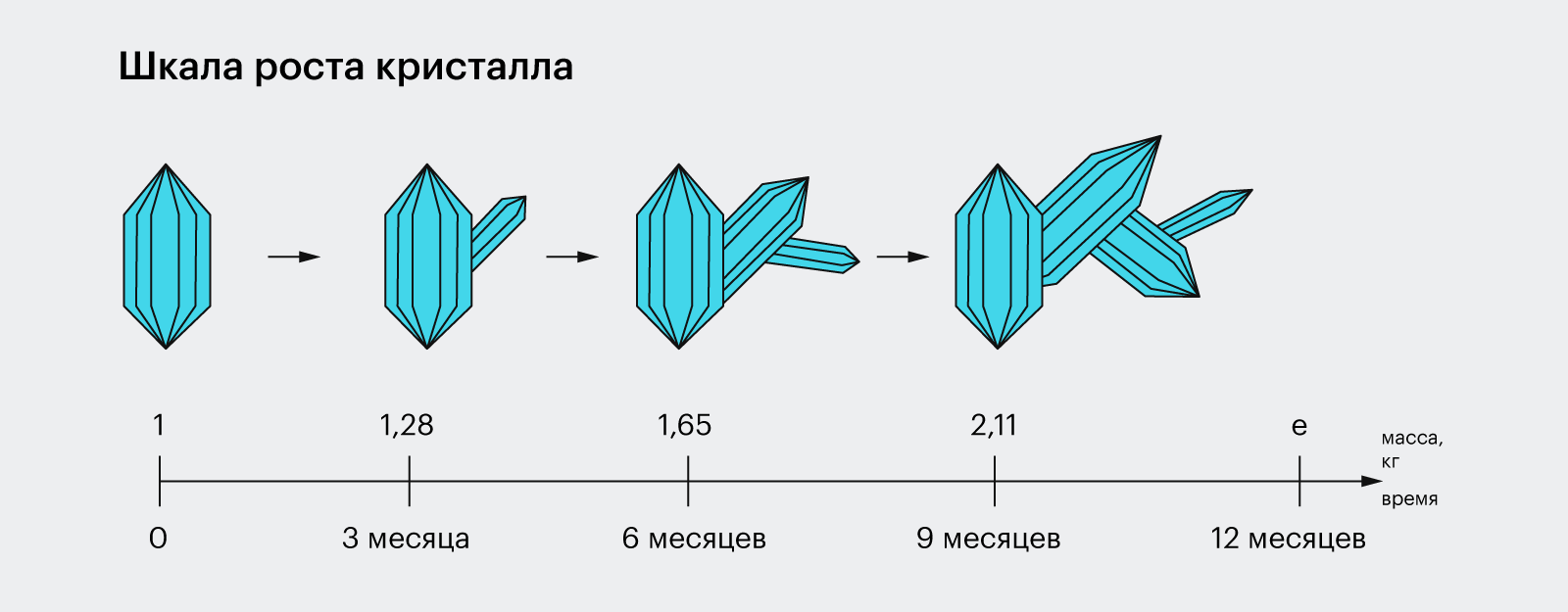
Представим кристалл, который весит 1 кг и растёт со скоростью 100% в год. Можно ожидать, что через год он будет весить 2 кг, но это не так.
Каждая новая выращенная часть начнёт растить свою собственную. Когда в кристалле будет 1,1 кг, он будет расти со скоростью 1,1 кг в год, а когда в нём будет 1,5 кг — со скоростью 1,5 кг в год. Математики подсчитали, что через год масса кристалла составит e, или ≈ 2,71828 кг.
Такой рост называется экспоненциальным. По экспоненте размножаются бактерии, увеличиваются популяции, приумножаются доходы, растут снежные комья, распадается радиоактивное вещество и остывают напитки.
Чтобы узнать, какой массы достигнет кристалл через три, пять, десять лет, нужно возвести e в соответствующую степень.
e3 ≈ 20,0855 кг
e5 ≈ 148,4132 кг
e10 ≈ 22 026,4658 кг
Но как рассчитать, когда кристалл будет весить тонну? Составим уравнение:
ex = 1000
Нам известны основание степени и результат возведения в степень — осталось найти её показатель. Ничего не напоминает? Это ведь и есть логарифм x = loge 1000! Или, если использовать сокращённую запись, x = ln 1000.
Подставим в калькулятор и выясним, что x ≈ 6,9. Именно столько лет потребуется кристаллу, чтобы его масса достигла тонны.
Десятичный логарифм — логарифм, основание которого равно 10. Он обозначается lg x и очень удобен, потому что с ним легко вычислять круглые числа.
Двоичный логарифм — логарифм, основание которого равно 2. Он обозначается lb x и часто используется программистами, потому что компьютеры думают и считают в двоичной системе.
Список операций, которые можно совершать с логарифмами, ограничен. Если вы запомните все и научитесь их выполнять, то сможете щёлкать логарифмические задачки, как семечки.
У всех логарифмов есть ограничения. Их основание и аргумент должны быть больше нуля, при этом основание не может быть равно единице. На математическом языке это звучит так:
Перейдём к свойствам логарифмов. Они работают в обе стороны, и их применяют как слева направо, так и справа налево.
1. Логарифм единицы по любому основанию всегда равен нулю:
Например: log17 1 = 0
2. Логарифм, где число и основание совпадают, равен единице:
Например: log17 17 = 1
3. Основное логарифмическое тождество:
Например: log17 175 = 5
4. Логарифм произведения чисел равен сумме их логарифмов:
Например: log5 12,5 + log5 10 = log5 (12,5 × 10) = log5 125 = 3
5. Логарифм дроби равен разности логарифмов числителя и знаменателя:
Например: log3 63 − log3 7 = log3 63/7 = log3 9 = 2
6. Если основание или аргумент возведены в степень, то их можно удобно выносить перед логарифмом:
Из этих двух формул следует:
Например: log23 49 = 9/3 × log2 4 = 3 × 2 = 6
7. Если нам неудобно основание логарифма, то его можно изменить:
Например: log25 125 = log5 125/log5 25 = 3/2 = 1,5
Из этой формулы следует, что мы можем поменять местами основание и аргумент вот так:
Например: log16 4 = 1/log4 16 = 1/2 = 0,5
А теперь возвращаемся к задачам, которые мы дали в начале статьи.
Пример 1
log3 81
Вспомните, что 81 — это 92. А 9 — это 32. Таким образом:
log3 81 = log3 92 = log3 32+2 = log3 34
Теперь логарифм не представляет для нас никаких сложностей. Воспользуемся свойством степени и вынесём четвёрку.
log3 34 = 4 × log3 3 = 4 × 1 =4
Ответ: 4.
Пример 2
lg 2 × lb 10
Переведём сокращённые записи в полный вид:
lg 2 × lb 10 = log10 2 × log2 10
Приведём оба логарифма к одному основанию.
log10 2 × log2 10 = 1/log2 10 × log2 10 = log2 10/log2 10 = 1
Ответ: 1.
Пример 3
log216 2 + log216 3
Воспользуемся свойством суммы.
log216 2 + log216 3 = log216 2 × 3 = log216 6
Представим 216 в виде степени числа 6 и вынесем с помощью свойства степени.
log216 6 = log63 6 = 1/3 × log6 6 = 1/3 × 1 = 1/3
Ответ: 1/3.
Чтобы работать с логарифмическими выражениями в Python, необходимо импортировать модуль math:
import math
И теперь посчитаем log2 8, используя метод math.log (b, a):
print (math.log (8, 2)) >>> 3.0
Обратите внимание на два момента. Во-первых, мы сначала передаём функции аргумент и только потом — основание. Во-вторых, функция всегда возвращает тип данных float, даже если результат целочисленный.
Если мы не передаём функции основание, то логарифм по умолчанию считается натуральным:
#math.e — метод для вызова числа Эйлера. print (math.log (math.e)) >>> 1.0
Для подсчёта десятичного и двоичного логарифма есть отдельные методы:
#Для десятичного. print (math.log10 (100)) >>> 2.0 #Для двоичного. print (math.log2 (512)) >>> 9.0
Ещё в Python есть специфичный метод, который прибавляет к аргументу единицу и считает натуральный логарифм от получившегося числа:
x = math.e print (math.log1p (x-1)) >>> 1.0
Когда х близок к нулю, этот метод даёт более точные результаты, чем math.log (1+x). Сравните:
x = 0.00001 print (math.log(x+1)) >>> 9.999950000398841e-06 print (math.log1p(x)) >>> 9.99995000033333e-06
Это все основные инструменты для работы с логарифмами в Python.

Научитесь: Профессия Python-разработчик
Узнать больше
Логарифм по основанию (a) от (b) – это число (t), которое показывает, в какую степень нужно возвести (a), чтобы получить (b).
Ограничения: числа (a) и (b) такие, что (a>0, ane 1, b>0).
Таким образом, верно основное логарифмическое тождество [Large{{color{royalblue}{a^t=b quadLeftrightarrowquad
log_a{b}=t}}}]
Т.к. мы имеем право возводить в любую степень, то (tin
mathbb{R}).
(blacktriangleright) Если (a,b,c) – числа, удовлетворяющие ограничениям: (a,b,c>0, ane 1), то справедливы следующие формулы:
[begin{array}{|ccc|}
hline textbf{(1)} log_a1=0&&textbf{(2)} log_aa=1\
&&\
textbf{(3)} log_{a^n}{b^m}=frac mnlog_ab&&textbf{(4)}
a^{log_bc}=c^{log_ba}\
&&\
textbf{(5)} log_a{bc}=log_ab+log_ac&&textbf{(6)}
log_a{dfrac bc}=log_ab-log_ac\
&&\
textbf{(7)} log_abcdot log_bc=log_ac & text{или}
&textbf{(7′}) log_bc=dfrac{log_ac}{log_ab}\
&&\
hline
end{array}]
Заметим, что при выполнении ограничений данные формулы верны в обе стороны!
Некоторые частные случаи, которыми удобно пользоваться:
(blacktriangleright) Частные случаи формул (3) и (4): [m=log_a{a^m} text{и} b=a^{log_ab}]
С помощью первой формулы нагляднее видно, как заменить число на логарифм по нужному основанию:
(4=log_2{2^4}=log_2{16});
а с помощью второй – как заменить число на степень с нужным основанием:
(4=3^{log_34}).
(blacktriangleright) Частные случаи формул (7) и (7’): [log_abcdot log_ba=1 text{и}
log_ab=dfrac1{log_ba}]
Пример:
(log_3{25}+dfrac2{log_{frac15}3}={small{text{(применили}}}
{small{text{ формулу}}}
(2))=log_3{25}+2log_3{dfrac15}=log_3{25}+log_3{dfrac1{25}}=log_3{left(25cdotdfrac1{25}right)}=0)
Содержание:
Множеством (областью) значений показательной функции
Такое значение аргумента единственное, так как если 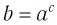
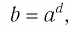
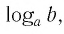
Таким образом, равенство 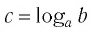
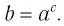
Определение:
Пусть 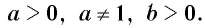
Приведем несколько примеров:
Нахождение логарифма числа называется логарифмированием.
Обозначим 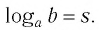
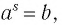
Это равенство называется основным логарифмическим тождеством.
Согласно этому тождеству, например, имеем: 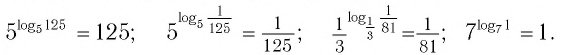
Например:
История логарифма
Логарифмы были изобретены в 1614 г. шотландским математиком Д. Непером (1550—1617) и независимо от него на 6 лет позднее швейцарским механиком и математиком И. Бюрги (1552—1632).
Оба исследователя хотели найти новое удобное средство арифметических вычислений, но их определения логарифма различны и у обоих не похожи на современные. Понимание логарифма как показателя степени с данным основанием впервые появилось в XVIII в. в работах английского математика В. Гардинера (1742). Широкому распространению этого определения логарифма более других содействовал Jl. Эйлер, который впервые применил в этой связи и термин «основание».
Термин «логарифм» принадлежит Неперу. Он возник из сочетания греческих слов логос — отношение и аритмос — число. Слово «логарифм», таким образом, означало «число отношения».
Пример:
а) Записать число 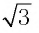
б) Записать число -5 в виде логарифмов по основанию 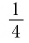
Решение:
а) По определению логарифма имеем:
б) По определению логарифма имеем:
Пример:
Между какими целыми числами находится число
Решение:
Пусть 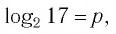
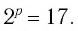
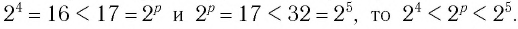
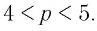
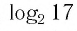
Ответ:
Пример:
Решить уравнение:
Решение:
а) Поскольку 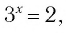
б)
Ответ:
Логарифмы по основанию 10 имеют особое название — десятичные логарифмы. Десятичный логарифм числа b обозначается 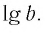
▲ Особое обозначение и название имеют не только десятичные логарифмы, но и логарифмы, основанием которых является число е:
Такие логарифмы называются натуральными.
Логарифмы по основанию е позволяют выражать математическую зависимость, которая характеризует многие биологические, химические, физические, социальные и другие процессы. По-видимому, этим объясняется и название «натуральные логарифмы», т. е. естественные (этот термин ввел в 1659 г. итальянский математик П. Менголи). Натуральные и десятичные логарифмы имели большое значение для облегчения вычислений в XVII—XX вв. до создания мощных современных вычислительных средств. Натуральные логарифмы имеют и большое теоретическое значение.▲
Основные свойства логарифмов
Теорема:
При любых положительных значениях b и с верно равенство:
Доказательство:
Докажем утверждение (1).
По основному логарифмическому тождеству
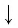
Таким образом, имеем:
Отсюда по следствию из п. 2.3 получаем равенство (1).
Докажем утверждение (2). Преобразуем левую часть равенства (2):
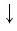
Заметим, что равенство (2) можно доказать тем же способом, что и равенство (1), — сделайте это самостоятельно.
Равенство (1) означает, что логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
Равенство (2) означает, что логарифм дроби с положительными. числителем и знаменателем равен разности логарифмов числителя и знаменателя.
Замечание. Равенства, доказанные в теореме 1 (как и другие равенства этого пункта), являются тождествами. Действительно, каждое из них превращается в верное числовое равенство при любых значениях a, b и с, для которых входящие в равенство выражения имеют смысл.
Теорема:
При любых значениях s и положительных значениях b верно равенство
Доказательство:
По основному логарифмическому тождеству
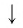
Таким образом, имеем
Отсюда по следствию из п. 2.3 получаем равенство (3).
Следствие 1. Если числа 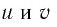
Следствие 2. При любом целом 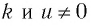
Пример №1
Найти значение выражения:
Решение:
Ответ:
Теорема:
При любых значениях 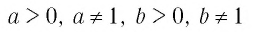
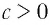
Доказательство:
Способ 1. По основному логарифмическому тождеству имеем
Прологарифмировав левую и правую части этого тождества по основанию а, получим
Применив тождество (3), имеем
Так как 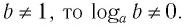
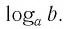
Способ 2. Пусть 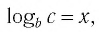
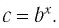
Откуда имеем
Итак,
Тождество (6) называется формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Обычно в таблицах, калькуляторах даются значения логарифмов по основанию 10, а когда нужно найти значение логарифма по другому основанию, пользуются формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Следствием из тождества (6) при основании а = с является формула
(убедитесь в этом самостоятельно).
Пример №2
Найти значение выражения, если
Решение:




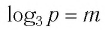
6)


Ответ:
Следствие 3. Имеют место тождества:
Тождества (8) и (9) можно доказать, используя уже доказанные тождества из этого пункта.
Пример №3
Упростить выражение
Решение:
Используя определение логарифма, представим числа 1 и 3 в виде логарифмов по основанию 2:
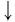
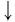
Ответ:
Развитие науки, прежде всего астрономии, уже в XVI в. привело к необходимости громоздких вычислений при умножении и делении многозначных чисел. Эти вычислительные проблемы были в некоторой степени решены с открытием логарифмов и созданием таблиц логарифмов.
Логарифмическая функция
Рассмотрим выражение 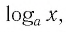
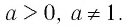
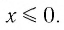
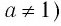
Определение:
Логарифмической функцией называется функция вида 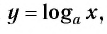
Область определения логарифмической функции — это естественная область определения выражения 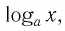
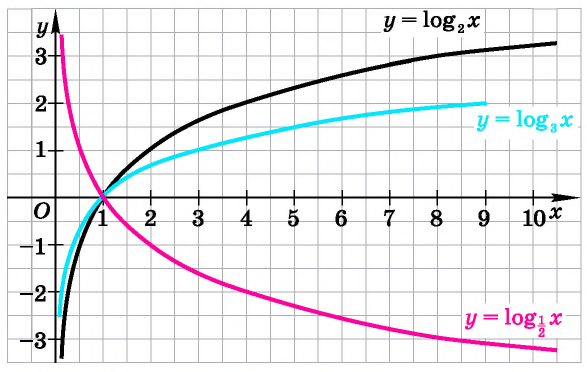
Графики некоторых логарифмических функций изображены на рисунке 34. Эти изображения (как и для графиков других функций) можно было получить, строя их по точкам. Отметим некоторые особенности изображенных графиков.
График функции 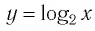
Когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» опускается вниз. А когда значения аргумента х увеличиваются, то график «медленно» поднимается вверх (ем. рис. 34). Аналогично для любой функции 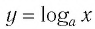
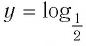
Заметим, что когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» поднимается вверх. А когда значения аргумента х увеличиваются, то график «медленно» опускается вниз. Аналогично для любой функции 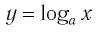
Теорема (о свойствах логарифмической функции 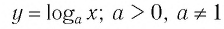
- Областью определения логарифмической функции является интервал
- Множеством (областью) значений логарифмической функции является множество R всех действительных чисел.
- Логарифмическая функция не имеет ни наименьшего, ни наибольшего значений.
- График логарифмической функции пересекается с осью абсцисс в точке (1; 0) и не пересекается с осью ординат.
- Значение аргумента х = 1 является нулем логарифмической функции.
- 6. При а > 1 логарифмическая функция принимает отрицательные значения на интервале (0; 1) и принимает положительные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
и принимает положительные значения на интервале (0; 1).
- Логарифмическая функция не является ни четной, ни нечетной.
- При а > 1 логарифмическая функция возрастает на всей области определения. При 0 < а < 1 логарифмическая функция убывает на всей области определения.
- Логарифмическая функция не является периодической.
Изображение графика логарифмической функции позволяет наглядно представить эти свойства.
Множество (область) значений логарифмической функции — проекция ее графика на ось Оу, а на рисунках 35 и 36 видно, что эта проекция есть ось Оу. Это значит, что для любой точки 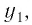
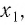
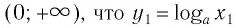
Множество (область) значений логарифмической функции — это множество всех действительных чисел, а в нем нет ни наименьшего числа, ни наибольшего (свойство 3).
График логарифмической функции проходит через точку (1; 0) и лежит в правой полуплоскости (свойства 4, 5).
При а > 1 график логарифмической функции лежит в IV координатном угле, когда 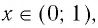
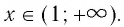
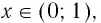
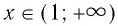
Область определения логарифмической функции — интервал 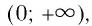
На рисунке 35 видно, что при а > 1 логарифмическая функция возрастает на области определения, а на рисунке 36 видно, что при 0 < а < 1 логарифмическая функция убывает на области определения (свойство 8).
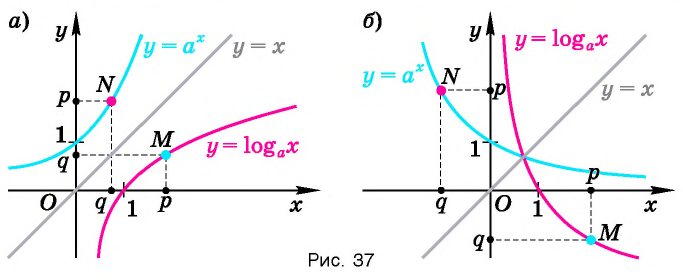
Пусть точка 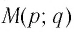
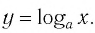
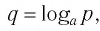
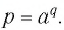
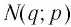
Заметим, что точки 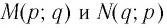
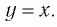
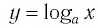
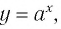
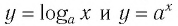
Последнее утверждение дает возможность, зная график функции 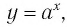
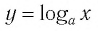
▲ Симметричность графиков функций 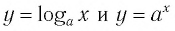
Функции 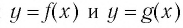
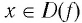
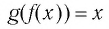
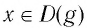
Покажем, что показательная и логарифмическая функции с одним, и тем же основанием а взаимно обратны.
Пусть 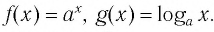
Для любого
Для любого
Покажем, что графики взаимно обратных функций 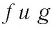
Пусть точка 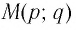
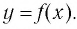
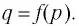
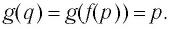
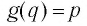
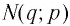
Таким образом, каждой точке М на графике функции 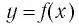
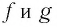
- Заказать решение задач по высшей математике
Логарифмы и их свойства
В предыдущем параграфе вы находили корни уравнения вида 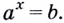
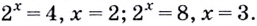
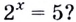
Для записи корней показательного уравнения используют понятие «логарифм» и соответствующий символ. Корнем уравнения 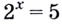
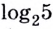
Рассмотрим общий случай-.
Пусть 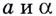
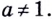
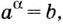
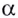
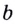
Логарифмом числа 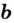
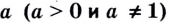
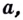
Логарифм числа 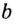
Примеры:
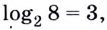
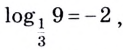
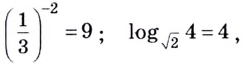
Основанием логарифма может быть произвольное положительное число, кроме единицы. Как известно, если 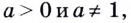
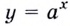
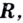
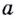
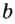
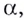
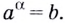
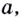
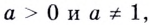
Полезно помнить, что для каждого
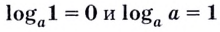
Нахождение логарифма числа называют логарифмированием. Эта операция обратная к операции возведения в степень с соответствующим основанием.
Согласно определению логарифма, если 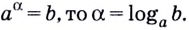
которое называют основным логарифмическим тождеством. Оно правильное для любых положительных
Например:
С помощью основного логарифмического тождества любое положительное число можно представить в виде степени, имеющей заданное основание.
Например:
Докажем ещё несколько важных свойств логарифмов (для положительных
1) По основному логарифмическому тождеству и основному свойству степени
Итак, 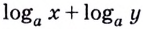
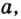
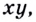
Эту формулу можно обобщить на три и более множителя:
Кратко говорят: логарифм произведения равен сумме логарифмов множителей.
2) Доказательство аналогичное предыдущему:
отсюда
Кратко говорят: логарифм частного равен разности логарифмов делимого и делителя.
3) Возведём обе части тождества 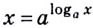
Итак,
Доказанные формулы можно использовать и справа налево, например:
В логарифмах переходить от одного основания к другому можно при помощи формулы перехода
где
Докажем эту формулу. Поскольку положительные числа 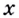
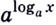
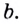
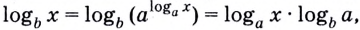
Обратите внимание! Как следствия из формулы перехода можно получить следующие формулы:
Докажите их самостоятельно.
Пример №4
Упростите выражение 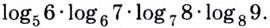
Решение:
Сведём все логарифмы к основанию 5. Имеем:
Особенно часто используют логарифмы по основаниям 10 и 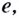
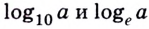
Рассмотренные в параграфе свойства логарифмов правиль-1 ные при условии, что переменные принимают положительные значения. С помощью модуля можно расширить использование некоторых формул. Например:
Для преобразования выражений, решения уравнений и неравенств используют и другие формулы, содержащие логарифмы:
Докажите их самостоятельно.
Пример №5
Вычислите:
Решение:
Пример №6
Решите уравнение:
Решение:
Пусть 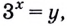
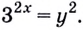
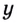
Получим: 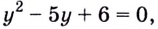
Поскольку 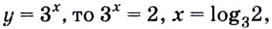
Ответ.
Пример №7
Найдите 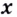
Решение:
Поскольку
Ответ.
Пример №8
Вычислите 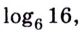
Решение:
Ответ.
- Корень из числа — нахождение и вычисление
- Теория множеств — виды, операции и примеры
- Числовые множества
- Вектор — определение и основные понятия
- Бесконечно убывающая геометрическая прогрессия
- Периодические дроби
- Степень с рациональным показателем
- Степень с действительным показателем
Начнем с простого. Как решить уравнение (displaystyle {{2}^{x}}=8)?
Очень легко – просто ответь на вопрос в какую степень нужно возвести число (2) чтобы получить (8)?
Решаем методом подбора: два в первой степени – нет, два во второй степени – нет, два в третей степени – ДА!
Двойку нужно возвести в ТРЕТЬЮ степень, чтобы получить восемь ((displaystyle {{2}^{3}}=8)) и значит решением уравнения будет число три ((x=3)).
Следующий вопрос. Как решить уравнение (displaystyle {{2}^{x}}=5)?
Опять просто ответь на вопрос в какую степень нужно возвести число (2), чтобы получить число (5)?
Попытаемся подобрать: два во второй степени равно четыре – мало, два в третьей степени равно восемь – много.
Метод подбора сразу ответ не дает… Да и вообще, в этом случае подобрать решение не получится – ведь это не только нецелое число, это число даже не рациональное.
Для нахождения таких решений было придумано понятие логарифм:
(displaystyle x={{log }_{2}}5).
В общем виде он записывается так:
То есть логарифм – это степень, в которую нужно возвести основание, чтобы получить аргумент.
Если ты посчитаешь на калькуляторе, то получишь (2,321928ldots ) и т.д. Это число иррациональное. Оно мало того, что не подбирается, оно еще и не кончается…
Ну и как с такими числами работать? Как их запоминать? Как их записывать?
В нашем случае решение уравнения можно записать как (2,321928ldots ) или как (displaystyle {{log }_{2}}5).
Согласись второе выражение гораздо удобнее, чем первое. И оно, кстати, абсолютно точное. Словами это произносится как:
Решением уравнения два в степени икс равно пяти является логарифм пяти по основанию два, или логарифм по основанию два от пяти.
Кстати, а ты заметил что и у степени числа и у логарифма основание всегда находится «ВНИЗУ». Легко запомнить правда? А вот «вверху», у степени находится ее показатель, а у логарифма – аргумент.
Выражение (displaystyle {{2}^{3}}=8) можно также записать в виде (displaystyle {{log }_{2}}8=3). Читается так:
«Логарифм восьми по основанию два равен трем»
или
«Логарифм по основанию два от восьми равен трем»
Теперь более общая запись:
Читается так:
«Логарифм по основанию (a) от (b) равен (c)»,
и означает:
«Чтобы получить число (b), нужно число (a) возвести в степень (c)»:
Иными словами, (displaystyle {{log }_{a}}b) – это степень, в которую нужно возвести (a), чтобы получить (b).
8 примеров вычисления логарифмов
Пример 1
Чему равен (displaystyle {{log }_{2}}4)?
(displaystyle {{log }_{2}}4=2), так как число (2) нужно возвести во вторую степень, чтобы получить (4).
Пример 2
Чему равен (displaystyle {{log }_{2}}frac{1}{8})?
Заметим, что (displaystyle 8={{2}^{3}}), тогда (displaystyle frac{1}{8}=frac{1}{{{2}^{3}}}={{2}^{-3}}), то есть (2) нужно возвести в степень (-3), чтобы получить (displaystyle frac{1}{8}).
Значит (displaystyle {{log }_{2}}frac{1}{8}=-3)
Пример 3
А чему равен (displaystyle {{log }_{2}}0,25)?
Обращать внимание нужно, в первую очередь, на основание. Возможно ли представить (0,25) как (2) в какой-то степени? Да, возможно: запишем это число в виде обычной дроби: (displaystyle 0,25=frac{1}{4}=frac{1}{{{2}^{2}}}={{2}^{-2}}).
Значит, (displaystyle {{log }_{2}}0,25=-2).
Пример 4
Чему равен (displaystyle {{log }_{7}}1)?
В какую степень надо возвести (7), чтобы получить (1)? Вспоминаем, что любое число в нулевой степени равно (1) (подробнее читай в разделе «Степень и ее свойства»).
Значит, (displaystyle {{log }_{7}}1=0). Более того, логарифм с любым основанием от единицы равен (0).
Пример 5
(displaystyle {{log }_{4}}2). В этом случае аргумент (2) равен корню основания: (displaystyle 2=sqrt{4}).
Но мы помним, что корень тоже можно представить в виде степени (с дробным показателем): (displaystyle 2=sqrt{4}={{4}^{frac{1}{2}}}text{ }Rightarrow text{ }{{log }_{4}}2=frac{1}{2}).
Когда нужная степень не подбирается
Как я уже говорил, далеко не всегда удается подобрать такую степень. Но это не значит, что такого числа не существует, просто его можно вычислить только на калькуляторе.
Например, (displaystyle {{log }_{2}}5=2,321928…).
Видим, что это число расположено между (displaystyle 2) и (displaystyle 3), и это понятно: ведь это значит, чтобы получить (5), нужно (2) возводить в степень больше (2), но меньше (3).
На ЕГЭ пользоваться калькулятором нельзя, но даже если бы было можно, нельзя записывать приближенные вычисления.
Поэтому, если перед нами задача первой части, ответ обязательно должен получиться «хороший», и его можно посчитать в уме.
В письменной части могут попасться и «плохие» числа; в этом случае пугаться не нужно, в ответе можно просто написать логарифм.
Например, ответ вполне может выглядеть так:
(displaystyle {{log }_{3}}10), или даже так: (displaystyle frac{2+{{log }_{3}}7}{5}).
Получается, что теперь мы можем мгновенно записать решение любого элементарного показательного уравнения:
(displaystyle {{3}^{x}}=8)? Легко: (displaystyle x={{log }_{3}}8).
(displaystyle {{17}^{x}}=0,387)? (displaystyle x={{log }_{17}}0,387)
(displaystyle {{0,56}^{x}}=23,7)? (displaystyle x={{log }_{0,56}}23,7).
И так далее.
Но увлекаться и халтурить тоже не стоит – если в ответе оставить (displaystyle x={{log }_{3}}81), высший балл за задачу не поставят.
То есть, если ответ возможно упростить и представить в виде рационального числа, это обязательно нужно будет сделать.
Потренируйся на следующих простых примерах:
Начнем с простого: допустим, что ( a=1). Тогда, например, число не существует, так как в какую бы степень мы не возводили ( 1), всегда получается ( 1).
Более того, ( displaystyle {{log }_{1}}b) не существует ни для какого ( displaystyle bne 1).
Но при этом ( displaystyle {{log }_{1}}1) может равняться чему угодно (по той же причине – ( 1) в любой степени равно ( 1)).
Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.
Похожая проблема у нас и в случае ( a=0): ( 0) в любой положительной степени – это ( 0), а в отрицательную его вообще нельзя возводить, так как получится деление на ноль (напомню, что ( displaystyle {{a}^{-c}}=frac{1}{{{a}^{c}}})).
При ( a<0) мы столкнемся с проблемой возведения в дробную степень (которая представляется в виде корня: ( displaystyle {{a}^{frac{m}{n}}}=sqrt[n]{{{a}^{m}}}).
Например, ( displaystyle {{log }_{4}}2=frac{1}{2}) (то есть ( displaystyle {{4}^{frac{1}{2}}}=sqrt{4}=2)), а вот ( displaystyle {{log }_{-4}}2) не существует.
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное.
Значит, аргумент должен быть положительным.
Например, ( displaystyle {{log }_{2}}left( -4 right)) не существует, так как ( 2) ни в какой степени не будет отрицательным числом (и даже нулем, поэтому ( displaystyle {{log }_{2}}0) тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ.
Приведу пример:
Решим уравнение ( displaystyle {{log }_{x}}left( x+2 right)=2).
Вспомним определение: логарифм ( displaystyle {{log }_{x}}left( x+2 right)) – это степень, в которую надо возвести основание ( x), чтобы получить аргумент ( displaystyle left( x+2 right)).
И по условию, эта степень равна ( 2): ( displaystyle {{x}^{2}}=x+2).
Получаем обычное квадратное уравнение: ( displaystyle {{x}^{2}}-x-2=0).
Решим его с помощью теоремы Виета: сумма корней равна ( 1), а произведение ( -2). Легко подобрать, это числа ( 2) и ( -1).
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу на ЕГЭ.
Почему?
Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
( displaystyle x=2text{: }{{log }_{2}}left( 2+2 right)={{log }_{2}}4=2) – верно.
( displaystyle x=-1text{: }{{log }_{-1}}left( -1+2 right)=2) – это явно неверно, так как основание не может быть отрицательным, то есть корень ( x=-1) – «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
( displaystyle left{ begin{array}{l}x>0\xne 1\x+2>0end{array} right.text{ }Leftrightarrow text{ }left{ begin{array}{l}x>0\xne 1.end{array} right.)
Тогда, получив корни ( x=2) и ( x=-1), сразу отбросим корень ( -1), и напишем правильный ответ.
Пример 1 (попробуй решить самостоятельно)
Найдите корень уравнения ( displaystyle {{log }_{x+1}}left( 2x+5 right)=2). Если корней несколько, в ответе укажите меньший из них.
Решение:
( displaystyle {{log }_{x+1}}left( 2x+5 right)=2).
Свойство 3 – разность логарифмов
Разность логарифмов с одинаковыми основаниями равна логарифму частного:( displaystyle lo{{g}_{a}}b-{{log }_{a}}c={{log }_{a}}frac{b}{c}).
Доказательство:
Все точно так же, как и в пункте 2:
Пусть ( displaystyle {{log }_{a}}b=x), тогда ( displaystyle {{a}^{x}}=b).
Пусть ( displaystyle {{log }_{a}}c=y), тогда ( displaystyle {{a}^{y}}=c).
Имеем:
( displaystyle {{log }_{a}}left( frac{b}{c} right)={{log }_{a}}left( frac{{{a}^{x}}}{{{a}^{y}}} right)={{log }_{a}}{{a}^{x-y}}=x-y={{log }_{a}}b-{{log }_{a}}c), ч.т.д.
( displaystyle {{log }_{a}}b-{{log }_{a}}c={{log }_{a}}left( frac{b}{c}cdot c right)-{{log }_{a}}c={{log }_{a}}frac{b}{c}+{{log }_{a}}c-{{log }_{a}}c={{log }_{a}}frac{b}{c}), ч.т.д.
Пример из прошлого пункта теперь становится еще проще:
( displaystyle {{log }_{5}}250-{{log }_{5}}2={{log }_{5}}frac{250}{2}={{log }_{5}}125={{log }_{5}}{{5}^{3}}=3).
Пример посложнее: ( displaystyle log _{2}^{2}2sqrt{3}-log _{2}^{2}sqrt{3}-{{log }_{2}}3).
Догадаешься сам, как решить?
Здесь нужно заметить, что у нас нету ни одной формулы про логарифмы в квадрате. Это что-то сродни выражению ( displaystyle {{2}^{{{x}^{2}}}}) – такое сразу не упростить.
Поэтому отвлечемся от формул про логарифмы, и подумаем, какие вообще формулы мы используем в математике чаще всего? Еще начиная с 7 класса!
Это – формулы сокращенного умножения. Нужно привыкнуть к тому, что они везде! И в показательных, и в тригонометрических, и в иррациональных задачах они встречаются. Поэтому их нужно обязательно помнить.
Нажми на ссылку «Формулы сокращенного умножения», и внимательно на них посмотри. Какую из них можно применить здесь?
Если присмотреться к первым двум слагаемым, становится ясно, что это разность квадратов:
( displaystyle log _{2}^{2}2sqrt{3}-log _{2}^{2}sqrt{3}=left( {{log }_{2}}2sqrt{3}-{{log }_{2}}sqrt{3} right)left( {{log }_{2}}2sqrt{3}+{{log }_{2}}sqrt{3} right)).
Дальше все просто – применяем только что выученные правила 2 и 3. Что получилось?
Ответ для проверки:
( displaystyle log _{2}^{2}2sqrt{3}-log _{2}^{2}sqrt{3}-{{log }_{2}}3=).
( displaystyle=left( {{log }_{2}}2sqrt{3}-{{log }_{2}}sqrt{3} right)left( {{log }_{2}}2sqrt{3}+{{log }_{2}}sqrt{3} right)-{{log }_{2}}3=).
( displaystyle={{log }_{2}}frac{2sqrt{3}}{sqrt{3}}cdot {{log }_{2}}left( 2sqrt{3}cdot sqrt{3} right)-{{log }_{2}}3=).
( displaystyle={{log }_{2}}2cdot {{log }_{2}}left( 2cdot 3 right)-{{log }_{2}}3=1cdot left( 1+{{log }_{2}}3 right)-{{log }_{2}}3=1.).
Упрости сам:
- ( displaystyle {{log }_{3}}4-{{log }_{3}}12)
- ( displaystyle {{log }_{0,3}}3-{{log }_{0,3}}10)
- ( displaystyle {{log }_{1,75}}28+{{log }_{1,75}}2-{{log }_{1,75}}32)
- ( displaystyle lg sqrt{0,05}-lg sqrt{5})
- ( displaystyle {{lg }^{2}}2sqrt{5}-{{lg }^{2}}5sqrt{2}-frac{3}{2}lg sqrt{frac{2}{5}})
Ответы:





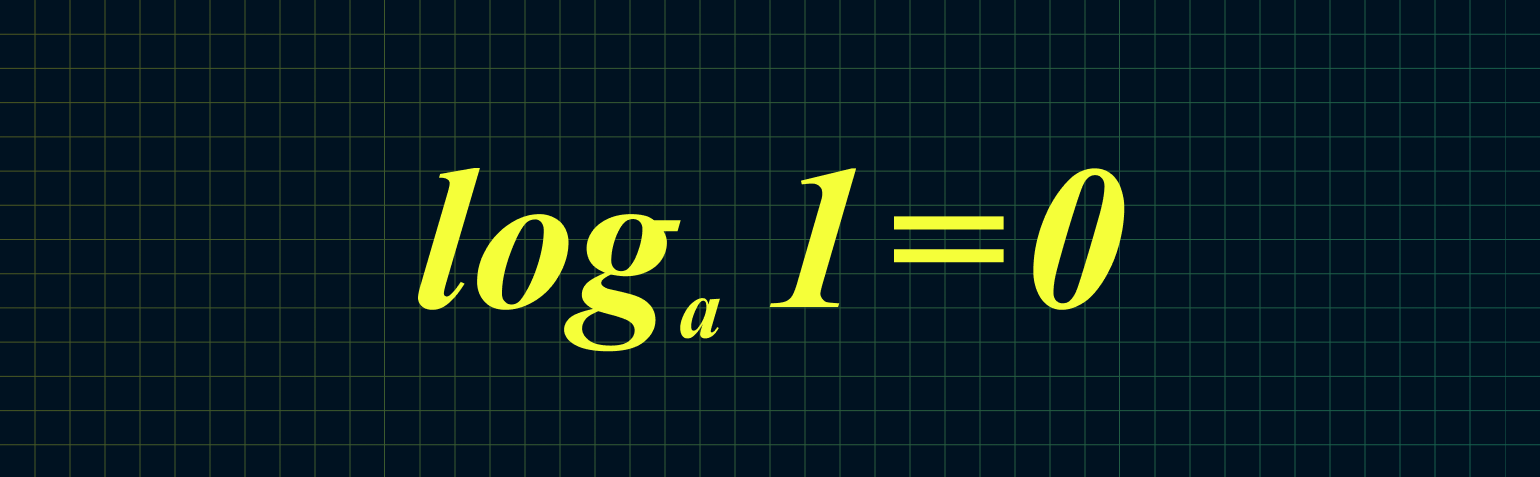
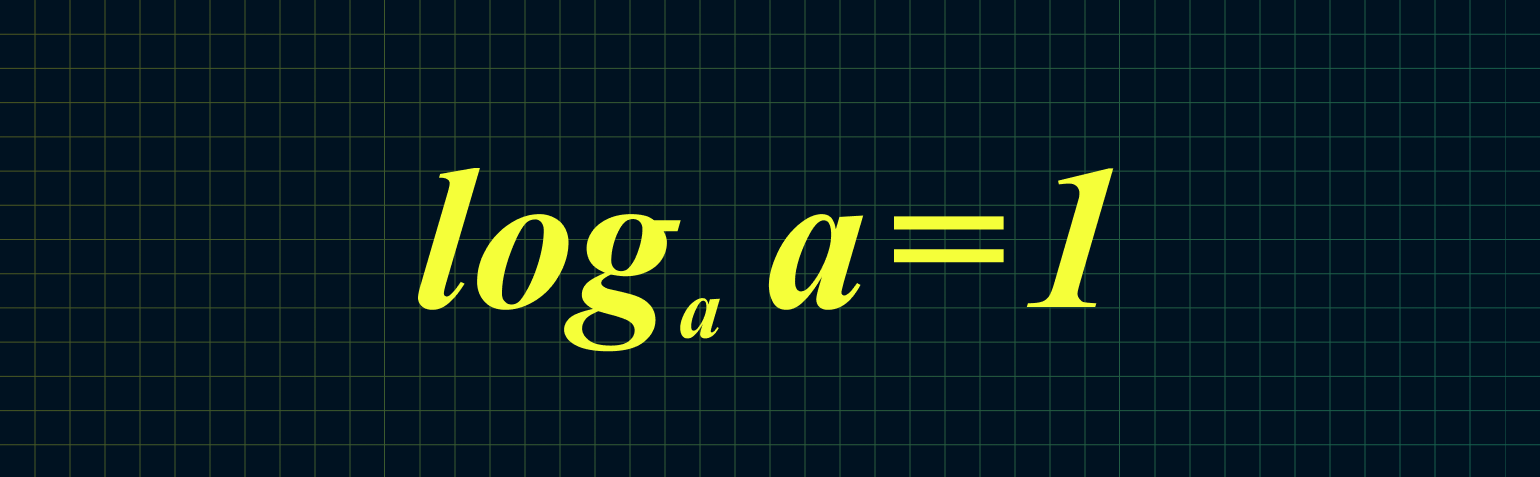
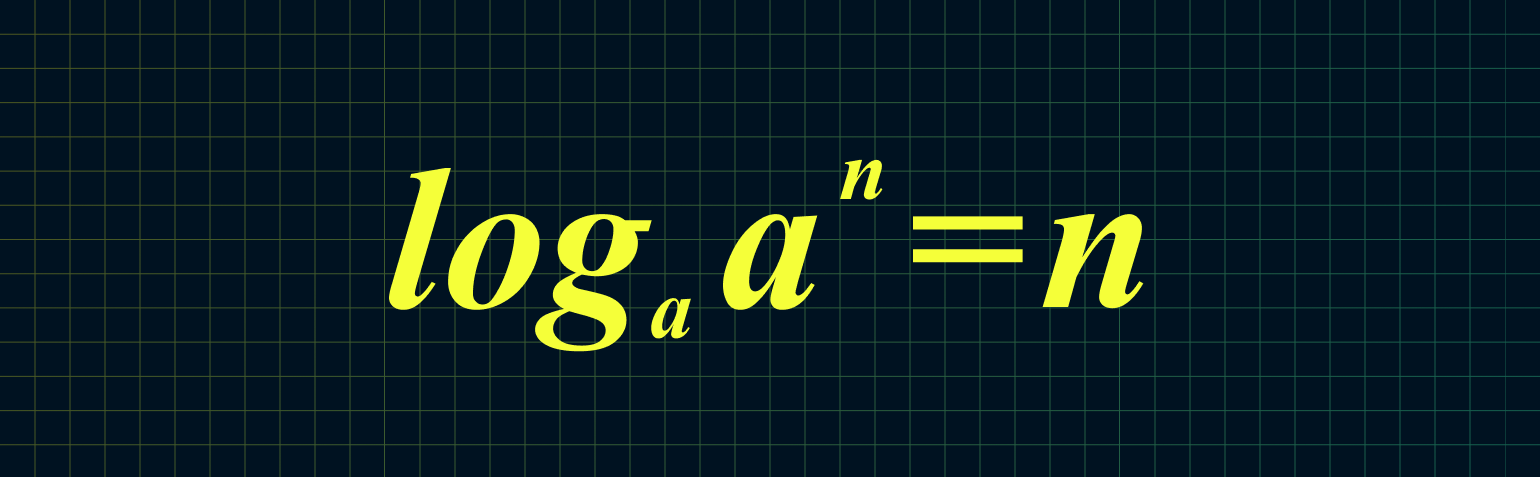
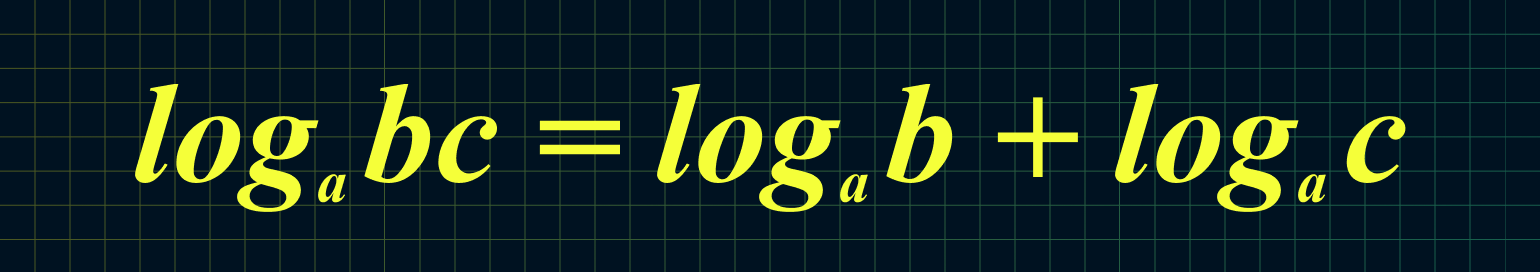
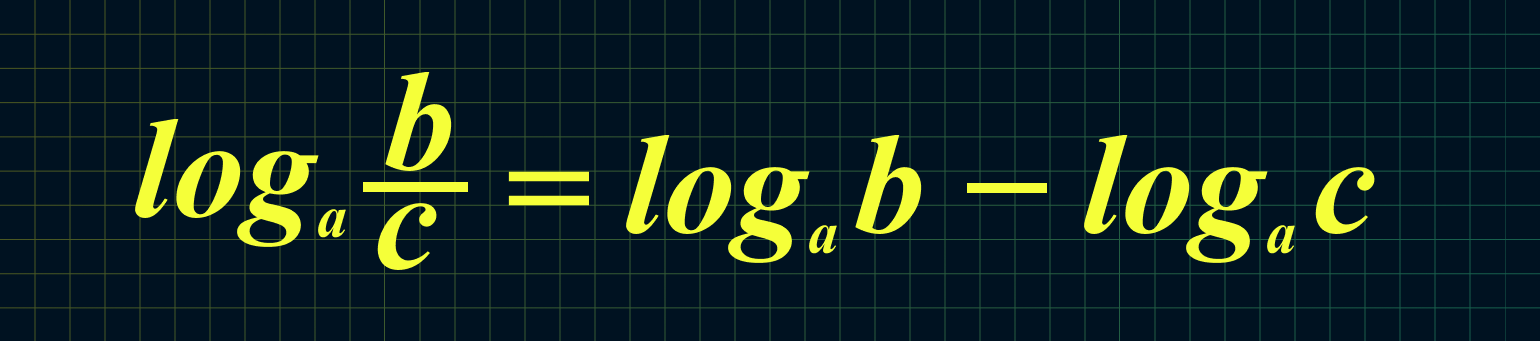
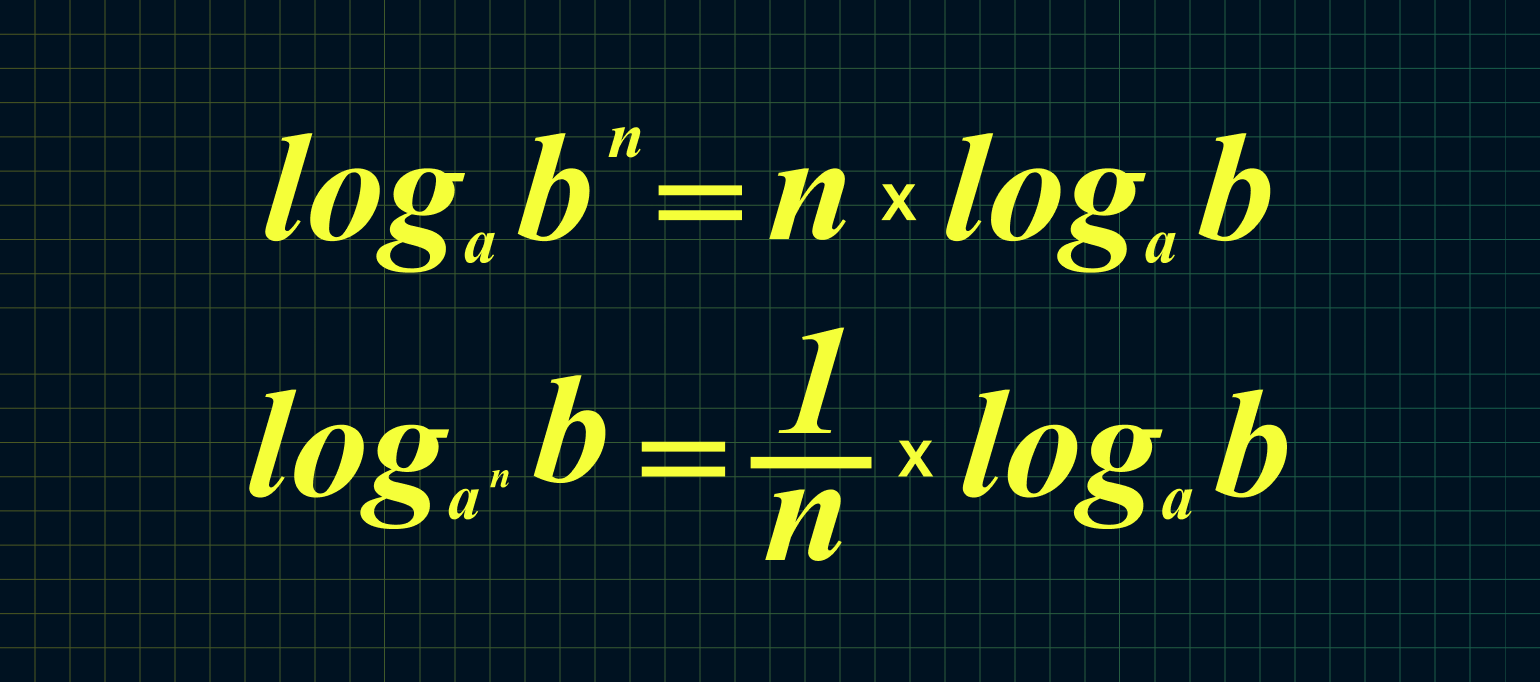
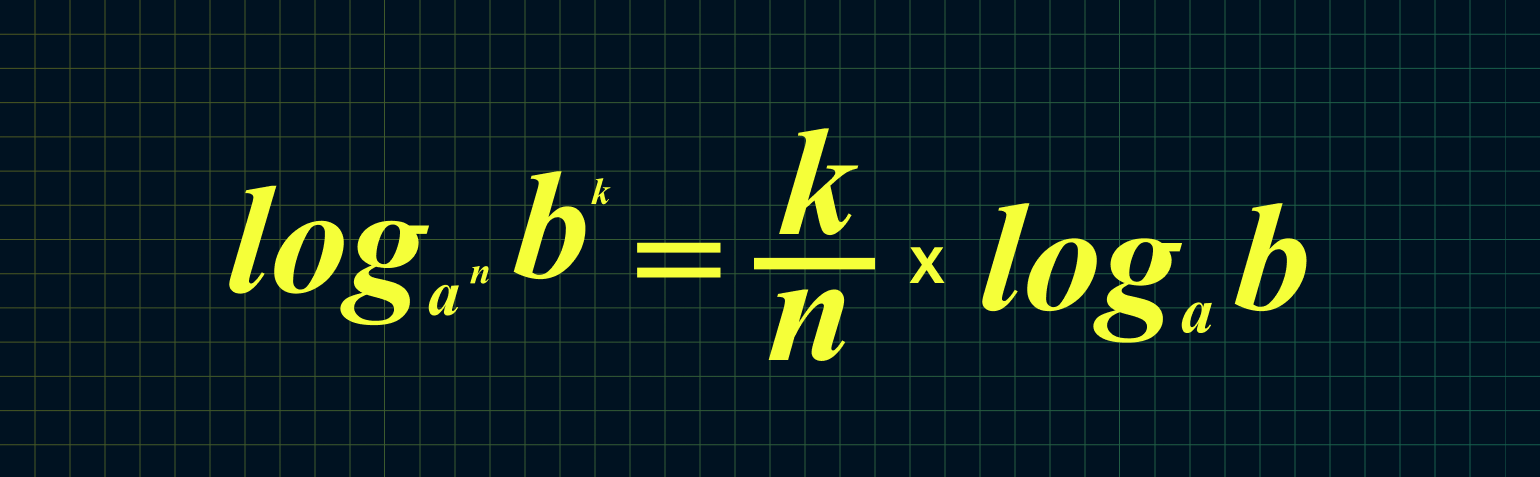
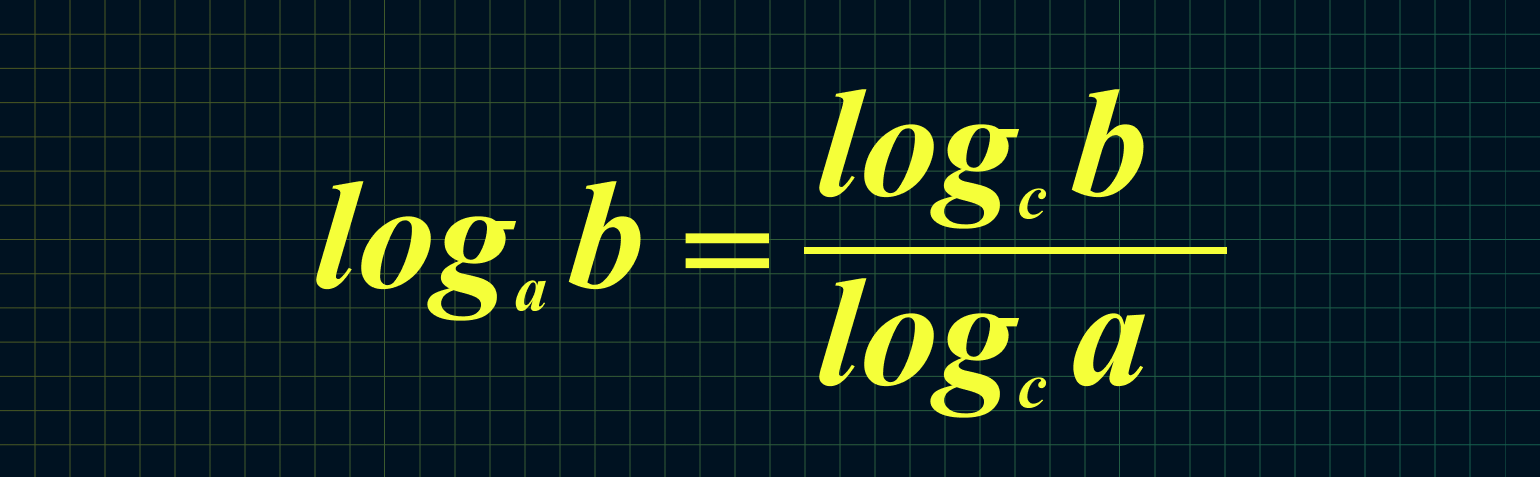
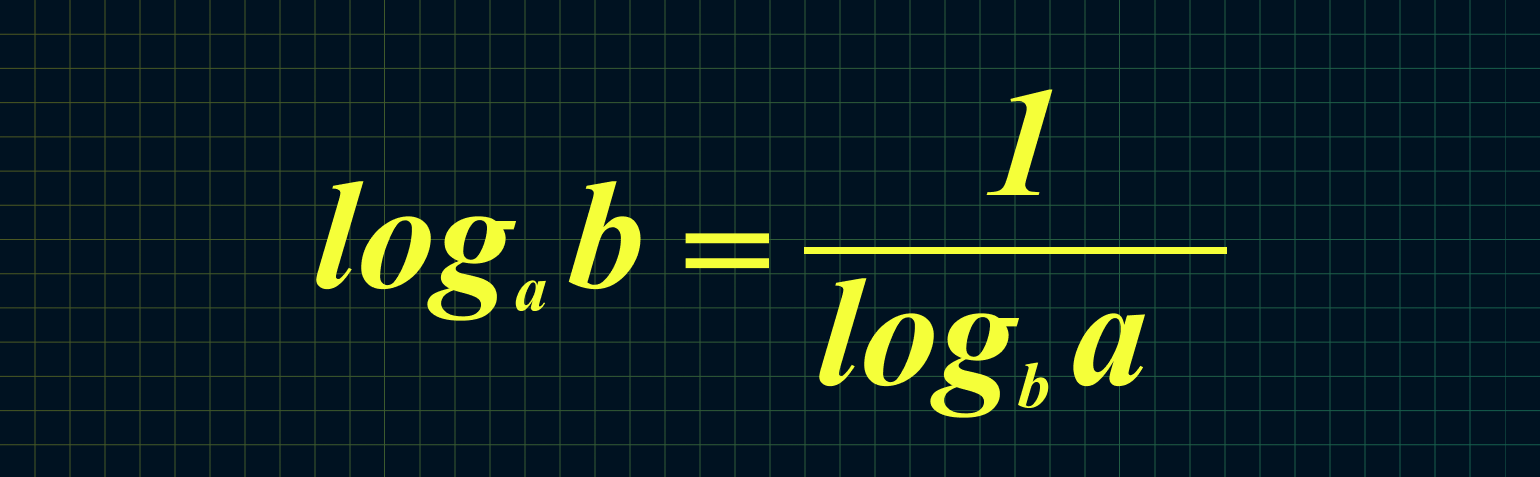
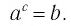
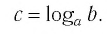
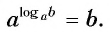
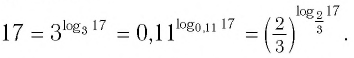
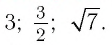
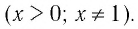
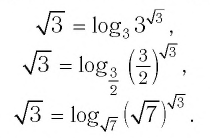
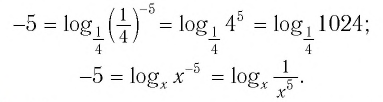
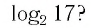
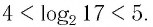
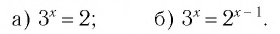
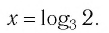
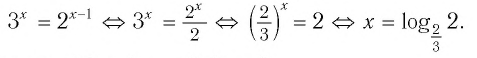
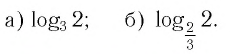
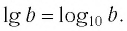
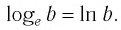
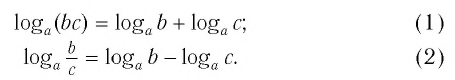
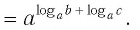
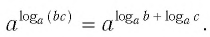
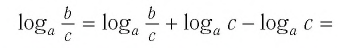
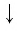
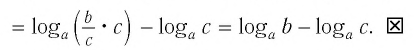

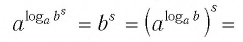
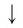
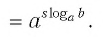
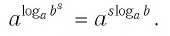

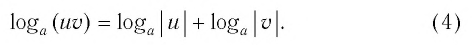
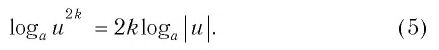
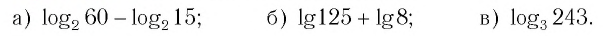
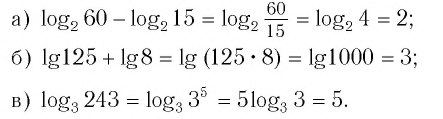
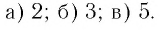

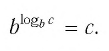
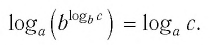
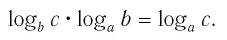

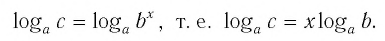
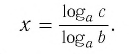
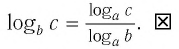

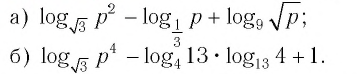
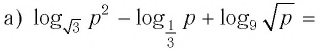
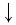
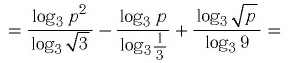
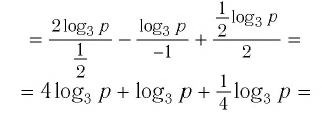
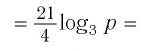
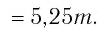
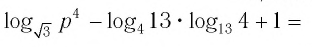
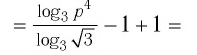
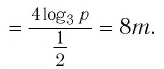
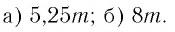

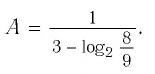
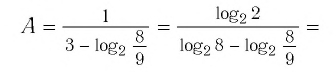
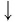
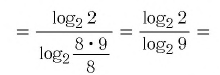
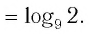
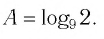
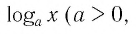
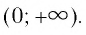
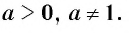
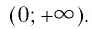
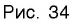
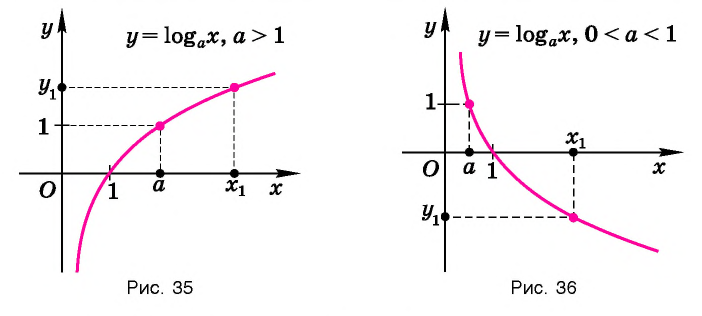
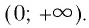
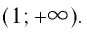 И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале
И при 0 < а < 1 логарифмическая функция принимает отрицательные значения на интервале 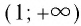 и принимает положительные значения на интервале (0; 1).
и принимает положительные значения на интервале (0; 1).