Как решение найти полный дифференциал функции - Исправление недочетов и поиск решений вместе с Examum.ru

Заказать задачи по любым предметам можно здесь от 10 минут

Полный дифференциал функции

Как найти?

Постановка задачи

Найти полный дифференциал функции двух переменных $ z = f(x,y) $

План решения

Формула полного дифференциала функции записывается следующим образом:

$$ dz = f’_x (x,y) dx + f’_y (x,y) dy $$

Находим первые частные производные функции $ z = f(x,y) $
Подставляя полученные производные $ f’_x $ и $ f’_y $ в формулу, записываем ответ

Примеры решений

Пример 1

Найти полный дифференциал функции двух переменных $ z = 2x + 3y $

Решение

Находим частные производные первого порядка:

$$ f’_x = 2 $$ $$ f’_y = 3 $$

Подставляем полученные выражения в формулу полного дифференциала и записываем ответ:

$$ dz = 2dx + 3dy $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ dz = 2dx + 3dy $$

Пример 2

Найти полный дифференциал функции нескольких переменных $ u = xyz $

Решение

Так как функция состоит из трёх переменных, то в формуле полного дифференциала функции необходимо это учесть и добавить третье слагаемое $ f’_z dz $:

$$ du = f’_x dx + f’_y dy + f’_z dz $$

Аналогично как и в случае функции двух переменных находим частные производные первого порядка:

$$ u’_x = yz $$ $$ u’_y = xz $$ $$ u’_z = xy $$

Используя формулу записываем ответ:

$$ du = yzdx + xzdy + xydz $$

Ответ

$$ du = yzdx + xzdy + xydz $$

Пример 3

Вычислить значение полного дифференциала функции $ z = x^3+y^4 $, при $ x = 1 $, $ y = 2 $, $ dx = 0.03 $ и $ dy = -0.01 $

Решение

Берем частные производные первого порядка:

$$ z’_x = 3x^2 $$ $$ z’_y = 4y^3 $$

Воспользовавшись формулой составляем полный дифференциал:

$$ dz = 3x^2 dx + 4y^3 dy $$

Из условия задачи известны все переменные для вычисления значения дифференциала. Подставив их и вычислим значение:

$$ dz = 3cdot 1^2 cdot 0.03 + 4 cdot 2^3 cdot (-0.01) = 0.09 — 0.32 = -0.23 $$

Ответ

$$ dz = -0.23 $$

Источник

При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции.

Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.

Понятие и геометрический смысл дифференциала

Пусть y = f (x) имеет производную не равную нулю.

Применяя свойства предела функции, получают равенство.

После умножения обеих частей на приращение аргумента Δx, образуется тождество:

в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.

Определение 1

Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)). Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x.

Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.

Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.

Определение 2

Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.

Формы записи дифференциала

Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:

dx = Δx

Отсюда получается формула:

dy = f'(x)dx

Для второго порядка вводится обозначение d2y.

Свойства дифференциала

Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:

Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически:

Полный дифференциал функции

Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.

Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых. Например, если z = f(x;y) то

Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.

Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.

Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.

Источник: https://nauka.club/matematika/algebra/differentsial-funktsii.html

Дифференциальные уравнения в полных дифференциалах

Дифференциальным уравнением в полных дифференциалах называется уравнение вида:

P(x,y)dx + Q(x,y)dy = 0, где левая часть является полным дифференциалом какой-либо функции двух переменных.

Обозначим неизвестную функцию двух переменных (её-то и требуется найти при решении уравнений в полных дифференциалах) через F и скоро вернёмся к ней. Первое, на что следует обратить внимание: в правой части уравнения обязательно должен быть нуль, а знак, соединяющий два члена в левой части, должен быть плюсом.

Второе — должно соблюдаться некоторое равенство, которое является подтверждением того, что данное дифференциальное уравнение является уравнением в полных дифференциалах.

Эта проверка является обязательной частью алгоритма решения уравнений в полных дифференциалах (он во втором параграфе этого урока), так процесс поиска функции F достаточно трудоёмкий и важно на начальном этапе убедиться в том, что мы не потратим время зря.

Итак, неизвестную функцию, которую требуется найти, обозначили через F. Сумма частных дифференциалов по всем независимым переменным даёт полный дифференциал. Следовательно, если уравнение является уравнением в полных дифференциалах, левая часть уравнения представляет собой сумму частных дифференциалов. Тогда по определению:

dF = P(x,y)dx + Q(x,y)dy.

Вспоминаем формулу вычисления полного дифференциала функции двух переменных:

Решая два последних равенства, можем записать:

Первое равенство дифференцируем по переменной «игрек», второе — по переменной «икс»:

Так как, получим, что является условием того, что данное дифференциальное уравнение действительно представляет собой уравнение в полных дифференциалах.

Алгоритм решения дифференциальных уравнений в полных дифференциалах

Шаг 1. Убедиться, что уравнение является уравнением в полных дифференциалах. Для того, чтобы выражение было полным дифференциалом некоторой функции F(x, y), необходимо и достаточно, чтобы . Иными словами, нужно взять частную производную по x одного слагаемого в левой части выражения и частную производную по y другого слагаемого и, если эти производные равны, то уравнение является уравнением в полных дифференциалах.

Шаг 2. Записать систему уравнений из частных производных, составляющих функцию F:

Шаг 3. Проинтегрировать первое уравнение системы — по x (y остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F:

, где — пока неизвестная функция от y.

Альтернативный вариант (если так интеграл найти проще) — проинтегрировать второе уравнение системы — по y (x остаётся константой и выносится за знак интеграла). Таким образом так же восстанавливается функция F:

, где — пока неизвестная функция от х.

Шаг 4. Результат шага 3 (найденный общий интеграл) продифференцировать по y (в альтернативном варианте — по x) и приравнять ко второму уравнению системы:

а в альтернативном варианте — к первому уравнению системы:

Из полученного уравнения определяем (в альтернативном варианте ).

Шаг 5. Результат шага 4 интегрировать и найти (в альтернативном варианте найти ).

Шаг 6. Результат шага 5 подставить в результат шага 3 — в восстановленную частным интегрированием функцию F. Произвольную постоянную C чаще записывают после знака равенства — в правой части уравнения. Таким образом получаем общее решение дифференциального уравнения в полных дифференциалах. Оно, как уже говорилось, имеет вид F(x, y) = C.

Источник: https://function-x.ru/differential_equations5.html

Источник

Простое объяснение принципов решения дифференциала функции и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения дифференциала функции

Дифференциалом функции называется произведение её производной и дифференциала независимой переменной

Для вычисления дифференциалов используются свойства дифференциалов, а также таблица их значений.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Примеры решения дифференциала функции

Задача

Найти дифференциал функции $y = 3x^{2} - sin(1 + 2x)$

Решение

Найдём производную данной функции.

Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :

Ответ

Задача

Найти дифференциал функции $y = ln(1 + e^{10x}) + sqrt{x^{2} + 1}$

Решение

Найдём производную данной функции.

$[y' = frac{10e^{10x}}{1 + e^{10x}} + frac{x}{sqrt{x^{2} + 1}}]$

Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :

$[dy = left(frac{10e^{10x}}{1 + e^{10x}} + frac{x}{sqrt{x^{2} + 1}}right)dx]$

Ответ

$[dy = left(frac{10e^{10x}}{1 + e^{10x}} + frac{x}{sqrt{x^{2} + 1}}right)dx]$

Задача

Найти дифференциал функции

Решение

Найдём производную данной функции.

Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :

Ответ

Задача

Найти дифференциал функции $y = sqrt{{sin}^2 x + 3{cos}^3 4x}$

Решение

Найдём производную данной функции.

В этом примере квадратный корень извлекается из суммы ${sin}^2 x + 3{cos}^3 4x$ . Поэтому сначала вычисляем производную от квадратного корня, а затем умножаем ее на производную от подкоренного выражения:
$y' = frac{1}{2sqrt{{sin}^2 x + 3{cos}^3 4x}}[2sin xcos x + 3cdot3{cos}^2 4xcdot(-sin 4x)cdot4]$

Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :

$dy = (frac{1}{2sqrt{{sin}^2 x + 3{cos}^3 4x}}[2sin xcos x + 3cdot3{cos}^2 4xcdot(-sin 4x)cdot4])dx$

Ответ

$dy = (frac{1}{2sqrt{{sin}^2 x + 3{cos}^3 4x}}[2sin xcos x + 3cdot3{cos}^2 4xcdot(-sin 4x)cdot4])dx$

Задача

Найти дифференциал функции $y = e^{sqrt{sin x}}$

Решение

Найдём производную данной функции.

По правилам дифференцирования показательной функции с основанием , производная этой функции равна произведению самой функции на производную функции, являющейся показателем степени:
$y' = e^{sqrt{sin x}}cdotfrac{1}{2sqrt{sin x}}cdotcos x$

Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :

$dy = e^{sqrt{sin x}}cdotfrac{1}{2sqrt{sin x}}cdotcos xdx$

Ответ

$dy = e^{sqrt{sin x}}cdotfrac{1}{2sqrt{sin x}}cdotcos xdx$

Задача

Найти дифференциал функции $y = e^{sin2x}$

Решение

Найдём производную данной функции.

$y' = 2e^{sin2x}cdotcos2x$

Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :

$dy = (2e^{sin2x}cdotcos2x)dx$

Ответ

$dy = (2e^{sin2x}cdotcos2x)dx$

Задача

Найти дифференциал функции $y = frac{sin x}{cos x}$

Решение

Найдём производную данной функции.

По правилу вычисления производной от дроби, получаем:

$[y' = frac{cos^{2}x + sin^{2}x}{cos^{2}x} = frac{1}{cos^{2}x}]$

Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :

$dy = frac{1}{cos^{2}x}dx$

Ответ

$dy = frac{1}{cos^{2}x}dx$

Задача

Найти дифференциал функции $y = tg {x^{3}}$

Решение

Найдём производную данной функции.

Функция $tg {x^{3}}$ является сложной, поэтому процесс нахождения производной будет происходить в два этапа.

Обозначим $x^{3} = u$ . Исходная функция примет следующий вид:

Найдём её производную по таблице основных тригонометрических функций:

${y_{u}}' = frac{1}{cos^{2}{u}}$

Далее найдём производную ${u_{x}}'$ :

${u_{x}}' = 3x^{2}$

Производная сложной функции будет равна произведению ${y_{u}}' = frac{1}{cos^{2}{u}}$ и ${u_{x}}' = 3x^{2}$ :

${y_{x}}' = {z_{u}}'cdot{{u_{x}}'} = frac{1}{cos^{2}{u}}cdot{3x^{2}} = frac{3x^{2}}{cos^{2}{(x^{3})}}$

Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :

$dy = frac{3x^{2}}{cos^{2}{(x^{3})}}dx$

Ответ

$dy = frac{3x^{2}}{cos^{2}{(x^{3})}}dx$

Пример 9

Задача

Найти дифференциал функции

Решение

Найдём производную данной функции.

Данная функция является сложной, т.к. подкоренным выражением является функция синус.

Найдём производную данной функции, как произведение производных корня и синуса:

$(sqrt{sin{x}})' = frac{1}{2sqrt{sin{x}}}$

Окончательно получаем:

$[(sqrt{sin{x}})' = frac{1}{2sqrt{sin{x}}}cos{x}]$

Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :

$dy = frac{1}{2sqrt{sin{x}}}cos{x}dx$

Ответ

$dy = frac{1}{2sqrt{sin{x}}}cos{x}dx$

Задача

Найти дифференциал функции $z = cos{sqrt{frac{1}{1 + x}}}$

Решение

Найдём производную данной функции.

Процесс нахождения произвоной данной функции будет происходить в три этапа: на первом этапе требуется определить производную функции косинус, на втором – производную от корня, на третьем – производную от дроби подкоренного выражения.

Найдём производную $(cos{sqrt{frac{1}{1 + x}}})'$

По таблице производных определяем, что $(cos{sqrt{frac{1}{1 + x}}})' = -sin{sqrt{frac{1}{1 + x}}}$

Т.к. аргумент косинуса сам является функцией от , то необходимо найти его производную по :
$(sqrt{frac{1}{1 + x}})' = frac{1}{2sqrt{frac{1}{1 + x}}}$

Подкоренное выражение является дробью, поэтому необходимо также найти производную этой дроби $(frac{1}{1 + x})'$ :

$(frac{1}{1 + x})' = -frac{1}{(1 + x)^2}$

Перемножая найденные производные, получаем окончательный результат:

$(cos{sqrt{frac{1}{1 + x}}})' = -sin{sqrt{frac{1}{1 + x}}}cdot{frac{1}{2sqrt{frac{1}{1 + x}}}}cdot{(-frac{1}{(1 + x)^2})} = -sin{sqrt{frac{1}{1 + x}}}cdot{frac{sqrt{1 + x}}{2}}cdot{(-frac{1}{(1 + x)^2})} = sin{sqrt{frac{1}{1 + x}}}cdot{(frac{sqrt{1 + x}}{2(1 + x)^2})} = sin{sqrt{frac{1}{1 + x}}}cdot{frac{1}{2}}cdot{(1 + x)^{-frac{3}{2}}} = sin{sqrt{frac{1}{1 + x}}}cdot{frac{1}{2cdot{(1 + x)^{frac{3}{2}}}}}$

Дифференциал будет равен произведению данной функции на дифференциал независимого аргумента :

$[dy = sin{sqrt{frac{1}{1 + x}}}cdot{frac{1}{2cdot{(1 + x)^{frac{3}{2}}}}}dx]$

Ответ

$[dy = sin{sqrt{frac{1}{1 + x}}}cdot{frac{1}{2cdot{(1 + x)^{frac{3}{2}}}}}dx]$

Источник

Ирина Алексеевна Антоненко

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение 1

Если для каждой пары $(x,y)$ значений двух независимых переменных из некоторой области ставится в соответствие определенное значение $z$, то говорят, что $z$ является функцией двух переменных $(x,y)$. Обозначение: $z=f(x,y)$.

В отношении функции $z=f(x,y)$ рассмотрим понятия общего (полного) приращения функции и полного дифференциала.

Пусть дана функция $z=f(x,y)$двух независимых переменных $(x,y)$.

Если аргументу $x$ дать приращение $Delta x$, а аргументу $y$ — приращение $Delta y$, то получается полное приращение заданной функции $z=f(x,y)$. Обозначение:

Пример 1

Записать полное приращение заданной функции

[z=x+y.]

Решение:

По определению полного приращения некоторой функции найдем:

$Delta z=x+Delta x+y+Delta y$ — полное приращение функции $z=f(x,y)$.

Пример 2

Вычислить полное приращение заданной функции $z=xy$ в точке $(1;2)$ при $Delta x=0,1;, , Delta y=0,1$.

Решение:

По определению полного приращения некоторой функции найдем:

$Delta z=(x+Delta x)cdot (y+Delta y)$ — полное приращение функции $z=f(x,y)$.

Следовательно,

[Delta z=(1+0,1)cdot (2+0,1)=1,1cdot 2,1=2,31.]

Определение 2

Если для каждой тройки $(x,y,z)$ значений трех независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией трех переменных $(x,y,z)$ в данной области.

Обозначение: $w=f(x,y,z)$.

Определение 3

Если для каждой совокупности $(x,y,z,…,t)$ значений независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией переменных $(x,y,z,…,t)$ в данной области.

Обозначение: $w=f(x,y,z,…,t)$.

«Полное приращение и полный дифференциал» 👇

Для функции трех и более переменных, аналогично как для функции двух переменных определяются полное приращение:

Пример 3

Записать полное приращение заданной функции

[w=(x+y)cdot z.]

Решение:

По определению полного приращения некоторой функции найдем:

$Delta w=((x+Delta x)+(y+Delta y))cdot (z+Delta z)$ — полное приращение функции $w=f(x,y,z)$.

Пример 4

Вычислить полное приращение заданной функции $w=xyz$ в точке $(1;2;1)$ при $Delta x=0,1;, , Delta y=0,1;, , Delta z=0,1$.

Решение:

По определению полного приращения некоторой функции найдем:

$Delta w=(x+Delta x)cdot (y+Delta y)cdot (z+Delta z)$ — полное приращение функции $w=f(x,y,z)$.

Следовательно,

[Delta z=(1+0,1)cdot (2+0,1)cdot (1+0,1)=1,1cdot 2,1cdot 1,1=2,541.]

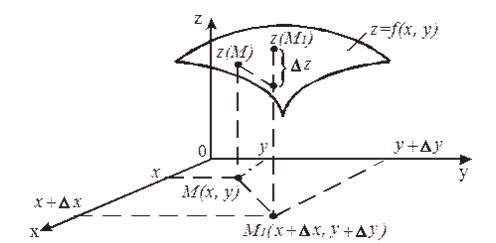
С геометрической точки зрения полное приращение функции $z=f(x,y)$ (по определению $Delta z=f(x+Delta x,y+Delta y)-f(x,y)$) равно приращению аппликаты графика функции $z=f(x,y)$ при переходе от точки $M(x,y)$ к точке $M_{1} (x+Delta x,y+Delta y)$ (рис. 1).

Рисунок 1.

Определение 4

Полный дифференциал заданной функции $z=f(x,y)$ является линейной частью приращения функции и записывается в виде

[dz=f’_{x} (x,y)cdot Delta x+f’_{y} (x,y)cdot Delta y.]

Пример 5

Записать полный дифференциал заданной функции

[z=x+2y.]

Решение:

Определим частные производные заданной функции:

[f’_{x} (x,y)=1,, , f’_{y} (x,y)=2.]

По определению полного дифференциала некоторой функции найдем:

[dz=1cdot Delta x+2cdot Delta y=Delta x+2cdot Delta y.]

Пример 6

Вычислить полный дифференциал заданной функции $z=xy$ в точке $(1;2)$ при $Delta x=0,1;, , Delta y=0,1$.

Решение:

Определим частные производные заданной функции:

[f’_{x} (x,y)=y,, , f’_{y} (x,y)=x.]

По определению полного дифференциала некоторой функции найдем:

[dz=ycdot Delta x+xcdot Delta y.]

Следовательно,

[dz|_{(1,2)} =2cdot 0,1+1cdot 0,1=0,2+0,1=0,3.]

Для функции трех и более переменных, аналогично как для функции двух переменных определяются полный дифференциал:

[dw=f’_{x} (x,y,z)cdot Delta x+f’_{y} (x,y,z)cdot Delta y+f’_{z} (x,y,z)cdot Delta z,] [dw=f’_{x} (x,y,z,…,t)cdot Delta x+f’_{y} (x,y,z,…,t)cdot Delta y+…+f’_{t} (x,y,z,…,t)cdot Delta t.]

Пример 7

Записать полный дифференциал заданной функции

[w=(x+y)cdot z.]

Решение:

Определим частные производные заданной функции:

[f’_{x} (x,y,z)=z,, , f’_{y} (x,y,z)=z,, , , f’_{z} (x,y,z)=x+y.]

По определению полного дифференциала некоторой функции найдем:

[dz=zcdot Delta x+zcdot Delta y+(x+y)cdot Delta z.]

Определение 5

Приращения независимых переменных, а именно, $Delta x,, , Delta y,, , Delta z,…,Delta t$ называют дифференциалами независимых переменных $x,y,z,…,t$. Обозначение: $dx,dy,dz,…,dt$.

В новых обозначениях выражения для полного дифференциала принимает следующий вид:

Замечание 1

Функция, имеющая непрерывные частные производные в заданной точке, является дифференцируемой в данной точке, при этом полный дифференциал функции в данной точке равен сумме произведений частных производных на дифференциалы независимых переменных соответственно.

Пример 8

Записать полный дифференциал заданной функции

[w=xcdot z.]

Решение:

Определим частные производные заданной функции:

[f’_{x} (x,y,z)=z,, , f’_{y} (x,y,z)=0,, , , f’_{z} (x,y,z)=x.]

По определению полного дифференциала некоторой функции найдем:

[dz=zcdot dx+0cdot dy+xcdot dz=zcdot dx+xcdot dz.]

Пример 9

Записать полный дифференциал заданной функции $z=xy$ в точке $(1;2)$.

Решение:

Определим частные производные заданной функции:

[f’_{x} (x,y)=y,, , f’_{y} (x,y)=x.]

По определению полного дифференциала некоторой функции найдем:

[dz=ycdot dx+xcdot dy.]

Запишем полный дифференциал в заданной точке:

[dz|_{(1,2)} =2cdot dx+1cdot dy=2dx+dy.]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Полный дифференциал | это… Что такое Полный дифференциал?
- Содержание
- Неформальное описание
- Определения
  - Для функций
  - Для отображений
- Связанные определения
- Свойства
- Примеры
- История
- См. также
  - Полезное
2.2. Полный дифференциал функции двух и трех переменных.
Исчисление III — Дифференциалы
- - Раздел 13.5: Дифференциалы
многомерное исчисление — В чем именно разница между производной и полной производной?
- Еще один способ сделать то же самое:

Полный дифференциал | это… Что такое Полный дифференциал?

ТолкованиеПеревод

Полный дифференциал

Дифференциа́л в математике — линейная часть приращения функции или отображения. Это понятие тесно связанное с понятием производной по направлению.

Обычно дифференциал f обозначается df, а его значение в точке x обозначается d_xf.

Содержание

1 Неформальное описание
2 Определения
- 2.1 Для функций
- 2.2 Для отображений
3 Связанные определения
4 Свойства
5 Примеры
6 История
7 См. также

Неформальное описание

Рассмотрим гладкую функцию f(x). Проведем касательную к ней в точке x, и отложим на этой касательной отрезок, такой длины, чтобы его проекция на ось

x была равна Δx. Проекция этого отрезка на ось y называется дифференциалом функции f(x) в точке x от Δx. Таким образом, дифференциал может пониматься как функция двух переменных x и Δx,

определяемой соотношением

в частности, разность приращения функции и её дифференциала — бесконечно малая величина:

f(x + Δx) = f(x) + d_xf(Δx) + o(Δx).

Определения

Для функций

Дифференциал гладкой вещественнозначной функции f определённой на M (M — область в или гладкое многообразие) представляет собой 1-форму и обычно обозначается df и определяется соотношением

где обозначает производную f по направлению вектора X в касательном расслоении M.

Для отображений

Дифференциал гладкого отображения из гладкого многообразия в многообразие есть отображение между их касательными расслоениями, , такое что для любой гладкой функции имеем

где Xf обозначает производную f по направлению X. (В левой части равенства берётся производная в N функции g по dF(X) в правой — в M функции по X).

Это понятие естественно обобщает дифференциал функции.

Связанные определения

Гладкое отображение называется субмерсией, если для любой точки , дифференциал сюръективен.
Гладкое отображение называется гладким погружением, если для любой точки , дифференциал инъективен.

Свойства

Дифференциал композиции равен композиции дифференциалов:

или

Примеры

Пусть в открытом множестве задана гладкая функция . Тогда df = f‘dx, где f‘ обозначает производную f, а dx является постоянной формой определяемой dx(V) = V.
Пусть в открытом множестве задана гладкая функция . Тогда . Форма dx_i может быть определена соотношением dx_i(V) = v_i, для вектора .
Пусть в открытом множестве задано гладкое отображение . Тогда
d_xF(v) = J(x)v,
где J(x) есть матрица Якоби отображения F в точке x.

История

Термин Дифференциал (от лат. differentia — разность, различие) введён Лейбницем. Изначально,

dx применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю. Подобный взгляд оказался неудобным в большинстве разделов математики (за исключением нестандартного анализа).

См. также

Внешний дифференциал

Wikimedia Foundation.
2010.

Игры ⚽ Нужно решить контрольную?

Полный Пэ (студия)
Полный дуплекс

Полезное

2.2. Полный дифференциал функции двух и трех переменных.

Линеаризация
функции двух и трех переменных.
Использование полного дифференциала
в приближенных вычислениях.

Сведения из теории

Из теории функций
двух переменных известно, что, если
функция
имеет в точке
непрерывные частные производные
и
,
то ее приращение
,
порожденное приращениями переменных
и
,
представимо в виде
.

Символ
означает, что, если
и
стремятся к нулю, то слагаемое
стремится к нулю еще быстрее. Если это
слагаемое отбросить, то получится
приближенное равенство

Выражение, которое
осталось справа, называется полным
дифференциалом
функции двух переменных
.
Обозначение
.
Если символы
и
заменить символами
и
, называемые дифференциалами
и
,
то полный дифференциал примет вид
.

Из определения
полного дифференциала следует, что для
любой фиксированной точки
разница между точным приращением функции
,
порожденным приращениями
и
,
и дифференциалом
,
вычисленным в точке
,
есть величина бесконечно малая, т.е.
.
Отсюда следует цепочка приближенных
равенств :



Если
обозначить
,
,
соответственно
,
,
то приближенная формула примет вид

Поясним смысл этой
формулы: исходная функция
с произвольной формулой
в окрестности точки
заменяется на линейную функцию двух
переменных вида
.
Главное достоинство последней функции

простота вычисления. Для этой замены
есть название

линеаризация
функции.

Геометрически
линеаризация функции двух переменных
означает замену ординаты поверхности,
являющейся графиком функции
,
на ординату касательной плоскости,
проведенной к графику функции, в точке
.

Для функции трех
переменных
полный дифференциал имеет вид
.
Линеаризация функции трех переменных
в окрестности точки
задается следующим приближенным
равенством

Рассмотрим на
примере, как линеаризация функции
используется для приближенного вычисления
значений функции при «неудобных»
значениях переменных.

Пример.
Вычислить приближённо с помощью полного
дифференциала значение выражения
.

Решение. Прежде
всего, нужно ввести функцию, частным
значением которой является искомое
выражение. В данном примере это будет
функция трех переменных
.
Искомое выражение является ее значением
при
.
Далее нужно подобрать значения
,
,
такие, чтобы они, во-первых, были близки
к
,
,
и, во-вторых, значение функции
вычислялось легко. Таковыми являются
,
,
.
Легко вычислить
.
Линеаризацию функции
нужно проводить в окрестности точки
.
Для этого вычислим значения частных
производных в точке
.

;

Формула линеаризации
функции имеет вид:

Тогда
.

Ответ.
.

Сведения из теории

Напомним, что
экстремумы бывают двух типов максимумы
и минимумы. Экстремумы характеризуют
функцию локально, только в окрестности
некоторой точки. Это вытекает из самого
определения экстремума.

Определение.
Говорят,
что функция двух переменных
имеет максимум ( минимум ) в точке
,
если существует окрестность этой точки,
для всех точек
которой выполняется неравенство
(соответственно для минимума
).

Доказано, что
функция
может принимать максимум или минимум
только в тех точках, в которых
и
или эти частные производные не существуют.
Известно также, что условие
еще не гарантирует наличие экстремума
в точке
.
Для этого еще должны выполняться так
называемые достаточные условия
экстремума. Они формулируются в виде
теоремы.

Теорема
(достаточные условия экстремума)

Пусть в точке
частные
производные
или эти частные производные не существуют.
Вычислим для этой точки три числа:
.
По ним вычислим выражение
.
Тогда:

если
,
то экстремум есть, при этом, если число
,
то минимум, а если
,
то максимум;
если
,
то экстремума нет;
если
,
для исследования функции на экстремум
нужны дополнительные исследования с
использованием частных производных
более высокого порядка.

Пример.
Исследовать на экстремумы функцию
.

Решение.

Прежде всего,
найдем точки, в которых
частные
производные
и
равны нулю:
.
Система имеет два решения
и
.

Далее найдем
формулы частных производных 2-го порядка.

Сначала исследуем
достаточные условия для точки
.

Вычислим
,
следовательно, в точке
экстремума нет.

Теперь исследуем
достаточные условия для точки
.

Вычислим
,
следовательно, в точке
экстремум есть. Так как
,
то минимум. Вычислим его

Ответ.
.

Исчисление III — Дифференциалы

Показать мобильное уведомление
Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.

е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 13.5: Дифференциалы

Это очень короткий раздел, и он здесь просто для того, чтобы признать, что точно так же, как у нас были дифференциалы для функций одной переменной, мы также имеем их для функций более чем одной переменной. Кроме того, как мы уже видели в предыдущих разделах, когда мы переходим к более чем одной переменной, все работает практически одинаково, но есть небольшие отличия.

Для заданной функции (z = fleft( {x,y} right)) дифференциал (dz) или (df) определяется выражением,

[dz = {f_x},dx + {f_y},dyhspace{0.5in}{mbox{or}}hspace{0. 5in}df = {f_x},dx + {f_y}, dy]

Существует естественное расширение функций трех и более переменных. Например, для данной функции (w = gleft({x,y,z} right)) дифференциал определяется как

[dw = {g_x},dx + {g_y},dy + {g_z},dz]
93}}}дс]

Обратите внимание, что иногда эти дифференциалы называются общими дифференциалами .

многомерное исчисление — В чем именно разница между производной и полной производной?

Все ли согласны с тем, что плакат пришел к правильному ответу?

Люди пишут $$frac{partial}{partial t}g(x(t),t)$$ или $$frac{text{d}}{text{d} t}g( x(t),t)$$

Первое обычно используется для обозначения «производной функции $g$ по второму аргументу». Второй обычно означает «полная производная». Есть вариации на этот счет. Некоторые опускают аргументы и просто пишут, например, $frac{partial}{partial t}g$

Так, например: если $x$ является скрытой функцией $t$, то обозначение $frac{d}{dt}f(x,t)$ называется полной производной и является сокращением для ( производная с одной переменной) $g′(t)$, где $g(t)=f(x(t),t)$. При применении цепного правила к последнему выражению вам понадобится какой-то способ обозначить «производную от f по ее первому аргументу». Многие люди написали бы для этого $frac{partial}{partial x}f$, но во многих случаях это сбивает с толку, как я объясню в примере ниже.

Широко распространенная здесь математическая нотация многих сбивает с толку, и я думаю, что в ней нет необходимости. Если вы хотите взять полную производную, явно создайте функцию (например, $g$ выше) и возьмите производную с одной переменной. В противном случае объяснение разницы между полными и частными производными потребует от вас таких призывов, как временная фиксация переменных или утверждение, что переменная фактически постоянна, или переключение между представлением о $x$ как о функции и как о выражении. Все это нечеткие вещи, которые вы можете успешно делать, когда уже чувствуете себя комфортно в том, что происходит. Но в противном случае стоит хорошенько подумать о том, что происходит на самом деле. 92$. В этом случае многие напишут

$frac{partial}{partial x}w$ и

$frac{partial}{partial x} f(x,y)$

(которые эквивалент). В этом есть смысл. В обоих случаях справа от дифференциального оператора находится выражение, содержащее $x$ и $y$. То, что получается в результате применения этого оператора, также является выражением в тех же переменных. Это также относится к тому, что означает $frac{d}{dx}$. Для конкретных выражений выше я бы просто использовал это. 92$. Переменные, фигурирующие в определении функции, строго говоря, невидимы для остального мира. Это просто удобный способ заявить, что «$f$ — это функция, которая принимает два аргумента. Она возводит в квадрат первый, возводит в квадрат второй и возвращает сумму квадратов». Вместо того, чтобы записывать это предложение (что люди должны были делать, прежде чем изобрести лучшую нотацию), вы можете вместо этого дать имена аргументам $f$, чтобы вы могли легко ссылаться на них при определении $f$.

Но когда вы пишете $frac{partial}{partial x} f$, вы используете некоторое знание того, как вы определили $f$ — что вы выбрали имя $x$ для первого аргумент. Может быть полезно иметь имена для аргументов функции, а не просто ссылаться на их позицию (первый, второй и т. д. аргумент), поэтому частичная нотация сохранилась, но я думаю, что для этого нотация должна быть улучшена.

Когда пишут $frac{partial}{partial x} f$, обычно имеют в виду «функцию, которая принимает два аргумента и возвращает чувствительность $f$ к первому аргументу». Итак, если вы в какой-то момент $(a,b)$ или $(x,y)$ или что-то еще, и вы качаете первый аргумент $a$ или $x$, насколько сильно колеблется вывод $f$ ? Это вопрос, на который должен ответить градиент функции. Вероятно, это то, что кто-то имеет в виду, когда говорит «нормальная производная». Они думают только об одной функции, возможно, с несколькими аргументами. И они пытаются сделать объект, который говорит вам, насколько чувствителен вывод функции к изменению каждого из входов.

Общая производная от обычно означает, что где-то вы неявно определили какие-то новые функции. В этом случае вы составили функции $x(r,theta) = r sin(theta)$ и $y(r,theta) = r cos(theta)$, и вы можете скомпоновать эти функции , создавая новую функцию:
$$g(r,theta) = f(x(r,theta),y(r,theta))$$

Еще раз обратите внимание, что $r$ и $theta$ выбраны только для того, чтобы дать человеческая информация о значении этой функции. Если бы мы обрабатывали вещи чисто символически, то определение $g$ могло бы также быть

$$g(input_1,input_2) = f(x(input_1,input_2),y(input_1,input_2))$$

Итак, когда задача попросила вас найти $frac{partial}{partial r} w$ есть две, в итоге идентичные, интерпретации того, что это значит. Либо создайте функцию $g$, как я сделал выше, и сообщите ее чувствительность по отношению к первому аргументу. ИЛИ подставьте выражения для $x$ и $y$ в выражение для $w$. Теперь у вас есть выражение для $w$ через $r$ и $theta$. Я предпочитаю подход, который думает о функциях. Вот как мы организуем код, и я думаю, что именно так мы должны организовать математику. Когда вы имеете дело с выражениями, у вас фактически есть тонна глобальных переменных.

Так как же нам вычислить $partial_1 g$, что является просто обозначением для «создать функцию с той же арностью (количеством входных данных), что и $g$, так, чтобы она вычисляла производную функции $g$ относительно его первого аргумента»? Это просто цепное правило.

$$[partial_1 g](r,theta) = [partial_1 f](x(r,theta), y(r,theta)) cdot [partial_1 x](r,theta ) + [partial_2 f](x(r,theta), y(r,theta)) cdot [partial_1 y](r,theta)$$

Мы можем понять, почему, размышляя о вещах в этом способ не популярен! Но это самый ясный, самый механический способ думать об этом. В противном случае вы полагаетесь на неявный каламбур $x$ как функции и выражения. Выберите один и придерживайтесь его! 92$ и, следовательно,

$[partial_1 f](x,y) = 2x$
$[partial_2 f](x,y) = 2y$

$x(r,theta) = rsin(theta)$ и, следовательно,

$[partial_1 x](r,theta) = sin(theta)$

аналогично

$[partial_1 y](r,theta) = cos(theta)$

ДАЛЕЕ, хотя в данный момент нам это не нужно

$[partial_2 x](r,theta) = rcdot cos(theta)$
$[partial_2 y](r,theta) = -rcdot sin(theta)$

Итак, снова функция

$$[partial_1 g](r,theta) = [partial_1 f](x(r,theta), y(r,theta)) cdot [ partial_1 x](r,theta) + [partial_2 f](x(r,theta), y(r,theta)) cdot [partial_1 y](r,theta)$$

подстановка функции, которые мы только что вычислили:

$$[partial_1 g](r,theta) = 2x(r,theta) cdot sin(theta) + 2y(r,theta) cdot cos( theta)$$

и подставив $x$ и $y$

$$[partial_1 g](r,theta) = 2rsin(theta) cdot sin(theta) + 2r cos(theta) cdot cos(theta)$$

, что после использования той самой триггерной идентификации, которую вы использовали, равно

$$[partial_1 g](r,theta) = 2r$$

Еще один способ сделать то же самое:

Когда вы видите обозначение $g'(x)$, вы можете сгруппировать это как $[g’](x)$.

Источник