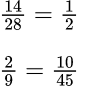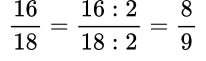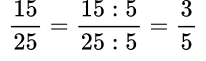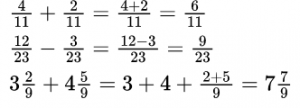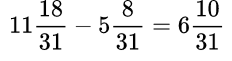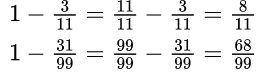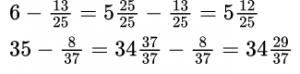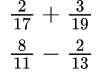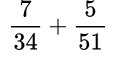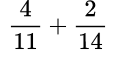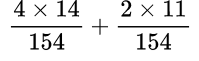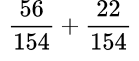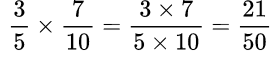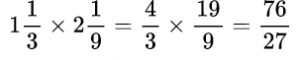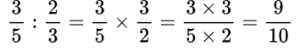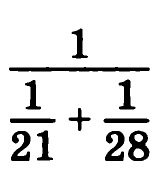Формулировка задачи: Найдите значение выражения (действия с дробями).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 1 (Действия с дробями).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
Найдите значение выражения 5/4 + 7/6 : 2/3.
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. И выполним необходимые действия в нужном порядке:
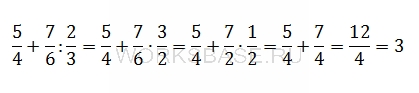
Ответ: 3
Пример задачи 2:
Найдите значение выражения (3,9 – 2,4) ∙ 8,2
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
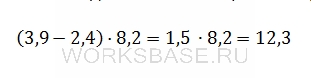
Ответ: 12,3
Пример задачи 3:
Найдите значение выражения 27 ∙ (1/3 – 4/9 – 5/27).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
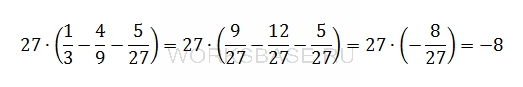
Ответ: –8
Пример задачи 4:
Найдите значение выражения 2,7 / (1,4 + 0,1)
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
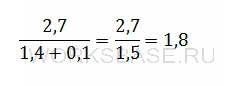
Ответ: 1,8
Пример задачи 5:
Найдите значение выражения 1 / (1/9 – 1/12).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
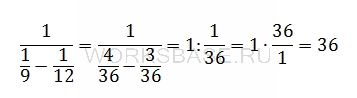
Ответ: 36
Пример задачи 6:
Найдите значение выражения (0,24 ∙ 10^6) / (0,6 ∙ 10^4).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
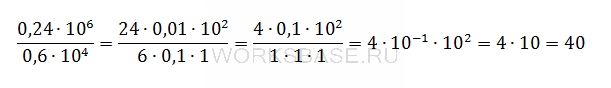
Ответ: 40
Пример задачи 7:
Найдите значение выражения (1,23 ∙ 45,7) / (12,3 ∙ 0,457).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
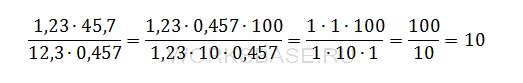
Ответ: 10
Пример задачи 8:
Найдите значение выражения (728^2 – 26^2) : 754.
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке. Также в данном случае нужно применить формулу разности квадратов:
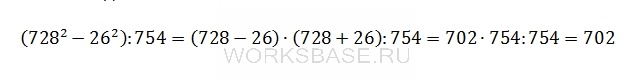
Ответ: 702
Загрузить PDF
Загрузить PDF
Действия с дробями не такие сложные, как кажутся, особенно если знать, что делать. Начните с изучения терминологии и основ, а затем перейдите к сложению, вычитанию, умножению и делению дробей. Как только вы поймете, что такое дроби и как с ними работать, вы будете быстро решать выражения с дробями.
-
1
Обратите внимание, что числитель находится сверху, а знаменатель — снизу. Дробь — это часть целого; верхнее число дроби называется числителем и характеризует данное количество частей целого. Нижнее число дроби называется знаменателем и указывает на количество частей, которые в сумме составляют целое.[1]
- Например, дана дробь 3/5. Здесь 3 — это числитель (то есть даны 3 части целого), а 5 — это знаменатель (то есть целое разделено на 5 частей). Другой пример: дробь 7/8. Здесь 7 — числитель, а 8 — знаменатель.
-
2
Преобразуйте целое число в дробь, записав под ним 1. Если дано целое число, которое нужно преобразовать в дробь, запишите это число в числителе, а в знаменателе запишите 1.[2]
- Например, чтобы преобразовать 7 в дробь, запишите 7/1.
-
3
Упростите дробь. Для этого найдите наибольший общий делитель (НОД) числителя и знаменателя. НОД — это наибольшее число, на которое можно разделить и числитель, и знаменатель. Затем просто разделите числитель и знаменатель на НОД, чтобы упростить дробь.[3]
- Например, дана дробь 15/45. Здесь НОД = 15, поскольку и 15, и 45 делятся на 15. Разделите: 15/15 = 1 — это новый числитель; 45/15 = 3 — это новый знаменатель. Таким образом, дробь 15/45 упрощается до 1/3.
-
4
Научитесь преобразовывать смешанные числа в неправильные дроби. Смешанное число включает целое число и дробь. Чтобы облегчить решение некоторых выражений с дробями, преобразуйте смешанное число в неправильную дробь (в такой дроби числитель больше знаменателя). Для этого умножьте целое число на знаменатель и к полученному результату прибавьте числитель. Теперь запишите полученное число в числителе, а знаменатель оставьте прежним.[4]
- Например, дано смешанное число 1 2/3. Умножьте 3 на 1 и получите 3. Прибавьте 3 к 2 и получите 5 (это новый числитель). Таким образом, 1 2/3 = 5/3.
Совет: преобразуйте смешанные числа в неправильные дроби, если вы их умножаете или делите.
-
5
Научитесь преобразовывать неправильные дроби в смешанные числа. В некоторых задачах неправильную дробь нужно превратить в смешанное число. Для этого разделите числитель на знаменатель — целочисленный результат деления превратится в целую часть смешанного числа, а остаток — в числитель дробной части (при этом знаменатель не изменится). Чтобы найти остаток, умножьте целое число на делитель (знаменатель) и результат вычтите из делимого (числителя). [5]
- Например, дана неправильная дробь 17/4. Разделите: 17 ÷ 4 = 4 ост. 1 (чтобы найти остаток, умножьте 4 * 4 = 16, а затем вычтите 17 – 16 = 1). Таким образом, 17/4 = 4 1/4.
Реклама
-
1
Сложите дроби с общим знаменателем. Для этого просто сложите их числители. Запомните: складывать можно только дроби с одинаковым знаменателем.[6]
- Например, дано выражение 5/9 + 1/9. Здесь просто сложите числители 5 + 1 = 6. Таким образом, 5/9 + 1/9 = 6/9 = 2/3.
-
2
Вычтите дроби с общим знаменателем. Для этого просто вычтите меньший числитель из большего. Запомните: вычитать (как и складывать) можно только дроби с одинаковым знаменателем.[7]
- Например, дано выражение 6/8 — 2/8. Здесь вычтите 6 – 2 = 4. Таким образом, 6/8 — 2/8 = 4/8 = 1/2.
-
3
Найдите общее кратное, чтобы сложить или вычесть дроби с разными знаменателями. Если у дробей разные знаменатели, найдите общее кратное обоих знаменателей и приведите дроби к общему знаменателю. Для этого умножьте числитель и знаменатель на некоторое число, которое приводит дробь к общему знаменателю. Затем сложите или вычтите числители, чтобы решить выражение.[8]
- Например, дано выражение 1/2 + 2/3. Начните с нахождения общего кратного. В нашем примере общее кратное равно 6, потому что 6 делится и на 2, и на 3. Чтобы привести дробь 1/2 к знаменателю 6, умножьте числитель и знаменатель на 3: 1 x 3 = 3 и 2 х 3 = 6; получится новая дробь 3/6. Чтобы привести дробь 2/3 к знаменателю 6, умножьте числитель и знаменатель на 2: 2 x 2 = 4 и 3 x 2 = 6; получится новая дробь 4/6. Теперь сложите числители: 3/6 + 4/6 = 7/6. Поскольку это неправильная дробь, ее можно преобразовать в смешанное число 1 1/6.
- Другой пример: 7/10 — 1/5. Здесь общим кратным является 10, потому что 10 делится на 10 и на 5. Чтобы привести дробь 1/5 к знаменателю 10, умножьте числитель и знаменатель на 2: 1 x 2 = 2 и 5 x 2 = 10; получится новая дробь 2/10. Обратите внимание, что дробь 7/10 уже имеет общий знаменатель. Теперь вычтите числители: 7/10 – 2/10 = 5/10 = 1/2.
-
4
Перемножьте дроби. Для этого просто перемножьте их числители, а затем перемножьте их знаменатели. Если дробь или дроби можно упростить, сделайте это до умножения.[9]
- Например, дано выражение 2/3 * 7/8. Перемножьте числители: 2 * 7 = 14. Затем перемножьте знаменатели: 3 * 8 = 24. Таким образом, 2/3 * 7/8 = 14/24 = 7/12 (если разделить числитель и знаменатель на 2).
-
5
Разделите дробь на дробь. Для этого переверните одну из дробей, а затем перемножьте числители и перемножьте знаменатели. То есть умножьте дробь на обратную дробь. Чтобы найти обратную дробь, поменяйте местами числитель и знаменатель. Теперь перемножьте числители и перемножьте знаменатели.[10]
- Например, дано выражение 1/2 ÷ 1/6. Переверните дробь 1/6 и получите 6/1. Теперь перемножьте: 1 x 6 = 6 (это новый числитель) и 2 x 1 = 2 (это новый знаменатель). Итак, 1/2 ÷ 1/6 = 6/2 = 3.
Реклама
Советы
- Внимательно прочитайте задачу (по крайней мере дважды), чтобы понять, что в ней нужно найти.
- Спросите у учителя, нужно ли преобразовывать неправильные дроби в смешанные числа и/или упрощать дроби.
- Чтобы найти обратное значение целого числа, запишите это число под 1. Например, 5 превратится в 1/5.
- Знаменателя, который равен нулю, не бывает, потому что на 0 делить нельзя.
Реклама
Об этой статье
Эту страницу просматривали 40 689 раз.
Была ли эта статья полезной?
Используя этот онлайн калькулятор с дробями, вы сможете сложить, вычесть, умножить, разделить или возвести в степень обыкновенные дроби, смешанные числа (дроби с целой частью), десятичные дроби и целые числа, соответственно найти их сумму, разность, произведение или частное.
Воспользовавшись онлайн калькулятором дробей, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения задач с дробями и закрепить пройденный на уроках материал.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Обыкновенная дробь – это запись числа в виде:
где число a называют числителем, а число b – знаменателем дроби.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Пример №1. У первой дроби можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.
Основное свойство дроби в основном применяют при сокращении обыкновенных дробей. Обыкновенные дроби бывают сократимые и несократимые.
- Сократимые – это дроби, у которых числитель и знаменатель делятся на одно и то же число.
- Несократимые – это дроби, у которых числитель и знаменатель не имеют общих делителей.
Сокращение дробей
Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.
Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби – четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:
Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.
Пример №4.
Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.
Вычитание обыкновенной дроби из целого числа
Вычитание обыкновенной дроби из единицы
Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.
Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).
Вычитание обыкновенной дроби из бóльшего числа
Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.
Пример №6.
Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.
Нахождение общего знаменателя
Наименьшее общее кратное. Приём №1.
Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.
Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7.
1. Нужно разложить на простые множители каждое число:
12=2×2×3
15=3×5
2. Затем найти одинаковые множители (подчеркиваем):
12=2×2×3
15=3×5
В данном случае это только множитель 3.
3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:
12 домножаем на 5: 12×5=60, или
15 домножаем на 2 и 2: 15×2×2=60
Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.
Перемножение знаменателей. Приём №2.
Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.
Пример №8.
Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.
Последовательный подбор. Приём №3.
Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.
Пример №9. Возьмем число 51, умножим на 2, получим 102 – видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.
После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.
Алгоритм сложения (вычитания)
- Находим общий знаменатель данных дробей.
- Находим дополнительный множитель к числителю каждой дроби, разделив общий знаменатель на числитель каждой дроби.
- Умножаем каждый числитель на дополнительный множитель.
- Выполняем сложение (вычитание) дробей с одинаковыми знаменателями.
Пример №10.
Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 – простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:
Выполняем умножение в числителе:
Выполняем сложение дробей с одинаковыми знаменателями:
Умножение обыкновенных дробей
Как перемножить дроби?
При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).
Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.
Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.
Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.
Пример №13. Нам даны смешанные дроби, переводим их в неправильные для выполнения умножения.
Деление обыкновенных дробей
Как разделить одну дробь на другую?
При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.
Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.
Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.
Пример №14. Делимое умножаем на число, обратное делителю.
Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление.
Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.
Задание OM2004
Сократите дробь 36n4n−2∙32n−1
Чтобы решить данное задание, необходимо понимать, что выполнять действия умножение и деление степеней мы можем в том случае, если они имеют одинаковые основания. Поэтому разложим на множители основание 36 нашего числителя так, чтобы вместо 36 были числа 4 и 3, которые есть в знаменателе.
(3∙3∙4)n4n−2∙32n−1
Теперь представим каждый множитель в виде степени:
3n∙3n∙4n4n−2∙32n−1
Разложим знаменатель дроби на множители по свойству степеней
3n∙3n∙4n4n∙4−2∙32n∙3−1
Теперь можно сократить числитель и знаменатель на 3n и в 4n степени
Получим дробь, которую преобразуем по свойству степеней:
14−2∙3−1 = 42∙311=16∙3=48
Ответ: 48
pазбирался: Даниил Романович | обсудить разбор
Задание OM1306o
Найдите значение выражения:
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:
теперь переходим от деления дробей к их умножению:
затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
сокращаем выражение на (a–5b):
Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений):
Подставим полученные значения в выражение и найдем конечный результат:
Ответ: 39
pазбирался: Даниил Романович | обсудить разбор
Задание OM1305o
Найдите значение выражения при x = 12:
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
Подставляем числовое значение для х в полученное выражение и находим результат:
Ответ: 0,6
pазбирался: Даниил Романович | обсудить разбор
Задание OM1304o
Найдите значение выражения
где a = 9, b = 36
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю – это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
9b² + 5a – 9b²
Приведем подобные слагаемые – это 9b² и – 9b², в числителе остается 5a. Запишем конечную дробь:
5a/b
Вычислим её значение, подставив числа из условия:
5•9/36 = 1,25
Ответ: 1,25
pазбирался: Даниил Романович | обсудить разбор
Задание OM1303o
Найдите значение выражения:
при x = √45 , y = 0,5
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель – это 15 x y, для этого необходимо первую дробь домножить на 5 y – и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y – (3 x + 5 y) = 5 y – 3 x – 5 y = – 3 x
Тогда дробь примет вид:
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: – 1/5 y
Подставим значение y = 0,5: – 1 / (5 • 0,5) = – 1 / 2,5 = – 0,4
Ответ: -0,4
pазбирался: Даниил Романович | обсудить разбор
Задание OM1302o
Найдите значение выражения:
при a = 13, b = 6,8
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй – в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:
Далее выносим из числителя второй дроби a:
Сокращаем (a-b):
И получаем:
a/2
Подставляем значение a = 13:
13 / 2 = 6,5
Ответ: 6,5
pазбирался: Даниил Романович | обсудить разбор
Задание OM0804o
Какое из данных ниже чисел является значением выражения?
Заметим, что в знаменателе присутствует разность (4 – √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² – (√14)². После этого знаменатель легко вычисляется:
16 – 14 = 2
Суммарно наши действия выглядят так:
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор
Задание OM0603o
Найдите значение выражения:
Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:
1/21 + 1/28 = 4/84 + 3/84
Затем складываем:
4/84 + 3/84 = 7/84
Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:
1 / ( 7 / 84 ) = 1 •84/7 = 84/7
Далее остается поделить 84 на 7:
84 / 7 = 12
Ответ: 12
pазбирался: Даниил Романович | обсудить разбор
Задание OM0602o
Найдите значение выражения:
Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.
1/3 • (6 • (1/3) — 17 )
Проведя вычисления в скобках, получим:
1/3 • ( 6 • (1/3) — 17 ) = 1/3 • (6 /3 — 17 ) = 1/3 • ( 2 — 17 ) = 1/3 • ( -15 )
Теперь умножим полученное значение -15 на 1/3:
1/3 • ( -15 ) = -5
Ответ: -5
pазбирался: Даниил Романович | обсудить разбор
Алла Василевская | Просмотров: 19.6k
В этом уроке мы познакомимся с понятием дробных выражений и с тем, как их считать. Узнаем интересные способы работы с дробями, в числителе или знаменателе которых стоят дроби.
Для начала определимся с определением дробного выражения.
Дробным выражением называется частное двух выражений или чисел, знак деления в котором обозначается чертой.
Пример:
$$mathbf{frac{1}{2}}$$
Мы привыкли называть такое выражение обыкновенной дробью. Она ничем не противоречит определению дробного выражения. Поэтому если вас спросят: «Является ли обыкновенная дробь дробным выражением?», то можно смело ответить: «Да, является!»
$$mathbf{frac{1+2}{3+4}}$$
$$mathbf{frac{5cdot(1+2)}{(3+5)div2}}$$
Мы не накладываем никаких ограничений на то, что из себя представляют выражения; нужно только то, чтобы это было деление, записанное как дробь.
Также никто не запрещает записать в одну или даже в обе части выражения, содержащие дроби.
Примеры:
$$mathbf{frac{1}{1+frac{1}{8}}}$$
$$mathbf{frac{3+12frac{1}{2}}{7frac{1}{3}-2frac{3}{4}}}$$
$$mathbf{frac{(frac{1}{2}+frac{1}{4})cdotfrac{2}{3}}{frac{2}{7}cdot(frac{3}{8}-frac{1}{4})}}$$
Можем пойти дальше и записать так называемую многоэтажную дробь. Это дробь, в числителе или в знаменателе (а иногда и в числителе и в знаменателе) которой стоят дробные выражения.
Примеры:
$$mathbf{frac{frac{1}{2}}{3}}$$
$$mathbf{frac{1}{frac{12}{19}}}$$
$$mathbf{frac{frac{12}{89}}{frac{74}{99}}}$$
Помимо определения дробного выражения необходимо знать определения числителя и знаменателя дробного выражения.
Эта информация доступна зарегистрированным пользователям
Если мы считаем дробное выражение делением, то числителем будет являться делимое, а знаменателем делитель.
Например, существует следующее дробное выражение:
$$mathbf{frac{3+10cdot2}{2+frac{1}{2}}}$$
В данном случае (mathbf{3+10cdot2}) будет являться числителем, а (mathbf{2+frac{1}{2}})- знаменателем.
Также можно преобразовывать обычные выражения в дробные.
Это можно делать при условии, что выражение представляет из себя частное двух выражений или чисел, но пока что записанное через обычный знак деления.
Эта информация доступна зарегистрированным пользователям
Примеры преобразования обычного выражения в дробное:
(mathbf{(3+4)div(200+123)=frac{3+4}{200+123}})
(mathbf{(1247+523cdot(54+78))div((345+67)cdot56cdot87cdot(63+85))=})
(mathbf{=frac{1247+523cdot(54+78)}{(345+67)cdot56cdot87cdot(63+85)}})
(mathbf{(4+frac{1}{2})div(frac{3}{5}cdot8+2)=frac{4+frac{1}{2}}{frac{3}{5}cdot8+2}})
(mathbf{(452+789cdot(frac{7}{9}+frac{1}{2}))div(frac{4}{741}+582cdot741)=})
(mathbf{=frac{452+789cdot(frac{7}{9}+frac{1}{2})}{frac{4}{741}+582cdot741}})
Сформулируем правило: для того, чтобы преобразовать выражение, представляющее из себя частное двух выражений или чисел, необходимо делимое поместить в числитель дробного выражения, а делитель- в знаменатель.
Теперь вы видите, насколько большой класс формул покрывается понятием дробного выражения.
Давайте пройдем небольшой тест и перейдем к изучению того, как вычислять значения дробных выражений.
Эта информация доступна зарегистрированным пользователям
Начнем с самого простого способа вычисления значений дробных выражений.
Он заключается в том, чтобы отдельно посчитать значения числителя и знаменателя и получить дробное выражение, в знаменателе и числителе которого стоят числа.
Далее надо смотреть, что получилось:
- может получиться правильная дробь, тогда это будет готовым ответом
- может получиться дробь неправильная, тогда необходимо выделить целую часть
- в числителе и знаменателе дробного выражения могут получиться дробные числа; в таком случае нужно поделить числитель на знаменатель, это и будет ответом
Эта информация доступна зарегистрированным пользователям
Пример 1
Вычислим значение выражения (mathbf{frac{1+2cdot4}{5-2}})
Решение:
Для начала вычислим значения числителя и знаменателя:
(mathbf{frac{1+2cdot4}{5-2}=frac{1+8}{3}=frac{9}{3}})
В данном примере числитель делится на знаменатель, поэтому из дроби получится натуральное число.
(mathbf{frac{9}{3}=3})
Пример 2
Вычислим значение выражения (mathbf{frac{7+2cdot3cdot2}{2cdot9}})
Решение:
Сначала вычислим числитель и знаменатель:
(mathbf{frac{7+2cdot3cdot2}{2cdot9}=frac{7+12}{18}=frac{19}{18}})
В данном случае получилась неправильная дробь, выделим целую ее часть, чтобы получить в ответе смешанное число:
(mathbf{frac{19}{18}=frac{19}{18}=1frac{1}{18}})
Пока что были рассмотрены случаи, в которых выражения в числителе и знаменателе представляли из себя арифметические действия над натуральными числами. Но вас нисколько не должны смущать случаи, в которых выражения содержат в себе дроби как обыкновенные, так и десятичные.
Пример:
(mathbf{frac{3+frac{3}{4}}{1.2+0.3}})
Решение:
Наверное, вы уже догадываетесь, что мы сделаем дальше. Правильно! Вычислим числитель и знаменатель:
(mathbf{frac{3+frac{3}{4}}{1.2+0.3}=frac{frac{3cdot4+3}{4}}{1.5}=})
(mathbf{=frac{frac{12+3}{4}}{1.5}=frac{frac{15}{4}}{1.5}})
В данном случае мы получили неправильную дробь в числителе и десятичную дробь в знаменателе.
Чтобы получить окончательный результат разделим одно на другое:
(mathbf{frac{frac{15}{4}}{1.5}=frac{15}{4}div1.5=frac{15}{4}divfrac{15}{10}=})
(mathbf{=frac{15}{4}cdotfrac{10}{15}=frac{15cdot10}{4cdot15}=frac{10}{4}=frac{5}{2}=2frac{1}{2}})
Прежде чем перейти к дополнительным приемам работы с дробными выражениями, решим небольшой тест для закрепления навыка вычисления дробных выражений.
Эта информация доступна зарегистрированным пользователям
Пока что во всех предыдущих случаях мы находили значения дробных выражений «в лоб», по достаточно простому алгоритму.
Но, как это часто бывает в математике, в некоторых случаях можно упростить себе подсчеты, вовремя заметив определенные вещи.
Вы уже наверняка хорошо освоили сокращение дробей.
Напомним, в чем его суть: если числитель представляет из себя произведение, и знаменатель также является произведением, и в этих произведениях есть одинаковый множитель, то мы можем сократить дробь на этот множитель.
Как же это относится к дробным выражениям?
Дело в том, что в некоторых случаях числитель и знаменатель могут быть произведениями или же могут стать произведениями в процессе подсчетов.
Тогда почему бы не сокращать их по возможности?!
Эта информация доступна зарегистрированным пользователям
Пример:
(mathbf{frac{7cdot(123+4)}{3cdot(120+7)}})
Начнем считать выражение и посмотрим, что получается.
(mathbf{frac{7cdot(123+4)}{3cdot(120+7)}=frac{7cdot127}{3cdot127}})
Числитель и знаменатель дробного выражения после первых преобразований превратились в произведения.
Также можно заметить, что в этих произведениях есть общий множитель: 127
Тогда мы можем поделить числитель и знаменатель дробного выражения на это число, тем самым значительно упростив выражение.
(mathbf{frac{7cdot127}{3cdot127}=frac{7}{3}=2frac{1}{3}})
Это и будет значением этого выражения.
Также мы можем быть еще более хитрыми и внимательными.
Найдем значение выражения (mathbf{frac{2cdot(478569-145236)}{(478569-145236)cdot3}})
Конечно же, можно начать вычислять сначала числитель, потом знаменатель. Для этого мы будем вычислять разность шестизначных чисел.
Но можно сделать проще: заметим, что числитель и знаменатель являются произведениями.
Числитель является произведением 2-х и выражения (478569-145236)
Знаменатель же является произведением выражения (478569-145236) и 3-х.
Выражение (478569-145236) является множителем и можно утверждать, что это один и тот же множитель в числителе и в знаменателе.
Значит, мы можем уверенно сокращать дробное выражение на это выражение.
(mathbf{frac{2cdot(478569-145236)}{(478569-145236)cdot3}=frac{2}{3}})
В данном случае мы сразу получили правильную дробь, это и будет являться значением выражения.
Отдельно стоит упомянуть работу с многоэтажными дробями.
Мы всегда можем идти по алгоритму с последовательным вычислением числителя и знаменателя — это гарантированно дает результат.
Но также можно запомнить два правила, которые существенно экономят время.
Первое правило говорит о том, что, если в числителе дробного выражения находится дробь (или же дробное выражение), мы можем домножить дробное выражение на знаменатель дроби (или дробного выражения), стоящей в числителе, тем самым уменьшив «этажность» дробного выражения.
Эта информация доступна зарегистрированным пользователям
Парочка примеров:
(mathbf{frac{frac{2}{3}}{4}=frac{frac{2}{3}cdot3}{4cdot3}=frac{2}{12}=frac{1}{6}})
(mathbf{frac{frac{3}{7+13}}{5}=frac{frac{3}{7+13}cdot(7+13)}{5cdot(7+13)}=})
(mathbf{=frac{3}{5cdot20}=frac{3}{100}=0.03})
Второе правило рассматривает случай, когда дробь (или дробное выражение) находится в знаменателе дробного выражения.
В таком случае уменьшить «этажность» дробного выражения поможет домножение всего дробного выражения на знаменатель дроби (или дробного выражения), стоящей в знаменателе.
Эта информация доступна зарегистрированным пользователям
И парочка примеров на этот случай:
(mathbf{frac{3}{frac{2}{7}}=frac{3cdot7}{frac{2}{7}cdot7}=frac{21}{2}=10frac{1}{2}})
(mathbf{frac{11}{frac{3}{1+7}}=frac{11cdot(1+7)}{frac{3}{1+7}cdot(1+7)}=})
(mathbf{=frac{11cdot(1+7)}{3}=frac{11cdot8}{3}=frac{88}{3}=29frac{1}{3}})
И в завершение еще дам такой пример:
(mathbf{frac{frac{3}{4+1}}{frac{7-2}{4}}=frac{frac{3}{5}}{frac{5}{4}}=})
(mathbf{=frac{frac{3}{5}cdot5}{frac{5}{4}cdot5}=frac{3}{frac{25}{4}}=frac{3cdot4}{frac{25}{4}cdot4}=frac{12}{25}})
Эта информация доступна зарегистрированным пользователям
Десять интересных математических фактов:
1. Известные всем знаки сложения и вычитания впервые были использованы только около 500 лет назад
2. 2 и 5— единственные простые числа, которые оканчиваются на 2 или 5
3. Несмотря на то, что сохранилось много трудов древнегреческого ученого Евклида, о его биографии почти ничего не известно
4. В римской системе счисления не существует нуля
5. Знак равенства «=» появился только в XVI веке
6. Слово «миг» обозначает не только короткое мгновение, но и вполне конкретный временной промежуток: 0,01 секунды
7. У древних египтян отсутствовала таблицы умножения и прочие математические правила
8. В свое время заниматься математикой в высоких кругах было настолько популярно, что даже Наполеон Бонапарт оставил после себя научные труды
9. Самые древние математические записи были найдены написанными на костях
10. Ученый Муавр с помощью математики смог рассчитать дату своей смерти