Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
2+1=3
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
x+2-2=7-2
x+0=7-2
x=7-2
Нужно остановиться на этом моменте подробно. Другими словами, мы +2 перенесли с левой части на правую и знак поменяли стало число -2.
x=5
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
x-4+4=12+4
x=12+4
Другими словами, мы -4 перенесли из левой части уравнения в правую и получили +4. При переносе через равно знаки меняются на противоположные.
x=16
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Решение:
Чтобы решить уравнение необходимо неизвестные перенести в одну сторону, а известные в другую. То есть переменные с x будут в левой части, а числа в правой части.
Сначала перенесем 2x с правой стороны в левую сторону уравнения и получим -2x.
4+3x=2x-5
4+3x-2x=-5
Далее 4 с левой стороны уравнения перенесем на правую сторону и получим -4
4+3x-2x=-5
3x-2x=-5-4
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Сделаем проверку, правильно ли решено уравнение? Для этого вместо переменной x в уравнение подставим -9.
4+3x=2x-5
4+3⋅(-9)=2⋅(-9)-5
4-27=-18-5
-23=-23
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
5x=20
5x:5=20:5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅4=20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Рассмотрим следующий пример:
Найдите корни уравнения .
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
1x=21 или x=21
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте перед переменной x убрать из знаменателя 5.
3x=45
Далее делим все уравнение на 3.
3x:3=45:3
(3:3)x=15
1x=15 или x=15
Сделаем проверку. Подставим в уравнение найденный корень.
5=5
Ответ: x=15
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Уравнения
Уравнение — это равенство, содержащее букву, значение которой надо найти. Например: 


Корень уравнения — это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.
Корень уравнения — это решение уравнения. Уравнение может иметь один и более корней или не иметь их вообще. Тогда говорят, что решить уравнение — значит найти все его корни или показать, что их нет вообще.
Для решения уравнений используют правило нахождения неизвестного:
1) слагаемого: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Решим уравнение 


Ответ: 
2) уменьшаемого: чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Решим уравнение 


Ответ: 
3) вычитаемого: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Решим уравнение 135 — 


Ответ: 
4) множителя: чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Решим уравнение 
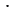


Ответ: 
5) делимого: чтобы найти неизвестное делимое, надо частное умножить на делитель.
Решим уравнение 

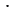

Ответ: 
6) делителя: чтобы найти неизвестный делитель, надо делимое разделить на частное.
Решим уравнение 184 : 


Ответ: 
При решении уравнений проводится проверка решения, для этого найденный корень (или корни) подставляются в уравнение вместо переменной. Если числовое равенство получается верным, то решение найдено верно. При оформлении решения проверка записывается под чертой после решения, а затем пишется ответ, при этом каждое действие записывается на новой строке (т.е. одна строка один знак равенства).
Например, решим уравнение 


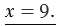
9 + 36 = 45;
45 = 45 — верно.
Ответ: 
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 524,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 525,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 585,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 593,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 624,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1018,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1686,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1751,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 494,
Мерзляк, Полонский, Якир, Учебник
Номер 569,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 131,
Мерзляк, Полонский, Якир, Учебник
Номер 453,
Мерзляк, Полонский, Якир, Учебник
Номер 639,
Мерзляк, Полонский, Якир, Учебник
Задание 786,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 803,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 828,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 932,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1147,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1258,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1277,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 85,
Мерзляк, Полонский, Якир, Учебник
Номер 110,
Мерзляк, Полонский, Якир, Учебник
Номер 321,
Мерзляк, Полонский, Якир, Учебник
Номер 515,
Мерзляк, Полонский, Якир, Учебник
Номер 557,
Мерзляк, Полонский, Якир, Учебник
Номер 689,
Мерзляк, Полонский, Якир, Учебник
Номер 814,
Мерзляк, Полонский, Якир, Учебник
Номер 836,
Мерзляк, Полонский, Якир, Учебник
Номер 1153,
Мерзляк, Полонский, Якир, Учебник
Номер 1166,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 193,
Мерзляк, Полонский, Якир, Учебник
Номер 210,
Мерзляк, Полонский, Якир, Учебник
Номер 215,
Мерзляк, Полонский, Якир, Учебник
Номер 216,
Мерзляк, Полонский, Якир, Учебник
Номер 217,
Мерзляк, Полонский, Якир, Учебник
Номер 218,
Мерзляк, Полонский, Якир, Учебник
Номер 219,
Мерзляк, Полонский, Якир, Учебник
Номер 401,
Мерзляк, Полонский, Якир, Учебник
Номер 417,
Мерзляк, Полонский, Якир, Учебник
Номер 518,
Мерзляк, Полонский, Якир, Учебник
Основные понятия уравнения
Определение
Уравнением называют равенство, в котором одна из переменных неизвестна, и её нужно найти. Значение этой неизвестной должно быть таким, чтобы равенство было верным.
К примеру: 3+4=7 это числовое равенство, при вычислении которого с левой стороны получается 7=7.
Уравнением же будет называться следующее равенство: 3+х=7, поскольку есть неизвестная переменная х, её значение можно найти.
Из этого уравнения следует, что переменная х=4, только при таком его значении равенство 3+х=7, будет верным.
Неизвестные переменные принято писать в виде маленьких латинских букв, можно любыми, но чаще используют x,y,z.
Получается, чтобы равенство сделать уравнением необходимо, чтобы в нем была буква, значение которой неизвестно.
Как мы понимаем существует множество примеров уравнений с разными арифметическими действиями.
Пример: х + 5 = 1= 9; z — 2 = 7; 9 * y = 18, 6 : f = 2
Помимо этого существуют уравнения со скобками. К таким уравнениям относится 8 : (х — 4) = 2 * (8 — х), неизвестных может быть несколько, они могут быть, как слева уравнения, так и справа или в обеих частях.
Помимо таких простых уравнений они могут быть с корнями, логарифмами, степенями и тд.
Уравнение может содержать несколько переменными, тогда их принято называть, соответственно уравнениями с двумя, тремя и более переменными.
Пример:
3 * а = 15 : х — уравнение с двумя переменными:
8 — а = 5 * х — z — уравнение с тремя переменными.
Корень уравнения
Мы часто слышим фразу на уроках математики, «найдите корень уравнения», давайте разберёмся, что же это значит.
Пример:
В примере 3+х=7, можно представить вместо буквы число, и уравнение тогда станет равенством, оно может быть либо верным, либо неверным, если поставить х=3, то первичное равенство примет вид 3+3 = 7 и станет неверным, а если х= 4 то равенство 3+4=7 будет верным, а значит х = 4 будет называться корнем или по другому решением уравнения 3+х=7.
Определение.
Отсюда можно выделить следующее определение: корень уравнения — это такое значение неизвестной переменной, при котором числовое равенство будет верным.
Стоит отметить, что корней может быть несколько или не быть вовсе.
Рассмотрим подробнее пример который не будет иметь корней. Таким примером станет 0 * х = 7, сколько бы чисел мы сюда не подставляли равенство не будет верным, так как умножая на ноль будет ноль, а не 7.
Но существуют и уравнения с множественным числом корней, к примеру, х — 3 = 6, в таком уравнении только один корень 9, а в уравнении квадратного вида х2 = 16, два корня 4 и -4, можно привести пример и с тремя корнями х * (х — 1) * (х — 2) = 0, в данном случае три решения ноль, два и один.
Для того чтобы верно записать результат уравнения мы пишем так:
- Если корня нет, пишем уравнение корней не имеет;
- Если есть и их несколько, они либо прописываются через запятые, либо в фигурных скобках, например, так: {-2, 3, 5};
- Еще одним вариантом написания корней, считается запись в виде простого равенства, к примеру неизвестная х а корни 3,5 тогда результат прописывается так: х=3, х=5.
- или прибавляя индекс снизух1 =3 , х2 = 5. данным способом указывается номер корня;
- Если решений уравнения бесконечное множество, то запись будет либо в виде числового промежутка от и до, или общепринятыми обозначениями. множество натуральных чисел N, целых – Z, действительных — R.
Стоит отметить, что если уравнение имеет два и более корней, то чаще употребляется понятие решение уравнения. Рассмотрим определение уравнения с несколькими переменными.
Решение уравнения с двумя и более переменными, означает, что эти несколько значений превращают уравнение в верное равенство.
Примеры:
Представим, что мы имеем следующее уравнение х + а = 5, такое уравнение имеет две переменные. Если мы поставим вместо них числа 3 и 6 то равенство не будет верным, соответственно и данные числа не являются решением для данного примера. А если взять числа 2 и 3 то равенство превратится в верное, а числа 2 и 3 будут решением уравнения. Представленные уравнения с несколькими переменными, тоже могут или не иметь корня вообще или наоборот иметь множество решений.
Правила нахождения корней
Таких правил существует несколько рассмотрим их ниже.
Пример 1
Допустим мы имеем уравнение 4 + х = 10, чтобы найти корень уравнения или значение х в данном случае необходимо найти неизвестное слагаемое, для этого есть следующее правило или формула. Для нахождения неизвестного слагаемого, нужно из суммы вычесть известное значение.
Решение:
х = 10 — 4
х = 6
Чтобы проверить является ли 6 решением, мы ставим его на место неизвестной переменной х в исходное уравнение, получаем следующее равенство 4 + 6 = 10, такое равенство является верным, что означает число корня уравнения, равно 6.
Пример 2
Возьмём уравнение вида х — 5 = 3, в данном примере х это неизвестное уменьшаемое, для того чтобы его найти необходимо следовать следующему правилу:
Для нахождения уменьшаемого необходимо сложить разность и вычитаемое.
Решение:
х = 3 + 5
х = 8
Проверяем правильность нахождения корня уравнения, подставляем, вместо переменной неизвестной, найденное число 8, получаем равенство 8 — 5 = 3, так как оно верное, то и корень уравнения найден правильно.
Пример 3
Берём уравнение, в котором неизвестное х будет вычитаемое к примеру: 8 — х = 4. для того чтобы найти х необходимо воспользоваться правилом:
Для нахождения вычитаемого, нужно из уменьшаемого вычесть разность.
Решение:
х = 8 — 4
х = 4
Проверяем правильность нахождения корня уравнения, для этого полученное значение ставим вместо неизвестного вычитаемого в исходный пример, и получаем следующее равенство 8 — 4 = 4, равенство верно, значит и корень найден правильно.
Нет времени решать самому?
Наши эксперты помогут!
Пример 4
Возьмём уравнение вида х * 3 = 9, в данном уравнении неизвестна переменная х, является множимым. Для того, чтобы найти корень такого уравнения необходимо использовать следующее правило.
Для нахождения неизвестного множимого, нужно произведение разделить на множитель.
Решение:
х = 9 : 3
х = 3
Для проверки подставим найденное значение х в исходное уравнение, получим равенство 3 * 3 =9, так как равенство является верным, то и решение уравнения верное.
Такое же правило действует и для множителя, чтобы его найти необходимо произведение разделить на множимое.
Пример 5
Возьмём уравнение следующего вида: х : 2 = 10 , в данном уравнении х- это неизвестное делимое, 2 — делитель, а 10 — частное. Для нахождения неизвестного значения х, воспользуемся правилом:
Чтобы найти делимое, необходимо частное умножить на делитель.
Решение:
х = 10 * 2
х = 20
Проверим, вместо неизвестного х, поставим его значение 20, получим следующее равенство 20: 2 = 10. Равенство верное, значит и решение было верным.
Пример 6
Теперь рассмотрим пример с делителем.
Возьмём уравнение 22: х = 11, где х неизвестный делитель. Для того чтобы его найти существует правило:
При нахождении неизвестного делителя нужно делимое разделить на частное.
Решение:
х = 22 : 11
х = 2
Проверяем, 2 ставим на место неизвестного х в исходное уравнение, получаем равенство 22 : 2 = 11. Так как равенство верно, то мы нашли верный корень уравнения.
Пример применения правил в более сложном уравнении: 2х — 5 =5
Решение:
2х = 5 + 5
2х = 10
х = 10 : 2
х = 5
Проверяем, для этого полученное значение х = 5, ставим в исходное уравнение, получаем равенство 2 * 5 — 5 = 5, так как равенство верно, корень найден правильно.
Квадратные уравнения
Существует также уравнения квадратного вида, например: 2х2 = 32, для того, чтобы найти неизвестное или корень квадратного уравнения, в таком уравнении необходимо:
Решение:
х2 = 32 : 2
х2 = 16
х = √16
х = 4
Проверим, для этого полученное значение подставим в исходное уравнение, и получим равенство 242 = 32. так как равенство верное, то и решение уравнения верно.
Как мы видим нахождение корня уравнения не такой сложный процесс, главное запомнить правила. Стоит отметить, что помимо решения различного вида задач, уравнения применяются в других различных науках. Применение уравнений можно найти в экономике, в физике, химии, биологии и других. При их помощи можно вычислить и описать процессы, происходящие вокруг нас.
Калькулятор квадратных корней
п.1. Определение уравнения и его корня
Уравнением с одной переменной x называют равенство f(x)=g(x), для которого поставлена задача найти все значения переменной x, которые обращают это равенство в истинное числовое равенство.
Значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называют корнем уравнения f(x)=g(x).
Например, для уравнения 15x+8=23 корнем является значение x=1.
В уравнении x(x + 5)(x — 3) = 0 три корня, $x_1 = 0,x_2 = -5,x_3 = 3$.
Уравнение $x^2 = -1$ действительных корней не имеет.
В уравнении 5(x + 3)=5x + 15 бесконечное количество корней, т.к. оно превращается в истинное равенство при любом $x in Bbb R$, т.е. является тождеством.
Решить уравнение означает найти все его корни или доказать, что их нет.
п.2. Примеры
Пример 1. Решите уравнение и выполните проверку x — (3 — 2x) = 9
Решение:
x-(3-2x)=9 $iff$ x-3+2x=9 $iff$ x+2x=9+3 $iff$ 3x=12 $iff$ x=4
Проверка:
$4 -(3 — 2 cdot 4)=9 implies 4 — 3 + 8 = 9 implies 9 equiv 9$
Ответ: x = 4
Пример 2. Решите уравнение и выполните проверку 7(x + 3) = 56
Решение:
7(x + 3)=56 |:7 $iff$ x + 3 = 8 $iff$ x = 8 — 3 $iff$ x=5
Проверка:
$7(5 + 3) = 56 implies 7 cdot 8 = 56 implies 56 equiv 56$
Ответ: x = 5
Пример 3. Решите уравнение и выполните проверку (3x + 4) : 2 = 14
Решение:
(3x + 4) : 2=14 |$times$2 $iff$ 3x + 4 = 28 $iff$ 3x = 28 — 4 $iff$ 3x = 24 $iff$ x=8
Проверка:
$(3 cdot 8 + 4) : 2 = 14 implies (24 + 4) : 2 = 14 implies 28 : 2 = 14 implies 14 equiv 14$
Ответ: x = 8
Пример 4. Решите уравнение $ frac{3x-7}{3} — frac {5x-11}{5} = 0$
Решение:
$frac {3x-7}{3} — frac {5x-11}{5} = 0 | times 15 iff5(3x-7)-3(5x-11)=0 iff$
$ iff 15x-35-15x+33=0 iff 0x=2 iff x in varnothing $
Решений нет.
Ответ: $x in varnothing $
Пример 5. Решите уравнение $frac {2x — 7}{2} = frac {3x+6}{3}$
Решение:
$frac {2x-7}{2}=frac {x+6}{3} | times 6 iff 3(2x-7)=2(x+6) iff 6x-21=2x+12 iff $
$iff 6x-2x=12+21 iff 4x=33 iff x= frac {33}{4} =8 frac 14$
Ответ: $8 frac 14$
Пример 6. Решите уравнение |x+1|=5
Решение:
$$|x+1|=5 iff left[ begin{array}{cc} {x+1=-5}\ {x+1=5} end{array} right. iff left[ begin{array}{cc} {x=-5-1}\ {x=5-1} end{array} right. iff left[ begin{array}{cc} {x_1=-6}\ {x_2=4} end{array} right. $$
Ответ: $ x_1=-6, x_2=4$
Пример 7*. Решите уравнение и выполните проверку |x + 1| = x + 3
Решение:
$$ |x + 1| = x + 3 iff left[ begin{array}{cc} {left{ begin{array}{c} x+1 ge 0 \ x+1=x+3 end{array} right.}\ {left{ begin{array}{c} x+1<0 \ -(x+1)=x+3 end{array} right.} end{array} right. iff left[ begin{array}{cc} {left{ begin{array}{c} x ge -1 \ 1=3 end{array} right.}\ {left{ begin{array}{c} x<-1 \ -x-1=x+3 end{array} right.} end{array} right. iff $$
$$ iff left[ begin{array}{cc} {emptyset}\ {left{ begin{array}{c} x<-1 \ -x-x=3+1 end{array} right.} end{array} right. iff left[ begin{array}{cc} {x<-1}\ {-2x=4} end{array} right. iff left[ begin{array}{cc} {x<-1}\ {x=-2} end{array} right. iff x=-2 $$
Проверка:
$$|-2+1|=-2+3 implies |-1|=1implies 1 equiv 1$$
Ответ: x = -2
Пример 8. При каком значении a уравнение 5ax + 18 = 3 будет иметь корень x = -3?
Решение:
Подставляем x=-3 в уравнение и решаем его относительно параметра a:
5a $cdot$ (-3) + 18 = 3 $iff$ -15a = 3 — 18 $iff$ -15a = -15 $iff$ a = -15:(-15)=1
a=1
Ответ: a = 1
Содержание:
- § 1 Что такое уравнение?
- § 2 Что такое корень уравнения?
- § 3 Написание и чтение уравнений
§ 1 Что такое уравнение?
В этом уроке Вы познакомитесь с такими понятиями, как уравнение и корень уравнения. Кроме того, узнаете, что значит решить уравнение и каким образом находить неизвестные переменные в нем.
Давайте рассмотрим задачу про грибы:
В корзине лежало несколько грибов. После того, как в нее положили еще 7 грибов, их стало 35. Сколько грибов было в корзине?
Решение:
Обозначим неизвестное число грибов, лежащих в корзине латинской буквой х, после того как в нее добавили еще 7 грибов, стало х + 7 грибов в корзине, то есть 35. Значит должно выполняться равенство х + 7 = 35. Теперь надо найти такое значение х, при котором выполняется данное равенство. По смыслу вычитания, таким значением будет разность чисел 35 минус 7, то есть 28. Или же х = 28. Значит, в корзине было 28 грибов.
Если в равенство входит буква, или правильно говорить переменная, то равенство может быть верным при одних значениях этой буквы, т.е. переменной и неверным при других ее значениях. Например, х + 11 = 24. Это равенство будет верным при х = 13, и неверным при х = 1 или х = 2 и так далее. Так вот, уравнением называют равенство, содержащее букву, значение которой надо найти. Или же уравнение – это равенство, содержащее переменную, значение которой надо найти.
§ 2 Что такое корень уравнения?
Значение буквы, или значение переменной при котором из уравнения получается верное числовое равенство, называют корнем уравнения.
Вернемся к последнему примеру.
Равенство х + 11 = 24 можно назвать уравнением, так как оно содержит переменную х, значение которой надо найти. Корнем данного уравнения является число 13, так при этом значении уравнение превращается в верное числовое равенство: 13 + 11 = 24.
Что же значит решить уравнение? Это значит, что надо найти все его корни или убедиться, что корней нет, то есть уравнение не имеет ни одного корня.
Например, решите уравнение: х + 22 = 56.
Решение: по смыслу вычитания, неизвестное слагаемое равно разности суммы и известного слагаемого, поэтому х = 56 – 22, то есть х = 34. Число 34 является корнем уравнения х + 22 = 56, так как 34 + 22 = 56. Обратите внимание, как находить корень в таких уравнениях: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Следующий пример, решите уравнение 21 – х = 19.
Решение: по смыслу вычитания, число 21 является суммой х и 19, то есть х + 19 = 21. Из этого уравнения находим неизвестное слагаемое х = 21 – 19, получим х = 2. Число 2 является корнем уравнения 21 – х = 19, так как равенство 21 – 2 = 19 является верным.
Обратите внимание, чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Рассуждая аналогичным образом, можно сформулировать еще одно правило, чтобы найти неизвестное уменьшаемое, надо к вычитаемому прибавить разность. Например, решите уравнение: у – 12 = 36. Для нахождения неизвестного уменьшаемого у, необходимо к разности 36 прибавить вычитаемое 12, получится 48. Ответ: корень уравнения у = 48. Действительно, если из 48 вычесть 12, получится 36.
§ 3 Написание и чтение уравнений
Кстати, уравнение принято оформлять в столбик, найденное значение переменной подчеркивать горизонтальной линией, а ниже производить проверку уравнения, подставив полученный корень в исходное равенство.
При чтении уравнений и буквенных выражений помните, что названия латинских букв – переменных Х, Y, Z – мужского рода, а названия остальных латинских букв – среднего рода, например, «х=5», или «y=2» или же «а=7».
Названия букв в математике не склоняются. Например, данное выражение (х + 11 = 30) читается так: сумма х и одиннадцати равна тридцати.
Другой пример, данное уравнение (р – 15 = 47) можно прочитать как разность P и пятнадцати равна сорока семи.
Таким образом, на этом уроке Вы познакомились с такими понятиями, как уравнение и корень уравнения, а также узнали, что решить уравнение – это значит найти все его корни или убедиться, что корней нет. Кроме того, научились находить неизвестные переменные в уравнении.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
- Дидактические материалы по математике 5 класс. Автор — Попов М.А. — 2013 год
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. — 2014 год
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. — 2010 год
- Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. — 2012 год
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009



