Основные определения
Наверное, каждый из нас сталкивался с треугольником. Это могло быть в школе, вузах, колледжах, на работе, во время помощи детям. Треугольник – это одна из самых простых геометрических фигур, но в то же время она выполняет очень важную роль. Множество свойств хранит треугольник. Но сегодня не будем вдаваться в подробности, а поговорим про периметр и порешаем задачи по нахождению его.
Если мы отметим на плоскости 3 точки и проведём к ним линии, то как раз получим треугольник.
Понятия
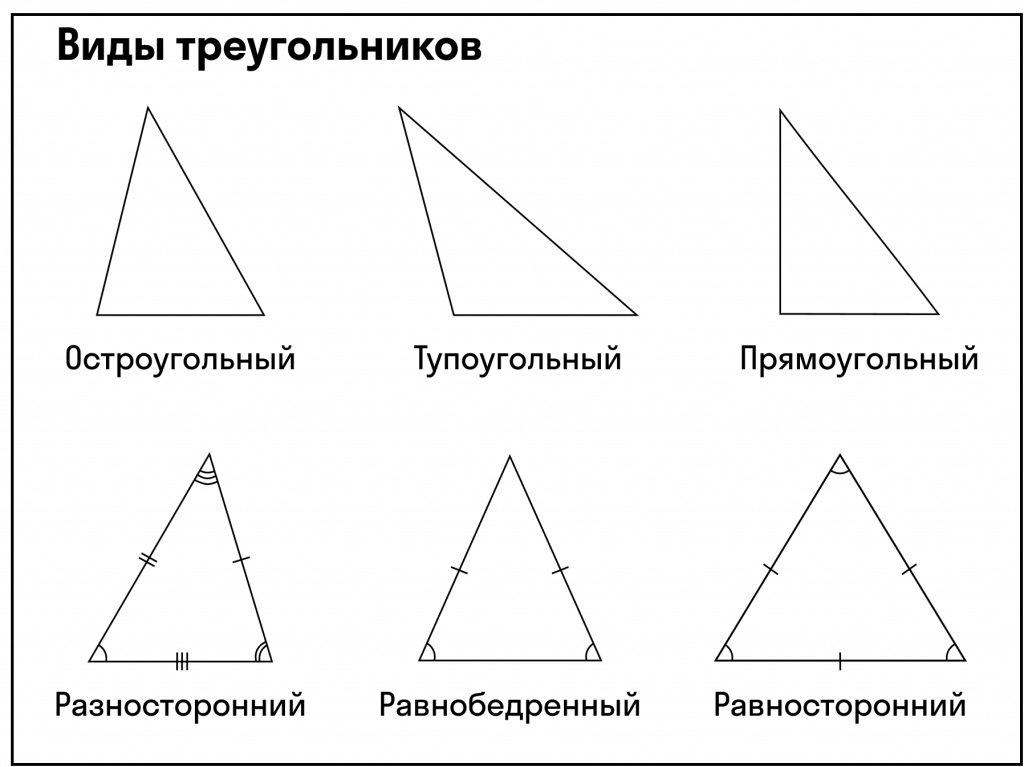
Треугольник – это геометрическая фигура, состоящая из трёх точек, которые соединены отрезками – сторонами. В зависимости от отношений между сторонами фигуры, то они бывают равносторонними, разносторонними и равнобедренными (р/б – равнобедренный, р/с – равносторонний).
Вершины треугольника – это точки, где соединяются 2 стороны фигуры.
Р/б треугольник – это треугольник у которого две стороны равны, но не равны третьей.
Р/с треугольник – это треугольник, у которого все стороны равны между собой.
Разносторонний треугольник – это треугольник, у которого все стороны не равны между собой.
Прямоугольный треугольник — это треугольник, у у которого один угол равен 90о. Самая длинная сторона называется гипотенузой, а две другие катетами.
Формула нахождения периметра
Из определения следует, что периметр геометрической фигуры – это сумма длин всех сторон, и треугольник не стал исключением. Общая формула имеет вид: Р = а + b + с. Периметр будет обозначаться Р. а, b и с — стороны треугольника. Решим задачу №1.
Задача 1
Пусть нам дан треугольник со сторонами 13 см, 15 см, 12 см. Нужно найти периметр данного треугольника.
Решение: [P=13+15+12=40] см.
Ответ: 40 см.
Периметр разностороннего треугольника
В прошлой задаче мы как раз нашли периметр разностороннего треугольника. Решим похожую задачу №2
Задача 2
Дан треугольник со сторонами 25 дм, 30 дм, 15 дм. Найдите периметр треугольника. Ответ выразите в метрах.
Решение:
P = 30 + 25 + 15 = 70 дм
70 : 10 = 7 м
Ответ: 7 м.
Периметр равнобедренного треугольника
Так как в р/б треугольнике 2 стороны равны (боковые), то формулу нахождения можно представить как: P = 2a + b. Решим 2 задачи.
Задачи 3 — 4
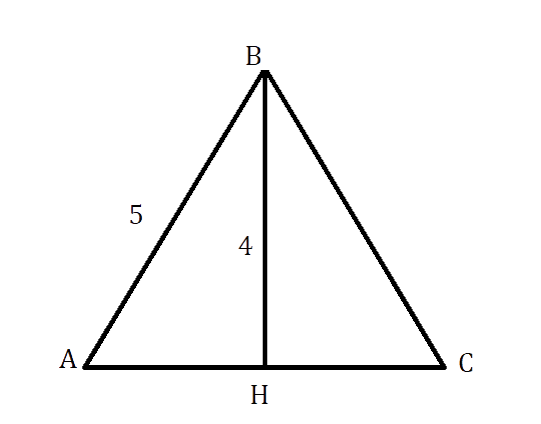
Дан равнобедренный треугольник АВС с биссектрисой, проведённой к основанию и равной 4 см, а также с боковой
стороной, равной 5 см. Найдите периметр данного треугольника.
Решение:
Так как ВН – биссектриса р/б треугольника АВС, то она является как высотой, так и медианой. Следовательно, ΔАВН прямоугольный и АН = НС.
В ΔАВН по теореме Пифагора [A H^{2}=A B^{2}-B H^{2}=25-16=9]см
АН = НС = √9 = 3 см
АС = АН + НС = 3 + 3 = 6 см
Р = 6 + 2*5 = 16 см
Ответ: 16 см.
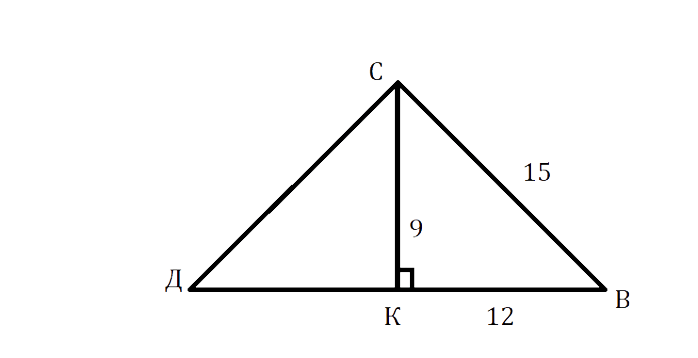
В треугольнике ДСВ ДС = СВ = 15 см, высота СК = 9 см. Найдите периметр этого треугольника.
Решение:
В ΔСКД по теореме Пифагора:
[text { ДК² }=text { ДС }^{2}-mathrm{CK}^{2}=225-81=144]см
ДК = √144 = 12 см.
Так как СК — высота в р/б треугольнике, проведённая к основанию, то она является медианой, следовательно, ДВ = ДК + КВ = 12 + 12 = 24 см.
Р = ДС + СВ + ДВ = 15 + 15 + 24 = 54 см.
Ответ: 54 см.
Нет времени решать самому?
Наши эксперты помогут!
Периметр равностороннего треугольника
А это один из самых “хороших” треугольников, его ещё называют правильным, так как все стороны и углы равны между собой. Формула нахождения периметра будет иметь вид: P = 3a.
Задачи 5 — 6
Дан равносторонний треугольник со стороной а = 13. Найдите периметр этого треугольника.
Решение:
Р = 3а = 3 * 13 = 39
Ответ: 39.
В равностороннем треугольнике АВС есть стороны: АВ = АС = СВ = 15 см, Найдите периметр данного треугольника.
Решение:
Р = 3АВ = 15 * 3 = 45 см.
Ответ: 45 см.
Периметр прямоугольного треугольника
Вычисляем по стандартной формуле: Р = а + в + с. Но у такого вида треугольников есть огромное преимущество – применение теоремы Пифагора.
Задачи 7 — 8
Дан прямоугольный треугольник с катетами а = 6 и в = 8. Найдите периметр.
Решение:
По теореме Пифагора: [c^{2}=в^{2}+a^{2}=64+36=100]
с = √100 = 10
Р = а + в + с = 6 + 8 + 10 = 24
Ответ: 24.
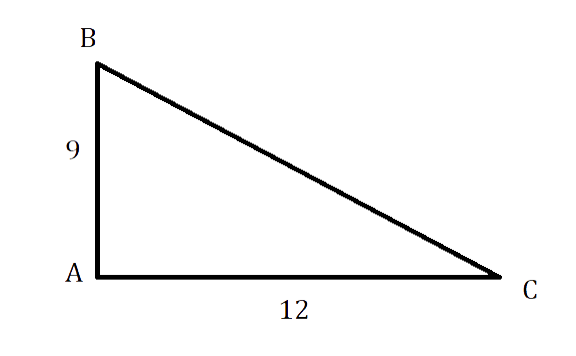
В прямоугольном треугольнике АВС, [angle mathrm{A}=90^{circ}, mathrm{AB}=9 mathrm{~см}, mathrm{AC} = 12см]. Надо найти периметр и площадь АВС.
Решение
По теореме Пифагора в ΔАВС:
[mathrm{CB}^{2}=mathrm{AC}^{2}+A mathrm{C}^{2}=144+81=225 mathrm{~см}]
СВ = √225 = 15 см
S = (АС * АВ) : 2 = (9 * 12) : 2 = 54 см
P = 15 + 9 + 12 = 36 см
Ответ: 36 см; 54 см.
Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Памятка
для решения задач, нахождение периметра фигур
1. Задача
Найди
периметр треугольника со сторонами 3см, 5см, 6см.
Объясняю:
Чтобы найти периметр треугольника, нужно все 3 стороны сложить.
Запись в тетради:
Р
= 3 + 5 + 6 = 14 (см)
Ответ:
14 см периметр треугольника.
2. Задача
Найди
периметр прямоугольника со сторонами 2см и 5см.
Объясняю:
1
способ: Чтобы найти периметр прямоугольника,
нужно все 4 стороны сложить.
Запись в тетради:
Р
= 2 + 5 + 2 + 5 = 14 (см) или Р = 2 + 2 + 5 + 5 = 14 (см)
Ответ:
14 см периметр прямоугольника.
2
способ: Чтобы найти периметр прямоугольника
применю формулу Р = (а + b)·2,
где а – длина одной стороны, b
– длина второй стороны.
В
формулу вместо букв поставлю известные данные Р = (2 + 5)·2
= 14 (см)
Запись в тетради:
Р
= (2 + 5)·2 = 14 (см)
Ответ:
14 см периметр прямоугольника.
3. Задача
Найди
периметр квадрата со стороной 3 см.
Объясняю:
1 способ:
Чтобы найти периметр квадрата, нужно все 4 стороны сложить
Запись в тетради:
Р = 3 + 3 + 3 + 3 = 12
(см)
Ответ: 12 см периметр
квадрата.
2 способ: Чтобы
найти периметр квадрата применю формулу Р = а·4,
где а – длина стороны квадрата. В формулу вместо буквы а,
поставлю известные данные
Запись в тетради:
Р = 3·4
= 12 (см)
Ответ: 12 см периметр
квадрата.
4. Задача
Длина одной
из сторон прямоугольника равна 6 см, длина другой стороны – на 4 см больше.
Найди периметр прямоугольника.
Объясняю:
У прямоугольника противоположные стороны равны. Чтобы найти периметр прямоугольника,
нужно все 4 стороны сложить. Но неизвестна вторая сторона, найду сначала её. В
задаче сказано, что она больше первой на 4см, буду прибавлять: 1) 6 + 4 = 10
(см) – вторая сторона. Все стороны известны, могу найти периметр, сложу все
четыре стороны: 2) 6 + 6 + 10 + 10 = 32 (см)
Запись в тетради:
1) 6
+ 4 = 10 (см) – вторая сторона.
2) 6
+ 6 + 10 + 10 = 32 (см) или Р = (6 + 10)·2 = 16·2
= 32 (см)
Ответ: 32 см периметр
прямоугольника.
5. Задача
Длина одной
из сторон прямоугольника равна 8 см, длина другой стороны – на 5 см меньше.
Найди периметр прямоугольника.
Объясняю:
У прямоугольника противоположные стороны равны. Чтобы найти периметр прямоугольника,
нужно все 4 стороны сложить. Но неизвестна вторая сторона, найду сначала её. В
задаче сказано, что она меньше первой на 5 см, буду вычитать: 1) 8 — 5 = 3
(см) – вторая сторона. Все стороны известны, могу найти периметр, сложу все
четыре стороны: 2) 8 + 8 + 3 + 3 = 22 (см)
Запись в тетради:
1) 8
— 5 = 3 (см) – вторая сторона.
2) 8
+ 8 + 3 + 3 = 22 (см) или Р = (8 + 3)·2 = 11·2
= 22 (см)
Ответ: 22 см периметр
прямоугольника.
6. Задача
Начерти
квадрат, периметр которого равен 16 см.
Объясняю: Чтобы начертить
квадрат, нужно знать длину стороны, а она неизвестна. Я знаю, что у квадрата
все четыре стороны равны, что периметр квадрата равен 16 см. Разделю периметр
16 см на 4 стороны, получу одну сторону.
Запись в тетради:
16 : 4 = 4 (см) – сторона
квадрата
Черчу квадрат
 |
Пример:
измеряя с помощью линейки длины сторон прямоугольника, получим (2) см и (4) см. Противолежащие им стороны имеют такую же длину — (2) см и (4) см.
Найдём сумму длин всех сторон этого прямоугольника.
Для этого сложим все эти длины.
Получим:
(2) см (+) (4) см (+) (2) см (+) (4) см (=) (12) см.
Периметр — это сумма длин всех сторон фигуры.
Значит,
складывая длины всех сторон прямоугольника, получаем периметр прямоугольника.
Периметр обозначается заглавной латинской буквой (Р).
Итак,
периметр прямоугольника (Р = 12) см.
Найдём периметр треугольника.
Сначала измерим стороны треугольника.
Длины сторон треугольника равны (4) см, (3) см, (6) см.
Значит,
сумма длин всех сторон треугольника, т. е. периметр треугольника
равен:
(Р) (=) (3) см (+) (4) см (+) (6) см (=) (13) см.
Дан квадрат, длина стороны которого равна (4) см.
У квадрата все стороны равны.
Периметр квадрата равен сумме длин всех сторон квадрата.
Получим:
(Р) (=) (4) см (+) (4) см (+) (4) см (+) (4) см (=) (16) см.
Если у треугольника все стороны равны, такой треугольник называется равносторонний.
Для определения периметра данного треугольника найдём сумму длин всех его сторон.
Получим:
(Р) (=) (5) см (+) (5) см (+) (5) см (=) (15) см.
Источники:
Рис. 1. Прямоугольник. © ЯКласс
Рис. 2. Треугольник. © ЯКласс
Рис. 3. Квадрат. © ЯКласс
Рис. 4. Равносторонний треугольник. © ЯКласс
Что такое периметр треугольника. Формула расчёта
В данной статье разберёмся, как найти периметр треугольника, а также рассмотрим несколько задач разного уровня сложности.
Периметр треугольника равен сумме длин его сторон. Общая формула выглядит следующим образом:
P = a + b + c, где a, b, c – длины сторон треугольника.
Как Вы можете заметить, найти по формуле периметр треугольника очень и очень просто, нужно просто сложить длину трёх его сторон. Как правило, в задачах на поиск периметра треугольника сложность состоит в другом – в поиске длины каждой из сторон или в поиске обходных путей для решения. Вы всё поймёте, если взглянете на примеры.
Примеры
Рассмотрим несколько задач на поиск периметра треугольника. В решении указана лишь логика и последовательность действий, но не верное оформление (в Вашем учебном заведения оно может быть другим).
Задача №1
Длина первой стороны треугольника 5 см, второй – 6 см, третьей – 9 см. Найди периметр треугольника.
- P = 5 + 6 + 9 = 20 см
Ответ: периметр треугольника равен 20 см.
Задача №2
Длина первой стороны треугольника 10 см, второй – в 2 раза меньше первой, а третьей – на 8 см больше, чем второй. Найди периметр треугольника.
- Периметр треугольника (ABC) = AB + AC + BC; AB = 10 см.
- AC = 10 : 2 = 5 см.
- BC = 5 + 8 = 13 см.
- ABC = 10 + 5 + 13 = 28 см.
Ответ: периметр треугольника равен 28 см.
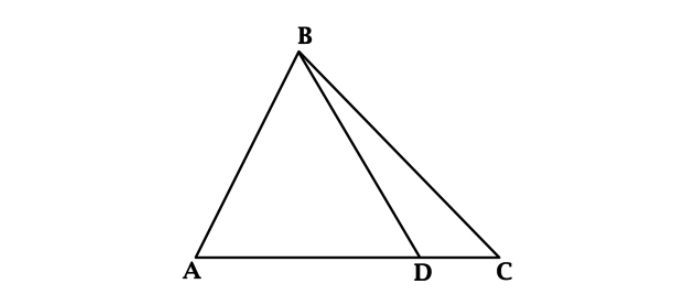
Задача №3
Точка D лежит на стороне AC треугольника ABC. Периметр треугольника ABD равен 10 см, периметр треугольника BDC равен 7 см, BD = 3 см. Найди периметр треугольника ABC.
- Периметр треугольника ABC = AB + AC + BC; периметр треугольника DBC = BD + DC + BC = 7 см; периметр треугольника ABD = AB + BD + AD = 10 см; BD = 3 см.
- Зная периметр DBC и длину стороны BD, мы можем найти сумму сторон DC + BC: 7 – 3 = 4 см.
- Зная периметр ABD и длину стороны BD, мы можем найти сумму сторон AB + AD: 10 – 3 = 7 см.
- AC = AD+DC. Зная это, меняем формулу периметра треугольника с AB + AC + BC на AB + AD + DC + BC. Обратите внимание на то, что суммы этих сторон нам уже известны: (AB + AD) + (DC + BC) = 7 + 4 = 11 см.
Как Вы могли заметить, при решении этой задачи мы не нашли длину ни одной из необходимых для расчёта периметра сторон. Это лишний раз показывает, что задачи на поиск периметра треугольника бывают интересными и не очень простыми.